В
настоящее время определение длин волн
спектральных линий является одним из
наиболее точных физических измерений.
Цель задания заключается в ознакомлении
с методами определения длин волн
спектральных
линий и с применением этих методов к
измерению длин волн нескольких
(56)
спектральных линий исследуемого
вещества. Существует много различных
способов, позволяющих вычислять длины
волн
спектральных
линий с точностью до
0,001 %.
Рассмотрим способы определения длины
волны для призменного спектрографа.
В этом
случае определение длины волны состоит
в сравнении данной длины волны со
стандартными
нормалями, для которых длины волн точно
измерены. Сравнение можно провести
несколькими способами.
1.
Для ориентировочного определения длины
волны можно воспользоваться графической
интерполяцией градуировочной
(дисперсионной) кривой спектрального
прибора или непосредственной
шкалой
длин волн, если последняя имеется в
приборе. С помощью компаратора измеряют
расстояние неизвестных линий до ближайших
известных линий. Затем, пользуясь
дисперсионной кривой, определяют
неизвестные
длины волн. Для получения достаточной
точности нужно иметь в данной области
спектра много известных линий сравнения,
в результате измерения которых получается
много точек на дисперсионной кривой.
Дисперсионную (градуировочную) кривую
в этом случае строят в очень большом
масштабе. Таким способом можно вычислить
длину волны с точностью до 10,5
Å.
2.
Если необходимо добиться большой
точности, то для определения длины волны
прибегают к математической интерполяции.
Если
исследуемая линия находится между двумя
линиями сравнения, расположенными
настолько близко к друг другу, что
участок дисперсионной
кривой
между ними можно с большой точностью
считать прямой линией, то пользуются
линейной интерполяцией.
В
случае линейной интерполяции поступают
следующим образом: пусть имеются две
спектральные линии
и
,
длины волн которых необходимо измерить
(рис. 7а). По обе стороны от них в эталонном
спектре
железа
находят линии, длины волн которых заранее
точно известны,
это нормали длин волн (берутся по атласу
железа). Необходимо на компараторе
измерить расстояние
и
неизвестных
линий
и
от
линий сравнения 1
и расстояние d
между линиями сравнения 1
и 2.
Определение
неизвестной длины волны в случае линейной
интерполяции
основывается на соотношении
(9)
где
коэффициент при
– средняя дисперсия на участке
спектральных линий 1
и 2
. Такой способ вычисления длины волны
вполне пригоден для приборов с
дифракционными решетками. Для призменных
приборов этот способ можно применять,
если (1-2)
не превосходит
50 Å.
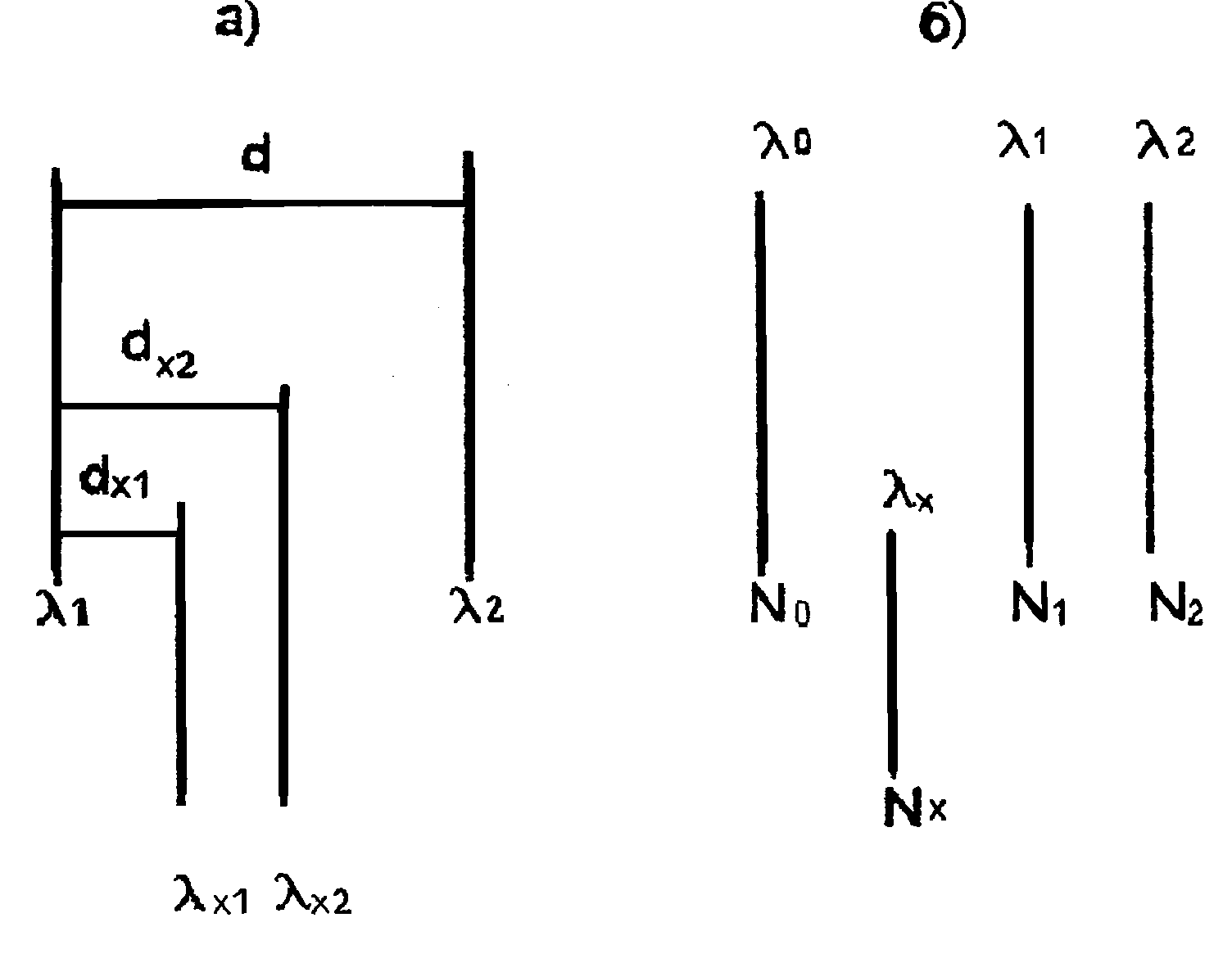
Рис. 7.
Расположение нормалей и измеряемых
длин волн в спектре для линейной (а) и
квадратичной (б) интерполяции
Более
точное определение длины волны можно
производить по интерполяционным формулам
второго порядка (интерполяция отрезком
параболы)
по трём «нормалям» эталонного спектра:
0,
1,
2,
расположенным
в небольшом спектральном участке (рис.
7б). При
этом обычно используют соотношение
, (10)
где
A
и B
– постоянные величины; l
– расстояние между «нормалью»
и измеряемой длиной волны. Для определения
x
следует на компараторе измерить положение
нормалей и неизвестной линии.
Пусть
отсчёты положения этих линий будут N0,
N1,
N2
и Nх.
Так как длины волн всех трех «нормалей»
известны, то согласно интерполяционной
формуле можно составить два уравнения:
;
.
Эти
уравнения дают возможность определить
постоянные А
и В,
входящие в них. Пользуясь далее этими
постоянными, можно вычислить неизвестную
длину волны
по формуле
. (11)
При
анализе погрешностей, возникающих в
процессе измерений и расчетов, следует
иметь в
виду, что
основная неточность возникает при
снятии отсчетов N.
Для компаратора Аббе
N
= ±
0,001 мм.
Легко
показать, что коэффициент А, равный
d/dn,
соответствует линейной дисперсии
спектрального прибора. Это, в частности,
следует из того факта, что формула (11)
является разложением функции x
= f(N)
в ряд
Тейлора
около точки (No,
о
), т.е.
Учитывая
это, можно определить погрешность
При
большей линейной дисперсии прибора
точность в определении x
будет увеличена.
Вычисленная
по формуле
(10) неизвестная
длина волны затем сверяется с табличными
данными. Таким образом можно определить,
какому элементу принадлежит данная
спектральная линия.
Если
же линии сравнения эталонного спектра
расположены на таком расстоянии друг
от друга, что необходимо учитывать
кривизну дисперсионной
кривой, то
при математической интерполяции для
спектров, полученных с призменными
спектрографами, пользуются формулой
Гартмана.
Дисперсионная
формула Гартмана имеет вид
(12)
где
0,
C,
d0
– три постоянные, подбираемые по трём
известным линиям;
и d
–
длина волны
и отсчет компаратора для неизвестной
линии. Эта формула представляет собой
кривую дисперсии призменного спектрографа
с хорошим приближением.
Для
определения постоянных формулы Гартмана
0,
C,
d
производится измерение трёх известных
линий –
1,
2
и 3
(нормалей) и отсчитываются положения
этих линий (d1,d2
и d3)
на компараторе. Составляются три
уравнения, из которых определяются
постоянные
Решение
этих уравнений дает следующие значения
постоянных:
;
.
Получив
численные значения этих постоянных по
формуле Гартмана, можно определить
длину волны x
неизвестной линии по отсчёту для неё.
Экспериментально
по полученному снимку спектра исследуемого
вещества:
1)
определяют длину волны двух спектральных
линий, используя линейную интерполяционную
формулу (9);
2)
вычисляют длину волны нескольких линий
исследуемого вещества, используя формулу
квадратичной интерполяции (11);
3)
по формуле Гартмана определяют длины
волн тех же спектральных линий.
Длины
волн следует подставлять в формулу для
расчёта с точностью до сотых долей
ангстрема.
Контрольные
вопросы к лабораторной работе № 5
-
Как выглядит
оптическая схема спектрографа ИСП-28? -
Какие основные
элементы содеожит любой спектраль-ный
прибор? -
Что является
диспергирующим элементом в спектро-графе
ИСП-28? -
Какую роль выполняют
коллиматорный и камерный объективы? -
Что называется
спектром? -
Для чего при снятии
спектров на ИСП-28 применяется диафрагма
Гартмана? -
Для какой
спектральной области предназначен
ИСП-28? -
Из какого материала
изготовлены призма и линзы спек-трографа? -
Как устроена
призма Корню? -
Чем отличается
линейная дисперсия от угловой? Для чего
вводятся эти понятия?
Редомендуемая
литература
[1], [12], [13], [14].
Таблица 4
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
03.05.2019796.16 Кб2№1.doc
- #
04.05.2019209.92 Кб1№2.doc
- #
- #
10.08.2019237.57 Кб1№3.doc
- #
- #
04.05.2019465.92 Кб3№5.doc
- #
04.05.2019826.37 Кб0№6.doc
- #
10.08.2019283.14 Кб1№7.doc
- #
04.05.2019471.55 Кб2№8.doc
Слайд 2
ГРАДУИРОВКА СПЕКТРОСКОПА
ОПРЕДЕЛЕНИЕ ДЛИНЫ ВОЛНЫ СПЕКТРАЛЬНЫХ ЛИНИЙ

Слайд 3
Цель работы:
научиться пользоваться спектроскопом, провести его градуировку, исследовать

спектры поглощения и испускания, ознакомиться с элементами качественного спектрального
анализа.
Приборы и принадлежности:
спектроскоп, индукционная катушка, источник постоянного тока на
6 – 12 В, источник света (лампа накаливания), спиртовая горелка, пробирка с раствором КМnО4.
Слайд 5
Ход лучей в спектроскопе
Лучи света выходят из коллиматора
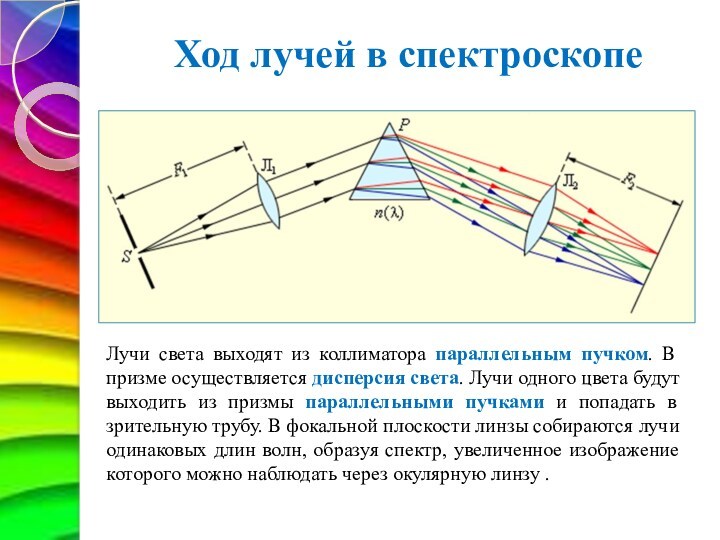
параллельным пучком. В призме осуществляется дисперсия света. Лучи одного
цвета будут выходить из призмы параллельными пучками и попадать в
зрительную трубу. В фокальной плоскости линзы собираются лучи одинаковых длин волн, образуя спектр, увеличенное изображение которого можно наблюдать через окулярную линзу .
Слайд 6
Отсчетный механизм спектроскопа и определение цены деления шкалы
Для

определения относительного положения полос спектра в окулярной трубе спектроскопа
имеется специальный треугольный указатель-маркер, который при помощи микрометрического винта (отсчетного
механизма спектроскопа) можно перемещать и совместить с любой спектральной линией.
Слайд 7
На основную шкалу спектроскопа (горизонтальный винт) нанесены миллиметровые
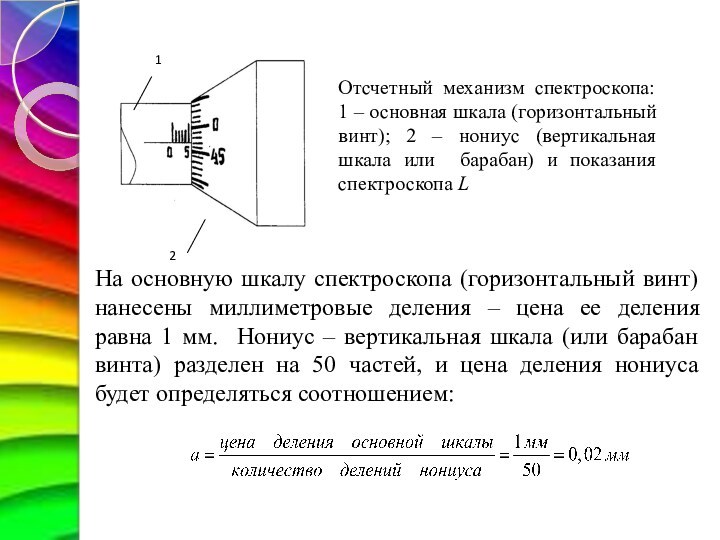
деления – цена ее деления равна 1 мм. Нониус
– вертикальная шкала (или барабан винта) разделен на 50 частей,
и цена деления нониуса будет определяться соотношением:
Слайд 8
Показания спектроскопа L можно найти по формуле:
L

= (N+na)
где N – число миллиметров, отсчитанное вдоль основной
шкалы (горизонтального винта); n – число делений на нониусе (шкале
барабана), а – цена деления нониуса.
Например,
Слайд 9
Градуировка спектроскопа
Шкала спектроскопа позволяет определить только относительное положение

спектральных линий и расстояние между ними, но не длину
волны соответствующих линий. Для того, чтобы с помощью спектроскопа можно
было определить длину волны линий исследуемого спектра, спектроскоп необходимо проградуировать, т.е. установить зависимость между длинами волн спектральных линий, наблюдаемых в поле зрения и делениями шкалы L отсчётного устройства спектроскопа.
Другими словами, проградуировать спектроскоп – значит построить график, у которого на оси Y отложены показания шкалы L отсчётного механизма спектроскопа в миллиметрах, а на оси Х – длина волны λ, нм
Слайд 11
Опыт 1. Градуировка спектроскопа
Расположить лампу дневного света (содержит

пары ртути) перед щелью коллиматора, зажечь лампу.
Лампа помещена
в футляр с отверстиями для исключения слишком большой освещен-ности рабочего
места и поля зрения спектроскопа через линзы.
Слайд 12
Опыт 1. Градуировка спектроскопа
С помощью окуляра добиться четкого

изображения спектра и маркера (треугольный указатель) в поле зрения
окуляра.
Навести маркер-указатель на определенную линию или полосу в спектре, и
провести измерение с отсчетного устройства.
Слайд 13
Опыт 1. Градуировка спектроскопа
Затем, вращая барабан, перевести указатель
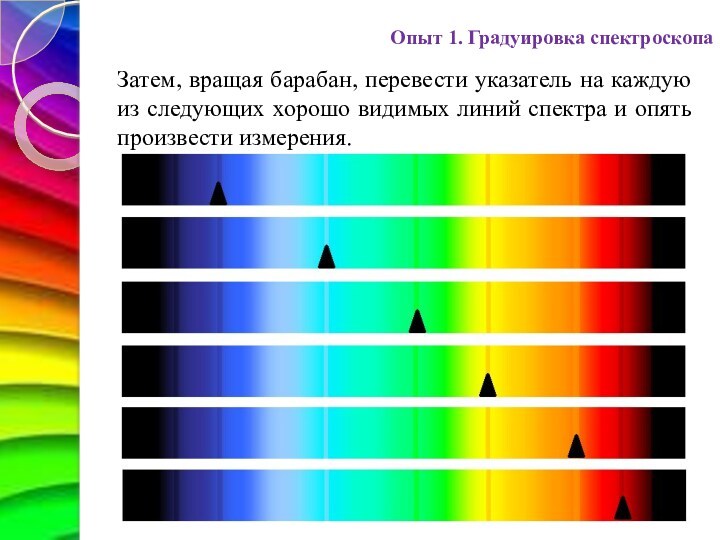
на каждую из следующих хорошо видимых линий спектра и
опять произвести измерения.
Слайд 14
Опыт 1. Градуировка спектроскопа
Таким образом, определить положение всех
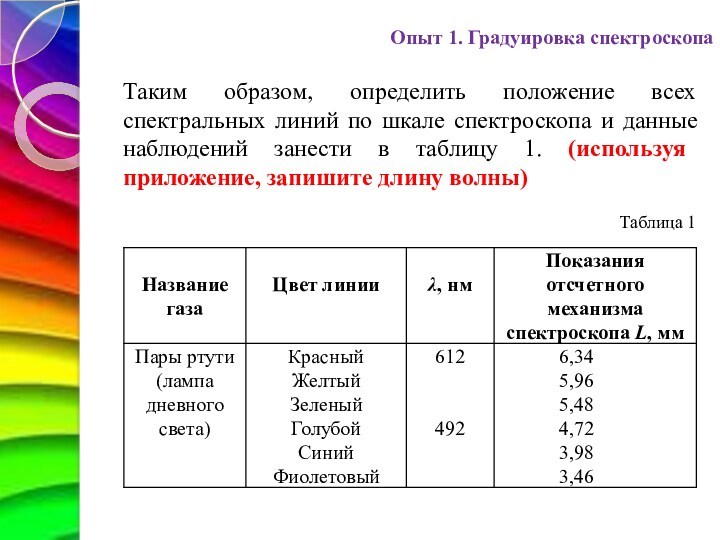
спектральных линий по шкале спектроскопа и данные наблюдений занести
в таблицу 1. (используя приложение, запишите длину волны)
Таблица 1
Слайд 16
Построить градуировочную кривую спектроскопа для лампы дневного света
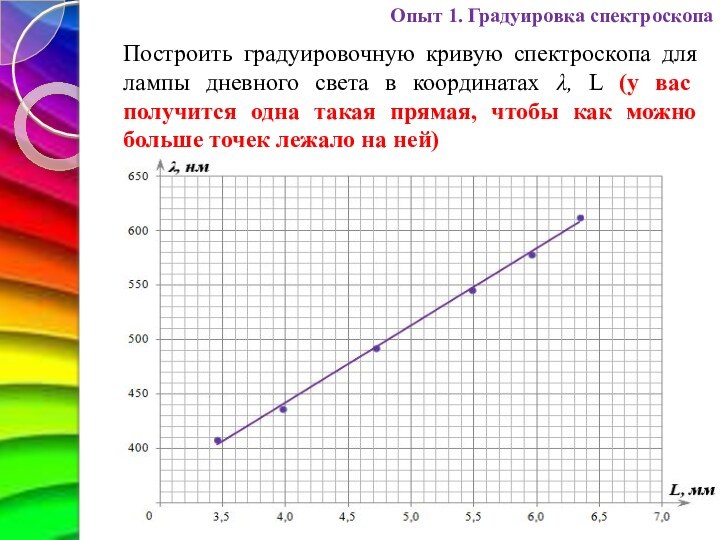
в координатах λ, L (у вас получится одна такая
прямая, чтобы как можно больше точек лежало на ней)
Опыт 1.
Градуировка спектроскопа
Слайд 17
Опыт 2. Исследование спектров испускания
Спиртовую горелку с раство-ром

соли NaCl в спирте поджечь и поместить перед щелью
коллиматора.
Пронаблюдать спектр испускания паров натрия в пламени горелки. (ниже
изображено то, что мы увидим в спектроскопе)
Слайд 18
Опыт 2. Исследование спектров испускания
Определить положение линии спектра
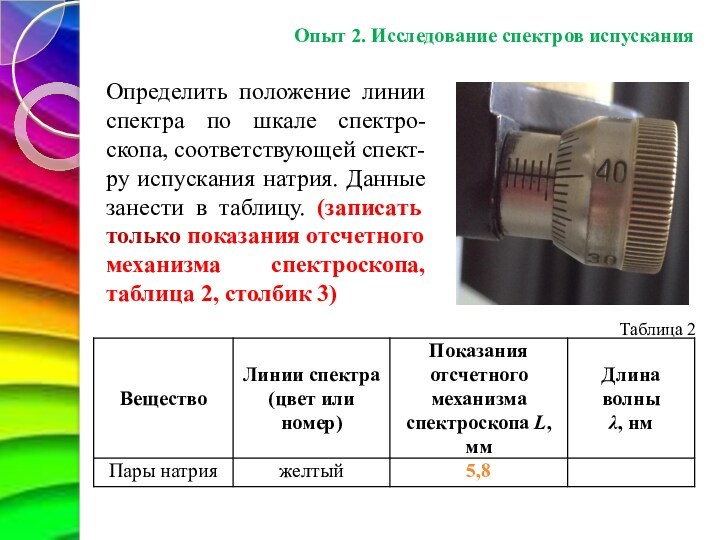
по шкале спектро-скопа, соответствующей спект-ру испускания натрия. Данные занести
в таблицу. (записать только показания отсчетного механизма спектроскопа, таблица 2,
столбик 3)
Таблица 2
Слайд 19
С помощью полученной ранее градуировочной кривой (график у
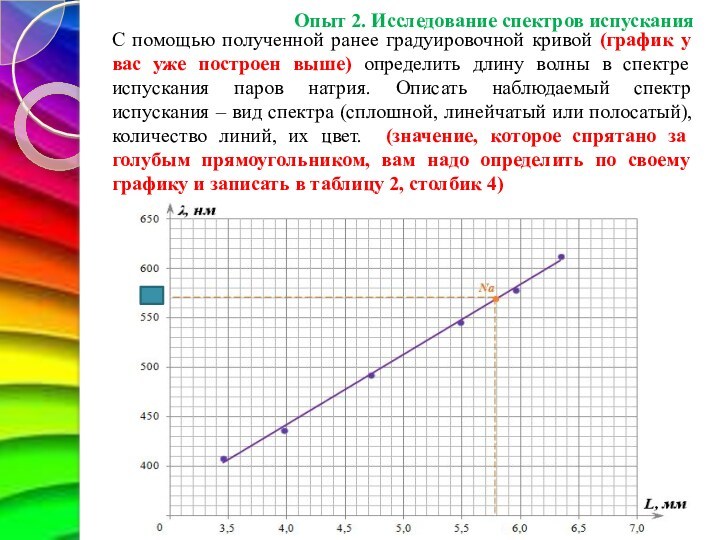
вас уже построен выше) определить длину волны в спектре
испускания паров натрия. Описать наблюдаемый спектр испускания – вид спектра
(сплошной, линейчатый или полосатый), количество линий, их цвет. (значение, которое спрятано за голубым прямоугольником, вам надо определить по своему графику и записать в таблицу 2, столбик 4)
Опыт 2. Исследование спектров испускания
Слайд 20
Опыт 3. Исследование спектров поглощения
Между осветителем (лам-пой накаливания)

и щелью коллиматора поместить ис-следуемое вещество (раст-вор КМnО4). Пронаблюдать
спектр поглощения (темные линии).
Слайд 21
Опыт 3. Исследование спектров поглощения
По шкале спектроскопа определить
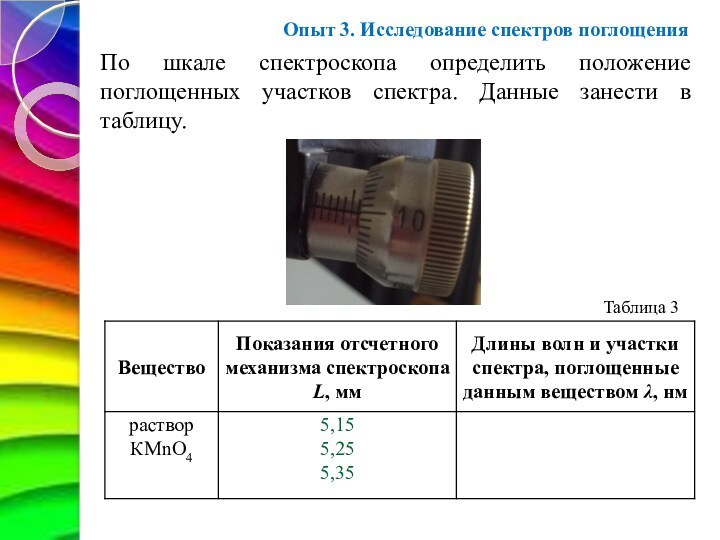
положение поглощенных участков спектра. Данные занести в таблицу.
Таблица 3
Слайд 22
С помощью градуировочной кривой (она уже у вас
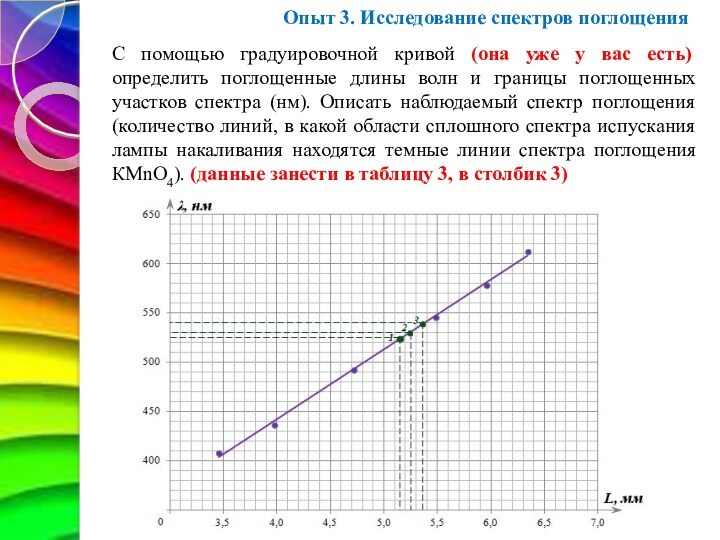
есть) определить поглощенные длины волн и границы поглощенных участков
спектра (нм). Описать наблюдаемый спектр поглощения (количество линий, в какой
области сплошного спектра испускания лампы накаливания находятся темные линии спектра поглощения КМnО4). (данные занести в таблицу 3, в столбик 3)
Опыт 3. Исследование спектров поглощения
Слайд 23
Контрольные вопросы
Из каких составных частей состоит спектроскоп и

каково их назначение?
Вычертить ход лучей в спектроскопе.
Что такое спектр
излучения?
Что такое спектр поглощения?
Объяснить происхождение линейчатых, сплошных и полосатых спектров.
Что
такое спектральный анализ?
Как проградуировать спектроскоп?
Как определить длину волны линии в спектре излучения какого-либо вещества?
Слайд 24
По результатам эксперимента сделать вывод

Длина волны всех спектральных линий Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Начальная орбита: 3 —> Конверсия не требуется
Конечная орбита: 7 —> Конверсия не требуется
Атомный номер: 17 —> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.00458824468631853 метр —>4588244.68631853 нанометр (Проверьте преобразование здесь)
21 Водородный спектр Калькуляторы
Длина волны всех спектральных линий формула
Длина волны всей спектральной линии = ((Начальная орбита^2)*(Конечная орбита^2))/([R]*(Атомный номер^2)*((Конечная орбита^2)-(Начальная орбита^2)))
λspectral = ((ninitial^2)*(nfinal^2))/([R]*(Z^2)*((nfinal^2)-(ninitial^2)))
Объясните модель Бора.
Модель Бора описывает свойства атомных электронов с помощью набора допустимых (возможных) значений. Атомы поглощают или испускают излучение только тогда, когда электроны скачкообразно переходят между разрешенными или стационарными состояниями. Модель Бора может объяснить линейчатый спектр атома водорода. Излучение поглощается, когда электрон переходит с орбиты с более низкой энергией на орбиту с более высокой энергией; тогда как излучение испускается, когда он движется с более высокой орбиты на более низкую.
Условие задачи:
Определить длину волны для линии в дифракционном спектре второго порядка, совпадающем с линией спектра третьего порядка, у которой длина волны 400 нм.
Задача №10.7.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(k_1=2), (k_2=3), (lambda_2=400) нм, (lambda_1-?)
Решение задачи:
Запишем формулу дифракционной решетки:
[dsin varphi = klambda;;;;(1)]
В этой формуле (d) – период решетки (также называют постоянной решетки), (varphi) – угол дифракции, (k) – порядок максимума, (lambda) – длина волны, падающей нормально на решетку.
Запишем формулу (1) для световой волны с длиной волны (lambda_1) и дифракционного максимума (k_1), а также для световой волны с длиной волны (lambda_2) и дифракционного максимума (k_2). Не забываем, что дифракционная решетка одна и та же, а указанные дифракционные максимумы совпадают, т.е. углы дифракции также одинаковы.
[left{ begin{gathered}
dsin varphi = {k_1}{lambda _1} hfill \
dsin varphi = {k_2}{lambda _2} hfill \
end{gathered} right.]
Тогда:
[{k_1}{lambda _1} = {k_2}{lambda _2}]
Откуда искомая длина волны (lambda_1) равна:
[{lambda _1} = frac{{{k_2}{lambda _2}}}{{{k_1}}}]
Посчитаем численный ответ:
[{lambda _1} = frac{{3 cdot 400 cdot {{10}^{ – 9}}}}{2} = 600 cdot {10^{ – 9}};м = 0,6;мкм]
Ответ: 0,6 мкм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.7.21 Определить длину волны для линии в дифракционном спектре третьего порядка
10.7.23 На дифракционную решетку нормально падает пучок света от разрядной трубки. Какова
10.7.24 Период дифракционной решетки равен 1,5 мкм. Чему равна ширина прозрачных щелей
Загрузить PDF
Загрузить PDF
Длина волны – это расстояние между двумя соседними точками, которые колеблются в одной фазе; как правило, понятие «длина волны» ассоциируется с электромагнитным спектром.[1]
Метод вычисления длины волны зависит от данной информации. Воспользуйтесь основной формулой, если известны скорость и частота волны. Если нужно вычислить длину световой волны по известной энергии фотона, воспользуйтесь соответствующей формулой.
-
1
Воспользуйтесь формулой для вычисления длины волны. Чтобы найти длину волны, разделите скорость волны на частоту. Формула:
[2]
-
2
Используйте соответствующие единицы измерения. Скорость измеряется в единицах метрической системы, например, в километрах в час (км/ч), метрах в секунду (м/с) и так далее (в некоторых странах скорость измеряется в британской системе, например, в милях в час). Длина волны измеряется в нанометрах, метрах, миллиметрах и так далее. Частота, как правило, измеряется в герцах (Гц).[3]
- Единицы измерения конечного результата должны соответствовать единицам измерения исходных данных.
- Если частота дана килогерцах (кГц), или скорость волны в километрах в секунду (км/с), преобразуйте данные значения в герцы (10 кГц = 10000 Гц) и в метры в секунду (м/с).
-
3
Известные значения подставьте в формулу и найдите длину волны. В приведенную формулу подставьте значения скорости и частоты волны. Разделив скорость на частоту, вы получите длину волны.[4]
- Например. Найдите длину волны, распространяющейся со скоростью 20 м/с при частоте колебаний 5 Гц.
-
4
Воспользуйтесь приведенной формулой, чтобы вычислить скорость или частоту. Формулу можно переписать в другом виде и вычислить скорость или частоту, если дана длина волны. Чтобы найти скорость по известным частоте и длине волны, используйте формулу:
. Чтобы найти частоту по известным скорости и длине волны, используйте формулу:
.[5]
Реклама
-
1
-
2
Перепишите представленную формулу, чтобы найти длину волны. Для этого проделайте ряд математических операций. Обе стороны формулы умножьте на длину волны, а затем обе стороны разделите на энергию; вы получите формулу:
. Если энергия фотона известна, можно вычислить длину световой волны.[7]
- Эту формулу можно использовать для вычисления максимальной длины световой волны, необходимой для ионизации металлов. В формулу подставьте энергию, необходимую для ионизации, и вычислите длину волны.[8]
- Эту формулу можно использовать для вычисления максимальной длины световой волны, необходимой для ионизации металлов. В формулу подставьте энергию, необходимую для ионизации, и вычислите длину волны.[8]
-
3
В полученную формулу подставьте известные значения и вычислите длину волны. В формулу подставьте только значение энергии, потому что две константы являются постоянными величинами, то есть не меняются. Чтобы найти длину волны, перемножьте константы, а затем результат разделите на энергию.[9]
- Например. Найдите длину световой волны, если энергия фотона равна 2,88 x 10-19 Дж.
Реклама
-
1
Проверьте ответ. Для этого умножьте длину волны на частоту. Если вы получите данное значение скорости, решение правильное; в противном случае проверьте вычисления. Если вы пользуетесь калькулятором, правильно вводите числа.
- Например. Найдите длину волны, которая распространяется со скоростью 343 м/с при частоте колебаний 70 Гц.
- Решите эту задачу как описано выше и получите значение 4,9 м.
- Проверьте ответ: 4,9 м х 70 Гц = 343 м/сек. Это данная в условии задачи скорость, поэтому решение верное.
- Например. Найдите длину волны, которая распространяется со скоростью 343 м/с при частоте колебаний 70 Гц.
-
2
Используйте экспоненциальную запись чисел, чтобы избежать ошибок при округлении чисел (в калькуляторе). Порой в вычислении длины волны участвуют очень большие числа, особенно когда присутствует скорость света. Это может привести к ошибкам округления чисел. Поэтому используйте экспоненциальную запись чисел.[10]
- Например. Свет проходит сквозь воду со скоростью 225000000 м/с. Найдите длину световой волны, если ее частота равна 4 x 1014 Гц.
-
3
Помните, что частота волны не меняется при изменении среды ее распространения. Во многих задачах волна распространяется в двух средах, и некоторые учащиеся пытаются вычислить две длины волны. Это ошибка, потому что в отличие от скорости распространения и длины волны частота волны не меняется при изменении среды ее распространения.[11]
- Например, световая волна длиной λ, распространяющаяся со скоростью v при частоте f, переходит из воздушного пространства в некоторую среду, показатель преломления которой равен 1,5. Как изменятся указанные три величины?
Реклама
Об этой статье
Эту страницу просматривали 158 348 раз.














