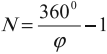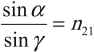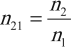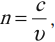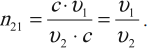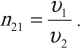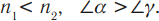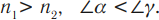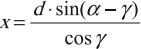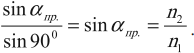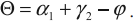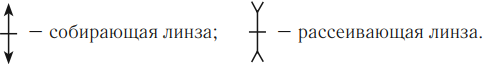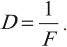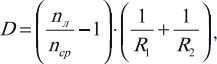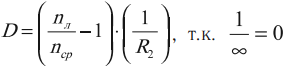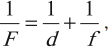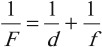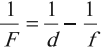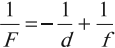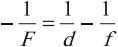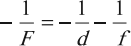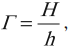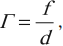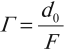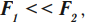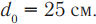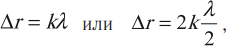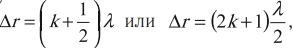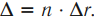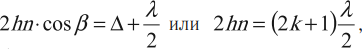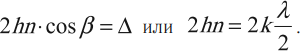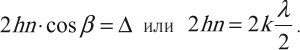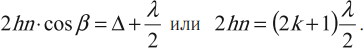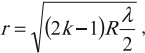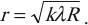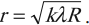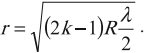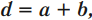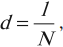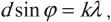Основные формулы по физике — ОПТИКА
Оптика — это раздел физики, изучающий природу светового излучения, его распространение и взаимодействие с веществом. Световые волны — это электромагнитные волны. Длина волны световых волн заключена в интервале [0,4·10-6 м ÷ 0,76·10-6 м]. Волны такого диапазона воспринимаются человеческим глазом.
Свет распространяется вдоль линий, называемых лучами. В приближении лучевой (или геометрической) оптики пренебрегают конечностью длин волн света, полагая, что λ→0. Геометрическая оптика во многих случаях позволяет достаточно хорошо рассчитать оптическую систему. Простейшей оптической системой является линза.
При изучении интерференции света следует помнить, что интерференция наблюдается только от когерентных источников и что интерференция связана с перераспределением энергии в пространстве. Здесь важно уметь правильно записывать условие максимума и минимума интенсивности света и обратить внимание на такие вопросы, как цвета тонких пленок, полосы равной толщины и равного наклона.
При изучении явления дифракции света необходимо уяснить принцип Гюйгенса-Френеля, метод зон Френеля, понимать, как описать дифракционную картину на одной щели и на дифракционной решетке.
При изучении явления поляризации света нужно понимать, что в основе этого явления лежит поперечность световых волн. Следует обратить внимание на способы получения поляризованного света и на законы Брюстера и Малюса.
Смотрите также основные формулы по физике — колебания и волны
Таблица основных формул по оптике
|
Физические законы, формулы, переменные |
Формулы оптики |
|
Абсолютный показатель преломления где с — скорость света в вакууме, с=3·108 м/с, v — скорость распространения света в среде. |
|
|
Относительный показатель преломления где n2 и n1 — абсолютные показатели преломления второй и первой среды. |
|
|
Закон преломления где i — угол падения, r — угол преломления. |
|
|
Формула тонкой линзы где F — фокусное расстояние линзы, d — расстояние от предмета до линзы, f — расстояние от линзы до изображения. |
|
|
Оптическая сила линзы где R1 и R2 — радиусы кривизны сферических поверхностей линзы. Для выпуклой поверхности R>0. Для вогнутой поверхности R<0. |
|
|
Оптическая длина пути: где n — показатель преломления среды; r — геометрическая длина пути световой волны. |
|
|
Оптическая разность хода: L1 и L2 — оптические пути двух световых волн. |
|
|
Условие интерференционного максимума: минимума: где λ0 — длина световой волны в вакууме; m — порядок интерференционного максимума или минимума. |
|
|
Оптическая разность хода в тонких пленках в отраженном свете: в проходящем свете: где d — толщина пленки; i — угол падения света; n — показатель преломления. |
|
|
Ширина интерференционных полос в опыте Юнга: где d — расстояние между когерентными источниками света; L — расстояние от источника до экрана. |
|
|
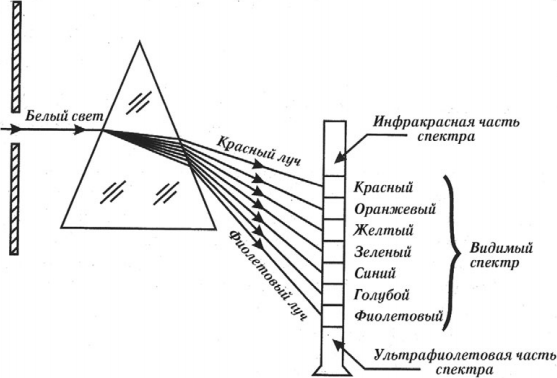
Условие главных максимумов дифракционной решетки: где d — постоянная дифракционной решетки; φ — угол дифракции. |
|
|
Разрешающая способность дифракционной решетки: где Δλ — минимальная разность длин волн двух спектральных линий, разрешаемых решеткой; m — порядок спектра; N — общее число щелей решетки. |
|
|
Закон Малюса: где I0 — интенсивность плоско-поляризованного света, падающего на анализатор; I — интенсивность света, прошедшего через анализатор; α — угол между плоскостью поляризации падающего света и главной плоскостью анализатора. |
|
|
Связь интенсивности естественного света Iест с интенсивностью света, прошедшего поляризатор (и падающего на анализатор): где k — относительная потеря интенсивности света в поляризаторе. |
|
|
Дисперсия вещества |
|
|
Средняя дисперсия |
|
|
Групповая скорость света |
|
|
Фазовая скорость света |
|
Поделитесь ссылкой с друзьями:
Похожие таблицы
Комментарии:
Download Article
Download Article
Wavelength is the distance of 1 frequency wave peak to the other and is most commonly associated with the electromagnetic spectrum.[1]
Calculating wavelength is dependent upon the information you are given. If you know the speed and frequency of the wave, you can use the basic formula for wavelength. If you want to determine the wavelength of light given the specific energy of a photon, you would use the energy equation. Calculating wavelength is easy as long as you know the correct equation.
-
1
Calculate wavelength with the wavelength equation. To find the wavelength of a wave, you just have to divide the wave’s speed by its frequency. The formula for calculating wavelength is:
.
[2]
-
2
Use the correct units. Speed can be represented using both metric and imperial units. You may see it as miles per hour (mph), kilometers per hour (kph), meters per second (m/s), etc. Wavelength is almost always given in metric units: nanometers, meters, millimeters, etc. Frequency is generally expressed in Hertz (Hz) which means “per second”.[3]
- Always keep units consistent across the equation. Most calculations are done using strictly metric units. If the frequency is in kilohertz (kHz) or the wave speed is in km/s you will need to convert these numbers to Hertz and m/s by multiplying by 1000 (10 kHz = 10,000 Hz).
Advertisement
-
3
Plug the known quantities into the equation and solve. If you want to calculate the wavelength of a wave, then all you have to do is plug the wave’s speed and wave’s frequency into the equation. Dividing speed by frequency gives you the wavelength.[4]
- For example: Find the wavelength of a wave traveling at 20 m/s at a frequency of 5 Hz.
-
4
Use this equation to solve for speed or frequency. You can rearrange this equation and solve for speed or frequency if given wavelength. To calculate speed given frequency and wavelength, use
. To calculate frequency given speed and wavelength, use
.[5]
Advertisement
-
1
-
2
Rearrange to solve for wavelength. You can rearrange the equation with algebra to solve for wavelength. If you multiply both sides of the equation by wavelength and then divide both sides by energy, you are left with
. If you know the energy of the photon, you can calculate its wavelength.[7]
This equation can also be used to determine the maximum wavelength of light necessary to ionize metals. Simply use the energy required for ionization and solve for the corresponding wavelength.
-
3
Plug in the known variables and solve. Once you have rearranged the equation, you can solve for the wavelength by plugging in the variables for energy. Because the other two variables are constants, they are always the same. To solve, multiply the constants together and then divide by the energy.[8]
- For example: Find the wavelength of a photon with an energy of 2.88 x 10-19 J.
Advertisement
-
1
Check your answer by multiplying the wavelength by the frequency. If you found the right value for the wavelength, multiplying by the frequency should get you the wave speed you started with. If it doesn’t, check your math. If you are using a calculator, make sure you have typed the numbers in correctly.
- For example: What is the wavelength of a 70 Hertz sound wave traveling at 343 meters per second?
- You follow the instructions above and get an answer of 4.9 meters.
- Check your work by calculating 4.9 meters x 70 Hz = 343 meters/second. This is the wave speed you started with, so your answer is correct.
- For example: What is the wavelength of a 70 Hertz sound wave traveling at 343 meters per second?
-
2
Use scientific notation to avoid calculator rounding errors. Wavelength calculations often involve very large numbers, especially if you’re working with light speed. This can lead to rounding errors on your calculator. Prevent this by writing your numbers in scientific notation and double checking the significant digits.[9]
- For example: Light travels through water at about 225,000,000 meters per second. If the wave’s frequency is 4 x 1014 Hz, what is its wavelength?
-
3
Do not change frequency when a wave enters a different medium. Many word problems involve a wave that crosses the boundary from one medium to another. A common mistake here is calculating a new frequency for the wave. In fact, the frequency of the wave remains the same when it crosses the boundary, while the wavelength and wave speed change.[10]
- For example: A light wave with frequency f, speed v, and wavelength λ crosses from air to a medium with refractive index 1.5. How do these three values change?
-
4
Check your units. The units you use will often tell you what to do when you are solving a problem. If they do not make sense when you finish, then check to see if you used the right units.
- For example, perhaps you used Joules when you should have used Hertz, so you ended up with the incorrect answer.
Advertisement
Calculator, Practice Problems, and Answers
Add New Question
-
Question
What is the formula for wavelength?
Meredith Juncker is a PhD candidate in Biochemistry and Molecular Biology at Louisiana State University Health Sciences Center. Her studies are focused on proteins and neurodegenerative diseases.
Scientific Researcher
Expert Answer
Wavelength can be calculated using the following formula: wavelength = wave velocity/frequency. Wavelength usually is expressed in units of meters. The symbol for wavelength is the Greek lambda λ, so λ = v/f.
-
Question
How do I calculate the wave length given only the frequency?
Meredith Juncker is a PhD candidate in Biochemistry and Molecular Biology at Louisiana State University Health Sciences Center. Her studies are focused on proteins and neurodegenerative diseases.
Scientific Researcher
Expert Answer
The speed of light never changes, so v will always equal 3.0 x 10^8 m/s. This value, divided by the given frequency, will give you wavelength.
-
Question
If the frequency of a radio wave is 4.5GHz, what is the wavelength of the wave (velocity of light=3x10m/s)?
Meredith Juncker is a PhD candidate in Biochemistry and Molecular Biology at Louisiana State University Health Sciences Center. Her studies are focused on proteins and neurodegenerative diseases.
Scientific Researcher
Expert Answer
f = 4.5 GHz = 4.5 x 10^9 Hz (Hz = s^-1)
v = 3.0 x 10^8 m/s
lambda = v/f= (3.0 x 10^8 m/s) / (4.5 x 20^9 s^-1)
= 0.0666 m
= 66.6 um
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
About This Article
Article SummaryX
To calculate wavelength, use the formula wavelength = speed divided by frequency. Just plug in the wave’s speed and frequency to solve for the wavelength. Remember to use the correct units when you’re using the formula and writing your answer. If you want to learn more, like how to calculate wavelength with the energy formula, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,482,315 times.
Did this article help you?
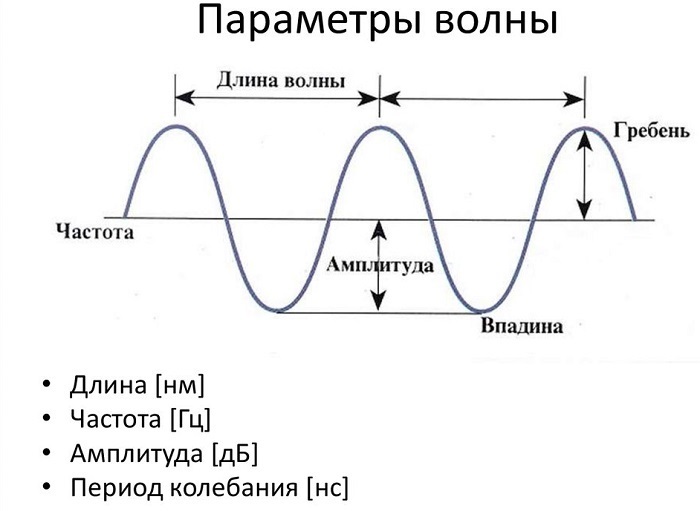
Длина волны — это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.
Цикл — это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.
На рисунке показаны основные параметры волны, используемые в физике:
Определение и формула длины волн
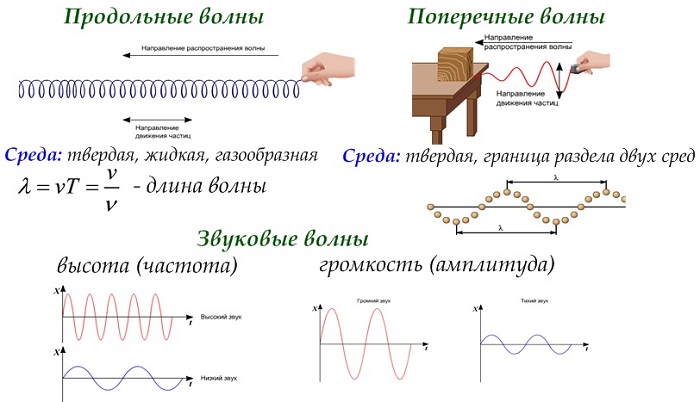
Волна — это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.
Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.
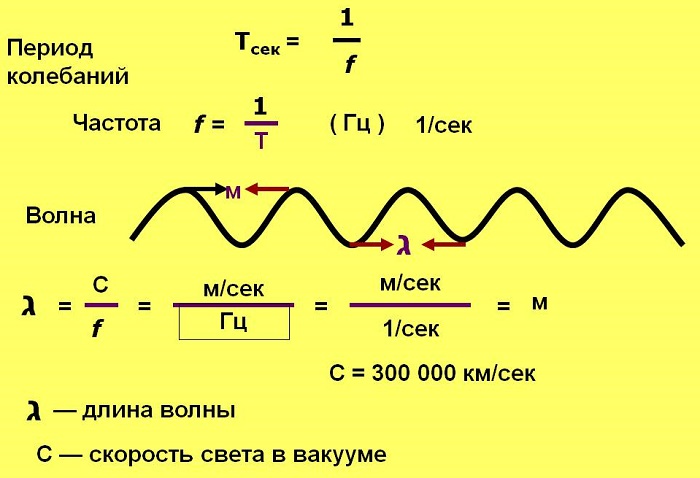
Греческая буква «λ» (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.
Период Т — время завершения полного колебания, единица измерения секунды (с).
Длинная волна соответствует низкой частоте, а короткая — высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.
У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.
Пространственный период волны — это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).
При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).
Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 108 м/с поделить на длину в метрах.
Единицы измерения длины волны λ — нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).
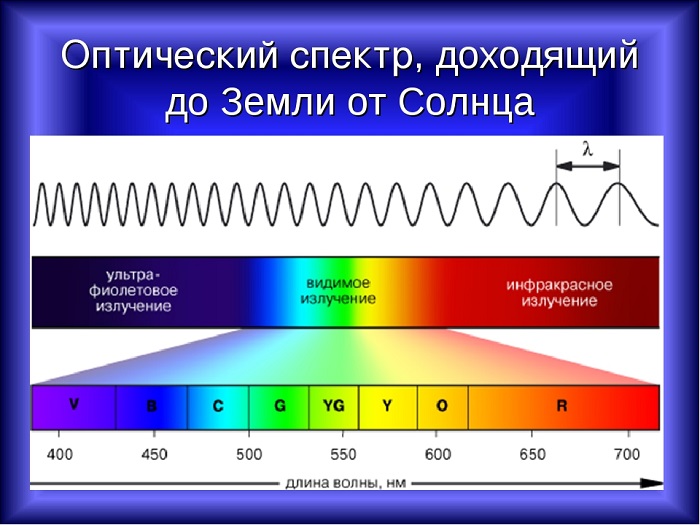
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.
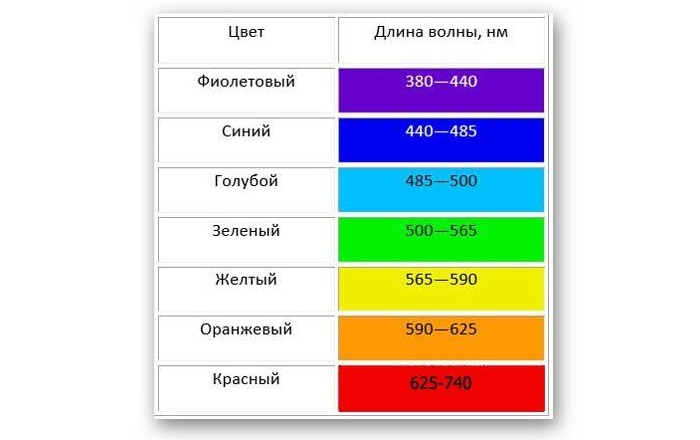
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной — красный, который составляет около 700 нм.
Таблица показывает длину волны в зависимости от цвета:
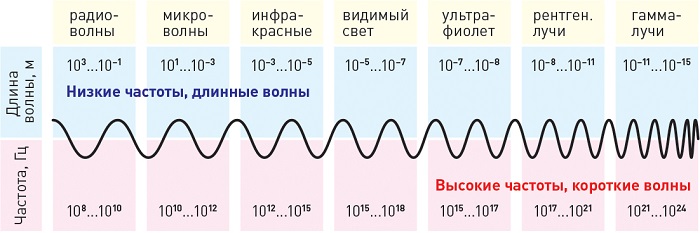
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.
Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.
Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:
Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.
Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Оптика
Оптика – это раздел физики, в котором изучаются закономерности световых явлений, природа света и его взаимодействие с веществом.
Световой луч – это линия, вдоль которой распространяется свет.
Закон независимости световых лучей:
при пересечении световых лучей каждый из них продолжает распространяться в прежнем направлении.
Источник света – это тело, которое излучает свет.
При излучении света источник теряет энергию, при поглощении его внутренняя энергия увеличивается, т. е. распространение света сопровождается переносом энергии.
Виды источников света:
- тепловые – это источники, в которых излучение света происходит в результате нагревания тела до высокой температуры;
- люминисцентные – это тела, излучающие свет при облучении их светом, рентгеновскими лучами, радиоактивным излучением и т. д.
Точечный источник света – это источник, представляющий собой светящуюся материальную точку, т. е. источник, размеры которого малы по сравнению с расстоянием до освещаемого предмета.
Если источник света находится в бесконечности, то его лучи падают на поверхность параллельным пучком.
Свет – это электромагнитная волна с частотой от 1,5·1011 Гц до 3·1016 Гц.
Скорость света в вакууме: ( c ) = 3·108 м/с.
Содержание
- Прямолинейное распространение света
- Закон отражения света
- Построение изображений в плоском зеркале
- Закон преломления света
- Полное внутреннее отражение
- Линзы. Оптическая сила линзы
- Формула тонкой линзы
- Построение изображений в линзах
- Оптические приборы. Глаз как оптическая система
- Интерференция света
- Дифракция света
- Дифракционная решетка
- Дисперсия света
- Основные формулы по теме «Оптика»
Прямолинейное распространение света
Закон распространения света:
свет в прозрачной однородной среде распространяется прямолинейно.
Экспериментальным доказательством прямолинейности распространения света является образование тени.
Тень – это область пространства, куда не попадает свет от источника.
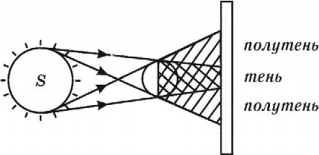
Полутень – это область пространства, куда частично попадает свет от источника.
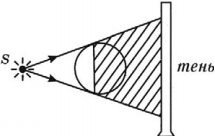
Если источник света точечный, то на экране образуется четкая тень предмета.
Если источник неточечный, то на экране образуется размытая тень (области тени и полутени).
Образованием тени при падении света на непрозрачный предмет объясняются такие явления, как солнечное и лунное затмения.
Закон отражения света
Отражение – это явление, при котором при падении световых лучей на непрозрачную гладкую поверхность они меняют направление распространения, возвращаясь в прежнюю среду.
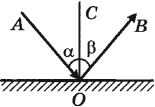
АО – падающий луч, ОВ – отраженный луч, СО – перпендикуляр
Угол падения – это угол между падающим лучом и перпендикуляром к отражающей поверхности.
Угол отражения – это угол между отраженным лучом и перпендикуляром к отражающей поверхности.
Законы отражения света
- Лучи падающий и отраженный лежат в одной плоскости с перпендикуляром, восстановленным в точку падения луча к отражающей поверхности.
- Угол отражения равен углу падения. ( anglebeta=anglealpha ), где ( alpha ) – угол падения, ( beta ) – угол отражения.
Виды отражения
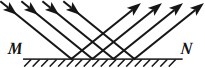
- Зеркальное – это отражение, при котором лучи, падающие на поверхность параллельным пучком, после отражения остаются параллельны.
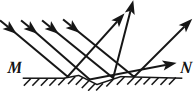
- Рассеянное – это отражение, при котором лучи, падающие на поверхность параллельным пучком, после отражения отклоняются в различных направлениях.
Если луч падает перпендикулярно отражающей поверхности, то угол падения равен нулю, и угол отражения тоже равен нулю. Поэтому луч отражается в обратном направлении.
Важно!
В оптике все углы отсчитываются от перпендикуляра к отражающей поверхности или к границе раздела сред.
Построение изображений в плоском зеркале
Построение изображения в плоском зеркале основано на законах отражения света.
Алгоритм построения изображения в плоском зеркале
- Проведите из данной точки на поверхность луч под произвольным углом. В точке падения луча на границу раздела сред проведите перпендикуляр.
- Отметьте угол падения ( alpha ).
- Постройте равный ему угол отражения ( beta ).
- Проведите из данной точки перпендикуляр к поверхности зеркала ( (alpha=0) ).
- Постройте равный ему угол отражения ( (beta=0) ) (эти лучи совпадают).
- Проведите пунктирной линией продолжения отраженных лучей за зеркало.
- Найдите точку пересечения продолжений отраженных лучей (эта точка является изображением данной точки в плоском зеркале).
- Аналогично постройте изображение второй точки.
- Соедините полученные изображения точек пунктирной линией.
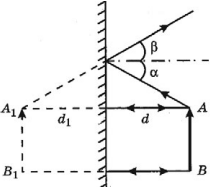
Изображение предмета в плоском зеркале мнимое, прямое, по размерам равное предмету, находящееся за зеркалом на таком же расстоянии, на каком предмет находится перед зеркалом.
Важно!
Если на поверхность плоского зеркала падает сходящийся пучок лучей, то изображение получается действительным.
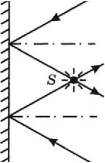
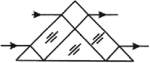
Если поверхность двух плоских зеркал образует угол ( varphi ), то количество изображений в такой системе зеркал можно определить по формуле:
где ( N ) – количество изображений.
Закон преломления света
Преломление света – это изменение направления распространения светового луча на границе раздела двух сред.
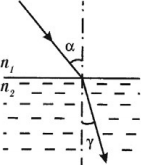
Угол преломления – это угол между преломленным лучом и перпендикуляром к границе раздела двух сред.
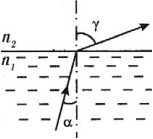
( gamma ) – угол преломления
Законы преломления света
- Лучи падающий и преломленный лежат в одной плоскости с перпендикуляром, восстановленным в точку падения луча к преломляющей поверхности.
- Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных двух сред и равная относительному показателю преломления двух сред:
где ( n_{21} ) – относительный показатель преломления.
Первой является среда, в которой распространяется падающий луч, второй является среда, в которой распространяется преломленный луч.
Относительный показатель преломления равен отношению абсолютного показателя преломления второй среды к абсолютному показателю преломления первой среды:
где ( n_1 ) – абсолютный показатель преломления первой среды; ( n_2 ) – абсолютный показатель преломления второй среды.
Абсолютный показатель преломления показывает, во сколько раз скорость света в вакууме больше, чем в данной среде:
где ( c ) – скорость света в вакууме, ( v ) – скорость распространения света в данной среде.
Относительный показатель преломления показывает, во сколько раз скорость распространения света в первой среде больше, чем во второй:
Среда, у которой абсолютный показатель преломления больше, является оптически более плотной средой.
Среда, у которой абсолютный показатель преломления меньше, является оптически менее плотной средой.
Следствия закона преломления света
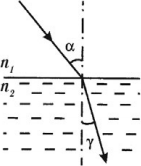
- Если свет падает из оптически менее плотной среды в оптически более плотную, то угол падения больше угла преломления:
- Если свет падает из оптически более плотной среды в оптически менее плотную, то угол падения меньше угла преломления:
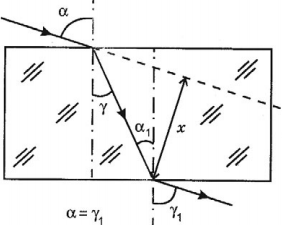
Если луч падает на плоско параллельную пластину, изготовленную из оптически более плотного вещества, чем окружающая среда, то луч не изменяет своего направления, а лишь смещается на некоторое расстояние.
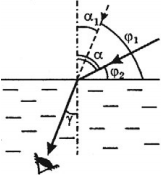
( x ) – смещение луча от первоначального направления:
где ( d ) – толщина пластины.
Важно!
Если в условии задачи говорится, что «кажется, что луч падает под углом ( varphi_1 ) к поверхности воды», то имеют в виду не кажущийся угол падения ( alpha_1 ), а угол между кажущимся падающим лучом и поверхностью воды ( varphi_1 ).
Полное внутреннее отражение
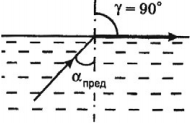
Если свет падает из оптически более плотной среды в оптически менее плотную среду, то с увеличением угла падения увеличивается угол преломления. При некотором значении угла падения угол преломления становится равным 90°. Преломленный луч будет скользить по поверхности раздела двух сред.
Предельный угол полного отражения – это угол падения, при котором угол преломления становится равным 90°:
Если вторая среда – воздух, ( n_2 ) = 1, то ( sinalpha_{пр.}=frac{1}{n_1}. ).
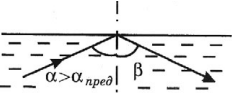
При дальнейшем увеличении угла падения угол преломления тоже увеличивается и наблюдается только отражение света. Это явление называется полным отражением света.
Применение явления полного внутреннего отражения
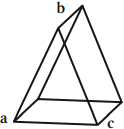
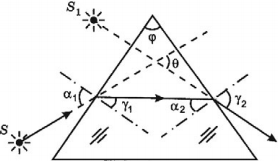
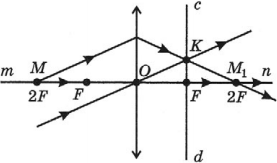
Треугольная призма – прозрачное тело, ограниченное с трех сторон плоскими поверхностями так, что линии их пересечения взаимно параллельны.
Если призма изготовлена из оптически более плотного вещества, чем окружающая среда, то луч, дважды преломляясь, отклоняется к основанию призмы, а мнимое изображение источника света смещается к вершине призмы.
Преломляющий угол призмы – это угол, лежащий против основания.
Угол отклонения луча призмой – это угол между направлениями падающего на призму и вышедшего из призмы лучей.
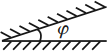
( varphi ) – преломляющий угол,
( theta ) – угол отклонения луча призмой.
Важно!
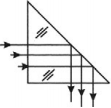
С помощью треугольной равнобедренной призмы с преломляющим углом 90° можно:
- повернуть луч на 90° (поворотная призма, используется в перископах);
- изменить направление луча на 180° (оборотная призма, используется в биноклях);
- изменить относительное расположение лучей.
Линзы. Оптическая сила линзы
Линза – это прозрачное тело, ограниченное двумя сферическими или криволинейными поверхностями, одна из которых может быть плоской.
Тонкая линза – физическая модель линзы, в которой ее толщиной можно пренебречь по сравнению с диаметром линзы.
Классификация линз
1. По форме:
- выпуклые – это линзы, у которых средняя часть толще, чем края;
- вогнутые – это линзы, у которых края толще, чем средняя часть.
2. По оптическим свойствам:
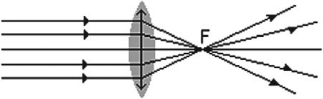
- собирающие – это линзы, после прохождения которых параллельный пучок лучей собирается в одной точке;
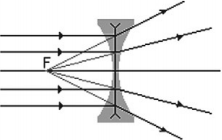
- рассеивающие – это линзы, после прохождения которых параллельный пучок лучей рассеивается.
Условные обозначения:
Величины, характеризующие линзу
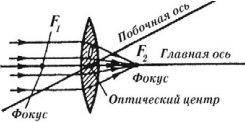
Главная оптическая ось – это прямая, проходящая через центры сферических поверхностей линзы.
Оптический центр линзы – это точка пересечения главной оптической оси с линзой, проходя через которую луч не изменяет своего направления.
Побочная оптическая ось – это любая прямая, проходящая через оптический центр линзы под произвольным углом к главной оптической оси.
Фокус линзы – это точка, в которой пересекаются после преломления лучи, падающие на линзу параллельно главной оптической оси.
Обозначение – ( F ).
Фокусное расстояние – это расстояние от оптического центра линзы до ее фокуса. Обозначение – ( F ), единица измерения – м.
Фокальная плоскость – это плоскость, проходящая через фокус линзы перпендикулярно ее главной оптической оси.
Побочный фокус – это точка пересечения побочной оптической оси с фокальной плоскостью.
Оптическая сила линзы – это величина, обратная фокусному расстоянию.
Обозначение – ( D ), единица измерения – диоптрия (дптр):
1 дптр – это оптическая сила линзы с фокусным расстоянием 1 м.
Важно!
Оптическая сила линзы зависит от показателя преломления линзы и от радиусов кривизны сферических поверхностей, ограничивающих линзу:
где ( n_л ) – показатель преломления линзы, ( n_{ср} ) – показатель преломления среды, ( R_1 ) и ( R_2 ) – радиусы сферических поверхностей.
Если поверхности выпуклые, то ( R_1 ) > 0 и ( R_2 ) > 0, если поверхности вогнутые, то ( R_1 ) < 0 и ( R_2 ) < 0.
Если одна из поверхностей линзы плоская, например первая, то ( R_1toinfty ), а вторая поверхность выпуклая: ( R_2 ) > 0, то
Формула тонкой линзы
где ( F ) – фокусное расстояние линзы, ( d ) – расстояние от предмета до линзы, ( f ) – расстояние от линзы до изображения.
Правило знаков:
- ( F ) > 0, если линза собирающая; ( F ) < 0, если линза рассеивающая;
- ( d ) > 0, если предмет действительный; ( d ) < 0, если предмет мнимый (если на линзу падает сходящийся пучок лучей);
- ( f ) > 0, если изображение действительное; ( f ) < 0, если изображение мнимое.
Линза собирающая, предмет действительный, изображение действительное:
Линза собирающая, предмет действительный, изображение мнимо:
Линза собирающая, предмет мнимый, изображение действительное:
Линза рассеивающая, предмет действительный, изображение мнимое:
Линза рассеивающая, предмет мнимый, изображение мнимое:
Увеличение линзы – это величина, равная отношению линейных размеров изображения к линейным размерам предмета.
Обозначение – ( mathit{Gamma} ), единицы измерения – нет.
где ( H ) – линейный размер изображения, ( h ) – линейный размер предмета.
где ( f ) – расстояние от линзы до изображения, ( d ) – расстояние от предмета до линзы.
Важно!
При расчете увеличения линзы знаки ( f ) и ( d ) не учитываются.
Построение изображений в линзах
Для построения изображения в линзах следует помнить:
- луч, идущий вдоль главной оптической оси линзы, не преломляется;
- луч, проходящий через оптический центр линзы, не преломляется;
- луч, падающий на собирающую линзу параллельно главной оптической оси, после преломления пройдет через фокус линзы;
- луч, падающий на рассеивающую линзу параллельно главной оптической оси, преломится так, что его мнимое продолжение пройдет через фокус линзы, а сам луч – противоположно мнимому продолжению;
- луч, падающий на собирающую линзу через фокус, после преломления пройдет параллельно главной оптической оси линзы;
- произвольный луч после преломления в собирающей линзе пойдет через побочный фокус (точку фокальной плоскости, в которой ее пересечет параллельная произвольному лучу побочная оптическая ось);
- произвольный луч, падающий на рассеивающую линзу, преломится так, что его мнимое продолжение пройдет через точку, в которой пересечет фокальную плоскость линзы побочная оптическая ось, параллельная произвольному лучу.
Изображение, даваемое тонкой линзой, может быть действительным или мнимым.
Действительное изображение получается в результате пересечения преломленных в линзе лучей, исходящих из данной точки.
Мнимое изображение получается в результате пересечения продолжений преломленных в линзе лучей, исходящих из данной точки.
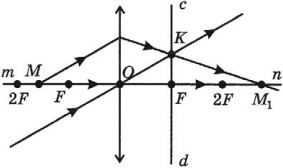
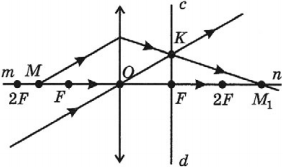
Построение изображений точки, даваемых собирающей линзой
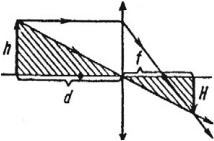
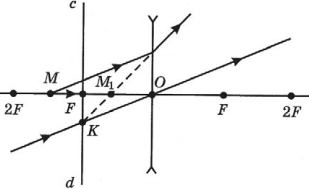
- Если точка находится за двойным фокусом линзы, то ее действительное изображение получается между фокусом и двойным фокусом по другую сторону от линзы.
- Если точка находится в двойном фокусе линзы, то его действительное изображение получается в двойном фокусе по другую сторону от линзы.
- Если точка находится между фокусом и двойным фокусом линзы, то его действительное изображение получается за двойным фокусом по другую сторону от линзы.
- Если точка находится в фокусе линзы, то его изображение находится в бесконечности.
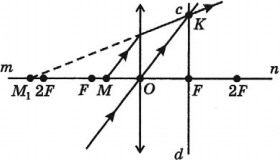
- Если точка находится между линзой и фокусом, то его мнимое изображение получается по ту же сторону от линзы.
Построение изображений предмета, даваемых собирающей линзой
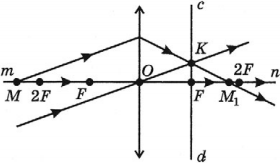
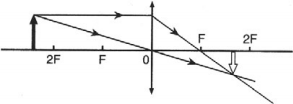
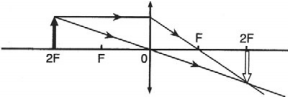
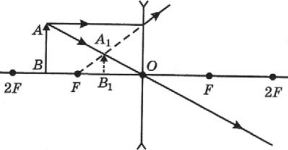
- Если предмет находится за двойным фокусом линзы, то его изображение получается действительным, перевернутым, уменьшенным, по другую сторону от линзы.
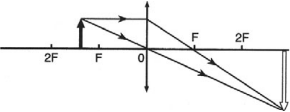
- Если предмет находится в двойном фокусе линзы, то его изображение получается действительным, перевернутым, равным по размерам предмету, в двойном фокусе по другую сторону от линзы.
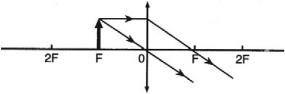
- Если предмет находится между фокусом и двойным фокусом линзы, то его изображение получается действительным, перевернутым, увеличенным, по другую сторону от линзы.
- Если предмет находится в фокусе линзы, то его изображение находится в бесконечности.
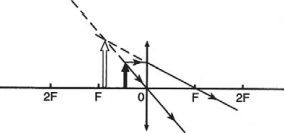
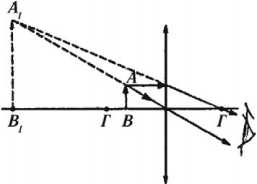
- Если предмет находится между линзой и фокусом, то его изображение получается мнимым, прямым, увеличенным, по ту же сторону от линзы.
Построение изображений точки, даваемых рассеивающей линзой
В рассеивающей линзе изображение точки всегда получается мнимым, по ту же сторону от линзы.
Построение изображений предмета, даваемых рассеивающей линзой
Изображение предмета в рассеивающей линзе всегда получается мнимым, прямым, уменьшенным, по ту же сторону от линзы.
Важно!
При решении задач на прохождение световых лучей сквозь линзы и получение изображений в них прежде всего выясните, о какой линзе идет речь: собирающей или рассеивающей. Обязательно сделайте чертеж, на котором соответствующими буквами укажите все основные расстояния: расстояние от предмета до линзы, расстояние от линзы до изображения, фокусное расстояние. Также обязательно укажите оптический центр линзы и оба фокуса по разные стороны от линзы.
При построении изображения следует заранее выучить, каким оно должно быть при соответствующем расположении предмета относительно линзы и где находиться (действительным или мнимым, увеличенным или уменьшенным, прямым или обратным). В противном случае при неверном построении, когда вы чуть-чуть искривите луч или он пойдет неточно через фокус или центр, изображение может оказаться не там, где надо, или вместо увеличенного уменьшенным, и тогда в решении появится ошибка.
Оптические приборы. Глаз как оптическая система
Оптические приборы – это устройства, предназначенные для получения на экране, светочувствительных пленках, фотопленках и в глазу изображений различных предметов.
Лупа – это короткофокусная двояковыпуклая линза, предназначенная для относительно небольшого увеличения изображения.
Увеличение лупы рассчитывается по формуле:
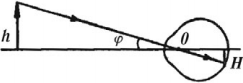
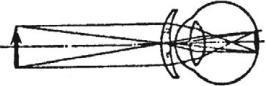
где ( d_0 ) – расстояние наилучшего зрения, ( d_0 ) = 0,25 м.
Для получения увеличенного изображения предмет помещают перед линзой на расстоянии немного меньше фокусного. Изображение получается мнимым.
Микроскоп – это оптический прибор, предназначенный для рассматривания очень мелких предметов под большим углом зрения.
Микроскоп состоит из двух собирающих линз – короткофокусного объектива и длиннофокусного окуляра, расстояние между которыми может изменяться:
где ( F_1 ) – фокусное расстояние объектива; ( F_2 ) – фокусное расстояние окуляра.
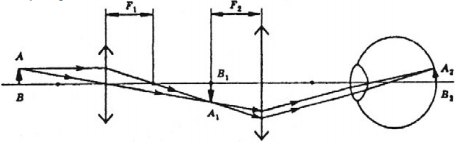
Фотоаппарат – прибор, предназначенный для получения действительных, уменьшенных, перевернутых изображений предметов на фотопленке.
Предметы могут находиться на разных расстояниях.
Мультимедийный проектор – оптическое устройство, с помощью которого на экране получают действительное, увеличенное изображение, снятое с источника видеосигнала.
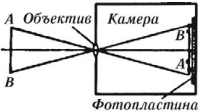
Человеческий глаз – оптическая система, подобная фотоаппарату.
Зрачок регулирует доступ света в глаз. Диаметр зрачка уменьшается при ярком освещении и увеличивается при слабом.
Хрусталик имеет форму двояковыпуклой линзы с показателем преломления 1,41. Он может изменять свою форму, в результате чего меняется его фокусное расстояние. При рассмотрении близких предметов хрусталик становится более выпуклым, при рассмотрении удаленных предметов – более плоским.
На сетчатке глаза образуется действительное, уменьшенное, перевернутое изображение предмета. Благодаря большому количеству нервных окончаний, находящихся на сетчатке, их раздражение передается в мозг и вызывает зрительные ощущения.
Зрение двумя глазами позволяет видеть предмет с разных сторон, т. е. осуществлять объемное зрение.
Если смотреть на предмет одним глазом, то, начиная с 10 м, он будет казаться плоским, если смотреть на предмет двумя глазами, то это расстояние увеличивается до 500 м.
Угол зрения – это угол, образованный лучами, идущими от краев предмета в оптический центр глаза.
( varphi ) – угол зрения.
Аккомодация глаза – это свойство глаза, обеспечивающее четкое восприятие равноудаленных предметов путем изменения фокусного расстояния оптической системы.
Предел аккомодации – от ( infty ) до 10 см.
Расстояние наилучшего зрения – это наименьшее расстояние, с которого глаз может без особого напряжения рассматривать предметы:
Дефекты зрения
- Близорукость – это дефект оптической системы глаза, при котором ее фокус находится перед сетчаткой. Близорукий глаз плохо видит отдаленные предметы.
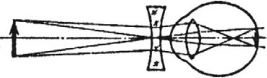
- Дальнозоркость – это дефект оптической системы глаза, при котором ее фокус находится за сетчаткой. Дальнозоркий глаз плохо видит близкие предметы.
Очки – это простейший прибор для коррекции оптических недостатков зрения.
Близорукость исправляют с помощью рассеивающих линз.
Дальнозоркость исправляют с помощью собирающих линз.
Интерференция света
Интерференция света – это явление перераспределения энергии в пространстве, происходящее в результате сложения когерентных волн, вследствие чего в одних местах возникают максимумы, а в других минимумы.
Когерентные волны – это волны, имеющие одинаковую частоту и постоянную во времени разность фаз.
Когерентные волны можно получить от одного источника в результате отражения, преломления или дифракции.
Два независимых источника света не могут быть когерентными, поэтому в опытах с интерференцией света световые пучки от одного источника разделяют на два пучка, заставляют их проходить разные расстояния, а потом соединяют.
Когерентными могут быть:
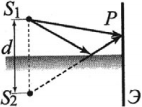
- волны, одна из которых падает на экран непосредственно от источника света, а другая создается его отражением в зеркале (зеркало Ллойда);
- волны, образованные отражением одной и той же волны от двух сдвинутых относительно друг друга поверхностей (тонкие пленки);
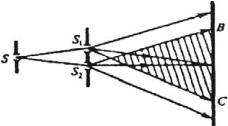
- волны, падающие от точечного источника на непрозрачную преграду с двумя узкими щелями, которые разделяют исходный пучок света на два когерентных пучка (опыт Юнга).
Интерференционная картина представляет собой чередование светлых (цветных) и темных полос.
Источником когерентных волн является лазер.
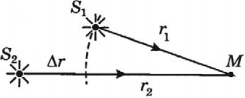
Геометрическая разность хода волн – это разность путей волн от двух когерентных источников ( S_1 ) и ( S_2 ) до точки пространства ( M ), в которой наблюдается интерференция.
Обозначение – ( Delta r ), единица измерения в СИ – м.
Условие максимума интерференции
Если геометрическая разность хода содержит целое число длин волн или четное число длин полуволн, то в месте их наложения друг на друга наблюдается усиление света – максимум:
где ( k ) = 0; 1; 2; 3… – порядок интерференционного максимума.
Условие минимума интерференции
Если геометрическая разность хода содержит нечетное число длин полуволн, то в месте их наложения друг на друга наблюдается ослабление света – минимум:
где ( k ) = 0; 1; 2; 3… – порядок интерференционного минимума.
Если свет распространяется в прозрачной среде с показателем преломления ( n ), то применяют понятие оптической разности хода.
Оптическая разность хода – это величина, равная произведению показателя преломления и геометрической разности хода волн.
Обозначение – ( Delta ), единица измерения в СИ – м.
Интерференция в тонких пленках
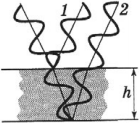
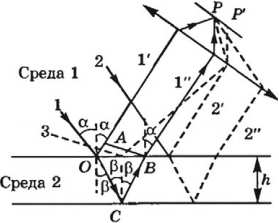
Наблюдаемое в природе радужное окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри, оксидные пленки на металлах) объясняется интерференцией света, возникающей в результате отражения света от передней и задней поверхностей пленки. На тонкую прозрачную пленку толщиной ( h ) падает световая волна, ограниченная лучами 1 и 2. В точке О свет частично отразится от верхней поверхности пленки (волна 1′), а частично преломится и отразится от задней ее поверхности в точке С, преломившись в точке В, выйдет в воздух параллельно волне 1′. Волны 1′ и 1″ когерентны. (То же самое справедливо и для луча 2.)
Если на пути этих лучей поставить собирающую линзу, то они будут накладываться в ее фокальной плоскости и давать интерференционную картину. ( То же самое справедливо и для луча 2.)
Максимум освещенности поверхности тонкой пленки в отраженном свете:
где ( Delta=2kfrac{lambda}{2} ) – оптическая разность хода световых волн при отражении от верхней и нижней поверхности, ( k ) = 1; 2; 3… – целое число длин полуволн, укладывающихся в этой разности хода, ( beta ) – угол преломления.
Минимум освещенности поверхности тонкой пленки в отраженном свете:
Максимум освещенности поверхности тонкой пленки в проходящем свете:
Минимум освещенности поверхности тонкой пленки в проходящем свете:
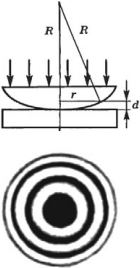
Примером интерференции являются кольца Ньютона, которые наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны. Воздушная прослойка постепенно утолщается от точки соприкосновения линзы к краям. Отраженные от верхней и нижней границ воздушной прослойки световые волны интерферируют между собой. При этом получается следующая картина: в точке соприкосновения наблюдается черное пятно, окруженное рядом концентрических светлых и темных колец убывающей ширины.
Радиус светлого кольца Ньютона в отраженном свете:
где ( R ) – радиус кривизны линзы, ( k ) – номер кольца, считая от центра интерференционной картины.
Радиус темного кольца Ньютона в отраженном свете:
Радиус светлого кольца Ньютона в проходящем свете:
Радиус темного кольца Ньютона в проходящем свете:
Важно!
При решении задач следует учитывать, в каком свете наблюдается интерференция: в отраженном или проходящем.
Использование интерференции света
- Интерферометры – это приборы, которые контролируют качество обработки поверхностей зеркал, точность изготовления деталей оптических инструментов и измерительных приборов.
- Просветление оптики – на поверхность линз наносят тонкую пленку с показателем преломления меньше, чем показатель преломления стекла. Подбирая толщину пленки и величину показателя преломления, добиваются «гашения отраженных волн», вследствие чего возрастает интенсивность света, пропускаемого линзой.
Дифракция света
Дифракция света – это явление отклонения волны от прямолинейного распространения при прохождении через малые отверстия и огибании волной малых препятствий.
Наилучшее условие для наблюдения дифракции создается, когда размеры отверстий или препятствий – порядка длины волны. Чтобы определить распределение интенсивности световой волны, распространяющейся в среде с неоднородностями, используют принцип Гюйгенса–Френеля.
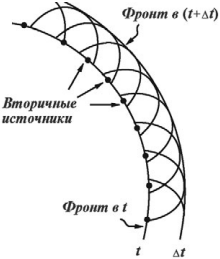
Принцип Гюйгенса–Френеля
Каждая точка фронта волны является источником вторичных волн, которые интерферируют между собой. Поверхность, касательная ко всем вторичным волнам, представляет новое положение фронта волны в следующий момент времени.
Все вторичные источники, расположенные на поверхности фронта волны, когерентны между собой, поэтому амплитуда и фаза волны в любой точке пространства – это результат интерференции волн, излучаемых вторичными источниками.
Дифракционная решетка
Дифракционная решетка – это оптический прибор, предназначенный для наблюдения дифракции света.
Дифракционная решетка представляет собой систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.
Дифракционную решетку применяют для разложения света в спектр и измерения длин световых волн.
Период решетки – это величина, равная сумме ширины прозрачной и непрозрачной полос решетки.
Обозначение – ( d ), единица измерения в СИ – м.
где ( a ) – ширина прозрачной полосы; ( b ) – ширина непрозрачной полосы.
Если решетка регулярна, т. е. ее прозрачные и непрозрачные полосы имеют одинаковую ширину, то период решетки можно рассчитать, разделив ее длину на число штрихов:
где ( l ) – длина решетки, ( N ) – число штрихов.
Формула дифракционной решетки
где ( d ) – период решетки; ( varphi ) – угол дифракции; ( k ) = 0; 1; 2… – порядок максимума, считая от центрального ( k ) = 0 и расположенного напротив центра решетки; ( lambda ) – длина волны, падающей на решетку нормально к ней.
Если дифракционная решетка освещается белым светом, то при ( k ) ≠ 0 разным длинам волн будут соответствовать разные дифракционные углы. Поэтому положение главных максимумов ненулевого порядка будет различным. Центральный максимум (( k ) = 0) остается белым, т. к. при ( k ) = 0 для всех длин волн ( varphi ) = 0, т. е. положение главного максимума для всех длин волн одинаково. Все остальные максимумы имеют вид радужных полос, называемых дифракционными спектрами первого порядка (( k ) = 1), второго порядка (( k ) = 2) и т. д. Ближе к центральному максимуму находится фиолетовый край спектра, дальше всего – красный, т. к. ( lambda_{фиол}<lambda_{кр} ), то и ( varphi_{фиол}<varphi_{кр} ).
Важно!
Поскольку углы, под которыми наблюдаются максимумы первого и второго порядка, не превышают 5°, можно вместо синусов углов использовать их тангенсы.
Дисперсия света
Дисперсия света – это зависимость показателя преломления среды от длины волны (частоты) падающего на вещество света.
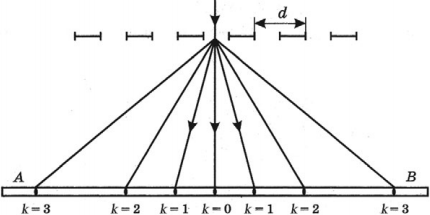
Опыт Ньютона (1672)
Из-за дисперсии световые волны с различной длиной волны поразному преломляются веществом, что приводит к разложению белого света на цветные монохроматические лучи – спектр.
Для лучей света различной цветности показатели преломления данного вещества различны, т. к. различны скорости распространения электромагнитных волн, у которых разная длина волны. Луч красного света преломляется меньше из-за того, что красный свет имеет в веществе наибольшую скорость, а луч фиолетового цвета преломляется больше, так как скорость для фиолетового цвета наименьшая. Это объясняется особенностями взаимодействия этих волн с электронами, входящими в состав атомов и молекул вещества среды, где они движутся.
Дисперсией света объясняется такое природное явление, как радуга.
Основные формулы по теме «Оптика»
Оптика
3 (60.87%) 115 votes
Загрузить PDF
Загрузить PDF
Длина волны – это расстояние между двумя соседними точками, которые колеблются в одной фазе; как правило, понятие «длина волны» ассоциируется с электромагнитным спектром.[1]
Метод вычисления длины волны зависит от данной информации. Воспользуйтесь основной формулой, если известны скорость и частота волны. Если нужно вычислить длину световой волны по известной энергии фотона, воспользуйтесь соответствующей формулой.
-
1
Воспользуйтесь формулой для вычисления длины волны. Чтобы найти длину волны, разделите скорость волны на частоту. Формула:
[2]
-
2
Используйте соответствующие единицы измерения. Скорость измеряется в единицах метрической системы, например, в километрах в час (км/ч), метрах в секунду (м/с) и так далее (в некоторых странах скорость измеряется в британской системе, например, в милях в час). Длина волны измеряется в нанометрах, метрах, миллиметрах и так далее. Частота, как правило, измеряется в герцах (Гц).[3]
- Единицы измерения конечного результата должны соответствовать единицам измерения исходных данных.
- Если частота дана килогерцах (кГц), или скорость волны в километрах в секунду (км/с), преобразуйте данные значения в герцы (10 кГц = 10000 Гц) и в метры в секунду (м/с).
-
3
Известные значения подставьте в формулу и найдите длину волны. В приведенную формулу подставьте значения скорости и частоты волны. Разделив скорость на частоту, вы получите длину волны.[4]
- Например. Найдите длину волны, распространяющейся со скоростью 20 м/с при частоте колебаний 5 Гц.
-
4
Воспользуйтесь приведенной формулой, чтобы вычислить скорость или частоту. Формулу можно переписать в другом виде и вычислить скорость или частоту, если дана длина волны. Чтобы найти скорость по известным частоте и длине волны, используйте формулу:
. Чтобы найти частоту по известным скорости и длине волны, используйте формулу:
.[5]
Реклама
-
1
-
2
Перепишите представленную формулу, чтобы найти длину волны. Для этого проделайте ряд математических операций. Обе стороны формулы умножьте на длину волны, а затем обе стороны разделите на энергию; вы получите формулу:
. Если энергия фотона известна, можно вычислить длину световой волны.[7]
- Эту формулу можно использовать для вычисления максимальной длины световой волны, необходимой для ионизации металлов. В формулу подставьте энергию, необходимую для ионизации, и вычислите длину волны.[8]
- Эту формулу можно использовать для вычисления максимальной длины световой волны, необходимой для ионизации металлов. В формулу подставьте энергию, необходимую для ионизации, и вычислите длину волны.[8]
-
3
В полученную формулу подставьте известные значения и вычислите длину волны. В формулу подставьте только значение энергии, потому что две константы являются постоянными величинами, то есть не меняются. Чтобы найти длину волны, перемножьте константы, а затем результат разделите на энергию.[9]
- Например. Найдите длину световой волны, если энергия фотона равна 2,88 x 10-19 Дж.
Реклама
-
1
Проверьте ответ. Для этого умножьте длину волны на частоту. Если вы получите данное значение скорости, решение правильное; в противном случае проверьте вычисления. Если вы пользуетесь калькулятором, правильно вводите числа.
- Например. Найдите длину волны, которая распространяется со скоростью 343 м/с при частоте колебаний 70 Гц.
- Решите эту задачу как описано выше и получите значение 4,9 м.
- Проверьте ответ: 4,9 м х 70 Гц = 343 м/сек. Это данная в условии задачи скорость, поэтому решение верное.
- Например. Найдите длину волны, которая распространяется со скоростью 343 м/с при частоте колебаний 70 Гц.
-
2
Используйте экспоненциальную запись чисел, чтобы избежать ошибок при округлении чисел (в калькуляторе). Порой в вычислении длины волны участвуют очень большие числа, особенно когда присутствует скорость света. Это может привести к ошибкам округления чисел. Поэтому используйте экспоненциальную запись чисел.[10]
- Например. Свет проходит сквозь воду со скоростью 225000000 м/с. Найдите длину световой волны, если ее частота равна 4 x 1014 Гц.
-
3
Помните, что частота волны не меняется при изменении среды ее распространения. Во многих задачах волна распространяется в двух средах, и некоторые учащиеся пытаются вычислить две длины волны. Это ошибка, потому что в отличие от скорости распространения и длины волны частота волны не меняется при изменении среды ее распространения.[11]
- Например, световая волна длиной λ, распространяющаяся со скоростью v при частоте f, переходит из воздушного пространства в некоторую среду, показатель преломления которой равен 1,5. Как изменятся указанные три величины?
Реклама
Об этой статье
Эту страницу просматривали 158 348 раз.