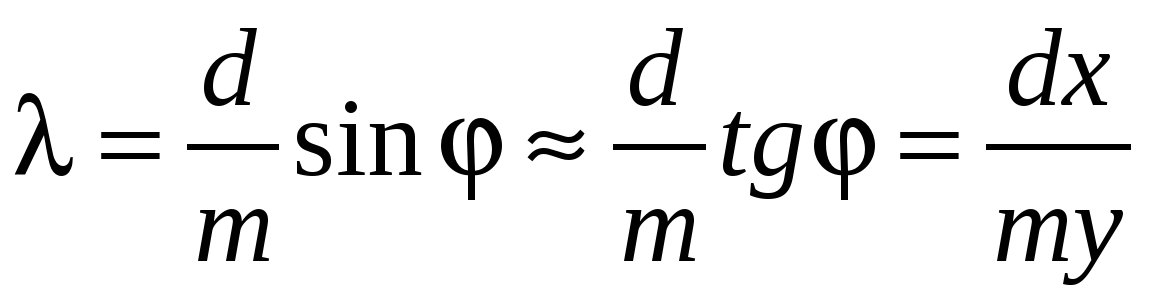Тема: Определение длины волны светового излучения с помощью дифракционной решётки
Цель: Познакомиться на опыте с явлением многолучевой интерференции световых волн. Используя решётку с известным расстоянием между штрихами измерить длину волны светового излучения.
Оборудование:
- Штатив.
- Дифракционная решётка 100 штрихов на мм.
- Измерительная лента.
Теория
Дифракция волн — огибание волнами различных препятствий (неоднородностей).
Препятствия нарушают прямолинейность распространения фронта волны.
Дифракция волн свойственна всякому волновому движению; проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней, однако проявляется всегда. Для увеличения яркости дифракционной картины нужно пропускать свет через несколько параллельных щелей. В этом случае кроме явления дифракции будет происходить ещё и явление интерференции, т.к. лучи, идущие от всех лучей, оказываются когерентными.
Когерентными называются волны, имеющие одинаковую частоту и постоянную разность фаз.
Дифракционная решетка – оптический прибор, представляющий собой большое число параллельных и очень близко расположенных узких щелей, которые пропускают или отражают свет.
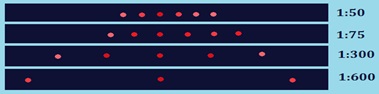
Дифракционные решетки с различным числом щелей на 1 мм:
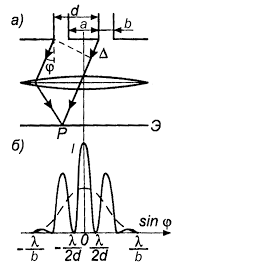
Параллельный пучок света с длиной волны λ, проходя через дифракционную решётку, вследствие дифракции за решёткой, распространяется по всевозможным направлениям и интерферирует. На экране, установленном на пути интерферирующего света, можно наблюдать интерференционную картину:
Максимумы света наблюдаются в точках экрана, для которых выполняется условие максимума:
Условие максимума: на разности хода волн укладывается четное число полуволн (целое число длин волн): Δ=k·λ, (1)
где Δ=АС — разность хода волн; λ — длина световой волны; k — номер максимума.
Центральный максимум (в точке О) называют нулевым; для него Δ=0. Слева и справа от него располагаются максимумы высших порядков.
Условие возникновения максимума можно записать иначе:
d·sinφ=k·λ
где k=0; ± 1; ± 2; ± 3…
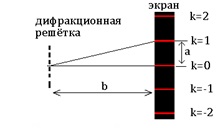
Здесь d — период дифракционной решётки в мм, φ — угол, под которым виден световой максимум k-го порядка в точке N на расстоянии а от нулевого максимума, а λ — длина волны.
Так как углы дифракции малы, то для них можно принять: sinφ ≈ tgφ, а tgφ=a/b.
Поэтому: 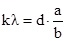
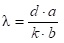
В данной работе формулу (2) используют для вычисления длины световой волны.
Из условия максимума следует sinφ=(k·λ)/d .
Пусть k=1, тогда sinφкр=λкр/d и sinφф=λф/d.
Известно, что λкр>λф , следовательно sinφкр>sinφф. Т.к. y= sinφф — функция возрастающая, то φкр>φф
Поэтому фиолетовый цвет в дифракционном спектре располагается ближе к центру.
Между максимумами расположены минимумы освещенности. Чем больше общее число щелей и чем ближе друг к другу они расположены, тем более широкими промежутками разделены максимумы.
Картина дифракции лазерного излучения красно цвета на решётках с различным числом щелей на 1 мм:
Ход работы
- Перенести рисунок в тетрадь.

- Подготовить таблицу для записи результатов измерений:
|
Порядок спектра, цвет k |
Постоянная d мм |
Расстояние от решётки до экрана, b мм |
Расстояние от нулевого максимума до максимума k-порядка а мм |
Длина волны, нм |
Средняя длина волны нм |
Относительная погрешность δ % |
|
1-ый, красный |
1:100=0,001 |
|||||
|
2-ой, красный |
1:100=0,001 |
|||||
|
1-ый, фиолетовый |
1:100=0,001 |
|||||
|
2-ой, фиолетовый |
1:100=0,001 |
- Укрепить в штативе линейку с экраном и закрепить на направляющей линейки дифракционную решётку.
- Установить расстояние от решётки до экрана 40 см (b).Результат записать в таблицу.
- Смотря через дифракционную решётку, направить прибор на источник света. Пронаблюдать спектр:
Измерить на экране расстояние а между нулевым максимумом и максимумом 1-го порядка для красного света. Результат записать в таблицу.
- Измерить на экране расстояние а между нулевым максимумом и максимумом 2-го порядка для красного света. Результат записать в таблицу.
- Повторить опыт, измерив на экране расстояние а между нулевым максимумом и максимумом 1-го и 2-го порядка для фиолетового света. Результат записать в таблицу.
- По формуле
рассчитать длину волны излучения.
- Найти среднее значение длины волны светового излучения для красного λкр ср=( λкр1+λкр2)/2
и фиолетового света .λф ср=( λф1+λф2)/2
- Зная истинное значение длины волны лазерного излучения , рассчитать относительную погрешность измерений:
δ=( λкр ср — λкр табл)/λкр табл *100% и δ=( λф ср — λф табл)/λф табл *100%
Диапазон длин волн, нм
Красный 625—740 нм (λкр табл= 680 нм)
Фиолетовый 380—440 нм (λф табл = 410 нм)
- Записать вывод по результатам выполненной работы.
- Ответить письменно на контрольные вопросы.
Контрольные вопросы
- Какие волны называются когерентными?
- В чём заключается явление дифракции?
- Какие свойства света подтверждает дифракция света?
- При каких условиях наблюдается дифракция света?
- Как образуется дифракционный спектр?
- Почему максимумы располагаются как слева, так и справа от нулевого максимума?
- В чём разница в дифракционных картинах решёток с 50 и 300 штрихами на одном миллиметре?
5.5. Дифракционная решетка
Широкое распространение в научном эксперименте и технике получили дифракционные решетки, которые представляют собой множество параллельных, расположенных на равных расстояниях одинаковых щелей, разделенных равными по ширине непрозрачными промежутками. Дифракционные решетки изготавливаются с помощью делительной машины, наносящей штрихи (царапины) на стекле или другом прозрачном материале. Там, где проведена царапина, материал становится непрозрачным, а промежутки между ними остаются прозрачными и фактически играют роль щелей.
Рассмотрим сначала дифракцию света от решетки на примере двух щелей. (При увеличении числа щелей дифракционные максимумы становятся лишь более узкими, более яркими и отчетливыми.)
Пусть а — ширина щели, a b — ширина непрозрачного промежутка (рис. 5.6).
Рис. 5.6. Дифракция от двух щелей
Период дифракционной решетки — это расстояние между серединами соседних щелей:
Разность хода двух крайних лучей равна
Если разность хода равна нечетному числу полуволн
то свет, посылаемый двумя щелями, вследствие интерференции волн будет взаимно гаситься. Условие минимумов имеет вид
Эти минимумы называются дополнительными.
Если разность хода равна четному числу полуволн
то волны, посылаемые каждой щелью, будет взаимно усиливать друг друга. Условие интерференционных максимумов с учетом (5.36) имеет вид
Это формула для главных максимумов дифракционной решетки.
Кроме того, в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, то есть главные минимумы решетки будут наблюдаться в направлениях, определяемых условием (5.21) для одной щели:
Если дифракционная решетка состоит из N щелей (современные решетки, применяемые в приборах для спектрального анализа, имеют до 200 000 штрихов, и период d = 0.8 мкм, то есть порядка 12 000 штрихов на 1 см), то условием главных минимумов является, как и в случае двух щелей, соотношение (5.41), условием главных максимумов — соотношение (5.40), а условие дополнительных минимумов имеет вид
Здесь k’ может принимать все целочисленные значения, кроме 0, N, 2N, . . Следовательно, в случае N щелей между двумя главными максимумами располагается (N–1) дополнительных минимумов, разделенных вторичными максимумами, создающими относительно слабый фон.
Положение главных максимумов зависит от длины волны l. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разлагаются в спектр, фиолетовый конец которого обращен к центру дифракционной картины, а красный — наружу. Таким образом, дифракционная решетка представляет собой спектральный прибор. Заметим, что в то время как спектральная призма сильнее всего отклоняет фиолетовые лучи, дифракционная решетка, наоборот, сильнее отклоняет красные лучи.
Важной характеристикой всякого спектрального прибора является разрешающая способность.
Разрешающая способность спектрального прибора — это безразмерная величина
Определение длины световой волны с помощью дифракционной решетки
Л а б о р а т о р н а я р а б о т а N 2 9
Определение длины световой волны с помощью дифракционной решетки
Дифракция света – явление огибания светом встречающихся на его пути препятствий, сопровождающееся пространственным перераспределением энергии световой волны — интерференцией.
Расчет распределения интенсивности света в дифракционной картине может быть осуществлен с помощью принципа Гюйгенса — Френеля. Согласно этому принципу каждая точка фронта световой волны, т. е. поверхности, до которой распространился свет, является источником вторичных когерентных световых волн (начальные фазы их и частоты одинаковы); результирующее колебание в любой точке пространства обусловлено интерференцией всех вторичных волн, приходящих в эту точку, с учетом их амплитуд и фаз.
Положение фронта световой волны в любой момент времени определяет огибающая всех вторичных волн; любая деформация фронта волны (она обусловлена взаимодействием света с препятствиями) приводит к отклонению световой волны от первоначального направления распространения – свет проникает в область геометрической тени.
2. Дифракционная решетка
Прозрачная дифракционная решетка представляет собой стеклянную пластинку или целлулоидную пленку, на которой через строго определенные расстояния специальным резцом нарезаны узкие шероховатые бороздки (штрихи), не пропускающие света. Сумма ширины ненарушенного, прозрачного промежутка (щели) и ширины бороздки называется постоянной или периодом решетки.
Пусть на решетку падает плоская монохроматическая световая волна с длиной волны 
Поместим на пути вторичных волн собирающую линзу. Она сфокусирует в соответствующем месте своей фокальной поверхности все вторичные волны, распространяющиеся под одним и тем же углом дифракции.
Для того, чтобы все эти волны при наложении максимально усиливали друг друга, необходимо, чтобы разность фаз волн, приходящих от соответствующих точек двух соседних щелей, т. е. точек, отстоящих на одинаковых расстояниях от краев этих щелей, была равна четному числу 

для точки P равна:

Следовательно, условие максимумов интенсивности результирующей световой волны при дифракции от дифракционной решетки можно записать следующим образом:

где 

Максимумы, удовлетворяющие условию (2), называются главными, число m называется порядком главных максимумов или порядком спектра. Значению m=0 соответствует максимум нулевого порядка (центральный максимум). Максимум нулевого порядка один, максимумов первого, второго и более высоких порядков — по два слева и справа от нулевого.
Положение главных максимумов зависит от длины 
3. Описание установки
Работа проводится на спектрогониометре ГС-5 с установленной на нем дифракционной решеткой. Гониометр — прибор, предназначенный для точного измерения углов. Внешний вид спектрогониометра ГС-5 изображен на рис.2.
Коллиматор 1, снабженный регулируемой микрометрическим винтом 2 спектральной щелью, крепится на неподвижной стойке. Щель обращена к источнику света (ртутной лампе). На предметном столике 3 устанавливается прозрачная дифракционная решетка 4.
Наблюдение дифракционной картины производится через окуляр 5 зрительной трубы 6.
Целью работы является изучение дифракционной решетки, нахождение ее характеристик и определение с ее помощью длины световых волн спектра излучения паров ртути.
В лаборатории физического практикума кафедры физики УГТУ-УПИ в качестве источника линейчатого спектра в лабораторной работе № 29 используется ртутная лампа, в которой при электрическом разряде генерируется линейчатый спектр излучения, которое пройдя коллиматор спектрогониометра ГС-5 падает на дифракционную решетку (фотография ГС-5 приведена на титульном файле). Экспериментатор определяет угол дифракции с точностью до нескольких секунд, наводя визирную линию окуляра на соответствующую линию спектра, затем по вышеописанной методике вычисляет длину волны выбранной линии.
В компьютерном варианте данной работы достаточно точно моделируются условия проведения опытов. На экране дисплея воспроизводится окуляр, визирную линию которого следует наводить на любую выбранную спектральную линию, точнее говоря на середину цветовой полоски, что повышает точность измерения углов до нескольких угловых секунд.
Как и реальном спектре паров ртути, в компьютерной работе также “генерируются” четыре наиболее ярких видимых линий спектра: фиолетовая, зеленая и две желтых линии. Спектры расположены зеркально симметрично относительно центрального (белого) максимума. Внизу под окуляром для лучшей ориентации на тонкой черной полоске приведены все линии спектра ртути. Причем две желтые линии сливаются в одну. Дело в том, что эти линии расположены рядом и имеют близкие значения длин волн – так называемый дуплет, однако на хорошей дифракционной решетке они разделяются (разрешаются), что видно в окуляре. В данной работе одной из задач и является определение разрешающей способности дифракционной решетки.
Итак, наведя курсор на «Измерения» и нажав левую клавишу мышки, можно приступать к измерениям. «Вращать» окуляр можно в четырех различных режимах как влево, так и вправо, до тех пор, пока в поле зрения окуляра не покажется цветная вертикальная линия. Следует навести черную вертикальную визирную линию окуляра на центральную часть цветной полоски, при этом на цифровом табло высвечиваются значения угла дифракции с точностью до нескольких угловых секунд. Спектральные линии расположены примерно от 60 до 150 градусов. При этом от тщательности проведения опытов зависит точность числовых значений углов и, как следствие, правильность полученных результатов. Экспериментатору предоставляется возможность самому выбирать последовательность выполнения измерений
Результаты измерений надо занести в соответствующие таблицы отчета и произвести необходимые вычисления.
4.1.Определение длины волны спектральных линий паров ртути.
Измерения проводятся для линий спектра первого порядка (m=1). Постоянная решетки d=833,3 нм., ее длина (ширина) равна 40 мм. Значение синуса угла можно определить по соответствующим таблицам или с помощью калькулятора, однако следует иметь в виду, что угловые секунды и минуты нужно переводить в десятичные разряды градусов, т. е. 30 минут равны 0,5 градуса и т. п.
Результаты измерений заносятся в таблицу 2 отчета (смотри Приложение). Значение длины волны 

4.2.Расчет характеристик дифракционной решетки.
Максимальное значение порядка m дифракционных спектров для какой-либо дифракционной решетки может быть определено в случае нормального падения света на решетку по следующей формуле:

Значение mmax определяется для наибольшей длины волны — в данной работе для второй желтой линии 


Разрешающая способность R дифракционной решетки характеризует ее способность разделять (разрешать) спектральные линии, мало отличающиеся по длинам волн. По определению

где 

Величина 



совпадает с первым добавочным минимумом в спектре этого же порядка m для другой линии 

Из этих уравнений следует, что

и разрешающая способность решетки оказывается равной

Таким образом, разрешающая способность решетки зависит от порядка m спектра и от общего числа N штрихов рабочей части решетки, т. е. той части, через которую проходит исследуемое излучение и от которой зависит результирующая дифракционная картина. По формуле (5) находится разрешающая сила R используемой дифракционной решетки для спектра первого порядка (m=1).
Из (5) следует, что две спектральные линии 


Используя найденное значение R, по формуле (5) вычисляется ( в нанометрах) линейное разрешение 




Угловая дисперсия D дифракционной решетки характеризует угловое расстояние между близкими спектральными линиями. По определению

где 

Формула для D получается дифференцированием соотношения(2): левой части по углу дифракции 



Таким образом, угловая дисперсия решетки зависит от порядка m спектра, постоянной d решетки и от угла дифракции 
По формуле (8) находится (в “/нм
Полученные результаты записываются в таблицу 2 отчета (смотри Приложение).
5. Kонтрольные вопросы
1. В чем состоит явление дифракции света?
2. Сформулируйте принцип Гюйгенса-Френеля.
3. Что такое разрешающая способность дифракционной решетки и от чего она зависит?
4. Как экспериментально определить угловую дисперсию D дифракционной решетки?
5. Какой вид имеет дифракционная картина, полученная от прозрачной решетки?
ПРИЛОЖЕНИЕ
ФОРМА ОТЧЕТА
Кафедра физики
по лабораторной работе 29
Изучение дифракционных решеток. Определение длины световой волны с помощью дифракционной решетки
Дата _________________________________
На внутренних страницах:
1. Расчетные формулы:




где 
m – порядок спектра ( m=1).
2. Источник излучения – ртутная лампа.
4. Результаты измерений углов дифракции и длин волн
спектральных линий паров ртути. Таблица 1
Порядок максимума, m
Угловое положение линии
Угол дифрак — ции

Слева от центр. макс. a 1
Справа от центр. макс. a 2
5. Расчет искомых величин.
Чтобы рассчитать число штрихов на рабочей части решетки, следует учесть, что d=833,3 нм, а длина (в нашем случае, ширина) решетки равна 40 мм.
Таблица 2 Xарактеристики дифракционной решетки

6. Оценка погрешностей измерений длин волн рассчитывается по формуле:

Табличные значения длин волн спектральных линий паров ртути:
Дифракционная решетка. Постоянная и период решетки. Использование в спектроскопии
Дифракционная решетка часто используется для определения спектра падающего на нее света, поскольку она позволяет расщеплять его на отдельные цвета. В данной статье рассмотрим, что такое дифракционная решетка, постоянная и период ее, и приведем пример решения задачи с использованием этого оптического прибора.
Явление дифракции
Суть его заключается в изменении направления распространения волны, когда она встречает на своем пути препятствие. Результат дифракции хорошо различим, если размеры препятствия сравнимы с длиной волны или меньше нее. Дифрагированная волна способна проникать в области за препятствием, куда она не смогла бы попасть, если бы двигалась вдоль прямой.

На рисунке ниже приведен пример дифракции морской волны.
Видно, как прямой фронт волны после прохождения препятствия приобретает форму окружности.
Математическое описание дифракции осуществляется с использованием принципа Гюйгенса-Френеля, который гласит, что каждая точка волнового фронта является источником вторичной волны некоторой интенсивности.
Дифракция часто сопровождается интерференцией. Благодаря этим двум явлениям можно наблюдать так называемые дифракционные картины.
Дифракционная решетка
Это решетка представляет собой прозрачную пластинку, на которую нанесены непрозрачные штрихи с определенным периодом. Когда свет проходит через такую пластинку, то она вносит периодическое возмущение в его волновой фронт. В результате возникает ряд вторичных источников, которые испускают когерентные волны. В результате интерференции когерентные волны образуют на экране совокупность максимумов и минимумов, то есть дифракционную картину.
Важной характеристикой решетки является число штрихов N, нанесенных на 1 мм ее длины. Эта величина N называется постоянной дифракционной решетки, d — период решетки, который равен обратному значению от N. Период обычно выражают в мкм. Геометрический смысл величины d простой — это расстояние между двумя соседними штрихами на решетке. Период d является параметром уравнения решетки, которое будет приведено в следующем пункте.
Описанная выше решетка называется проходящей или прозрачной. Существует также отраженная дифракционная решетка, которая представляет собой совокупность периодических бороздок, нанесенных на гладкую поверхность материала. Примером этого вида решетки является DVD-диск.
Уравнение решетки
В приближении дальнего поля (дифракция Фраунгофера) уравнение для решетки выглядит следующим образом:
Это выражение показывает, при каких углах θm будут возникать максимумы (яркие полосы) на экране. Здесь m = 0, ±1, 2, 3, . Эти числа называются порядком дифракции. Величина λ — это длина волны, которая дифрагирует на решетке, d — период, то есть величина, обратная постоянной дифракционной решетки. Длина самой решетки, как видно из формулы, никакой роли не играет. Углы θm измеряются между двумя прямыми: перпендикуляром, восстановленным к центру решетки, и прямой, направленной от центра к максимуму порядка m.
Приведенная формула непосредственно следует из условия интерференционного максимума. В лабораторных работах ее используют для определения либо постоянной дифракционной решетки, когда λ известна, либо длины волны, когда d известен.
Использование дифракционной решетки в спектроскопии
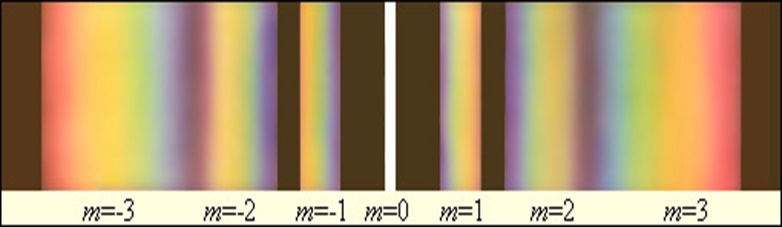
Приведенное выше уравнение решетки позволяет сделать вывод, что углы θm, в которых появляются максимумы, зависят от длины волны. Чем больше она, тем больше эти углы (длинные волны лучше дифрагируют, чем короткие). Это означает, что если на решетку направить белый свет, то она его разложит на ряд цветов подобно дисперсионной призме. Причем последовательность цветов, начиная от центра (m=0), будет идти от фиолетового к красному.
Каждый максимум для соответствующего порядка дифракции и белого света будет представлять собой «радугу». Единственным максимумом, который всегда будет белым, является центральный или нулевой (m=0).
Явление разложения белого света на отдельные составляющие позволяет использовать дифракционную решетку в спектроскопии. Например, пропуская свет от далекой галактики через решетку, а затем анализируя полученный спектр, можно с достоверностью сказать, какие элементы присутствуют в галактике, какая у них температура, с какой скоростью движется эта галактика относительно нас (в последнем случае учитывается эффект Доплера).
Пример решения задачи
Покажем, как пользоваться уравнением решетки, на примере решения простой задачи. Пусть постоянная дифракционной решетки равна 300 штрихов на 1 мм. Необходимо определить, при каком угле будет наблюдаться максимум первого порядка для фиолетовой (400 нм) и для красной (700 нм) волн.
Учитывая, что число штрихов N обратно пропорционально периоду d, перепишем уравнение решетки в виде:
Угол для первого максимума равен:
Подставляем данные в единицах СИ в это выражение, получаем:
Для фиолетового: θ1 = arcsin(400*10-9*300*103) = 6,89o.
Для красного: θ1 = arcsin(700*10-9*300*103) = 12,12o.
Если экран поставить на расстоянии 1 метра от решетки, тогда на нем красная и фиолетовая полосы для первого порядка дифракции будут находиться на расстоянии около 9 см друг от друга.
http://pandia.ru/text/77/487/2144.php
http://1ku.ru/obrazovanie/34998-difrakcionnaja-reshetka-postojannaja-i-period-reshetki-ispolzovanie-v-spektroskopii/
Министерство
высшего и среднего специального
образования
РСФСР
Дальневосточный
ордена Трудового Красного Знамени
политехнический
институт имени В.В.Куйбышева
ФИЗИКА
Определение
длины волны света
при
помощи дифракционной решетки
Методические
указания по выполнению
лабораторной
работы № 74
Владивосток
1987
УДК
536.625/076.5/07/
Одобрено
методическим советом университета
Методические
указания предназначены для проведения
лабораторного практикума по курсу общей
физики для студентов дневного, вечернего
и заочного отделений.
Методические
указания составила преподаватель
кафедры физики Н.А. Король.
Лабораторная
работа № 74
Определение
длины волны света при помощи
дифракционной
решетки
Цель
работы: изучить явление дифракции света,
определить длину волны света.
Приборы
и оборудование: источник света,
дифракционная решетка, экран.
Дифракцией
называется огибание волнами препятствий,
соизмеримых с длиной волны. Свет –
электромагнитные волны, лежащие в
диапазоне волн
до

поэтому на препятствиях, размеры которых
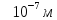
он будет дифрагировать.
|
где |
Ширина
каждой зоны выбирается так, чтобы
разность хода для лучей, идущих от краев
этих зон, была равна
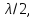
всего на ширине щели уместится
зон. Так как свет на щель падает нормально,
то плоскость щели совпадает с фронтом
волны, следовательно, все точки фронта
в плоскости щели будут колебаться с
одинаковой фазой. Амплитуды вторичных
волн в плоскости щели будут равны, т.к.
выбранные зоны Френеля имеют одинаковые
площади и одинаково наклонены к
направлению наблюдения.
Из
выражения (1) вытекает, что число зон,
укладывающихся на ширине щели, зависит
от угла
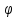
От числа зон, в свою очередь, зависит
результат лжения ичных волн: если число
зон – четное
|
|
(2) |
|
|
(3) |
то
в точке
наблюдается дифракционный минимум,
т.к. колебания от каждой пары соседних
зон взаимно гасят друг друга. Если же
число зон – нечетное
то
наблюдается дифракционный максимум,
соответствующий действию одной
нескомпенсированной волны. В точке
наблюдается центральный дифракционный
максимум, т.к. для направления
щель действует как одна зона.
На
условии (2) и (3) можно найти направление
на точках экрана, в которых амплитуда
(а, следовательно, и интенсивность) равна
нулю:

или максимальна: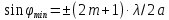
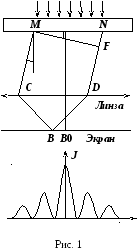
Распределение интенсивности на экране,
получаемое вследствие дифракции,
приведено на рис.1, б.
Таким
образом, на экране в стороны от центральной
белой полосы (центрального максимума)
будут наблюдаться чередующиеся темные
(минимумы) и светлые (максимумы) полосы.
Положение
дифракционных максимумов зависит от
длины волны
(см. выражение 3). Поэтому в случае белого
света центральный максимум (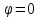
останется общим для всех длин волн, и в
центре дифракционной картины расположится
белая полоса, а последующие максимумы
для разных длин волн уже не совпадают
между собой, ближе к центру будут
находиться максимумы, соответствующие
более коротким волнам (фиолетовые
полосы).
Большое
практическое значение имеет дифракция,
наблюдаемая при прохождении света через
дифракционную решетку – систему
параллельных щелей равной ширины,
лежащих в одной плоскости и разделенных
равными по ширине непрозрачными
промежутками.
Дифракционная
картина на решетке определяется как
результат взаимной интерференции волн,
идущих от всех щелей, т.е. в дифракционной
решетке осуществляется многолучевая
интерференция когерентных дифракционных
пучков света, идущих от всех щелей.
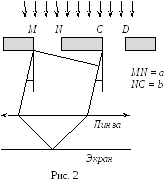
Для
наглядности рассмотрим дифракционную
решетку, состоящую из двух щелей:
и
(рис.2). Если ширина каждой щели
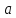
а ширина непрозрачных участков между
щелями
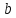
то величина
называется постоянной (периодом)
дифракционной решетки. Пусть плоская
монохроматическая волна падает нормально
к плоскости решетки. Так как щели
находятся друг от друга на расстояниях
одинаковых, то разности хода лучей
идущих от двух соседних щелей, будут
для данного направления
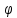
в пределах всей дифракционной решетки:
|
|
(4) |
В
тех направлениях, в которых ни одна из
щелей не посылает свет, он не будет
распространяться и при двух щелях, т.е.
прежние (главные) минимумы интенсивности
будут наблюдаться в направлениях,
определяемых условием:
|
|
(5) |
|
|
Кроме
того, вследствие взаимной интерференции
световых лучей, посылаемых двумя щелями,
в некоторых направлениях они будут
гасить друг друга, т.е. возникнут
дополнительные минимумы:
Наоборот,
действие одной щели будет усиливать
действие другой, если
|
|
(6) |
Т.е.
направлениям (6) соответствуют так
называемые главные максимумы. Если
дифракционная решетка состоит из
щелей, то условием главных минимумов
является условие (5), условием главных
максимумов – условие
|
|
(6),
а условием дополнительных минимумов
где
может принимать все целочисленные
значения, кроме
Следовательно,
в случае
щелей между двумя главными максимумами
располагается
дополнительных минимумов, разделенных
вторичными максимумами, создающими
весьма слабый фон. Чем больше число
щелей
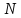
тем больше количество световой энергии
пройдет через решетку, тем больше
минимумов образуется между соседними
главными максимумами, тем, следовательно,
более интенсивными и более острыми
будут максимумы. Положение главных
максимумов зависит от длины волны
(см. (6)). Поэтому при пропускании через
решетку белого света все максимумы,
кроме центрального (
разложатся в спектр, фиолетовая область
которого будет обращена к центру
дифракционной картины, красная – наружу.
Это свойство дифракционной решетки
используется для исследования
спектрального состава света (определение
длин волн и интенсивностей всех его
монохроматических компонентов), т.е.
дифракционная решетка может быть
использована как спектральный прибор.
Из
условия (6) определяется длина волны
монохроматического света
(7)
где
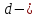
дифракционной решетки,
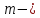
дифракционного максимума (спектра).
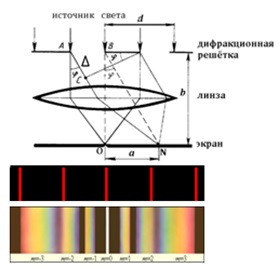
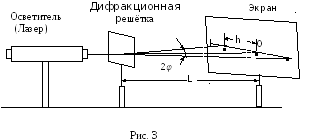
Экспериментальная
установка для определения длины волны
с помощью дифракционной решетки
представлена на рис.3. В качестве источника
света использован He-Ne
лазер, в качестве дифракционной решетки
прозрачная решетка. Все элементы
установки установлены на единой
оптической скамье. Точка О на рис. 3
определяет положение главного
дифракционного максимума порядка m
= 0. Слева и справа от нее точками отмечены
два симметричных дифракционных максимума
порядка m,
углы между которыми составляют 2φ. Углы
дифракции обычно составляют малую
величину (2φ << 1 рад ≈ 57о),
при этом условии tgφ
≈ sinφ.
Из рис. 3 следует:
где
расстояние от центрального максимума
до дифракционного максимума m-ого
порядка,
расстояние от решетки до экрана.
|
|
(8) |
Тогда
Порядок
выполнения работы
При
выполнении работы рекомендуется
придерживаться следующего порядка:
-
Устанавливают
осветитель (ОКГ) на расстоянии 70-80 см
от экрана так, чтобы лазерный луч
попадал в центр экрана. -
Между
осветителем и экраном в непосредственной
близости от лазера помещают дифракционную
решетку. При этом плоскость решетки
должна быть перпендикулярна лучу
лазера. На экране наблюдают дифракционную
картину в виде дифракционных максимумов
по обе стороны от центрального максимума. -
Измеряют
расстояние
от решетки до экрана и расстояния
от каждого максимума порядка m
до центрального максимума. Рекомендуется
измерять расстояния для всех наблюдаемых
дифракционных максимумов. -
По
формуле (8) вычисляют длину волн света,
излучаемого лазером, для всех порядков
дифракционных максимумов, и по ним
рассчитывают среднее значение длины
волны лазерного излучения. Затем
определяют погрешность результата,
принимая λm
за
прямые измерения. -
Постоянная
решетки
,
данная в мм, написана на самой решетке.
Контрольные
вопросы
-
Что
называют дифракцией света? -
В
чем заключено понятие зоны Френеля? -
Какими
условиями определяются положения
дифракционных максимумов интенсивности
света на экране от одной щели, от решетки? -
Как
выглядит дифракционная картина,
полученная в монохроматическом свете?
В «белом» свете?
Литература
-
Савельев
И.В. Курс общей физики, Т. 3. М.: Наука,
1968. -
Яворский
В.М. Курс общей физики. Т.3. М.: Высшая
школа, 1966. -
Рымкевич
П.А. Курс физики. М.: Наука, 1974.
Методические
указания по выполнению
лабораторной
работы № 74
Определение
длины волны света при
помощи
дифракционной решетки
Составила
Н.А. Король
Редактор
С.А.Хмелева
Техн.
редактор Л.П. Абраменко
Подписано
в печать 01.10.87.
Формат
60×84/16. Бумага типографская. Печать
офсетная. Усл.печ.л. 0,46. Уч.-изд.л. 0,29.
Тираж 200 экз.
Заказ
551.
Бесплатно.
Редакционно-издательский
отдел ДВПИ. Владивосток, Пушкинская, 10
Фотоофсетная
лаборатория ДВПИ. Владивосток, Ленинская,
53
Лабораторная работа №10
ДИФРАКЦИЯ СВЕТА. ОПРЕДЕЛЕНИЕ ДЛИНЫ МОНОХРОМАТИЧЕСКОЙ ВОЛНЫ.
Цель работы: провести наблюдения явлений дифракции света на дифракционной решетке и щели; определить длину монохроматической волны с помощью дифракционной решетки и зная длину световой волны определить ширину щели.
Оборудование: оптическая скамья, лазер, дифракционная решетка, регулируемая щель, экран.
Теоретические сведения:
Дифракция — это явление огибаниия светом препятствий и попаданием его в область геометрической тени, дифракция возникает при распространении света в среде с резкими неоднородностями (препятствиями). Явление дифракции состоит в нарушении закона прямолинейного распространения света.
Явления дифракции можно объяснить с помощью принципа Гюйгенса: любая точка в пространстве, до которой дошел фронт волны, становится точечным источником вторичных сферических волн.
Френель ввел представление о том, что волновое возмущение в любой точке исследуемого пространства можно рассматривать как результат интерференции сферических волн от вторичных источников, на которые разбивается волновой фронт.
Огибающая этих волн дает положение волнового фронта в каждый последующий момент времени. Волновой фронт — это геометрическое место точек среды колеблющихся в одной фазе и световые лучи перпендикулярны волновому фронту.
Для определения результата дифракции в исследуемой точке пространства, волновую поверхность условно разбивают на участки (зоны Френеля) таким образом, чтобы волны, посылаемые соседними участками в данную точку пространства, приходили в нее в противофазе, т.е. гасили друг друга. Причем, разность фаз соответствует разности хода волн .
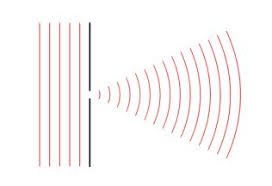
Осветим непрозрачный экран с отверстием параллельным пучком света (см. рис.1). Согласно принципу Гюйгенса – Френеля свет попадает в зону геометрической тени.
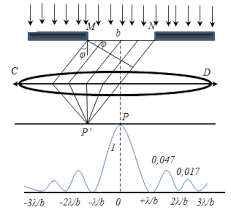
Рассмотрим дифракцию в параллельных лучах на одной щели. Пусть параллельный пучок монохроматического света падает нормально на непрозрачный экран, в котором прорезана длинная узкая щель шириной b. Фронт световой волны доходит до плоскости щели, тогда согласно принципу Гюйгенса — Френеля все точки волны являются точечными источниками вторичных когерентных сферических волн, следовательно, световые лучи попадают в зону геометрической тени Рассмотрим световые лучи, идущие под углом к первоначальному направлению распространения волны (см. рис.2).
Если собрать их линзой на экране в точке Р’, можно наблюдать результат их интерференции. Оптическая разность хода между двумя крайними лучами равна . Если угол
таков, что равно четному числу полуволн
(
)
тогда фронт световой волны (в пределах щели) разбивается на четное число плоских зон Френеля (условие min интенсивности в дифракционной картине).
Если же , то поверхность фронта волны разбивается на нечетное число зон Френеля —
, где
(условие max интенсивности для дифракции от одной щели).
В направлении угла = 0 лежит самый яркий максимум, максимум нулевого порядка, поскольку разность хода любых лучей, посылаемых щелью, в этом случае равна нулю. Поэтому лучи приходят в точку наблюдения в одной фазе, максимально усиливая друг друга.
При освещении щели монохроматическим светом на экране наблюдается дифракционная картина(см. рис.2), состоящая из симметрично расположенных относительно центрального максимума нулевого порядка темных и светлых полос. Если щель освещается белым светом, то максимумы всех порядков, кроме нулевого, окрашены во все цвета радуги. Центральный же максимум – белый, т.к. при разность хода любых лучей, независимо от длины волны, равна нулю.
|
|
|
Рис.3 |
Для увеличения интенсивности и более четкого разделения цветов пользуются не одной щелью, а дифракционной решеткой (рис.3а).
Она представляет собой N параллельных щелей одинаковой ширины (b), разделенных непрозрачными промежутками шириной (a). Расстояние d равное сумме этих двух промежутков a + b = d называется периодом или постоянной дифракционной решетки.
Пусть на решетку, состоящую из N щелей, падает параллельный пучок монохроматического света (рис.3а).
Согласно принципу Гюйгенса-Френеля все щели будут излучать вторичные когерентные волны. Расположив параллельно решетке линзу, в фокальной плоскости которой находится экран, можно наблюдать дифракционную картину. Для того, чтобы найти распределение интенсивности на экране, нужно учесть не только интерференцию волн, вышедших из каждой отдельной щели, но и интерференцию волн, пришедших в данную точку наблюдения P из соседних щелей.
Условие min интенсивности для одной щели является также условием главных max интенсивности и для дифракционной решетки (см. рис. 3b). Лучи, идущие от крайних точек двух соседних щелей, имеют разность хода . Следовательно, такая же разность хода и у вторичных волн, идущих от соответствующих пар точек фронта падающей волны.
Если разность хода между лучами укладывается целое число длин волн, то при интерференции возникнут главные максимумы, которые удовлетворяют условию:
, m = 0, 1, 2 – порядок главных максимумов.
Главный максимум, соответствующий , называется центральным, а максимумы при m = 1, 2, 3… называются главными максимумами первого, второго, третьего порядков, соответственно.
Между главными максимумами возникают минимумы, число которых зависит от числа щелей N в дифракционной решетке. Чем больше N, тем резче главные максимумы и больше их интенсивность.
При освещении решетки белым светом происходит разложение его в спектр, световые полосы, соответствующие максимумам всех порядков, кроме нулевого, окрашены.
С помощью дифракционной решетки с известным периодом можно определить длину световой волны
, воспользовавшись условием максимума для малых углов,
, по формуле:
где — расстояние от центрального максимума (m = 0) до максимума
— порядка;
— расстояние от решетки до экрана.
Эксперимент и обработка результатов.
Установка (см.рис. 4), на которой выполняется данная работа, состоит из источника света (2) (полупроводниковый лазер), экрана (6) на держателе (5), держателя (3), в котором можно укрепить либо щель с регулируемой шириной, либо дифракционную решетку (4). Элементы установки располагаются на оптической скамье (1).
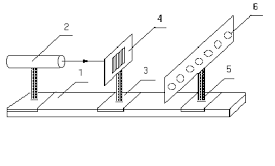
ВНИМАНИЕ! Попадание в глаз прямого лазерного пучка опасно для зрения. При работе с лазером его излучение можно наблюдать только в отраженном свете.
Задание 1.
1. На дальнем от лазера конце оптической скамьи установить экран.
2. Между лазером и экраном (на расстоянии y 100 см от экрана) установить дифракционную решетку так, чтобы ее плоскость была перпендикулярна лучу лазера.
3. Включить лазер при этом на экране должна появиться дифракционная картина.
4. Наложить на экран лист бумаги и отметить положение максимумов интенсивности.
5. Измерить расстояние между лазером и экраном.
6. Измерить на листе бумаги расстояние между центральным максимумом порядка m = 0 и соседним максимумом первого порядка (m=1).
7. Определить длину волны излучения лазера по формуле:
.
Задание 2.
1. На той же установке между лазером и экраном поставить держатель с регулируемой щелью вместо дифракционной решетки.
2. Включить лазер при должна возникнуть дифракционная картина.
3. С помощью микрометрического винта добиться наиболее четкой картинки на экране,
4. Наложить на экран лист бумаги и отметить положения дифракционных максимумов на листе.
5. Измерить расстояние между лазером и экраном.
6. Измерить расстояние между центральным максимумом порядка m = 0 и соседним максимумом первого порядка (m=1).
7. определить ширину щели по формуле:
, значение длины волны взять из первого задания.
Оформление результатов.
Результаты должны содержать схему установки, все основные формулы, описывающие дифракцию от щели и дифракционной решетки, а также расчетную формулу, по которой определялась длина волны излучения лазера. В отчете должны быть представлены результаты всех измерений и
Контрольные вопросы.
1. В чем заключается явление дифракции света?
2. Сформулировать принцип Гюйгенса. Как с его помощью можно качественно объяснить дифракцию света?
3. В чем заключается дополнение Френеля к принципу Гюйгенса?
4. В каких направлениях и почему наблюдаются максимум при дифракции от одной щели?
5. В каких направлениях и почему наблюдаются минимум при дифракции от одной щели?
6. В каком направлении наблюдается максимум нулевого порядка?
7. Чем отличается дифракционная картина от одной щели при освещении ее монохроматическим и белым светом?
8. Как устроена дифракционная решетка и что является ее периодом?
9. Условие главных максимумов дифракции на решетке.
10. Как получить формулу для определения длины волны излучения лазера?
4





















 Рассмотрим
Рассмотрим
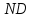 ,
,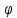 ,
,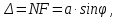
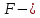
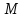
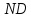 .
.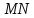
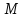
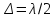
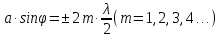
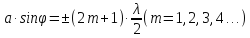
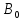

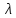
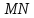
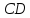
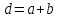
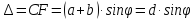
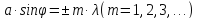
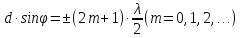
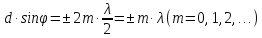
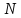

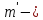
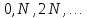
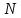
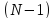
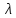
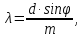
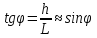
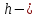
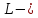
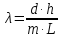
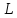
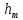
 ,
,