Уравнение высоты треугольника
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Высота треугольника онлайн
С помощю этого онлайн калькулятора можно найти высоту треугольника. Для нахождения высоты треугольника введите известные элементы треугольника и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Открыть онлайн калькулятор
Высота треугольника. Определение
Определение 1. Отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
Высота треугольника может содержаться внутри треугольника (Рис.1), совпадать со стороной треугольника (при прямоугольном треугольнике высота совпадает с катетом (Рис.2) ), проходить вне треугольника (при тупоугольном треугольнике(Рис.3)).
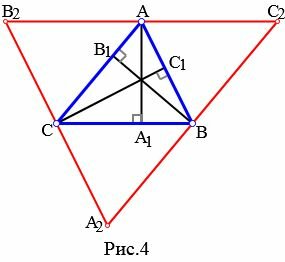
Теорема о пересечении высот треугольника
Теорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.
Доказательство. Рассмотрим произвольный треугольник ABC (Рис.4). Докажем, что высоты ( small AA_1 ,) ( small BB_1 ,) ( small CC_1 ) пересекаются в одной точке. Из каждой вершины треугольника проведем прямую, параллельно противоположной стороне. Получим треугольник ( small A_2B_2C_2. ) Покажем, что точки ( small A, B, C ) являются серединами сторон треугольника ( small A_2B_2C_2. ) ( small AB=A_2C ) так как они являются противоположными сторонами параллелограмма ( small ABA_2C. ) ( small AB=CB_2 ) так как они являются противоположными сторонами параллелограмма ( small ABCB_2. ) Тогда ( small CB_2=CA_2, ) то есть точка ( small C ) является серединой стороны ( small A_2B_2 ) треугольника ( small A_2B_2C_2. ) Аналогично доказывается, что точки ( small A ) и ( small B ) являются серединами сторон ( small B_2C_2 ) и ( small A_2C_2, ) соответственно.
Далее из ( small AA_1⊥BC ) следует, что ( small AA_1⊥B_2C_2 ) поскольку ( small BC ǁ B_2C_2 ). Аналогично, ( small BB_1⊥A_2C_2, ) ( small CC_1⊥A_2B_2. ) Получили, что ( small AA_1,) ( small BB_1, ) ( small CC_1) являются серединными перпендикулярами сторон ( small B_2C_2, ) ( small A_2C_2, ) ( small A_2B_2, ) соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке.
Точка пересечения высот треугольника называется ортоцентром.
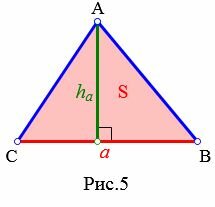
Высота треугольника по основанию и площади
Пусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).
Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:
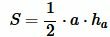
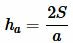 . . |
(1) |
Пример 1. Сторона треугольника равна ( small a=5 ) а площадь ( small S=7. ) Найти высоту треугольника.
Применим формулу (1). Подставляя значения ( small a ) и ( small S ) в (1), получим:
Ответ:
Высота треугольника по трем сторонам
Формула площади треугольника по трем сторонам имеет следующий вид (см. статью на странице Площадь треугольника онлайн):
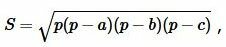 |
(2) |
где ( small a, b, c ) стороны треугольника а полупериод ( small p ) вычисляется из формулы:
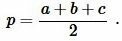 |
(3) |
Высота треугольника, отпущенная на сторону ( small a) вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления высоты треугольника по трем сторонам:
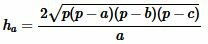 . . |
(4) |
Пример 2. Известны стороны треугольника: ( small a=5, ) ( small b= 4, ) ( small c=7. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Найдем, сначала полупериод ( small p ) треугольника из формулы (3):
Подставляя значения ( small a , b, c ) и ( small p ) в (4), получим:
Ответ:
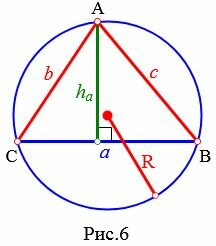
Высота треугольника по двум сторонам и радиусу описанной окружности
Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:
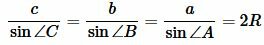 |
(5) |
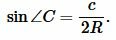 |
(6) |
Далее, из теоремы синусов имеем:
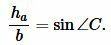 |
(7) |
Подставляя (6) в (7), получим:
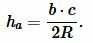 |
(8) |
Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:
(small max (b,c) ≤2R Пример 3. Известны стороны треугольника: ( small b=7, ) ( small c= 3 ) и радиус описанной окружности ( small R=4. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Проверим сначала условие (9):
(small max (7,3) ≤2 cdot 4 Ответ: ( small 2frac<5><8>. )
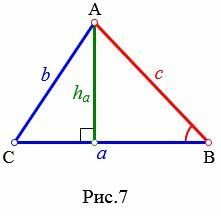
Высота треугольника по стороне и прилежащему к ней углу
Найдем высоту ( small h_a ) треугольника на рисунке 7. Из теоремы синусов имеем:
( small frac<large h_a><large sin angle B>=frac<large c><large sin 90°>, )
| ( small h_a=c cdot sin angle B. ) | (11) |
Пример 4. Известны сторона ( small c=12 ) треугольника и прилежащий угол ( small angle B=30°. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Для нахождения высоты треугольника подставим значения ( small c=12 ) и ( small angle B=30° ) в (11). Имеем:
Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
http://matworld.ru/geometry/vysota-treugolnika.php
2.9. Типовая задача с треугольником
Многие помнят из школы признаки равенства треугольников, признаки подобия треугольников и мучительное заучивание доказательств теорем. Как в
сердцАх сказал один мой одноклассник, «не понимаю, на### доказывать равенство треугольников, если и так видно, что они одинаковые». Мы тоже не
будем ничего доказывать, поскольку аналитическая геометрия рассматривает треугольник совсем с другой стороны.
Типовая задача, как правило, формулируется так: Даны три вершины треугольника. Требуется найти… много чего требуется
найти…. Повезёт, если будет пункта 3-4, но чаще всего их 5-6 и даже больше. И вам повезло – разберём всё! Или почти всё:
Задача 95
Даны вершины треугольника . Требуется:
1) составить уравнения сторон и найти их угловые коэффициенты;
2) найти длину стороны ;
3) найти ;
4) составить прямой , проходящей через точку
параллельно прямой
;
5) составить уравнение высоты и найти её длину;
6) вычислить площадь треугольника ;
7) составить уравнение медианы ;

.
и для особо опасных энтузиастов:
9) найти уравнение биссектрисы ;
10) найти центр тяжести треугольника;
11) составить систему линейных неравенств, определяющих треугольник.
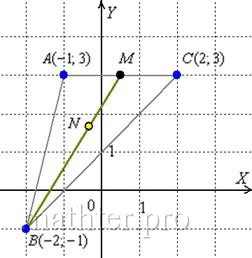
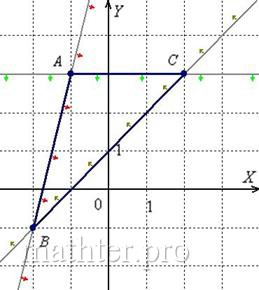
С чего начать решение? Начать целесообразно с выполнения чертежа. По условию этого можно не делать, но для самоконтроля и
самопроверки всегда строим чертёж на черновике, не устану это рекомендовать:
Ещё раз напоминаю, что самый выгодный масштаб 1 единица = 1
см (2 тетрадные клетки). Всё хорошо видно, и расстояния удобно измерять линейкой.
Вперёд без страха и сомнений:
1) Составим уравнения сторон и найдём их угловые
коэффициенты.
Поскольку известны вершины треугольника, то уравнения каждой стороны составим по двум
точкам.
Составим уравнение стороны по точкам
:
Для проверки мысленно либо на черновике подставляем координаты каждой точки в полученное уравнение.
Теперь
найдём угловой коэффициент. Для этого перепишем общее уравнение в виде уравнения с угловым коэффициентом:
Таким образом, угловой коэффициент:
Самостоятельно разбираемся со сторонами и сверяемся, что
получилось:
2) Найдём длину стороны . Используем соответствующую формулу для точек
:
Сторону легко измерить обычной линейкой, хотя это не сильно строгая проверка 
3) Найдём . Это Задача 31, повторим:
Используем формулу 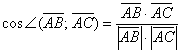
Найдём векторы:
Таким образом:
, и сам угол:
, ну что же, похоже на правду, желающие могут приложить транспортир, у кого
он есть.
Внимание! При выполнении этого пункта лучше не использовать формулы ориентированного угла
между прямыми, так как они всегда дают острый угол.
4) Составим уравнение прямой , проходящей через точку
параллельно прямой
. Это стандартная задача, и мы ленимся отработать её вновь!
Из общего уравнения прямой вытащим направляющий вектор
.
Составим уравнение прямой по точке
и направляющему вектору
:
5) Составим уравнение высоты и найдём её длину.
Первую часть задания мы тоже решали:
Из уравнения стороны снимаем вектор нормали
. Уравнение высоты
составим по точке
и направляющему вектору
:
Обратите внимание, что координаты точки нам не известны.
Иногда уравнение высоты находят из соотношения угловых коэффициентов перпендикулярных прямых: . В данном случае
, тогда:
. Уравнение высоты
составим по точке
и угловому коэффициенту
:
Длину высоты можно найти двумя способами.
Существует окольный путь:
а) находим – точку
пересечения высоты и стороны ;
б) находим длину отрезка по двум
известным точкам.
Но зачем? – ведь есть удобная формула расстояния от точки до прямой
:
6) Вычислим площадь треугольника. Используем «школьную» формулу:
7) Уравнение медианы составим в два шага:
а) Найдём точку – середину стороны
. Используем формулы координат середины отрезка.
Известны концы , и тогда середина:
б) Уравнение медианы составим по точкам
:
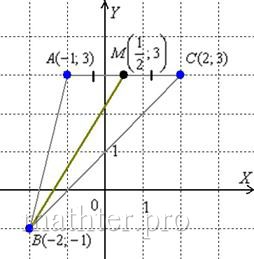
– для проверки подставим координаты точек
.

высоты и медианы:
в
Первое уравнение умножили на 5, складываем их почленно:
– подставим в первое уравнение:
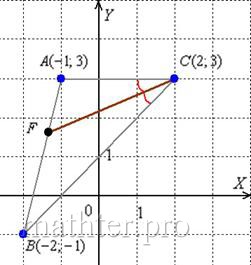
9) Биссектриса делит угол пополам:
Из свойств биссектрисы внутреннего угла следует соотношение длин следующих отрезков:
Длины сторон уже найдены в предыдущих пунктах: .
Таким образом, . Координаты точки
найдём по формулам деления отрезка в данном отношении. Да,
параметр «лямбда» получился просто сказочным, ну а кому сейчас легко? Точки известны и понеслась нелёгкая:
Примечание: на последнем шаге я умножил числитель и знаменатель на сопряжённое выражение – чтобы использовать формулу
и
избавиться от иррациональности в знаменателе.
Разбираемся со второй координатой:
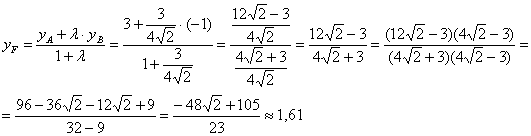
аким образом:
И предчувствие вас не обмануло, уравнение биссектрисы составим по точкам
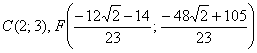
:
обратите внимание на технику упрощений:
Проверил, всё сходится. На практике, конечно, вычисления почти всегда будут проще. Никого не хотел запугать, так уж получилось =)
10) Найдём центр тяжести треугольника.
Но сначала поймём, что такое центр тяжести плоской фигуры. Мысленно вырежьте из тонкого однородного картона любую фигуру. …Почему-то фигура зайца
в голову пришла. Так вот: если слегка насадить данную фигуру центром тяжести (какой же я изверг =)) на вертикально расположенную иголку, то
теоретически фигура не должна свалиться.
Центром тяжести треугольника является точка пересечения его медиан. В треугольнике три медианы и пересекаются они в одной точке.
Из пункта 7 нам уже известна одна из медиан: . Как решить задачу?
Напрашивается очевидный алгоритм: можно найти уравнение второй медианы (любой из двух оставшихся) и точку пересечения этих медиан. Но есть путь
короче! Нужно только знать полезное свойство:
Точка пересечения медиан делит каждую из медиан в
отношении , считая от вершины треугольника. Поэтому справедливо
отношение
Нам известны концы отрезка – точки и
.
По формулам деления отрезка в данном отношении:
Таким образом, центр тяжести треугольника:
И заключительный пункт задачи, для освоения которого нужно уметь решать недавно разобранные линейные
неравенства:
11) Составим систему линейных неравенств, определяющих треугольник.
Для удобства я перепишу найденные уравнения сторон:
Рассмотрим прямую . Треугольник лежит в полуплоскости, где находится
вершина . Составим вспомогательный многочлен
и вычислим его значение в точке
:
. Поскольку сторона
принадлежит треугольнику, то неравенство будет нестрогим:
Внимание! Если вам не понятен этот алгоритм, то обратитесь к
Задаче 90.
Рассмотрим прямую . Треугольник расположен ниже данной прямой, поэтому
очевидно неравенство .
И, наконец, для составим многочлен
, в который подставим координаты точки
:
.
Таким образом, получаем третье неравенство: .
Итак, треугольник определяется следующей системой линейных
неравенств:
Готово.
Какой можно сделать вывод?
Многие задачи аналитической геометрии прозрачны и просты,
главное, не допустить вычислительных ошибок.
Следует отметить, что по настоящему трудные задачи в аналитической геометрии встречаются редко, и вы справитесь практически с любой из них!
Главное, придерживаться методики решения и проявить маломальское упорство.
Ну что, может ещё задачку? Да ладно, не надо стесняться, я же по глазам вижу, что хотите =)
Но сейчас на очереди другая увлекательная тема, продолжаем изучать геометрию плоскости:


| Оглавление |
Автор: Aлeксaндр Eмeлин
8
Даны вершины
треугольника.
Найти:
-
длину стороны ВС;
-
уравнение высоты ВС;
-
уравнение высоты, проведённой из вершины
А; -
длину высоты, проведённой из вершины
А; -
угол В.
Сделать чертёж.
Дано: А(-8;3), В(4;-2), С(7;2).
РЕШЕНИЕ
-
Длину стороны ВС находим по формуле
.
По условию имеем В(4;-2), С(7;2).
-
Найдём уравнение стороны ВС. Найдём
уравнение прямой, на которой лежит
сторона ВС. Используем уравнение прямой,
проходящей через две точки
,
полагая
-
Найдём уравнение высоты, проведённой
из вершины А. При составлении уравнения
прямой, на которой лежит высота
треугольника, воспользуемся формулой
и условием перпендикулярности двух
прямых
:
Определим угловой коэффициент прямой
ВС. Для этого разрешим уравнение стороны
ВС относительно у:
Следовательно, высота, проведённая из
точки А, имеет угловой коэффициент
Тогда, уравнение высоты, опущенной из
вершины А(-8;3) на сторону ВС:
-
Найдём длину высоты, проведённой из
вершины А. Она равна расстоянию от точки
А(-8;3) до прямой ВС заданной уравнением
.
По формуле
вычисляем расстояние от точки А до
прямой ВС, полагая
-
Найдём угол В. Угол В равен углу между
прямыми ВС и АВ и может быть найден с
помощью формулы
.
Угловой коэффициент прямо ВС известен
и равен
.
Найдём угловой коэффициент прямой АВ
по формуле:
Тогда получаем,
И угол равен
Выполним чертёж. В прямоугольной
декартовой системе координат хОу строим
исходные точки и получаем треугольник
АВС. Затем из вершины А опустим
перпендикуляр на сторону ВС, получим
АК.
18
Даны координаты вершин пирамиды А1А2А3А4.
Найти:
-
координаты вектора
и длину ребра
;
-
угол между рёбрами
и
;
-
площадь грани
;
-
объём пирамиды;
-
уравнение плоскости
;
-
уравнение прямой
;
-
угол между ребром
и гранью
;
-
уравнение высоты, опущенной из вершины
на грань
;
Сделать чертёж.
Дано: А1(7;2;2), А2(5;7;7), А3(5;3;1),
А4(2;3;7).
РЕШЕНИЕ
-
Вектор
равен
Длину ребра
можно найти как расстояние между двумя
точками
и
,
оно равно
Получаем
-
Угол между рёбрами
и
найдём как угол между векторами
и
.
Вектор
Таким образом, имеем два вектора
и
,
угол между ними найдём по формуле:
Скалярное произведение двух векторов
в числителе дроби находили как сумму
произведений одноимённых координат
(проекций).
-
Площадь грани
равна половине площади параллелограмма,
построенного на векторах, как на
сторонах. И площадь треугольника
можно вычислить через векторное
произведение
Координаты вектора
или
Векторное произведение вычислим через
определитель 3-го порядка, разложив его
по элементам первой строки:
Модуль векторного произведения
-
Объём треугольной пирамиды А1А2А3А4
можно рассматривать как одну шестую
часть объёма параллелепипеда, построенного
на векторах
,
и
как на рёбрах:
Смешанное произведение трёх векторов
равно
-
Уравнение плоскости
имеет вид
или для нашей задачи
Разложим определитель по элементам
первой строки:
-
Уравнения прямой
найдём в канонической форме, для этого
воспользуемся уравнением прямой,
проходящей через две заданные точки
и
:
,
-
Углом ψ между ребром
и гранью
будет острый угол между прямой
и её проекцией на плоскость
.
Для нахождения угла ψ воспользуемся
формулой
Канонические уравнения прямой
получим как:
Отсюда l=5; m=1;
n=-5, где l,
m, n –
координаты направляющего вектора прямой
:
;
Уравнение плоскости
было получено в пункте 5:
Отсюда А=5; В=7; С=-4, где А, В, С – координаты
нормального вектора плоскости
:
Тогда получаем
-
Уравнения высоты, опущенной из вершины
на грань
.
Канонические уравнения прямой, проходящей
через точку
,
имеют вид
,
где l, m, n
– координаты направляющего вектора
прямой.
Так как высота перпендикулярна плоскости
,
то из условия перпендикулярности прямой
и плоскости
координаты направляющего вектора
прямой, перпендикулярной плоскости
можно заменить координатами нормального
вектора плоскости l=A=5;
m=B=7; n=C=-4.
Окончательно получим
Выполним чертёж пирамиды как пересечения
плоскостей её граней:
Грань А1А2А4:
Грань А1А2А3:
Грань А1А3А4:
Грань А2А3А4:
28
Составить уравнение и построить линию,
каждая точка которой равноотстоит от
оси ординат и от окружности
РЕШЕНИЕ
В системе координат хОу строим ось
ординат х=0 и окружность
Пусть точка М(х; у) – произвольная точка
искомого геометрического места точек.
Опустим перпендикуляры на ось ординат
и на окружность.
Тогда расстояние от произвольной точки
М(х; у) до оси ординат
–
абсцисса точки М(х; у), а расстояние от
точки М(х; у) до окружности
.
Приравнивая эти расстояния и снимая
знак модуля, получаем
Получили уравнение параболы, строим
верхнюю часть окружности и параболы,
так как чертёж симметричный:
Соседние файлы в папке Приборостроителям
- #
- #
- #
- #
- #
- #
- #
- #
- #
Даны вершины А(х1,у1),
В(х2,у2), С(х3,у3) треугольника
АВС.
Требуется найти:
1) уравнение стороны АВ;
2) уравнение высоты СН и длину
этой высоты;
3) уравнение медианы АМ;
4) точку N пересечения медианы АМ и СН;
5) уравнение прямой, параллельной
стороне АВ и проходящей через вершину С;
6) внутренний угол при вершине А и внешний угол при вершине С.
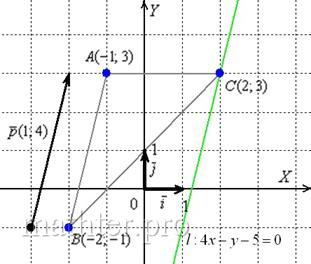
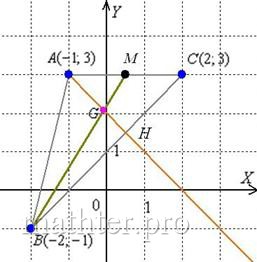
А(1;7), В(-3;-1), С(11;-3)
Решение
1) Уравнение
прямой АВ:
4(y-7)=8(x-1)
8x-4y+20=0
2x—y+5=0– общее уравнение прямой АВ
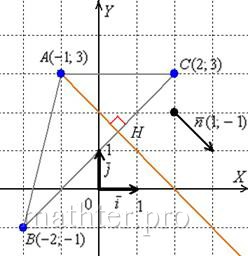
2) СНАВ =>
2x—y+5=0=> и
Уравнение высоты CH:
y+3= (x-11)
2у+6= -х+11
x+2y-5=0 – общее уравнение высоты CH.
Найдем длину высоты CH как
расстояние от точки С до прямой АВ, общее уравнение
которой Ax+By+C=0,
А=2, В=-1, С=5
CH=
CH=
1) Найдем
координаты точки М как середины отрезка ВС:
,
М()
Уравнение медианы АМ
3(y-7)= -9(x-1)
9x+3y-30=0
3х+y-10=0-
общее уравнение медианы АМ
2) Найдем
точку пересечения N медианы АМ и высоты CH:
N(3;1)
5) Так как прямая
параллельна АВ, то её угловой коэффициент равен . Найдем её уравнение по формуле:
y+3=2 (x-11)
2x—y-25=0 – общее уравнение прямой,
параллельной прямой АВ и проходящей через точку С.
3) Косинус
внутреннего угла при вершине А:
(-3-1;-1-7)=(-4;-8)
(11-1;-3-7)=(10;—10)
Косинус внешнего угла при вершине С:
(-10,10)
(-3—11;-1+3)=(-14;2)
Ответ:
1) 2x—y+5=0
2) x+2y-5=0, CH=
3) 3х+y-10=0
4) 2x—y-25=0
5) ,
Уравнение высоты треугольника
Длина сторон треугольника:
|AB| = 15
|AC| = 11.18
|BC| = 14.14
Расстояние d от точки M: d = 10
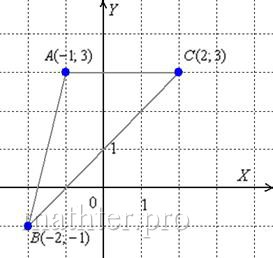
Даны координаты вершин треугольника: A(-5,2), B(7,-7), C(5,7).
2) Длина сторон треугольника
Расстояние d между точками M1(x1; y1) и M2(x2; y2) определяется по формуле:

Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями:
Уравнение прямой AB
Каноническое уравнение прямой: или
или y = -3/4x -7/4 или 4y + 3x +7 = 0
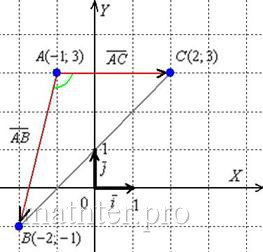
Уравнение прямой AC
Каноническое уравнение прямой: или
или y = 1/2x + 9/2 или 2y -x — 9 = 0
Уравнение прямой BC
Каноническое уравнение прямой: или
или y = -7x + 42 или y + 7x — 42 = 0
3) Угол между прямыми
Уравнение прямой AB:y = -3/4x -7/4
Уравнение прямой AC:y = 1/2x + 9/2
Угол φ между двумя прямыми, заданными уравнениями с угловыми коэффициентами y = k1x + b1 и y2 = k2x + b2, вычисляется по формуле:
Угловые коэффициенты данных прямых равны -3/4 и 1/2. Воспользуемся формулой, причем ее правую часть берем по модулю:
tg φ = 2
φ = arctg(2) = 63.440 или 1.107 рад.
9) Уравнение высоты через вершину C
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
y = 4/
3x + 1/3 или 3y -4x — 1 = 0
Данное уравнение можно найти и другим способом. Для этого найдем угловой коэффициент k1 прямой AB.
Уравнение AB: y = -3/4x -7/4, т.е. k1 = -3/4
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k1*k = -1.
Подставляя вместо k1 угловой коэффициент данной прямой, получим :
-3/4k = -1, откуда k = 4/3
Так как перпендикуляр проходит через точку C(5,7) и имеет k = 4/3,то будем искать его уравнение в виде: y-y0 = k(x-x0).
Подставляя x0 = 5, k = 4/3, y0 = 7 получим:
y-7 = 4/3(x-5)
или
y = 4/3x +
1/3 или 3y -4x — 1 = 0
Найдем точку пересечения с прямой AB:
Имеем систему из двух уравнений:
4y + 3x +7 = 0
3y -4x — 1 = 0
Из первого уравнения выражаем y и подставим во второе уравнение.
Получаем: x = -1; y = -1
D(-1;-1)
9) Длина высоты треугольника, проведенной из вершины C
Расстояние d от точки M1(x1;y1) до прямой Ax + By + С = 0 равно абсолютному значению величины:
Найдем расстояние между точкой C(5;7) и прямой AB (4y + 3x +7 = 0)
Длину высоты можно вычислить и по другой формуле, как расстояние между точкой C(5;7) и точкой D(-1;-1).
Расстояние между двумя точками выражается через координаты формулой:
5) уравнение окружности, для которой высота CD есть диаметр;
Уравнение окружности радиуса R с центром в точке E(a;b) имеет вид:
(x-a)2 + (y-b)2 = R2
Так как CD является диаметром искомой окружности, то ее центр Е есть середина отрезка CD.
Воспользовавшись формулами деления отрезка пополам, получим:
Следовательно, Е(2;3) и R = CD / 2 = 5. Использую формулу, получаем уравнение искомой окружности: (x-2)2 + (y-3)2 = 25
6) система линейных неравенств, определяющих треугольник АВС.
Уравнение прямой AB: y = -3/4x -7/4
Уравнение прямой AC : y = 1/2x + 9/2
Уравнение прямой BC : y = -7x + 42
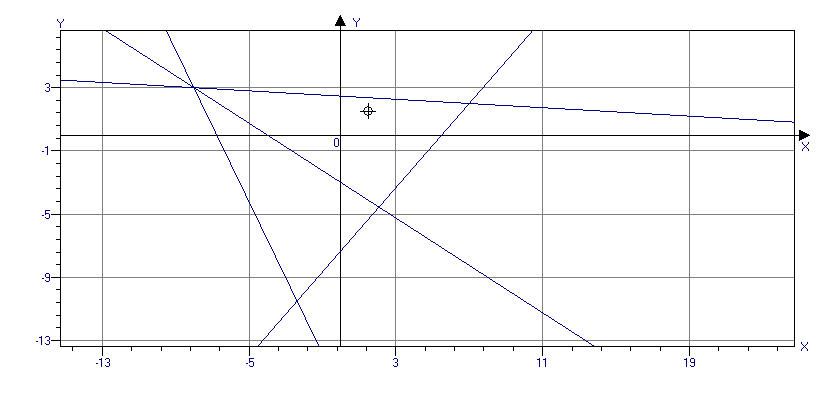
Система линейных неравенств:
y ≥ -3/4x -7/4 или y + 3/4x ≥ -7/4 или 3x + 4y ≥ -7
y ≤ 1/2x + 9/2 или y — 1/2
x ≤ 9/2 или — x + 2y ≤ 9
y ≤ -7x + 42 или y + 7x ≤ 42 или 7x + y ≤ 42
python — По заданным координатам вершин треугольника вычислить длины его медиан
Вопрос задан
2 года 1 месяц назад
Изменён
2 года 1 месяц назад
Просмотрен
321 раз
Есть код, но он не проходит такой тест:
- x1=3
- y1=0
- x2=0
- y2=4
- x3=0
- y3=0
- m1= 3.
605551275463989 (должно быть 4.27)
- m2= 4.0 (должно 2.5)
- m3= 4.272001872658765 (только это верно)
Вроде нужно В функцию
med передать не четыре переменных, а шесть. Добавить x3, y3.
В вызова функции тоже должно быть шесть переменных. Но сделать толково не получается
def med(x1,y1,x2,y2):
import math
med=math.sqrt((x1-(x2+x3)/2)**2+(y1-(y2+y3)/2)**2)
return med
x1=float(int(input("x1=" )))
y1=float(int(input("y1=" )))
x2=float(int(input("x2=" )))
y2=float(int(input("y2=" )))
x3=float(int(input("x3=" )))
y3=float(int(input("y3=" )))
print("m1=",med(x1, y1, x2, y2))
print("m2=",med(x2, y2, x3, y3))
print("m3=",med(x2, y2, x1, y1))
- python
А в чем проблема то?
В Википедии даётся формула
дальше ее всего лишь надо реализовать:
def med(p1, p2, p3):
a = (p1[0] - p2[0])**2 + (p1[1] - p2[1])**2
b = (p3[0] - p2[0])**2 + (p3[1] - p2[1])**2
c = (p3[0] - p1[0])**2 + (p3[1] - p1[1])**2
return math. sqrt(2*a + 2*b - c) / 2
sqrt(2*a + 2*b - c) / 2
и вызывать
med((x1, y1), (x2, y2), (x3, y3))
по хорошему предварительно надо проверить, что точки вообще образуют треугольник, но это вопрос уже из другой серии
1
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
Как найти треугольник на координатной плоскости
Все математические ресурсы среднего уровня SSAT
10 диагностических тестов
225 практических тестов
Вопрос дня
Карточки
Learn by Concept
SSAT Middle Level Math Help »
Геометрия »
Координатная геометрия »
Как найти треугольник на координатной плоскости
Найдите площадь указанного выше треугольника, учитывая, что его высота равна 12, а основание равно 10.
Возможные ответы:
Правильный ответ:
Объяснение:
Так как это прямоугольный треугольник, формула площади проста:
Таким образом, решение:
Сообщить об ошибке
Дан треугольник, указанный выше, равносторонний периметр в единицах, как показано в системе координат.
Возможные ответы:
Правильный ответ:
Пояснение:
Используя систему координат, можно увидеть, что длина основания треугольника равна 6 единицам. Поскольку это равносторонний треугольник, две другие стороны также должны иметь длину по 6 единиц каждая. Следовательно, периметр равен:
Сообщить об ошибке
Периметр показанного выше равнобедренного треугольника равен 22, а основание равно 6.
Найдите длины левой и правой сторон соответственно. Предположим, что никакая другая сторона не имеет длины 6,9.0005
Возможные ответы:
Правильный ответ:
Объяснение:
С периметром 22 и основанием 6 это означает, что две другие стороны должны в сумме: равно 6, две оставшиеся стороны должны быть равны друг другу.
Таким образом, чтобы быть равными друг другу, а также дать в сумме 16, каждая сторона должна иметь длину 8 единиц.
Сообщить об ошибке
Учитывая, что основание приведенного выше треугольника равно 5, а высота равна 6, каков периметр треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Во-первых, используйте теорему Пифагора, чтобы найти длину гипотенузы:
где и равны 5 и 6 соответственно, а является гипотенузой.
Таким образом,
Наконец, периметр равен сумме сторон треугольника или:
Сообщить об ошибке
Дан треугольник , где находится в точке и находится в точке , найдите площадь.
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти площадь этого треугольника, нам сначала нужно определить длины сторон AB и BC. Во-первых, точка B имеет ту же координату x, что и точка A, и ту же координату y, что и точка C. Таким образом, точка B должна находиться в точке (-2,-2).
Тогда длина стороны AB должна быть:
, а длина стороны BC:
Используя формулу площади,
, мы можем найти площадь BC (сторону и площадь основания) высота (сторона AB):
Сообщить об ошибке
Дан треугольник , где сторона и сторона , найдите периметр.
Возможные ответы:
Правильный ответ:
Объяснение:
Используйте теорему Пифагоре, чтобы найти длину боковой AC:
Затем периметр — это просто сумма всех трех сторон:
Сообщение о ошибке
Выше выше. треугольник имеет основание 6 и высоту 4. Найдите периметр.
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку ось Y делит основание пополам, мы можем разделить треугольник на два равных прямоугольных треугольника. Таким образом, основание прямоугольного треугольника вдвое меньше, чем у большего треугольника, или 3. Высота по-прежнему равна 4. Чтобы найти гипотенузу, воспользуйтесь теоремой Пифагора: основание, как указано в задаче, и каждую из двух других сторон (которые также являются гипотенузами прямоугольных треугольников).
Следовательно, периметр равен:
Сообщить об ошибке
Учитывая высоту единиц и основание единиц, найдите площадь треугольника, показанного выше.
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь любого треугольника рассчитывается по формуле:
Таким образом, площадь этого треугольника равна:
Сообщить об ошибке
Учитывая, что треугольник , найдите высоту треугольника.
Возможные ответы:
Правильный ответ:
Объяснение:
Используйте теорему Пифагора,
где это гипотенуза, это основание и это высота.
Перестановка для вычисления высоты, дает:
Сообщить об ошибке
Уведомление об авторских правах
Все математические ресурсы среднего уровня SSAT
10 диагностических тестов
225 практических тестов
Вопрос дня
Карточки
Учитесь по концепции
Онлайн-калькулятор: Площадь треугольника
Хотя у нас есть несколько калькуляторов для нахождения площади треугольника (см.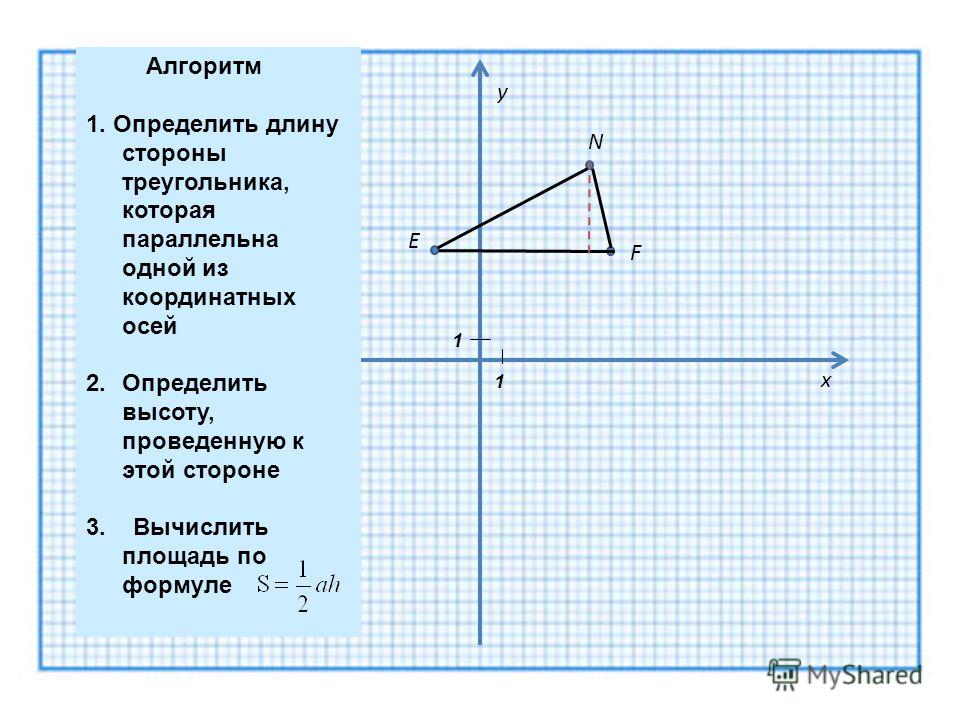
Поддерживаются следующие формулы:
- Формула умножения половины основания на высоту — если известно основание и высота треугольника
- Формула Герона — если известны все три стороны треугольника
- Формула сторона-угол-сторона — если известны две стороны и прилежащий угол
- Формула координат — если известны координаты трех вершин треугольника
- Формула равностороннего треугольника — формула равностороннего треугольника, являющаяся упрощенной формулой Герона
Вы можете найти все формулы с описанием под калькулятором.
Площадь треугольника
Найти площадь по основанию и высотедлины всех сторондве стороны и прилежащий уголкоординаты вершиныдлина стороны равностороннего треугольника
Первая вершина y
Вторая вершина x
Вторая вершина y
Третья вершина x
Третья вершина y
Длина стороны
Точность вычисления
Digits after the decimal point: 2
Half of base times height formula
Heron’s formula
Side angle side formula
Coordinates formula
Equilateral triangle formula
Area of the triangle
Half of base times формула высоты
Вы можете найти площадь треугольника из длины основания и длины соответствующей высоты.
где A площадь, a длина основания, h длина высоты.
Формула Герона
Вы можете найти площадь треугольника, если знаете длины всех сторон. Формула
где A площадь, a , b , c длины сторон, p периметр деленный на 2 (полупериметр).
Формула названа в честь Героя Александрийского, греческого инженера и математика, жившего в 10 — 70 г. н.э. Доказательство можно найти в его книге Метрика , написанная около 60 г. н.э.
Формула сторона-угол-сторона
Эта формула, также называемая SAS, позволяет найти площадь треугольника, если известны две стороны и угол при общей вершине (включенный угол). Формула
, где A — площадь, a и b — длины сторон, альфа — угол при общей вершине.
На самом деле, эта форма непосредственно следует из половины формулы умножения основания на высоту, потому что высота треугольника будет равна .

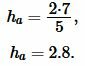
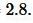
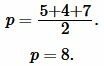
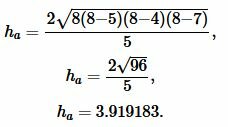
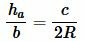















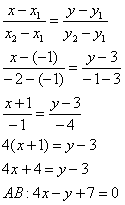
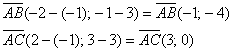
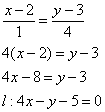
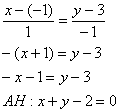
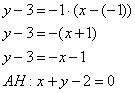
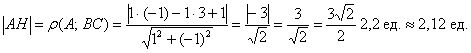
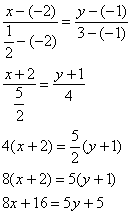
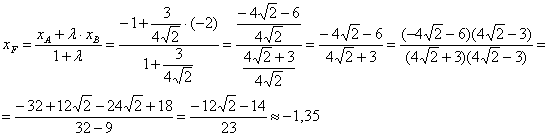
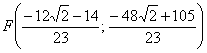
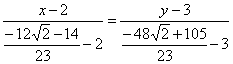
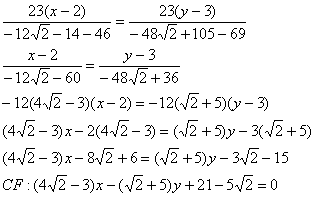
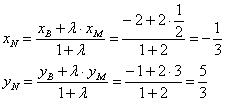
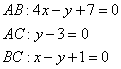
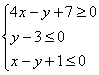
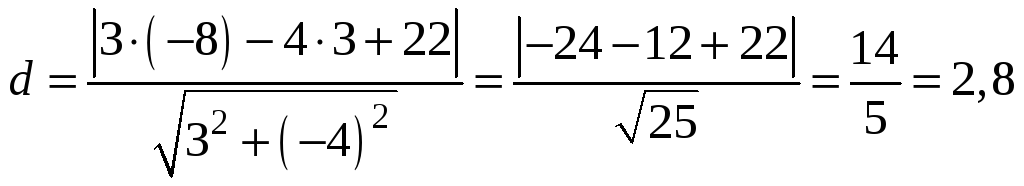
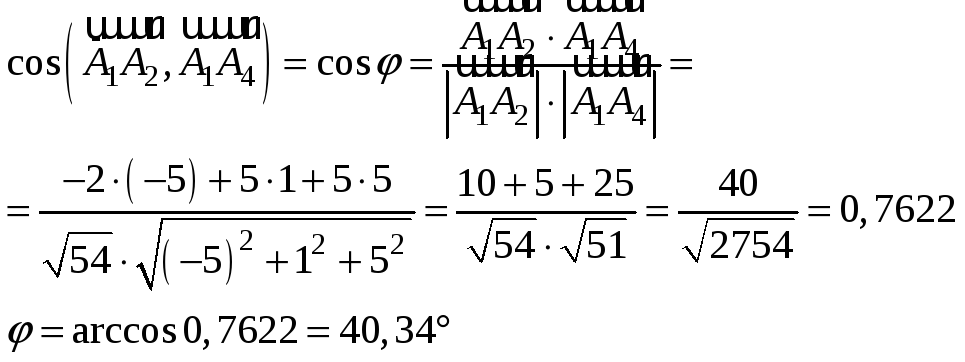
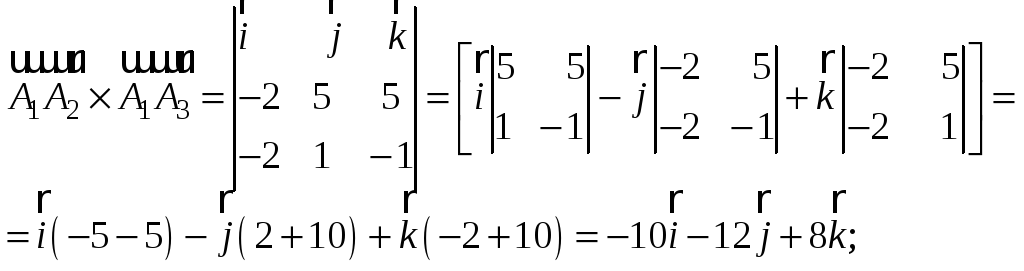


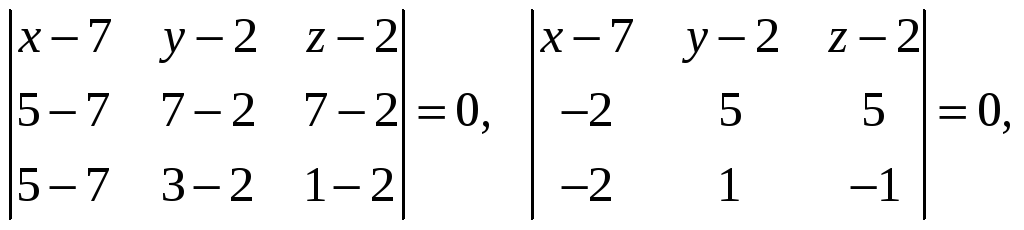
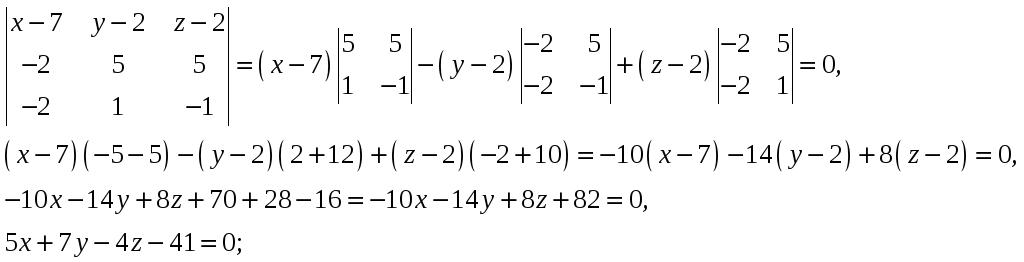

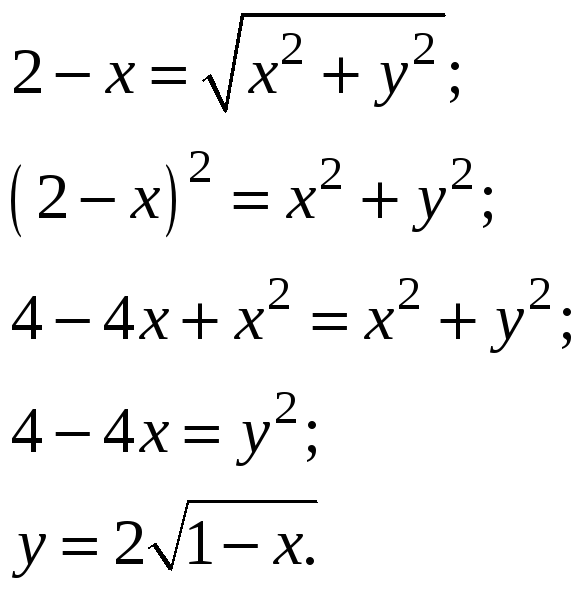





 605551275463989 (должно быть 4.27)
605551275463989 (должно быть 4.27) sqrt(2*a + 2*b - c) / 2
sqrt(2*a + 2*b - c) / 2

