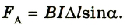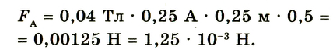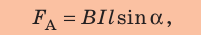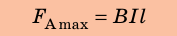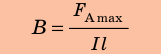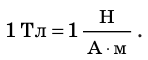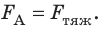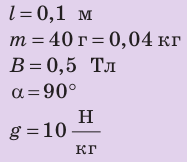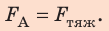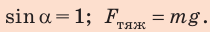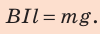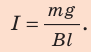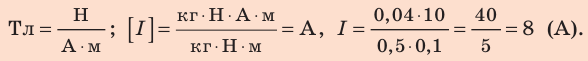Опыт
показывает, что проводники, по которым
текут электрические токи, взаимодействуют
друг с другом. Так, например, два тонких
прямолинейных параллельных проводника
притягиваются друг к другу, если
направления протекающих в них токов
совпадают, и отталкиваются, если
направления токов противоположны (рис.
2).
Рис.
2. Взаимодействие параллельных проводников
с током.
Определяемая
экспериментально сила взаимодействия
проводников, отнесенная к единице длины
проводника (т.е., действующая на 1м
проводника) вычисляется по формуле:
,
где
и
–
силы токов в проводниках,
– расстояние между ними в системе СИ,
— так называемая, магнитная постоянная
().
Связь
между электрической
и магнитной
постоянными
определяется соотношением:
где
=
3·108
м/с
– скорость света в вакууме.
На
основании эмпирической формулы для
установлена
единица
силы тока в системе СИ – Ампер (А).
Ампер
– сила такого неизменяющегося тока,
который, проходя по двум прямолинейным
проводникам бесконечной длины и ничтожно
малого кругового сечения, расположенным
в вакууме на расстоянии 1 м один от
другого, вызывает силу взаимодействия
между ними, равную 2·10-7
Н на 1 м длины.
Итак,
при протекании электрического тока по
проводнику в окружающем его пространстве
происходят какие-то изменения, что
заставляет проводники с током
взаимодействовать, а магнитную стрелку
вблизи проводника с током поворачиваться.
Таким образом, мы пришли к выводу, что
взаимодействие между магнитами,
проводником и током, между проводниками
с током осуществляется посредством
материальной среды, получившей название
магнитного
поля.
Из опыта Эрстеда следует, что магнитное
поле имеет направленный
характер,
поскольку угол поворота стрелки зависит
от величины и направления протекающего
тока. Это подтверждается также и опытами
по взаимодействию проводников с током.
1.3. Индукция магнитного поля
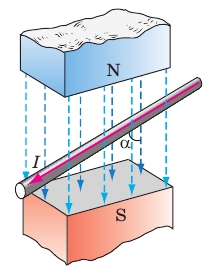
Рассмотрим
взаимодействие прямого проводника с
током с магнитным полем подковообразного
магнита. В зависимости от направления
тока проводник втягивается или
выталкивается из магнита (рис. 3).
Рис.
3. Взаимодействие прямого проводника с
током с магнитным полем
подковообразного
магнита.
Мы
пришли к заключению, что на проводник
с током, помещенный в магнитное поле,
действует сила. Причем эта сила зависит
от длины проводника и величины протекающего
по нему тока, а также от его ориентации
в пространстве. Можно найти такое
положение проводника в магнитном поле,
когда эта сила
будет
максимальной.
Это и позволяет ввести понятие силовой
характеристики магнитного поля.
Силовой
характеристикой магнитного поля является
физическая величина, определяемая в
данном случае как
,
Она
получила название индукции
магнитного поля.
Здесь
— максимальная сила, действующая на
проводник с током
в магнитном поле,—
длина проводника,—
сила тока в нем.
Единица
измерения вектора магнитной индукции
– тесла
.
1
Тл – индукция такого магнитного поля,
которое действует с силой 1 Н на каждый
метр длины прямолинейного проводника,
расположенного перпендикулярно
направлению поля, если по проводнику
течет ток 1
А:
1
Тл=1 Н/(А·м).
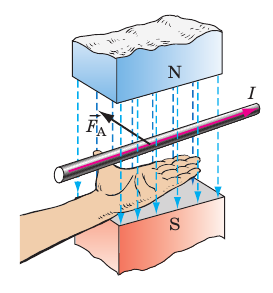
Индукция
магнитного поля – величина векторная.
Направление вектора
магнитной индукции
в нашем случае связано с направлениями
и
правилом
левой руки (рис.
4):
если
вытянутые пальцы направить по направлению
тока в проводнике,
а силовые линии
магнитного поля будут входить в ладонь,
то отогнутый большой палец укажет
направление силы
,
действующей
на проводник с током со стороны магнитного
поля.
Рис.
4. Правило левой руки
Численное
значение
вектора
можно
определить и через момент сил, действующих
на рамку с током в магнитном поле:
,
—
максимальный вращательный момент,
действующий на рамку
с током в магнитном
поле,
—
площадь рамки,—
сила тока в ней.
За
направление вектора
в
этом случае (рис. 5) принимается направление
нормали
к
плоскости витка, выбранное так, чтобы,
глядя навстречу
,
ток по витку протекал бы против часовой
стрелки.
Единица
измерения вектора магнитной индукции
– тесла
.
За
направление вектора
в
этом случае (рис. 5) принимается направление
нормали
к
плоскости витка, выбранное так, чтобы,
глядя навстречу
,
ток по витку протекал бы против часовой
стрелки.
Рис.
5. Ориентирующее действие магнитного
поля на рамку с током.
Силовые
линии магнитного поля (линии
индукции магнитного поля)
– это линии, в каждой точке которых
вектор
направлен
по касательной к ним.
Модуль
магнитной индукции пропорционален
густоте силовых линий, т.е. числу линий,
пересекающих поверхность единичной
площади, перпендикулярную этим линиям.
В
таблице 1 приведены картины силовых
линий для различных магнитных полей.
Так,
например, направление линий магнитной
индукции прямого провода с током
определяется
по правилу
буравчика (или «правого винта»):
если
направление поступательного движения
буравчика совпадает с направлением
тока в проводнике, то направление
вращения ручки буравчика совпадает с
направлением вектора магнитной индукции.
Таким
образом, силовые линии магнитного поля
бесконечного прямого проводника с током
представляют собой концентрические
окружности, лежащие в плоскости,
перпендикулярной проводнику. С увеличением
радиуса r
окружности
модуль вектора индукции магнитного
поля уменьшается.
Для
постоянного магнита за направление
силовых линий магнитного поля принято
направление от северного полюса магнита
N
к южному S.
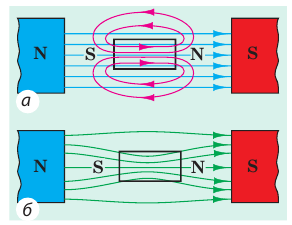
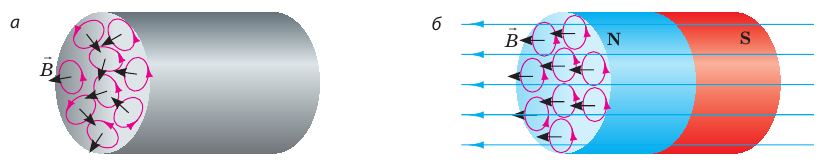
Картина
линий индукции магнитного поля для
соленоида поразительно похожа на картину
линий индукции магнитного поля для
постоянного магнита. Это навело на мысль
о том, что внутри магнита имеется много
маленьких контуров с током. Соленоид
тоже состоит из таких контуров – витков.
Отсюда и сходство магнитных полей.
Таблица
1
Силовые
линии магнитного поля
|
Источник |
Картина |
|
Прямой провод |
|
|
Кольцевой виток с |
|
Таблица
1 (продолжение)
-
Источник
магнитного поляКартина
силовых линийПостоянный
магнит
Катушка
с током
(соленоид)Магнитное
поле
Земли
Принцип
суперпозиции для вектора
:
результирующая индукция поля в некоторой
точке равна векторной сумме индукций
отдельных полей:
.
Важная
особенность линий магнитной индукции
– они не имеют ни начала, ни конца, т.е.
линии
магнитной индукции всегда замкнуты.
Этим магнитное поле отличается от
электростатического. Его силовые линии
имеют источники: они начинаются на
положительных зарядах и заканчиваются
на отрицательных.
Поля
с замкнутыми силовыми линиями называют
вихревыми.
Магнитное поле – вихревое поле.
Замкнутость
линий магнитной индукции – фундаментальное
свойство магнитного поля. Оно заключается
в том, что магнитных
зарядов в природе нет.
Источниками магнитного поля являются
движущиеся
электрические заряды.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
07.11.2018669.18 Кб6_7.doc
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Сила и закон Ампера:
Действие магнитного поля на проводник с током в 1820 г. исследовал экспериментально Андре Мари Ампер. Меняя форму проводников и их расположение в магнитном поле, Ампер сумел определить силу, действующую на отдельный участок проводника с током (элемент тока). В его честь ее назвали силой Ампера.
Исследуем с помощью динамометра модуль силы Ампера, действующей на участок прямолинейного проводника длиной I с током силой l со стороны магнитного поля индукцией В (рис. 150).
Согласно экспериментальным данным и результатам вычислений модуль силы:
- пропорционален длине проводника, находящегося в магнитном поле (F ~ l)
- пропорционален модулю индукции магнитного поля (F ~ В); пропорционален силе тока в проводнике (F ~ l);
- зависит от ориентации проводника в магнитном поле, т. е. от угла
Обобщая полученные результаты, запишем выражение для силы Ампера
в виде
где В — индукция магнитного поля, l — длина участка проводника, находящегося в магнитном поле, I — сила тока в проводнике, 
Закон Ампера
Это выражение называют законом Ампера:
- модуль силы, с которой магнитное поле действует на находящийся в нем прямолинейный проводник с током, равен произведению индукции В этого поля, силы тока I, длины участка проводника l и синуса угла между направлениями тока и индукции магнитного поля.
Сила Ампера 
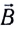
Правило левой руки
Ампера используют правило левой руки (рис. 151):
если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора индукции магнитного поля входила в ладонь, а четыре вытянутых пальца указывали направление тока, то отогнутый на 90° большой палец укажет направление силы Ампера.
Магнитное взаимодействие проводников с током используется для определения в СИ одной из основных единиц — единицы силы тока — ампера.
Один ампер есть сила постоянного тока, поддерживаемого в каждом из двух прямолинейных параллельных проводниках бесконечной длины и ничтожно малого кругового сечения, расположенных на расстоянии 1 м один от другого в вакууме, который вызывает между этими проводниками силу взаимодействия, равную 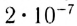
Магнитное поле
Обобщение учеными результатов теоретических и экспериментальных исследований различных взаимодействий в природе привело к выводу, что материя может существовать не только в форме вещества, по и в форме поля. Изучая физику в предыдущих классах, вы узнали о существовании электрического и магнитного полей, благодаря которым взаимодействуют наэлектризованные тела. Работы Дж. Максвелла, М. Фарадея и других ученых показали, что эти поля взаимосвязаны и фактически являются проявлениями более универсального электромагнитного поля. И только выбор системы отсчета определяет, что мы наблюдаем — электрическое или магнитное поле. Изучить все свойства электромагнитного поля довольно сложно. Поэтому в физике изучают постепенно отдельные проявления этого ноля. Одним из этапов изучения электромагнитного поля является изучение магнитного поля, которое проявляется в случае, когда заряженные частицы или тела в определенной системе отсчета движутся равномерно. В этом разделе рассматриваются не только условия, при которых магнитное поле наблюдается, но и физические величины, которые описывают его свойства, законы, по которым взаимодействуют магнитные поля и вещественные объекты. Знание этих законов позволяет производить важные для практики расчеты результатов взаимодействия магнитного поля с различными физическими телами.
Явления, которые мы называем магнитными, известны человечеству очень давно. Необычные свойства магнетита (разновидности железной руды) использовались в Древнем Китае, а потом и в других странах для изготовления компасов. Магнитам приписывали магические свойства, их действием объясняли непонятные явления природы, пробовали лечить болезни.
Систематизированные исследования магнитов провел английский физик У. Гильберт в XVI в. Он не только исследовал взаимодействие постоянных .магнитов, но и установил, что Земля является большим магнитом.
Учение о магнитах развивалось длительное время обособленно, как отдельная отрасль науки, пока ряд открытий и теоретических исследований в XIX в. не доказали его органическую связь с электричеством.
Одним из фундаментальных доказательств единства электрических и магнитных явлений является опыт Г.Х. Эрстеда, датского физика, который в 1820 г. заметил, что магнитная стрелка изменяет ориентацию вблизи проводника с током (рис. 2.1).
Pиc. 2.1. Опыт Эрстеде
Было вполне очевидно, что причиной изменения ориентации стрелки является электрический ток -направленное движение заряженных частиц в проводнике. C подробным описанием этого опыта вы встречались в 9-м классе.
Магнитное действие движущихся заряженных тел исследовал также американский физик Г. Роуланд в 1878 г. Основная часть его установки представляла собой эбонитовый диск 1, покрытый тонким слоем золота (рис. 2.2). Диск был насажен на вал и мог свободно вместе с ним вращаться между двумя стеклянными пластинами 2. Над эбонитовым диском были укреплены на тонкой нити две намагниченные стальные иголки 3, чувствительные к магнитному полю. Когда диску сообщили некоторый заряд и начали вращать, иголки повернулись на некоторый угол, что свидетельствовало о наличии магнитного поля. При увеличении скорости вращения иголки поворачивались на больший угол.
Рис. 22. Главная часть установки Роуланда по выявлению магнитного поля движущегося электрически заряженного диска
Опытами Г. Роуланда было подтверждено открытие Эрстеда о связи магнитного поля с движущимися электрически заряженными частицами или телами.
 |
Генри Роуланд (184β-1901) — американский физик; научные работы в области электродинамики, оптики, спектроскопии и теплоты. Он доказал, что заряженные тела, если они движутся, вызывают магнитное взаимодействие. |
Магнитные явления хотя и связаны с электрическими, но не идентичны им. Это подтверждают опыты.
Если взять два длинных параллельных проводника и присоединить к источнику тока, то заметим, что они взаимодействуют между собой (рис. 2.3) в зависимости от направления тока в них. При токах противоположных направлений проводники отталкиваются (рис. 2.3-а). Если токи одного направления, то проводники притягиваются друг к другу (рис. 2.3-б).
Pиc. 23. Магнитное взаимодействие проводников с током
Действие проводника с током на магнитную стрелку или другой проводник с током происходит при отсутствии непосредственного контакта между ними, благодаря наличию вокруг проводника магнитного поля.
Магнитное поле имеет свои особенности, которые выделяют его среди других полей:
- магнитное поле наблюдается всегда, когда есть движущиеся заряженные частицы или тела;
- магнитное поле действует только на движущиеся заряженные тела или частицы.
Другие свойства будут описаны далее.
Магнитная индукция
Наблюдения за магнитными взаимодействиями в лаборатории или в природе показывают, что действия магнитного поля па физические тела или проводники с током при равных условиях могут быть различными.
Интенсивность магнитного взаимодействия может быть различной.
Если для выявления магнитного поля Земли магнитную стрелку компаса приходится устанавливать на специальных опорах, которые существенно уменьшают силы трения, то действие электромагнита, в обмотках которого проходит электрический ток, будет заметным даже тогда, когда стрелка будет просто лежать на столе.
Различным будет и взаимодействие параллельных проводников с током. Сила взаимодействия этих проводников будет изменяться, если будет изменяться сила тока в них или расстояние между ними, — она будет увеличиваться при увеличении силы тока или при уменьшении расстояния.
Для всех таких случаев говорят о «сильном» или «слабом» поле. Аналогичные случаи рассматривались при изучении свойств электрического поля, при рассмотрении действия электрического поля на заряженные тела. Для количественной характеристики электрического поля введена напряженность электрического поля. Для магнитного же поля используется также силовая характеристика и соответствующая ей физическая величина магнитная индукция. Магнитная индукция является векторной величиной и обозначается буквой В. Поскольку для исследования магнитного поля длительное время пользовались магнитной стрелкой на острие, то магнитная индукция как характеристика магнитного поля была связана с действием магнитного поля па магнитную стрелку. Так, направление полюсов стрелки послужило базой для установления направления вектора магнитной индукции изучаемого поля. Условились, что за направление магнитной индукции принимается направление северного полюса стрелки.
Магнитная индукция — векторная величина, имеющая направление.
Исследуем с помощью магнитной стрелки магнитное поле проволочного витка с током.
Замкнув цепь, в которую включен виток, начнем обносить магнитную стрелку на острие вокруг витка. Заметим, что ориентация стрелки при этом будет меняться. В разных точках она будет иметь различную ориентацию. Наиболее ощутимым будет действие поля на стрелку в центре витка (рис. 2.4).
Puc. 2.4. Продольная ось магнитной стрелки, находящаяся в центре витка с током, перпендикулярна его плоскости
Таким образом, мы установили, что магнитная индукция витка или прямоугольной рамки будет иметь максимальное значение в центре.
Продольная ось магнитной стрелки плоскости витка. Аналогичное явление будет наблюдаться и тогда, когда возьмем прямоугольную рамку или моток провода произвольной формы.
В отличие от напряженности электрического поля магнитная индукция как векторная величина не совпадает по направлению с направлением силы, которая действует на проводник с током. Выясним, как направление вектора магнитной индукции зависит от направления тока в витке.
Магнитная индукция — это силовая характеристика поля. Она определяет силу, которая действует на проводник с током или на движущуюся частицу.
Отметив направление магнитной стрелки при определенном направлении тока в витке, изменим направление последнего на противоположное. Магнитная стрелка развернется на 1800, показывая, что направление магнитной индукции также изменилось. Таким образом, направление магнитной индукции витка с током зависит от направления тока и нем.
Чтобы каждый раз, когда нужно знать направление магнитной индукции, не проводить опыты со стрелкой, пользуются правилом правого винта (буравчика).
Это правило позволяет запомнить связь направления тока в витке с направлением магнитной индукции его поля. Для этого необходимо представить, как будет двигаться правый винт, приставленный перпендикулярно к плоскости витка, при вращении его по направлению тока в витке.
Если направление вращения правого винта, расположенного в центре витка с током, совпадает с направлением тока, то его поступательное движение показывает направление магнитной индукции (рис. 2.5).
Магнитное поле существует и вокруг прямого проводника с током. Для подтверждения этого магнитную стрелку будем обносить вокруг проводника, не изменяя расстояния (рис. 2.6).
|
Pиc. 2.5. Определение |
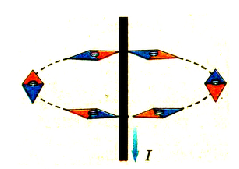 Pиc. 2.6. Исследование магнитного поля прямого проводника с током при помощи магнитной стрелки |
В разных точках ее ориентация будет различной, но ось стрелки всегда будет направлена по касательной к траектории движения.
Соответственно и магнитная индукция проводника с током будет иметь такое ясе направление.
При изменении направления тока в проводнике на противоположное стрелка развернется на 180° и покажет направление магнитной индукции, которое также будет противоположным к прежнему.
Таким образом, направление магнитной индукции прямого проводника зависит от направления тока в нем. Для облегчения его определения, как и в предыдущем случае, на основании анализа результатов эксперимента, сформулировано правило правого винта (рис. 2.7): если направление поступательного движения правого винта совпадает с направлением тока в проводнике, то направление его вращения показывает направление магнитной индукции.
Pиc. 2.7. Определение направления магнитной индукции поля прямого проводника с током при помощи правою винта (буравчика)
Для измерения магнитной индукции применяется специальная единица тесла (Тл). Эта единица названа в честь сербского ученого и изобретателя Николы Теслы.
 |
Никола Тесла (1856-1943) — родился в Сербии, изобретатель и физик. Известен благодаря своим изобретениям в области электротехники и электроники; работал инженером на предприятиях Венгрии, Франции, США. |
В практике используются долевые величины:
- 1 миллитесла = 1 мТл = 10-3 Тл,
- 1 микротесла 1 мкТл 10-6 Тл.
Значения магнитной индукции измеряют специальными приборами, которые называются магнитометрами или индикаторами магнитной индукции (рис. 2.8).
Pиc. 2.8. Лабораторный магнитометр для школьных опытов
Часто вместо прямых измерений пользуются формулами, которые позволяют рассчитать магнитную индукцию на основании параметров проводника. Таким примером может быть расчет модуля магнитной индукции прямого проводника с током. Экспериментально подтверждено, что магнитная индукция поля прямого проводника с током прямо пропорциональна силе тока в проводнике и обратно пропорциональна расстоянию от его оси:
Магнитная индукция прямого проводника с током пропорциональна силе тока в нем и обратно пропорциональна расстоянию от проводника до точки наблюдения.
Коэффициент пропорциональности в этой формуле зависит от выбора системы единиц измерений. В Международной системе единиц (СИ) он имеет значение
где μ0 — магнитная постоянная, ее числовое значение 1,256 × × 10-6 Н/А2.
Тогда окончательно для рассчетов модуля магнитной индукции поля прямого проводника с током имеем формулу:
где μ0 — магнитная постоянная; I — сила тока в проводнике: r — расстояние от проводника до данной точки поля.
Пример №1
Каково значение модуля магнитной индукции в точке поля, удаленной на 3 см от бесконечно длинного проводника, по которому проходит ток 6 А?
| Дано: r = 3 см, I = 6 А. |
Решение Магнитная индукция прямого проводника с током рассчитывается по формуле: 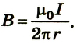 |
| В — ? |
Подставив значения физических величин, получим
Ответ: магнитная индукция поля прямого проводника с током равна 4 • 10-5 Тл.
Действие магнитного поля на проводник с током и сила Ампера
Поскольку вокруг проводников с током возникает магнитное поле, естественно предположить, что в магнитном поле на них действует сила.
На проводник с током в магнитном поле действует сила.
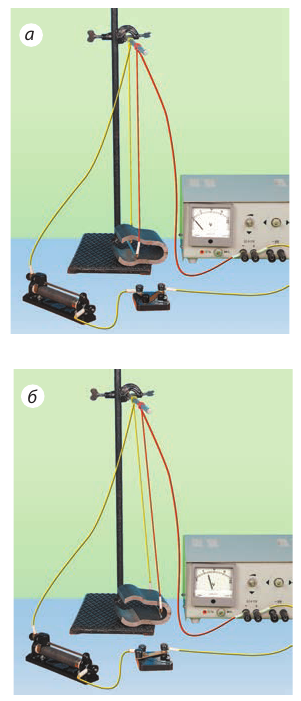
Проведем исследование с целью определения, от чего зависит модуль и направление этой силы. Для этого используем установку, в которой прямой проводник подвешен в магнитном поле постоянного магнита так, что его можно включать в электрическую цепь, силу тока в которой можно изменять при помощи реостата. Амперметр будет измерять силу тока в цепи.
Замкнув электрическую цепь, заметим, что проводник отклонится от положения равновесия, а динамометр покажет некоторое значение силы. Увеличим силу тока в проводнике в 2 раза и увидим, что сила, действующая на проводник, также увеличится в 2 раза. Любые другие изменения силы тока будут вызывать соответствующие изменения силы. Сопоставление результатов всех измерений позволяет сделать вывод, что сила F, которая действует на проводник с током, пропорциональна силе тока к нем:
F~I.
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Сила Ампера пропорциональна силе тока в проводнике.
Pиc. 2.9. Установка для изучения действия магнитного поля на проводник с током
Расположим еще один магнит рядом с первым. Длина проводника, находящегося в магнитном поле, увеличится приблизительно в 2 раза. Значение силы, действующей на проводник, в этом случае также увеличится в 2 раза. Таким образом, сила FΔ, действующая на проводник с током в магнитном поле, пропорциональна длине проводника Δl, который расположен в магнитном поле:
F~ΔI.
Сила Ампера пропорциональна длине активной части проводника.
Сила увеличится также тогда, когда применим другой, более мощный магнит с большей магнитной индукцией поля.
Это позволит сделать вывод, что сила Ампера FА зависит от магнитной индукции поля:
F~B.
Опыт позволяет убедиться и в том, что наибольшее значение силы Ампера будет тогда, когда угол между проводником и вектором магнитной индукции будет равен 90°. Если этот угол будет равен нулю, т. е. вектор магнитной индукции будет параллельным проводнику, то сила Ампера также будет равна нулю. Отсюда легко сделать вывод, что сила Ампера зависит от угла между вектором магнитной индукции и проводником.
Окончательно для расчетов имеем формулу
Направление силы Ампера определяется по правилу левой руки (рис. 2.10): если левую руку разместить так, чтобы линии магнитной индукции входили в ладонь, а четыре от. ставленных пальца показывали направление тока в проводнике, то отставленный под углом 90″ большой палец покажет направление силы, действующей на проводник с током в магнитном поле.
Pиc. 2.10. При помощи левой pуκu можно определить направление силы Ампера
Если левую руку разместить так. чтобы линии магнитной индукции входили в ладонь, а четыре отставленных пальца показывали направление тока в проводнике, то отставленный под углом 90° большой палец покажет направление силы, действующей на проводник с током в магнитном поле.
Взаимодействие проводников с током
Взаимодействие проводников с током объясняется действием силы Ампера (рис. 2.11).
Каждый из проводников имеет свое магнитное поле, которое действует на соседний проводник с током и способствует появлению силы Ампера. Так, проводник AA‘ по которому проходит ток I1, имеет магнитное поле, модуль индукции B1 которого, как указывалось ранее, равен
где r — расстояние от проводника до точки наблюдения.
Если проводник CC’ длиной Δl находитсяy на расстоянии r от проводника AA’ и в нем проходит ток I2, то на него действует сила Ампера FА, поскольку он находится в магнитном поле проводника AA’ . Значение этой силы равно
Поскольку проводники параллельны и угол между проводником CC’ и вектором магнитной индукции B1 равен 90°, то sinα = 1.
Подставим в последнюю формулу значение магнитной индукции поля проводника AA’:
Силу взаимодействия двух параллельных проводников с током можно определить, зная только расстояние между ними и силу тока в них.
Как и при любом взаимодействии, такая сила, согласно третьему закону Ньютона, действует на каждый из проводников. Только направления их противоположны.
Таким образом, два параллельных проводника нзнимодей-ствуют между собой благодаря магнитным полям, которые образуются вокруг проводников, по которым проходит электрический ток.
Пример №2
Определить модуль силы Ампера, которая действует на проводник с током длиной 25 см в магнитном поле с индукцией 0,04 Тл, если между вектором магнитной индукции и направлением тока угол 30° сила тока в проводнике 0,25 А.
|
Дано: |
Решение Подставим значения всех величин: |
| FA— ? |
Ответ: модуль силы равен 1,25 • 10-3 Н.
Использование действия силы Ампера
Силу Ампера применяют для преобразования энергии электрического тока в механическую энергию проводника. Такое превращение происходит во многих электротехнических устройствах. Рассмотрим некоторые из них.
Eлектроиэмеритальные приборы магнитоэлектрической системы
Электроизмерительный прибор магнитоэлектрической системы состоит из постоянного магнита и проволочной рамки, расположенной между его полюсами (рис. 2.12). Полюса магнита имеют специальные насадки, создающие однородное магнитное поле, в котором вращение рамки не приводит к изменению угла между магнитной индукцией и проводниками рамки. Этот угол всегда равен 90°.
Pиc. 2.12. Устройство электроизмерительного прибора магнитоэлектрической системы
C рамкой соединены две спиральные пружины, которые подводят к рамке электрический ток. Во время прохождения электрического тока по витком рамки возникает сила Ампера, пропорциональная силе тока в рамке. Чем больше сила действует на витки рамки, тем больше закручиваются спиральные пружины, которых возникает сила упругости. Когда сила Ампера и сила упругости станут равными, вращение рамки прекратится.
Стрелка, прикрепленная к рамке, показывает угол поворота рамки. Этот угол пропорционален силе тока в рамке.
Электрический двигатель постоянного тока
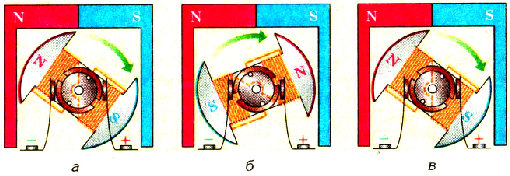
Электрический двигатель применяют для преобразования энергии электрического тока в механическую энергию вращения вала двигателя. Принцип его действия подобен принципу действия электроизмерительного прибора магнитоэлектрической системы, описанного выше. Только в его конструкции отсутствует пружина, поэтому рамка может поворачиваться на любой угол. Электрический ток к рамке, размещенной на валу и имеющей стальной сердечник, подается через специальные скользящие контакты-щетки (рис. 2.13).
Рис. 213. Устройство двигателя постоянного тока
При замыкании цепи питания двигателя ток проходит по рамке и она взаимодействует с магнитным полем постоянного магнита или электромагнита и поворачивается до тех пор, пока ее плоскость не станет параллельной вектору магнит ной индукции. Чтобы она могла нужно сменить направление силы тока в ней, вследствие чего поменяет направлению сила Ампера, действующая на рамку с током в магнитном поле. В двигателе этот процесс осуществляется с помощью двух неподвижных графитометаллических щеток и двух полуколец на валу, к которым подведены концы рамки.
На рисунке 2.14-а показан момент, когда ток в якоре такого направления, что его полюса отталкиваются от одноименных полюсов статора. После поворачивания на некоторый угол якорь окажется в положении, когда разноименные полюса притягиваются (рис 2.14-6). Вследствие инерции якорь проходит это положение равновесия, а благодаря кольцам, которых касаются токоподводящие щетки (рис. 2.14-в), направление тока в якоре изменяется па противоположное и вращение якоря продолжается (см. рис. 2.14-а).
Pиc. 2.14 Схемы, которые объясняют действие коллекторного электродвигателя постоянного тока
В промышленных образцах электродвигателей постоянного тока ротор имеет несколько рамок-обмоток. Поэтому и количество пар скользящих контактов в них больше: оно согласуется с количеством обмоток. В целом такое устройство называют коллектором. В новейших моделях двигателей постоянного тока роль коллектора выполняет специальное устройство с электронными приборами.
Таким образом, действие силы Ампера нашло применение в различных технических устройствах: электроизмерительных приборах, электрических двигателях и т. п.
Сила ампера
Вы узнали, что магнитное поле действует на проводник с током с некоторой силой. А из курса физики 8 класса помните, что сила — это векторная физическая величина, поэтому, чтобы полностью определить силу, нужно уметь рассчитывать ее значение и определять направление. От чего зависит значение силы, с которой магнитное поле действует на проводник с током, как направлена эта сила и почему ее называют силой Ампера, вы узнаете из данного параграфа.
Характеристика силы действующей на проводник с током
Между полюсами подковообразного постоянного магнита подвесим на тонких и гибких проводах прямой алюминиевый проводник (рис. 4.1, а). Если через проводник пропустить ток, проводник отклонится от положения равновесия (рис. 4.1, б). Причина такого отклонения — сила, действующая на проводник с током со стороны магнитного поля. Доказал наличие этой силы и выяснил, от чего зависят ее значение и направление, А. Ампер. Именно потому эту силу называют силой Ампера.
Рис. 4.1. Опыт, демонстрирующий действие магнитного поля на алюминиевый проводник: при отсутствии тока магнитное поле на проводник не действует (а); если в проводнике течет ток, на проводник действует магнитное поле и проводник отклоняется (б)
Сила Ампера — это сила, с которой магнитное поле действует на проводник с током.
Сила Ампера прямо пропорциональна силе тока в проводнике и длине активной части проводника (то есть части, расположенной в магнитном поле). Сила Ампера увеличивается с увеличением индукции магнитного поля и зависит от того, под каким углом к линиям магнитной индукции расположен проводник.
Значение силы Ампера 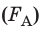
где 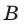
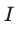
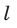
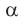
Обратите внимание! Магнитное поле не будет действовать на проводник с током 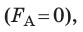
Рис. 4.2. Угол 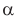
Чтобы определить направление силы Ампера, используют правило левой руки:
Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец укажет направление силы Ампера (рис. 4.3).
Рис. 4.3. Определение направления силы Ампера по правилу левой руки
Формула для определения модуля магнитной индукции
Если проводник расположен перпендикулярно линиям магнитной индукции 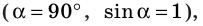
Отсюда получаем формулу для определения модуля магнитной индукции:
Обратите внимание! Значение магнитной индукции не зависит ни от силы тока в проводнике, ни от длины проводника, а зависит только от свойств магнитного поля.
Например, если уменьшить силу тока в проводнике, то уменьшится и сила Ампера, с которой магнитное поле действует на проводник, а вот значение магнитной индукции останется неизменным.
В СИ единица магнитной индукции — тесла (Тл), единица силы — ньютон (Н), силы тока — ампер (А), длины — метр (м), поэтому:
1 Тл — это индукция такого однородного магнитного поля, которое действует с максимальной силой 1 Н на проводник длиной 1 м, в котором течет ток силой 1 А.
- Заказать решение задач по физике
Пример №3
Докажите, что два параллельных проводника, в которых текут токи одного направления, притягиваются.
Анализ физической проблемы. Около любого проводника с током существует магнитное поле, следовательно, каждый из двух проводников находится в магнитном поле другого. На первый проводник действует сила Ампера со стороны магнитного поля, созданного током во втором проводнике, и наоборот. Определив по правилу левой руки направления этих сил, выясним, как будут вести себя проводники.
Решение
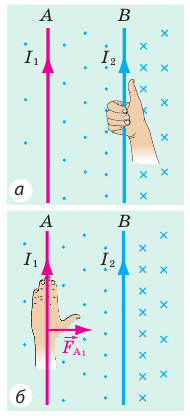
Решая задачу, выполним пояснительные рисунки: изобразим проводники А и В, покажем направления тока в них и т. д.
Выясним направление силы Ампера, которая действует на проводник А, находящийся в магнитном поле проводника В.
- С помощью правила буравчика найдем направление линий магнитной индукции магнитного поля, созданного проводником В (рис. 1, а). Выясняется, что вблизи проводника А магнитные линии направлены к нам (обозначено «•»).
- Воспользовавшись правилом левой руки, определим направление силы Ампера, действующей на проводник А со стороны магнитного поля проводника В (рис. 1, б).
Рис. 1
3. Приходим к выводу: проводник А притягивается к проводнику В.
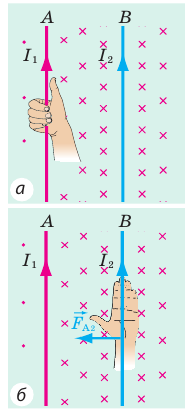
Теперь выясним направление силы Ампера, которая действует на проводник В, находящийся в магнитном поле проводника А.
1) Определим направление линий магнитной индукции магнитного поля, созданного проводником А (рис. 2, а). Выясняется, что вблизи проводника В магнитные линии направлены от нас (обозначено
2) Определим направление силы Ампера, действующей на проводник В (рис. 2, б).
Рис. 2
3) Приходим к выводу: проводник В притягивается к проводнику А.
Ответ: два параллельных проводника, в которых текут токи одного направления, притягиваются.
Пример №4
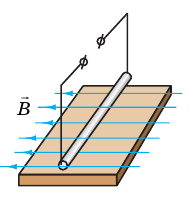
Прямой проводник (стержень) длиной 0,1 м и массой 40 г находится в горизонтальном однородном магнитном поле индукцией 0,5 Тл. Стержень расположен перпендикулярно магнитным линиям поля (рис. 3).
Рис. 3
Ток какой силы и в каком направлении следует пропустить по стержню, чтобы стержень не давил на опору (завис в магнитном поле)?
Анализ физической проблемы. Стержень не будет давить на опору, если сила Ампера уравновесит силу тяжести. Это произойдет при условиях: 1) сила Ампера будет направлена противоположно силе тяжести (то есть вертикально вверх); 2) значение силы Ампера будет равно значению силы тяжести:
Дано:
Найти:
Поиск математической модели, решение
1. Определим направление тока. Для этого расположим левую руку так, чтобы линии магнитного поля входили в ладонь, а отогнутый на 90° большой палец был направлен вертикально вверх. Четыре вытянутых пальца укажут направление от нас. Следовательно, ток в проводнике нужно направить от нас.
2. Учитываем, что
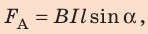
Следовательно,
Из последнего выражения найдем силу тока:
Проверим единицу, найдем значение искомой величины.
Вспомним:
Ответ: 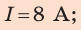
Подводим итоги:
Силу, с которой магнитное поле действует на проводник с током, называют силой Ампера. Значение силы Ампера находят по формуле: 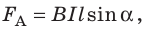
Направление силы Ампера определяют по правилу левой руки: если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец укажет направление силы Ампера.
Магнитные свойства веществ и гипотеза Ампера
Наверное, каждый из вас видел магниты и даже исследовал их свойства. Если поднести магнит к кучке мелких предметов, некоторые из них (гвоздики, кнопки, скрепки) притянутся к магниту, а некоторые (кусочки мела, медные и алюминиевые монетки, комочки земли) никак не отреагируют. Почему так? Действительно ли магнитное поле не оказывает никакого влияния на некоторые вещества? Именно об этом пойдет речь в параграфе.
Действия электрического и магнитного полей на вещество
Изучая в 8 классе электрические явления, вы узнали, что под влиянием внешнего электрического поля происходит перераспределение электрических зарядов внутри незаряженного тела (рис. 5.1). В результате в теле образуется собственное электрическое поле, направленное противоположно внешнему, и именно поэтому электрическое поле в веществе всегда ослабляется.
Рис. 5.1. В результате действия электрического поля отрицательно заряженной палочки ближняя к ней часть проводящей сферы приобретает положительный заряд
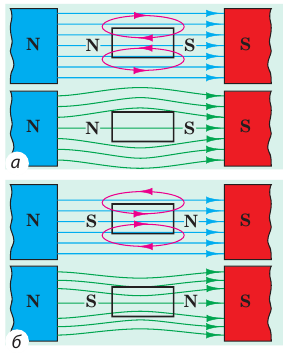
Вещество изменяет и магнитное поле. Есть вещества, которые (как в случае с электрическим полем) ослабляют магнитное поле внутри себя. Такие вещества называют диамагнетиками. Многие вещества, наоборот, усиливают магнитное поле — это парамагнетики и ферромагнетики.
Дело в том, что любое вещество, помещенное в магнитное поле, намагничивается, то есть создает собственное магнитное поле, магнитная индукция которого разная для разных веществ.
Слабомагнитные вещества
Вещества, которые намагничиваются, создавая слабое магнитное поле, магнитная индукция которого намного меньше магнитной индукции внешнего магнитного поля (то есть поля, вызвавшего намагничивание), называют слабомагнитными веществами. К таким веществам относятся диамагнетики и парамагнетики.
Диамагнетики (от греч. dia — расхождение) намагничиваются, создавая слабое магнитное поле, направленное противоположно внешнему магнитному полю (рис. 5.2, а). Именно поэтому диамагнетики незначительно ослабляют внешнее магнитное поле: магнитная индукция магнитного поля внутри диамагнетика 
Рис. 5.2. Образцы из диамагнетика (а) и парамагнетика (б) во внешнем магнитном поле: красные линии — линии магнитного поля, созданного образцом; синие — магнитные линии внешнего магнитного поля; зеленые — линии результирующего магнитного поля
Если диамагнетик поместить в магнитное поле, он будет выталкиваться из него (рис. 5.3).
Рис. 5.3. Пламя свечи выталкивается из магнитного поля, так как продукты сгорания — диамагнитные частицы
К диамагнетикам относятся инертные газы (гелий, неон и др.), многие металлы (золото, медь, ртуть, серебро и др.), молекулярный азот, вода и т. д. Тело человека — диамагнетик, так как оно в среднем на 78 % состоит из воды.
Парамагнетики (от греч. para — рядом) намагничиваются, создавая слабое магнитное поле, направленное в ту же сторону, что и внешнее магнитное поле (рис. 5.2, б). Парамагнетики незначительно усиливают внешнее поле: магнитная индукция магнитного поля внутри парамагнетика 
К парамагнетикам относятся кислород, платина, алюминий, щелочные и щелочноземельные металлы и другие вещества. Если парамагнитное вещество поместить в магнитное поле, то оно будет втягиваться в это поле.
Ферромагнетики
Если слабомагнитные вещества извлечь из магнитного поля, их намагниченность сразу исчезнет. Иначе происходит с сильномагнитными веществами — ферромагнетиками.
Ферромагнетики (от лат. ferrum — железо) — вещества или материалы, которые остаются намагниченными и при отсутствии внешнего магнитного поля.
Ферромагнетики намагничиваются, создавая сильное магнитное поле, направленное в ту же сторону, что и внешнее магнитное поле (рис. 5.4, 5.5, а). Если изготовленное из ферромагнетика тело поместить в магнитное поле, оно будет втягиваться в него (рис. 5.5, б).
Рис. 5.4. Железный гвоздь намагничивается в магнитном поле так, что конец гвоздя, расположенный вблизи северного полюса магнита, становится южным полюсом, поэтому гвоздь притягивается к магниту
Рис. 5.5. Ферромагнетики создают сильное магнитное поле, направленное в ту же сторону, что и внешнее магнитное поле (а); линии магнитной индукции как будто втягиваются в ферромагнитный образец (б)
К ферромагнетикам относится небольшая группа веществ: железо, никель, кобальт, редкоземельные вещества и ряд сплавов. Ферромагнетики значительно усиливают внешнее магнитное поле: магнитная индукция магнитного поля внутри ферромагнетиков 
Так, кобальт усиливает магнитное поле в 175 раз, никель — в 1120 раз, а трансформаторная сталь (на 96-98 % состоит из железа) — в 8000 раз.
Ферромагнитные материалы условно делят на два типа. Материалы, которые после прекращения действия внешнего магнитного поля остаются намагниченными длительное время, называют магнитожесткими ферромагнетиками. Их применяют для изготовления постоянных магнитов. Ферромагнитные материалы, которые легко намагничиваются и быстро размагничиваются, называют магнитомягкими ферромагнетиками. Их применяют для изготовления сердечников электромагнитов, двигателей, трансформаторов, то есть устройств, которые во время работы постоянно перемагничиваются (о строении и принципе действия таких устройств вы узнаете позже).
Обратите внимание! При достижении температуры Кюри (см. таблицу) ферромагнитные свойства магнитомягких и магнитожестких материалов исчезают — материалы становятся парамагнетиками.
Температура Кюри для некоторых ферромагнетиков
| Вещество (или материал) | Температура,°С |
| Гадолиний | +19 |
| Железо | +770 |
| Кобальт | +1127 |
| Неодимовый магнит NdFeB | +320 |
| Никель | +354 |
Гипотеза Ампера
Наблюдая действие проводника с током на магнитную стрелку (см. рис. 1.1) и выяснив, что катушки с током ведут себя как постоянные магниты (см. рис. 1.3), А. Ампер выдвинул гипотезу о магнитных свойствах веществ. Ампер предположил, что внутри веществ существует огромное количество незатухающих малых круговых токов и каждый из них, как маленькая катушка, является магнитиком. Постоянный магнит состоит из множества таких элементарных магнитиков, ориентированных в определенном направлении.
Механизм намагничивания веществ Ампер объяснял так. Если тело не намагничено, круговые токи ориентированы беспорядочно (рис. 5.7, а). Внешнее магнитное поле пытается сориентировать эти токи так, чтобы направление магнитного поля каждого тока совпадало с направлением внешнего
Рис. 5.7. Механизм намагничивания тел согласно гипотезе Ампера: а — круговые токи ориентированы беспорядочно, тело не намагничено; б — круговые токи ориентированы в определенном направлении, тело намагничено
магнитного поля (рис. 5.7, б). У некоторых веществ такая ориентация токов (намагничивание) остается и после прекращения действия внешнего магнитного поля. Таким образом, все магнитные явления Ампер объяснял взаимодействием движущихся заряженных частиц.
Гипотеза Ампера послужила толчком к созданию теории магнетизма. На основе этой гипотезы были объяснены известные свойства ферромагнетиков, однако она не могла объяснить природу диа- и парамагнетизма, а также то, почему только небольшое количество веществ имеет ферромагнитные свойства. Современная теория магнетизма основана на законах квантовой механики и теории относительности А. Эйнштейна.
Подводим итоги:
Любое вещество, помещенное в магнитное поле, намагничивается, то есть создает собственное магнитное поле.
| Диамагнетики | Парамагнетики | Ферромагнетики |
| Намагничиваются, создавая слабое магнитное поле, направленное противоположно внешнему магнитному полю | Намагничиваются, создавая слабое магнитное поле, направленное в сторону внешнего магнитного поля | Намагничиваются, создавая сильное магнитное поле, направленное в сторону внешнего магнитного поля; остаются намагниченными после прекращения действия внешнего магнитного поля |
| Незначительно ослабляют внешнее магнитное поле, выталкиваются из него | Незначительно усиливают внешнее магнитное поле, втягиваются в него | Усиливают внешнее магнитное поле в сотни и тысячи раз, втягиваются в него |
| Инертные газы, медь, золото, ртуть, серебро, азот, вода и др. Кислород, платина, алюминий, щелочные металлы и др. | Кислород, платина, алюминий, щелочные металлы и др. | Железо, никель, кобальт, редкоземельные вещества (например, неодим), ряд сплавов |
- Закон взаимодействия прямолинейных параллельных проводников с током
- Сила Лоренца
- Правило Буравчика в физике
- Шунт и добавочное сопротивление
- Работа по перемещению заряда в электростатическом поле
- Закон Ома для однородного участка электрической цепи
- Закон Ома для полной цепи
- Закон Ома для цепи переменного тока с последовательным соединением сопротивлений
Ток в двух параллельных проводниках
Два проводника с током взаимодействуют друг с другом, поскольку каждый из них находится в магнитном поле другого.
Ток в двух параллельных проводниках
Если направления токов одинаковы, то параллельные проводники притягиваются, если же направления токов противоположны — отталкиваются.
Если
| F | сила, действующая между параллельными проводниками, | Ньютон |
|---|---|---|
| μа = μ0μ | абсолютная магнитная проницаемость, | |
| μ0 | магнитная постоянная, | 1.257 · 10-6 Гн/м |
| μ | относительная магнитная проницаемость | |
| I1 | сила тока в первом проводнике, | Ампер |
| I2 | сила тока во втором проводнике, | Ампер |
| l | длина проводников, | метр |
| r | расстояние между проводниками, | метр |
то на второй проводник, находящийся в поле первого проводника, действует сила
[ F = B_{1} I_{1} l_{1} ]
где
[ В_{1} = H_{1} ]
Поскольку напряженность магнитного поля $Н_{1}$ на расстоянии r от проводника дается выражением
[ Н_{1}= frac{I_{1}}{2πr} ]
получаем следующую формулу для силы, действующей между проводниками:
[ F = frac{μ_{a} I_{1} I_{2} l}{2πr} ]
Вычислить, найти силу взаимодействия двух параллельных проводников с током
Ток в двух параллельных проводниках |
стр. 668 |
|---|
6.5. Взаимодействие двух проводников с током
Применим закон Ампера для вычисления силы взаимодействия двух длинных прямолинейных проводников с токами I1 и I2, находящихся на расстоянии d друг от друга (рис. 6.26).
Рис. 6.26. Силовое взаимодействие прямолинейных токов:
1 — параллельные токи; 2 — антипараллельные токи
Проводник с током I1 создает кольцевое магнитное поле, величина которого в месте нахождения второго проводника равна
Это поле направлено «от нас» ортогонально плоскости рисунка. Элемент второго проводника 
Подставляя (6.23) в (6.24), получим
При параллельных токах сила F21 направлена к первому проводнику (притяжение), при антипараллельных — в обратную сторону (отталкивание).
Аналогично на элемент 

Итак, сила взаимодействия двух прямолинейных бесконечно длинных параллельных проводников, рассчитанная на элемент длины 
На рис. 6.27 представлен опыт, демонстрирующий притяжение параллельных токов и отталкивание антипараллельных. Для этого используются две алюминиевые ленты, подвешенные вертикально рядом друг с другом в слабо натянутом состоянии. При пропускании через них параллельных постоянных токов силой около 10 А ленты притягиваются. а при изменении направления одного из токов на противоположное — отталкиваются.
Рис. 6.27. Силовое взаимодействие длинных прямолинейных проводников с током
На основании формулы (6.25) устанавливается единица силы тока — ампер, являющаяся одной из основных единиц в СИ.
Ампер — это сила неизменяюшегося тока, который, протекая по двум длинным параллельным проводникам, расположенным в вакууме на расстоянии 1 м, вызывает между ними силу взаимодействия 2×10 –7 Н на каждый метр длины провода.
Пример. По двум тонким проводам, изогнутым в виде одинаковых колец радиусом R = 10 см, текут одинаковые токи I = 10 А в каждом. Плоскости колец параллельны, а центры лежат на ортогональной к ним прямой. Расстояние между центрами равно d = 1 мм. Найти силы взаимодействия колец.
Решение. В этой задаче не должно смущать, что мы знаем лишь закон взаимодействия длинных прямолинейных проводников. Поскольку расстояние между кольцами много меньше их радиуса, взаимодействующие элементы колец «не замечают» их кривизны. Поэтому сила взаимодействия дается выражением (6.25), куда вместо 

Объясняем закон Ампера простым языком
Проводник, по которому течёт электрический ток, взаимодействует с существующими магнитными полями. На этом основана работа многих электротехнических устройств. Закон Ампера позволяет рассчитать такие взаимодействия. Он стал основой многих открытий в физике и часто применяется в современной технике. А имя Андре-Мари Ампера увековечено наряду с именами других 72 величайших ученых в списке, помещенном на первом этаже Эйфелевой башни.
Общее представление об электромагнитном поле
Длительное время представления об электрическом и магнитном поле не связывались между собой. Практические эксперименты подтверждали, что каждое из них имеет свои особенные свойства. Исследования Фарадея и Максвелла показали, что существует электромагнитное поле, которое может проявлять себя как электрическое или магнитное. Его можно описать с мощью вектора напряжённости. Если знать величину и направление данного вектора, то можно рассчитать силу воздействия.
Первым из учёных, кто обратил внимание на взаимное влияние магнитного поля и тока был известный учёный Х. К. Эрстед. Он исследовал влияние проводника с текущим по нему током на положение стрелки компаса. После этого учёные стали систематически изучать различные варианты взаимодействия.
Ампер появился на свет в 1775 году в Лионе. С детства он проявлял страсть к математике. Будучи подростком, изучал труды Эйлера и Лагранжа. Профессором математики Ампер стал в 1809 году, а в 1814 году был избран в академию наук. Хотя он преимущественно занимался математикой, его интересовала физика и некоторые другие науки.
Ампер был не первым человеком, который проявил интерес к связи магнитных и электрических полей, однако он впервые постарался найти точное математическое описание происходящих процессов. Им был не только установлен факт взаимодействия между электрическими токами, но и сформулирован закон данного явления.
Ампер доказал, что проводники начинают взаимодействовать, если по каждому из них протекает ток. В этом случае между ними возникают силы отталкивания или притягивания. В 1826 году Ампер впервые опубликовал результаты своего исследования, с помощью которого он изучал взаимодействие параллельных токов.
На рисунке ниже представлена схема одного из экспериментов Ампера, с помощью которого измеряется сила, действующая на проводник с током в магнитном поле. Стрелка красного цвета на рисунке показывает направление тока.
Основываясь на экспериментах, учёный сделал предположение, которое впоследствии получило название «гипотеза Ампера». Понимая, как влияет ток на магнитное поле, он сумел доказать, что вещество состоит из совокупности чрезвычайно маленьких круговых токов. Каждый из них порождает очень слабое магнитное поле. Поскольку все эти токи ориентированы хаотично, то внешне магнитное поле практически не проявляется. Однако в магнитах все круговые токи одинаково направлены и их воздействие складывается. Этим объясняются их особые свойства и практическое использование.
Ампер, используя свой закон, также объяснил эффект намагничивания. Согласно ему, у некоторых веществ под воздействием магнитного поля происходит упорядочивание круговых токов, и они постепенно ориентируются в одну сторону.
Эта гипотеза стала одним из источников теории магнетизма. Она смогла объяснить явление только частично, так как не дала ответа на вопрос о том, почему некоторые вещества подвергаются воздействию внешнего магнитного поля незначительно. Также остался необъяснённым вопрос, почему при намагничивании одни вещества создают магнитный поток сонаправленный внешнему полю (парамагнетики), а другие — противоположно направленный (диамагнетики).
Формулировка закона Ампера
При исследовании параллельных проводников с током было выяснено, что между ними действует сила притяжения, если токи однонаправленные, и отталкивания, если токи противоположно направленные. Сила взаимодействия токов зависит пропорционально от произведения сил токов и длины проводника. Справедливо также утверждение, что она обратно пропорциональна имеющемуся между проводами расстоянию. Математическая формулировка выглядит следующим образом:
Закон Ампера в такой формулировке показывает, что расчет силы магнитного поля производится по отношению к единице длины проводника. Силу, которую проводник с током испытывает в магнитном поле, называют силой Ампера.
Взаимодействие токов возможно лишь при наличии магнитных полей вокруг проводников. Эти поля создают движущиеся заряды. У магнитов постоянных магнитное поле, как утверждает закон Ампера, тоже возникает под воздействием электрических микротоков, но только тех, которые циркулируют внутри молекул вещества.
При описании магнитного поля принято использовать силовую характеристику, аналогичную вектору напряженности электрополя. Ее называют вектором магнитной индукции и обозначают латинской буквой «B». В системе СИ за единицу измерения данной характеристики принята Тесла: 1 Тл = 1 Н/А×м.
Направление вектора МИ определяется по правилу буравчика. Если штопор направить перпендикулярно плоскости проводника с током, то движение краёв рукоятки укажет направление вектора напряжённости. Подразумевается, что рукоятка будет вращаться по ходу часовой стрелки, если наблюдать сзади.
Взаимодействие тока и магнитного поля
Вектор магнитной индукции считается положительно направленным, если он совпадает с магнитной стрелкой, ориентированной на северный полюс. Используя это правило, можно определить направление вектора МИ в любой точке пространства и наглядно представить структуру магнитного поля. На рисунке ниже приведен пример расположения линий МИ для постоянного магнита и катушки с током.
Ампер смог рассчитать, как будет проходить взаимодействие между магнитным полем с заданной напряжённостью и проводником, по которому течёт ток. Согласно его закону действие магнитного поля на проводник с током описывается с помощью такой формулы:
Данная формула представлена в векторной форме. Умножение между векторами производится по особым правилам. В результате этой операции получится вектор, абсолютная величина которого определяется по следующей дифференциальной формуле:
Для прямолинейного провода данная формула в скалярной форме имеет вид:
Хотя, кажется, что закон достаточно прост, он стал важным достижением в развитии физической науки.
Направление электромагнитной силы
Если взять проводник с током и расположить его между полюсами магнита, как показано на рисунке ниже, то сила Ампера находится по формуле:
F = B × L × I, поскольку α = 90 градусов и sinα = 1.
Определение вектора действия силы выполняется согласно правилу левой руки. В этом случае нужно расположить ладонь левой руки перпендикулярно к силовым линиям магнитного поля. Пальцы при этом должны быть направлены в ту сторону, в которую течет ток. В таком положении перпендикулярно отставленный большой палец будет показывать направление электромагнитной силы.
При определении вектора силы, действующей на проводник, нужно учитывать, что ток всегда направлен от плюса к минусу. Это сложилось исторически, а потом стало традицией, несмотря на то, что в проводниках ток представляет собой движение электронов, то есть, отрицательных частиц.
В рассматриваемой ситуации можно регулировать силу взаимодействия, увеличивая или уменьшая силу тока. При этом напряжённость магнитного поля остается неизменной.
Проиллюстрировать применение правила левой руки можно на простом примере. Как уже было сказано выше, параллельные проводники с однонаправленными токами притягиваются. Правило поможет разобраться, почему это происходит.
Вокруг каждого проводника, по которому протекает ток, возникает магнитное поле. Нужно определить, как будет направлен вектор его напряжённости. Если взгляд направить вдоль проводника, то линии магнитной индукции поля будут видны в виде окружностей. Другими словами, если мысленно обхватить проводник правой рукой, направив большой палец по течению тока, то остальные четыре пальца будут соответствовать линиям напряженности магнитного поля.
Помещая первый проводник параллельно второму проводнику в магнитное поле, созданное последним, можно определить направление электромагнитной силы, используя правило левой руки. Расположив ее таким образом, чтобы получить линии МИ, входящие в ладонь, а направление пальцев, совпадающее с направлением тока, можно увидеть, что отогнутый большой палец указывает на второй проводник.
Понятно, что данное правило одинаково относится к обоим проводникам. Следовательно, можно определить направление электромагнитной силы в различных ситуациях. Аналогично можно видеть, что при противоположном направлении токов, действует сила отталкивания.
Влияние замкнутого контура
Используя закон Ампера можно сделать вывод о том, каким будет магнитное поле замкнутого контура. Например, можно вертикально ориентировать рамку в поле, силовые линии которого направлены сверху вниз.
Чтобы определить, какое направление будет иметь магнитная индукция в этой ситуации, следует также воспользоваться правилом левой руки. Так как ток в нижней части рамки направлен вправо, руку нужно расположить так, чтобы пальцы были направлены, если смотреть на рисунок, тоже вправо. При этом ладонь должна быть открыта вверх. Большой палец в такой ситуации будет направлен в сторону от наблюдателя.
Применив это правило для верхней части рамки, можно увидеть, что сила Ампера действует по направлению к наблюдателю. То есть, рамке придано вращательное движение. Однако по мере приближения к горизонтальному положению эта сила уменьшается.
Если рамка будет обладать инерцией и благодаря ей проскочит горизонтальное положение, то описанные выше силы вновь начнут действовать: вначале слабо, а затем будут увеличиваться по мере достижения рамкой вертикального положения.
Использование бесконечно малых величин
В указанных выше формулах применяются бесконечно малые величины (dF, dl). Их использование расширяет возможности расчёта параметров. Обычно экспериментально исследуются сравнительно простые ситуации, но при этом возникает необходимость получить формулы универсального характера.
В реальной жизни возможны, например, ситуации, когда напряжённость магнитного поля меняется по сложному закону или рассматриваются контуры проводников произвольной конфигурации.
Использование бесконечно малых величин даёт возможность обобщить результаты основополагающих экспериментов для самых разных ситуаций. Для этого могут быть применены методы дифференциального и интегрального исчисления.
При рассмотрении бесконечно малого участка провода речь идёт о величине, которая достаточно мала, чтобы считать её прямолинейной. В этом случае возможно применение уже существующих закономерностей. При помощи методов интегрирования можно перейти к проводам, которые имеют контур различной степени сложности или к рассмотрению магнитного поля сложной конфигурации.
Практическое применение
Сила Ампера используется практически во всех электромеханических устройствах, где необходимо с помощью электрических процессов вызвать движение реальных объектов. Одним из примеров применения являются измерительные приборы.
На рисунке приведен пример схемы измерительного прибора. К оси присоединен источник питания (4). Ось закреплена в подшипниках (5), поэтому может свободно вращаться. На оси есть прямоугольная рамка (1), через которую течёт ток. Она расположена между полюсами постоянного магнита (2). Контакты сделаны в виде спиральных пружин. К оси прикреплена стрелка (6), острие которой передвигается по шкале измерения (7).
При пропускании тока через проводник появляется магнитное взаимодействие, и рамка начинает вращаться. При этом смещается стрелка указателя до тех пор, пока сила Ампера не уравновесит силу упругости обеих пружин. Полученный показатель будет характеризовать ток, протекающий через проводник. Чем больше сила тока, тем сильнее отклонится стрелка.
На законе Ампера основывается и такая отрасль, как электротехника. Например, электромагнитная индукция применяется в электродвигателях.
Двигатель обеспечивает преобразование электроэнергии во вращение вала. Ток на рамку поступает через скользящие щётки. Она взаимодействует с постоянным магнитом, что приводит к её повороту под действием силы Ампера. В современных двигателях может использоваться одновременно несколько рамок. Это позволяет увеличить мощность мотора и сделать вращение оси более плавным.
Двигатели, работающие на основе рассматриваемого эффекта, активно используются в различных видах электротранспорта — трамваях, троллейбусах, электропоездах.
Еще одно применение закона Ампера — это громкоговорители. Внутри них находится постоянный магнит. Изменение силы тока вызывает изменение силы воздействия магнитного поля, что приводит к вибрации мембраны, производящей звук нужной частоты.
Притяжение между проводниками с током легло в основу точного определения единицы измерения 1 Ампер. При этом рассматривалась абстрактная ситуация, предполагающая наличие двух параллельно расположенных проводников с бесконечной длиной. Считалось, что каждый из них имеет бесконечно малое сечение, размерами которого можно пренебречь.
Принято, что на всём протяжении они находятся точно на расстоянии один метр и в вакууме. При прохождении тока величиной 1 Ампер сила, действующая на каждый метр проводников, должна составлять 0.0000002 Ньютона. Это определение вступило в силу в 1948 году.
Видео по теме
Взаимодействие параллельных проводников с током (параллельных токов)
Определить в некоторой точке пространства вектор индукции магнитного поля B, порождаемого постоянным электрическим током I, можно с помощью Закона Био-Савара. Это делается путем суммирования всех вкладов в магнитное поле от отдельных элементов тока.
Магнитное поле элемента тока dI, в точке, заданной вектором r, по Закону Био-Савара находится так (в системе СИ):
Одна из типичных задач состоит в том, чтобы далее определить силу взаимодействия двух параллельных токов. Ведь токи, как известно, порождают собственные магнитные поля, а ток, находящийся в магнитном поле (другого тока) испытывает на себе действие силы Ампера.
Под действием силы Ампера, противоположно направленные токи взаимно отталкиваются, а токи направленные в одну сторону — взаимно притягиваются.
Прежде всего для прямого тока I нам необходимо найти магнитное поле B на некотором расстоянии R от него.
Для этого вводится элемент длины тока dl (по направлению тока), и рассматривается вклад от тока в месте расположения данного элемента длины — в общую индукцию магнитного поля применительно к выбранной точке пространства.
Сначала будем записывать выражения в системе СГС, то есть появится коэффициент 1/с, а в конце приведем запись в системе СИ, где появится магнитная постоянная.
По правилу нахождения векторного произведения, вектор dB — результат векторного произведения dl на r для любого элемента dl, в каком бы месте рассматриваемого проводника он не находился, всегда будет направлен за плоскость рисунка. Результат будет равен:
Произведение косинуса на dl можно выразить через r и угол:
Значит выражение для dB примет вид:
Далее выразим r через R и косинус угла:
И выражение для dB примет вид:
Далее необходимо это выражение проинтегрировать в пределах от -пи/2 до +пи/2, и в результате получим для B в точке на расстоянии R от тока следующее выражение:
Можно сказать, что вектор B найденной величины, для выбранной окружности радиуса R, через центр которой перпендикулярно проходит данный ток I, всегда будет направлен по касательной к данной окружности, какую бы точку окружности мы ни выбрали. Здесь присутствует осевая симметрия, так что вектор B в любой точке окружности получается одной и той же длины.
Теперь рассмотрим параллельные постоянные токи и решим задачу нахождения сил их взаимодействия. Допустим, что параллельные токи направлены в одну и ту же сторону.
Изобразим магнитную силовую линию в форме окружности радиуса R (о которой речь шла выше). И пусть второй проводник расположен параллельно первому в какой-то точке данной силовой линии, то есть в месте с индукцией, значение которой (в зависимости от R) мы только что научились находить.
Магнитное поле в этом месте направлено за плоскость рисунка, и оно действует на ток I2. Выделим элемент длины тока l2, равный одному сантиметру (единица длины в системе СГС). Далее рассмотрим силы, действующие на него. Будем использовать Закон Ампера. Индукцию в месте расположения элемента длины dl2 тока I2 мы нашли выше, она равна:
Следовательно сила, действующая со стороны всего тока I1 на единицу длины тока I2 будет равна:
Это и есть сила взаимодействия двух параллельных токов. Поскольку токи однонаправленные и они притягиваются, то сила F12 со стороны тока I1 направлена так, что она тянет ток I2 в сторону тока I1. Со стороны же тока I2 на единицу длины тока I1 действует сила F21 равной величины, но направленная в сторону противоположную силе F12, в соответствии с третьим законом Ньютона.
В системе СИ, сила взаимодействия двух постоянных параллельных токов находится по следующей формуле, где коэффициент пропорциональности включает в себя магнитную постоянную:
http://profazu.ru/knowledge/electrical/zakon-ampera.html
http://electricalschool.info/spravochnik/electroteh/2369-vzaimodeystvie-parallelnyh-provodnikov-s-tokom.html
- Главная
- Справочник
- Законы
- Закон Ампера
- Закон Ампера
- Значение закона Ампера
Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.
Ампер первым установил, что проводники, по которым течет электрический ток, взаимодействуют механически (притягиваются или отталкиваются).
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения: ( overrightarrow{F} ),( overrightarrow{F}_{A} ). Сила (( overrightarrow{F} )), которая действует на прямолинейный проводник с током (I), всегда перпендикулярна проводнику и направлению вектора магнитной индукции (( overrightarrow{B} )). В том случае, если прямолинейный проводник расположен параллельно вдоль направления линий магнитного поля, поле не действует.
Конкретное направление силы Ампера можно найти с помощью правила левой руки. Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 90 градусов большой палец укажет направление силы Ампера.
Еще Ампер установил, что два параллельных проводника с током притягиваются, если токи имеют одинаковые направления и отталкиваются, если токи текут в противоположные стороны. Это просто объяснить, если представить, что один проводник создает магнитное поле, а другой проводник в него помещен и это поле действует на него. Можно использовать правило левой руки и выяснить, как направлена сила.
Сила взаимодействия параллельных токов. Закон Ампера
Если взять два проводника с электрическими токами, то они будут притягиваться друг к другу, если токи в них направлены одинаково и отталкиваться, если токи текут в противоположных направлениях. Сила взаимодействия, которая приходится на единицу длины проводника, если они параллельны, может быть выражена как:
где $I_1{,I}_2$ — токи, которые текут в проводниках, $b$- расстояние между проводниками, $в системе СИ {mu }_0=4pi cdot {10}^{-7}frac{Гн}{м} (Генри на метр)$ магнитная постоянная.
Закон взаимодействия токов был установлен в 1820 г. Ампером. На основании закона Ампера устанавливают единицы силы тока в системах СИ и СГСМ. Так как ампер равен силе постоянного тока, который при течении по двум параллельным бесконечно длинным прямолинейным проводникам бесконечно малого кругового сечения, находящихся на расстоянии 1м друг от друга в вакууме вызывает силу взаимодействия этих проводников равную $2cdot {10}^{-7}Н$ на каждый метр длины.
Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы
Правило левой руки
Для определения направления вектора силы Ампера применяется “правило левой руки”.
Рис. 2. Правило левой руки для определения направления силы Ампера.
Левая рука располагается так, чтобы пальцы ладони (все кроме большого) указывали направление тока в проводнике. Затем плоскость ладони устанавливается перпендикулярно плоскости, в которой находятся проводник с током и вектор магнитной индукции B. Вектор B должен входить в ладонь. Тогда большой палец левой руки, развернутый под прямым углом, укажет направление силы Ампера.
Закон Ампера для проводника произвольной формы
Если проводник с током находится в магнитном поле, то на каждый носитель тока действует сила равная:
где $overrightarrow{v}$ — скорость теплового движения зарядов, $overrightarrow{u}$ — скорость упорядоченного их движения. От заряда, это действие передается проводнику, по которому заряд перемещается. Значит, на проводник с током, который находится в магнитном, поле действует сила.
Выберем элемент проводника с током длины $dl$. Найдем силу ($overrightarrow{dF}$) с которой действует магнитное поле на выделенный элемент. Усредним выражение (2) по носителям тока, которые находятся в элементе:
где $overrightarrow{B}$ — вектор магнитной индукции в точке размещения элемента $dl$. Если n — концентрация носителей тока в единице объема, S — площадь поперечного сечения провода в данном месте, тогда N — число движущихся зарядов в элементе $dl$, равное:
Умножим (3) на количество носителей тока, получим:
Зная, что:
где $overrightarrow{j}$- вектор плотности тока, а $Sdl=dV$, можно записать:
Действие магнитного поля на проводник с током
На прошлом уроке мы с вами установили, что о существовании магнитного поля можно судить по наличию силы, действующей на проводник с током. Эту силу называют силой Ампера,
в честь французского учёного Адре Мари Ампера.
Тогда логично предположить, что если мы поместим проводник с током в магнитное поле, например в поле постоянного магнита, то на него будет действовать сила со стороны этого поля — магнитная сила. Проверим это предположение на опыте. Для этого возьмём проводник с током и расположим его так, чтобы только один его прямолинейный участок оказался в магнитном поле, а остальные части цепи находились в областях пространства, где магнитное поле слабое и его действием на эти части цепи можно пренебречь. Замкнув цепь, мы заметим, что проводник придёт в движение.
Уберём магнит, и проводник двигаться не будет. Значит, со стороны магнитного поля на проводник с током действует сила так же, как действует сила со стороны магнитного поля на магнитную стрелку. Изменяя направление тока или направление силовых линий магнитного поля, легко заметить, что при этом меняется и направление движения проводника, а значит, и направление действующей на проводник силы.
Направление действующей на проводник с током силы Ампера в магнитном поле можно определить, пользуясь правилом левой руки. Руку располагают так, чтобы силовые линии поля перпендикулярно входили в ладонь, четыре пальца были направлены по току, тогда отставленный на 90° большой палец расположится вдоль направления действующей на проводник силы
.
Рассмотрим теперь, от чего зависит величина этой силы. Для этого опять обратимся к опыту. Подвесим к левому плечу коромысла рычажных весов линейный проводник и поместим его между полюсами магнита так, чтобы он был перпендикулярен силовым линиям магнитного поля. Последовательно с этим проводником включим амперметр и реостат, с помощью которого можно менять силу тока в нашем проводнике. Уравновесим весы и замкнём цепь.
Не трудно заметить, что равновесие весов нарушилось. Чтобы его восстановить, на правую чашку придётся положить добавочный груз, вес которою будет равен силе, действующей на проводник вертикально вниз.
Теперь будем изменять ток в нашем проводнике в целое число раз. Как видим, увеличение силы тока в целое число раз приводит к увеличение в целое число раз силы, действующей на проводник. То есть сила, с которой магнитное поле действует на проводник с током прямо пропорциональна силе этого тока.
А теперь проверим, зависит ли эта сила от длины проводника. Для этого будем помещать в магнитное поле проводники разной длины при одном и том же токе. Как видим, сила, с которой магнитное поле действует на проводник с током, прямо пропорциональна длине части проводника, расположенной в магнитном поле.
На основании проведённых опытов мы с вами можем утверждать, что максимальная сила, действующая со стороны магнитного поля на участок проводника, по которому идёт ток, прямо пропорциональна произведению силы тока на длину участка проводника.
Однако при этом отношение силы к длине проводника и к току в нём есть величина постоянная, не зависящая ни от длины проводника, ни от тока в нём. Следовательно, величина этого отношения может служить характеристикой магнитного поля. Эту величину и называют индукцией магнитного поля или просто магнитной индукцией.
В системе единиц СИ за единицу индукции магнитного поля принимается индукция такого однородного магнитного поля, которое действует с силой один ньютон на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению индукции поля, если по этому проводнику течёт ток в один ампер:
Эта единица измерения названа теслой в честь великого сербского инженера и изобретателя Николы Тесла.
Напомним вам, что индукция магнитного поля — это векторная величина.
А её направление в данной точке совпадает с направлением силовой магнитной линии, проходящей через эту точку. Так же в системе СИ индукция магнитного поля является силовой характеристикой магнитного поля, подобно тому, как напряжённость электрического поля является силовой характеристикой поля электрического.
Зная индукцию магнитного поля, можно рассчитать максимальную силу Ампера, действующую на проводник с током со стороны магнитного поля:
.
В общем же случае, сила Ампера будет зависеть и от ориентации проводника в магнитном поле. И действительно, если в нашем первом опыте менять ориентацию проводника в магнитном поле, то можно заметить, что модуль действующей силы зависит от угла между направлениями тока в проводнике и магнитной индукции. Причём модуль силы обращается в ноль тогда, когда направление тока в проводнике и направление вектора магнитной индукции совпадают.
Таким образом, в общем случае модуль силы Ампера равен произведению силы тока, модуля вектора магнитной индукции, длины отрезка проводника и синуса угла между направлениями вектора магнитной индукции и элемента тока:
Это выражение называют законом Ампера.
Он был установлен Адре Мари Ампером в 1820 году.
В случае, когда магнитное поле создаётся несколькими источниками, то индукцию результирующего магнитного поля определяют по принципу суперпозиции: если магнитное поле в некоторой точке пространства создаётся несколькими источниками, то индукция результирующего магнитного поля в этой точке равна векторной сумме индукций магнитных полей, созданных каждым источником:
Теперь, для закрепления материала давайте с вами решим такую задачу. В однородном магнитном поле, индукция которого равна 0,25 Тл и имеет вертикальное направление, на двух идеальных нитях горизонтально подвешен прямолинейный проводник массой 40 г. Активная длина проводника располагается в вакууме и равна 20 см. Какой ток течёт по проводнику, если нити отклонились на 45о от вертикали?
В заключении отметим, что силы, действующие на проводник с током в магнитном поле, широко используются в технике. Электродвигатели и генераторы, телефоны и микрофоны — во всех этих и множестве других приборах используется взаимодействие токов, токов и магнитов и так далее.
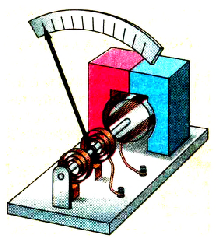
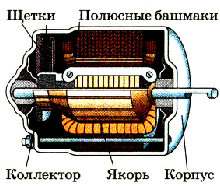
Рассмотрим принцип действия электроизмерительных приборов магнитоэлектрической системы, предназначенных для измерения силы тока и напряжения в цепях постоянного тока.
Итак, приборы магнитоэлектрической системы состоят из постоянного магнита, создающего постоянное магнитное поле, усиливаемое специальными «полюсными башмаками». Между башмаками устанавливается катушка, изготовленная, как правило, из алюминиевого каркаса (рамки) и обмотки, к которой подводится ток. Внутри рамки помещают железный цилиндр, который обеспечивает радиальное направление линий магнитной индукции в той области, где находятся витки катушки. Рамка укреплена на двух полуосях, на одной из которых закреплена показывающая стрелка. Вращение стрелки уравновешивается спиральными пружинами.
В таких приборах вращающий момент амперовых сил пропорционален силе проходящего по подвижной катушке тока. Противодействующий механический момент создаваемый спиральными пружинами, пропорционален углу закручивания. Следовательно, угол отклонения катушки, и скреплённой с нею стрелки, будет пропорционален силе протекающего по обмотке тока. А линейная зависимость между током и углом отклонения обеспечивает равномерность шкалы прибора.
И давайте рассмотрим ещё принцип работы громкоговорителя, который является одним из самых важных изобретений ХХ века. Именно его появление (наряду с микрофоном) обеспечило возможность развития систем звукозаписи и звуковоспроизведения.
Громкоговоритель — это прибор, который служит для возбуждения звуковых волн под действием переменного электрического тока, меняющегося со звуковой частотой. Иными словами, громкоговоритель применяется для преобразования электрических колебаний в звуковые.
Патент на первую электродинамическую головку (капсюль) был получен известным изобретателем Александром Беллом в 1876—1877 гг. В нём мембрана из магнитомягкого материала колебалась в магнитном поле постоянного магнита и электромагнита. До конца 1920-х годов большинство громкоговорителей использовало именно этот принцип работы.
Но такие громкоговорители имели высокий уровень нелинейных и частотных искажений. В 1924 году американцы Честер Рейс и Эдвард Келлог из запатентовали наиболее близкую к современной конструкцию динамического громкоговорителя. Уже через два года это устройство появилось в промышленных громкоговорителях и в радиоприёмниках.
Интересно отметить, что почти одновременно работы по созданию электродинамических громкоговорителей велись и в России. В 1923 году в Петрограде была создана Центральная радиолаборатория, позднее переименованная в Институт радиовещательного приёма и акустики имени Александра Степановича Попова. А уже в 1926 году был создан первый электромагнитный громкоговоритель «Рекорд» и электромагнитный рупорный уличный громкоговоритель. Первые мощные громкоговорители были созданы в 1930—1932 гг. для звукоусиления на Красной площади в Москве.
За многие десятилетия акустические системы претерпели массу изменений. Однако их принцип работы до сих пор остаётся неизменным.
Итак, у громкоговорителя есть две части — подвижная и неподвижная. Подвижную часть, закрытую пылезащитным колпачком, называют диффу́зором. Он создаёт механические колебания, которые мы воспринимаем как звук.
За диффу́зором располагается центрирующая шайба, в которой находится звуковая катушка. Катушка может свободно перемещаться в магнитном поле мощного постоянного магнита, кольцевой формы, который крепится к корзине. В зависимости от силы поступаемого на обмотку электрического сигнала, прочно прикреплённая к диффузору катушка приводит последний в колебательные движения. Эти колебания возбуждают окружающий воздух, образовывая направленную звуковую волну.
Общим недостатком всех громкоговорителей является их малый КПД — всего порядка 1—3 %. Но на практике и этих процентов хватает с лихвой.
В настоящее время наряду с электромеханическими громкоговорителями широкое применение получили пьезоэлектрические громкоговорители (или излучатели). Их принцип действия основан на пьезоэлектрическом эффекте, который проявляется в виде деформации некоторых типов кристаллов в электростатическом поле.
Пьезогромкоговорители очень удобны в изготовлении и компактны. Поэтому их широко применяют радио- и мобильных телефонах, ноутбуках, часах-будильниках и даже в устройствах для отпугивания грызунов и насекомых.
Опыты Ампера
Андре-Мари Амперу повезло родиться в богатой аристократической семье, имевшей поместье недалеко от Лиона. На образование ребенка родители не скупились: учителя, приходившие обучать богатого отпрыска, давали ему знания из самых различных областей. Никто не посмел бы отнести мальчика к разряду недорослей: он рано заинтересовался математическими трудами известных ученых и часами проводил время за чтением фолиантов из обширной отцовской библиотеки. А в 13 лет Андре-Мари написал свою первую работу по математике и отправил ее в Лионскую академию.
Во время Великой Французской буржуазной революции был казнен отец Ампера, и юноше пришлось заняться преподаванием, чтобы заработать. Начав с частных уроков математики, он через некоторое время был приглашен в Центральную школу старинного городка Бурк-ан-Бреса для преподавания физики и химии. Потом был Лионский колледж, а в 1807 году, в возрасте 32 лет, он становится профессором Политехнической школы.
Время расцвета научной деятельности Ампера приходится на 1814—1824 годы и связано, главным образом, с Академией наук, в число членов которой он был избран 28 ноября 1814 года за свои заслуги в области математики. Впрочем, наш рассказ — об открытиях, сделанных ученым в области изучения свойств электричества.
В 1820 году датский физик Ханс Христиан Эрстед случайно заметил, что если по проволоке проходит ток, то отклоняется стрелка лежащего рядом компаса. На заседании академии 4 сентября 1820 года был продемонстрирован опыт Эрстеда. А уже к концу сентября Ампер доложил об открытии сил притяжения между двумя параллельными проводниками с током.
Продолжая эти эксперименты, Ампер обнаружил, что катушка с током действует как постоянный магнит (в дальнейшем, работая в этом направлении, Майкл Фарадей открыл явление электромагнитной индукции). Ампер изобрел устройство со свободно подвешенной иглой, которая отклонялась под действием тока через катушку, причем отклонение было тем больше, чем больше сила тока. Усовершенствование этого устройства привело к появлению измерительного прибора — гальванометра. Но даже работая с его прототипом, Ампер установил, что ток течет в замкнутой электрической цепи. В дальнейшем Кирхгоф и Ом установили законы электрических цепей.
Единицы мощности
Перевод ватты в амперы и наоборот — понятие относительное, потому как это разные единицы измерения. Амперы — это физическая величина силы электрического тока, то есть скорость прохождения электричества через кабель. Ватт — величина электрической мощности, или скорость потребления электроэнергии. Но такой перевод необходим для того, чтобы рассчитать, соответствует ли значение силы тока значению его мощности.
Связь с другими единицами СИ
Что такое амперы с точки зрения связи между электрическими единицами, можно увидеть на примерах:
- при силе тока в 1 ампер (А) поперечное сечение проводника за одну секунду пропускает через себя заряд в 1 кулон (Кл);
- при подаче заряда силой 1 ампер к обкладкам конденсатора с ёмкостью 1 Ф напряжение на пластинах будет расти, увеличиваясь каждую секунду на 1 В;
- ёмкость гальванических источников и аккумуляторов измеряется в ампер-часах (А*ч, или А*h), 1 А*ч = 3660 Кл, такое количество электричества протекает через проводник за 1 час;
- отдаваемая максимальная мощность (ватт) выпрямителей или блоков питания – вторая по значению характеристика подобных источников, имеет маркировку В*А;
- величина электричества в разряде молнии равна приблизительно 500 килоамперам (1 кА = 10³ А);
- лампочка накаливания мощностью 0,1 киловатт (кВт) потребляет 0,5 А.
Единица измерения индукции
Единица индукции в системе СИ определяется как индукция такого магнитного поля, в котором на 1 м проводника при силе тока действует сила Ампера величиной 1 Н. Единица называется тесла (Тл).
$1 Тл = {1 Нover {1 A*1 м}}$ (3).
Единица индукции названа в честь выдающегося сербского инженера, физика Николы Тесла (1856-1943 г.г.). Тесла изобрел электромеханические генераторы, высокочастотный трансформатор. Исследовал свойства токов высокой частоты, изобрел многофазный электродвигатель и системы передачи электроэнергии с помощью переменного тока. Тесла сформулировал основные принципы радиосвязи, изобрел мачтовую антенну для приемки и передачи радиосигналов.
Рис. 3. Портрет Никола Тесла.
Применение
Закон Ампера, а точнее следствия, вытекающие из него, используются в каждом электромеханическом устройстве, где необходимо вызвать движение рабочих элементов. Самым распространённым механизмом, работа которого базируется на законе Ампера, является электродвигатель.
Применение электромоторов настолько широкое, что его можно увидеть практически во всех сферах человеческой деятельности:
- на производстве, в качестве приводов станков и различного оборудования;
- в бытовой сфере (бытовая электротехника);
- в электроинструментах;
- на транспорте;
- в устройствах автоматики, в офисной технике и во многих других сферах.
Из закона Ампера вытекает возможность получения электротока путём перемещения проводников, находящихся в магнитном поле. На данном принципе построены все генераторы электрического тока. Благодаря этой уникальной возможности, у нас появился доступ к использованию электроэнергии для различных потребностей.
Мы буквально окружены проявлением закона Ампера. Например, просмотр телепередачи сопровождается звуком, который транслируется через динамики. Но диффузор динамика приводит в движение сила Ампера. Мы разговариваем по телефону – там тоже есть динамик и микрофон. Принцип действия современных микрофонов также основан на законе Ампера.
Вход в помещение через автоматическую раздвижную дверь, поднятие на лифте, поездка в троллейбусе, трамвае, запуск двигателя автомобиля – всё это было бы невозможным, если бы не существовало взаимодействия электрического тока с силами магнитной индукции.
Ампер открыл перед человечеством такие возможности, без которых развитие научно-технического прогресса было бы невозможным. Влияние этого закона в электротехнике сравнимо с законами Ньютона, которые в своё время совершили революцию в механике. В этом огромная заслуга учёного-физика Мари Ампера, труды которого увенчались открытием в 1820 г. знаменитого закона.
Источник

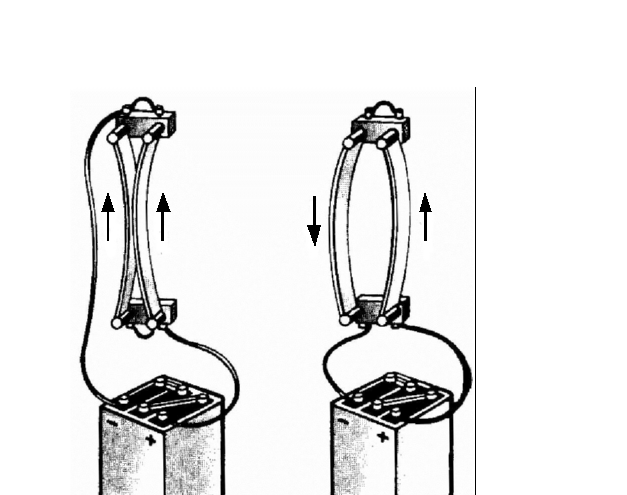
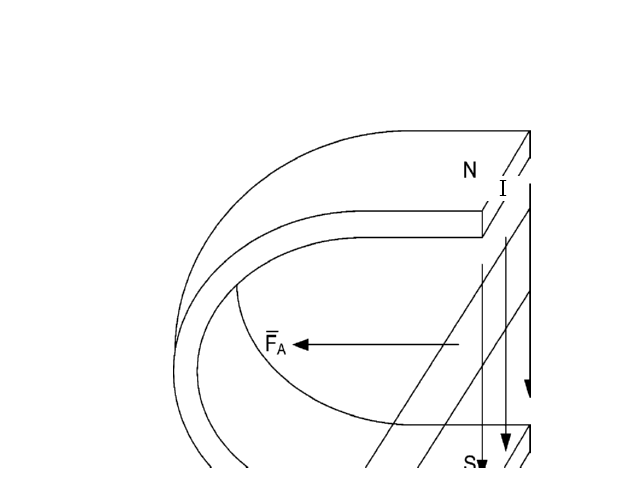
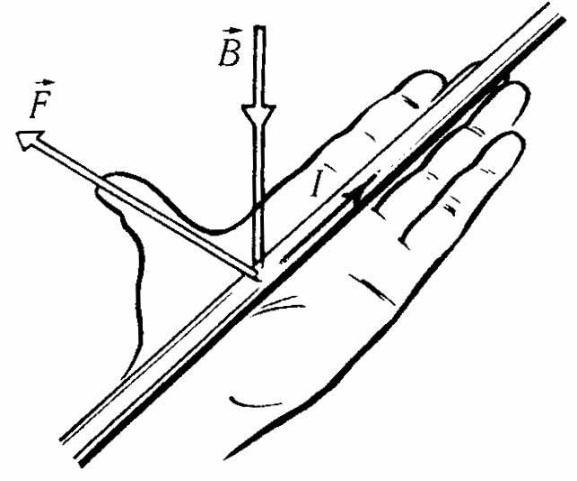


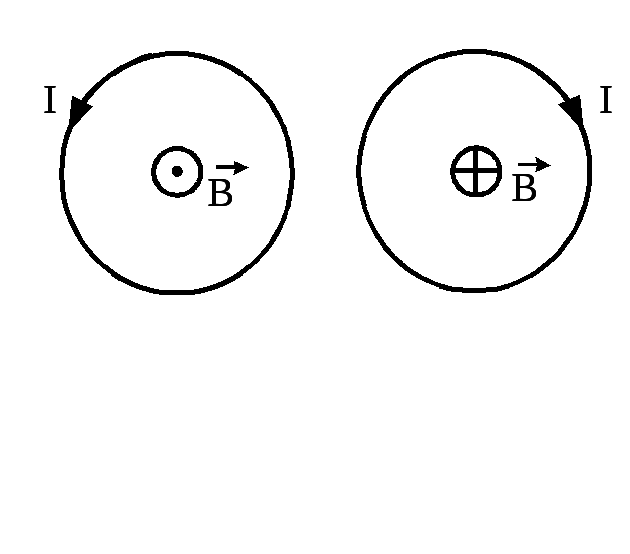
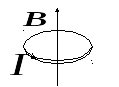
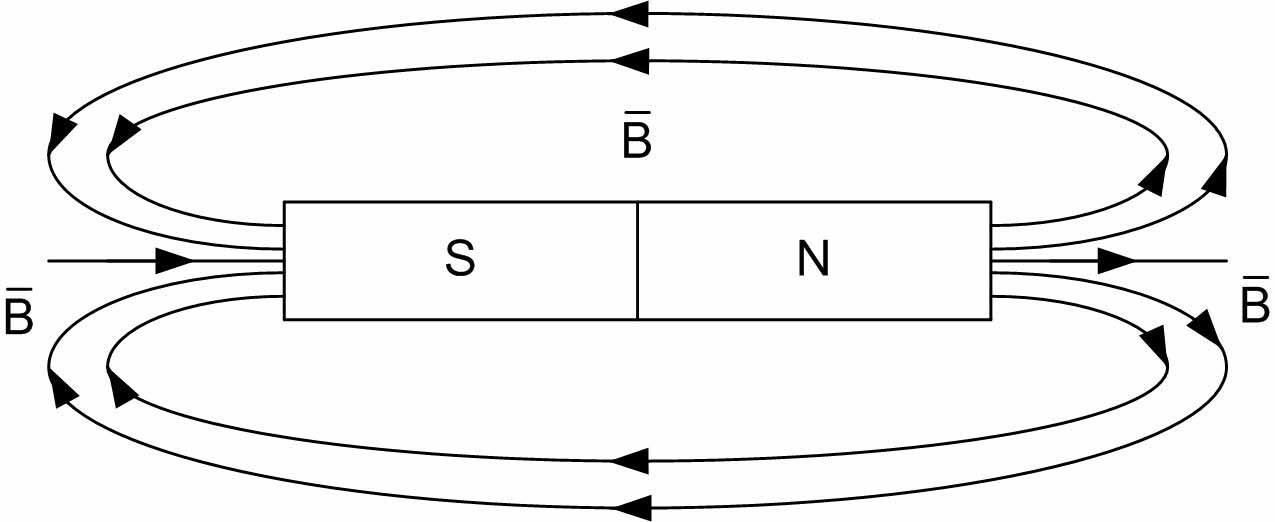
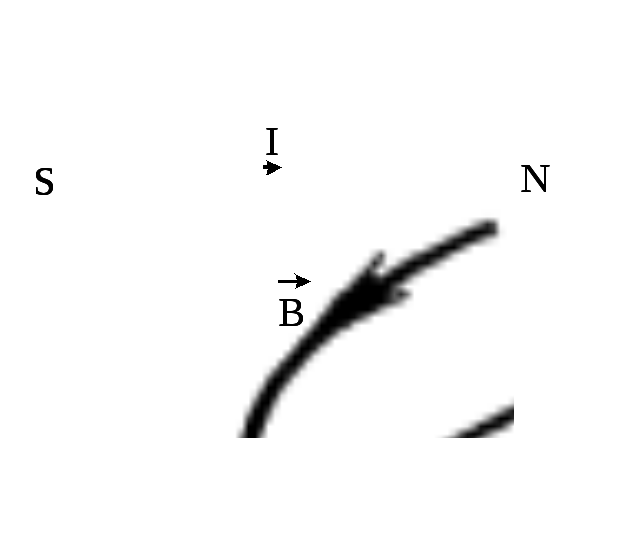

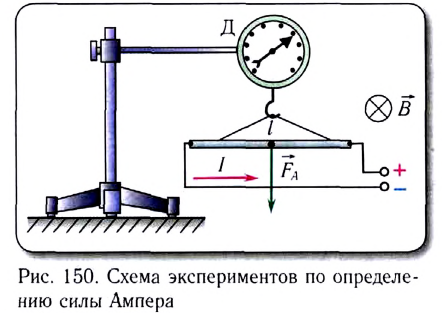
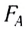
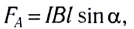
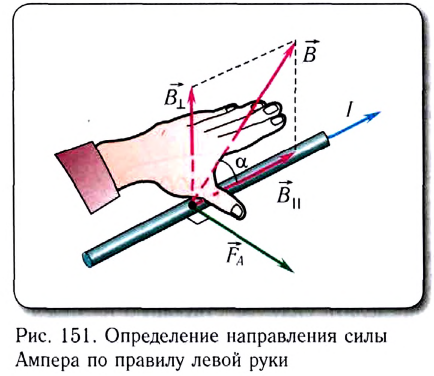
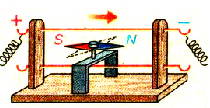
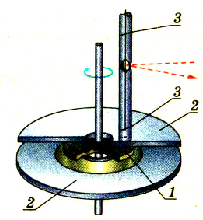
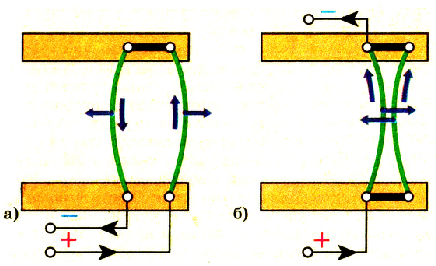
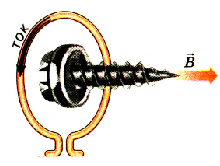
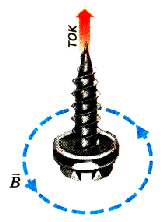
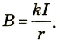
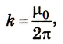

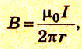
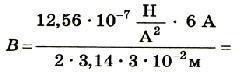
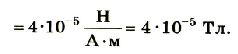
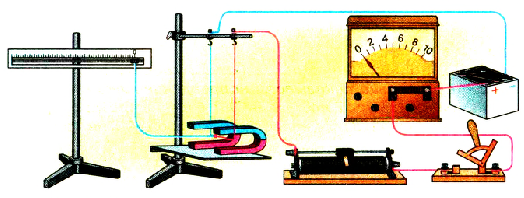
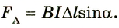
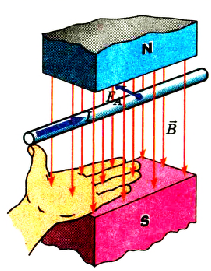
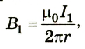
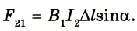
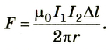
 = 30%
= 30%