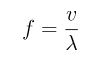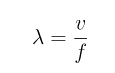Определения
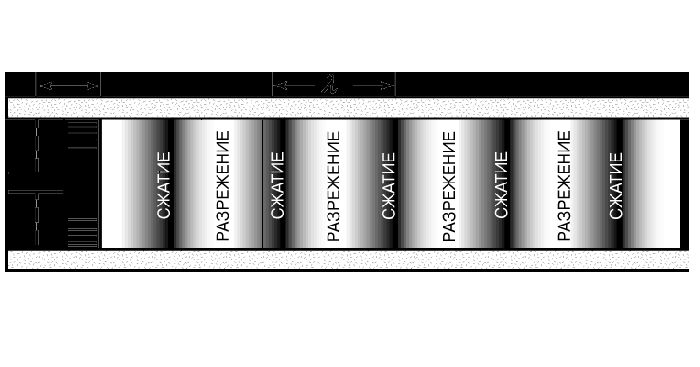
Звук — это волновой процесс. Если струна скрипки или арфы колеблется, в окружающем ее воздуха
образуются зоны
сжатия и разрежения, которые и представляют собой звук. Эти зоны сжатия и разрежения перемещаются по воздуху в
форме продольных волн, которые имеют ту же частоту, что и источник звука. В продольных волнах молекулы воздуха
движутся параллельно движению волны.
Воздух сжимается в том же направлении, в котором распространяются звуковые волны. Эти волны передают энергию
голоса или колеблющейся струны. Отметим, что воздух не перемещается, когда звуковая волна проходит через него.
Перемещаются только колебания, то есть зоны сжатия и разрежения. Более громкие звуки получаются при более
сильных сжатиях и разрежениях.
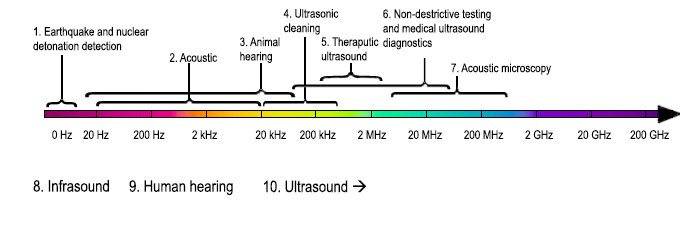
Спектр звуковых колебаний. 1 — землетрясения, молнии и обнаружение ядерных взрывов; 2 — акустический
диапазон; 3 — Слух животных; 4, Ультразвуковая очистка; 5. Терапевтическое применение ультразвука; 6 —
Неразрушающий контроль и медицинская ультразвуковая диагностика; 7 — Акустическая микроскопия; 8 —
Инфразвук; 9 — Слышимый диапазон; 10 — Ультразвук
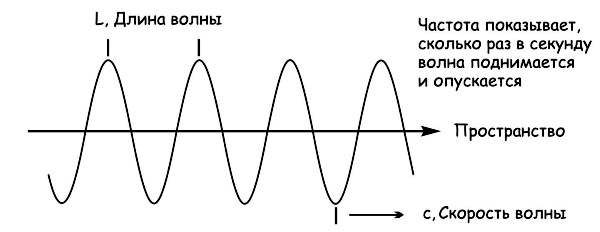
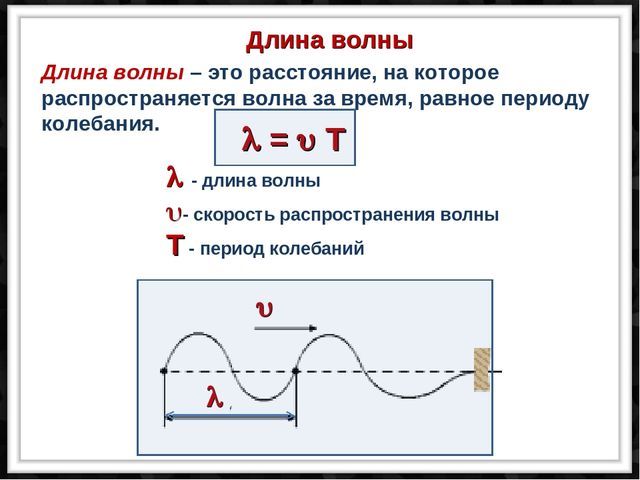
Количество этих колебаний в секунду называется частотой и измеряется в герцах. Период колебаний — это
длительность одного цикла колебаний, измеренная в секундах. Длина волны — это расстояние между двумя соседними
повторяющимися зонами волнового процесса. Если предположить, что скорость распространения волны в среде
постоянная, то длина волны обратно пропорциональна частоте.
При 20 °C звук распространяется в сухом воздухе со скоростью около 343 метра в секунду или 1 километр
приблизительно за 3 секунды. Звук распространяется быстрее в жидкостях и еще быстрее в твердых телах.
Например, в воде звук распространяется в 4,3 раза быстрее, чем в воздухе, в стекле — в 13 раз и в алмазе в 35
раз быстрее, чем в воздухе.
Хотя звуковые волны и морские волны движутся намного медленнее электромагнитных волн, уравнение, описывающее
их движение будет одинаковым для всех трех типов волн:
или
где f — частота волны, v — скорость распространения волны и λ — длина волны
Описание
Данный калькулятор определяет длину волны звуковых колебаний (только звуковых!), если известны их
частота и
скорость распространения звука в среде. Он также может рассчитать частоту, если известны длина волны и
скорость или скорость звука, если известны частота и длина волны.
Пример: Рассчитать длину звуковой волны, распространяющейся в морской воде от гидроакустического
преобразователя с частотой 50 кГц, если известно, что скорость звука в соленой воде равна 1530 м/с.
Random converter
- Калькуляторы
- Акустика — звук
Калькулятор звуковой частоты и длины волны
Этот калькулятор определяет длину волны звуковых колебаний (только звуковых!), если известны их частота и скорость распространения звука в среде. Он также может рассчитать частоту, если известны длина волны и скорость или скорость звука, если известны частота и длина волны.
Пример: Рассчитать длину звуковой волны, распространяющейся в морской воде от гидроакустического преобразователя с частотой 50 кГц, если известно, что скорость звука в соленой воде равна 1530 м/с.
Частота
f
Длина волны
λ
Скорость звука
v
или Среда
Поделиться ссылкой на этот калькулятор, включая входные параметры
Для расчета выберите среду или введите скорость звука, затем введите частоту и нажмите кнопку Рассчитать для расчета длины волны. Можно также ввести длину волны и рассчитать частоту.
Определения и формулы
Звук — это волновой процесс. Если струна скрипки или арфы колеблется, в окружающем ее воздуха образуются зоны сжатия и разрежения, которые и представляют собой звук. Эти зоны сжатия и разрежения перемещаются по воздуху в форме продольных волн, которые имеют ту же частоту, что и источник звука. В продольных волнах молекулы воздуха движутся параллельно движению волны. Воздух сжимается в том же направлении, в котором распространяются звуковые волны. Эти волны передают энергию голоса или колеблющейся струны. Отметим, что воздух не перемещается, когда звуковая волна проходит через него. Перемещаются только колебания, то есть зоны сжатия и разрежения. Более громкие звуки получаются при более сильных сжатиях и разрежениях.
Спектр звуковых колебаний. 1 — землетрясения, молнии и обнаружение ядерных взрывов; 2 — акустический диапазон; 3 — Слух животных; 4, Ультразвуковая очистка; 5. Терапевтическое применение ультразвука; 6 — Неразрушающий контроль и медицинская ультразвуковая диагностика; 7 — Акустическая микроскопия; 8 — Инфразвук; 9 — Слышимый диапазон; 10 — Ультразвук
Количество этих колебаний в секунду называется частотой и измеряется в герцах. Период колебаний — это длительность одного цикла колебаний, измеренная в секундах. Длина волны — это расстояние между двумя соседними повторяющимися зонами волнового процесса. Если предположить, что скорость распространения волны в среде постоянная, то длина волны обратно пропорциональна частоте.
При 20 °C звук распространяется в сухом воздухе со скоростью около 343 метра в секунду или 1 километр приблизительно за 3 секунды. Звук распространяется быстрее в жидкостях и еще быстрее в твердых телах. Например, в воде звук распространяется в 4,3 раза быстрее, чем в воздухе, в стекле — в 13 раз и в алмазе в 35 раз быстрее, чем в воздухе.
Хотя звуковые волны и морские волны движутся намного медленнее электромагнитных волн, уравнение, описывающее их движение будет одинаковым для всех трех типов волн:
или
где
f — частота волны,
v — скорость распространения волны и
λ — длина волны
Продольные и поперечные волны
В различных средах звук распространяется в виде различных видов волн. В жидкостях и газах звук распространяется в виде продольных волн. В твердых телах звук может распространяться как в виде продольных, так и в виде поперечных волн.
Для лучшего понимания обоих типов волн удобно воспользоваться механическим аналогом, которым послужит пружина Слинки. Эта пружина представляет собой модель среды (жидкости или газа). Если ее растянуть, а затем сжимать, а затем отпускать один конец, сжатие в форме волны перемещается вперед, передавая таким образом энергию с одного конца пружины в другой. Если звук распространяется в жидкости или газе, он идет от источника в форме периодических сжатий и разрежений газа или жидкости, которые перемещаются от источника звука.
Мы можем сравнить витки пружины с молекулами воздуха или воды, которые сталкиваются друг с другом. Поскольку направление движения этих сжатий и разрежений параллельно направлению движения самой волны, такие волны называются продольными.
Если начать двигать один конец пружины перпендикулярно ее оси, то создается поперечная волна. Она называется поперечной, потому что движение витков пружины перпендикулярно направлению движения волны по пружине. В такой волне энергия передается вдоль пружины, а ее витки движутся в направлении, перпендикулярном передаче энергии.
Отметим, что в нашем эксперименте пружина представляет собой среду, в которой распространяется волна, и эта среда не движется вместе с волной. Она только колеблется. Это поведение волны легко наблюдать в твердом теле, однако это справедливо также для воздуха, воды и вообще любой жидкости или газа. То есть, колебания переносятся молекулами жидкости или газа, в то время как среднее положение молекул среды не изменяется с течением времени. Это справедливо для любых типов волн.
Примеры
Возьмем на клавиатуре несколько нот и покажем их частоту и длину волны. Предположим, что звук движется в воздухе со скоростью 340 м/с. Тогда можно рассчитать длину волны нот:
| Научное и традиционное название ноты | Частота, Гц | Период, мс | Длина волны, см |
|---|---|---|---|
| A3, ля малой октавы | 220 | 4,55 | 156 |
| A4, ля первой октавы | 440 | 2,27 | 78 |
| A5, ля второй октавы | 880 | 1,14 | 39 |
| A6, ля третьей октавы | 1760 | 0,57 | 19,5 |
Акустика — звук
На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!
Канал Конвертера единиц TranslatorsCafe.com на YouTube
Sound waves are defined as longitudinal waves that form a pattern of disruptions created by the flow of energy across materials such as air, liquid, or solid. To put it another way, they can be defined as a vibration that travels through the medium as mechanical waves. They travel quickly in solids, slowly in liquids, and very slowly in gaseous media. The speed of sound waves vary drastically from medium to medium. For example, the speed of sound is 343 m/s in air, 1403 m/s in water and 1007 m/s in helium.
Sound Wavelength
The wavelength is defined as the distance between the two nearest points in phase with each other. It is defined as the distance over which the shape of a sound wave repeats. Its SI unit is given by meters (m). It is represented by the symbol λ (lambda) and its dimensional formula is given by [M0L1T0]. It is equal to the ratio of the velocity of the sound wave to its frequency.
Formula
λ = v/f
where,
v is the velocity of sound wave,
f is the frequency of sound wave.
Derivation
We know that wavelength is the distance travelled by the sound wave at a constant velocity in time t.
λ = vt …….. (1)
Also, it is known that the frequency of a wave is defined as the reciprocal of time.
f = 1/t
t = 1/f …….. (2)
Using (2) we get,
λ = v (1/f)
λ = v/f
This derives the formula for sound wavelength.
Sample Problems
Problem 1. Calculate the wavelength of a sound wave travelling in air at a frequency of 20 Hz.
Solution:
We have,
v = 343
f = 20
Using the formula we have,
λ = v/f
= 343/20
= 17.15 m
Problem 2. Calculate the wavelength of a sound wave travelling in air at a frequency of 65 Hz.
Solution:
We have,
v = 343
f = 65
Using the formula we have,
λ = v/f
= 343/65
= 5.27 m
Problem 3. Calculate the wavelength of a sound wave travelling in water at a frequency of 5 Hz.
Solution:
We have,
v = 1403
f = 20
Using the formula we have,
λ = v/f
= 1403/5
= 280.6 m
Problem 4. Calculate the wavelength of a sound wave travelling in helium at a frequency of 35 Hz.
Solution:
We have,
v = 1007
f = 35
Using the formula we have,
λ = v/f
= 1007/35
= 28.77 m
Problem 5. Calculate the wavelength of a sound wave that travelled in the air for 6 seconds.
Solution:
We have,
v = 343
t = 6
Using the formula we have,
λ = vt
= 343 × 6
= 2058 m
Problem 6. Calculate the wavelength of a sound wave that travelled in water for 8.5 seconds.
Solution:
We have,
v = 1403
t = 8.5
Using the formula we have,
λ = vt
= 1403 × 8.5
= 11925.5 m
Problem 7. Calculate the wavelength of a sound wave that travelled in helium for 12 seconds.
Solution:
We have,
v = 1007
t = 12
Using the formula we have,
λ = vt
= 1007 × 12
= 12084 m
Last Updated :
28 Apr, 2022
Like Article
Save Article
Звуковая волна – период, длина, частота и скорость распространения
Калькуляторы онлайн перевода длины звуковой, инфразвуковой или ультразвуковой
волны в частоту и наоборот. Таблица соответствия
нот полного звукоряда частотам.
Звуковая волна – это механические колебания, которые в результате колебаний молекул вещества распространяются в какой-либо
среде (в газе, жидкости или твёрдом теле) и, достигнув органов слуха человека, воспринимаются им как звук. Источник, создающий
возмущение (колебания воздуха), называется источником звука.
Как уже было сказано, для распространения звука необходима какая-либо упругая среда. Поэтому в вакууме ори, не ори – тебя никто не
услышит, по причине того, что звуковые волны распространяться не смогут, так как там нечему колебаться.., да и слушать там, по большому
счёту, тоже некому.
Так же, как и в случае с электромагнитными волнами, соотношение, связывающее длину звуковой волны с частотой колебаний,
в общем случае выглядит следующим образом:
λ (м) = V (м/сек) / F (Гц), где V (м/сек) — это скорость распространения
звука в среде.
Период колебаний также не претерпел никаких изменений и по-прежнему равен:
T(сек) = 1 / F (Гц) = λ (м) / V (м/сек).
Частота колебаний звукового сигнала F (Гц) – это параметр стабильный, практически не зависящий от среды распространения.
А вот скорость звука V (м/сек), а соответственно и длина звуковой волны – это величины, которые зависят
не только от плотности вещества, но и от его упругости, а в случае с жидкостями и газами ещё – и от температуры, и атмосферного
давления.
Зависимость скорости звуковой волны от свойств упругой среды легко прослеживается по следующей формуле:
V (м/сек) = √Eупр (паскаль) / ρ (кг/м3)
,
где Eупр представляет собой модуль объёмной упругости среды, а ρ – плотность среды.
Модуль упругости, так же как и плотность – это справочные величины, прописанные для конкретных материалов.
В качестве примера, ниже приведена таблица величины скорости распространения звука в различных средах:
| Среда | Скорость звука, м/сек |
| Воздух при 0° | 331 |
| Воздух при 30° | 350 |
| Вода | 1450 |
| Медь | 3800 |
| Дерево | 4800 |
| Железо | 4900 |
| Сталь | 5600 |
Для газов параметры модуля объёмной упругости и плотности имеют ярко выраженную зависимость от температуры и атмосферного давления.
Если углубиться, то скорость звука в газах можно вычислить по следующей формуле:
V (м/сек) = √γ*Ратм / ρ ,
где
γ = cp/сv – это отношение удельной теплоёмкости при постоянном давлении
к удельной теплоёмкости при постоянном объёме, а Pатм – атмосферное давление,
которое связано с температурой газообразной среды.
Поэтому, чтобы никого сильно не грузить, приведу и приближённую зависимость скорости звука (при нормальном
атмосферном давлении) от температуры среды:
V (м/сек) = (331 + 0,6 * T°), где 331 м/сек – это скорость звука при 0°С,
а T° – температура в градусах Цельсия.
Теперь можно совместить формулы и получить простое соотношение, связывающее длину звуковой волны с частотой колебаний с учётом
температуры среды:
λ (м) = (331 + 0,6 * T°) / F (Гц).
Всё это без лишнего напряга несложно посчитать при помощи листа бумаги или деревянных счёт, ну а для пущего упрощения жизни человека,
приведу и пару он-лайн считалок для перевода одного из параметров в другой.
Калькуляторы предполагают расчёты длины и частоты звуковой волны для воздушной среды при нормальном атмосферном
давлении (760 мм ртутного столба).
Онлайн калькулятор расчёта длины звуковой волны по частоте
|
Частота звуковых колебаний f |
||
Температура Т(°С) (по умолчанию 20°) |
||
Длина волны |
Онлайн калькулятор расчёта частоты по длине звуковой волны
|
Длина волны λ при заданной Т |
||
Температура Т(°С) (по умолчанию 20°) |
||
Частота колебаний |
Полный диапазон звуковых частот условно находится в пределах:
16…20 000 Гц.
Ниже ( 0,001…16Гц ) – инфразвук.
Выше ( 20…100кГц ) – низкочастотный ультразвук,
ещё выше (100кГц…1МГц) – высокочастотный ультразвук.
А для интересующихся приведу таблицу соответствия нот стандартного музыкального звукоряда частотам.
| Частота (Гц) | ||||||||||||
| Октава | Нота | |||||||||||
| До | До — диез | Ре | Ми — бемоль | Ми | Фа | Фа — диез | Си | Си- диез | Ля | Соль-бемоль | Соль | |
| C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B | |
| 0 | 16.35 | 17.32 | 18.35 | 19.45 | 20.60 | 21.83 | 23.12 | 24.50 | 25.96 | 27.50 | 29.14 | 30.87 |
| 1 | 32.70 | 34.65 | 36.71 | 38.89 | 41.20 | 43.65 | 46.25 | 49.00 | 51.91 | 55.00 | 58.27 | 61.74 |
| 2 | 65.41 | 69.30 | 73.42 | 77.78 | 82.41 | 87.31 | 92.50 | 98.00 | 103.8 | 110.0 | 116.5 | 123.5 |
| 3 | 130.8 | 138.6 | 146.8 | 155.6 | 164.8 | 174.6 | 185.0 | 196.0 | 207.7 | 220.0 | 233.1 | 246.9 |
| 4 | 261.6 | 277.2 | 293.7 | 311.1 | 329.6 | 349.2 | 370.0 | 392.0 | 415.3 | 440.0 | 466.2 | 493.9 |
| 5 | 523.3 | 554.4 | 587.3 | 622.3 | 659.3 | 698.5 | 740.0 | 784.0 | 830.6 | 880.0 | 932.3 | 987.8 |
| 6 | 1047 | 1109 | 1175 | 1245 | 1319 | 1397 | 1480 | 1568 | 1661 | 1760 | 1865 | 1976 |
| 7 | 2093 | 2217 | 2349 | 2489 | 2637 | 2794 | 2960 | 3136 | 3322 | 3520 | 3729 | 3951 |
| 8 | 4186 | 4435 | 4699 | 4978 | 5274 | 5588 | 5920 | 6272 | 6645 | 7040 | 7459 | 7902 |
Длина звуковой волны

4.1
Средняя оценка: 4.1
Всего получено оценок: 61.
4.1
Средняя оценка: 4.1
Всего получено оценок: 61.
Звук – это механические волны, распространяющиеся в упругих средах, которые могут воспринимать слуховые анализаторы человека. Звук, как и любой другой волновой процесс, имеет ряд характеристик. Рассмотрим такую важную характеристику звука, как длина волны.
Звуковые волны в разных средах
В большинстве случаев мы воспринимаем звук, распространяющийся в воздухе. Воздушная звуковая волна – это ряд распространяющихся в воздухе колебаний плотности – сжатий и разрежений. То есть, звук представляет собой продольную механическую волну.
Для распространения механической волны необходимо наличие упругой среды, которой является не только воздух. А, значит, звук может распространяться и в других средах – в жидкостях и кристаллах. Однако, упругость жидкостей и кристаллов гораздо выше, чем упругость воздуха, поэтому колебания точек в таких средах среде происходит с гораздо большими внутренними напряжениями. Это приводит к тому, что колебания распространяются намного быстрее.
Длина звуковой волны
Если скорость распространения звука в различных средах различна, а его частота фиксирована, то расстояние между соседними сжатиями или разрежениями будет также различно.
Это расстояние и называется длиной звуковой волны. Поскольку частота и период связаны простой обратной зависимостью, формулу длины звуковой волны можно получить как на основе частоты колебаний, так и на основе периода:
$$lambda = vT={vover nu},$$
где:
- $lambda$ – длина волны (м);
- $v$ – скорость звука в среде (м/с);
- $T$ – период звуковых колебаний (с);
- $nu$ – частота звуковых колебаний (Гц).
Из формулы можно видеть, что длина волны прямо пропорциональна скорости звука в среде. При одной и той же частоте длина волны будет наименьшей в газах при невысоких давлениях, будет больше в жидкостях, и самой большой будет в кристаллах. Например, для частоты 500гц:
|
Среда |
v (м/с) |
λ(м) |
|
Воздух |
330 |
0.66 |
|
Вода |
1500 |
3 |
|
Металл |
6000 |
12 |
Роль длины звуковой волны
Звуковые волны способны отражаться от границ сред. Это свойство используется в ряде случаев и человеком и Природой. Если в среде есть какие-то неоднородности – то звуковые волны отражаются от них, и по картине отражения можно делать выводы о расположении неоднородностей. Такой процесс называется эхолокацией. Природное использование эхолокации – поведение летучих мышей и дельфинов. Человек использует эхолокацию в целях дефектоскопии промышленных установок, а также в медицинской практике, для исследования внутренних органов.
Однако, для отражения волны граница между средами должна иметь размеры больше ее длины. Если длина волны будет больше, волна будет просто огибать неоднородность, не отражаясь. Отсюда следует важный вывод, что для обнаружения небольших неоднородностей длина звуковой волны должна быть как можно меньше.
Именно поэтому и человек и Природа для эхолокации использует ультразвук. Малая длина волны ультразвука способствует обнаружению самых мелких неоднородностей.
Что мы узнали?
Звук представляет собой распространяющиеся в среде сжатия и расширения. Длина звуковой волны – это расстояние между ближайшими сжатиями или расширениями. В разных средах длина волны различна, короткие ультразвуковые волны удобны для эхолокации.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.1
Средняя оценка: 4.1
Всего получено оценок: 61.
А какая ваша оценка?