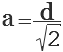Как найти длины сторон квадрата 3 класс

Математика

Компоненты арифметических действий и их взаимосвязь.

1. Компоненты при сложении:

1слагаемое, 2слагаемое, сумма.

1. Компоненты при вычитании:

уменьшаемое, вычитаемое, разность.

1. Компоненты при умножении:

1 множитель, 2множитель, произведение.

1. Компоненты при делении:

делимое, делитель ,частное.

1. Назвать результаты всех действий:

при сложении — сумма

при вычитании — разность

при умножении — произведение

при делении – частное

1. Как найти неизвестное слагаемое?

Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

Х+4=12                        или                4+х=12

Х=12-4                                        х=12-4                                        

Х=8                                                 х=8

8+4=12                                        4+8=12

  12=12                                        12=12

1. Как найти неизвестное уменьшаемое?

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

Х-7=3

Х=3+7

Х=10

10-7=3

        3=3

1. Как найти неизвестное вычитаемое?

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

8-х =5

х=8-5

х=3

8-3=5

   5=5

9                Как найти неизвестный множитель?        

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

х·3=6                                4·х=8

х=6:3                                х=8:4

х=2                                х=2        

2·3=6                                4·2=8

   6=6                                   8=8

10           Как найти неизвестное делимое?

Чтобы найти неизвестное делимое, надо частное умножить на делитель.

х:5=3

х=3·5

х=15

15:5=3

     3=3

1. Как найти неизвестный делитель?

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

6:х=2

х =6:2

х=3

6:3=2

   2=2

Геометрический материал.

1. Что такое квадрат?

Квадрат – это прямоугольник, у которого все стороны равны.

1. Что такое прямоугольник?

Прямоугольник – это четырёхугольник, у которого все углы прямые. Противоположные стороны прямоугольника  равны.

1. Что такое треугольник?

Треугольник – многоугольник, у которого три угла и три стороны.

15     Что такое четырёхугольник?

Четырёхугольник – геометрическая фигура, у которой четыре угла и четыре стороны.

1. Что такое периметр?

Периметр( Ρ) – это сумма длин сторон какой-нибудь геометрической фигуры.

1. Что такое площадь?

Площадь(S) – это внутренняя часть какой-нибудь геометрической  фигуры

(прямоугольника, квадрата и т.д)

1. Как найти периметр квадрата?

У квадрата 4 стороны, равные между собой. Чтобы найти сторону квадрата, нужно Ρ□ разделить на 4.

a□ = Ρ□ : 4

1. Как найти периметр прямоугольника?

Чтобы найти периметр прямоугольника, нужно сложить все 4 стороны   прямоугольника

 Или

сложить длину и ширину прямоугольника и умножить на 2.

        Ρ▬=a+b+a+b

или

    Ρ▬=(a+b)·2

1. Как найти периметр треугольника?

Чтобы найти периметр треугольника, нужно сложить все 3 стороны.

1. Как найти сторону квадрата, если известен периметр? 

У квадрата 4 стороны, равные между собой. Чтобы найти сторону квадрата, нужно Ρ разделить на 4.

a=Ρ:4

1.         Как найти сторону прямоугольника, если известен периметр и другая сторона? 

Чтобы найти сторону прямоугольника, нужно Ρ▬разделить на 2  и  вычесть другую сторону.

a▬=Ρ▬:2 – b

b▬=Ρ▬:2 – a

22        В каких единицах измеряется периметр?

    Периметр измеряется в мм, см, дм, метрах.

23         Как найти площадь квадрата?

Площадь квадрата равна произведению двух его сторон.

S□ =  a · a

24          Как найти площадь прямоугольника?

Чтобы найти площадь прямоугольника, надо длину прямоугольника умножить на его ширину.

S█ =  a · b

25          Как найти сторону прямоугольника, если известна площадь и другая его сторона?

Чтобы найти одну из сторон прямоугольника,  нужно площадь прямоугольника разделить на известную сторону.

a▬=S▬ :  b

b▬= S ▬ : a

   26        В каких единицах измеряется площадь?

   Площадь измеряется в квадратных единицах: мм², см², дм², м².

27      Назвать единицы длины.

Единицы длины — мм, см, дм, м, км.

28           Рассказать таблицу мер длины.

1см  =  10мм

1дм  =  10см

1дм  =  100мм

1м  =    10 дм

1м  =  100 см

1км = 1000м

29       Сколько  квадратных сантиметров

в 1квадратном метре?

1м²  =  10 000см²  

30      Сколько  квадратных  дециметров  

в 1 квадратном  метре?

1м²  =  100дм²  

31            Рассказать  таблицу мер площади.

1м²  =  100дм²  = 10 000см²  

1дм²  = 100см²  =  10 000мм²

1см²  =  100мм²

Масса.

32            Назвать единицы массы.

Масса измеряется в граммах, килограммах, центнерах, тоннах.

33           Рассказать таблицу мер массы.

1кг  = 1000г

1ц  =  100кг

1т  =  10ц

1т  =  1000кг

Время.

34        Назвать  единицы измерения времени.

Время  измеряется секундами, минутами, часами, сутками, неделями, месяцами, годами, веками.

35           Рассказать таблицу мер времени.

1мин  =  60сек.

1час  =  60мин

1час  =  3600сек.

1сут.  =  24часа

1год  =  12мес.  =  365сут.  или  366сут.

1век  =  100лет

Взаимосвязь скорости, времени и расстояния.

36     Как  найти  скорость?

Чтобы найти скорость ( v ), надо расстояние ( S ) разделить на время ( t ), затраченное в пути.

v = S : t

37    Как найти время?

Чтобы найти время ( t ), надо расстояние ( S ) разделить на скорость ( v ).

t = S : v

38    Как найти расстояние?

Чтобы найти расстояние ( S ),  нужно скорость ( v ) умножить на время ( t ).

S = v · t

Взаимосвязь цены, количества, стоимости.

39    Что такое цена?

Цена – стоимость одного предмета, единицы товара.

40     Как найти стоимость?

Чтобы найти стоимость, нужно цену умножить на количество.

Ст = Ц · К

41     Как найти цену?

Чтобы найти цену, нужно стоимость разделить на количество.

Ц  =  Ст : К

42   Как найти  количество?

Чтобы найти количество, нужно стоимость разделить на цену.

К = Ст : Ц

Задачи на дроби.

43

Дробь  — ⅔

2 – числитель

3 – знаменатель

44  Как найти дробь числа?

Чтобы найти дробь числа, нужно число разделить на знаменатель, а потом умножить на числитель.

45      Как найти число по дроби?

Чтобы  найти число по дроби, нужно число разделить на числитель и умножить на знаменатель.

Взаимосвязь работы, времени и производительности.

46    Что такое производительность?

         Как найти производительность?

Производительностью ( v ) называют работу, выполненную за единицу времени.

Чтобы найти производительность ( v ), надо всю выполненную работу разделить на время.

v  =  A  :  t

47    Как найти выполненную работу?

Выполненная работа равна производительности, умноженной на время работы.

A  =  v  · t

48   Как найти время работы?

Чтобы узнать время работы, надо работу разделить на производительность.

t  =  A  :  v

49   Как  найти среднее арифметическое?

Чтобы найти среднее арифметическое надо сумму разделить на число слагаемых.

• Предыдущее

Вы перешли к вопросу Как найти ученику 3 — го класса сторону квадрата если известна площадь?. Он относится к категории Математика,
для 1 — 4 классов. Здесь размещен ответ по заданным параметрам. Если этот
вариант ответа не полностью вас удовлетворяет, то с помощью автоматического
умного поиска можно найти другие вопросы по этой же теме, в категории
Математика. В случае если ответы на похожие вопросы не раскрывают в полном
объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части
сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете
ознакомиться с вариантами ответов пользователей.

Найдите правильный ответ на вопрос ✅ «Как найти ученику 3-го класса сторону квадрата если известна площадь? …» по предмету 📘 Математика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.

Смотреть другие ответы

Как найти сторону квадрата?

Часто в геометрии необходимо найти длину стороны квадрата, при этом известны такие его параметры: периметр, площадь, длина диагонали.

Квадрат — это ромб или прямоугольник, стороны которого равны между собой. Углы квадрата также равны между собой и имеют по 90° каждый. Рассмотрим, как найти сторону квадрата имея один из вышеперечисленных параметров.

Нахождение стороны квадрата по его периметру

В этом случае, чтобы найти длину стороны квадрата, необходимо число значения периметра квадрата разделить на 4 (поскольку квадрат имеет 4 стороны, равные между собой): z = P/4, где z — это длина стороны квадрата; P — это периметр квадрата.

Единицей измерения одной стороны квадрата будет та же самая единица измерения длины, как у его периметра. Например, если задан периметр квадрата в миллиметрах, то также длина его стороны будет в миллиметрах.

Например: Задан периметр квадрата 40 метров. При решении этой задачи мы получим: z = 40/4 = 10. Длина стороны квадрата — 10 метров.

Нахождение стороны квадрата по его площади

В этом случае, чтобы найти длину стороны, необходимо добыть квадратный корень числа значения площади (поскольку площадь квадрата равна квадрату его стороны): z = vS, где z — это длина стороны квадрата; S — это площадь квадрата.

Единицей измерения одной стороны квадрата будет та же самая единица измерения длины, как у его площади. Например, если задана площадь квадрата в миллиметрах квадратных — длина его стороны будет просто в миллиметрах.

Например: Задана площадь квадрата 16 квадратных метров. При решении этой задачи мы получим: z = v9 = 3. Длина стороны квадрата — 4 метра.

Нахождение стороны квадрата по его диагонали

В этом случае длина стороны квадрата будет равна длине диагонали квадрата, разделенной на корень квадратный из 2 (за теоремой Пифагора, поскольку смежные стороны квадрата и его диагональ составляют равнобедренный прямоугольный треугольник). Чтобы найти сторону квадрата по диагонали необходимо: z = d/v2 (так как z 2 + z 2 = d 2 ), где: z — это длина стороны квадрата; d — это длина диагонали квадрата.

Единицей измерения одной стороны квадрата будет та же самая единица измерения длины, как у его диагонали. Например, если задана диагональ квадрата в миллиметрах, то также длина его стороны будет в миллиметрах.

Например: Задана диагональ квадрата 20 метров. При решении этой задачи мы получим: z = 20/v2, это приблизительно равно 20/1,4142. Длина стороны квадрата — 20/v2 метров, или, приблизительно, 14,142 метров.

Теперь Вы знаете, как найти длину стороны квадрата, если заданы его периметр, площадь или длина диагонали.

Сторона квадрата

Квадрат, наряду с кругом, считается идеальной геометрической фигурой. Квадрат является не только параллелограммом, но и ромбом, и прямоугольником одновременно, так как у него все стороны равны и все углы прямые. Более того, квадрат является представителем ряда правильных многоугольников, поэтому к нему относятся и их свойства тоже. Вычислить сторону квадрата можно несколькими различными способами: через периметр квадрата, через площадь квадрата или через диагональ квадрата, а также радиусы вписанной и описанной окружностей.

Поскольку все стороны квадрата между собой равны, а периметр многоугольника – это сумма всех его сторон, то найти сторону можно, разделив периметр на четыре (количество равных сторон):

Площадь квадрата – это его сторона, возведенная во вторую степень, следовательно, если нам нужно найти сторону через площадь, то необходимо извлечь из нее квадратный корень:

Если дана диагональ квадрата, то исходя из теоремы Пифагора в прямоугольном треугольнике, который образует диагональ, сторона будет равна диагонали, деленной на корень из двух:
a 2 +a 2 =d 2
2a 2 =d 2

Сторона квадрата

Четырехугольник, у которого все четыре стороны равны, противоположные — параллельны, а углы — прямые, называется квадратом. Диагональ квадрата (d) делит его на 2 одинаковых прямоугольных треугольника, у которых гипотенузой является диагональ (d) квадрата, а катетами — две одинаковых стороны квадрата (а). Как известно по теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Т.е. d 2 = а 2 + а 2 = 2а 2 .
Отсюда, сторона квадрата (а) равна диагонали квадрата (d) деленной на корень квадратный из двух.