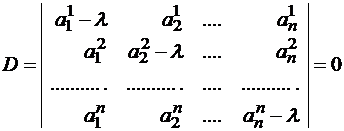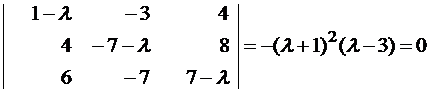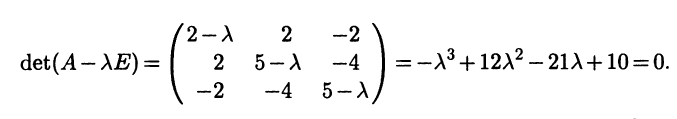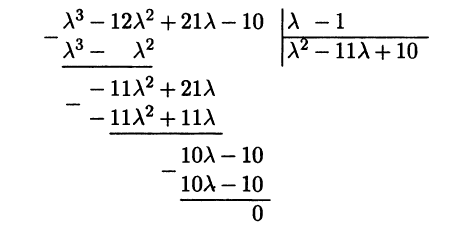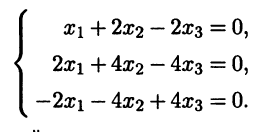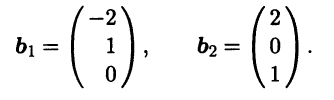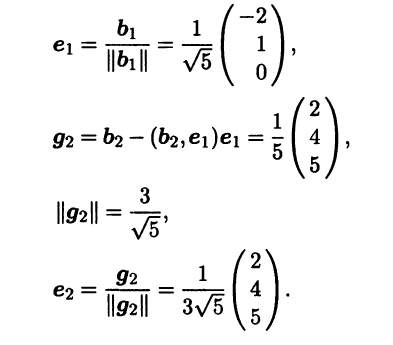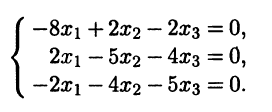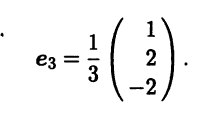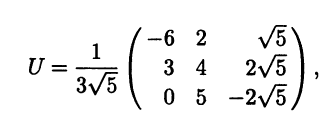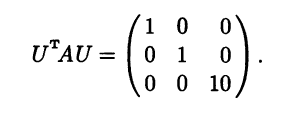Prerequisite: Eigenvalues and eigenvectors
Let A and B be two matrices of order n. B can be considered similar to A if there exists an invertible matrix P such that B=P^{-1} A P This is known as Matrix Similarity Transformation.
Diagonalization of a matrix is defined as the process of reducing any matrix A into its diagonal form D. As per the similarity transformation, if the matrix A is related to D, then
and the matrix A is reduced to the diagonal matrix D through another matrix P. Where P is a modal matrix)
Modal matrix: It is a (n x n) matrix that consists of eigen-vectors. It is generally used in the process of diagonalization and similarity transformation.
In simpler words, it is the process of taking a square matrix and converting it into a special type of matrix called a diagonal matrix.
Steps Involved:
Step 1: Initialize the diagonal matrix D as:
where λ1, λ2, λ3 -> eigen values
Step 2: Find the eigen values using the equation given below.
where, A -> given 3×3 square matrix. I -> identity matrix of size 3×3. λ -> eigen value.
Step 3: Compute the corresponding eigen vectors using the equation given below.
where, λi -> eigen value. Xi -> corresponding eigen vector.
Step 4: Create the modal matrix P.
Here, all the eigenvectors till Xi have filled column-wise in matrix P.
Step 5: Find P-1 and then use the equation given below to find diagonal matrix D.
Example Problem:
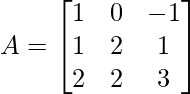
Problem Statement: Assume a 3×3 square matrix A having the following values:
Find the diagonal matrix D of A using the diagonalization of the matrix. [ D = P-1AP ]
Solution:
Step 1: Initializing D as:
Step 2: Find the eigen values. (or possible values of λ)
Step 3: Find the eigen vectors X1, X2, X3 corresponding to the eigen values λ = 1,2,3.
Step 5: Creation of modal matrix P. (here, X1, X2, X3 are column vectors)
Step 6: Finding P-1 and then putting values in diagonalization of a matrix equation. [D = P-1AP]
We do Step 6 to find out which eigenvalue will replace λ1, λ2, and λ3 in the initial diagonal matrix created in Step 1.
![Rendered by QuickLaTeX.com begin{array}{l} begin{array}{l} quad P=left[begin{array}{ccc} 1 & -2 & 1 \ -1 & 1 & -1 \ 0 & 2 & -2 end{array}right] \ operatorname{det}(P)=(1)[(-2)(1)-(-1)(2)]-(-2)[(-2)(-1)-(0)(-1)]+(1)[(2)(-1)- \ (0)(1)] \ =[0+(4)+(-2)] \ =2 end{array}\ text { Since } operatorname{det}(P) neq 0 Longrightarrow text { Matrix } P text { is invertible. } end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-95a4873225048341204822e8e209f569_l3.png)
We know that
On solving, we get
Putting in the Diagonalization of Matrix equation, we get
![Rendered by QuickLaTeX.com begin{array}{l} quad D=P^{-1} A P \ D=frac{1}{2}left[begin{array}{ccc} 0 & -2 & 1 \ -2 & -2 & 0 \ -2 & -2 & -1 end{array}right]left[begin{array}{ccc} 1 & 0 & -1 \ 1 & 2 & 1 \ 2 & 2 & 3 end{array}right]left[begin{array}{ccc} 1 & -2 & 1 \ -1 & 1 & -1 \ 0 & 2 & -2 end{array}right] \ D=left[begin{array}{lll} 1 & 0 & 0 \ 0 & 2 & 0 \ 0 & 0 & 3 end{array}right] end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-701b5697ed528cee5a6dafd21522243b_l3.png)
Matlab
clear all
clc
disp("MATLAB Implementation for Diagonalization
of a Square Matrix | GeeksforGeeks")
A = input("Enter a matrix A : ");
[P , D] = eig(A);
D1 = inv(P)*(A)*(P);
disp("Diagonal form 'D' of Input Matrix 'A' is:")
disp(D1)
Output:
For the Matrix:
For the Matrix:
Last Updated :
27 Apr, 2022
Like Article
Save Article
Собственные числа и собственные векторы линейного оператора
Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x 1, x 2, . x m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x 1, x 2, . x m оператора A с попарно различными собственными числами λ1, λ2, …, λm линейно независимы.
3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.
Итак, если имеется n линейно независимых собственных векторов x 1, x 2, . x n, соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 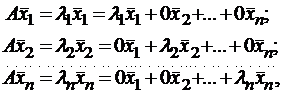

Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.
Теорема. Матрица линейного оператора A в базисе < ε i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.
Правило отыскания собственных чисел и собственных векторов
Система (1) имеет ненулевое решение, если ее определитель D равен нулю
Пример №1 . Линейный оператор A действует в R3 по закону A· x =(x1-3x2+4x3, 4x1-7x2+8x3, 6x1-7x2+7x3), где x1, x2, . xn — координаты вектора x в базисе e 1=(1,0,0), e 2=(0,1,0), e 3=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e 1=(1,4,6)
A· e 2=(-3,-7,-7)
A· e 3=(4,8,7) 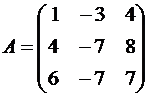
Составляем систему для определения координат собственных векторов:
(1-λ)x1-3x2+4x3=0
x1-(7+λ)x2+8x3=0
x1-7x2+(7-λ)x3=0
Составляем характеристическое уравнение и решаем его:
Пример №2 . Дана матрица 
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор
Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой ai k =ak i .
Замечания .
- Все собственные числа симметрической матрицы вещественны.
- Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.
Свойства собственных векторов
Для любого собственного значения Хк(А) существует п- кг линейно независимых собственных векторов
образующих фундаментальную систему решений однородной системы уравнений (А — ХкЕ)Х = 0. Здесь гк = г(А — ХкЕ) — ранг матрицы А — ХкЕ.
Множество всех собственных векторов А(Хк), соответствующих собственному значению Хк <А)матрицы Л, совпадает с общим решением однородной системы уравнений (Л — ХкЕ)Х = ©, т. е.
Любые два собственных вектора F и F(X2), соответствующие различным собственным значениям А, ф А2 характеристического уравнения А — ХЕI = 0 матрицы А, являются линейно независимыми.
Если F(A,j), F(Х2) линейно независимые, то равенство F(X<)a + + Е(А9)Р = 0 выполняется только при а = Р = 0. Предположим, что F(Xl)а + Е(А9)Р = 0 при р * 0. Так как F(Xl) и F(X2) — собственные векторы, то они удовлетворяют уравнению АХ = XX, т. е.
Умножим первое равенство на а, второе на Р и сложим, получим
По предположению F(Xx)a + Е(А9)р = 0, тогда Составим и решим систему уравнений
Так как по условию X,, * Xv а по предположению р * 0, то F(X2) = 0. Это противоречит тому, что собственным вектором может быть только ненулевой вектор.
Система собственных векторов, составленная из систем собственных векторов, соответствующих различным собственным значениям АДА!), А2(Л). АП(Л), является линейно независимой.
Пример 7.1. Найти собственные значения и собственные векторы матрицы
Решение. Составим систему (А — ХЕ)Х = 0, которая в координатной записи имеет вид
Приравняем определитель матрицы этой системы к нулю
Раскроем этот определитель по правилу треугольника, получим характеристическое уравнение
Найдем характеристические значения матрицы А (корни этого уравнения):
Для каждого из характеристических значений найдем собственные векторы.
При = 1 система (7.1) принимает вид
Система является разрешенной. Включим в набор разрешенных неизвестных х< и хт Свободной неизвестной х3 придадим значение д’3 = 1, получим решение С(Х1) = (1, 0, -1), которое является собственным вектором.
Аналогично найдем соответствующие собственным значениям Х2 и Х3 собственные векторы
Приведение квадратной матрицы к диагональному виду
Матрицу А можно привести к диагональному виду с помощью матрицы Г, если матрица Т
г АТявляется диагональной.
Для нахождения матрицы Т необходимо найти собственные значения и собственные векторы матрицы А. Матрицу Т составляют из собственных векторов-столбцов. Если эта матрица является квадратной, то матрицу А можно привести к диагональному виду.
Пример 7.2. Матрицу
привести к диагональному виду.
Решение. В предыдущем примере для матрицы А были найдены собственные значения
и соответствующие им собственные векторы Из этих векторов составим матрицу Т
Найдем обратную матрицу Т 1 с использованием присоединенной матрицы.
Найдем произведение матриц Т 1 АТ:
Упражнения
7.1. Найти собственные значения и собственные векторы матрицы А. Записать матрицу Т приводящую матрицу А к диагональному виду и Гр
Приведение квадратной матрицы к диагональному виду. Критерии приводимости квадратной матрицы к диагональному виду
Страницы работы
Фрагмент текста работы
§ 2. Приведение квадратной матрицы к диагональному виду
Говорят, что квадратная матрица А с элементами из поля P приводится к диагональному виду над P, если существует невырожденная квадратная матрица Т с элементами из P такая, что матрица – диагональная.
Критерии приводимости квадратной матрицы к диагональному виду. 1. Если А – квадратная матрица -го порядка с элементами из поля P, – линейное пространство над Р, – тот линейный оператор, матрица которого в некотором базисе пространства совпадает с А, то для приводимости матрицы А к диагональному виду над полем Р необходимо и достаточно, чтобы в существовал базис, состоящий из собственных векторов оператора f.
2. Для того чтобы квадратная матрица А n-го порядка приводилась к диагональному виду над полем Р необходимо и достаточно, чтобы все корни ее характеристического уравнения принадлежали этому полю и для каждого из них выполнялось условие
, (7)
где – кратность корня характеристического уравнения матрицы А.
При решении задач первый критерий, пожалуй, проще в применении, хотя студенты обычно предпочитают второй.
В том случае, когда все характеристические числа матрицы А различны и принадлежат полю Р, эта матрица приводится к диагональному виду над Р. Если матрица А приводится к диагональному виду – матрице , то диагональными элементами последней являются собственные значения матрицы А, а матрица Т, приводящая А к диагональному виду, есть не что иное, как матрица перехода от исходного базиса к базису из собственных векторов.
Из всего вышесказанного вытекает, что для приведения квадратной матрицы к диагональному виду над полем Р следует:
1) составить характеристический многочлен матрицы А и найти его корни. Если какой-либо из них не принадлежит полю Р, то А к диагональному виду не приводится;
2) если все корни характеристического уравнения принадлежат полю Р, то для кратных корней проверить условие (7) (для однократных оно выполняется всегда). Если для какого-то из корней (7) не выполняется, то А к диагональному виду не приводится;
3) если для каждого из собственных значений условие (7) выполняется, то А к диагональному виду приводится. Записываем этот диагональный вид – матрицу , располагая на ее главной диагонали собственные значения в произвольном порядке, причем каждое из значений повторяется столько раз, какова его кратность;
4) для каждого из найденных собственных значений находим собственные векторы и составляем из них базис;
5) записываем матрицу Т, приводящую А к диагональному виду, – матрицу перехода от исходного базиса к базису из собственных векторов, сохраняя порядок, установленный матрицей .
Пример 1. Найти диагональный вид матрицы А над полем действительных чисел и невырожденную матрицу Т, приводящую к этому диагональному виду, если
.
►Проводим решение по намеченному плану.
+
.
2.Все корни действительны и однократны, поэтому матрица А приводится к диагональному виду.
3. .
4. Все собственные векторы можно найти с помощью алгебраических дополнений. Кроме того, вспомним, что, если мы нашли один собственный вектор, то любой вектор, ему коллинеарный, также является собственным с тем же самым собственным значением.
: ; ,
(алгебраические дополнения к элементам первой строки);
: ; =
(алгебраические дополнения к элементам второй строки);
: ; ,
(алгебраические дополнения к элементам первой строки).
5. Составляем матрицу перехода от исходного базиса к, построенному базису , записывая в столбцы матрицы координатные столбцы векторов , и соответственно:
.◄
Пример 2. Проверить, приводится ли матрица А к диагональному виду. Если приводится, найти этот диагональный вид и невырожденную матрицу Т, приводящую нему.
.
►Составляем и решаем характеристическое уравнение:
.
Матрица имеет только одно собственное значение , но его кратность равна трем. Проверяем выполнение условия (4.58):
.
Условие не выполняется, значит, матрица к диагональному виду не приводится.◄
Пример 3. Проверить, приводится ли матрица А к диагональному виду. Если приводится, найти этот диагональный вид и невырожденную матрицу Т, приводящую нему.
.
► Решение опять проводим по намеченному плану.
–
.
2. Проверяем выполнение условия (7) для кратного корня:
. (8)
Таким образом, , условие выполняется, матрица к диагональному виду приводится.
3. .
4. Так как , то , т. е для первого собственного значения можно найти два линейно независимых собственных вектора. По одной из строк матрицы (8), разделив все ее элементы на общий множитель, выписываем единственное уравнение для отыскания координат собственных векторов и решаем его: , . В качестве двух линейно независимых решений можно взять, например
http://bstudy.net/719731/estestvoznanie/svoystva_sobstvennyh_vektorov
http://vunivere.ru/work86118
Во
многих практических задачах бывает
важно привести матрицу линейного
преобразования к простейшей форме.
Очевидно, простейшей формой для матрицы
является диагональная форма. В настоящей
главе мы рассмотрим достаточные условия
того, чтобы, за счет выбора базы линейного
пространства, можно было получить
диагональную матрицу линейного
преобразование
.
Для
решения этой задачи сначала докажем
теорему, непосредственно использующую
определение собственных значений и
собственных векторов линейного
преобразования:
|
Теорема: (10.5) |
Линейное |
►Действительно,
равенство:
==
равносильно тому, что в
—
ой строке матрицы преобразования
в указанной базе, равны нулю все элементы,
стоящие вне главной диагонали, а на
главной диагонали стоит число
:
=

.
◄
Следующая теорема
устанавливает важное отношение между
собственными векторами:
|
Теорема: (10.6) |
Собственные |
►Допустим,
что всё-таки нашлись такие, не равные
нулю, числа
и
,
что выполняется равенство: +
=0. (16)
Применим
к (16) преобразование
:
+
=0,
и вычтем из этого равенства равенство
(16), умноженное на число
.
Получим невозможное равенство:
(
–
)
=0,
так
как по условию собственные числа
и
— различны.
◄
Следствие:
Всякая матрица, все
характеристические корни которой
действительны, подобна
диагональной матрице, то есть матрица
преобразования
приводится
к диагональной форме,
если существует база
,
составленная из собственных векторов
линейного преобразования
.
Рассмотренные примеры достаточно полно
иллюстрируют особенности поиска
диагональной матрицы для разных линейных
преобразований
.
☺☺
Пример
10–15:Найти собственные
векторы линейного преобразования
,
заданного в некотором базисе
матрицей:
.
Решение:
1).
Составляем характеристический многочлен
и находим его корни, используя свойства
определителя и правила нахождения
корней многочлена:
=
=
=
,
откуда
корни многочлена
:
=
-1,
= 6.
2).
Записываем систему уравнений для
нахождения собственных векторов
линейного преобразования, соответствующим
найденным собственным значениям:

3).
Для собственного значения
=
-1 система (A)
принимает вид:

Так
как определитель системы равен нулю,
то независимых уравнений только одно.
Назначаем свободной неизвестной
=–
,
тогда
=
,
получаем собственный вектор:
=
(1,
-1).
4).
Для собственного значения
=
6 система (A)
принимает вид:
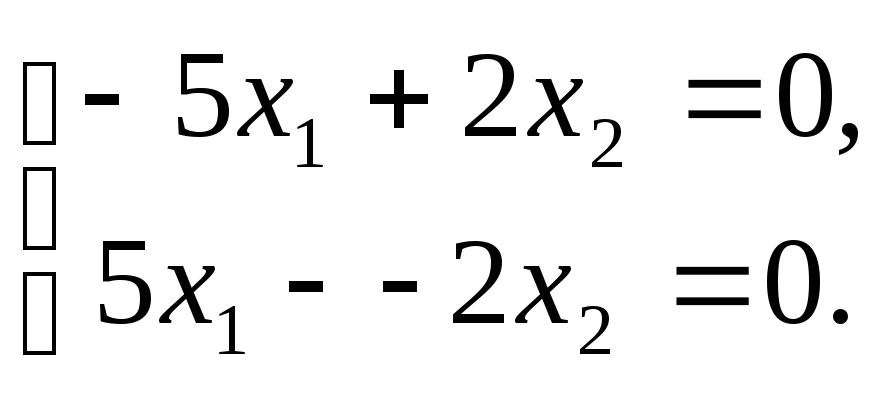
Так
как определитель системы равен нулю,
то независимых уравнений только одно.
Назначаем свободной неизвестной
=5
,
тогда
=2,
получаем собственный вектор:
=
(2,
5).
3)
Построим базис из собственных векторов
и составляем для этого базиса диагональную
матрицу линейного преобразования:
=
.
Ответ:
собственные значения:
=
-1,
= 6; собственные векторы:
=
-1 имеем:
=
(1,
-1), для
=
6
имеем:
=
(2,
5).
Диагональная
форма матрицы линейного преобразования
в базисе
имеет простейший вид:
.
Пример
10–16:Линейное
преобразование
,
заданного матрицей:

.Можно ли привести матрицу преобразования
к диагональному виду. Если можно, найти
базис, в котором такая запись возможна.
Решение:
1).
Составляем характеристический многочлен
и находим его корни, используя свойства
определителя и правила нахождения
корней многочлена:
=
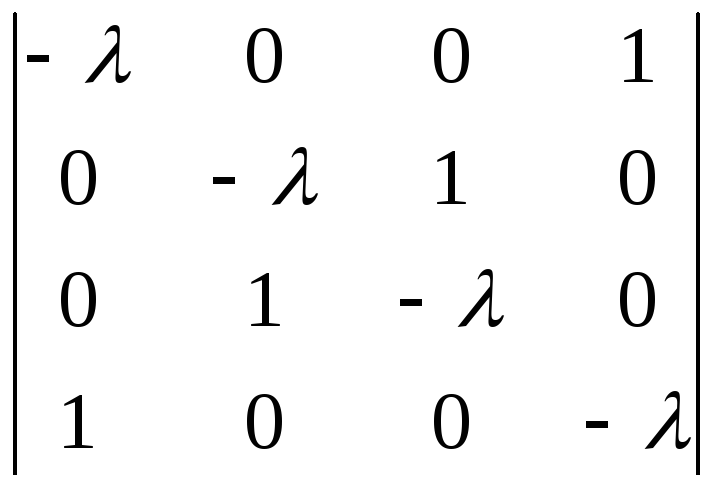
(1)
=
(2)
→
=(1–
)·

(3)
=(1–)·
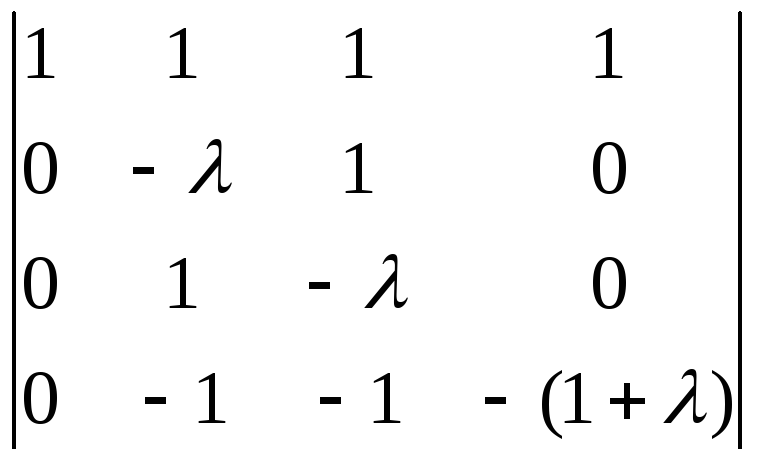
(4)
→
=(1–
)·

(5)
=–(1–)·(1+
)·
=
.
Выполнены
операции:
(1):
[R1]+[R2]+[R3]+[R4].
(2):
вынесен общий множитель первой строки.
(3):
[R4]–[R1].
(4):
разложим определитель по первому
столбцу. (5):
разложим
определитель по третьему столбцу.
Получены
характеристические корни: =
=1,
=
=–1.
2).
Записываем систему уравнений для
нахождения собственных векторов
линейного преобразования, соответствующим
найденным собственным значениям:

3).
Для собственного значения =
1 система (A)
принимает вид:

(B)
Ранг
системы уравнений (B)
равен двум. Это значит, что ФСР этой
системы уравнений содержит два независимых
решения. Примем: =
,
=
.
Найдём
фундаментальную систему решений для
системы (B):
-
x1
x2
x3
x4
α1
0
1
1
0
α2
1
0
0
1
Векторы-решения
и
есть ФСР для
=1,
тогдасобственные
векторы: =(0,1,1,0),
=(1,0,0,1).
4).
Для собственного значения =–1
система (A)
принимает вид:
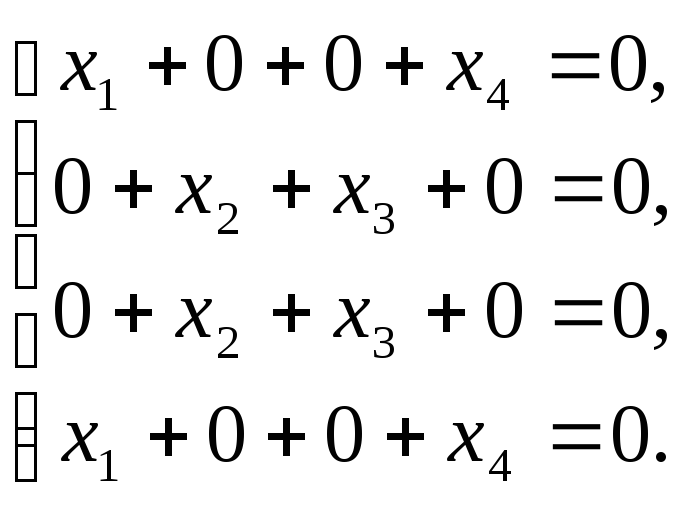
(C)
Ранг
системы уравнений (C)
равен двум. Это значит, что ФСР этой
системы уравнений содержит два независимых
решения. Примем: =
,
=
.
Найдём
фундаментальную систему решений для
системы (C):
-
x1
x2
x3
x4
α1
0
1
-1
0
α2
1
0
0
-1
Векторы-решения
и
есть ФСР для
=–1,
тогдасобственные
векторы: =(0,1,-1,0),
=(1,0,0,-1).
5).
В соответствии с теоремой 10.4 совокупность
векторов ,
,
,
независима, и её достаточно, чтобы
построить базу линейного пространства
.
Это значит: матрица заданного линейного
преобразования к диагональному виду
приводится.
Ответ:
матрица
приводится к диагональному виду:
в базе: =(0,1,1,0),
=(1,0,0,1),
=(0,1,-1,0),
=(1,0,0,-1).
☻
Набор поясняющих
примеров иллюстрирует наиболее сложные
теоретические вопросы и предлагает
рациональные схемы вычислений участвующих
величин.
Соседние файлы в папке ЛА и АГ пособие
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Матрица А линейного оператора А при замене базиса преобразуется согласно формуле А’ = U-1AU, где U — матрица перехода (см. теорему 4.6). Если речь идет об евклидовом пространстве и переходе из одного ортонормированного базиса в другой, матрица перехода U является ортогональной (см. теорему 7.5). Согласно свойству 7.2, такая матрица удовлетворяет соотношению U-1 = UT. Поэтому для случая ортонормиро- ванных базисов формулу преобразования матрицы линейного оператора можно записать следующим образом:
А’ = UTAU. (7.5)
Теорема 7.7. Для любой симметрической матрицы М существует такая ортогональная матрица U, что UTMU = Λ, где Λ = diag(λ1, …, λn) — диагональная матрица, диагональными элементами которой являются собственные значения матрицы М, повторяющиеся согласно их кратности.
◄ Доказательство теоремы основано на следствии 6.4, теореме 7.5 и свойстве 7.2. Согласно следствию 6.4, для симметрической матрицы М порядка n существует такая невырожденная матрица Р, что Р-1МР = Λ = diag(λ1, …, λn), где в последовательности λ1, …, λn указаны все собственные значения матрицы М с учетом их кратностей. Из доказательства того же следствия вытекает, что Р является матрицей перехода между ортонормированными базисами. Поэтому Р — ортогональная матрица (см. теорему 7.5) и Р-1 = РT (см. свойство 7.2). Следовательно, РTМР = Р-1МР = Λ, т.е. в качестве матрицы U в формулировке теоремы можно взять Р. ►
Преобразование (7.5) с ортогональной матрицей U иногда называют ортогональным преобразованием матрицы А. Поэтому теорему 7.7 можно сформулировать так: любая симметрическая матрица ортогональным преобразованием приводится к диагональному виду. Чтобы найти соответствующую матрицу U, о которой говорится в этой теореме, необходимо:
1) найти собственные значения матрицы М;
2) для каждого собственного значения найти набор собственных векторов, соответствующих этому собственному значению, при этом эти собственные векторы должны быть линейно независимыми и их количество должно равняться кратности собственного значения;
3) преобразовать системы собственных векторов, полученные для каждого собственного значения, в ортонормированные при помощи процесса ортогонализации Грама — Шмидта. Объединить ортонормированные системы для каждого собственного значения в единую систему векторов, которая будет ортонормированным базисом евклидова пространства;
4) выписать матрицу U, столбцами которой являются координаты векторов построенной ортонормированной системы.
Пример 7.4. Найдем ортогональное преобразование, приводящее симметрическую матрицу
к диагональному виду.
1. Находим собственные значения матрицы А. Для этого составляем ее характеристическое уравнение
Это уравнение третьей степени. Так как его коэффициенты являются целыми числами, то целое число может быть его корнем лишь в случае, если оно делитель свободного члена. Поэтому мы можем поискать корни среди чисел ±1, ±2, ±5. Подстановкой в уравнение убеждаемся, что одним из корней является λ1 = 1.
Найденный корень позволяет разложить левую часть харак-теристического уравнения на линейный и квадратичный мно-жители, например, при помощи деления характеристического многочлена на х — 1 «в столбик»
Получаем разложение
(λ — 1)(λ2 — 11λ + 10) =0,
откуда находим оставшиеся два корня λ2 = 1, λ3 = 10. Таким образом, имеются два собственных значения: 1 кратности 2 и 10 кратности 1.
2-3. Найдем для собственного значения λ1,2 = 1 кратности 2 два линейно независимых собственных вектора. Для этого нужно найти фундаментальную систему решений однородной системы линейных алгебраических уравнений (А — Е)х = 0, т.е. системы
Ранг матрицы этой системы равен единице (все строки матрицы системы пропорциональны), поэтому можно отбросить второе и третье уравнения, оставив первое
х1 + 2x2 — 2х3 = 0.
В качестве независимых переменных выбираем x2, х3. Фундаментальную систему решений составляют x2 = 1, х3 = 0, х1 = — 2 и x2 = 0, х3 = 1, x1 = 2, т.е. векторы
Найденные собственные векторы, соответствующие собственному значению λ1,2 = 1, линейно независимы, но ортогональными не являются. Построим по ним другую, ортонормированную пару собственных векторов е1, e2 при помощи метода ортогонализации Грама — Шмидта:
Для собственного значения λ3 = 10 система линейных алгебраических уравнений имеет вид (А — 10Е)х = 0, или
В качестве ее фундаментальной системы решений можно взять одно ненулевое решение, например вектор b3 = (1 2 -2)T . Нормируя этот вектор, получаем
Найденные векторы e1, е2, е3 образуют ортонормированный базис из собственных векторов.
4. Составим из найденных векторов еi матрицу
которая и является искомой.
Убедиться в том, что матрица U определена правильно, можно при помощи подстановки матрицы U и заданной матрицы А в следующее тождество:
Замечание 7.4. В случае n = 3 при λ1 = λ2 ≠ λ3 собственные векторы удобнее с точки зрения экономии вычислений находить в следующем порядке. Сначала для собственного значения кратности 1 (λ3 = 10 в рассмотренном примере) найти собственный вектор и нормировать его. Обозначим полученный вектор, например, е3. Затем для собственного значения кратности 2 (λ1,2 = 1 в рассмотренном примере) найти один собственный вектор и нормировать его. Получим вектор e1. Векторы е1 и е3 будут ортогональными согласно теореме 6.4. Недостающий третий вектор ортонормированного базиса может быть найден при помощи векторного произведения: е2 = e1 × е3.
Описанный прием позволяет избежать процесса ортогона- лизации. Точно так же можно не применять процесс ортогона- лизации при n = 2, так как, зная один вектор е1 ортонормированного базиса, мы можем получить второй поворотом первого на 90°. Для этого достаточно поменять две координаты вектора e1 местами, а у первой из них к тому же изменить знак. При n > 3 приемов, аналогичных описанным, нет.
Вопросы и задачи
- Опишите множество всех ортогональных матриц второго порядка.
- Пользуясь результатами задачи 7.1, докажите, что любой ортогональный оператор в евклидовом пространстве V2 является либо поворотом вектора на некоторый угол, либо симметрией относительно некоторой прямой, либо произведением таких операторов.
- Докажите, что произведение ортогональных операто-ров является ортогональным оператором. Можно ли утверждать, что: а) сумма ортогональных операторов есть ортогональный оператор? б) произведение ортогонального оператора на число есть ортогональный оператор?
- Докажите, что линейный оператор А в евклидовом пространстве тогда и только тогда является ортогональным, когда А*А = I.
- Докажите, что если Н — инвариантное подпростран-ство для ортогонального оператора А, то и H⊥ — тоже инвариантное подпространство этого оператора.
- Докажите, что собственными значениями ортогонального оператора могут быть лишь числа 1 и -1.
- Приведите пример ортогонального оператора, не имеющего собственных векторов. Какой может быть размерность евклидова пространства, в котором есть такие операторы?
- Докажите, что любой ортогональный оператор в пространстве V3 имеет собственный вектор. Используя результаты задач 7.2 и 7.5, опишите множество ортогональных операторов в V3.
- Докажите, что любому перемещению твердого тела вокруг неподвижной точки из одного положения в другое соответствует ортогональный оператор в пространстве V3 и что эти положения связаны между собой вращением тела вокруг неподвижной оси. Эта ось проходит через неподвижную точку и параллельна собственному вектору указанного ортогонального оператора.
- Приведите пример оператора, одновременно являющегося и самосопряженным, и ортогональным.
- Приведите к диагональному виду ортогональным преобразованием следующие симметрические матрицы:
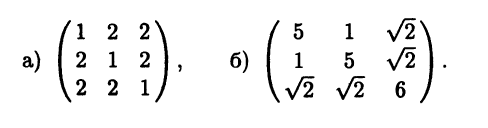
-
Линейные операции над векторами
-
Базис. Cкалярное произведение
-
Векторное и смешанное произведения векторов
-
Декартова система координат. прямая на плоскости
-
Плоскость в пространстве
-
Прямая в пространстве
-
Кривые второго порядка — I
-
Кривые второго порядка — II
-
Поверхности второго порядка
-
Матрицы и операции с ними
-
Обратная матрица
-
Ранг матрицы
-
Системы линейных алгебраических уравнений
-
Свойства решений однородных и неоднородных СЛАУ
Подобие числовых матриц
Квадратные матрицы и
n-го порядка называются подобными, если существует такая невырожденная матрица
, что
Преобразование матрицы по формуле
называется преобразованием подобия, а матрица
— преобразующей.
Свойства подобных матриц
1. Каждая квадратная матрица подобна самой себе: .
2. Если матрица подобна матрице
, то и
подобна
при
.
3. Если матрица подобна матрице
, а
подобна
, то
подобна
, где
.
4. Подобие является частным случаем эквивалентных преобразований.
5. В случае ортогональности преобразующей матрицы подобные матрицы являются конгруэнтными.
Поясним свойства 4, 5. Напомним, что эквивалентные матрицы связаны соотношением , где
и
— невырожденные (элементарные) матрицы. Если
, то получаем преобразование подобия
. Если же матрица
ортогональная
, то подобные матрицы, связанные равенством
, оказываются конгруэнтными, так как
.
Подобные матрицы возникают во многих алгебраических задачах при замене переменных. Например, при решении системы уравнений с невырожденной квадратной матрицей
можно сделать линейную замену неизвестных: ввести столбец
— новых неизвестных
и новый столбец свободных членов с
, для которых система уравнений будет выглядеть так
или
.
Матрица полученной системы подобна матрице исходной системы. Например, если в результате преобразования подобия полученная матрица
имеет диагональный вид:
, то решение системы
находится просто:
, после чего нетрудно вычислить и решение исходной системы
.
Приведение матрицы к диагональному виду при помощи преобразования подобия
Рассмотрим задачу приведения квадратной матрицы к диагональному виду
при помощи преобразования подобия.
Теорема 7.5 о приведении матрицы к диагональному виду. Для того чтобы квадратная матрица n-го порядка приводилась к диагональному виду
, необходимо и достаточно, чтобы она имела
линейно независимых собственных векторов.
Действительно, запишем равенство в виде
, т.е.
или , где
— столбцы матрицы
. Отсюда получаем систему уравнений для столбцов
матрицы
(7.18)
Поэтому, если матрицу можно привести преобразованием подобия к диагональному виду
, то для столбцов матрицы
выполняются равенства (7.18), т.е. столбцы
являются собственными векторами матрицы
, причем они линейно независимы, так как матрица
невырожденная. Необходимость доказана. Пусть, наоборот, матрица
имеет
линейно независимых собственных векторов
, удовлетворяющих (7.18). Тогда, составив из них матрицу
, получим для нее равенство
, равносильное (7.18). Учитывая, что матрица
невырожденная (из-за линейной независимости ее столбцов), получаем
, т.е. матрица
подобна диагональной. Достаточность доказана.
Следствие 1. Если матрица имеет простой спектр, то она приводится к диагональному виду.
Действительно, в этом случае по свойству 1 собственных векторов все собственные векторы будут линейно независимы.
Следствие 2. Если матрица приводится к диагональному виду
, то числа
(среди которых могут быть равные) являются собственным значениями матрицы
, а столбцы
преобразующей матрицы
являются соответствующими собственными векторами матрицы
.
Следствие 3. Если — линейно независимые собственные векторы матрицы
, соответствующие ее собственным значениям
(среди которых могут быть равные), то матрица
приводится к диагональному виду
при помощи преобразующей матрицы
, составленной из собственных векторов.
Чтобы привести квадратную матрицу (n-го порядка) к диагональному виду при помощи преобразования подобия
и найти преобразующую матрицу
, нужно выполнить следующие действия.
1. Найти л линейно независимых собственных векторов матрицы
(при этом использовать алгоритм в разд. 7.2.1 с учетом пункта 2 замечаний 7.5).
2. Из собственных векторов составить преобразующую матрицу
(см. следствие 3 теоремы 7.5).
3. По собственным значениям матрицы составить матрицу
— диагональный вид матрицы
. Иначе матрицу
можно найти, выполняя преобразование подобия
.
Пример 7.9. Привести данные матрицы к диагональному виду и найти соответствующие преобразующие матрицы:
Решение. Матрица . 1. Собственные векторы и собственные значения этой матрицы были найдены в примере 7.8. Для собственных значений
и
возьмем соответствующие собственные векторы (полагая
):
. Эти столбцы линейно независимы (по свойству 1 собственных векторов).
2. Составляем из собственных векторов преобразующую матрицу .
3. Находим диагональный вид матрицы
, выполняя преобразование подобия:
На главной диагонали (согласно следствию 2 теоремы 7.5) стоят собственные значения матрицы .
Преобразующую матрицу можно было составить по-другому: . Тогда в результате преобразования подобия получили бы диагональную матрицу
.
Матрица . 1. Собственные векторы и собственные значения этой матрицы были найдены в примере 7.8. Для собственных значений
и
возьмем соответствующие собственные векторы (полагая
):
. Эти столбцы линейно независимы, поэтому матрицу
можно привести к диагональному виду.
2. Составляем из собственных векторов преобразующую матрицу . Выполняем преобразование подобия
На главной диагонали матрицы стоят (согласно следствию 2 теоремы 7.5) собственные значения матрицы
.
Матрица . Найдем собственные векторы матрицы
, используя алгоритм, изложенный в разд.7.2.1.
1. Составляем характеристический многочлен .
2. Решаем характеристическое уравнение .
3. Для собственного значения составляем однородную систему уравнений
, которую решаем методом Гаусса. Приводим расширенную матрицу системы к упрощенному виду
Ранг матрицы равен единице , количество неизвестных
. Поэтому фундаментальная система решений содержит
решение. Выражаем базисную переменную
через свободную:
. Полагая
, находим решение
.
4. Все собственные векторы, соответствующие собственному значению , имеют вид
, где
— произвольная постоянная. отличная от нуля.
Как видим, матрица второго порядка имеет только один линейно независимый собственный вектор, поэтому ее нельзя привести к диагональному виду при помощи преобразования подобия.
Пример 7.10. Привести матрицу к диагональному виду и найти соответствующую преобразующую матрицу. Найти выражение для степени
с натуральным показателем
.
Решение. 1. Собственные векторы и собственные значения этой матрицы были найдены в примере 7.8. Выберем три линейно независимых собственных вектора (см. пример 7.8):
Векторы и
соответствуют собственному значению
, вектор
-собственному значению
.
2, 3. Составляем из этих собственных векторов преобразующую матрицу , при помощи которой матрица
приводится к диагональному виду
Найдем m-ю степень матрицы , учитывая, что
Нетрудно получить степень диагональной матрицы, так как произведение диагональных матриц является диагональной матрицей:
Следовательно,
Связь подобия числовых матриц с эквивалентностью их характеристических матриц
Получим необходимое и достаточное условие подобия числовых квадратных матриц и
n-го порядка. Напомним, что с этими числовыми матрицами связаны λ-матрицы
и
, которые называются характеристическими. Две λ-матрицы называются эквивалентными, если одна из них получена из другой при помощи элементарных преобразований. Согласно пункту 6 замечаний 7.4, если λ-матрицы
и
эквивалентны, то существуют такие обратимые λ-матрицы
и
, что
.
Критерий подобия числовых матриц
Теорема 7.6 (критерий подобия числовых матриц). Для того чтобы числовые матрицы и
были подобными необходимо и достаточно, чтобы их характеристические λ-матрицы
и
были эквивалентны.
В самом деле, если числовые матрицы подобны, т.е. , то
Значит, характеристические матрицы эквивалентны, так как числовую матрицу можно считать частным случаем λ-матрицы, а невырожденная числовая матрица является элементарной (следствие 3 теоремы 3.3). Необходимость доказана.
Для доказательства достаточности запишем условие эквивалентности λ-матриц и
:
Перепишем равенство в виде
(7.19)
Разделим λ-матрицу слева на
, а λ-матрицу
справа на
(7.20)
Здесь остатки и
— обратимые числовые матрицы, так как
и
— обратимые λ-матрицы (см. пункт 3 замечаний 7.3). Подставим выражения (7.20) в (7.19):
Преобразуем равенство
Отсюда следует, что , в противном случае равенство ложное, так как степень многочлена в левой части не менее второй, а в правой части — не более первой. При
получаем
(7.21)
Сравнивая это равенство с (7.19), делаем вывод, что λ-матрицы и
в (7.19) можно заменить числовыми матрицами
и
. Приравнивая в (7.21) коэффициенты при одинаковых степенях
, находим
(7.22)
Следовательно, , т.е. матрицы
и
подобны.
Следствие. Если матрицы и
подобны, т.е.
, то в качестве преобразующей матрицы
можно взять матрицу
— левое или правое значения соответствующих λ-матриц из равенства
(7.23)
В самом деле, из доказательства теоремы следует, что λ-матрицы в (7.23) можно заменить числовыми матрицами:
где преобразующая матрица согласно (7.20) равна правому остатку при делении
на
, который по теореме Безу равен правому значению
. Учитывая (7.22), получаем
. Равенство
доказывается аналогично на основании теоремы Безу.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

![Rendered by QuickLaTeX.com D=left[begin{array}{ccc} lambda_{1} & 0 & 0 \ 0 & lambda_{2} & 0 \ 0 & 0 & lambda_{3} end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3cee524be22e1360cec9e36c6dc6e6ac_l3.png)
![Rendered by QuickLaTeX.com begin{array}{l} A t, lambda=i \ {[A-lambda I] X_{i}=0} end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2412ee29fc689f726190dc0b6eb3567e_l3.png)
![Rendered by QuickLaTeX.com A=left[begin{array}{ccc} 1 & 0 & -1 \ 1 & 2 & 1 \ 2 & 2 & 3 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7f7076d949d44df81d04a07e77719019_l3.png)
![Rendered by QuickLaTeX.com begin{array}{l} Longrightarrow operatorname{det}(A-lambda I)=operatorname{det}left(left[begin{array}{ccc} 1-lambda & 0 & -1 \ 1 & 2-lambda & 1 \ 2 & 2 & 3-lambda end{array}right]right)=0 \ Longrightarrowleft(lambda^{3}-6 lambda^{2}+11 lambda-6right)=0 & \ Longrightarrow(lambda-1)(lambda-2)(lambda-3)=0 \ Longrightarrow & lambda=1,2,3 end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aecb25e925f13c740b8dafd0698fd52d_l3.png)
![Rendered by QuickLaTeX.com At $lambda=1$ A - $(1) I$ $X_{1}=0$ $Longrightarrowleft[begin{array}{ccc}1-1 & 0 & -1 \ 1 & 2-1 & 1 \ 2 & 2 & 3-1end{array}right]left[begin{array}{l}x_{1} \ x_{2} \ x_{3}end{array}right]=left[begin{array}{l}0 \ 0 \ 0end{array}right]$ $Longrightarrowleft[begin{array}{ccc}0 & 0 & -1 \ 1 & 1 & 1 \ 2 & 2 & 2end{array}right]left[begin{array}{l}x_{1} \ x_{2} \ x_{3}end{array}right]=left[begin{array}{l}0 \ 0 \ 0end{array}right]$ On solving, we get the following equations: $x_{3}=0left(x_{1}right)$ $x_{1}+x_{2}=0 Longrightarrow x_{2}=-x_{1}$ $therefore X_{1}=left[begin{array}{c}x_{1} \ -x_{1} \ 0left(x_{1}right)end{array}right]$ $Longrightarrow X_{1}=left[begin{array}{c}1 \ -1 \ 0end{array}right]$ Similarly, for $lambda=2$ $X_{2}=left[begin{array}{c}-2 \ 1 \ 2end{array}right]$ and for $lambda=3$ $X_{3}=left[begin{array}{c}1 \ -1 \ -2end{array}right]$](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54df2258de67c7cf854e845a2919dc0c_l3.png)
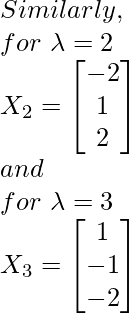
![Rendered by QuickLaTeX.com P=left[X_{1} X_{2} X_{3}right]=left[begin{array}{ccc} 1 & -2 & 1 \ -1 & 1 & -1 \ 0 & 2 & -2 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-09e5d83615881301779f489beb4f4c6b_l3.png)
![Rendered by QuickLaTeX.com P^{-1}=frac{1}{2}left[begin{array}{ccc} 0 & -2 & 1 \ -2 & -2 & 0 \ -2 & -2 & -1 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9a106923a45ac3b418199d0adac54ab7_l3.png)