2018-05-31
Найти добротность математического маятника длины $l = 50 см$, если за промежуток времени $tau = 5,2 мин$ его полная механическая энергия уменьшилась в $eta = 4,0 cdot 10^{4}$ раз.
Решение:
Для незатухающего осциллятора механическая энергия $E = frac{1}{2} m dot{x}^{2} + frac{1}{2} m omega_{0}^{2}x^{2}$. Для затухающего осциллятора.
$x = a_{0}e^{ — beta t} cos ( omega t + alpha), omega = sqrt{ omega_{0}^{2} — beta^{2} }$
и $E(t) = frac{1}{2} m dot{x}^{2} + frac{1}{2} m omega_{0}^{2} x^{2} = frac{1}{2} ma_{0}^{2} e^{ — 2 beta t} ( beta^{2} cos^{2} ( omega t + alpha) + 2 beta omega cos ( omega t + alpha) sin ( omega t + alpha) + omega^{2} sin^{2} ( omega t + alpha ) ) + frac{1}{2} ma_{0}^{2} omega_{0}^{2} e^{ — 2 beta t} cos^{2} ( omega t + alpha) = frac{1}{2} ma_{0}^{2} omega_{0}^{2} e^{ — 2 beta t} + frac{1}{2} ma_{0}^{2} beta^{2} e^{ — beta t} cos ( 2 omega t + 2 alpha) + frac{1}{2} ma_{0}^{2} beta omega e^{ — 2 beta t} sin ( 2 omega t + 2 alpha)$
Если $beta ll omega$, то среднее из последних двух членов относительно времени $t$ будет обращаться в нуль и
$langle E(t) rangle = frac{1}{2} ma_{0}^{2} omega_{0}^{2} e^{ — 2 beta t}$ — это соответствующая механическая энергия.
В момент времени $tau$ она уменьшается в $frac{1}{ eta}$
$e^{ — 2 beta tau} = frac{1}{ eta}$ или $tau = frac{ ln eta}{2 beta}$.
$beta = frac{ln eta}{2 tau}$
и $lambda = frac{2 pi beta}{ sqrt{ omega_{0}^{2} — beta^{2} } } = frac{2 pi}{ sqrt{ left ( frac{ omega_{0} }{ beta} right )^{2} — 1 } } = frac{2 pi}{ sqrt{ frac{2g tau^{2} }{l ln^{2} eta} — 1 } } $ поскольку $omega_{0}^{2} = frac{g}{l}$.
и $Q = frac{ pi}{ lambda} = frac{1}{2} sqrt{ frac{2g tau^{2} }{l ln^{2} eta} — 1 } approx 130$.
ФИЗИКА
Модуль 1.7
ГЛАВА 7 Затухающие
и вынужденные колебания
1 Затухающие
колебания
Во всякой реальной
колебательной системе всегда имеется
либо сила трения (в механической системе),
либо активное электрическое сопротивление
(в колебательном контуре), действие
которых приводит к уменьшению энергии
системы. Если убыль энергии не восполняется,
колебания будут затухать.
Начнем с рассмотрения
механических колебаний. В простейшем
случае сила трения (например, сила
вязкого трения) пропорциональна скорости:
. (7.1)
Здесь
— постоянная, которую мы будем называть
коэффициентом
трения или коэффициентом сопротивления
среды. Знак
минус обусловлен тем, что сила
и скорость
направлены
в противоположные стороны, вследствие
чего их проекции на ось х
имеют разные знаки.
Уравнение второго
закона Ньютона при наличии силы трения
имеет вид
. (7.2)
Применив обозначения
,
,
( 7.3)
напишем уравнение
(7.2) следующим образом:
. (7.4)
Отметим, что
— собственная
частота
колебательной системы, т. е. та частота,
с которой колебалась бы система в
отсутствие трения.
Попробуем искать
решение уравнения (7.4) в виде
(7.5)
где
некоторая функция от
.
Дифференцирование по
дает:
,
.
После подстановки
выражений для
,
и
в уравнение (7.4) и сокращения на отличный
от нуля множитель
получим дифференциальное уравнение
для
:
. (7.6)
Решение уравнения
(7.6) зависит от знака коэффициента,
стоящего при
.
Рассмотрим случай, когда этот коэффициент
положителен (т. е.
— трение мала). Введя обозначение
, (7.7)
придем к уравнению
,
решением которого
является функция
(см. (5.9) и (5.6)).
Таким образом, в
случае малого трения ()
решением уравнения (7.4) будет функция
. (7.8)
Здесь
— постоянные, значения которых зависят
от начальник условий,
— величина; определяемая формулой
(7.7), называется циклической частотой
затухающих колебаний.
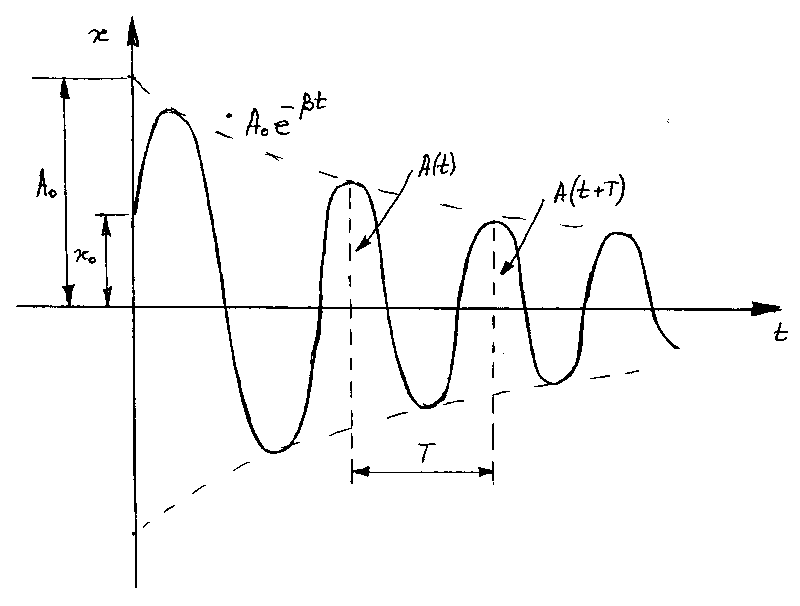
График функции
(7.8) дан на рис.1. Штриховыми линиями
показаны пределы, в которых находится
смещение колеблющейся частицы.
Рис. 1
В соответствии с
видом функции (7.8) движение частицы
можно рассматривать как гармоническое
колебание частоты
с амплитудой, изменяющейся по закону
. (7.9)
Верхняя из штриховых
кривых на рис. 1 дает график этой функции,
причем
представляет
собой амплитуду и начальный момент
времени. Начальное смещение
зависит, кроме,
также от начальной фазы
:
.
Скорость затухания
колебаний определяется величиной
.
которую называют
коэффициентом
затухания.
Найдем время
,
за которое
амплитуда
уменьшается в
раз. По
определению
,
откуда
.
Следовательно,
коэффициент затухания
обратен тому
промежутку времени, за
который амплитуда
уменьшается и
раз,
Согласно формуле
(7.7) период затухающих колебаний
. (7.10)
При
незначительном трении
период колебаний
практически равен
.
С ростом коэффициента затухания период
колебаний увеличивается.
Отношение значений
амплитуды, соответствующих моментам
времени, отличающимся на период, равно
Это отношение
называют декрементом
затухания,
а его логарифм — логарифмическим
декрементом затухания
. (7.11)
Для характеристики
колебательной системы обычно используется
логарифмический декремент затухания
.
Выразив в соответствии с (7.11)
через
и
можно закон убывания амплитуды со
временем написать в виде
За время
,
за которое амплитуда уменьшается в
раз, система
успевает совершить
колебаний. Из условия
получается, что
.
Следовательно, логарифмический декремент
затухания обратен числу колебаний,
совершаемых за то время, за которое
амплитуда уменьшается в
раз.
Для характеристики
колебательной системы употребляется
также величина
(7.12)
называемая
добротностью
колебательной системы. Она пропорциональна
числу колебаний
,
совершаемых системой за то время
,
за которое амплитуда колебаний
уменьшается
в е
раз.
Энергия колебательной
системы пропорциональна квадрату
амплитуды. В соответствии с этим энергия
системы при затухающих колебаниях
убывает по закону,
(7.13)
(
— значение энергии при
).
Как и всякая производная,
определяет скорость возрастания
, а величина
— скорость убывания энергии. Согласно
(7.13)
скорость убывания
энергии
. (7.14)
Если энергия мало
изменяется за время, равное периоду
колебаний, убыль энергии за период
можно найти, умножив выражение (7.14) на
:
(напомним, что
обозначает приращение, а
— убыль энергии). Приняв во внимание
формулы (7.11) и (7.12), придем к соотношению
(7.15)
из которого
следует, что при слабом затухании
колебаний добротность с точностью до
множителя
равна
отношению энергии, запасенной в системе
в данный момент, к убыли энергии за один
период колебаний.
Из формулы (7.10)
вытекает, что при
период колебаний обращается в
бесконечность, т. е. движение перестает
быть периодическим. В случае, когда
(трение велико), общее решение уравнения
(7.4) имеет вид
, (7.16)
где
,
,
— постоянные,
значения которых зависят от начальных
условий.
(В этом можно
убедиться подстановкой функции (7.16) в
уравнение (7.4).) Следовательно, движение
носит апериодический
(непериодический) характер— выведенная
из положения равновесия система
возвращается обратно, не совершая
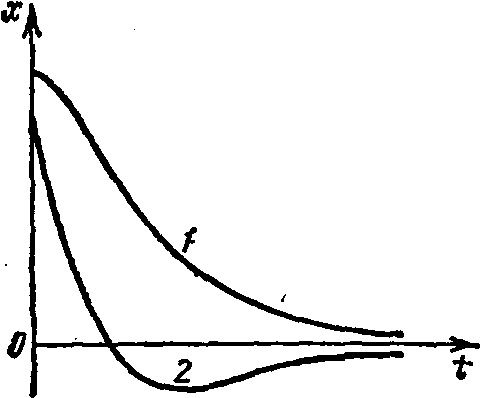
колебаний. На рис. 2 показаны два возможных
способа возвращения системы в положение
равновесия при апериодическом движении.
Каким из этих способов приходит система
в положение равновесия, зависит от
начальных условий.
Рис. 2
2 Вынужденные
колебания
Допустим, что
механическая колебательная система
подвергается действию внешней силы,
изменяющейся со временем по гармоническому
закону;
. (7.17)
В этом случае
уравнение второго закона Ньютона имеет
вид
.
Введя обозначения
(7.3), преобразуем уравнение следующим
образом:
. (7.18)
Здесь
— коэффициент затухания,
— собственная частота колебательной
системы,
— частота вынуждающей силы.
Дифференциальное
уравнение (7.18) описывает вынужденные
колебания. Из теории линейных
дифференциальных уравнений с постоянными
коэффициентами известно, что общее
решение неоднородного уравнения (т.е.
уравнения, в правой части которого
стоит не равная тождественно нулю
функция от
)
равно сумме общего решения соответствующего
однородного уравнения (т. е. того же
уравнения, в котором правая часть
принята равной тождественно нулю) и
частного решения неоднородного
уравнения. Общее решение однородного
уравнения мы уже знаем, оно имеет вид
, (7.19)
где
(см.
формулу (7.8)).
Остается найти
частное (т. е. не содержащее произвольных
постоянных) решение уравнения (7.18).
Попробуем искать это решение в виде
, (7.20)
где
— неизвестный пока сдвиг фаз между
силой и вызываемыми ею колебаниями.
Попытаемся выяснить, не существует ли
таких значений
и
,
при которых функция (7.20) удовлетворяет
уравнению (7.18). Для этого подставим в
уравнение (7.18) выражение (7.20) и его
производные
, (7.21)
, (7.22)
разворачивая
одновременно
и
по формулам для синуса и косинуса
разности:
Сгруппировав
соответствующим образом члены уравнения,
получим
(7.23)
Для того чтобы
уравнение (7.23) удовлетворялось при
любых значениях
,
коэффициенты при
и
в
обеих частях уравнения должны быть
одинаковыми. Отсюда получаются условия
, (7.24)
, (7.25)
Из этих соотношений
можно найти значения
и
, при которых функция (7.20) удовлетворяет
уравнению (7.18). Возведя равенства (7.24)
и (7.25) в квадрат и сложив их друг с другом,
получим
,
откуда

Из
уравнения (7.25) следует, что
. (7.27)
Подставив в (7.20)
значения
и
,
определяемые формулами (7.26) и (7.27),
получим частное решение неоднородного
уравнения (7.18):
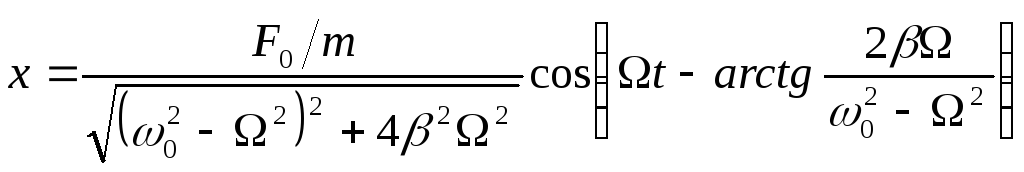
Функция (7.28) в
сумме с (7.19) дает общее решение уравнения
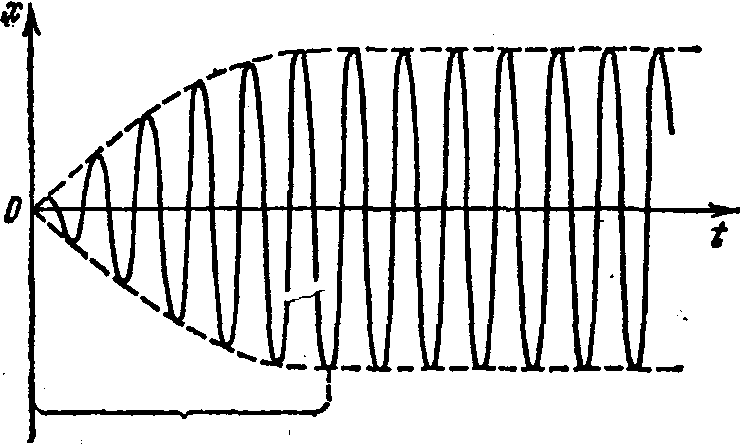
(7.18). Слагаемое (7.19) играет заметную роль
только в начальной стадии процесса,
при установлении колебаний (рис. 3). С
течением времени из-за экспоненциального
множителя
роль
слагаемого (7.19) уменьшается, и по
прошествии достаточного времени им
можно пренебречь, сохранив в решении
только слагаемое (7.28), которое описывает
установившиеся вынужденные колебания.
Отметим, что на рис.3 изображен простейший
случай установления колебаний.
установление
колебаний
Рис. 3
Обсудим полученные
результаты. Из формулы (7.28) следует, что
установившиеся вынужденные колебания
представляют собой гармонические
колебания с частотой, равной частоте
вынуждающей силы. Амплитуда колебаний
пропорциональна амплитуде силы. Для
данной колебательной системы (для
заданных
и
амплитуда зависит от частоты силы).
Колебания отстают по фазе от силы,
причем отставание также зависит от
частоты силы.
Зависимость
амплитуды вынужденных колебаний от
частоты вынуждающей силы приводит к
тому, что при некоторой частоте амплитуда
достигает максимального значения.
Колебательная система оказывается
особенно отзывчивой на действие
вынуждающей силы при данной частоте.
Это явление называется резонансом,
а соответствующая частота — резонансной
частотой.
Чтобы определить
резонансную частоту
,
нужно найти максимум функции (7.26) или,
что то же самое, минимум выражения,
стоящего под корнем в знаменателе.
Продифференцировав это выражение по
и приравняв производную нулю, получим
условие, определяющее
.
Это уравнение
имеет три решения:
и
.
Решение, равное нулю, соответствует
максимуму знаменателя (т. е. минимуму
амплитуды). Из остальных двух решений
отрицательное должно быть отброшено,
как не имеющее физического смысла
(частота не может быть отрицательной).
Таким образом, для резонансной частоты
получается одно значение:
(7.29)
Подставив это
значение в (7.26), получим выражение для
амплитуды при резонансе:
(7.30)
Из этого выражения
следует, что в отсутствие трения
амплитуда при резонансе обращалась бы
в бесконечность. Согласно (7.29) резонансная
частота при тех же условиях (при
)
совпадает с собственной частотой
колебаний системы
Зависимость
амплитуды вынужденных колебаний от
частоты вынуждающей силы (или, что то
же самое, от частоты колебаний) показана
графически на рис. 5.
Кривые на графике
соответствуют различным значениям
параметра
.
В соответствии с (7.29) и (7.30), чем меньше
,
тем выше и правее лежит максимум
резонансной кривой. При очень большом
затухании (таком, что
)
выражение для резонансной частоты
становится мнимым. Это означает, что
резонанс в этом случае не наблюдается
– с увеличением частоты амплитуда
монотонно убывает (см. рис. 5).

Рис. 5
Изображенная на
рис. 5 совокупность графиков функции
(7.26) называется резонансными кривыми.
По поводу этих кривых можно сделать
следующие замечания. При стремлении
частоты к нулю все кривые приходят к
одному и тому же предельному значению,
равному
,
т. е.
.
Это значение представляет собой смещение
из положения равновесия, которое
получает система под действием постоянной
силы
.
При стремлении
к бесконечности все кривые асимптотически
стремятся к нулю, так как при большой
частоте сила так быстро изменяет свое
направление, что система не успевает
заметно сместиться из положения
равновесия. Наконец, отметим, что чем
меньше
,
тем сильнее изменяется с частотой
амплитуда вблизи резонанса, тем острее
получается максимум.
Согласно формуле
(7.30) при малом затухании (т.
е. при
)
амплитуда при резонансе
.
Разделим это
выражение на смещение
из положения равновесия под действием
постоянной силы
,
равное
.
В результате получим, что
, (7.31)
(см. формулу
(7.12)). Следовательно, добротность
показывает, во сколько раз амплитуда
при резонансе превышает смещение
системы из положения равновесия под
действием постоянной силы, модуль
которой равен амплитуде вынуждающей
силы (это справедливо лишь при небольшом
затухании).
Вынужденные
колебания отстают по фазе от вынуждающей
силы, причем отставание лежит в пределах
от 0 до
.
Зависимость
от
при разных значениях
показана
на рис. 6. Частоте
соответствует
.
Резонансная частота меньше собственной
(см. формулу
(7.29)), поэтому в момент резонанса
.
При слабом затухании
и значение
при резонансе
можно считать равным
.

Рис. 6
Явление резонанса
приходится учитывать при конструировании
машин и различных сооружений. Резонансная
частота этих устройств не должна быть
близка к частоте возможных внешних
воздействий. Например, резонансная
частота вибраций корпуса корабля и
крыльев самолета должна сильно отличаться
от частоты колебаний, которые могут
возбуждаться вращением гребного винта
или пропеллера. Иначе возбуждаются
вибрации, которые могут вызвать
катастрофу.
Задачи
Задача 1
Амплитуда затухающих колебаний за один
период уменьшается в 3 раза. Определить
логарифмический декремент затухания
и найти, при каких значениях фазового
угла достигается максимальное смещение
от положения равновесия.
Решение
По определению
логарифмический декремент затухания
равен

Из условия задачи
следует, что
= 1,09.
Для ответа на
второй вопрос запишем уравнение
затухающих колебаний.
и вычислим
производную
,
Условие максимума
имеет вид
,
где введено
обозначение фазового угла
,
а
— момент времени, когда
.
Таким образом,
.
Подставляем
численные значения, находим
,
.
Задача 2
Стальной шарик диаметром
= 2 см совершает на легкой пружине
вертикальные колебания в воздухе с
циклической частотой
= 5 рад/с. Если шарик опустить в жидкость,
то частота уменьшится до величины
= 4 рад/с. Определить кинематическую
вязкость жидкости
.
Решение
Из формулы
и
имеем:
,
,
отсюда
.
Кинетический
коэффициент вязкости можно найти,
используя формулу Стокса:
,
откуда

Подставляя
численные значения (
кг/м3),
получаем
.
Задача 3
Найти добротность математического
маятника длины
= 50 см, если за время
= 5,2 мин его энергия колебаний уменьшается
в
раз.
Решение
Прежде всего
выясним, можно ли в данном случае
пользоваться формулой
,
справедливой для малого затухания ().
Если
~
,
то из условия задачи следует, что
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
При наличии механических колебаний происходит периодическое изменение кинетической и потенциальной энергии. Обращение в ноль кинетической энергии и скорости связано с максимальным отклонением тела от положения равновесия. Энергия такого колеблющегося тела достигает максимального значения. Если груз располагается на горизонтальной пружине, то потенциальная энергия считается энергией упругих деформаций пружины. У математического маятника – это энергия в поле тяготения Земли.
Когда тело принимает положение равновесия при движении, это говорит о наличии минимальной его скорости. Тогда кинетическая энергия обладает максимальным значением, а потенциальная – минимальным. По 3-му закону Ньютона формула силы натяжения записывается как T=mg при вертикальном подвешивании тела на нити. Уменьшение потенциальной приводит к увеличению кинетической. Дальнейшее движение показывает, что происходит уменьшение кинетической и увеличение потенциальной.
Гармонические колебания – это пример превращения кинетической энергии в потенциальную и наоборот.
Рисунок 2.4.1. Модель превращения энергии при колебаниях.
Математический и пружинный маятник
Когда колебательная система не имеет силы трения, тогда остается неизменной полная механическая энергия.
Формулы, характеризующие груз на пружине:
E=Ek+Ep=mυ22+kx22, ω02=km,(Ep)max=kxm22, (Ek)max=mυm22=mω02xm22=(Ep)max.
Выражения при малых колебаниях математического маятника записываются:
E=Ek+Ep=mυ22+mgh=mυ22+mgx22l, ω02=gl,(Ep)max=mghm=mgxm22l, (Ek)max=mυm22=mω02xm22=(Ep)max.
Значение hm является максимальной высотой подъема маятника, xm и υm=ω0xm – максимальными значениями отклонения физического маятника от положения равновесия и его скорости.
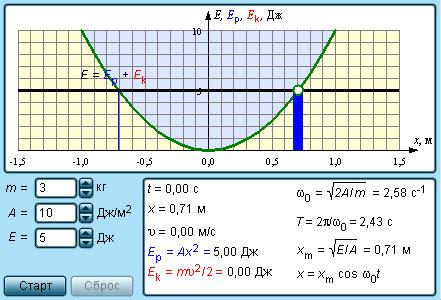
Для объяснения превращения энергии при свободных механических колебаниях без силы трения приводится иллюстрация.
Если рассматривать колебания с грузом массой m на пружине с жесткостью k, тогда смещение груза x(t) из положения равновесия и его скорость υ(t) могут изменяться со временем согласно законам:
x(t)=xmcos (ω0t), где ω02=km,
υ(t)=-ωxmsin (ω0t).
Формулы кинетической и потенциальной энергии запишутся так:
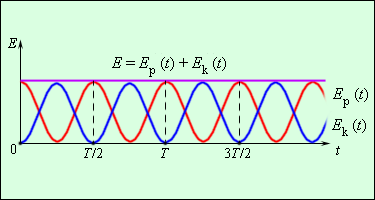
Ep(t)=12kx2=12kxm2 cos2ω0t=14kxm2(1+cos 2ω0t),
Ek(t)=12mυ2=12kω02xm2 sin2ω0t=14kxm2(1-cos 2ω0t).
Рисунок 2.4.2 показывает два графика функций изменения Ep(t) и Ek(t). Обе энергии в период колебаний T=2πω0, достигают максимальных значений по два раза. Значение их суммы не изменяется Ep(t)+Ek(t)=E=const.
Рисунок 2.4.2. Превращения энергии при свободных колебаниях.
Реальные условия для колебательной системы – это наличие воздействия сил трения (сопротивления).
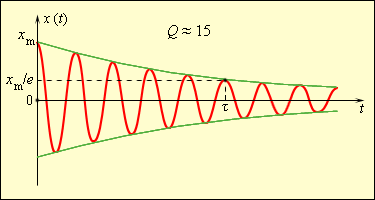
При переходе части механической энергии во внутреннюю энергию теплового движения атомов и молекул колебания становятся затухающими, как показано на рисунке 2.4.3.
Рисунок 2.4.3. Свободные затухающие механические колебания.
Скорость затухания колебаний зависит от величины сил трения.
Частота. Добротность. Формулы
Промежуток времени τ с уменьшением колебаний в e≈2,7 раз называют временем затухания.
Скорость затухания зависит от частоты свободных колебаний, как видно из формулы. При увеличении действия сил трения происходит уменьшение собственной частоты. Если действия силы трения достаточно велико, то изменение частоты становятся заметными.
Колебательная система с затухающими колебаниями характеризуется добротностью Q.
Определение параметра представляет собой произведение числа полных колебаний N за время затухания τ на значение π:
Q=πN=πτT.
Повышение Q колебательной системы происходит при медленных затуханиях свободных колебаний. На рисунке 2.4.3 показано, что Q имеет значение, приближенное к 15.
Добротность механических колебательных систем может достигать огромных значений. Для определения Q колебательной системы применяют формулу:
Q=2πЗапас энергии в колебательной системеПотеря энергии за 1 период колебаний.
То есть добротность способна характеризовать относительную убыль (затухание) энергии при наличии действия силы трения на данном промежутке времени, равняющемуся одному периоду колебаний.
К нему прикреплена легкая пружина жесткости )!. Свободный конец пружины начали перемещать в горизонтальном направлении вдоль пружины с некоторой постоянной скоростью. Через сколько времени надо остановить этот конец пружины, чтобы после остановки брусок не колебался? Решение Пусть имеется неподвижная система координат Оху.
Введем систему координат О, х, у,, движущуюся со скоростью У вдоль осн х по отношению к системе Оху так, что х=х, +У! (см. рис.4.5). В системе О,х,у, свободный конец пружины покоится, а брусок движется влево со скоростью У. Пружина с бруском представляет собой колебательную 132 Глава 4 Г систему с собственной частотой «зв = ~ —. Движение бруска в системе о о, х х1 Рнс.4.5 О, х,у, описывается уравнением х, = ав сов (азв1+ а), (1) дх, В момент 1=0 смещение бруска х =О, а скорость )л = — ‘=-)л. 1 Через время, равное целому числу периодов колебаний после начала 2ю Ги движения конца пружины 1=пТ =л — =2лп ~ — (и = 1,2, 3 …), скорость «зо бруска в системе координат О,х,у, будет равна -)л, а в системе Оху он будет покоится.
Следовательно, при остановке свободного конца пружины в указанные моменты времени в системе Оху брусок будет покоится и колебаний не возникнет. Ответ: 1 = 2лн ~ —, (л = 1, 2, 3 …). Колебания и волны (ЗЗ 4.1.5. Сплошной однородный цилиндр радиуса г катается без скольжения по внутренней стороне цилиндрической поверхности радиуса Я, совершая малые колебания. Найти их период. Решение Допустим, что цилиндр отклонился от вертикали на угол (о(см.
рис.4.6). Приращение его потенциальной энергии составляет Е, = тя(Л вЂ” г)(1 — соз(в), где т — масса цилиндра. Кинетическая энергия цилиндра: т(l~ (в~ Е 2 2 где У = аг, К — скорость цилиндра, в — угловая скорость цилиндра относительно его собственной оси, ! = те с2 — момент инерции цилиндра. Далее получаем Рис.4.6 т)г~ те~в~ Зсиг~в~ Е = 2 4 4 Угловая скорость — и угловая скорость в связаны между собой сс (о ос! соотношением (см. рис.4,6): — (Е-г) = ак с(ф> с!с Отсюда Зсиг~(К вЂ” г) (Ыд1 ! ~Зт(й — г) 1(с((о1 Предположим, что ср «1, т.е.
колебания малые. Тогда ! Е„н — (сия(Я вЂ” г))(о~ (2) 2 Выражение в квадратных скобках в (!) представляет собой т,е, а в (2)- lс,е . Следовательно аь = р,„ьт,,)ш = гдт. Отсюда получаем окончательно Т = 2л(З(Ю -г)!2ф’ ~. 134 Глава 4 Ответ: Т= 2л~3(И -г)12я)» 4.1.6. Тонкое кольцо радиуса К совершает малые колебания около точки О (см.
рис.4.7). Найти период колебаний, если они происходят: а) в плоскости рисунка; б) в направлении, перпендикулярном к плоскости рисунка. Найти приведенную длину физического маятника в случаях а) и б). Решение а) Рассмотрим сначала случай колебаний кольца в плоскости рисунка. При отклонении центра кольца от вертикали, проходящей через а) Рис.4.7 ~очку подвеса, на небольшой угол 1е (~к<1) на кольцо действует момент силы тяжести, возвращающий его в положение равновесия 1см.
рис.4.7б): Ф =-таей з1и ге= -глу)11е (1) Основное уравнение динамики твердого тела (1.4.1) выглядит в данном случае следующим образом 7 — =М, Ы'(е 12) ~Й’ где 1 — момент инерции кольца относительно точки О. Согласно теореме Штейнера (1.4.2) (3) 1с+гла 135 Колебания и яолнм где 1 = лО! — моменг инерции кольца относительно оси, проходящей через его центр масс перпендикулярно плоскости кольца, а = й.
Отсюда получаем 1 = 2тК’, Подставляя (1) и (4) в (2), получим 2т(! — + тЛ!((а = О, 2е( (а Й’ откуда приходим к уравнению малых колебаний кольца Ы'(о — +и ‘(а=О, г о (4) гл Гй где ио = — = (†— круговая частота колебаний. Следовательно, Т )(2!! г=2 1 = — гл)1 =3 2 Далее по аналогии со случаем а) получим Гзг Т=2л ~ —. ~г~ ‘ Напомним, что приведенной длиной физического маятника называется длина такого математического маятника, период которого совпадает с периодом данного физического маятника: б) В этом случае уравнение движения кольца аналогично уравнению (2), но в выражении для 1 (см.(3)) меняется 1с.
Теперь !с представляет собой момент инерции кольца относительно оси, совпадающей с его диаметром. Используя общую формулу для момента инерции тела относительно оси 1 = ~~)и,г, (где т,, — элементарные массы, на которые разбивается тело; расстояние ~’-й массы до оси) и переходя в пределе т, -ь О к интегрированию, получим величину 1с кольца относительно его диаметра: й2 !. = —. 2 (5) Подставляя (5) в (3), получим момент инерции кольца относительно оси, проходящей через точку О: 136 Глава 4 1 1„„= —, (6) где ! — момент инерции физического маятника относительно оси вращения, т — масса маятника, 1 — расстояние от оси вращения до центра масс маятника.
Подставляя (4) и (5) в (6), а также учитывая, что 1=И в обоих случаях, получим 3 г — тй б) 1„= = — Гг. 3 тл 2 гЮ Ггг ]и Ответ:а) Т=2л ~ —, 1„=2И; б) Т=2гг ~ —, 1„= — Я. ’12я «л 2 4.2. Затухающие колебания Осгговные формулы ° Уравнение движения осциллятора с учетом затухания г( х г(х т =-Йх — г— (4.2.1) г(гг г(! Последний член в (4.2.1) представляет собой силу сопротивления среды, которая пропорциональна скорости тела; г носит название коэффициента сопротивления. ° Запишем (4.2.1) в другой форме — е2!3 — +ага х=О, г( х в(х (4.2.2) г!гг Й где коэффициент !3 = г/2т — называется коэффициентом затухания, а),’= ‘г!гл ° Решение уравнения (4.2.2): х = а ее ~ соз(ах + а), (4.2.3) где ав, а — произвольные постоянные, аг = [аз, — )Т ] — циклическая г » вг частота затухающих колебаний, Т= 2гв’аг- их период, а(!) = а,ехр(-рг)- амплитуда затухающих колебаний.
° Логарифмический декремент затухания: 2 =!п[а(!)! а(! е Т)] =г9Т, (4.2.4) 137 Колебания и волны М, = !/2 — число колебаний, в течение которых амплитуда спадает в е раз. ° Добротность колебательной системы: Я = я/Я = я/!/,. ° Энергия осциллятора при слабом затухании (,В <е лЬ): ЕВ) = Ео ехр(-2Ф), (4.2.6) где Е, = /га,’/2- энергия осциллятора при / = О. Из (4.2.6) следует, что г/Е=2ДЕг//. ° Изменение энергии осциллятора за период: АЕ = -2Д7′ Е = -2АЕ (4.2.7) Примеры решения задач 4.2.1.
Точка совершает затухающие колебания с частотой в = 25с’. Найти коэффициент затухания /х если в начальный момент скорость точки равна нулю, а ее смещение из положения равновесия в // = 1,02 раза меньше амплитуды. Решение Смещение точки из положения равновесия при затухающих колебаниях описывается уравнением (4.2.3): я=а,е~сок(ох+ а). (1) Из этого уравнения следует, что сдвиг фазы между смещением и скоростью точки отличается от к/2 . Отсюда следует, в частности, что максимальная величина смещения и минимальная величина скорости точки достигаются не одновременно.
В этом одно из отличий затухающих и незатухающих колебаний. Дифференцируя (1) по времени, найдем скорость точки )л(/) = ао е ~ [-фсок(ая + а) — ав1п(ох + а)1. В соответствии с условием задачи )л(0) = а, [-фсок(а) — ев(п(а)] = О, л(0)/ ав = сока= 1/// Отсюда получаем !яа= -/Ра, сока= 1///. (2) Поскольку //и в положительны, то из (2) следует, что а< О. Далее из(2) получаем ,В=в! !яа~ = в[! — сок’ а)’/сока= в [(1/сок’ а) -1)н’ = в[//’ — 1)н’.
138 Глава 4 Ответ: г8= ш(г?’ -!1 4.2.2. Математический маятник совершает колебания в среде, для которой логарифмический декремент затухания Лс = 1.5. Каким будет значение Л, если сопротивление среды увеличить в и = 2 раза? Во сколько раз следует увеличить сопротивление среды, чтобы колебания стали невозможны? Решение В соответствии с формулами (4.2.3) и (4.2.4) имеем г гнг (1) Из (1) при Л = Лв, )5 = Дг получаем (коэффициент затухания Дг соответствует случаю, когда логарифмический декремент затухания равен =Р (2) (шв -г8в 1 Возводя обе части равенства (2) в квадрат и разрешая полученное уравнение относительно Дг, получаем д Лешо (3) (4лг + Л ]»‘ Для случая, когда коэффициент гб увеличен по условию задачи по сравнению с первоначальным значением в н = /РДг = 2 раза, получаем, используя (!) и (3) 2глгД, 2 т (Шо — (нг(гв) 1 (( в )г 1)иг А 2 ге 2лнЛо нг ‘ шо (4л +Ло ) иг (4гг +Лв (1 н )) (лЛОогв) Полагая в (4) и = 2, получаем Л| и 3,3 .
Колебания маятника стануг невозможны при Л = . Это реализуется в случае, когда знаменатель в (4) обращается в нуль. В результате приходим к уравнению 1+(1-и )(Лв/2л) =О, 139 Колебания и волны откуда и’= !1+(2юЛо)’)и’ж4,3. Ответ: Л~ =лЛдl!1+ (1- л’)Лв/2л) ! ‘ =3,3; л = !1+(2шЛв) ] ~ н43 4.2.3. Найти добротность математического маятника длины 50 см, если за промежуток времени г = 5,2 мин его полная механическая энергия уменьшилась в !2 = 4х10″ раз. Решение Согласно формуле (4.2.5) Х Х 0= — = —, л ~г’ 2л’ 2л (д где Т= — = , шв ы ~ — — собственная частота незатухающих 2 р2 ) из ‘ !1~ ! колебаний математического маятника.
Предположим, что затухание в системе мало. В этом случае, согласно (4.2.6) Ейй = Ев ехр(-2,Й). Отсюда найдем Р Подставляя выражение для Т и Р’в формулу для Д, получим л!«1, —,8 )и 1 гон 1 4г оЛ, 1 4уг~ Так как Д!, = Я/л» 1, то колебания действительно слабо затухающие, и, следовательно, предположение, сделанное выше, верно.
1и2 Ответ: Д = — — 1~ н130. 1~4яг’ 2~! !пг 14О Глава 4 4.3. Вынужденные колебания Основные формулы где й = Хо ((йго йг ) +48 ш ) (й — сдвиг между фазами установившегося колебания и вынуждающей силы, который определяется выражением 2,8йг г йь’ -йг’ ° Максимум амплитуды смешения достигается при йг „= [йзг~ — 2р»] ~~ ° Амплитуда смещения при резонансе равна Хо а,„, = м’ 2г)(йг г дг)аг (4.3.3) (4.3.4) Примеры решения задач 4.3.1. Шарик массы нг может совершать незатухающие гармонические колебания около точки х = 0 с собственной частотой йг, .
|
0 / 0 / 0 Регистрация: 26.05.2012 Сообщений: 25 |
|
|
1 |
|
Найти добротность математического маятника04.06.2012, 06:07. Показов 16109. Ответов 3
Найти добротность математического маятника длиной l=0,5м, если за промежуток Тау=5,2мин его полная механическая энергия уменьшилась в n=4*104 раз.
0 |
|
4444 / 2448 / 227 Регистрация: 20.08.2011 Сообщений: 3,108 |
|
|
05.06.2012, 02:15 |
2 |
|
Найти добротность математического маятника длиной l=0,5м, если за промежуток Тау=5,2мин его полная механическая энергия уменьшилась в n=4*104 раз. Q=1/βT,
0 |
|
0 / 0 / 0 Регистрация: 26.05.2012 Сообщений: 25 |
|
|
06.06.2012, 20:11 [ТС] |
3 |
|
Всё очень печально ):
0 |
|
4444 / 2448 / 227 Регистрация: 20.08.2011 Сообщений: 3,108 |
|
|
07.06.2012, 14:00 |
4 |
|
Всё очень печально ): Не по теме: Согласен, печально. Ну, что это за задача с решением в одну строчку! Только развернешься, а она уже закончилась!
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
07.06.2012, 14:00 |
|
4 |