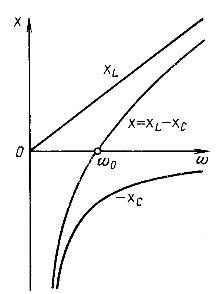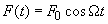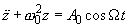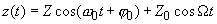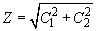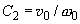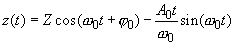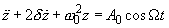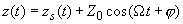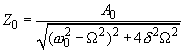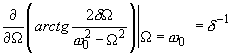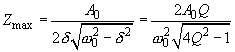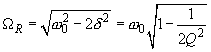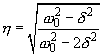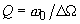Методы определения добротности
Пользуясь
определением добротности, можно показать,
что
,
(9)
RП
= r + R + RL,
где RП
– полное сопротивление цепи; r
– внутреннее сопротивление источника
тока; R
– сопротивление, включенное в контур;
RL
– активное сопротивление катушки
индуктивности.
1. Расчет
теоретического значения добротности.
Добротность контура Qтеор
можно рассчитать по формуле (9), зная
параметры электрической цепи RП,
L
и C.
2. Определение
добротности по измерениям резонансного
напряжения U0
рез
и амплитуды вынуждающей ЭДС 0.
Соотношение (8) при малых коэффициентах
затухания принимает вид
,
откуда
.
(10)
3. Определение
добротности по ширине резонансной
кривой.
Шириной резонансной кривой называется
разность частот, при которых достигается
эффективное значение резонансного
напряжения на конденсаторе, равное (см.
рис. 3)
.
Разность этих
частот
= 2
– 1
является
полосой пропускания контура.
Энергия, запасенная
в контуре при резонансе, на границах
полосы пропускания уменьшается в два
раза.
Пользуясь
соотношениями (9) и (10) и преобразуя
уравнение (5), получаем, что с достаточной
степенью точности
.
(11)
Таким
образом, зная
и рез,
можно вычислить добротность контура.
Расчет добротности
этим методом производится с помощью
полученной экспериментально резонансной
кривой в координатах U0
, .
По ней определяются для
значения
1
и 2
слева и справа от рез.
Вместо рез
и циклических частот 1
и 2
используются соответствующие частоты
генератора
.
(12)
Метод измерения и описание аппаратуры
Для выполнения
работы используется простейший
колебательный контур из последовательно
соединенных катушки индуктивности L,
конденсатора C
и сопротивления R.
Резонансные кривые снимают при различных
сопротивлениях, включенных в контур.
Наблюдение за изменением амплитуды
колебаний на конденсаторе производится
с помощью электронного осциллографа.
Для этого сигнал с конденсатора подается
на вход осциллографа, и при изменении
частоты генератора измеряется амплитуда
напряжения. При этом диапазон частот
выбирается достаточно широким в обе
стороны по отношению к резонансной
частоте. Резонансная частота соответствует
наибольшей амплитуде измеряемого
напряжения при заданном сопротивлении
контура. Определение добротности контура
производится двумя из вышеописанных
способов: по ширине резонансной кривой
и по отношению резонансного напряжения
к амплитуде вынуждающей ЭДС. Полученные
результаты позволяют вычислить омическое
сопротивление контура и оценить значение
внутреннего сопротивления генератора.
Порядок выполнения работы
-
Включите генератор
синусоидальных колебаний и электронный
осциллограф и соберите схему для
измерений в соответствии с указаниями
на стенде. -
Рассчитайте
собственную частоту контура по формуле
.
Параметры L,
C,
RL,
r
контура
даны на стенде. Значения L,
C
и f0
запишите в
табл. 1.
-
Определите по
осциллографу амплитуды вынужденных
колебаний напряжения U0,
снимаемого с конденсатора в делениях
масштабной сетки на экране осциллографа,
при фиксированных значениях частоты
F
генератора в выбранном диапазоне частот
при R1.
Полученные данные занесите в табл. 1. -
Повторите опыт
(пункт 3) при другом сопротивлении R2,
включенном в контур. -
Не изменяя
настройки генератора определите
амплитуду колебаний ЭДС генератора,
соответствующую резонансной частоте,
полученной экспериментально в п. 3,4.
Для этого установите на генераторе
резонансную частоту, выход генератора
подключите непосредственно к входу
электронного осциллографа с помощью
переключателя на стенде, и зафиксируйте
амплитуду сигнала 0.
Результат занесите в табл. 1 и табл. 2. -
По данным табл.
1 постройте резонансные кривые при
различных сопротивлениях контура R1
и R2. -
На каждой
резонансной кривой отметьте уровень,
соответствующий 0,7U0
рез.
Таблица 1
|
№ |
Частота |
U0, |
|
|
п/п |
F, |
R1 |
R2 |
|
1 2 … 11 |
С
= … Ф; f0
= … КГц;
L
= … Гн; 0
= … В.
Соседние файлы в папке 2000
- #
09.06.201525.6 Кб260.DOC
- #
09.06.2015182.78 Кб2701.DOC
- #
09.06.2015304.64 Кб2602.DOC
- #
09.06.2015189.95 Кб2603.DOC
- #
09.06.2015293.89 Кб4604.DOC
Что такое добротность колебательного контура?
как измерить добротность в радиолюбительских условиях.
«Добротность обозначается символом Q (от английского quality factor) и является тем параметром колебательной системы,
который определяет ширину резонанса и характеризует, во сколько раз запасы энергии в системе больше, чем потери энергии за
время изменения фазы на 1 радиан.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность
колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания
»
— авторитетно учит нас Википедия.
Да уж. Напустили тумана ироды — без поллитры не разберёшься. А ведь придётся, раз впряглись.
Для начала возьмём ёжика. Хорошее животное! Хотя выдающимся умом не обладает, но думаю, что и оно в курсе, что
«quality factor» — это показатель качества колебательного контура и в первую очередь, конструктивного качества катушки индуктивности.
Теперь возьмём женщину в теле — добротную женщину. Таких женщин рисовали художники 18-го, 19-го веков, а поэты писали: «Её
выпуклости меня восхищают, её впуклости сводят с ума».
Так вот. К чему это я?
А к тому, что для получения в сухом остатке высокодобротного колебательного контура, придётся поискать в загашнике и высококачественный
конденсатор с низким током утечки, и катушку индуктивности — крепкую, добротную и красивую, словно выпавшую из картины
венецианского мастера в Пушкинском музее.
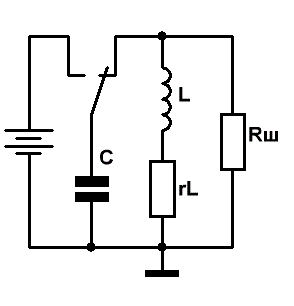
Приведём эквивалентную схему колебательного контура.
Здесь L и C — собственные индуктивность и ёмкость компонентов, входящих в состав колебательного
контура,
rL — сопротивление катушки, эквивалентное потерям электрической энергии в проводе катушки индуктивности,
Rш — сумма сопротивлений, обусловленных потерями в изоляции провода, каркасе, экране, сердечнике катушки индуктивности,
а также потерями, вызванные наличием токов утечки в конденсаторе.
Рис.1
При подключении к контуру внешних цепей, параллельно Rш добавляется дополнительное сопротивление Rн, вносимое этими внешними цепями.
По большому счёту, на Рис.1 не хватает ещё одной ёмкости, равной сумме паразитных ёмкостей катушки индуктивности, внешних цепей и
паразитной ёмкости монтажа. На высоких частотах эти привнесённые ёмкости могут иметь существенные величины, соизмеримые с ёмкостью самого
контурного конденсатора. На добротность эти ёмкости существенного влияния не оказывают, но при расчёте резонансной частоты их необходимо
учитывать и суммировать со значением основной ёмкости С.
Теперь давайте разберёмся, что такое «скорость затухания собственных колебаний в системе» и, каким боком она связана с добротностью.
Для начала мысленно спаяем схему, нарисованную на Рис.1, и замкнём переключатель на батарейку (в левое по схеме положение).
Конденсатор С зарядится до уровня, равного напряжению питания.
Теперь перещёлкнем переключатель в правое по схеме положение.
Благодаря энергии, запасённой в конденсаторе, в образовавшейся LC-цепи возникнут свободные колебания на частоте резонанса
колебательного контура, равной fо= 1/2π√LС.
Поскольку у нас ни с какой стороны не вечный двигатель — свободные колебания затухают, причём скорость затухания зависит от потерь
в конденсаторе и катушке индуктивности: чем они меньше, тем медленнее затухание.
Число колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в еπ = 23,14 раза,
как раз и будет числено равняться добротности контура Q.
Число периодов свободных колебаний в контуре можно подсчитать счётчиком импульсов и таким образом узнать добротность
колебательного контура, генератор сигналов в этом случае не нужен.
Собственно говоря, на таком принципе и строится большинство промышленных измерителей добротности.
Вспоминаем дальше: «Добротность является тем параметром колебательной системы, который определяет ширину резонанса».
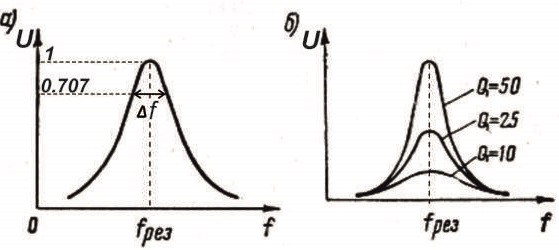
Рисуем резонансную кривую (амплитудно частотную характеристику) колебательного контура.
По частотной характеристике условно определяется полоса пропускания контура Δf.
При этом сделано допущение, что напряжение внутри этой полосы имеет право снижаться до уровня 0,707 от максимального.
Исходя из этого, формула для определения добротности приобретает следующий вид:
Q = f рез/Δf
.
Рис.2
Из формулы естественным образом вытекает, что чем выше добротность — тем уже полоса пропускания резонансного контура,
соответственно, чем ниже — тем шире.
А как измерить добротность контура, не прибегая к изготовлению специальных устройств, в домашней лаборатории?
1. Если речь идёт о низких (звуковых) частотах, то тут всё просто.
В этом случае, Q равна отношению реактивного сопротивления индуктивного или ёмкостного характера (характеристического сопротивления)
к полному последовательному сопротивлению потерь в резонансном контуре. В виду того, что конденсаторы на данных частотах практически не
вносят потерь, то добротность контура равна добротности катушки индуктивности, величина которой напрямую зависит от активного сопротивления
катушки.
А поскольку данное сопротивление можно легко измерить обычным омметром, то имеет полный смысл проделать эту не сильно замысловатую
манипуляцию, после чего перейти на страницу ссылка на страницу и в первой таблице произвести расчёт
добротности. Естественным образом, подразумевается, что катушка намотана на соответствующем для данных частот сердечнике, не вносящих
существенных потерь в работу колебательного контура.
2. На высоких частотах (радиочастотах) значение активного сопротивления катушки может составлять доли ома, к
тому же возможно проявление влияния добротности конденсатора на общую добротность цепи, поэтому такими же примитивными
методами, как в случае НЧ обойтись не удастся.
Рискну сделать осторожное предположение, что в радиолюбительской лаборатории у нас затерялся высокочастотный генератор с 50-омным
выходом и такой же высокочастотный осциллограф, или, на худой конец, измеритель ВЧ напряжений.
В этом случае мы воспользуемся ещё одним определением Q. Добротность резонансного контура равна фактору увеличения напряжения и
может быть выражена отношением напряжения, развиваемого на реактивных элементах к входному напряжению, поданному последовательно с
контуром.
Спаяем пару резисторов.
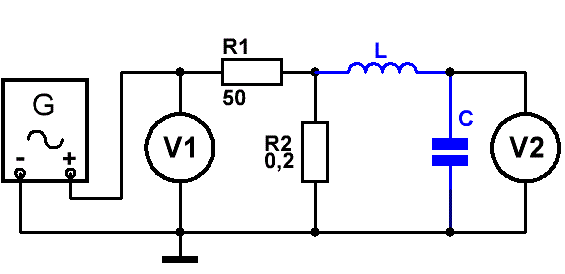
Добротность измеряется при настройке генератора сигналов на частоту резонанса контура, соответствующую максимальному выходному
напряжению.
Добротность Q рассчитывается как отношение выходного напряжения на резонансном контуре к напряжению, поданному на него.
В нашем случае
Q = 250
x V2/V1 .
Рис.3
Так как в случае высокодобротных элементов, сопротивление контура на резонансной частоте может превышать значение в сотню
килоом, для корректного измерения добротности, входные импедансы измерителя ВЧ напряжений, либо осциллографа должны превышать
это значение как минимум на порядок.
Все наши рассуждения и формулы корректны для ненагруженных параллельных колебательных контуров, то есть для случаев, когда на выходе
отсутствует реальная нагрузка.
В реальной схеме контур связан с источником колебаний и нагрузкой, которые вносят в него дополнительные потери, снижающие добротность.
Эквивалентная добротность Q параллельного колебательного контура с учётом этих потерь вычисляется по следующей формуле:
Q = Q0
x Rш/(Rш+Rо) , где
Q0 — добротность ненагруженного контура,
Rш — шунтирующее сопротивление, равное R(источника) ll R(нагрузки),
Rо — эквивалентное сопротивление ненагруженного контура, равное сопротивлению контура на резонансной частоте,
значение которого можно посчитать на той же странице ссылка на страницу во 2-ой таблице.
А на следующей странице порассуждаем на тему: что надо сделать, чтобы намотать катушку с максимально-возможной добротностью.
Колебательный контур является типичным представителем резонансных колебательных систем, играющих важную роль в большинстве разделов физики — в механике это различного типа маятники и звуковые резонаторы (струны, мембраны, трубы, свистки, органы), в электродинамике — колебательные контуры, закрытые и открытые резонаторы с распределенными параметрами, в оптике — лазерные резонаторы, эталоны Фабри — Перо и т.д. Принципы описания всех колебательных систем настолько общи, что теория колебаний стала самостоятельным разделом физики. Поэтому изучение параметров, свойств и характеристик колебательного контура полезно рассматривать как общее введение в мир резонансных колебательных систем.
В теории колебаний выделяются два класса явлений — явления в линейных и нелинейных колебательных системах. Линейными называются такие системы, параметры которых не зависят от амплитуды колебаний. Например, для маятников это означает такие малые колебания, при которых упругость пружин и стержней не зависит от амплитуды колебания, а натяжение нити подвеса определяется только гравитационными силами. Для электрических колебательных контуров независимыми от амплитуды токов и напряжений должны оставаться такие величины, как индуктивность $L$, емкость $C$ и сопротивление $R$.
Резонансные системы имеют два важных свойства.
-
Свойство избирательно реагировать на внешние источники сигналов, выделяя только те из них, частоты которых совпадают с собственной частотой колебательной системы.
-
Свойство запасать энергию колебаний, возбужденных внешним источником, поддерживая колебания в течение определенного времени после выключения внешнего источника.
Колебательный контур характеризуется двумя основными параметрами: частотой собственных (резонансных) колебаний $omega _{0} $ и добротностью $Q$, характеризующей отношение мощности энергии собственного колебания к мощности потерь за период.

На рис. 18 приведены примеры «параллелей» электрических и механических колебательных систем. В электрических резонаторах происходит периодический переход электрической энергии, запасенной в конденсаторе $(W_Э =frac 12 CU^2),$ в магнитную энергию катушки индуктивности $(W_M =frac 12 LI^2)$ и обратно. В маятниках происходит аналогичный циклический переход энергии из потенциальной (поднятого груза или сжатой пружины) в кинетическую и обратно.
Свободные колебания происходят в замкнутой цепи без вынуждающей силы (рис. 19,а).
Согласно второму закону Кирхгофа для такой цепи можно написать:
$$
Rcdot I+U_{C} =-Lcdot frac{dI}{dt}.
$$
Выражая $U_{C} $ через заряд $q$, получим уравнение
$$
Rcdot I+Lcdot frac{dI}{dt} +frac{q}{C} =0 mbox{ (СИ). }
$$
Дифференцируя по времени и учитывая равенство $I=frac{dq}{dt} $, получаем
$$
Lfrac{d^{2} I}{dt^{2} } +Rfrac{dI}{dt} +frac{I}{C} =0 mbox{ (СИ). }
$$
Разделив на $L$ и вводя обозначения
$delta =frac{R}{2cdot L} $ и $omega _{0}^{2} =frac{1}{LC} $,
получим общее уравнение для свободных колебаний линейной резонансной системы:
$$
I»+2delta , I’+omega _{0}^{2} I=0,
$$
где параметр $delta $ называется затухание, а параметр $omega _{0} $ — собственная частота, или частота свободных колебаний. Оно решается подстановкой $I=Acdot e^{iomega , t} $, которая приводит к характеристическому уравнению
$$
-omega ^{2} +2iomega , delta +omega _{0}^{2} =0,
$$
с решением
$$
lambda , _{1,2} =i, delta pm sqrt{omega _{0}^{2} -delta ^{2} } .
$$
Общее решение имеет две составляющие
$$
I=Acdot e^{iomega _{1} , t} +Bcdot e^{iomega _{2} , t} .
$$
Константы $A$ и $B$ определяются начальными данными задачи, например, зарядом $q_{0} $ или напряжением на конденсаторе $U_{0} $. Характер начальных данных определяется конкретной физической системой.
Частный пример схемы для возбуждения свободных колебаний в колебательном контуре приведен на рис. 19,б. Конденсатор $C$ заряжается от батареи до напряжения $U_{0} $ (положение «а» переключателя), а затем переключается в точку «б». Свободные колебания будут представлять собой циклический переход энергии электрического поля (в конденсаторе) в энергию магнитного поля (в индуктивности) и обратно.
Подставив найденные значения $A$ и $B$, получим общее решение для свободных колебаний в контуре
$$
I=ifrac{U_{0} }{Lsqrt{omega _{0}^{2} -delta ^{2} } } e^{-delta , t} frac{e^{isqrt{omega _{0}^{2} -delta ^{2} } , t} -e^{-isqrt{omega _{0}^{2} -delta ^{2} } , t} }{2} .
$$
Если бы колебательный контур состоял только из идеальных (без потерь) реактивных элементов (индуктивности $L$ и емкости $C$), то переход энергии из электрической в магнитную и обратно совершался бы без потерь, а в контуре существовали бы незатухающие свободные колебания с собственной частотой $omega _{0} =2pi , f=sqrt{frac{1}{LC}}.$
Наличие в схеме активного элемента $R$ приводит к тому, что часть энергии за каждый период переходит в тепло и колебания затухают с некоторой постоянной времени $tau $. Роль частоты в уравнении теперь играет величина $omega _{p} =sqrt{omega _{0}^{2} -delta ^{2} } $, зависящая от отношения реактивной мощности к потерям на активном сопротивлении $R$. При этом вовсе не обязательно в схему должен быть включен отдельный резистор. В его качестве может выступать, например, омическое сопротивление провода, которым намотана катушка индуктивности, а также сопротивление утечки изоляторов конденсатора. Кроме того, часть энергии колебаний может излучаться контуром в окружающее пространство в виде электромагнитной волны. На этом основано действие так называемых связанных контуров: если вблизи данного колебательного контура расположен другой, то в нем «наводятся» (возникают) колебания за счет того, что часть энергии трансформируется из первого контура во второй. Передача энергии совершается переменным электромагнитным полем, возникающим вокруг первого контура.
Если затухание мало, т. е. $delta <omega _{0} $, то мы получаем уравнение слабо затухающих колебаний в виде
$$
I=-frac{U_{0} }{Lomega _{p} } e^{-delta , t} sin omega _{p} t=-I_{0} e^{-delta , t} sin omega _{p} t.
$$
При этом резонансная частота приближается к частоте собственных колебаний:
$$
omega _{p} =sqrt{omega _{0}^{2} -delta ^{2} } approx omega _{0} left(1-frac{1}{2} frac{delta ^{2} }{omega _{0}^{2} } right).
$$
Таким образом, при малом затухании резонансная частота практически совпадает с собственной, однако колебания при этом не являются гармоническими. Для гармонических колебаний должно соблюдаться условие $Ileft(tright)=Ileft(t+Tright)$, где $T$ — период колебания. В нашем случае $Ileft(tright)ne Ileft(t+Tright)$, и о периоде можно говорить лишь как о времени, через которое повторяются нули функции (рис. 20). Именно в этом смысле мы будем ниже использовать термин «период колебаний».

Введем понятия добротности $Q$ и логарифмического декремента затухания $gamma $ контура. Из отношение амплитуд $n$–того и $(n + k)$–го колебаний равно
$I_{n} I_{n+k}^{-1} = e^{kdelta T}$, где $T=2, pi omega ^{-1} $ — период колебания («повторения нулей»). Логарифмическим декрементом затухания $gamma $ называется величина
$$
gamma =delta , T=frac{1}{k} ln frac{I_{n} }{I_{n+k} } =ln frac{I_{n} }{I_{n+1} } .
$$
Из уравнения для тока видно, что величина $delta $ обратно пропорциональна времени, за которое амплитуда колебаний уменьшается в $e$ раз. Из последнего уравнения следует, что декремент затухания $gamma $ показывает уменьшение амплитуды за период колебания:
$$
gamma =delta , T=frac{2; pi , delta }{omega } .
$$
С логарифмическим коэффициентом затухания однозначно связан другой, более распространенный параметр, характеризующий колебательную систему, добротность $Q$.
Добротность контура $Q$ определяется соотношением
$$
Q=frac{omega _{0} L}{R} =frac{1}{omega _{0} CR} =frac{rho }{R},
$$
где $rho =sqrt{frac LC} $ (СИ).
Физический смысл добротности заключается в отношении запасенной в контуре энергии к энергии потерь за период колебания
$$
Q=omega cdot frac{W_0}{Delta W},
$$
откуда можно найти связь добротности с другими параметрами контура
$$
Q=frac{pi }{gamma } =frac{pi }{delta , T} =frac{omega }{2, delta } =omega frac{L}{R} mbox{ (СИ).}
$$
Экспериментально добротность определяется по резонансной кривой как отношение резонансной частоты $omega _{p} $ к полосе частот $2cdot Delta omega $, определяемой на уровне $U_{1,2} =pm frac{U_p}{sqrt{2}}$:
$$
Q=frac{omega _{з}}{2cdot Delta omega } =frac{f_{з}}{2cdot Delta f} ,
$$
где $U_{p} $ — амплитуда колебания на резонансной частоте контура. Величина $rho =sqrt{frac LC}$ называется характеристическим (волновым) сопротивлением контура.
При большом затухании, т.е. при $delta >omega _{0} $, величина $omega _{0}^{2} -delta ^{2} $ отрицательна, корень из нее мнимый. Такой случай называется апериодическим процессом. Общее решение, аналогичное, полученному ранее, будет иметь вид
$$
I=-frac{U_{0} }{Lsqrt{(delta ^{2} -omega _{0}^{2} )} } e^{-delta , , t} mbox{sh}sqrt{(delta ^{2} -omega _{0}^{2} )} , t.
$$
График этой функции приведен на рис. 21.
Критическим условием, при котором затухающие колебания переходят в апериодический процесс, является условие $delta =omega _{0} $. В этом случае решение общего уравнения имеет вид
$$
I=-frac{U_{0} }{omega L} (omega t)e^{-delta , t} , =-frac{U_{0} }{L} t, e^{-delta , t} .
$$
Остается добавить, что аналогичные параметры могут быть введены для любой резонансной колебательной системы независимо от ее физической природы (механические, термодинамические, электромагнитные, оптические, аэро– и гидродинамические системы).
Колебательный контур, рассмотренный в предыдущем разделе, представлял собой замкнутую электрическую цепь, в которой совершаются свободные колебания.
В случае вынужденных колебаний мы должны подводить к контуру электрическую энергию от внешнего источника (генератора). Есть много способов для подключения источника внешней энергии к контуру, которые сводятся к той или иной комбинации двух основных: в разрыв цепи контура (рис. 22, а) или параллельно емкостной и индуктивной ветвям контура (рис. 22,б).
В зависимости от способа включения различают соответственно последовательный (рис. 22,а) и параллельный (рис. 22,б) колебательные контуры. Они предъявляют разные требования к согласованию с генератором и нагрузкой. Поэтому нужно отличать собственные параметры контура от параметров нагруженного контура, получаемые с учетом влияния генератора и «нагрузки» (входного сопротивления той цепи, в которую включен контур). В параллельном контуре (рис. 22,б) возникает резонанс токов. Для его поддержания в качестве вынуждающей силы необходимо применение генератора стабильного тока. В последовательном контуре (рис. 22,а) имеет место резонанс напряжений, и для его поддержания должен применяться внешний генератор стабильного напряжения.
Закон Кирхгофа, позволяющий исследовать процессы в контуре (рис. 22,а) в зависимости от частоты, записывается в виде
$$
U=U_{R} +U_{L} +U_{C} =IR+iI(omega L-frac{1}{omega C} )=Icdot Z.
$$
Контур представляет для генератора некоторое комплексное сопротивление
$$
Z=R_L +icdot (omega L-frac{1}{omega C} ),
$$
$$
left|Zright| = sqrt{R_L^2 +(omega L-frac{1}{omega C})^2}, mbox{tg}varphi =frac{omega L-frac{1}{omega C} }{R_L}
$$
где $left|Zright|$ — модуль комплексного сопротивления; $R_{L}$ — омическое сопротивление катушки индуктивности; $varphi $ — сдвиг фазы между активным и реактивным сопротивлениями, равный сдвигу фазы между током $I$ в цепи и входным напряжением $U$.
Из последнего выражения видно, что сопротивление цепи будет минимально и равно активному сопротивлению $R_{L} $ на некоторой частоте $omega _{0} $, определяемой условием
$$
omega _0 L=frac{1}{omega _0 C} , mbox{ где } omega _{0} =frac{1}{sqrt{LC}} mbox{ (СИ).}
$$
Таким образом, на резонансной частоте сопротивление контура минимально, чисто активно, а ток в цепи совпадает по фазе с входным напряжением (напряжением генератора). Фактически это и есть определение резонанса в последовательном колебательном контуре.
Для практических целей представляет интерес исследовать поведение напряжений на реактивных элементах контура в зависимости от частоты генератора и определить его добротность $Q$.
Поскольку фазы $U_{L} $ и $U_{C} $ независимо от частоты всегда сдвинуты относительно тока $I$ на $+$ и $-90^{circ}$ соответственно, то достаточно исследовать зависимость от частоты их модулей. Это можно сделать исходя из уравнений
$$
U_{R} =IR, U_{L} =Iomega L, U_{C} =frac{I}{omega C}, I=frac{U}{Z} .
$$
Для примера раскроем уравнения для $I$ и $U_{L} $. Используя введенное для свободных колебаний понятие добротности $Q=left(omega _{0} RCright)^{-1}$, получим следующее выражение для тока в последовательном контуре:
$$
I=frac{U}{sqrt{R^{2} +(omega L-frac{1}{omega C} )^{2} } } =frac{U}{R} frac{1}{sqrt{1+Q^{2} (frac{omega }{omega _{0} } -frac{omega _{0} }{omega } )^{2} } } .
$$
Тогда напряжение на индуктивности будет равно
$$
U_{L} =omega LI=Ufrac{Qfrac{omega }{omega _{0} } }{sqrt{1+Q^{2} (frac{omega }{omega _{0} } -frac{omega _{0} }{omega } )^{2} } } .
$$
Аналогичное уравнение можно получить для напряжения на $C$. При $omega =omega _{0} $ напряжения на $L$ и $C$ будут равны $U_{L0} =U_{C0} =Qcdot U$, т.е. в $Q$ раз больше напряжения вынуждающей эдс.
На самом деле максимумы напряжения на элементах $L$ и $C$ несколько выше и смещены от резонансной частоты и выражаются следующими соотношениями:
$$
omega _{Lmax } =omega _{0} sqrt{frac{2}{2-frac{R^{2} C}{L} } } =omega _{0} sqrt{frac{2}{2-left(frac{1}{Q} right)^{2} } } , omega _{Cmax } =frac{omega _{0}^{2} }{omega _{L} } .
$$
При добротности контура $Q ge 10$ сдвиг частот максимумов $U_{L} $ и $U_{C} $ относительно резонансной частоты $omega _{0} $ не превышает 1% и экспериментально резонансную частоту и добротность можно определять по резонансной кривой любого из напряжений $U_{L} $ и $U_{C} $. Напряжение на реактивных элементах $U_{L} $ и $U_{C} $ при $omega =omega _{0} $ в $Q$ раз больше, чем входное напряжение $U$, поэтому резонанс в последовательном контуре называется резонансом напряжений.
Важно отметить, что для нашего анализа существенно, что само входное напряжение $U$ от частоты не зависит. В противном случае все параметры зависели бы не только от самого контура, но и от параметров источника сигнала. Как было показано в предыдущем параграфе, для этого выходное сопротивление генератора должно быть много меньше $R$.
Схема подключения параллельного контура представлена на рис. 21,б. Из–за комплексного характера нагрузки ток генератора является комплексной величиной. Поэтому модуль тока $I$ может оказаться меньше не только суммы модулей токов индуктивной и емкостной ветвей контура, но и каждого из них в отдельности. Именно это и происходит при резонансе в параллельном контуре: токи в индуктивной и емкостной ветвях контура в $Q$ раз больше, чем ток, потребляемый от генератора тока. Поэтому резонанс в параллельном контуре называется резонансом токов.
Комплексное сопротивление параллельного контура равно
$$
Z=frac{Z_{1} Z_{2} }{Z_{1} +Z_{2} } =
frac{(R_{L} +iomega L)(iomega C)^{-1}}{R_{L} +i(omega L-(omega C)^{-1} )} approx
frac{LC^{-1}}{R_{L} +i(omega L-(omega C)^{-1})} .
$$
Мы пренебрегли величиной $R_{L} $ в числителе, поскольку она в $Q$ раз меньше индуктивного сопротивления, но этого нельзя делать в знаменателе, поскольку при резонансе величина в скобках стремится к нулю.
Условие резонанса для параллельного контура то же, что и для последовательного — равенство реактивных сопротивлений ветвей с $L$ и $C$:
$$
omega _{0} L=frac{1}{omega _{0} C}, mbox{ где } omega _{0} =frac{1}{sqrt{LC} } mbox{ (СИ). }
$$
Таким образом, при резонансе сопротивление контура становится чисто активным и равным
$$
R_{э} =frac{L}{ C R_{L} } =frac{rho ^{2} }{R_{L} } ,
$$
где — $rho =sqrt{frac LC} $ волновое сопротивление контура.
Сопротивление $R_{э} $ отдельного физического эквивалента в контуре не имеет, а является комбинацией волнового сопротивления $rho $ и сопротивления потерь $R_{L} $. Поэтому оно не составляет отдельной ветви параллельного контура и не ответвляет в себя ток. Следовательно, «переносить» его куда–либо или к чему–нибудь «подсоединять» (например, к внутреннему сопротивлению источника тока) бессмысленно. На схеме это просто условное обозначение того факта, что на резонансной частоте параллельный колебательный контур представляет для внешнего генератора некоторое чисто активное сопротивление величиной $R_{э} $, а в формулах символическая запись определенной комбинации $rho $ и $R_{L} $, даваемой последней формулой.
Добротность параллельного контура
$$
Q=frac{omega _{0} L}{R_{L} } =frac{1}{R_{L} omega _{0} C} =frac{R_{э} }{rho } =R_{э} sqrt{frac{C}{L} } .
$$
Собственные параметры параллельного контура, т.е. резонансная частота $omega _{0} $ и добротность $Q$ будут такими же, как и в последовательном контуре при тех же $C$, $L$ и $R_{L}.$
Предположим, что к контуру (см. рис. 3.8) приложено синусоидальное напряжение , амплитуда которого неизменна, а частота может изменяться в пределах от 0 до
.
Изменение частоты приводит к изменению параметров контура, изменяется его реактивное, а следовательно, и полное сопротивление, а также угол φ (аргумент комплексного сопротивления). Зависимости от частоты параметров цепи назовем частотными характеристиками цепи, зависимости действующих или амплитудных значений тока и напряжения от частоты резонансными кривыми.
На рис. 5.1 построены частотные характеристики и
. Изменение реактивного сопротивления приводит к изменению режима цепи. На рис. 5.2 приведен примерный вид резонансных кривых
и кривой
для цепи, добротность которой
. При ω = 0 напряжение, приложенное к цепи, во времени не изменяется, поэтому ток в цепи отсутствует. При изменении частоты от 0 до
реактивное сопротивление
имеет емкостный характер и изменяется от
до 0 (см. рис. 5.1). Вследствие этого ток возрастает от 0 до максимального резонансного значения
, а угол сдвига фаз между напряжением и током изменяется от —π/2 до 0. При изменении частоты от
до
результирующее реактивное сопротивление возрастает от 0 до
и имеет индуктивный характер.
Вследствие этого ток уменьшается от наибольшего значения до 0, а угол φ возрастает от 0 до π/2. Напряжение изменяется пропорционально току.
В выражении напряжения на индуктивности оба сомножителя зависят от частоты. При ω = 0 сопротивление
, ток I = 0, и, следовательно,
. При изменении частоты от 0 до
оба сомножителя увеличиваются и
возрастает. При дальнейшем увеличении частоты (
) ток I уменьшается, но за счет роста ωL напряжение
продолжает возрастать. Анализ, который здесь не приводится, показывает, что для цепи с добротностью
это возрастание
продолжается непрерывно до значения U, а для цепи с добротностью
напряжение
при некоторой частоте
достигает максимума
, а затем уменьшается. При
и
, следовательно,
.
Теперь рассмотрим зависимость напряжения на емкости от частоты. При ω = 0 тока в цепи нет, поэтому
. При возрастании ω, начиная от нуля,
непрерывно уменьшается. Анализ показывает, что для цепи с добротностью
напряжение
непрерывно уменьшается, а при
напряжение сначала из-за возрастания тока I увеличивается, достигает при некотором значении частоты
максимума
, а затем уменьшается.
Уменьшение напряжения с ростом частоты начинается при частоте
, меньшей
, вследствие непрерывного уменьшения
. При
как I, так и
равны нулю, поэтому
. Заметим, что
. При
, как было отмечено,
.
График зависимости тока от частоты показывает, что рассматриваемая цепь обладает «избирательными свойствами». Цепь обладает наименьшим сопротивлением для тока той частоты, которая наиболее близка к ее резонансной частоте.
Избирательными свойствами таких цепей широко пользуются в электросвязи и радиотехнике, при этом режим резонанса является нормальным режимом работы. Наоборот, в устройствах, где резонансный режим не предусмотрен, появление резонанса нежелательно, так как возникающие значительные напряжения на катушке и конденсаторе могут оказаться опасными для изоляции.
Рис. 5.1
Рис. 5.2
Выясним влияние параметров цепи на форму резонансной кривой . Для удобства сравнения резонансных кривых друг с другом будем строить их в относительных единицах:
где — действующий ток при резонансе;
— относительная частота.
Преобразуем выражение полного сопротивления цепи:
Разность характеризует расстройку контура относительно резонансной частоты. Произведение
называется обобщенной расстройкой. С учетом этих обозначений сопротивление
Ток в цепи
Выражение (5.5) показывает, что влияние параметров цепи на вид резонансной кривой полностью учитывается добротностью Q.
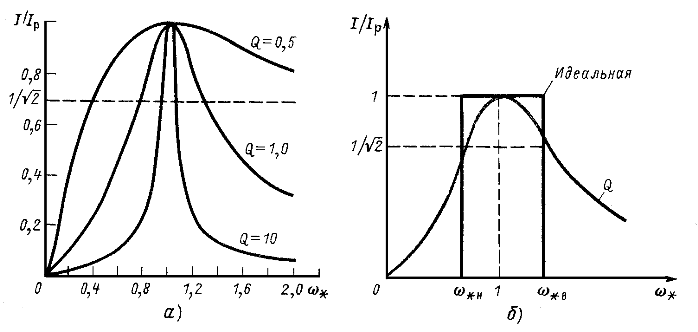
На рис. 5.3,а представлен ряд резонансных кривых. Чем больше Q, тем острее резонансная кривая, тем лучше «избирательные свойства» цепи, что и послужило одной из причин назвать Q добротностью контура. Заметим, что наибольшие достигаемые на практике значения Q контуров, состоящих из катушек индуктивности и конденсаторов, лежат в пределах 200-500.
Для оценки избирательных свойств цепи вводят условное понятие ширины резонансной кривой или полосы пропускания контура , которую определяют как разность верхней и нижней частот, между которыми отношение
превышает
. На рис. 5.3, а проведена горизонтальная линия, соответствующая
. Ее пересечение с резонансными кривыми определяет граничные частоты полосы пропускания соответствующих контуров. Из рисунка видно, что чем выше добротность, тем уже полоса пропускания контура.
Рис. 5.3
Высшая и низшая
относительные частоты показаны на рис. 5.3,б для контура с известной добротностью Q. На этом же рисунке построена идеальная резонансная кривая, для которой вне полосы пропускания ток равен нулю, т. е. у которой идеальные избирательные свойства. На рис. 5.3, а также проведена горизонтальная линия, соответствующая
. Ее пересечение с резонансными кривыми определяет полосы пропускания соответствующих контуров. Из рисунка видно, что чем выше добротность, тем уже полоса пропускания контура.
Если диапазон изменения частоты составляет несколько порядков, то часто выбирают для частоты логарифмический масштаб, т. е. или
. Интервал частот
, для которого
, называют декадой (десятикратное изменение частоты). Число декад
. Интервал частот, для которого
, называют октавой (удвоение частоты), причем 1 декада
октавы.
Пример 5.1.
Определить добротность контура по известной резонансной кривой
Решение.
На границах полосы пропускания , т.е. как следует из (5.5),
и
, откуда
так как и
(рис. 5.3, б).
Сложим (а) и (б):
или
т. е должно быть , т. е.
.
Вычтем (б) из (а):
или
откуда
Идеальный случай.
Пусть на шарик в пружинном маятнике действует периодическая внешняя сила
(1)
В этом случае для смещения шарика вблизи положения равновесия вместо уравнения (1) пункта 2.3.1 получаем
(2)
где 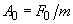
Нетрудно проверить, что решение уравнения (1) в случае
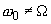
(3)
где
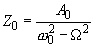
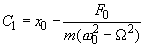
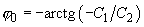
Первое слагаемое в (3) описывает свободные колебания, а второе – так называемые вынужденные колебания с амплитудой
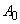
В предельном случае точного совпадения частот
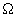
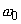
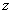
(4)
Такое движение можно рассматривать как колебания с линейно нарастающей со временем амплитудой. Явление раскачки колебаний под действием периодической внешней силы называется резонансом.
Следует подчеркнуть, что неограниченный резонансный рост амплитуды вынужденных колебаний есть идеализация системы. Во-первых, когда амплитуда колебаний становится достаточно большой, осциллятор, как правило, перестаёт быть линейным. Во-вторых, при записи уравнения (12) не учитывались силы трения, приводящие к затуханию колебаний. Рассмотрим роль последнего фактора более подробно.
Вынужденные колебания при наличии трения.
Если на осциллятор с трением действует внешняя сила (1), то уравнение таких колебаний имеет вид
(5)
где
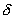
Общее решение (5) имеет вид [1–3]
(6)
где
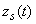
Благодаря трению
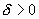
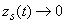
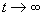
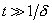
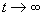
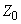
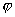
(7)
(8)
Как следствие из формулы (8), коэффициент
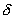
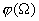
(9)
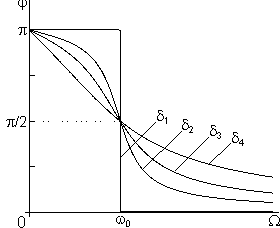
Важным отличием от случая вынужденных колебаний осциллятора без трения является наличие сдвига фазы
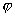
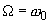
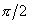
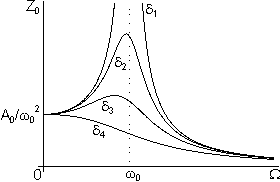
Другим существенным следствием наличия затухания является качественное изменение вида резонансной кривой. На рис. 1 приведена зависимость
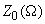
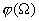
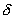
Рис. 1а. Резонансные кривые (АЧХ) линейного осциллятора для различных значений коэффициента трения:
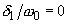
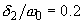
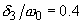
Рис. 1б. Зависимость сдвига фаз
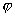
Максимальное значение амплитуды вынужденных колебаний (7), определяется формулой
(10)
Этому максимуму соответствует резонансная частота
(11)
при условии, что
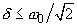
(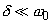
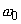
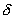
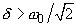
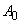
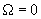
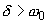
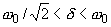
Как видно из формулы (7), при слабом затухании
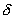
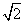
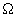
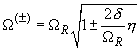
(12)
Величину

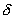
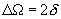
(13)
Таким образом, ширина резонансной кривой определяется добротностью и собственной частотой. Чем больше добротность колебательной системы, тем меньше ширина резонансного пика. Как видно из формулы (13), добротность колебательной системы можно оценить из экспериментальных АЧХ осциллятора и соответственно определить коэффициент затухания.
Выводы.
Литература.
- С.Э. Хайкин. Механика. – М.: ОГИЗ, 1947. – 574 с.
- Д. В. Сивухин. Механика. – М.: Наука, 1989. – 576. с.
- Карлов Н.В., Кириченко Н.А. Колебания, волны, структуры. – М.: ФИЗМАТЛИТ, 2003. – 496 с.