Способы доказательства теорем и приемы решения геометрических задач
Аксиома есть очевидная истина, не требующая доказательства.
Теорема или предложение есть истина, требующая доказательства.
Доказательство есть совокупность рассуждений, делающих данное предложение очевидным.
Доказательство достигает своей цели, когда при помощи его обнаруживается, что данное предложение есть необходимое следствие аксиом или какого-нибудь другого предложения, уже доказанного.
Всякое доказательство основано на том начале, что при правильном умозаключении из истинного предложения нельзя вывести ложного заключения.
Состав теоремы. Всякая теорема состоит из двух частей, a) условия и b) заключения или следствия.
Условие иногда называют предположением. Оно дано и поэтому иногда получает название данного.
Обратная теорема. Предложение, у которого заключение данной теоремы делается условием, а условие заключением, называется теоремой обратной данной.
В таком случае данная теорема называется прямой.
Две теоремы в совокупности, прямая и обратная, называются взаимно-обратными теоремами.
Они находятся в таком взаимном отношении, что, выбрав любую из них за прямую, можно другую принять за обратную.
В двух взаимно-обратных предложениях одно из них вытекает как необходимое следствие другого.
Если в теореме мы обозначим условие буквой, стоящей на первом месте, а заключение буквой, стоящей на втором месте, то прямую теорему можно схематически представить выражением (Aa), а обратную выражением (aA).
Выражение (Aa) схематически представляет предложение: если имеет место A, то имеет место a.
Если для данного предложения (Aa) имеет место и теорема (aA), то обе теоремы (Aa) и (aA) называются взаимно-обратными теоремами.
Примером двух таких взаимно-обратных теорем могут послужить теоремы:
Первая теорема. В треугольнике против равных сторон лежат равные углы.
Вторая теорема. В треугольнике против равных углов лежат равные стороны.
В первой теореме данным условием будет равенство сторон треугольника, а заключением равенство противолежащих углов, а во второй наоборот.
Не всякая теорема имеет свою обратную.
Примером арифметического предложения, не имеющего своего обратного, может послужить следующая теорема. Если в двух произведениях множители равны, то и произведения равны.
Обратное предположение несправедливо. Действительно, из того, что произведения равны, не следует, что множители равны.
Примером геометрического предложения, для которого обратное предложение не имеет места, может послужить теорема: во всяком квадрате диагонали равны.
Предложение обратное этому будет: если диагонали четырехугольника равны, то он будет квадратом.
Это предположение неверно, ибо диагонали бывают равными не в одном квадрате.
Так как обратное предположение не всегда справедливо, то каждый раз обратное предложение требует особого доказательства.
В теории геометрических доказательств весьма важно иногда знать, когда данное предложение допускает свое обратное.
Для этой цели может послужить следующее правило обратимости. Когда в предположении всем возможным и различным условиям соответствуют все возможные и различные заключения, обратное предложение имеет место.
Рассмотрим для примера.
Прямое предложение. Если два треугольника имеют по две равные стороны, то третья сторона будет больше, равна или меньше третьей стороны другого треугольника, смотря по тому, будет ли угол между равными сторонами больше, равен или меньше соответствующего угла другого треугольника.
В этом предложении трем различным и возможным предположениям об угле соответствуют три различных и возможных заключения о противолежащей стороне, поэтому, согласно с правилом обратимости, данная теорема допускает обратное предположение:
Когда два треугольника имеют по две равных стороны, угол между ними будет больше, равен или меньше соответствующего угла другого треугольника, смотря по тому, будет ли третья сторона больше, равна или меньше третьей стороны данного треугольника.
Кроме обратной прямая теорема может иметь свою противоположную.
Противоположная теорема есть такая, в которой из отрицания условия вытекает отрицание заключения.
Противоположная теорема может иметь свою обратную.
Чтобы обобщить все эти теоремы, мы их представим схематически в следующей общей форме:
-
Прямая или основная теорема. Если имеет место условие или свойство A, то имеет место заключение или свойство B.
-
Обратная. Если имеет место B, то имеет место A.
-
Противоположная. Если не имеет места A, то не имеет места B.
-
Обратная противоположной. Если не имеет места B, то не имеет места A.
Следующие примеры поясняют на частных случаях взаимное отношение этих теорем:
-
Прямая теорема. Если при пересечении двух данных прямых третьей соответственные углы равны, то данные прямые параллельны.
-
Обратная теорема. Если две прямые параллельны, то при пересечении их третье, соответственные углы равны.
-
Противоположная. Если при пересечении двух прямых третьей соответственные углы не равны, прямые не параллельны.
-
Обратная противоположной. Если прямые не параллельны, соответственные углы не равны.
При геометрическом изложении теорем достаточно доказать только две из этих трех теорем, тогда остальные две теоремы справедливы без доказательства.
На этой связи теорем основан прием, по которому для доказательства обратной теоремы ограничиваются часто только доказательством теоремы противоположной.
Способы геометрических доказательств
Для доказательства геометрических теорем существует два основных способа: синтетический и аналитический.
Эти методы называют иногда сокращенно синтезом и анализом.
Синтез есть такой метод доказательства, в котором данное предложение является необходимым следствием другого, уже доказанного.
В синтезе цепь доказательств начинается с какого-нибудь известного предложения и оканчивается данным предложением. При доказательстве исходное предложение сопоставляется с аксиомой или с другим уже известным предложением. Синтетический способ удобен для вывода таких новых предложений, которые заранее не обозначены. Для доказательства же данного предложения он представляет много неудобств. В нем не видно: a) какую из известных теорем нужно выбрать для того, чтобы доказываемое предложение вытекало как ее необходимое следствие, и b) какое из следствий выбранного предложения приводит к доказываемому предложению.
Синтез называют поэтому не методом открытия новых истин, а методом их изложения.
Впрочем и при самом изложении теорем методом синтетическим является неудобство в том отношении, что не видно, почему за исходную истину в цепи доказательств выбрано то, а не другое предложение, то, а не другое его следствие.
Примером синтетического способа доказательства может послужить следующая теорема.
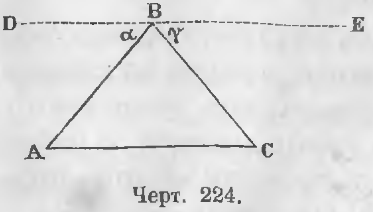
Теорема. Сумма углов треугольника равна двум прямым.
Дан треугольник ABC (черт. 224).
Требуется доказать, что A + B + C = 2d.
Доказательство. Проведем прямую DE параллельную AC.
Сумма углов, лежащих по одну сторону прямой, равна двум прямым, следовательно,
α + B + γ = 2d
Так как
α = A, γ = C
то, заменяя в предыдущем равенстве углы α и γ равными им углами, имеем:
A + B + C = 2d (ЧТД).
Здесь исходным предложением в цепи доказательств выбрана теорема о сумме углов, лежащих по одну сторону прямой.
Она поставлена в связь с теоремами о равенстве углов накрест-лежащих при пересечении двух параллельных третьею косвенною.
Доказываемая теорема есть необходимое следствие всех предложенных теорем и является в цепи доказательств последним заключением.
Анализ есть способ обратный синтезу. В анализе цепь рассуждений начинается доказываемой теоремой и оканчивается какой-нибудь другой уже известной истиной.
Анализ является в двух видах. От доказываемого предложения мы можем перейти к предложению, служащему его ближайшим основанием или его ближайшим следствием.
Переходя от данного предложения к предложению, служащему его ближайшим основанием, мы смотрим на данное предложение как на необходимое следствие.
Переходя от данного предложения к его ближайшему следствию, мы смотрим на данное предложение как на основание для цепи умозаключений.
Первый способ анализа. Совершая анализ переходом к основанию, отыскивают то первое ближайшее предложение, из которого данное вытекает как необходимое следствие. Если это предложение было прежде доказано, то доказано и данное предложение, если же нет, то отыскивают второе предложение, служащее основанием для первого.
Такой переход к основанию следует продолжать до тех пор, пока не дойдем до предложения вполне доказанного. Данное предложение явится как необходимое следствие последнего доказанного предложения.
Обозначая каждое предложение буквой и ставя ее впереди или позади другой, смотря по тому, будет ли оно служить основанием или следствием другого предложения, мы схематически можем этот прием анализа выразить в виде
H — K — L — M
где M есть данное предложение, L его ближайшее основание, а H предложение, вполне доказанное. Если верно предложение H, то верно предложение K; если верно K, то верно L; если верно L, то верно и M.
Второй способ анализа состоит в переходе от данного предложения к его следствию. Этот прием применяют чаще, потому что легче находить необходимое следствие, нежели отыскивать основание какой-нибудь истины. По этому способу выводят из данного предложения ту теорему, которая служит его ближайшим следствием. Если это следствие есть предложение прежде доказанное, то на нем и останавливаются; если же нет, переходят к следующему ближайшему следствию и вообще продолжают такой последовательный вывод следствий до тех пор, пока не дойдут до предложения, вполне доказанного.
Если последнее предложение не верно, то и данное не верно, ибо неверное следствие нельзя получить из верного предложения.
Если же последнее предложение верно, то для убеждения в верности данного предложения требуется, чтобы были соблюдены некоторые условия.
Схематически этот прием анализа можно представить в виде
M — N — O — P — Q — R — S
где M данное предложение, N предложение, служащее его ближайшим следствием, а S то последнее предложение, в справедливости которого мы вполне убеждены.
Из двух предложений R и S, стоящих в такой связи, что если справедливо R, то справедливо и предложение S, мы, как известно, не всегда можем обратно заключать, что если справедливо S, то справедливо и предложение R.
Чтобы последнее заключение имело место, требуется, чтобы теоремы R и S были взаимно-обратными предложениями.
Итак, для того, чтобы убедиться, что теоремы R и S стоят в такой связи, что она удовлетворяет схеме R — S и схеме S — R, требуется доказать, что предложения R и S взаимно-обратны.
Таким образом, чтобы можно было по верности последнего предложения S заключить о верности данного предложения M, требуется доказать, что каждые два рядом стоящие предложения R и S, P и R, O и P, N и O, M и N удовлетворяют закону обратимости.
Если это доказано, то цепь предложений можно обратить, и рядом со схемой M — N — O — P — Q — R — S справедлива и схема
S — R — Q — P — O — N — M
по которой мы имеем право заключить, что если справедливо предложение S, то справедливо и предложение M.
Так как затруднительно всякий раз доказывать обратимость двух предложений, то этого избегают, соединяя способ аналитический с синтетическим. После того, как из предложения M выведено предложение S как его следствие, смотрят, нельзя ли обратно вывести предложение M как необходимое следствие предложения S.
Если синтез есть способ, называемый дедукцией или выводом, то анализ можно назвать редукцией (приведение, наводка).
Примером аналитического способа доказательства может послужить следующая теорема.
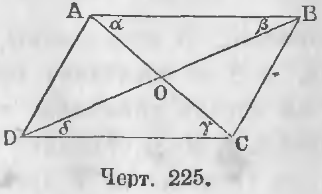
Теорема. Диагонали параллелограмма пересекаются пополам.
Доказательство. Если диагонали пересекаются пополам, то треугольники AOB и DOC равны (черт. 225). Равенство же треугольников AOB и DOC вытекает из того, что AB = CD как противоположные стороны параллелограмма и ∠α = ∠γ, ∠β = ∠δ как накрест-лежащие углы.
Таким образом мы видим, что последовательно данное предложение заменяется другим и такое замещение совершается до тех пор, пока не дойдем до предложения уже доказанного.
Сравнение синтеза с анализом. Способ аналитический вернее ведет к доказательству данной теоремы, ибо от данной теоремы легче переходить к его ближайшему основанию или следствию.
Хотя анализ лучше синтеза объясняет, почему выбран тот или другой путь для доказательства теоремы, однако неопределенность при доказательствах не устраняется вполне в том смысле, что при последовательных заменах одного предложения другим, мы не всегда можем дойти до предложения нам известного, ибо иногда не видно, какое из следствий или какое из оснований данного предложения нужно выбрать для того, чтобы его доказать. Затруднения увеличиваются еще больше, когда приходится для доказательства проводить новые вспомогательные прямые. Иногда трудно дать верные указания, какие из них облегчают доказательство данной теоремы.
Анализ, как и все логические приемы, только облегчает и помогает находить доказательство данного предложения, но не всегда необходимо ведет к самому доказательству.
Кроме этих прямых существует непрямой способ доказательства, известный под именем доказательства от противного или способа приведения к нелепости.
Способ доказательства от противного состоит в том, что для доказательства данного предложения убеждают в невозможности предположения противоположного.
На этом основании это доказательство называется доказательством от противного. Оно достигает своей цели всякий раз, когда из двух предложений, данного и противоположного, одно непременно имеет место.
В этом случае для доказательства данного, допустив противоположное предложение, выводят из него такие следствия, которые противоречат аксиомам или теоремам, уже доказанным. Если одно из следствий этого предложения ложно, то и противоположное предложение ложно, а следовательно данное предложение справедливо.
Этот прием часто применяют для доказательства теорем обратных или противоположных данным.
Не трудно заметить, что этот способ есть второй способ анализа, в котором от данного предложения последовательно переходят к его следствиям.
Примером применения такого способа может послужить приведенное выше доказательство теоремы: против равных углов в треугольнике лежат равные стороны (теорема 26).
В геометрии также применяют способы, зависящие от самого содержания геометрических истин. Геометрические истины относятся к геометрическим протяжениям. Эти протяжения обладают определенными свойствами, подлежащим внешним чувствам. Геометрическое протяжение может рассматриваться как целое, доступное наблюдению внешними чувствами. Убедительности доказательства содействует и самое чувственное созерцание. Обойтись без него в геометрии невозможно.
К числу приемов, имеющих место в геометрии, принадлежат: способ наложения, способ пропорциональности и способ пределов.
Способ наложения состоит в том, что одну геометрическую величину накладывают на другую. Этим способом убеждаются в равенстве или неравенстве геометрических протяжений, смотря по тому, совмещаются или не совмещаются ни при наложении.
Способ пропорциональности состоит в применении к геометрическим протяжениям свойств пропорций. Этот способ применяется при доказательстве теорем, относящихся к подобным фигурам и к пропорциональным отрезкам.
Способ пределов состоит в том, что вместо данных протяжений рассматривают свойства протяжений близких по своим свойствам к данному, и выводы, получаемые из рассмотрения одних, применяют к другим сходным протяжениям.
Способы решения геометрических задач
При решении геометрических задач синтез и анализ применяют точно так же как и при доказательстве теорем.
Решая задачу синтетически, берут такую другую задачу, которую умеют решить, потом из ее решения выводят решение следующей задачи, как ее необходимое следствие, и поступают так до тех пор, пока не доходят до решения данной задачи.
Синтетический метод решения задачи обладает всеми теми же недостатками, какими обладает и синтетический метод доказательства.
Поэтому чаще и успешнее для решения задач применяют анализ.
При решении задачи анализом заменяют данную задачу новой. Эту новую задачу будем называть заменяющей.
Если две задачи находятся в таком отношении, что условия второй есть необходимые следствия условий первой, то первую задачу будем называть начальной, а вторую — производной.
При анализе существуют два способа.
Первый способ. Заменяющую задачу выбирают так, чтобы условия данной задачи вытекали как необходимое следствие условий новой заменяющей задачи, т. е. по нашей терминологии от данной задачи переходят к первой начальной задаче. Если решение этой задачи известно, то решение данной является как необходимое следствие решения начальной задачи. Если же ее решение неизвестно, то от нее переходят ко второй, третьей начальной задаче и продолжают так поступать до тех пор, пока не получат задачу, решение которой известно.
Решив эту последнюю задачу, вместе с этим последовательно доходят и до решения данной задачи.
Второй способ. Можно переходить от данной задачи к такой другой, условия которой являются следствием условий данной, т. е. от данной задачи переходят к ее производной.
Заменяя таким образом последовательно одну задачу другой ее производной, мы можем дойти до задачи, решение которой уже известно. Решение этой задачи дает иногда возможность решить и данную задачу.
Такой переход от данной задачи к ее производной применяют чаще, ибо переходить к следствию легче, нежели подыскивать основание для какой-нибудь истины.
В этом частном случае анализа обыкновенно полагают, что задача решена, и из этого предположения выводят соотношения, дающие возможность решить данную задачу.
При переходе от данной задачи к ее заменяющей весьма важно обращать внимание на то, будут ли две задачи обладать свойством взаимной обратимости. Эта взаимность в условиях двух задач является тогда, когда одна задача, будучи начальной для другой, может быть в то же время и ее производной; иначе когда две задачи находятся в таком отношении, что условия одной могут быть и необходимыми следствиями другой и наоборот.
Если две задачи, данная и новая, обладают такими свойствами, то новая задача вполне заменяет данную. В этом случае все решения одной будут и решениями другой.
Если же условия двух задач не обладают свойствами взаимной обратимости, то, заменяя данную задачу новой, мы можем найти или лишние решения или иметь некоторые из решений потерянными.
Если заменяющая задача будет производной для данной, то мы можем найти некоторые лишние решения; если же она будет начальной для данной, то мы можем найти некоторые решения потерянными.
Так как чаще от данной задачи переходят к задаче производной, то чаще приходится получать решения лишние.
Чтобы отделить лишние решения и отыскать потерянные, поверяют все найденные решения.
Поверка есть способ отделения посторонних (лишних) решений. Она дополняет анализ.
Аналитическое решение задачи указывает на то построение, которое нужно сделать для решения задачи. Совершая это построение, поступают при решении задачи способом обратным анализу, т. е. прибегают к синтетическому способу. Этот синтетический способ часто может заменить и самую поверку найденных решений.
Совместное применение синтеза и анализа дает средство избегнуть тех ошибок, которые могут получиться при применении только одного из этих методов решения.
Решим одну и ту же задачу синтетически и аналитически. Для примера может послужить следующая задача.
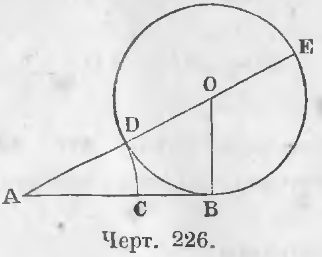
Задача. Разделить данный отрезок AB в крайнем и среднем отношении.
Решение. Восставим из конца отрезка AB перпендикуляр BO равный половине AB (черт. 226). Из центра O опишем окружность радиусом BO, соединим центр O с точкой A и отложим на отрезке AB отрезок AC равный AD, тогда отрезок AC или AD будет искомый.
Доказательство. Прямая AB — касательная к окружности, следовательно
AE/AB = AB/AD
откуда имеем:
(AE — AB)/AB = (AB — AD)/AD
Так как DE = AB и AD = AC, то в предыдущей пропорции имеем:
AE — AB = AE — DE = AD = AC
AB — AD = AB — AC = BC
откуда имеем пропорцию
AC/AB = BC/AC
Это решение синтетическое. В нем мы отправляемся от известной теоремы о свойствах касательной и решение данной задачи вытекало как необходимое следствие этой теоремы.
Решение аналитическое. Допустим, что задача решена, а следовательно и отрезок AC найден, тогда
AB/AC = AC/CB (1)
откуда
(AB + AC)/AB = (AC + CB)/AC
или
(AB + AC)/AB = AB/AC (2).
Из последней пропорции видно, что AB есть касательная, AB + AC пересекающаяся, AC ее внешний и AB внутренний отрезок.
Отсюда вытекает и само построение. Нужно из конца B восставить перпендикуляр равный ½AB, провести окружность, соединить O с A и отложить на отрезке AB часть AC = AD.
В этом аналитическом решении мы данную задачу, удовлетворяющую условию (1), заменяем задачей, удовлетворяющей условию (2).
Условие (2) указывает и путь для решения самой задачи построением.
Обыкновенно, найдя решение задачи способом аналитическим, совершают построение, в котором, применяя способ рассуждений синтетический, доказывают, что это построение действительно разрешает задачу и этим доказательством заменяют поверку, имеющую в виду устранить посторонние решения.
В данном примере между задачами, удовлетворяющим условиям (1) и (2), существует полная обратимость, ибо из условий (1) вытекают условия (2) как необходимое следствие и наоборот, поэтому здесь нет ни потерянных, ни посторонних решений.
Исследование второстепенных и вспомогательных приемов решения задач еще не достигло в своей обработке полной и совершенной законченности. Мы пока устраняемся от их подробного рассмотрения.
Как правило, у большинства учеников самый нелюбимый блок в экзаменах — геометрия, потому что он тяжело даётся. А кто-то и вовсе его не понимает. А в геометрии есть самый нелюбимый тип заданий — это задачи на доказательство. Почему так происходит и как помочь ученику научиться их решать?
Что такое задача на доказательство
Задача на доказательство — это утверждение, которое нужно доказать, используя различные теоремы, аксиомы, следствия и признаки геометрии. Другими словами, нам нужно решить задачу и получить то же самое, что написано в условии, тогда задание будет выполнено. Поэтому задачи на доказательство на самом деле несильно отличаются от задач на нахождение чего-либо — просто то, что нужно найти, уже известно заранее. Звучит даже легче, не правда ли? Так почему же многие школьники всё равно намеренно пропускают эти задания и не решают их?
Всё дело в том, что задачи на доказательство очень похожи на то, как доказываются теоремы. А доказательство теорем начинается в 7 классе, когда происходит деление на Алгебру и Геометрию как отдельные предметы в школах. Однако обычно доказательство теорем выглядит следующим образом:
- учитель доказывает теорему у доски,
- ученики переписывают себе всё в тетрадь, иногда даже не понимая, что они пишут,
- дальше звучит знакомая всем фраза «Выучите доказательство, потом ответите его на оценку»,
- а дальше зачастую происходит зубрёжка переписанной теоремы.
Даже человек без педагогического образования догадается, что к пониманию, как осуществляется доказательство, это не приведёт. Да и зачем, если ни на одном экзамене не просят доказывать теоремы? Наоборот, нужно просто использовать уже готовые и доказанные формулировки. Но навык это очень полезный, и вот почему.
Где мы встречаемся с доказательствами
Умение доказывать геометрические задачи проверяют 2 главных школьных экзамена по математике — ОГЭ и ЕГЭ.
- В ОГЭ доказательство находится в № 24 как самостоятельная задача, которая приносит 2 балла максимум,
- в ЕГЭ доказательства встречаются в пунктах а) в № 13 (стереометрическая задача) и № 16 (планиметрическая задача), которые сами по себе приносят по 1 баллу, но без корректных доказательств практически невозможно перейти к пункту б) с решением, что в совокупности приносит по 3 балла за каждую задачу.
Как вы можете заметить, доказательства достаточно важны и приносят неплохие баллы сдающим экзамены. Но это не единственная их польза. Все задания на доказательство помогают ученикам выстраивать логические цепочки и учат рассуждать, а это пригодится не только на экзаменах, но и в жизни.
Так как помочь школьникам научиться их решать?
Как научить школьника решать задачи на доказательство
Доказательство, как я уже говорила, несильно отличается от решения всех геометрических задач. Алгоритм в обоих случаях такой:
- построить чертеж,
- отметить на чертеже, что дано,
- отметить на чертеже, что нужно найти,
- построить логическую цепочку от того, что нужно найти до того, что дано,
- записать шаги доказательства.
Кроме того, в ходе решения или доказательства нужно не забывать выносить всю теорию на чертёж, а также строить чертеж, причем как можно большего размера — так будет лучше видно детали.
Но вернёмся к объяснению задач на доказательство ученикам. Самое главное — объяснить, как должно строиться доказательство, потому что именно здесь у учеников возникают проблемы. Обычно они двух видов:
- слабые ученики просто не берутся за доказательство, потому что не понимают, что делать,
- а сильные в ходе доказательства могут опускать и не расписывать некоторые важные пункты, потому что для них они кажутся очевидными, что приводит к нарушению логики и потере баллов.
Удобная аналогия для решения задач на доказательство
А секрет прост. Доказательство должно быть похоже на заплетание косички:
- три пряди, на которые мы делим все волосы — это то, что нам дано,
- готовая косичка — то, что должно получиться или то, что нужно доказать,
- процесс вплетания прядей — построение логической связи.
Заметили сходство с алгоритмом выше?
Если вы сможете донести это до учеников, то проблема с пропуском важных этапов решится. Ведь мы не можем пропустить прядь, пока плетём косичку? Тогда она у нас просто не получится.
Если пример с косичкой не поможет, то можно провести аналогию с объяснением доказательства очень-очень слабому ученику. Нужно посоветовать ему представить, что, записывая доказательство, он объясняет его другу, который ничего не понимает и всегда задаёт один и тот же вопрос «Почему?». Тогда «отвечая» каждый раз на «Почему?», ученик автоматически будет всё подробно расписывать, а у эксперта при проверке такого вопроса не возникнет.
Давайте объединим все вышеуказанные приёмы и алгоритм и разберём несложную задачу на доказательство. Я буду писать объяснение от первого лица, которое вы можете использовать на уроке, и к нему иногда добавлять поясняющие комментарии.
Разбор задачи на доказательство
Шаг 1. Понять, что нам дано
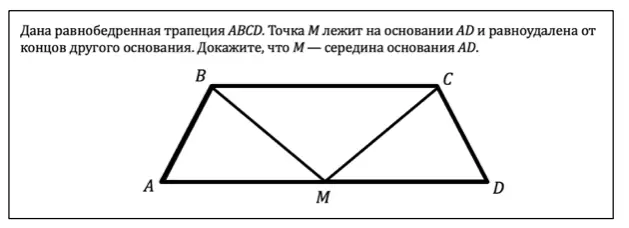
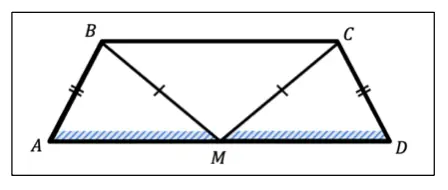
К счастью, первый пункт алгоритма можно опустить, потому что чертёж нам уже дан. Далее нужно вынести на чертёж всё что дано, а именно:
- АВ = CD, так как по условию трапеция равнобедренная, а значит её боковые стороны равны,
- ВМ = СМ, так как точка М равноудалена концов основания ВС.
Шаг 2. Понять, что нужно доказать
Теперь отмечаем то, что нужно доказать:
- нужно доказать, что М — середина AD, а значит отрезки АМ и MD должны быть равны.
Итак, получается следующая картина:
А теперь нужно построить логическую цепочку от того, что нужно найти, до того, что дано.
Я не оговорилась, нужно идти от вопроса к тому, что есть. Скажите ученикам, чтобы они представили, будто раскручивают клубок с рассуждениями, а когда дойдут до точки начала, будут закручивать его обратно и записывать всё по порядку. Кстати, вот вам ещё один приём, который поможет научить учеников доказывать задачи.
Шаг 3. Выстроить логическую цепочку
- Итак, как мы можем доказать, что AM = MD? Верно, из треугольников ABM и MCD, ведь если мы докажем, что данные треугольники равны, то и все их элементы тоже будут равны. Сейчас мы раскрутили первый виток нашего клубочка.
- Как нам доказать, что треугольники ABM и MCD равны? Правильно, у нас уже есть две равные стороны, осталось доказать, что углы ABM DCM равны. Ещё виток раскрутили!
- А как доказать, что углы ABM DCM равны? Конечно, можно воспользоваться свойством равнобедренной трапеции, а также получившимся равнобедренным треугольником ВМС. Вот мы и раскрутили клубок! А теперь будем его закручивать, подробно всё расписывая.
Не забывайте про ученика-почемучку, которому вы как будто объясняете доказательство. А также не забудьте в решение выписать всё то, что вы уже вынесли на чертёж, начинать нужно именно с этого.
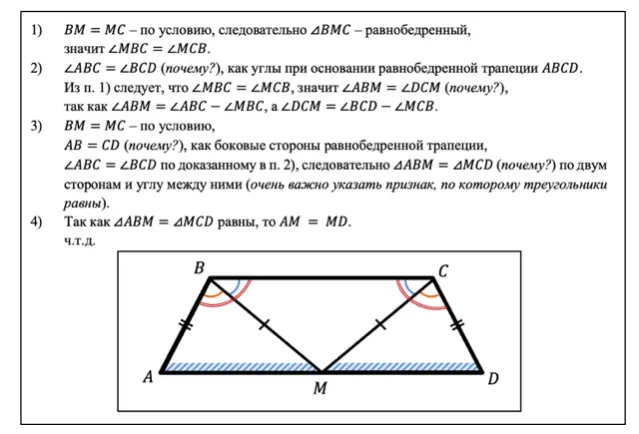
- ВМ = МС по условию, следовательно треугольник BMC — равнобедренный, значит углы МВС и МСВ равны.
- Углы АВС и BCD равны (почему?), как углы при основании равнобедренной трапеции ABCD.
Из п. 1) следует, что углы МВС и МСВ равны, значит углы АВM и DCM равны (почему?), так как АВM = АВС — МВС, а DCM = BCD — МСВ. - ВМ = МС по условию,
АВ = CD (почему?), как боковые стороны равнобедренной трапеции,
углы АВС и BCD равны по доказанному в п. 2), следовательно треугольники ABM и MCD равны (почему?) по двум сторонам и углу между ними (очень важно указать признак, по которому треугольники равны). - Так как треугольники ABM и MCD равны, то AM = MD.
Что и требовалось доказать.
Вот так легко мы доказали задачу, используя:
- алгоритм решения геометрической задачи,
- косичку,
- ученика-почемучку
- и клубочек.
Теперь вы знаете, как объяснить доказательство самому слабому ученику, а также как подсказать сильному, чтобы он не упускал важные факты. И пусть мы разобрали задачу уровня ОГЭ, в ЕГЭ на более сложных примерах все эти принципы работают с таким же успехом.
Прежде чем говорить
о доказательстве, продолжим характеристику
основных форм мышления. Введем некоторые
необходимые понятия.
Умозаключением
называется процесс получения нового
суждения-вывода из одного или нескольких
данных суждений.1
Силлогизм
– это умозаключение, в котором на
основании двух суждений (большей посылки
и меньшей посылки) выводится третье
суждение (вывод, заключение).
Большая посылка
– это некоторое общее суждение (аксиома,
теорема, определение, допущение и т.
д.); меньшая посылка – частное суждение.
Пример.
Если три стороны одного треугольника
равны трем сторонам другого треугольника,
то такие треугольники равны (общее
суждение).
В треугольниках
АВС и А1В1С1
АВ = А1В1,
АС = А1С1,
ВС = В1С1
(частное суждение).
Треугольник АВС
равен треугольнику А1В1С1
(новое суждение-вывод) .
Теперь мы в состоянии
принять рабочее понятие доказательства,
достаточное для нужд школьного курса
планиметрии.
Доказательство
– логическое действие, в процессе
которого истинность какого-либо
математического предложения обосновывается
с помощью других предложений, признанных
истинными. Это действие обычно представляет
собой цепочку силлогизмов.
Доказательство
включает в себя три основных элемента:
Тезис,
установить истинность которого –
главная цель доказательства. Форма
выражения тезиса – суждение.
Аргументы
(основания) доказательства – положения,
на которые опирается доказательство и
из которых при условии их истинности
необходимо следует истинность
доказываемого тезиса. Форма выражения
аргументов – суждения. Связывая
аргументы, приходим к умозаключениям,
которые строятся по определенным
правилам.
Демонстрация
– логический процесс взаимосвязи
суждений, в результате которого
осуществляется переход от аргументов
к тезису.
К
тезису, аргументам и демонстрации
предъявляют определенные требования,
нарушение которых приводит к ошибкам
в доказательствах.
Требования
к доказываемому предложению (тезису):
– тезис
должен быть сформулирован ясно и
определенно. Пример небрежной формулировки
тезиса: большей дуге соответствует
большая хорда (это справедливо для дуг
одной и той же или равных окружностей
и при условии, что большая дуга меньше
полуокружности);
– тезис
должен оставаться неизменным на
протяжении всего доказательства.
Требования к
аргументам:
– аргументы
доказательства должны быть суждениями
истинными и доказанными.
– аргументы
должны быть такими суждениями, истинность
которых доказана независимо от тезиса.
К
типичным случаям нарушения первого
требования относят:
а)
использование в качестве аргумента
доказательства такого положения, которое
само нуждается в доказательстве;
б)
использование в качестве аргумента
доказательства ложного суждения;
в)
использование в качестве основания
суждения, с помощью которого можно
доказать не только данный тезис, но и
заведомо ложные утверждения.
В
демонстрации,
т.е. в переходе от аргументов к тезису,
также возможны ошибки, обусловленные
нарушением правила вывода, используемых
в этом переходе. Различают ошибки двух
видов:
– тезис
не вытекает из аргументов, а произвольно
присоединяется к ним;
– тезис
выведен из аргументов путем ошибочного
умозаключения.
Очевидно,
что число таких ошибок уменьшилось,
если бы правила вывода были предметом
изучения в школе.
Методы доказательства
теорем.
По способу связи
аргументов от условия к заключению
доказательства подразделяются на прямые
и косвенные.
Прямое доказательство
основано на каком-нибудь несомненном
начале, из которого непосредственно
устанавливается истинность теоремы.
Методы прямого
доказательства:
– синтетический,
– аналитический,
– метод математической
индукции.
Синтетический
метод: при
построении цепочки силлогизмов мысль
движется от условия теоремы к ее
заключению.
В учебниках
приводятся преимущественно синтетические
доказательства. Их преимущества –
полнота, сжатость, краткость. Недостатки
– отсутствие мотивации шагов, обоснования
дополнительных построений; они носят
значительно более формальный характер,
чем аналитические доказательства.
Пример.
Теорема о хордах окружности.
Теорема. Если две
хорды окружности пересекаются, то
произведения отрезков одной хорды равно
произведению отрезков другой хорды.
Дано: АВ и СД –
хорды окружности, Е – точка их пересечения.
Доказать: АЕВЕ
= СЕДЕ.
(1)
Доказательство
(синтетическое)
Рассмотрим
треугольники АДЕ и СВЕ. В этих треугольниках
углы 1 и 2 равны, так как они вписанные и
опираются на одну и ту же дугу ВМД, а
углы 3 и 4 равны как вертикальные. По
первому признаку подобия треугольников
АДЕ
~ СВЕ.
Отсюда следует, что
,
или АЕВЕ
= СЕДЕ.
Теорема доказана .
Аналитический
метод: при
поиске доказательства мысль движется
от заключения теоремы к ее условию.
Преимущества этого метода – есть
отправное звено доказательства,
дополнительные построения мотивированы,
увеличивается творческая активность
учащихся. Недостатки – большие потери
времени, искусственные дополнительные
построения трудно обосновать.
Пример.
Теорема о хордах окружности.
Доказательство
(аналитическое)
Чтобы доказать
равенство (1), достаточно показать, что
(2).
Для того, чтобы
найти пропорцию (2), достаточно доказать
подобие треугольников, стороны которых
являются членами этой пропорции. Для
получения таких треугольников соединяем
точки С и В, А и Д.
Чтобы обосновать
верность пропорции (2), достаточно
доказать, что АДЕ
~ СВЕ.
Эти треугольники подобны по первому
признаку подобия треугольников: 1
= 2
как вписанные углы, опирающиеся на одну
и ту же дугу ВМД, а 3
= 4
как вертикальные. Следовательно, теорема
верна .
Любое аналитическое
доказательство обратимо в синтетическое
и наоборот. Это широко используется в
учебном процессе. Технологии могут быть
таковы:
1) синтетическое
доказательство предваряется аналитическими
поисками его плана;
2) синтетическое
доказательство заменяется аналитическим,
в качестве домашнего задания – изучение
синтетического доказательства по
учебнику;
3) при использовании
лекционного метода (преимущественно
за пределами курса основной школы) часто
используется чисто синтетический метод
доказательства.
Метод математической
индукции не
имеет распространения в геометрии, так
как основан на свойствах множества
натуральных чисел, выходит за рамки
основной школы, поэтому мы не будет
подвергать его специальному изучению.
Косвенное
доказательство:
истинность теоремы устанавливается
посредством опровержения некоторых
суждений, содержащихся в теореме.
Наиболее
распространенный и единственно применимый
в курсе планиметрии метод косвенного
доказательства – доказательство
от противного.
Логико-математическая
сущность метода от противного: вместо
прямой (р
q) доказывается обратная противоположной
теорема ().
Поэтому доказательство
методом от противного строится по
следующей схеме:
1) пусть неверно
q, то есть истинно
;
2) докажем, что
ложно р, то есть истинно
;
3) убедились, что
из
;
4) следовательно,
р
q (в силу равносильности импликаций р
q и
),
что и требовалось доказать.
Курс геометрии
основной школы широко применяет
доказательства от противного, начиная
буквально с первых уроков в седьмом
классе. При этом необходимо использовать
алгоритмический подход.
Алгоритм
доказательства от противного.
1. Допускаем, что
заключение теоремы ложно. Тогда будет
верно противоречащее ему утверждение.
2. Вычленяем
возможные случаи.
3. Убеждаемся, что
в каждом случае приходим к следствию,
которое противоречит:
– условию теоремы,
– ранее установленным
математическим фактам.
4. Наличие противоречия
заставляет отказаться от принятого
заключения.
5. Признаем
справедливость заключения доказываемой
теоремы.
Мы охарактеризовали
основные логические
методы доказательства
теорем: прямые и косвенные, которые в
свою очередь могут быть аналитическими
и синтетическими, доказательствами от
противного.
Можно говорить об
основных математических
методах
доказательства теорем. В геометрии к
ним можно отнести следующие базовые
методы:
1) метод
геометрических преобразований:
эффективен, соответствует современной
концепции обучения геометрии в школе,
но требует развитого абстрактного и
пространственного мышления; методика
его использования в школе недостаточно
отработана;
2) метод
равенства и подобия треугольников –
соответствует
классической концепции обучения
геометрии в школе,
известен со времен Евклида, поэтому
методика его хорошо разработана; навыки
его применения формируются постепенно,
в процессе решения задач и доказательства
теорем.
Кроме указанных
базовых математических методов
доказательства теорем планиметрии
можноговорить
о более частных методах: метод симметрии,
метод поворота, векторный метод,
алгебраический метод, метод подобия,
координатный метод и др.
Методы доказательства,
используемые в курсе геометрии основной
школы, можно обобщить в виде схемы I.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Face it: Proofs are not easy. And in geometry, things seem to get worse, as now you have to turn pictures into logical statements, making conclusions based on simple drawings. The different types of proofs you learn in school can be overwhelming at first. But once you understand each type, you’ll find it much easier to wrap your head around when and why to use different types of proofs in geometry.
The Arrow
The direct proof works like an arrow. You start with the information given and build on it, moving in the direction of the hypothesis you wish to prove. In using the direct proof, you employ inferences, rules from geometry, definitions of geometric shapes and mathematical logic. The direct proof is the most standard type of proof and, for many students, the go-to proof style for solving a geometric problem. For example, if you know that point C is the midpoint of the line AB, you can prove that AC = CB by using the definition of the midpoint: The point that falls equal distance from each end of the line segment. This is working off the definition of the midpoint and counts as a direct proof.
The Boomerang
The indirect proof is like a boomerang; it allows you to reverse the problem. Instead of working just off the statements and shapes you are given, you change the problem by taking the statement you wish to prove and assuming it’s not true. From there, you show that it cannot possibly not be true, which is enough to prove it is true. Though it sounds confusing, it can simplify many proofs that seem difficult to prove through a direct proof. For example, imagine you have a horizontal line AC that passes through point B, and at point B is a line perpendicular to AC with endpoint D, called line BD. If you want to prove that the measure of angle ABD is 90 degrees, you can start by considering what it would mean if the measure of ABD were not 90 degrees. This would lead you to two impossible conclusions: AC and BD are not perpendicular and AC is not a line. But both of these were facts stated in the problem, which is contradictory. This is enough to prove that ABD is 90 degrees.
The Launching Pad
Sometimes you meet with a problem that asks you to prove something is not true. In such a case, you can use the launching pad to blast yourself away from having to directly deal with the problem, instead providing a counterexample to show how something’s not true. When you use a counterexample, you only need one good counterexample to prove your point, and the proof will be valid. For example, if you need to validate or invalidate the statement “All trapezoids are parallelograms,” you only need to provide one example of a trapezoid that is not a parallelogram. You could do this by drawing a trapezoid with only two parallel sides. The existence of the shape you just drew would disprove the statement “All trapezoids are parallelograms.”
The Flowchart
Just as geometry is a visual mathematics, the flowchart, or flow proof, is a visual type of proof. In a flow proof, you begin by writing down or drawing all the information you know next to one another. From here, make inferences, writing them on the line below. In doing this, you are “stacking” your information, making something like an upside-down pyramid. You use the information you have to make more inferences on the lines below until you get to the bottom, a single statement that proves the problem. For example, you might have a line L that crosses through point P of the line MN, and the question asks you to prove MP = PN given that L bisects MN. You could start by writing the given information, writing “L bisects MN at P” at the top. Below it, write the information that follows from the given information: Bisections produce two congruent segments of a line. Next to this statement, write a geometric fact that will help you get to the proof; for this problem, the fact that congruent line segments are equal in length helps. Write that. Below these two pieces of information, you can write the conclusion, which naturally follows: MP = PN.