Как найти доли в прямоугольниках

Тема: Доли» (3 класс)
Цели:

• Дать общее представление о доле числа.
• Познакомить с их записью и чтением.
• Учить называть, записывать и сравнивать доли.
• Развивать самостоятельность, логическое
  мышление.
• Развивать навыки устных вычислений.

Задачи:

• Выполнить практические задачи по инструкции
  учителя.
• Выполнить наглядное сравнение долей.
• Решить задачи с использованием нового
  материала.
• Повторить умножение и деление.

ХОД УРОКА

I. Чистописание

12     21
– Дайте характеристику каждому числу.

II. Устный счёт

60 :
10             6 * 7
42 * 1              90 *
0
17 : 17             7 * 8
40 : 5              
45 : 45

1	24	8	64	56	42	9	6	12	0
н	о	д	с	и	а	к	м	ф	р

– Проверим: возьмите простой карандаш и под
каждым ответом поставьте соответствующую букву.

6    42   1    8   42  
0   56   1
м    а     н    д   
а    р    и    н

– Если ответы верны, то получится слово. (Мандарин)

– Вы скажете, причём тут мандарин, когда у нас
математика?

– А он нам поможет назвать тему урока.

III. Сообщение темы урока

– Вот у меня мандарин. Я его очистила. Когда мы
начинаем его есть, то мы его делим на что? (На
дольки)
– Мандарин состоит из долек. Если мы посмотрим на
чеснок, он тоже состоит из долей.
– Так тема урока – «Доли». (Запись в тетради)

IV. Объяснение нового материала

1. – У вас на партах лежит
геометрическая фигура. Как она называется? (Круг)
– Сложите круг пополам.
– Разверните.
– Сколько равных частей получили? (2)
– Итак, мы разделили круг пополам, т.е. на две
равные части.
– Как они называются?  (Половинки)

2. Яблоко.

– Теперь я возьму яблоко, разрежу его пополам.
– Сколько равных частей я получила?  (2
равные части)

– Можно сказать, что половина яблока – это одна
вторая доля яблока.

– А записывают это так:  .
– Сколько частей взяли? (1)
– На сколько частей разделили? (2)
– Мы получили  .
– В математике число, которое записано над
чертой, называют числитель, а число, которое
записано под чертой – знаменатель.
– Итак, числитель – показывает, сколько равных
частей взяли, а знаменатель – показывает, на
сколько равных частей разделили целое.

(Запись в тетради:)

– Итак, мы яблоко разделили на две равные доли и
получили долю яблока.
– Доля – это часть целого.

3. – Теперь возьмите круг, который вы
согнули пополам. Сложите ещё пополам.
– Разверните. Сколько теперь равных частей
получили? (4)

4. Яблоко

– Я возьму и каждую долю яблока разрежу
пополам.
– Сколько равных частей получили? (4)

– А записывают это так: .
– В числителе записываем 1, а в знаменателе – 4.

5. – Посмотрите на  и .
– Сравните: что больше: и ?

(Запись в тетради:   >  )

– Вывод: чем больше частей, тем доля
меньше.

V. Самостоятельная работа

Карточки: изображено 6 кругов, каждый разделён
на доли: на 3, 8, 2, 4, 6,12. Надо подписать:  ,, , , , .

VI. Физминутка

VII. Закрепление. Работа по учебнику

1. Стр. 80 №1.

– Итак, пирог разделён на 6 равных частей. (Показ
на доске)

– Взяли 1 такую часть

– Это  доля
пирога.
– И вам нужно узнать, какая доля получится, если
разделить на 2 равные части каждую шестую долю
пирога.
– Значит, что мы должны сделать с каждой шестой? (Разделить
на 2 равные части)
– У вас у каждого «пирог», разделённый на 6 равных
частей.
– Разделите каждую шестую долю пирога на две
равные части.
– Проверяю. (У доски варианты деления)
– Сколько равных частей получили? (12)
– Значит, какая доля получится? ( )
– Сравните: какая доля больше:  или  ?
(Запись в тетради: > )

Вывод: чем больше частей, тем доля
меньше.

2. Стр. 80 №2.

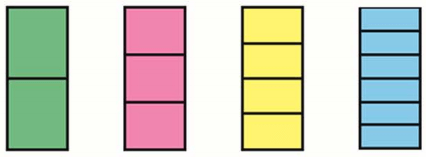
– У вас на картинке прямоугольники, которые
разделены на доли.
– Какого цвета  доля?
(Розового)
– Какого цвета
доля? (Синего)
– Какого цвета
доля? (Зелёного)
– Какого цвета  доля?
(Жёлтого)

– Какая доля меньше  или  ?
(Запись в тетради:   < )
– Чем больше частей, тем доля меньше.
– Какая доля больше:  или ?

(Запись в тетради:  >  )

– Какая доля самая маленькая? ()
– Запишите в тетради доли прямоугольника,
начиная с наименьшей, т. е. с самой маленькой.
– Проверим.

3.  Стр. 80 № 3.

– Прочитаем задание.
– Какую фигуру надо начертить?
– Чему равна сторона квадрата?
– Начертите квадрат со стороной 3 см.
– Подпишите.
– Читаем дальше, что нужно сделать?
– Выполним 1 часть.
– Значит, на сколько равных частей надо
разделить квадрат? (На 9)
– Как разделим? / на квадратные см/
– Что такое квадратный см?
– Разделите.
– Сколько частей получили? (9)
– Назовите 1 такую часть. ()
– Закрасьте .
– Закрасьте  самостоятельно.
– Проверяем.

VII. Итог урока

– Какая тема урока была?
– Что такое доля?
– Мы учились делить на доли и записывать доли.
– Как называется число, которое пишем над чертой?
– Что показывает числитель?
– Как называется число, которое под чертой?
– Что показывает знаменатель?
– А ещё мы учились сравнивать доли. Какой вывод
сделали?
– Урок закончен. Спасибо.

Рассмотри, как разделен на равные части один и тот же прямоугольник. Назови доли прямоугольника, начиная с наименьшей.
Какая доля меньше:
одна третья или одна шестая?
одна третья или половина этого прямоугольника?

Какая доля больше: одна шестая или одна четвертая?

Добрый день, мои дорогие друзья.

Сегодня я хочу рассказать вам, как находить
несколько долей, то есть частей целого – вот, например,
как дольки у мандарина, помните?

Итак, приступим. Вот посмотрите на этот сливовый пирог.

Его испёк наш придворный повар и разрезал на
шесть равных долей. Теперь каждая из этих долей – одна шестая
часть. Одна шестая – это дробное число или дробь. Это слово
родственно слову «дробить», то есть разбивать, разделять на мелкие части.

В числе одна шестая нижняя часть, её называют знаменатель,
показывает, на сколько равных долей разрезали пирог, а верхняя часть, её
называют числитель, показывает, сколько долей взяли.

Почувствовав аромат пирога, прибежала наша
Решалочка. Она съела один кусочек, потом взяла ещё один. Как вы думаете, какую
часть пирога съела Решалочка? Одна шестая, да ещё одна шестая – это две из
шести частей – или две шестых.

А какая часть пирога осталась? Один, два, три,
четыре. Четыре шестых.

А если бы пирог был разрезан не на шесть, а на десять
равных долей? Тогда каждая доля была бы уже не одной шестой, а одной десятой. А
теперь я четыре кусочка отложу для моих помощников – знаков арифметических
действий. Какую часть пирога я отложила? Четыре десятых.

А какая часть пирога осталась? Шесть десятых.

Конечно, находить доли целого можно не
только у пирога или какого-то другого предмета круглой формы. Это может быть
отрезок, геометрическая фигура. Или любой другой предмет. Главное при этом, чтобы
доли, на которые его разделили, были равными.

Вот посмотрите на этот прямоугольник. Какой его
участок стал жёлтого цвета? Помните, как это определять? На сколько всего
равных долей разделён прямоугольник? На восемь. Восьмёрку пишем в нижней части
числа.

А сколько из них закрашено жёлтым цветом? Пять.
Пятёрку пишем над восьмёркой. Закрашено пять восьмых. А сколько частей остались
зелёными? Три восьмых.

А теперь посмотрите на этот отрезок. Какой его
участок стал красного цвета?

Отрезок разделён на семь долей, а стали красными
три из них. Значит, красная область составляет три седьмых части. А сколько
частей остались чёрными? Четыре седьмых.

А теперь посмотрите на этот треугольник.

Определите, сколько его частей не закрашено
розовым цветом? Две третьих.

А какая область закрашена синим цветом вот у этой
звёздочки?

Четыре пятых части.

Знаете, ребята, можно делить на части
не только какие-то предметы или геометрические фигуры, но и части величин или
чисел.

Вот, например, ваш урок длится три четверти часа,
то есть три четвёртых – это одно и то же. Сколько это минут?

Нам надо найти, сколько минут составляют три
четверти часа. Вы помните, как это делается? В дроби нижняя часть показывает,
на сколько долей делим целое, а верхняя – сколько из них мы берём, то
есть на сколько нужно умножить одну часть.

Один час равен шестидесяти минутам. Значит, за
целое принимаем число шестьдесят. Находим одну четвёртую часть часа –
шестьдесят делим на четыре. А потом умножаем на три. Так мы находим три из
четырёх частей, или три четвертых, или три четверти часа. Это сорок пять мнут.

А как найти, к примеру, шесть седьмых частей числа
двадцать восемь?

Делим двадцать восемь на семь. и затем полученное
число умножаем на шесть. Шесть седьмых числа двадцать восемь равно двадцати
четырём.

Ну что, ребята, вы поняли? В дроби нижняя
часть числа показывает, на сколько равных долей разделили целое, а верхняя
– сколько таких долей взяли.

А теперь я предлагаю вам решить задачу.

Муравьи Касьян и Демьян на зиму заготовили тридцать
шесть сушёных гусениц. За первый месяц зимовки они съели две шестых своих
запасов. Сколько ещё сушёных гусениц осталось у муравьёв?

Я жду вашего решения…

А теперь давайте проверим, так ли вы решили.

1) 36 : 6 ∙ 2 = 12 (г.) – съели

2) 36 – 12 = 24 (г.) – осталось

Ответ: осталось 24 сушёных гусеницы.

В первом действии вам надо было узнать, сколько
сушёных гусениц съели муравьи.

Чтобы найти две шестых от числа тридцать шесть,
надо было разделить его на шесть и умножить на два. Съели муравьи двенадцать
гусениц.

А теперь можно узнать, сколько гусениц осталось.
Вычитаем из тридцати шести двенадцать, получается двадцать четыре.

Я надеюсь, вы поняли, как найти несколько
долей целого? Предмет, объект или число, которое принимаем за целое, надо разделить
на знаменатель дроби, а потом полученный результат умножить на числитель.

Ну вот и подошла сегодня к концу наша встреча. Я
надеюсь, что вы были внимательны, всё поняли и всё запомнили. Поэтому я говорю
вам ребята: до свидания! Успешной работы и отличных отметок!

Математика, 3 класс

Урок №32. Доли. Образование и сравнение долей

Перечень вопросов, рассматриваемых в теме:

— что такое «доля»?

— как записывать, сравнивать доли?

— что значит разделить на равные части (доли) предметы, геометрические фигуры?

Глоссарий по теме:

Доля – каждая из равных частей единицы.

Деление – действие, обратное умножению.

Делимое – число, которое делят.

Делитель – число, на которое делят.

Частное – результат деления.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017, с. 92-93.

2. Рудницкая В. Н. Тесты по математике:3 класс. М.:Издательство «Экзамен», 2016, с. 44-47.

3. Рудницкая В.Н. КИМ ВПР. Математика .3 класс. М.: Издательство «Экзамен», 2018, с. 39-42.

Теоретический материал для самостоятельного изучения

Людям часто приходится делить целое на доли. Самая известная доля — это, конечно, половина. Слова с приставкой «пол» можно услышать, пожалуй, каждый день: полчаса, полкилограмма, полбулки.

Но есть и другие употребительные доли. Например, четверть, десятая, сотая. Когда образуются доли? Тогда, когда один предмет (буханка хлеба, лист бумаги) или единица измерения (час, килограмм) делятся на равные части. Доля это каждая из равных частей единицы. Название доли зависит от того, на сколько равных частей разделили единицу. Разделили на две части название доли «половина», на три — «треть», на четыре — «четверть». А если на пять, на шесть, семь частей, то пользуются словами «пятая, шестая, седьмая» и т. д. Четверти по-другому называют четвёртыми, трети – третьими, а половины – вторыми долями.

Для записи любой доли используют горизонтальную черточку. Ее называют дробной чертой. Над ней ставится единица, а под чертой пишется число равных частей, на которые единица делится.

В русском языке слово «дробь» появилось в VIII веке, оно происходило от глагола «дробить» — разбивать, ломать на части. В первых учебниках математики (в XVII веке) дроби так и назывались – «ломаные числа». У других народов называние дроби также связано с глаголами «ломать», «разбивать», «раздроблять».

Современное обозначение дробей берет своё начало в Древней Индии; его стали использовать и арабы, а от них в ХII – XIV веках было заимствовано европейцами.

Первым европейским ученым, который стал использовать и распространять современную запись дробей, был итальянский купец и путешественник, сын городского писаря Фибоначчи (Леонардо Пизанский). В 1202 году он ввёл слово «дробь». Названия «числитель» и «знаменатель» ввёл в ХIII веке Максим Плануд – греческий монах, ученый – математик.

Каждому из вас приходилось делить апельсин. Неразделенный апельсин считается целое, а его части – доли.

Доля — это каждая из равных частей единицы.

В апельсине восемь долек. Мы разделим их пополам. Получились две части или в математике говорят одна вторая и записывается так: .

Число под чертой указывает, на сколько частей разделили, а число, над чертой – сколько таких частей взяли.

Познакомимся с различными записями долей.

На первом рисунке закрашена одна вторая.

На втором рисунке две третьих.

На третьем рисунке закрашено три четвертых.

На четвёртом рисунке закрашено четыре пятых рисунке.

На пятом рисунке закрашена одна шестая.

Доли можно сравнивать. На рисунке один и тот же прямоугольник разделён на равные части. Сравним их.

Наименьшей частью будет одна шестая, а наибольшая одна вторая.

Сравним другие доли. Одна третья меньше одной второй. Одна четвертая больше одной шестой.

Задания тренировочного модуля:

1. Продолжите цепочку равенств:

Правильный ответ:

2. Соотнесите рисунок с ответом.

Правильный ответ:

Инфоурок

›

Начальные классы

›Презентации›Презентация к уроку «Решение задач. Геометрические задачи на нахождение доли площади прямоугольника» 3 класс УМК «Школа России»