Доля в процентах
Как известно, доля представляет собой какую-то часть от целого числа.
Рассмотрим на нескольких примерах, как найти долю в процентах.
1) Целое (A) и части от целого (A1, A2, A3…) выражены в каких-либо единицах (рублях, сантиметрах и др.).
В этом случае посчитать, чему равна доля каждой части, можно по формуле:
An (%) = An / A * 100%.
Например:
Доходы предприятия в 2016 году составили 8 млн рублей. Из них:
5 млн рублей — доходы от основной деятельности.
1 млн рублей — доходы от инвестиционной деятельности.
2 млн рублей — прочие доходы.
Посчитаем, чему равна доля в процентах каждой статьи доходов от общей суммы доходов.
5 / 8 * 100% = 0,625 * 100% = 62,5%. Это доля доходов от основной деятельности.
1 / 8 * 100% = 0,125 * 100% = 12,5%. Это доля доходов от инвестиционной деятельности.
2 / 8 * 100% = 0,250 * 100% = 25%. Это доля доходов от прочей деятельности.
2) Если числовое значение доли от целого уже известно и выражено в виде обыкновенной или десятичной дроби, то достаточно умножить данную дробь на 100%.
Например:
Торт разрезали на 4 равные части, соответственно каждый кусок торта представляет собой 1/4 часть от целого.
Доля в процентах = 1/4 * 100% = 25%.
Как найти долю в процентах от числа
Процент можно легко рассчитать следующим способом: доля полки (%) = (количество фейсингов / общее число фейсингов) x 100.
- Процент можно рассчитать как долю полки в процентах.
- Для нахождения доли от числа нужно разделить число на знаменатель дроби и умножить на числитель.
- Чтобы найти число по доле, нужно умножить долю на число долей.
- Долю от общего числа можно рассчитать по формуле Рекламный трафик / Общий трафик * 100% или с помощью бесплатного сервиса.
- В Excel процент можно рассчитать с помощью формулы = числитель / знаменатель * 100%.
- Для нахождения процентного соотношения чисел нужно разделить одно число на другое и умножить на 100%.
- Для нахождения одной пятой доли от числа нужно умножить число на 1/5. Например, 1/5 часть от 45 равна 9.
- Как определить долю от числа
- Как найти долю числа и число по его доле
- Как посчитать долю от общего числа калькулятор
- Как рассчитать долю в процентах в Excel
- Сколько в процентах от числа
- Как посчитать сколько процентов
- Как вывести долю от числа
- Как найти одну пятую долю от числа 45
- Что такое доля числа
- Как получить процент от двух чисел
- Как найти процент от общего числа формула
- Как узнать на сколько процентов увеличилось число
- Как узнать процент доли
- Как рассчитать долю рынка в процентах формула
- Как рассчитать изменение показателя в процентах
- Как найти соотношение между числами
- Как найти долю двух чисел
- Как найти 2 от 5
- Как определить долю в статистике
- Как рассчитать долю от общей суммы
Как определить долю от числа
Ответ:. Для нахождения какой-либо доли от числа необходимо разделить число на знаменатель дроби и полученный результат умножить на числитель дроби.
Как найти долю числа и число по его доле
Чтобы найти число по его доле, нужно долю этого числа умножить на число долей.
Как посчитать долю от общего числа калькулятор
Инструкция Рассчитать эту задачу можно по формуле: Рекламный трафик / Общий трафик * 100%. Однако, вы можете использовать и бесплатный сервис, который моментально произведет нужные вычисления.
Как рассчитать долю в процентах в Excel
Вычисление процентов:
- Щелкните любую пустую ячейку.
- Введите формулу =42/50 и нажмите клавишу RETURN. Результат — 0,84.
- Выделите ячейку с результатом, полученным на шаге 2.
- На вкладке Главная нажмите кнопку. Результат составляет 84,00 %, то есть процент правильных ответов в тесте.
Сколько в процентах от числа
Для того что бы найти процентный состав числа а от числа в, нужно число а разделить на число а на число в и результат умножить на 100 %.
Как посчитать сколько процентов
1% — это сотая часть числа. Разделив число на 100, мы как раз и получаем один процент. Чтобы найти проценты от какого-либо числа надо это число разделить на 100 и результат деления умножить на количество процентов. Например, чтобы найти 30% от 250, надо 250 поделить на сто (получим 2,5) и потом 2,5 умножить на 30.
Как вывести долю от числа
Сколько процентов составляет одно число от другого числа
Чтобы вычислить процентное отношение чисел, нужно одно число разделить на другое и умножить на 100%.
Как найти одну пятую долю от числа 45
Число 45 — составляет 5/5 всего значения числа; неизвестное число Х — составляет 1/5 часть от всего значения числа; Х = 45 * 1/5 = 9. Ответ: 1/5 часть от 45 равна 9.
Что такое доля числа
Доля есть каждая из равных частей, на которые разделено целое. Половина пирога на рисунке — это вторая доля; четверть — четвёртая доля. Для обозначения доли используют двухуровневую запись из двух чисел, разделённых горизонтальной чертой. Например, двенадцатую долю обозначают так: 1 12.
Как получить процент от двух чисел
Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100. Например: вычислить, сколько процентов составляет число 52 от числа 400. По правилу: 52: 400 ⋅ 100 % = 13 %.
Как найти процент от общего числа формула
Это определенная часть из 100 долей целого. Математическая формула расчета процентов выглядит следующим образом: (искомая часть / целое число) * 100. Чтобы найти процент от числа, применяется такой вариант формулы: (число * процент) / 100.
Как узнать на сколько процентов увеличилось число
Чтобы вычислить, на сколько процентов одно число больше другого, нужно первое число разделить на второе, умножить результат на 100 и вычесть 100. Таким же образом можно определить на сколько процентов увеличилось число.
Как узнать процент доли
Процент можно легко рассчитать следующим способом: доля полки (%) = (количество фейсингов / общее число фейсингов) x 100.
Как рассчитать долю рынка в процентах формула
В чем измеряется доля рынка? Формула доли рынка будет выглядеть так: объем проданных товаров или услуг вашей фирмы делим на общий объем продаж конкурентов и умножаем на 100%.
Как рассчитать изменение показателя в процентах
Для того, чтобы вычислить на сколько процентов повысилась стоимость надо вычислить сколько процентов от первоначальной цены составляет полученная разница. Для этого мы разницу делим на первоначальную стоимость и затем полученный результат умножаем на сто. 840 / 4200 * 100 = 0,2 * 100 = 20%.
Как найти соотношение между числами
Теория: Отношением двух чисел называют их частное. Например, отношение числа (a) к числу (b) записывают так: (a: b), или a b. При делении одного числа на другое мы находим, во сколько раз одно число больше другого или, наоборот, какую часть одно число составляет от другого.
Как найти долю двух чисел
Чтобы найти долю числа, нужно разделить это число на, где. То есть число под чертой в записи подскажет, на сколько частей или долей разделили целое.
Как найти 2 от 5
1. Для того, чтобы вычислить, чему равно 2/5 от числа 150, необходимо данное число умножить на данную дробь, тогда получим следующее выражение, вычислим, чему равно его значение: 150 * 2/5 = 30 * 2 = 60 единиц. Ответ: 2/5 от 150 составляют 60 единиц.
Как определить долю в статистике
Доля единицы, таким образом, является обратным числом положительного целого числа, 1/n. Примеры — 1/1, 1/2, 1/3, 1/4 и т.
Как рассчитать долю от общей суммы
Чтобы определить долю товара в общей выручке, необходимо знать цену единицы указанного товара и объем его продаж. Доля в выручке определяется как отношение выручки от реализации конкретного товара к общей сумме выручки, умноженное на 100%.
Оставить отзыв (1)
- Как вычислить долю в процентах от числа
- Как найти процент доли от числа
- Как находить долю от числа
- Как определить долю числа в процентах
- Как посчитать долю в процентах от числа
- Как посчитать долю от общего числа калькулятор
- Как посчитать долю от числа пример
- Как посчитать долю числа в процентах
- Как посчитать процентную долю от числа
- Как узнать долю процента от числа
- Как узнать процентную долю от числа
Содержание материала
- Проценты в обыкновенную дробь
- Видео
- Проценты: правила
- Нахождение одного процента от числа
- Составление пропорции
- Соотношения чисел
- Второй способ нахождения процента
- Сколько процентов составляет одно число от другого?
- Онлайн-сервисы для вычислений
- На сколько процентов одно число больше другого
- Прибавить проценты к числу
- Как найти процентное соотношение чисел
- Отнять от числа проценты
Проценты в обыкновенную дробь
Чтобы представить проценты в виде обыкновенной дроби нужно проценты представить в виде десятичной дроби. Затем десятичную дробь преобразовать в обыкновенную дробь.
Преобразовать 25% в обыкновенную дробь
25%100%
=
0.25
=
25100
=
1 × 25 4 × 25
=
14
Проценты: правила
Рассмотрим четыре известных способа поиска процентов.
Нахождение одного процента от числа
Найти процент от числа можно несколькими способами.
Первый способ
-
Найдем, чему равен 1%.
-
Умножим полученное значение на количество искомых процентов.
Пример: найти 12% от числа 48.
-
48 : 100 = 0,48.
-
0,48 × 12 = 5,76.
Второй способ
-
Переведем проценты в десятичную дробь.
-
Умножим число на полученную десятичную дробь.
Давайте снова найдем 12% от 48, но другим способом.
-
12 : 100 = 0,12.
-
48 × 0,12 = 5,76.
Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?
Как решаем:
- Переведем 15% в рубли:
250 : 100 = 2,5 — это 1% от стоимости шоколада,
значит, 2,5 × 15 = 37,5 — это 15%.
- Вычислим цену со скидкой 15%: 250 − 37,5 = 212,5.
- 212,5 < 225.
Ответ: выгоднее воспользоваться скидкой 15%.
Составление пропорции
Равенство двух отношений называют пропорцией.
a : b = c : d или a/b = c/d
- a, d — крайние члены
- b, c — средние члены
Читается: а относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.
Рассмотрим пример. Насколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?
Как решаем:
Найдем, сколько рублей составляет выгода, то есть скидка в 14%. Обозначим стоимость футболки за 100%, значит 1390 рублей = 100%. Тогда 14% это х рублей. Получаем пропорцию:
1390 руб. = 100% x руб. = 14%
Перемножим крест-накрест и найдем x:
x = 1390 × 14 : 100 x = 194,6
Ответ: выгода по скидке составила 194,6 рубля.
Соотношения чисел
Есть случаи, при которых можно использовать простые дроби. Например, 10% — это десятая часть целого. Чтобы найти 10% от числа a, нужно разделить его на 10. Собрали примеры соотношения чисел в таблице.
| Процент | Дробь | Как найти % от числа a |
|---|---|---|
| 10% | 1/10 | a : 10 |
| 20% | 1/5 | a : 5 |
| 25% | 1/4 | a : 4 |
| 50% | 1/2 | a : 2 |
| 75% | 3/4 | a : 4 × 3 |
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Как решаем:
- 100% — 25% = 75%,
значит, нужно заплатить 75% от первоначальной цены.
- Используем правило соотношения чисел:
75% — это 3/4 от числа, значит, 8500 : 4 × 3 = 6375 (рублей).
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Видео
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись 

Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
300 × 0,5 = 150
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Сколько процентов составляет одно число от другого?
Чтобы вычислить процентное отношение двух чисел, нужно вычислить их отношение и умножить его на 





То есть число 




Решение. Зарплата сотрудника составляет от зарплаты начальника
Зарплата начальника составляет
от зарплаты сотрудника.
Сколько процентов составляет число от числа от числа = неопределённость
Округлять до знаков после запятой.
Онлайн-сервисы для вычислений
В нахождении нужных процентов могут помочь различные сервисы-калькуляторы, работающие в режиме онлайн. Например, популярный сайт имеет в своём функционале различные инструменты, помогающие, в том числе, высчитать процент от любого числа.
Порядок действий:
- Перейдите на .
- Введите искомые показатели в соответствующие клетки.
- Нажмите на «Рассчитать». Вы сразу же получите искомый результат.
Также указанный калькулятор позволяет высчитать какую долю от 1 составляет 2, прибавить % к числу или вычесть из него. Всё очень быстро и удобно.
На сколько процентов одно число больше другого
Чтобы вычислить, на сколько процентов одно число больше другого, нужно первое число разделить на второе, умножить результат на 100 и вычесть 100.
Вычислим, на сколько процентов число 20 больше числа 5: 205 · 100 — 100 = 4 · 100 — 100 = 400 — 100 = 300% Число 20 больше числа 5 на 300%. Например, зарплата начальника равна 50000 рублей, а сотрудника — 35000 рублей. Найдем, на сколько процентов зарплата начальника больше: 5000035000 · 100 — 100 = 1,43 * 100 — 100 = 143 — 100 = 43% Таким образом, зарплата начальника на 43% выше зарплаты сотрудника.
Прибавить проценты к числу
Чтобы прибавить к числу p процентов, нужно умножить это число на (1 + p100)
Прибавим 30% к числу 200: 200 · (1 + 30100) = 200 · 1,3 = 260 200 + 30% равняется 260. Например, абонемент в бассейн стоит 1000 рублей. Со следующего месяца обещали поднять цену на 20%. Вычислим, сколько будет стоить абонемент. 1000 · (1 + 20100) = 1000 · 1,2 = 1200 Таким образом, абонемент будет стоить 1200 рублей.
Как найти процентное соотношение чисел
Также могут возникнуть ситуации, когда нужно высчитать процентное соотношение двух чисел. К примеру, какой процент число B составляет от числа А, на сколько процентов (B) вы выполнили свою работу от заданной нормы (A), на сколько (B) повысилась цена товара от первоначальной (A) и так далее.
Для определения такого результата существуют следующая формула:
B / A * 100 =
К примеру, нам нужно высчитать, какая доля от числа 500 составляет число 85.
Используя приведённую формулу, выполняем несложные арифметические операции:
85 / 500 * 100 = 17%
Таким образом, число 85 составляет 17% от 500.
Проверяем полученное число по формуле первого способа:
500 / 100 * 17 = 85.
Всё сошлось.
Отнять от числа проценты
Давайте отнимем 



Чтобы отнять от числа 
Уменьшить число на % — 0% =
Округлять до знаков после запятой.
Теги
Математика, 3 класс
Урок №34. Задачи на нахождение доли числа и числа по его доле.
Перечень вопросов, рассматриваемых в теме:
— как решать задачи на нахождение доли числа и числа по его доли?
— какие наиболее эффективные способы используются для нахождения доли величины и величины по ее доле?
— каким образом сравнивать разные доли одной и той же величины?
Глоссарий по теме:
Задача – это текст, содержащий численные компоненты
Доля – это каждая из равных частей единицы.
Условие – это часть задачи, в которой рассказывается о том, что неизвестно, содержит числовые данные.
Вопрос – это часть задачи, в которой сообщается о том, что нужно узнать.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 97.
2. Волкова С. И. Проверочные работы 3 класс. Издательство «Просвещение» 2017, с. 38-39.
3. Волкова С. И. Тесты 3 класс. Издательство «Просвещение»2017, с. 20-27.
4.Рудницкая В. Н. Тесты по математике 3 класс. М.: Издательство «Экзамен», 2016 с. 44-47.
Теоретический материал для самостоятельного изучения
Появление долей связывается с практическими потребностями: задачи, где нужно производить деление на части, были очень распространены. Кроме того, в жизни человеку приходилось не только считать предметы, но и измерять величины. Люди встретились с измерениями длин, площадей земельных участков, объемов, массы тел. При этом случалось, что единица измерения не укладывалась целое число раз в измеряемой величине. Например, измеряя длину участка шагами, человек встречался с таким явлением: в длине укладывалось десять шагов, и оставался остаток меньше одного шага.
Таким образом, во всех цивилизациях понятие доли возникло из процесса дробления целого на равные части. Русский термин «дробь», как и его аналоги в других языках, происходит от лат. fractura, который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять.
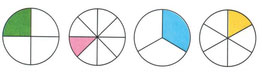
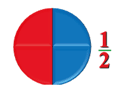
Доля это каждая из равных частей единицы. Название доли зависит от того, на сколько равных частей разделили единицу. Разделили на две части название доли «половина», на три — «треть», на четыре — «четверть».
Использование знаний о долях применяется для решения задач.
Рассмотрим рисунок.
12 см
1) Полоску длиной 12 см разделили на 2 части. Одна часть, или ее называют одна вторая, составляет 6 см. Составим выражение:
12 : 2 = 6 см
2) Полоску этой же длины разделим на 3 части. Одна третья составляет 4 см.
12 см
12 : 3 = 4 см
3) Найдем одну шестую полоски. Одна шестая составляет 2 см.
12 см
12 : 6 = 2 см
Вывод: чтобы найти долю от числа, надо число разделить на количество частей (долей).
Рассмотрим рисунок.
1) Длина второй части отрезка составляет 8 см. Чему равна длина всего отрезка?
? см
8 ∙ 2 = 16 см
По 8 см возьмем 2 раза получим 16 см.
2) Длина четвертой части отрезка составляет 4 см. Найдем длину всего отрезка.
? см
4 ∙ 4 = 16 см
4 умножим на 4, получим 16 см.
3) Найдем длину отрезка, если восьмая часть составляет 2 см.
? см
2 ∙ 8 = 16 см
Вывод: чтобы найти число по его доле, надо долю этого числа умножить на число долей.
Решим задачу.
6 листов составляют половину тетради. Сколько всего листов в тетради? Половин в тетради может быть только две. Если в каждой по 6 листов, то вся тетрадь содержит: 6 ∙ 2 = 12 (листов).
Вывод: чтобы найти число по его доле, надо долю этого числа умножить на число долей.
Решим задачу.
Чему равна треть суток?
В сутках 24 часа. Чтобы найти треть суток, нужно 24:4=8 (часов).
Вывод: чтобы найти долю от числа, надо число разделить на количество частей (долей)
Задания тренировочного модуля:
1. Выберите верный ответ.
В мотке 24 м кружев. Отрезали восьмую часть мотка. Сколько кружев отрезали?
16 м
32 м
3 м
4м
Правильный ответ:
3м
2. Соотнесите ответы.
Длина коридора 12 м. Мальчик прошел по коридору 4 м. Какую часть коридора он прошёл?
Правильный ответ:
Содержание
- Нахождение доли от числа и числа по доле.
- Тренажер по математике 3 класс «Нахождение доли от числа и числа по доле.»
- Что значит часть от числа математика
- Половина
- Треть
- Четверть
- Запись и чтение долей
- Сравнение долей
- Урок 21 Бесплатно Отношения
- Отношение
- Отношение и часть от числа
- Отношения в задачах
- Интересная информация
- Заключительный тест
Нахождение доли от числа и числа по доле.
Инструкция
1 Как найти долю от числа
Для того, чтобы обозначить какую-то часть (долю) числа, люди придумали дроби. Дробь состоит из числителя (над чертой) и знаменателя (под чертой). Знаменатель показывает, на сколько частей разделили число, а числитель — сколько таких частей взяли. Например, дробь 3/5 означает, что целое, например, тортик, разделили на 5 кусков, а затем взяли 3 куска.
Вместо тортика можно взять число, например, 15. Найдем 3/5 от числа 15. Для этого сначала нужно разделить число 15 на 5 частей (то есть найти 1/5 часть числа 15), а затем взять 3 части (умножить на 3):
Найдем 1/2 от числа 8. Для этого нужно разделить 8 на 2, а затем умножить на 1.
Рассмотрим еще пример: найдем 3/4 от числа 20:
2 Как найти число по доле
Найдем число, если 2/3 от этого числа равно 10. Дробь 2/3 говорит нам о том, что число разделили на 3 части и взяли 2 таких части. Чтобы найти это число, мы сначала должны узнать, сколько составляет одна часть (1/3) . Для этого разделим 10 на 2 (взяли же 2 части). А затем умножим полученную часть на 3:
Рассмотрим еще пример: найдите число по доле: 2/7 = 16
Надеемся, что это объяснение поможет вам находить долю от числа и число по доле!
Наберите ответ при помощи кнопок на экране, затем нажмите кнопку «Проверить». Затем — кнопку «Дальше». Всего в тренажере 50 заданий, выпадающих в случайном порядке.
Тренажер по математике 3 класс «Нахождение доли от числа и числа по доле.»
Если у вас не открываются игры или тренажёры, читайте здесь .
Источник
Что значит часть от числа математика
В этой теме мы познакомимся с образованием долей, научимся их записывать, читать и сравнивать.
Доли появляются, если нам нужно разделить ЦЕЛОЕ на равные части, например, яблоко:

На доли можно разделить окружность:
Доля – это каждая из равных частей целого.
Название доли зависит от того, на сколько частей разделили целое.
Половина
Половина — это самая известная доля.
Например, яблоко разделили на две части, получилась половина яблока.
Любую долю можно записать как деление двух чисел. Мы разделили целое на две доли, каждую из долей мы можем записать в виде дроби, в которой черта обозначает знак деления.
Прочитать такую долю можно как ОДНА ВТОРАЯ.
Треть
Если целое разделили на три части, то получили ТРЕТЬ, третью часть.
Прочитать такую долю можно как ОДНА ТРЕТЬЯ.
Четверть
Если целое разделили на четыре части, получили ЧЕТВЕРТЬ, четвёртую часть.
Прочитать такую долю можно как ОДНА ЧЕТВЁРТАЯ.
Запись и чтение долей



Сравнение долей
Для примера сравним две доли: одну шестую и одну третью.
Какая доля больше? Рассмотри рисунок:
Красным закрашены названные доли. Посмотри, какая доля больше? Одна третья.
Значит, одна третья часть БОЛЬШЕ, чем одна шестая часть.
Сравним ещё две доли: одну восьмую и одну четвёртую.
Какая доля больше? Рассмотри рисунок:
Красным закрашены названные доли. Посмотри, какая доля больше? Одна четвёртая.
Значит, одна четвёртая часть БОЛЬШЕ, чем одна восьмая часть.
Вывод: Чем долей больше, тем одна её часть МЕНЬШЕ.
Поделись с друзьями в социальных сетях:
Источник
Урок 21 Бесплатно Отношения
В этом уроке мы узнаем, что такое отношения. Также поймем, что нам показывает отношение двух чисел. И в завершение узнаем, как определить часть одного числа от другого.
Отношение
Начнем с определения:
Отношением двух чисел называют частное этих двух чисел.
Записать отношение числа a к числу b мы можем как (mathbf) или же через дробную черту: (mathbf<frac>)
У нас получается дробное выражение, поэтому возможны варианты во что оно преобразуется:
- может получиться натуральное число
- обыкновенная дробь
- смешанное число
Посмотрим на разные примеры.
Пример 1
Найдем отношение чисел 256 и 8
По определению, отношением двух чисел будет являться их частное, что мы и посчитаем.
Ответом будет 32.
Иными словами, 256 относится к 8 как 32 к 1
В последней фразе была как раз упомянута суть отношения, мы акцентируем на этом внимание.
Отношение одного числа к другому показывает, как одно число соотносится с другим, иными словами, во сколько раз оно его больше или меньше:
- если отношение получилось больше 1, значит, первое число больше второго
- если меньше 1, то второе число больше первого
- если отношение оказалось равно 1, значит, числа равны
Пример 2
Найдите отношение 15 к 12
По определению посчитаем частное, а далее посмотрим на полученный результат.
Данный пример иллюстрирует, в каких случая получается смешанное число.
Отношение равняется смешанному числу в тех случаях, когда первое число больше второго, и при этом первое на второе не делится.
Мы можем прочитать результат так: 15 больше 12 в (mathbf<1frac<1><4>>) раза.
Пример 3
Найдем отношение 16 к 24.
Снова идем по алгоритму: делим первое число на второе.
В этом случае мы получили в ответе правильную дробь.
Нам это говорит о том, что первое число меньше второго.
А если мы хотим сказать, как именно первое число меньше второго, то это можно сделать так: первое число меньше второго в (mathbf<frac<2><3>>) раза.
Мы можем сформулировать вывод и так: 16 составляет (mathbf<frac<2><3>>) от 24-х, то есть мы отвечаем на вопрос, какой частью является первое число от второго.
Также важно отметить, что отношение числа a к числу b не всегда равно отношению числа b к числу a.
Пример 4
Есть два числа, 14 и 28
Посчитаем отношение 14 к 28
И посчитаем отношение 28 к 14
Как вы видите, получились разные значения.
Как можно заметить, это взаимно обратные числа.
Отметим еще одно свойство отношений: если есть два числа a и b, то отношение a к b взаимно обратно отношению b к a.
Если дано отношение первого числа ко второму, то мы без труда сможем найти отношение второго к первому, даже не зная самих чисел, просто посчитав обратное к отношению число.
Пример 5
Дано, что отношение числа a к числу b равно (mathbf<frac<2><5>>), найдем отношение b к a
Для этого надо найти обратное число к (mathbf<frac<2><5>>)
Значит, отношение b к a равняется (mathbf<2frac<1><2>>)
В конце этой части добавим еще одно простое, но важное свойство.
Отношение двух чисел не изменится, если каждое из них домножить или разделить на одно и тоже число.
Это легко доказать, показав, что при делении этот множитель сократится.
Пример 6
Отношение числа 10 к числу 30 равно (mathbf<frac<1><3>>)
Домножим каждое из чисел на 2 и заметим, что отношение 20 к 60 также равно (mathbf<frac<1><3>>)
Пройти тест и получить оценку можно после входа или регистрации
Отношение и часть от числа
Посмотрим, какие еще можно сделать выводы, зная отношение.
Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь.
Так мы получим число, которое будет частью исходного.
Допустим, изначально у нас было число 4, и мы решили найти от него (mathbf<frac<3><8>>)
Перемножив, мы получим:
А теперь найдите отношение полученного числа к изначальному.
Для этого разделите одно на другое:
То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение.
Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби.
Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b.
Пример 1
Известно, что некая дробь от числа 10 равна (mathbf<2frac<1><2>>)
Найдем, какая именно это дробь.
Решение:
Дробь от числа равна отношению полученного числа к изначальному.
Теперь разделим одно на другое и получим ответ.
Ответ: дробь, взяв которую от 10 получили (mathbf<2frac<1><2>>), равняется (mathbf<frac<1><4>>)
Пример 2
Отношение первого числа ко второму равно (mathbf<1frac<1><5>>), также известно, что первое число равно 6.
Найдем второе число.
Решение:
Мы знаем, что отношение обратно дроби.
Найдем обратное число к (mathbf<1frac<1><5>>)
Теперь можно найти второе число, домножим первое на эту дробь:
Второе число равно 5
Проверка:
Найдем отношение первого числа ко второму, то есть 6 к 5
Получилось то же отношение, что и в условии.
Пример 3
Решим похожую задачу:
Отношение числа а к числу b равно (mathbf<1frac<1><2>>)
Известно, что число b равняется 8-ми, надо найти число а.
Решение:
Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения:
Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь.
В нашем случае на дробь надо делить число b :
Ответ: число a равняется 12
Пройти тест и получить оценку можно после входа или регистрации
Отношения в задачах
Теперь научимся находить отношения в задачах.
Сразу перейдем к примерам, чтобы посмотреть, за какими формулировками могут стоять отношения.
Задача 1
Длина улицы составляет 25 километров. Освещено 15 километров улицы.
а) Найдите, какая часть улицы освещена.
б) Во сколько раз вся улица длиннее ее освещенной части?
Решение:
В начале урока мы находили отношение меньшего числа к большему, тем самым определили, какую часть первое число составляет от второго.
Именно это и спрашивается в первом вопросе.
Для нахождения отношения длины освещенного участка к длине всей улицы поделим одну величину на другую:
Значит, длина освещенного участка составляет (mathbf<frac<3><5>>) от длины всей улицы.
Во втором вопросе нас спрашивают: «Во сколько раз больше?» — это соответствует отношению большего числа к меньшему.
Для нахождения этого отношения необходимо поделить длину всей улицы на длину ее освещенной части:
Что отвечает на вопрос второго пункта.
Также важно помнить, что если подаются какие-либо величины, то всегда надо следить, чтобы мера измерения была одинаковой.
То есть если нам подали что-то в тоннах и килограммах и мы хотим найти отношения этих величин, то надо либо тонны переводить в килограммы, либо наоборот.
Задача 2
Масса груза составляет 2 тонны. Известно, что часть груза- это одежда и ее масса 350 кг.
Найдите, какую часть от массы груза составляет масса одежды.
Решение:
Для начала преобразуем преобразуем тонны в килограммы. Получается, что масса груза равна 2000 кг.
Теперь найдем искомое отношение:
Теперь попробуйте порешать задачи самостоятельно, а если будет сложно, используйте подсказки.
Пройти тест и получить оценку можно после входа или регистрации
Интересная информация
Сегодня вы узнаете о математических фокусах!
Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам.
Фокус 1
Попросите зрителя загадать число и никому не говорить.
Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число.
Теперь вы можете уверенно сказать, что у зрителя получилось число 4.
Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка.
Попробуй доказать это на формулах, взяв за задуманное число Х
Фокус 2
В нем вы можете угадать День рождения человека.
Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.).
Для того чтобы сказать по полученному числу День рождения человека, надо вычесть из числа, названного зрителем, 250 — получится трехзначное или четырехзначное число, где первые одна или две цифры — это день рождения, а последние две — месяц.
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Источник