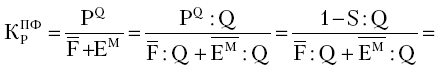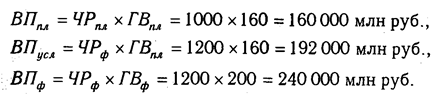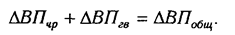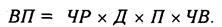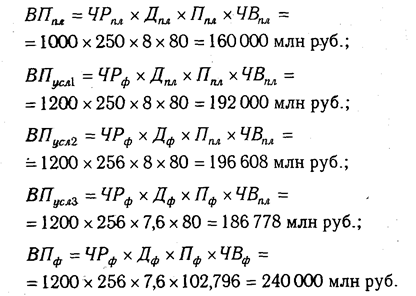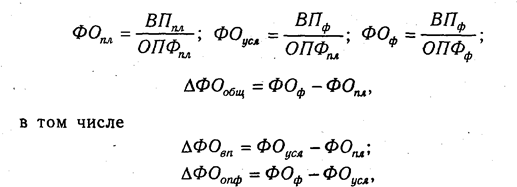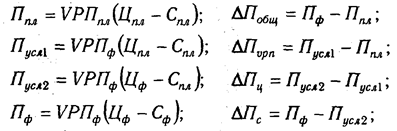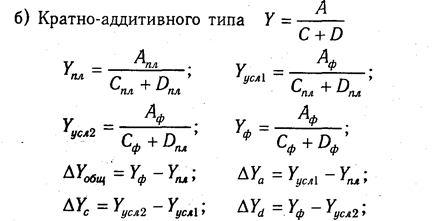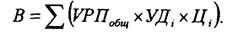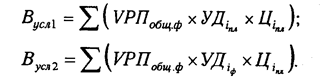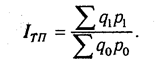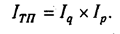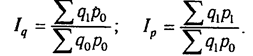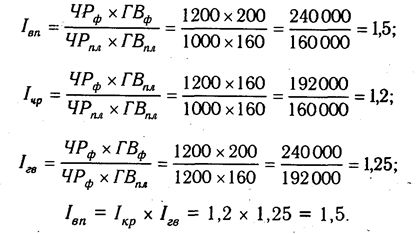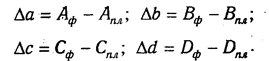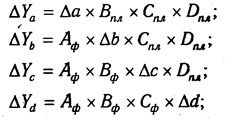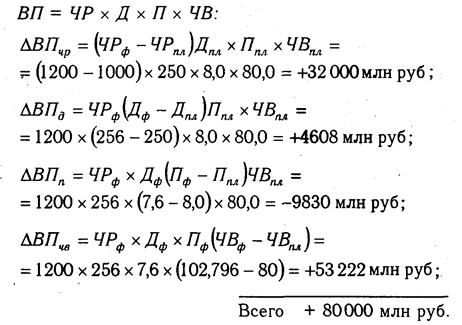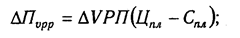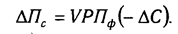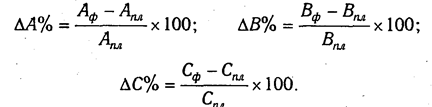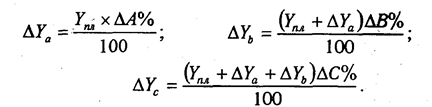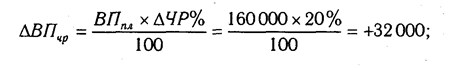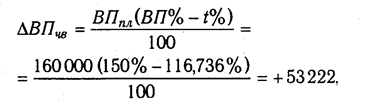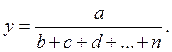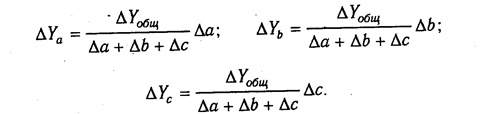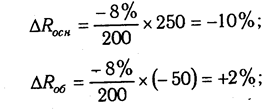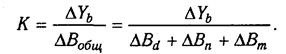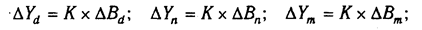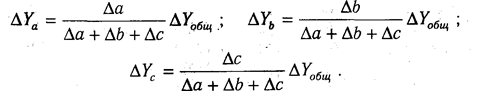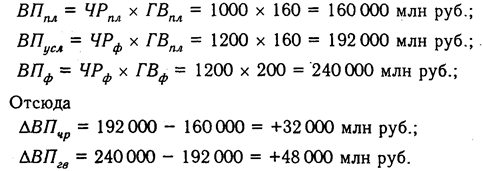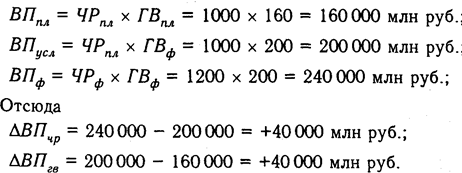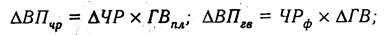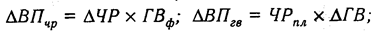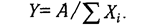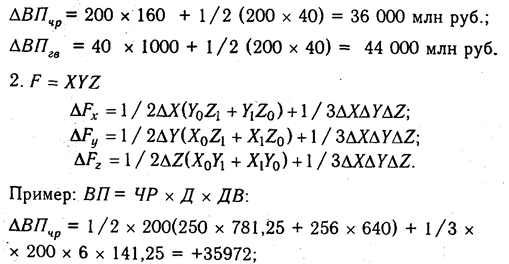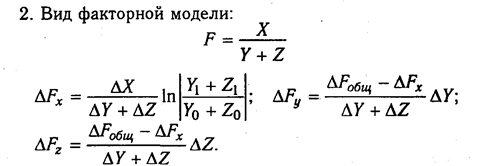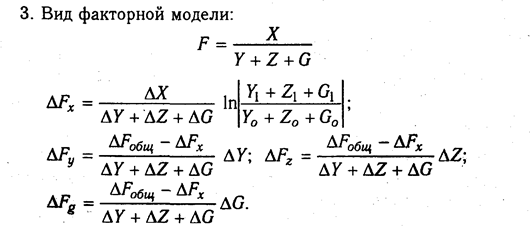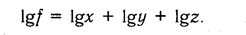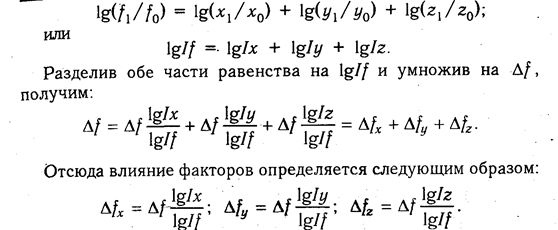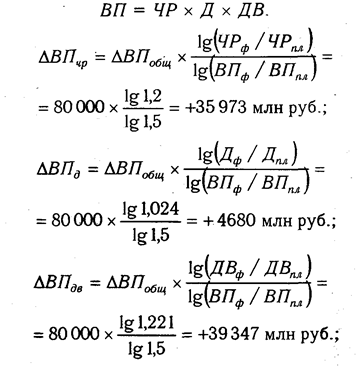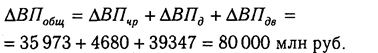Способы выявления влияния факторов на результативный показатель
Одной
из важнейших методологических задач в
экономическом анализе является
определение величины влияния факторов
на прирост результативных показателей.
В детерминированном факторном анализе
для этого используются следующие методы:
цепной подстановки, абсолютных разниц
относительных разниц, долевого участия,
логарифмический, балансовый и т.д.
Наиболее
распространенным является метод цепной
подстановки.
Данный
способ используется для расчета влияния
факторов во всех типах детерминированных
факторных моделей: аддитивных,
мультипликативных, кратных и
комбинированных. Способ цепных подстановок
заключается в определении ряда
промежуточных значений результативного
показателя путем последовательной
замены базисных значений факторов на
отчетные. Разность промежуточных
значений равна изменению результативного
показателя за счет заменяемого фактора.
Число расчетов результативного показателя
на единицу больше числа факторов. При
расчетах используется следующий порядок.
При наличии количественных и качественных
показателей в первую очередь производится
подсчет количественных факторов, а
затем качественных.
Рассмотрим
пример применения этого способа.
Таблица
5.1.
Показатели, определяющие объем выпуска продукции
|
Показатель |
Условное |
Уровень |
Отклонение |
||
|
базовый |
отчетный |
абсолютное |
относительное, |
||
|
Валовая |
Вп |
4800 |
5920 |
+1120 |
+23,3 |
|
Среднесписочная |
Чр |
15 |
16 |
+1 |
+6,7 |
|
Среднегодовая |
Гв |
320 |
370 |
+50 |
15,625 |
|
Количество |
Д |
200 |
205 |
+5 |
+2,5 |
|
Средняя |
П |
8 |
7,8 |
-0,2 |
-2,5 |
|
Среднечасовая |
ЧВ |
200 |
231,4 |
+31,4 |
+15,7 |
Между
показателями данной таблицы существует
взаимосвязь, которая может быть выражена
в виде следующей факторной модели:
ВП
= ЧР ∙ ГВ.
лгоритм
расчета способом цепной подстановки
имеет вид:
ВП0
= ЧР0
∙ ГВ0
= 15 ∙ 320 = 4800 тыс. руб.
ВПусл
= ЧР1
∙ ГВ0
= 16 ∙ 320 = 5120 тыс. руб.
ВП1
= ЧР1
∙ ГВ1
= 16 ∙ 370 = 5920 тыс. руб.
Второй
показатель валовой продукции отличается
от первого тем, что при его расчете взята
численность рабочих текущего периода
вместо базисного. Выработка продукции
одним рабочим и там и там базисная. Можно
сказать, что за счет передержки численности
рабочих выпуск продукции вырос на 320
тыс. руб. (5120 — 4800).
Третий
показатель валовой продукции отличается
от второго тем, что при его расчете
выработка рабочих взята фактическая
вместо базисной. Численность и там и
там фактическая. Таким образом, за счет
роста производительности труда
объем валовой продукции вырос на 800 тыс.
руб. (5920 — 5120).
Следовательно,
рост объема производства произошел за
счет следующих факторов:
|
1) |
+320 |
|
2) |
+800 |
|
Итого |
+1120 |
Алгебраическая
сумма влияния факторов обязательно
должна быть равна общему приросту
результативного показателя:
Δ
ВПчр
+ Δ ВПгв
= Δ ВПобщ
.
Отсутствие
такого равенства говорит о допущенных
ошибках в расчетах.
Для
определения большего количества
факторов, например, четырех, рассчитывается
пять значений результативного показателя.
Схематически это можно представить
следующим образом (табл. 5.2)
Таблица
5.2.
Схема
расчета пяти значений результативного
показателя
|
Уровень |
Условия |
|||
|
Фактор |
Фактор |
Фактор |
Фактор |
|
|
Базисный |
план |
план |
план |
план |
|
Условный |
факт |
план |
план |
план |
|
Условный |
факт |
факт |
план |
план |
|
Условный |
факт |
факт |
факт |
план |
|
Фактический |
факт |
факт |
факт |
факт |
В
качестве примера рассмотрим четырехфакторную
модель валовой продукции:
ВП
= ЧР ∙ Д ∙ П ∙ ЧВ.
Исходные
данные возьмем из таблицы 5.1:
ВП0
= ЧР0
∙ Д0
∙ П0
∙ ЧВ0
= 15 ∙ 200 ∙ 8 ∙ 200 = 4800 тыс. руб.
ВПусл1
= ЧР1
∙ Д0
∙ П0
∙ ЧВ0
= 16 ∙ 200 ∙ 8 ∙ 200 = 5120 тыс. руб.
ВПусл2
= ЧР1
∙ Д1
∙ П0
∙ ЧВ0
= 16 ∙ 205 ∙ 8 ∙ 200 = 5248 тыс. руб.
ВПусл3
= ЧР1
∙ Д1
∙ П1
∙ ЧВ0
= 16 ∙ 205 ∙ 7,8 ∙ 200 = 5116,8 тыс. руб.
ВП1
= ЧР1
∙ Д1
∙ П1
∙ ЧВ1
= 16 ∙ 205 ∙ 7,8 ∙ 231,4 = 5920 тыс. руб.
Объем
выпуска продукции
за отчетный период вырос на 1120 тыс. руб.,
в том числе за счет изменения:
1)
численности рабочих:
Δ
ВП(ЧР) = ВПусл1 — ВП0 = 5120 —
4800 = +320 тыс. руб.;
2)
количества отработанных дней одним
рабочим за год:
Δ
ВП(Д) = ВПусл2 — ВПусл1 =
5248 — 5120 = +128 тыс. руб.;
3)
средней продолжительности рабочего
дня:
Δ
ВП(П) = ВПусл3 — ВПусл2 =
5116,8 — 5248 = -131,2 тыс. руб.;
4)
среднечасовой выработки:
Δ
ВП(ЧВ) = ВП1 — ВПусл3 = 5920 —
5116,8 = 803,2 тыс. руб.
Итого:
+1120 тыс. руб.
Следовательно,
применение способа цепной подстановки
требует знания взаимосвязи факторов,
их соподчиненности, умения правильно
их классифицировать и систематизировать.
В
мультипликативных моделях детерминированного
факторного анализа применяется способ
абсолютных разниц. Несмотря на
ограниченное использование, благодаря
простоте он получил широкое применение
в экономическом анализе.
Сущность
этого способа заключается в том, что
величина влияния факторов определяется
умножением абсолютного прироста значения
исследуемого фактора на базовую
(плановую) величину факторов, которые
находятся справа от него, и на фактическую
величину факторов, расположенных слева
от него в модели.
Алгоритм
расчета для мультипликативной
четырехфакторной модели валовой
продукции представляет собой следующее.
ВП
= ЧР ∙ Д ∙ П ∙ ЧВ.
Δ
ВПчр = Δ ЧР ∙ Д0 ∙ П0 ∙
ЧВ0 = (+1) ∙ 200 ∙ 8 ∙ 200 = + 320 тыс. руб.
Δ
ВПд = ЧР1 ∙ Δ Д ∙ П0 ∙
ЧВ0 = 16 ∙ (+5) ∙ 8 ∙ 200 = + 128 тыс. руб.
Δ
ВПп = ЧР1 ∙ Д1 ∙ Δ П ∙
ЧВ0 = 16 ∙ 205 ∙ (-0,2) ∙ 200 = -131,2 тыс.
руб.
Δ
ВПчв = ЧР1 ∙ Д1 ∙ П1
∙ Δ ЧВ = 16 ∙ 205 ∙ 7,8 ∙ (+31,4) = +803,2 тыс. руб.
Итого:
+1120 тыс. руб.
Результаты
с помощью способа абсолютных разниц
получаются те же, что и способом цепной
подстановки. Необходимо иметь в виду,
что если имеется несколько количественных
и качественных факторов, то сначала
исследуется влияние факторов первого
порядка, а затем более низкого.
Данный
способ применяется для измерения влияния
факторов на прирост результативного
показателя только в мультипликативных
моделях. Используются относительные
приросты факторных показателей,
выраженные в виде коэффициентов или
процентов.
Для
расчета влияния первого фактора
необходимо базовую величину результативного
показателя умножить на относительный
прирост первого фактора, выраженного
в виде десятичной дроби.
Для
расчета влияния второго фактора нужно
к базовой величине результативного
показателя прибавить изменение его за
счет первого фактора и затем полученную
сумму умножить на относительный прирост
второго фактора.
Влияние
третьего фактора определяется аналогично:
к базовой величине результативного
показателя необходимо прибавить его
прирост за счет первого и второго
факторов и полученную сумму умножить
на относительный прирост третьего
фактора и т.д.
Рассмотрим
данную методику на примере, приведенном
в
Δ
ВПчр = ВП0 ∙ Δ ЧР / ЧР0
= 4800 ∙ 1 / 15 = +320 тыс. руб.
Δ
ВПд = (ВП0 + Δ ВПчр ) ∙
Δ Д / Д0 = (4800 + 320) ∙ 5 / 200 = +128 тыс. руб.
Δ
ВПп = (ВП0 + Δ ВПчр + Δ
ВПд ) ∙ Δ П / П0 = (4800 + 320 + 128) ∙
-0,2 / 8 = -131,2 тыс. руб.
Δ
ВПчв = (ВП0 + Δ ВПчр + Δ
ВПд + Δ ВПп ) ∙ Δ ЧВ / ЧВ0
= (4800 + 320 + 128 — 131,2) ∙ 31,4 / 200 = 803,2 тыс. руб.
Результаты
расчетов такие же, как и при использовании
предыдущих способов.
Данный
способ удобно применять в тех случаях,
когда требуется рассчитывать влияние
большего количества факторов (8 и более).
Этот способ значительно сокращает число
вычислительных действий, что говорит
о его преимуществе.
Иногда,
чтобы определить влияние факторов на
прирост результативного показателя,
используется метод пропорционального
деления. Он используется, когда мы
имеем дело с аддитивными моделями Y = Σ
xi и моделями кратно-аддитивного
характера:
Y
= a / b + c + d +….+n; Y = a + b + c +… + n / k.
Когда
имеется одноуровневая модель, например,
Y = a + b + c, расчет проводится следующим
образом:
Δ
Ya = Δ
Yобщ / Δ
a + Δ b + Δ c ∙
Δ a;
Δ
Yb = Δ
Yобщ / Δ
a + Δ b + Δ c ∙
Δ b;
Δ
Yc = Δ
Yобщ / Δ
a + Δ b + Δ c ∙
Δ c.
В
моделях кратно-аддитивного типа сначала
определяем методом цепной подстановки,
как изменился результативный показатель
за счет числителя и знаменателя, а затем
следует расчет влияния факторов второго
порядка
способом пропорционального деления
вышеперечисленными алгоритмами.
Пример.
Уровень
фонда заработной платы повысился на
21,7% в связи с ростом среднегодовой
заработной платы на 3250 руб. Среднегодовая
заработная плата возросла за счет роста
выплат по тарифным ставкам — на 346
руб., за счет роста выплат доплат и
надбавок — на 2129 руб., за счет роста
выплат дополнительной заработной
платы — на 775 руб. Определим, как
изменился фонд заработной платы за счет
каждого фактора.
Δ
ФЗПтс = +21,7% / 3250 ∙ 346 = +2,3%; Δ ФЗПдн
= +21,7% / 3250 ∙ 2129 = +14,2%; Δ ФЗПдз = +21,7%
/ 3250 ∙ 775 = +5,2%.
Для
решения такого типа задач можно
использовать способ долевого участия.
Сначала
определяется доля каждого фактора в
общей сумме их приростов, которая затем
умножается на общий прирост результативного
показателя (табл. 5.3).
Δ
Ya = Δ а / Δ a + Δ b + Δ c ∙ Δ Yобщ
; Δ Yc = Δ с / Δ a + Δ b + Δ c ∙ Δ Yобщ
; Δ Yb = Δ b / Δ a + Δ b + Δ c ∙ Δ Yобщ
.
Таблица
5.3.
Соседние файлы в папке АХД
- #
- #
- #
- #
- #
- #
FAQТЦО РоссияКак определить долю прямого и косвенного участия одной организации в другой?
Одним из основных критериев для признания лиц взаимозависимыми является наличие доли прямого и (или) косвенного участия одной организации в другой, превышающей 25%.
ОПРЕДЕЛЕНИЕ ДОЛИ ПРЯМОГО УЧАСТИЯ
Согласно пп. 1 п. 2 ст. 105.1 Налогового Кодекса РФ, доля прямого участия одной организации в другой организации может быть рассчитана тремя способами:
- расчет непосредственно принадлежащей одной организации доли голосующих акций другой организации (способ 1);
- расчет непосредственно принадлежащей одной организации доли в уставном (складочном) капитале (фонде) другой организации (способ 2);
- расчет непосредственно принадлежащей одной организации доли, определяемой пропорционально количеству участников в другой организации (при невозможности использования первых двух способов) (способ 3).
Ниже представлены примеры расчетов.
Пример. Уставный капитал ОАО «А» составляет 32 млн рублей, из которых 25 млн рублей приходится на обыкновенные акции номиналом 1000 рублей, а 7 млн рублей – на привилегированные номиналом 5000 рублей. Привилегированные акции не являются голосующими. Распределение акций ОАО «А» между владельцами представлено в таблице 1 (графы 1-4).
Необходимо определить доли прямого участия организаций ООО «В», ООО «С» и прочих в ОАО «А».
Таблица 1
Определение доли участия в уставном капитале ОАО «А»
| . | Обыкновенные акции | Привилегированные акции | Доля участия в УК | Доля прямого участия,% | |||
| шт. | млн руб. | шт. | млн руб. | млн руб. | Способ 1 | Способ 2 | |
| A | 1 | 2 | 3 | 4 | 5=2+4 | 6 | 7 |
| ООО «B» | 9 500 | 9,5 | 700 | 3,5 | 13,0 | 38,0 | 40,6 |
| ООО «С» | 8 600 | 8,6 | 500 | 2,5 | 11,1 | 34,4 | 34,7 |
| Прочие | 6 900 | 6,9 | 200 | 1,0 | 7,9 | 27,6 | 24,7 |
| Итого | 25 000 | 25,0 | 1 400 | 7,0 | 32,0 | 100 | 100 |
В данном случае определить долю прямого участия можно, применив способ 1 или способ 2, как следствие, способ 3 для расчетов не используется.
Способ 1: В расчетах доли участия данным способом будут учитываться только обыкновенные акции, так как привилегированные акции при заданных условиях не являются голосующими. Таким образом, доля прямого участия ООО «В» в ОАО «A» составляет 38%: 9,5 млн рублей/25 млн руб *100%= 38%.
Доли прямого участия других организаций в ОАО «А», рассчитанные по способу 1, указаны в графе 6 таблицы 1.
Способ 2: Данный способ учитывает владение как обыкновенными, так и привилегированными акциями. С учетом исходных данных, доля прямого участия ООО «В» в уставном капитале ОАО «А» будет равна 40,6%:
13,0 млн руб./32,0 млн руб. *100% = 40,6%.
Доли прямого участия других организаций в ОАО «А», рассчитанные по способу 2, указаны в графе 7 таблицы 1.
При невозможности использования первых двух способов (при возникновении сложностей с определением количества голосующих акций или доли в уставном (складочном) капитале общества) применяется способ 3. В данном случае доля участия одной организации определяется пропорционально количеству участников в другой организации.
Пример. Акции ОАО «А» распределены между тремя владельцами. Таким образом, доля прямого владения каждой организации в ОАО «А» будет составлять 33,3%.
Важно! В письме Министерства финансов РФ N 03-01-18/33535 от 16 августа 2013 года говорится, что при возможности использования нескольких из указанных выше способов в целях определения взаимозависимости используется доля, которая является максимальной из долей, определенных различными способами.
ОСОБЫЙ СЛУЧАЙ. Определение прямой доли участия в случае наличия собственных акций (долей), принадлежащих организации
В случае наличия собственных акций (долей), принадлежащих организации (то есть в случае прямого участия организации в собственном капитале), при расчете доли прямого участия других организаций в этой организации необходимо учитывать тот факт, что, согласно Федеральным законам «Об акционерных обществах» и «Об обществах с ограниченной ответственностью», собственные акции, приобретенные организацией, не являются голосующими. Как следствие, эти акции исключаются из расчета доли участия одной организаций в другой.
Пример. Акционерный капитал ЗАО «А» состоит из 5 тыс. акций, из которых 2,9 тыс. акций находятся в собственности ОАО «В», 1 тыс. акций в собственности ОАО «С». Оставшаяся часть (1,1 тыс. акций) выкуплена непосредственно самой компаний — ЗАО «А». Номинальные доли организаций в уставном капитале ЗАО «А» представлены на схеме 1.
Необходимо определить прямую долю участия ОАО «В» и ОАО «С» в ЗАО «А».
Схема 1
НАЛИЧИЕ СОБСТВЕННЫХ АКЦИЙ (ДОЛЕЙ), ПРИНАДЛЕЖАЩИХ ОРГАНИЗАЦИИ
Для определения долей участия из расчетов необходимо исключить собственные акции, принадлежащие ЗАО «А».
Таким образом, прямая доля участия ОАО «В» в ОАО «А» будет равна 74,4%:
2 900/(5 000-1 100)*100=74,4%;
прямая доля участия ОАО «С» в ОАО «А» — 25,6%:
1 000/(5 000-1 100)*100=25,6%.
ОПРЕДЕЛЕНИЕ ДОЛИ КОСВЕННОГО УЧАСТИЯ
Для расчета доли косвенного участия одной организации в другой организации необходимо выполнить следующие действия:
- найти все последовательности участия одной организации в другой организации через прямое участие каждой предыдущей организации в каждой последующей организации;
- определить доли прямого участия каждой предыдущей организации в каждой последующей организации соответствующей последовательности;
- просуммировать произведения долей прямого участия одной организации в другой организации через участие каждой предыдущей организации в каждой последующей организации всех последовательностей.
Пример. На схеме 2 представлено последовательное участие организаций в капитале. Необходимо определить косвенное участие ООО «D» в ООО «А».
Схема 2
КОСВЕННОЕ УЧАСТИЕ ОРГАНИЗАЦИЙ В КАПИТАЛЕ
Порядок расчета косвенного участия будет следующим:
- Находим последовательности участия ООО «D» в ООО «А»: D-B-C-A.
- Доли прямого участия каждой предыдущей организации в последующей известны: 24%, 40%, 35%.
- Перемножаем эти доли: 0,24*0,40*0,35*100%=3,36%.
Таким образом, доля косвенного участия ООО «D» в ООО «А» составляет 3,36%.
Источники:
Налоговый Кодекс РФ статья 105.2;
Письмо Минфина РФ от 2 июля 2013 г. N ОА-4-13/11912;
Письмо Минфина РФ от 16 августа 2013 г. N 03-01-18/33535.
Комплексная оценка эффективности хозяйственной деятельности организации
Объем производства продукции в стоимостном выражении является результатом воздействия всех видов ресурсов. Использование производственных и финансовых ресурсов может носить как экстенсивный, так и интенсивный характер. Понятие всесторонней интенсификации охватывает и характеризует использование не только живого, но и овеществленного труда, т. е. всей совокупности производственных и финансовых ресурсов.
Возможность обеспечить неуклонный рост и достаточно высокие темпы экономической эффективности производства дает переход к преимущественно интенсивному типу развития. Соотношение экстенсивности и интенсивности производства анализируется по соотношению качественных и количественных показателей использования ресурсов.
Конечный результат хозяйственной деятельности предприятия (объем продукции, прибыль и рентабельность, финансовое состояние и платежеспособность) складывается под воздействием как интенсивных, так и экстенсивных факторов, как качественных, так и количественных показателей использования ресурсов.
Анализ интенсификации производства и влияния ее на результаты хозяйственной деятельности предприятия может быть рассмотрен на следующем примере с использованием рекомендованной А.Д. Шереметом и Р.С. Сайфулиным методики. Исходные данные для расчета показателей интенсификации использования ресурсов можно получить из форм бухгалтерской и статистической отчетности: № 1 «Бухгалтерский баланс», П-1 «Сведения о производстве и отгрузке товаров и услуг», П-4 «Сведения о численности, заработной плате и движении работников», 5-з «Сведения о затратах на производство и реализацию продукции (работ, услуг) предприятия», 11 «Сведения о наличии и движении основных фондов (средств) и других нефинансовых активов», 1-предприятие «Основные сведения о деятельности организации», 1-т «Сведения о численности и заработной плате работников по видам деятельности».
В отчетном году по сравнению с предыдущим годом динамика качественных показателей имеет следующий вид: производительность труда составила 126,62%, выпуск продукции на 1 руб. оплаты труда — 116,02%, материалоотдача — 98,16%, фондоотдача — 116,15%, амортизациоотдача — 91,77%, оборачиваемость оборотных средств — 119,03% (табл. 7.1).
| № п/п | Показатели | Предыдущий год | Отчетный год | Темпы динамики, % |
|---|---|---|---|---|
| А | Б | 1 | 2 | 3 |
| 1 | Объем продукции в действующих ценах (без НДС и акциза), тыс. руб. | 44 540 | 54 500 | 122,36 |
| 2 | Промышленно-производственный персонал, человек | 1 190 | 1 150 | 96,64 |
| 3 | Оплата труда, тыс. руб. | 14 100 | 14 870 | 105,46 |
| 4 | Материальные затраты, тыс. руб. | 24 790 | 30 900 | 124,65 |
| 5 | Основные промышленно-производственные фонды, тыс. руб. | 13 860 | 14 600 | 105,34 |
| 6 | Амортизация, тыс. руб. | 540 | 720 | 133,33 |
| 7 | Оборотные средства, тыс. руб. | 10 660 | 10 960 | 102,81 |
| 8 | Производительность труда, руб. | 37 428 | 47 391 | 126,62 |
| 9 | Продукция на 1 руб. оплаты труда, руб. | 3,159 | 3,665 | 116,02 |
| 10 | Материалоотдача, руб. | 1,797 | 1,764 | 98,16 |
| 11 | Фондоотдача, руб. | 3,214 | 3,733 | 116,15 |
| 12 | Амортизациоотдача, руб. | 82,481 | 75,694 | 91,77 |
| 13 | Оборачиваемость оборотных активов, раз | 4,178 | 4,973 | 119,03 |
В экономическом анализе для количественной оценки роли факторов (экстенсивного и интенсивного характера) определяется доля их влияния на 100% прироста продукции. Для расчета доли влияния экстенсивности использования ресурса находят соотношение прироста ресурса в расчете на 1% прироста объема продукции путем деления темпа прироста (падения) каждого ресурса на темп прироста (падения) объема продукции. Для расчета доли влияния интенсивности использования ресурса полученный результат по каждому ресурсу вычитают из 100%.
На анализируемом предприятии (табл. 7.1) наблюдается следующее:
- снижение численности работников (экстенсивный фактор) по сравнению с предыдущим годом на 3,36% привело к уменьшению прироста объема продукции на 0,15 пунктов (–3,36 : 22,36), или на 15% (–0,15 x 100), а доля прироста продукции за счет интенсивного фактора (производительности труда) составила 115% [(100 — (–15)];
- доля прироста продукции за счет повышения оплаты труда (экстенсивный фактор) составила 24,4% (5,46 : 22,36 x 100), а за счет увеличения зарплатоотдачи (интенсивный фактор) — 75,6% (100 — 24,4); доля прироста продукции за счет увеличения материальных затрат (экстенсивный фактор) составила 1,102 пункта (24,65 : 22,36), или 110,2% (1,102 x 100), а за счет снижения материалоотдачи (интенсивный фактор) уменьшение прироста объема продукции составило 10,2% (100 –110,2);
- доля прироста продукции за счет увеличения среднегодовой стоимости основных фондов (экстенсивный фактор) определена в размере 0,239 пункта (5,34 : 22,36), или 23,9%, а за счет увеличения фондоотдачи (интенсивный фактор) — в размере 76,1% (100 — 23,9);
- доля прироста продукции за счет увеличения суммы амортизационных отчислений (экстенсивный фактор) составила 1,491 пункта (33,33 : 22,36), или 149,1% (1,491 x 100), а за счет снижения амортизациоотдачи (интенсивный фактор) снижение прироста продукции составило 49,1% (100 — 149,1);
- за счет увеличения средней суммы оборотных активов (экстенсивный фактор) доля прироста объема продукции составила 0,126 пункта (2,81 : 22,36), или 12,6%, следовательно, доля прироста продукции за счет ускорения их оборачиваемости (интенсивный фактор) определяется в размере 87,4% (100 — 12,6).
Приведенные данные показывают, что качественный уровень использования ресурсов повысился, кроме отдачи материальных ресурсов и амортизациоотдачи основных фондов, что видно в табл. 7.2.
Данные таблицы показывают, что использование трудовых ресурсов, основных фондов и оборотных активов на предприятии преимущественно интенсивное. Использование материальных ресурсов — полностью экстенсивное при отрицательной интенсификации, т. е. ухудшении качественного уровня использования материальных ресурсов — материалоотдачи.
| Вид ресурсов | Динамика качественных показателей, коэффициент | Прирост ресурсов на 1% прироста объема продукции, пункты | Доля влияния на 100% прироста продукции факторов | Относительная экономия, перерасход ресурсов (+, -) | |
|---|---|---|---|---|---|
| экстенсивного характера | интенсивного характера | ||||
| А | 1 | 2 | 3 | 4 | 5 |
| Промышленно-производственный персонал | 1,266 | -0,150 | -15,0 | +115,0 | -3 956,6 |
| Оплата труда | 1,160 | 0,244 | +24,4 | +75,6 | -2 383,0 |
| Материальные затраты | 0,982 | 1,102 | +110,2 | -10,2 | +567,0 |
| Основные промышленно-производственные фонды | 1,161 | 0,239 | +23,9 | +76,1 | -2 359,0 |
| Амортизация | 0,918 | 1,491 | +149,1 | -49,1 | +59,0 |
| Оборотные активы | 1,190 | 0,126 | +12,6 | +87,4 | -2 084,0 |
| Комплексная оценка интенсификации | 1,088 | 0,559 | +55,9 | +44,1 | -625,9 |
Расчет относительной экономии ресурсов можно рассмотреть на примере численности работников. Если среднегодовую численность работников в отчетном году сравнить с численностью работников предыдущего года, скорректированную на коэффициент изменения объема продукции, то результат покажет относительную экономию численности работников: 306 чел. (1 150 — 1 190 x 1,2236). Умножив сэкономленную численность работников на среднегодовую заработную плату 1 работника в отчетном году, получим относительную экономию численности работников, выраженную через их заработную плату. В нашем примере это 3 956,6 тыс. руб. ((14 870 : 1 150) x 306)). Это общий результат интенсификации использования трудовых ресурсов, часть которого может отразиться в повышении заработной платы работников, а другая часть — в снижении себестоимости продукции за счет относительной экономии заработной платы. Расчет относительной экономии заработной платы для условий нашего примера:
14 870 — 14 100 x 1,2236 = -2 383,0 тыс. руб.
Материальные ресурсы были использованы с относительным перерасходом в размере 567,0 тыс. руб. (30 900 — 24 790 x 1,2236).
По основным промышленно-производственным фондам получена относительная экономия в сумме 2 359,0 тыс. руб. (14 600 — 13 860 x 1,2236), а вот по амортизации допущен перерасход в размере 59,0 тыс. руб. (720 — 540 x 1,2236).
Относительная экономия по оборотным средствам составила 2 084,0 тыс. руб. (10 960 — 10 660 x 1,2236).
Комплексную оценку степени всесторонней интенсификации получают с помощью сведения различных показателей в единый интегральный показатель, вбирающий в себя все качественные характеристики частных показателей интенсификации. Пример комплексной оценки всесторонней интенсификации может быть дан по показателям относительной экономии различных ресурсов. В нашем случае совокупная относительная экономия всех ресурсов составила 7 832,6 тыс. руб. Эта сумма складывается из экономии фонда оплаты труда, отражающей снижение трудоемкости производства — 3 956,6 тыс. руб., из экономии по основным промышленно-производственным фондам — 2 359,0 тыс. руб., из экономии оборотных средств — 2 084,6 тыс. руб. и относительного перерасхода по материальным ресурсам — 567 тыс. руб.
Необходимо также рассчитать совокупную долю влияния экстенсивности и интенсивности по всем ресурсам. Для этого определяются все ресурсы как сумма оплаты труда, материальных затрат, основных фондов и оборотных средств.
Для предыдущего года:
14 100 + 24 790 + 13 860 + 10 660 = 63 410 тыс. руб.
Для отчетного года:
14 870 + 30 900 + 14 600 + 10 960 = 71 330 тыс. руб.
Далее исчисляется динамика совокупных ресурсов 71 330 : 63 410 = 1,1249. Сопоставлением динамики продукции и динамики совокупных ресурсов определяется динамика качественного показателя: 1,2236 : 1,1249 = 1,0877. Прирост совокупных ресурсов на 1% прироста объема продукции составит 12,49% : 22,36% = 0,559. Следовательно, доля экстенсивности на 100 % прироста продукции составит 55,9%, а интенсивности — 44,1%. Относительная экономия ресурсов — 6 259 тыс. руб. (2 383 — 567 + 2 359 + 2 084).
Таким образом, совокупный социально-экономический эффект повышения интенсивности составил 7 832,6 тыс. руб., а совокупный экономический эффект, отраженный в показателях предприятия, -6 259,0 тыс. руб. Разница в 1 573,6 тыс. руб. (7 832,6 — 6 259,0) отражает прирост средней оплаты труда работников. Экономия по себестоимости составила 1 757 (2 383 — 567 — 59), а экономия примененного авансированного капитала — 4 384 тыс. руб. (2 359 — 59 + 2 084).
Обобщающим показателем всесторонней интенсификации предприятия является уровень рентабельности производственных фондов, определяемый отношением прибыли от продажи товаров, продукции, работ, услуг (РQ) к среднегодовой стоимости основных производственных фондов (F) и материальных оборотных средств (ЕM). Этот показатель вбирает в себя все качественные характеристики частных показателей интенсификации, что видно из следующего моделирования уровня рентабельности производственных фондов:
 |
(7.1) |
| где | M : Q | — | материалоемкость продукции; |
| ФОТ : Q | — | зарплатоемкость продукции, которая отражает трудоемкость продукции; | |
| A : Q | — | амортизациемкость продукции; | |
| F : Q | — | фондоемкость продукции; | |
| ЕM | — | уровень оборотных средств на 1 руб. продукции (или фондоемкость продукции по оборотным средствам). |
В динамике уровня рентабельности производственных фондов отражается рост всесторонней интенсификации хозяйственной деятельности, что делает этот показатель наиболее обобщающим показателем эффективности производства.
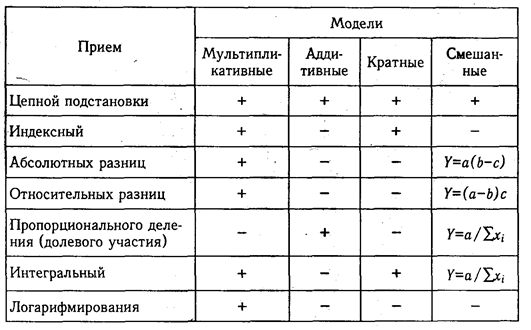
Способы:
— цепной подстановки;
— индексный;
— абсолютных разниц;
— относительных разниц;
— пропорционального деления;
— долевого участия;
— интегральный;
— логарифмирования.
6.1. Способ цепной подстановки
Типы детерминированных моделей, в которых применяется способ цепной подстановки. Сущность и правила его применения. Алгоритмы расчета влияния факторов этим спосбом в различных типах моделей.
Одним из важнейших методологических вопросов в АХД является определение величины влияния отдельных факторов на прирост результативных показателей. В детерминированном факторном анализе (ДФА) для этого используются следующие способы: цепной подстановки, индексный, абсолютных разниц, относительных разниц, пропорционального деления, интегральный, логарифмирования и др.
Первых четыре способа основываются на методе элиминирования. Элиминировать — значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, потом изменяются два, затем три и т.д., при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.
Наиболее универсальным из них является способ цепной подстановки. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и т.д. факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня того или другого фактора позволяет элиминироваться от влияния всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.
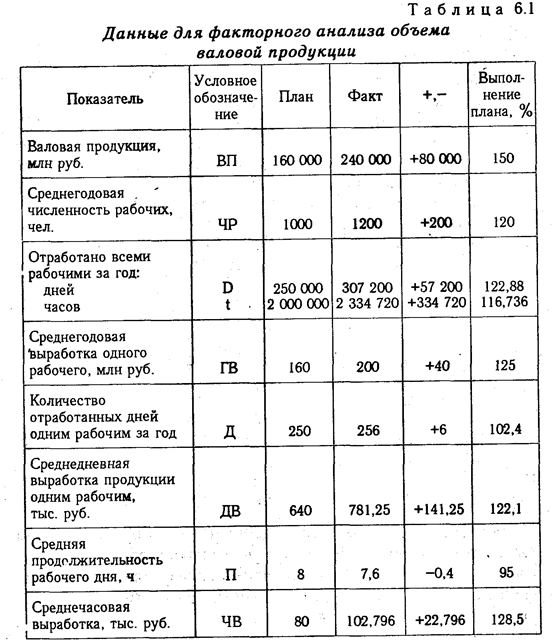
Порядок применения этого способа рассмотрим на следующем примере (табл. 6.1).
Как нам уже известно, объем валовой продукции (ВП) зависит от двух основных факторов первого уровня: численности рабочих (ЧР) и среднегодовой выработки (ГВ). Имеем двухфакторную мультипликативную модель: ВП = ЧР х ГВ.
Алгоритм расчета способом цепной подстановки для этой модели:
Как видим, второй показатель валовой продукции отличается от первого тем, что при его расчете принята фактическая численность рабочих вместо запланированной. Среднегодовая выработка продукции одним рабочим в том и другом случае плановая. Значит за счет увеличения количества рабочих выпуск продукции увеличился на 32 000 млн руб. (192 000 — 160 000).
Третий показатель отличается от второго тем, что при расчете его величины выработка рабочих принята по фактическому уровню вместо плановой. Количество же работников в обоих случаях фактическое. Отсюда за счет повышения производительности труда объем валовой продукции увеличился на 48 000 млн руб. (240 000 — 192 000).
Таким образом, перевыполнение плана по объему валовой продукции явилось результатом влияния следующих факторов:
а) увеличения численности рабочих + 32 000 млн руб.
б) повышения уровня производительности труда + 48 000 млн руб.
Итого +80 000 млн руб.
Алгебраическая сумма влияния факторов обязательно должна быть равна общему приросту результативного показателя:
Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах.
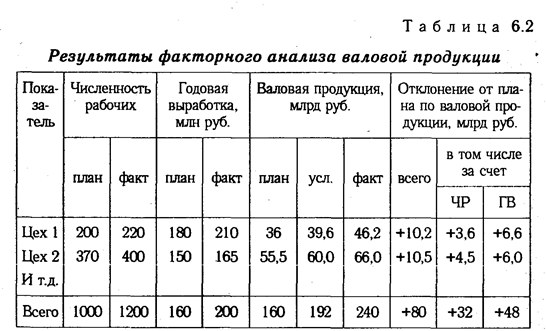
Для наглядности результаты анализа приведены в табл. 6.2.
Если требуется определить влияние трех факторов, то в этом случае рассчитывается не один, а два условных дополнительных показателя, т.е. количество условных показателей на единицу меньше числа факторов. Проиллюстрируем это на четырехфакторной модели валовой продукции:
Исходные данные для решения задачи приведены в табл.6.1:
План по выпуску продукции в целом перевыполнен на 80 000 млн руб. (240000 — 160000), в том числе за счет изменения:
а) количества рабочих
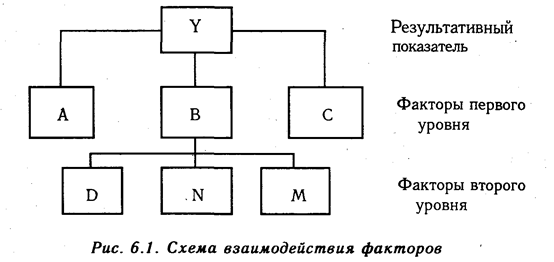
Используя способ цепной подстановки, рекомендуется придерживаться определенной последовательности расчетов: в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Если же имеется несколько количественных и несколько качественных показателей, то сначала следует изменить величину факторов первого уровня подчинения, а потом более низкого. В приведенном примере объем производства продукции зависит от четырех факторов: количества рабочих, количества отработанных дней одним рабочим, продолжительности рабочего дня и среднечасовой выработки. Согласно схеме 5.2, количество рабочих в данном случае — фактор первого уровня подчинения, количество отработанных дней – второго уровня, продолжительность рабочего дня и среднечасовая выработка — факторы третьего уровня. Это и обусловило последовательность размещения факторов в модели и соответственно очередность их исследования.
Таким образом, применение способа цепной подстановки требует знания взаимосвязи факторов, их соподчиненности, умения правильно их классифицировать и систематизировать.
Мы рассмотрели пример расчета влияния факторов на прирост результативного показателя в мультипликативных моделях.
В кратных моделях алгоритм расчета факторов на величину исследуемых показателей следующий:
где ФО — фондоотдача; ВП —валовая продукция; ОПФ — среднегодовая стоимость основных производственных фондов.
Методика расчета влияния факторов в смешанных моделях:
а) Мультипликативно-аддитивного типа П = VPП (Ц — С)
где П — сумма прибыли от реализации продукции; VPП — объем реализации продукции; Ц — цена реализации; С — себестоимость единицы продукции;
Аналогичным образом рассчитывают влияние факторов и по другим детерминированным моделям смешанного типа.
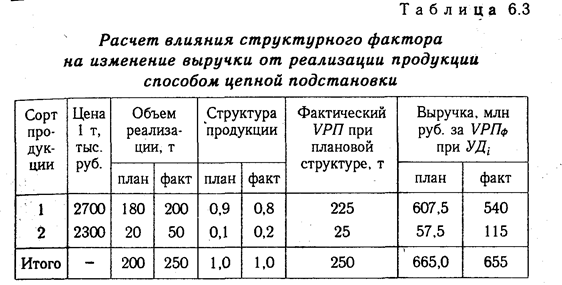
Отдельно необходимо остановиться на методике определения влияния структурного фактора на прирост результативного показателя с помощью этого способа. Например, выручка от реализации продукции (В) зависит не только от цены (Ц) и количества проданной продукции (VPH), но и от ее структуры (УДi). Если возрастет доля продукции высшей категории качества, которая продается по более высоким ценам, то выручка за счет этого увеличится, и наоборот. Факторная модель этого показателя может быть записана так:
В процессе анализа необходимо элиминироваться от воздействия всех факторов, кроме структуры продукции. Для этого сравниваем следующие показатели выручки:
Разность между этими показателями учитывает изменение выручки от реализации продукции за счет изменения ее структуры (табл. 6.3.).
Из таблицы видно, что в связи с увеличением удельного веса продукции второго сорта в общем объеме его реализации выручка уменьшилась на 10 млн руб. (655 — 665). Это неиспользованный резерв предприятия.
6.2. Индексный метод
Сущность и назначение индексного метода. Алгоритм расчета влияния факторов этим методом для разных моделей.
Индексный метод основан на относительных показателях динамики, пространственных сравнений, выполнения плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому или по другому объекту).
С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.
Для примера возьмем индекс стоимости товарной продукции:
Он отражает изменение физического объема товарной продукции (q) и цен (р) и равен произведению этих индексов:
Чтобы установить, как изменилась стоимость товарной продукции за счет количества произведенной продукции и за счет цен, нужно рассчитать индекс физического объема Iq и индекс цен 1p:
В нашем примере объем валовой продукции можно представить в виде произведения численности рабочих и их среднегодовой выработки. Следовательно, индекс валовой продукции 1вп будет равен произведению индекса численности рабочих lчр и индекса среднегодовой выработки 1гв:
Если из числителя вышеприведенных формул вычесть знаменатель, то получим абсолютные приросты валовой продукции в целом и за счет каждого фактора в отдельности, т.е. те же результаты, что и способом цепной подстановки.
6.3. Способ абсолютных разниц
Сущность, назначение и сфера применения способа абсолютных разниц. Порядок и алгоритмы расчета влияния факторов этим способом
Способ абсолютных разниц является одной из модификаций элиминирования. Как и способ цепной подстановки, он применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных и мультипликативно-аддитивных моделях: Y = (а — b)с и У = a(b — с). И хотя его использование ограничено, но благодаря своей простоте он получил широкое применение в АХД. Особенно эффективно применяется этот способ в том случае, если исходные данные уже содержат абсолютные отклонения по факторным показателям.
При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.
Рассмотрим алгоритм расчета для мультипликативной факторной модели типа Y=axbxcxd. Имеются плановые и фактические значения по каждому факторному показателю, а также их абсолютные отклонения:
Определяем изменение величины результативного показателя за счет каждого фактора:
Как видно из приведенной схемы, расчет строится на последовательной замене плановых значений факторных показателей на их отклонения, а затем на фактический уровень этих показателей.
Рассмотрим методику расчета влияния факторов этим способом для четырехфакторной мультипликативной модели валовой продукции:
Таким образом, способ абсолютных разниц дает те же результаты, что и способ цепной подстановки. Здесь также необходимо следить за тем, чтобы алгебраическая сумма прироста результативного показателя за счет отдельных факторов была равна общему его приросту.
Рассмотрим алгоритм расчета факторов этим способом в смешанных моделях типа V = (а — b)с. Для примера возьмем факторную модель прибыли от реализации продукции, которая уже использовалась в предыдущем параграфе:
П = VРП(Ц — С).
Прирост суммы прибыли за счет изменения объема реализации продукции:
цены реализации:
себестоимости продукции:
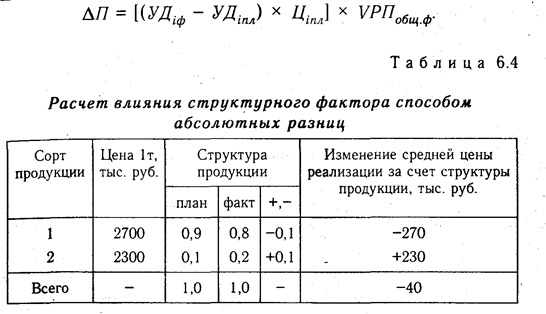
Расчет влияния структурного фактора при помощи этого способа проводится следующим образом:
Как видно из табл. 6.4, за счет изменения структуры реализации средняя цена за 1 т молока уменьшилась на 40 тыс. руб., а за весь фактический объем реализации продукции прибыли было получено меньше на 10 млн руб. (40 тыс. руб. х 250 т).
6.4. Способ относительных разниц
Сущность и назначение способа относительных разниц. Сфера его применения. Алгоритм расчета влияния факторов этим способом.
Способ относительных разниц, как и предыдущий, применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных и аддитивно-мультипликативных моделях типа V = (а — b)с. Он значительно проще цепных подстановок, что при определенных обстоятельствах делает его очень эффективным. Это прежде всего касается тех случаев, когда исходные данные содержат уже определенные ранее относительные приросты факторных показателей в процентах или коэффициентах.
Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа V = А х В х С. Сначала необходимо рассчитать относительные отклонения факторных показателей:
Тогда изменение результативного показателя за счет каждого фактора определяется следующим образом:
Согласно этому правилу, для расчета влияния первого фактора необходимо базисную (плановую) величину результативного показателя умножить на относительный прирост первого фактора, выраженного в процентах, и результат разделить на 100.
Чтобы рассчитать влияние второго фактора, нужно к плановой величине результативного показателя прибавить изменение его за счет первого фактора и затем полученную сумму умножить на относительный прирост второго фактора в процентах и результат разделить на 100.
Влияние третьего фактора определяется аналогично: к плановой величине результативного показателя необходимо прибавить его прирост за счет первого и второго факторов и полученную сумму умножить на относительный прирост третьего фактора и т.д.
Закрепим рассмотренную методику на примере, приведенном в табл. 6.1:
Как видим, результаты расчетов те же, что и при использовании предыдущих способов.
Способ относительных разниц удобно применять в тех случаях, когда требуется рассчитать влияние большого комплекса факторов (8-10 и более). В отличие от предыдущих способов значительно сокращается количество вычислений.
Разновидностью этого способа является прием процентных разностей. Методику расчета влияния факторов с его помощью рассмотрим на том же примере (табл. 6.1).
Для того чтобы установить, насколько изменился объем валовой продукции за счет численности рабочих, необходимо плановую его величину умножить на процент перевыполнения плана по численности рабочих ЧР%:
Для расчета влияния второго фактора необходимо умножить плановый объем валовой продукции на разность между процентом выполнения плана по общему количеству отработанных дней всеми рабочими D% и процентом выполнения плана по среднесписочной численности рабочих ЧР%:
Абсолютный прирост валовой продукции за счет изменения средней продолжительности рабочего дня (внутрисменных простоев) устанавливается путем умножения планового объема валовой продукции на разность между процентами выполнения плана по общему количеству отработанных часов всеми рабочими t% и общему количеству отработанных ими дней D%:
Для расчета влияния среднечасовой выработки на изменение объема валовой продукции необходимо разность между процентом выполнения плана по валовой продукции ВП% и процентом выполнения плана по общему количеству отработанных часов всеми рабочими t% умножить на плановый объем валовой продукции ВПпл:
Преимущество этого способа состоит в том, что при его применении не обязательно рассчитывать уровень факторных показателей. Достаточно иметь данные о процентах выполнения плана по валовой продукции, численности рабочих и количеству отработанных ими дней и часов за анализируемый период.
6.5. Способ пропорционального деления и долевого участия
Сущность, назначение и сфера применения способа пропорционального деления. Порядок и алгоритмы расчетов влияния факторов этим способом.
В ряде случаев для определения величины влияния факторов на прирост результативного показателя может быть использован способ пропорционального деления. Это касается тех случаев, когда мы имеем дело с аддитивными моделями типа V = 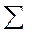
В первом случае, когда имеем одноуровневую модель типа V= а + b + с. расчет проводится следующим образом:
Например, уровень рентабельности снизился на 8% в связи с увеличением капитала предприятия на 200 млн руб. При этом стоимость основного капитала возросла на 250 млн руб., а оборотного уменьшилась на 50 млн руб. Значит, за счет первого фактора уровень рентабельности снизился, а за счет второго — повысился:
Методика расчета для смешанных моделей несколько сложнее. Взаимосвязь факторов в комбинированной модели показана на рис. 6.1.
Когда известны 
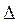
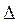
Величина коэффициента (К) определяется следующим образом:
Умножив этот коэффициент на абсолютное отклонение В за счет соответствующего фактора, найдем изменение результативного показателя:
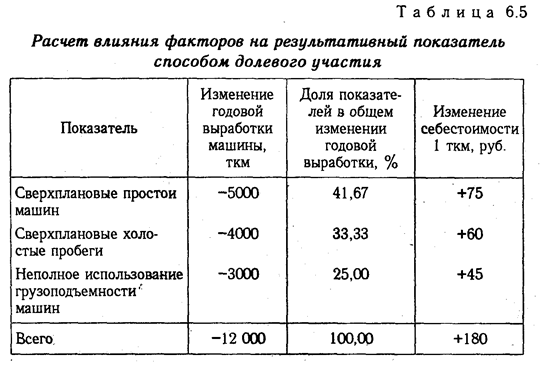
Например, себестоимость 1 ткм за счет снижения среднегодовой выработки автомобиля повысилась на 180 руб. При этом известно, что среднегодовая выработка автомашины снизилась из-за:
а) сверхплановых простоев машин -5000 ткм
б) сверхплановых холостых пробегов -4000 ткм
в) неполного использования грузоподъемности -3000 ткм
Всего-12000 ткм
Отсюда можно определить изменение себестоимости под влиянием факторов второго уровня:
Для решения такого типа задач можно использовать также способ долевого участия. Сначала определяется доля каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост результативного показателя (табл. 6.5):
Аналогичных примеров применения этого способа в АХД можно привести очень много, в чем вы сможете убедиться в процессе изучения отраслевого курса анализа хозяйственной деятельности предприятия.
6.6. Интегральный способ в анализе хозяйственной деятельности
Основные недостатки метода элиминирования. Проблема разложения дополнительного прироста от взаимодействия факторов между ними. Сущность интегрального метода и сфера его применения. Алгоритмы расчета влияния факторов в разных моделях интегральным способом.
Элиминирование как способ детерминированного факторного анализа имеет существенный недостаток. При его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом же деле они изменяются совместно, взаимосвязано и от этого взаимодействия получается дополнительный прирост результативного показателя, который при применении способов элиминирования присоединяется к одному из факторов, как правило к последнему. В связи с этим величина влияния факторов на изменение результативного показателя меняется в зависимости от места, на которое поставлен тот или иной фактор в детерминированной модели.
Рассмотрим это на примере, который дан в табл. 6.1. Согласно приведенным в ней данным, количество рабочих на предприятии увеличилось на 20%, производительность труда — на 25%, а объем валовой продукции — на 50%. Это значит, что 5% (50 — 20 — 25), или 8000 млн руб. валовой продукции составляет дополнительный прирост от взаимодействия обоих факторов.
Когда мы подсчитаем условный объем валовой продукции, исходя из фактического количества рабочих и планового уровня производительности труда, то весь дополнительный прирост от взаимодействия двух факторов относится к качественному фактору — изменению производительности труда:
Если же при расчете условного объема валовой продукции взять запланированное количество рабочих и фактический уровень производительности труда, то весь дополнительный прирост валовой продукции относится к количественному фактору, который мы изменяем во вторую очередь:
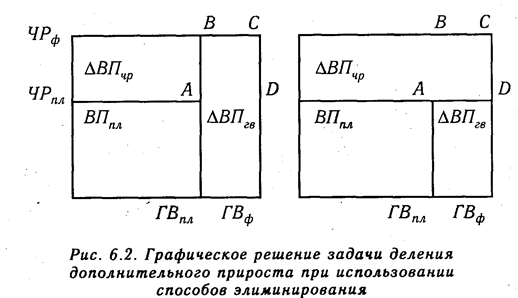
Покажем графическое решение задачи в разных вариантах (рис. 6.2).
В первом варианте расчета условный показатель имеет форму: ВПусл = ЧРф х ГВпл, во втором – ВПусл = ЧРпл х ГВф.
Соответственно отклонения за счет каждого фактора в первом случае
во втором
На графиках этим отклонениям соответствуют разные прямоугольники, так как при разных вариантах подстановки величина дополнительного прироста результативного показателя, равная прямоугольнику ABCD, относится в первом случае к величине влияния годовой выработки, а во –втором, к величине влияния количества рабочих. В результате этого величина влияния одного фактора преувеличивается, а другого — приуменьшается, что вызывает неоднозначность оценки влияния факторов, особенно в тех случаях, когда дополнительный прирост довольно существенный, как в нашем примере.
Чтобы избавиться от этого недостатка, в детерминированном факторном анализе используется интегральный метод, который применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида
Использование этого способа позволяет получать более точные результаты расчета влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния факторов потому, что в данном случае результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, который образовался от взаимодействия факторов, раскладывается между ними поровну.
На первый взгляд может показаться, что для распределения дополнительного прироста достаточно взять его половину или часть, соответствующую количеству факторов. Но это сделать чаще всего сложно, так как факторы могут действовать в разных направлениях. Поэтому в интегральном методе пользуются определенными формулами. Приведем основные из них для разных моделей.
В нашем примере (см. табл. 6.1) расчет проводится следующим образом:
Для расчета влияния факторов в кратных и смешанных моделях используются следующие рабочие формулы.
Таким образом, использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и сделать не очень сложные расчеты с помощью калькулятора или другой вычислительной техники. При этом достигается более высокая точность расчетов.
6.7. Способ логарифмирования в анализе хозяйственной деятельности
Сущность, сфера применения и отличительные черты способа логарифмирования. Алгоритмы расчета влияния факторов этим способом.
Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. В данном случае результат расчета, как и при интегрировании, не зависит от месторасположения факторов в модели и по сравнению с интегральным методом обеспечивается еще более высокая точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. В этом его преимущество, а недостаток — в ограниченности сферы применения.
В отличие от интегрального метода при логарифмировании используются не абсолютные приросты показателей, а индексы их роста (снижения).
Математически этот метод описывается следующим образом. Допустим, что результативный показатель можно представить в виде произведения трех факторов: f = хуz. Прологарифмировав обе части равенства, получим
Учитывая, что между индексами изменения показателей сохраняется та же зависимость, что и между самими показателями, произведем замену абсолютных их значений на индексы:
Из формул вытекает, что общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму индекса результативного показателя. И не имеет значения, какой логарифм используется — натуральный или десятичный.
Используя данные табл. 6.1, вычислим прирост валовой продукции за счет численности рабочих (ЧР), количества отработанных дней одним рабочим за год (Д) и среднедневной выработки (ДВ) по факторной модели:
Сравнив полученные результаты расчета влияния факторов разными способами по данной факторной модели, можно убедиться в преимуществе способа логарифмирования. Это выражается в относительной простоте вычислений и повышении точности расчетов.
Рассмотрев основные приемы детерминированного факторного анализа и сферу их применения, результаты можно систематизировать в виде следующей матрицы:
Знание сущности данных приемов, области их применения, процедуры расчетов — необходимое условие квалифицированного проведения количественных исследований.
Теория по эконометрике
Оценка влияния факторов на зависимую переменную (коэффициенты эластичности, бета–коэффициенты, дельта–коэффициенты)
Для экономического анализа уравнения регрессии используют:
1. Средний коэффициент эластичности
.
Он показывает, на сколько процентов изменяется в среднем Y при увеличении только фактора Xj на один процент.
2. С помощью бета-коэффициентов
можно упорядочить факторы по степени их влияния на Y: больший модуль бета-коэффициента соответствует более сильному влиянию.
3. Дельта–коэффициент
показывает долю влияния фактора Xj на результат Y в суммарном влиянии всех факторов, включенных в модель (где — коэффициент корреляции между Xj и Y).
Продолжение примера 3. По приведенным формулам были рассчитаны коэффициенты эластичности, бета- и дельта–коэффициенты:
|
Фактор |
j |
j |
j |
|
X1 |
0,892 |
0,571 |
0,532 |
|
X2 |
0,242 |
0,243 |
0,082 |
|
X3 |
— |
0,429 |
0,386 |
Видно, что при увеличении числа легких «грузовиков» на 1 % чистая годовая прибыль возрастает в среднем на 0,892 %, а при увеличении числа тяжелых «грузовиков» на 1 % — в среднем на 0,242 %. Интерпретация коэффициента эластичности фиктивных переменных лишена смысла.
По бета–коэффициентам видно, что изменение числа легких «грузовиков» наиболее сильно влияет на изменение прибыли.
В суммарном влиянии на прибыль доля влияния числа легких «грузовиков» составляет 53,2 %, тяжелых — 8,2 %, формы собственности 38,6 %.