Как найти дополнение для графа

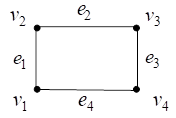
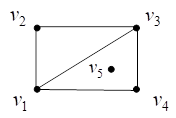
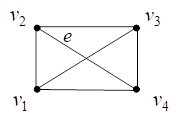
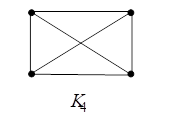
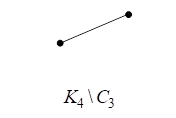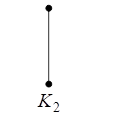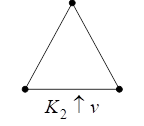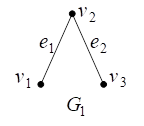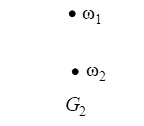Consider a set A and U denotes the universal set then complement of set A can be found by

Ac =U-A.

But, a graph G(v, e) is a set of vertices and edges, is it possible to find the Complement of a graph? This question is answered below. 

Complement of Graph

The complement of a graph G is a graph G’ on the same set of vertices as of G such that there will be an edge between two vertices (v, e) in G’, if and only if there is no edge in between (v, e) in G.

Complement of graph G(v, e) is denoted by G'(v, e’).

Note: The number of vertices remains unchanged in the complement of the graph.

Example:

In the above example in graph G there is a edge between (a, d),(a, c),(a, d).
Complement of Graph G is G' having edges between (a, b),(b, c),(b, d). 

Properties of Complemented Graph

1. If E be the set of edges of graph G’ then E(G’)={ (u, v) | (u, v) ∉ E(G) }

2. Union of graph G and its complement G’ will give a complete graph(K_n).

3. The intersection of two complement graphs has no edges, also known as null graph

4. If G is a disconnected graph then its complement G’ would be a connected graph.

5. Order of a Graph and its Complement are Same. The order of the graph is the number of vertices in it.

Example:

Order of a graph G on a set of vertices is given by G={a, b, c, d, e} is number of vertices in the graph G i.e., 5.

6. Size of a Graph and its complement cannot be the same. The size of a graph is the number of edges in it.

Example:

Size of a graph G on the set of edges is G= {(b, d), (c, e) } is the number of edges in the graph i.e., 2.

Note:

1. If G be a graph with edges E and K_n denoting the complete graph, then the complement of graph G can be given by

E(G') = E(Kn)-E(G).

2. The sum of the Edges of a Complement graph and the main graph is equal to the number of edges in a complete graph, n is the number of vertices.

E(G')+E(G) = E(Kn) = n(n-1)÷2.

Practice Questions:

Question 1. Consider a simple graph G, where E denotes the edges and V denotes the vertices |E(G)|= 30, |E(G’)|= 36. Find |V(G)|=?

Solution: 

        We know,
        E(G')+E(G)=E(Kn)=n(n-1)÷2.
        ⇒ 36+30=n(n-1)÷2
        ⇒ 66=n(n-1)÷2
        ⇒ 66×2=n2-n
        ⇒ n2-n-132=0
        ⇒ n2-12n+11n-132=0
        ⇒ n(n-12)+11(n-12)=0
        ⇒ (n-12)(n+11)=0
Therefore, n=12 and n=-11.
Since vertices cannot be negative
n=12.

Question 2. Consider a simple graph G, where E denotes the edges and V denotes the vertices |E(G)|= 12, |V(G)|= 8. Find the number of edges in complement graph |E(G’)|= ?.

Solution: 

       We know,
       E(G')+E(G)=E(Kn)=n(n-1)÷2.
       ⇒ E(G') + 12 =8(8-1)÷2      [here n denotes number of vertices, i.e. given 8]
       ⇒ E(G')+12 = 8(7)÷2
       ⇒ E(G')+12= 4×7
       ⇒ E(G')+12=28
       ⇒ E(G')=28-12
       ⇒ E(G')=16.

Last Updated :
04 Feb, 2022

Like Article

Save Article

91

Удаление вершины
из графаGприводит к
подграфу
,
содержащему все вершины графаG,
за исключением
,
и все рёбра графаG, не
инцидентные
.
Другими словами,
есть максимальный подграф графаG,
не содержащий
.

Удаление ребра e_jиз графаGприводит к
остовному подграфу, содержащему все
рёбра графаG, за исключениемe_j,
т.е.G–e_jесть максимальный подграф графаG,
не содержащийe_j.

Удаление произвольного множества вершин
или рёбер из Gопределяется
как последовательное удаление всех
элементов этого множества.

Если

и

не смежны вG, тодобавление
ребра
()
образует наименьший надграф графаG,
содержащий ребро
().

Эти понятия иллюстрируются на рис.
2.2.1.

Рис. 2.2.1

Существуют
графы, для которых результат удаления
вершины или ребра, а также добавления
ребра не зависит от выбора вершины или
ребра. Для графаG,
обладающего этим свойством, обозначим
соответствующие графы черезG–v,G+e, см. рис. 2.2.2.

Рис.
2.2.2

Введём операцию подразделения ребра
графаG(V,E).
Пусть
– произвольное ребро этого графа
иw– некоторый объект,
не принадлежащий множествуV.
Операция подразделения ребра
заключается
в построении графа
,
множество вершин которого
,
а множество рёбер
содержит все рёбра исходного графа, за
исключением выделенного ребра
,
и два дополнительных новых ребра:

Граф
называетсяподразделением графа
,
если он может быть получен из графа

путём применения конечного числа
операций подразделения рёбер.

Обратная подразделению ребра графа
операциясостоит в замене двух рёбер,
инцидентых вершине второй степени,
одним ребром при удалении этой вершины.

Графы

и

называются
гомеоморфными
(обозначение
G₁G₂),
если существуют такие их подразделения,
которые изоморфны. Другими словами, два
графа гомеоморфны, если они изоморфны
с точностью до вершин второй степени.
На рис. 2.2.3 изображены два неизоморфных
графа

и
.
Эти графы гомеоморфны, т.к. каждый из
них может быть подразделён до графа G.

Рис. 2.2.3

Естественно
стремиться представить структуру
рассматриваемого графа с помощью графов
меньшего размера и более простой
структуры. Операции над графами позволяют
образовывать новые графы из нескольких
более простых.

Дополнение графа

ПустьG(V,E)
– обыкновенный граф. Дополнение


графа G
(также обыкновенный граф) имеет в качестве
множества вершин множество V,
любые две несовпадающие вершины в

смежны тогда и только тогда, когда они
не смежны в G.
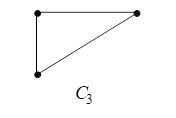
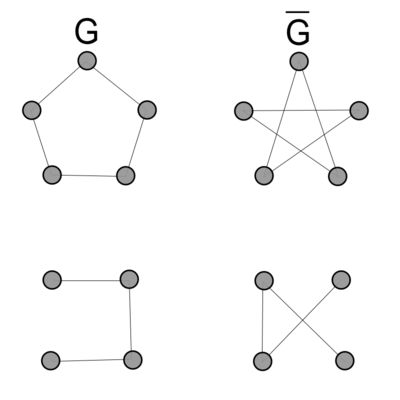
На рис. 2.2.4 изображены графы
,


и их дополнения

и

соответственно.

Рис. 2.2.4

Очевидно,
что

и

тогда и только тогда, когда
.

Граф,
изоморфный своему дополнению, называетсясамодополнительным.
Например,

и граф, изображённый на рис. 2.2.5, –
самодополнительные.

Рис. 2.2.5

Теорема
2.2.1. Пусть G
– обыкновенный граф с матрицей смежности
вершин А. Тогда матрицей смежности
вершин графа

является матрица
,
образованная поэлементным логическим
отрицанием матрицы А, исключая диагональные
элементы, которые остаются нулевыми.

Если
число вершин графа G
равно p,
то матрицы А и

имеют одинаковую размерность
.
Если G
– неориентированный обыкновенный граф,
то элемент

()
матрицы А равен 1, если вершины

и

смежны, и 0
в противном случае. Так как

и

()
смежны в
тогда
и только тогда, когда они не смежны в G,
то

равно 1 (0) в

тогда и
только тогда, когда

равно 0 (1) в А.

Если
G
– обыкновенный орграф, то элемент

()
матрицы А равен 1, если существует дуга

в G,
и 0 в противном случае. Элемент
()
в

равен 1 (0) тогда и только тогда, когда не
существует (существует) дуга

в G,
т.е. элемент

равен 0 (1) в
А.

в
А и

в
,
т. к. G
и

– обыкновенные графы.

Пример
2.2.1. Матрицы
смежности вершин А графа

и

графа
,
изображённых на рис. 2.2.4, имеют вид:

,
.

Правильность
построения матрицы

можно легко проверить по рис. 2.2.4.

Соседние файлы в папке конспектик

• #
• #
• #
• #
• #
• #

Дополнение графа (обратный граф) — граф [math]displaystyle{ G’ }[/math], имеющий то же множество вершин, что и заданный граф [math]displaystyle{ G }[/math], но в котором две несовпадающие вершины смежны тогда и только тогда, когда они не смежны в [math]displaystyle{ G }[/math].

Формально для простого графа [math]displaystyle{ G=(V,E) }[/math] и [math]displaystyle{ K=mathcal P(V^2) }[/math] — множества всех двухэлементных подмножеств его вершин — дополнение [math]displaystyle{ G’ }[/math] определяется как пара [math]displaystyle{ (V,K setminus E) }[/math] — граф с исходным набором вершин и с набором ребёр, полученным из полного графа удалением имевшихся в заданном графе.

Дополнение пустого графа (содержащего только вершины, но не рёбра) является полным графом, и наоборот. Независимое множество графа является кликой в дополнении графа, и наоборот. Дополнение любого графа без треугольников не содержит клешней.

Самодополнительный граф — это граф, который изоморфен своему дополнению. Кографы определяются как графы, которые можно построить из единственной точки несвязанным объединением и операцией дополнения. Кографы образуют семейство самодополнительных графов — дополнение любого кографа является другим (возможно, отличным от исходного) кографом.

Литература

• Харари Ф. Теория графов. — 2-е издание. — М.: УРСС, 2003. — 295 с. — ISBN 5-354-00301-6.

Определение. Дополнением графа называется такой граф , в котором две вершины смежны тогда и только тогда, когда они не смежны в .

Граф имеет те же вершины, что и граф . Граф имеет те и только те рёбра, которые добавляются в граф , чтобы он стал полным.

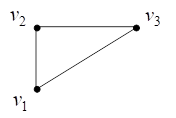
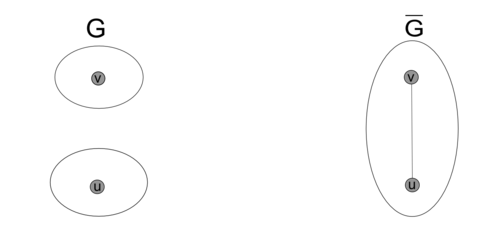
Например, на рис. 9 представлена диаграмма дополнения графа на рис. 1.

Рис. 9. Дополнение

Определение. Объединением графов и , не имеющих общих вершин и ребер, называется граф .

Граф содержит вершины и ребра, принадлежащие хотя бы одному из графов.

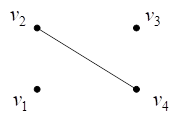
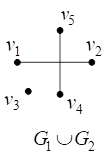
Например, на рис. 10 представлены диаграммы графов и и диаграмма их объединения .

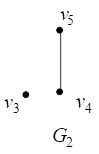
Рис. 10. Объединение графов

Определение. Соединением Графов и , не имеющих общих вершин и ребер, называется граф .

Граф соединения графов и содержит вершины и рёбра, принадлежащие хотя бы одному из графов и , и рёбра, соединяющие каждую вершину с каждой вершиной .

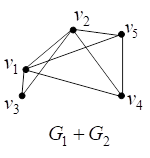
Например, на рис. 11 представлены диаграммы графов и и диаграмма их соединения .

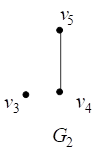
Рис. 11. Соединение графов

Определение. Удалением вершины графа называется операция, состоящая в удалении этой вершины Вместе с инцидентными ей ребрами.

Для обозначения удаления вершины графа используется символ .

Например, На рис. 12 представлен результат удаления вершины графа на рис. 1.

Рис. 12. Диаграмма графа

Определение. Удалением ребра графа называется операция удаления этого ребра при сохранении всех вершин графа.

Для обозначения удаления ребра графа используется символ .

Например, на рис. 13 представлен результат удаления ребра графа на рис. 1.

Рис. 13. Диаграмма графа

Определение. Добавлением новой вершины графа называется операция добавления этой вершины к множеству вершин , при сохранении всех ребер графа .

Для обозначения добавления новой вершины графа используется символ .

Например, на рис. 14 представлен результат добавления вершины графа на рис. 1.

Рис. 14. Диаграмма графа

Определение. Добавлением нового ребра графа называется операция добавления этого ребра к множеству ребер , при сохранении всех вершин .

Для обозначения добавления нового ребра графа используется символ .

Например, На рис. 15 представлен результат добавления ребра графа на рис. 1.

Рис. 15. Диаграмма графа

Определение. Стягиванием Подграфа графа называется операция, состоящая в следующем:

1) нахождение множества ;

2) нахождение множества ;

3) добавление к множеству новой вершины;

4) добавление к множеству новых ребер, инцидентных новой вершине и соединяющих новую вершину с оставшимися старыми вершинами.

Для обозначения стягивания подграфа графа используется символ .

Например, На рис. 16 представлены диаграммы графов и и диаграмма стягивания подграфа графа .

Рис. 16. Диаграмма графа

Определение. Размножением вершины графа называется операция, состоящая в следующем:

1) удаление из графа вершины вместе с инцидентными ей ребрами;

2) добавление пары новых вершин вместе с соединяющим их ребром;

3) соединение каждой из новых вершин с другими вершинами.

Для обозначения размножения вершины графа используется символ .

Например, На рис. 17 представлена диаграмма графа и диаграмма размножения его вершины.

Рис. 17. Диаграмма графа

Задачи и упражнения

30. Определите типы графов на рис. 23 и на
рис. 24.

31. Графы и заданы диаграммами:

Постройте диаграммы следующих графов, являющихся результатами операций над графами и :

1) , ;

2) , , , ;

3) , , , ;

4) , , ;

5) , ;

6) , , , ;

7) , , , ;

, где , , Æ;

9) .

32. Постройте диаграммы следующих графов, являющихся результатами операций над графами и задачи 4.1:

1) , ;

2) , , , ;

3) , , , ;

4) , , ;

5) , ;

6) , , , ;

7) , , , ;

, где , , Æ;

9) .

< Предыдущая		Следующая >

Дополнительный граф

<wikitex>

Определение:

Пусть дан граф . Дополнительным графом (англ. complement graph) к $G$ называется граф то есть граф с вершинами из $V$ и теми и только теми ребрами из $E$, которые не вошли в $G$.

Пример графа с 6-ю вершинами и его дополнение.

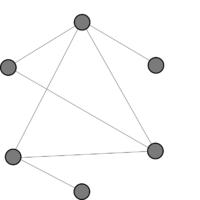
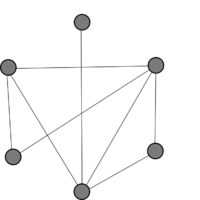
Теорема:

Дополнительный граф к дополнительному графу $G$ есть граф $G$.

Доказательство:

Теорема:

В дополнительном графе к . количество ребер равняется .

Доказательство:

Так как множества ребер в $G$ и $overline{G}$ дизъюнктны, то $leftvert E rightvert + leftvert overline{E} rightvert =$ , из чего следует утверждение теоремы.

Теорема:

Дополнительный граф к несвязному графу связен.

Доказательство:

Для графа с одной вершиной утверждение очевидно. Докажем его для остальных графов. Пусть $G$ — данный граф. Рассмотрим произвольные вершины $v$ и $u$ из $G$. Возможны два случая: $v$ и $u$ лежат в одной или в разных компонентах связности. Пусть $v$ и $u$ лежат в разных компонентах связности $G$. Тогда ребро $(u, v) notin G Rightarrow (u, v) in overline{G} Rightarrow u$ и $v$ лежат в одной компоненте связности $overline{G}$. Пусть $v$ и $u$ лежат в одной компоненте связности $G$. $G$ — несвязный $Rightarrow exists w in G$, не лежащая в одной компоненте связности с $v$ и $u$. Тогда по предыдущему пункту $(v, w) in overline{G}$ и $(u, w) in overline{G} Rightarrow v$ и $u$ лежат в одной компоненте связности $overline{G}$. То есть $forall u, v in V$ $u$ и $v$ лежат в одной компоненте связности $overline{G}$, то есть $overline{G}$ связен.

Самодополнительный граф

Определение:

Самодополнительным графом (англ. self-complement) называется граф, изоморфный своему дополнительному.

Теорема:

Любой самодополнительный граф имеет $4k$ или $4k + 1$ вершину.

Доказательство:

Обозначим $leftvert V rightvert$ за $n$, $leftvert E rightvert$ за $a$. Граф самодополнителен $Rightarrow$ количество его ребер равно количеству ребер в его дополнении. Но по одной из предыдущих теорем, $- a = leftvert overline{E} rightvert = a Rightarrow 4a = n cdot left ( n — 1 right )$, из чего следует утверждение теоремы.

Теорема:

Для любых $k > 0$ существует самодополнительный граф с $4k$ или $4k + 1$ вершиной.

Доказательство:

Будем доказывать по индукции. Для $k = 1$ утверждение справедливо. Пусть у нас есть самодополнительный граф $G$ с $n$ вершинами, построим самодополнительный граф с $n + 4$ вершинами. Добавим к $G$ 4 вершины $v_1, v_2, v_3, v_4$ и ребра: Добавим ребра $(v_1, v_2), (v_2, v_3), (v_3, v_4)$ Если $u$ была вершиной в $G$, добавим ребра $(u, v_1), (u, v_4)$ Назовем полученный граф $A$. Докажем, что $A$ самодополнителен. Рассмотрим биекцию на множестве вершин $A$ и $overline{A}$: Среди всех вершин, принадлежавших $G$ биекция будет такая же, как и у $G$ с $overline{G}$; $v_1 rightarrow v_2, v_2 rightarrow v_4, v_3 rightarrow v_1, v_4 rightarrow v_3$. Тогда между ребрами $A$ и $overline{A}$ тоже будет биекция.

</wikitex>

См. также

• Основные определения теории графов
• Отношение связности, компоненты связности

Источники информации

• Харари Ф. Теория графов. /пер. с англ. — изд. 2-е — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
• Википедия — дополнение графа
• Википедия — самодополнительный граф