Порой обучение продвигается с трудом. Сложная теория, непонятные задания… Хочется бросить. Не сдавайтесь, все сложности можно преодолеть. Рассказываем, как
Не понятна формулировка, нашли опечатку?
Выделите текст, нажмите ctrl + enter и опишите проблему, затем отправьте нам. В течение нескольких дней мы улучшим формулировку или исправим опечатку
Что-то не получается в уроке?
Загляните в раздел «Обсуждение»:
- Изучите вопросы, которые задавали по уроку другие студенты — возможно, ответ на ваш уже есть
- Если вопросы остались, задайте свой. Расскажите, что непонятно или сложно, дайте ссылку на ваше решение. Обратите внимание — команда поддержки не отвечает на вопросы по коду, но поможет разобраться с заданием или выводом тестов
- Мы отвечаем на сообщения в течение 2-3 дней. К «Обсуждениям» могут подключаться и другие студенты. Возможно, получится решить вопрос быстрее!
Подробнее о том, как задавать вопросы по уроку
Если заданы два
множества, то можно не только найти их
пересечение и объединение, но и вычесть
из одного множества другое. Результат
вычитания называют разностью и
определяют следующим образом.
Определение.
Разностью множеств А и В называют
множество, содержащее все элементы,
которые принадлежат множеству А и не
принадлежат множеству В.
Разность множеств
А и В обозначают А В. По определению: А
В ={х/х∈А
и х∉В}.
В школьном курсе
математики чаще всего приходится
выполнять вычитание множеств в случае,
когда одно из них является подмножеством
другого, при этом разность множеств А
В называют дополнением множества В
до множества А, и обозначают символом
В´А,
а наглядно изображают так:
Определение:
Пусть В⊂ А.
Дополнением множества В до множества
А называется множество, содержащее все
элементы множества А, которые не
принадлежат множеству В.
По определению:
В´А
={х/х∈А
и х∉В}.
Выясним, как
находить дополнение подмножества на
конкретных примерах.
Если элементы
множеств А и В перечислены и В ⊂
А, достаточно перечислить элементы,
принадлежащие множеству А и не
принадлежащие множеству В. Например, А
= {1, 2, 3, 4, 5}, В = {2, 4}, то В´А
= {1, 3, 5}.
В том случае, когда
указаны характеристические свойства
элементов множеств А и В и известно, что
В ⊂ А, то
множество В´А
задают также с помощью характеристического
свойства, общий вид которого «х∈А
и х∉В».
Так, если А – множество четных чисел, а
В – множество кратных 4 чисел, то В´А
— это множество, содержащее такие
четные числа, которые не делятся на 4.
Например, 22∈
В´А.
Вычитание–
это третья операция над множествами.
Условились считать, чтопересечение
– более «сильная» операция, чем вычитание.Что касается вычитания и объединения,
то их считают равноправными.
Вычитание множеств
обладает рядом свойств. В частности
можно доказать, что для любых множеств
А, В и С справедливы следующие равенства:
1) (А
В) С =
(А С) В);
2)
(А∪ В)
С = (А С)∪ (В
С);
-
(А
В)∩ С
= (А∩ С)
(В∩ С); -
А
(В∪ С)
= (А В)
∩(А С); -
А
(В∩ С)
= (А В)
∪(А С).
8. Понятие разбиения множества на классы с помощью одного, двух, трех свойств
Понятия множества
и операций над множествами позволяют
уточнить наше представление о классификации
– действии распределения объектов по
классам.
Классификацию мы
выполняем достаточно часто. Так,
натуральные числа представляем как два
класса – четные и нечетные. Углы на
плоскости разбиваем на три класса:
прямые, острые и тупые.
Любая классификация
связана с разбиением некоторого множества
объектов на подмножества. При этом
считают, что множество Х разбито на
классы Х₁, Х₂,
…, Хn,…, если:
-
подмножества Х₁,
Х₂, …, Хn,…
попарно не пересекаются; -
объединение
подмножеств Х₁,
Х₂, …, Хn,
… совпадает с множеством Х.
Если не выполнено
хотя бы одно из условий, классификацию
считают неправильной. Например, если
из множества Х треугольников выделить
подмножества равнобедренных, равносторонних
и разносторонних треугольников, то
разбиения мы не получим, поскольку
подмножества равнобедренных и
равносторонних треугольников пересекаются
(все равносторонние треугольники
являются равнобедренными). В данном
случае не выполнено первое условие
разбиения множества на классы.
Так как разбиение
множества на классы связано с выделением
его подмножеств, то классификацию можно
выполнять при помощи свойств элементов
множеств.
Рассмотрим,
например, множество натуральных чисел.
Его элементы обладают различными
свойствами.
Положим,.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000что нас интересуют числа, обладающие
свойством «быть кратным 3». Это свойство
позволяет выделить из множества
натуральных чисел подмножество, состоящее
из чисел, кратных 3. Тогда про остальные
натуральные числа можно сказать, что
они не кратны 3, т.е. получаем еще одно
подмножество множества натуральных
чисел. Так как выделенные подмножества
не пересекаются, а их объединение
совпадает с множеством натуральных
чисел, то имеем разбиение этого множества
на два класса.
NN
Вообще, если на
множестве Х задано одно свойство, то
это множество разбивается на два класса.
Первый – это класс объектов, обладающий
этим свойством, а второй – дополнение
первого класса до множества Х. Во втором
классе содержатся такие объекты множества
Х, которые заданным свойством не обладают.
Такую классификацию называют
дихотомической.
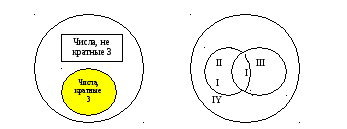
Рассмотрим ситуацию,
когда для элементов множества заданы
два свойства. Например, «быть кратным
3» и «быть кратным 5». При помощи этих
свойств из множества натуральных чисел
можно выделить два подмножества: А –
подмножество чисел, кратных 3, и В –
подмножество чисел, кратных 5. Эти
множества пересекаются, но ни одно из
них не является подмножеством другого.
Проанализируем получившийся рисунок
(справа). Конечно, разбиения множества
натуральных чисел на подмножества А и
В не произошло. Но круг, изображающий
множество N, можно
рассматривать как состоящий из четырех
непересекающихся областей – на рисунке
они пронумерованы. Каждая область
изображает некоторое подмножество
множестваN. ПодмножествоIсостоит из чисел, кратных
3 и 5; подмножествоII– из
чисел, кратных 3 и не кратных 5; подмножествоIII– из чисел, кратных 5
и не кратных 3; подмножествоIY– из чисел, не кратных 3 и не кратных 5.
Объединение этих четырех подмножеств
есть множествоN.
Таким образом,
выделение двух свойств привело к
разбиению множества Nнатуральных чисел на четыре класса.
Не следует думать,
что задание двух свойств элементов
множества всегда приводит к разбиению
этого множества на четыре класса.
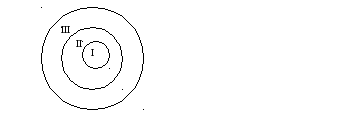
Например, при помощи двух таких свойств
«быть кратным 3» и «быть кратным 6»
множество натуральных чисел разбивается
на три класса: I– класс
чисел, кратных 6;II– класс
чисел, кратных 3; но не кратных 6;III- класс чисел, не кратных 3.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Дополнение | Теория множеств
Зарегистрируйтесь для доступа к 15+ бесплатным курсам по программированию с тренажером
Прежде чем мы определим, что такое дополнение множества, вспомним определения универсального множества и подмножества — эти термины будут часто использоваться в этом уроке. Универсальное множество — это множество всех элементов, которые рассматриваются в конкретной задаче или ситуации.
Допустим, нам нужно найти все целые числа, которые удовлетворяют неравенству
. В этой задаче множество целых чисел
является универсальным множеством. Ответ
является подмножеством универсального множества.
Допустим, у нас есть множество
, которое является подмножеством некоторого универсального множества
. Дополнение
— это множество элементов универсального множества, которые не являются элементами
. В нашем примере выше, дополнение
— это множество, содержащее все целые числа, которые не удовлетворяют неравенству.
Мы можем проиллюстрировать это определение на новом примере.
Если нашим универсальным множеством являются города России, то возможным подмножеством является множество городов миллионников:
Москва, Санкт-Петербург, Новосибирск, Екатеринбург, Казань, Нижний Новгород, Челябинск, Самара, Уфа, Ростов-на-Дону, Омск, Волгоград, Воронеж, Краснодар, Красноярск, Пермь
.
Тогда дополнением
будет множество, содержащее все остальные города, которые не являются миллионниками.
Существуют различные способы обозначения дополнения множества с помощью нотации. Например, можно использовать знак простого числа. Иногда используется надстрочная строчная буква
. Над именем исходного множества может стоять черточка или символ подчеркивания.
В этом уроке мы подробно рассмотрим дополнение множества, его определение и свойства.
Что такое дополнение множества?
Если универсальное множество
имеет подмножество
, то дополнение множества
(представляется как
), является отличным от элементов множества
, которое включает элементы универсального множества, но не элементы множества
.
Это тождество можно записать так:
Другими словами, дополнение множества
— это разность между универсальным множеством и множеством
.
Условные обозначения
Дополнение любого множества представляется как
и т.д. Другими словами, если задано универсальное множество
и подмножество универсального множества
, то разность универсального множества
и подмножества универсального множества
является дополнением подмножества, то есть
.
Если универсальным множеством являются все простые числа до
, а множество
, то дополнение множества
отлично от элементов
. Рассмотрим на таком примере:
Диаграмма
Для лучшего понимания посмотрите на приведенную ниже диаграмму Венна, которая ясно показывает дополнение множества
, то есть
:
Здесь
не является частью множества
, и множество
также не является частью
.
и
являются подмножествами
.
Свойства дополнения множества
Ниже перечислены свойства дополнения множества, которые включают в себя:
-
Законы дополнения
-
Закон двойного дополнения
-
Закон пустого множества
-
Закон универсального множества
Законы дополнения
-
Если
является подмножеством универсального множества, то
также является подмножеством универсального множества.Поэтому объединение
и
является универсальным множеством, представленным как -
Пересечение множеств
и
дает пустое множество »
«, представленное как
Рассмотрим на такое примере:
-
Если
и
и -
и
-
Кроме того,
Закон двойного дополнения
-
Дополнением дополненного множества является исходное множество
-
Дополнение множества
, где само
является дополнением
, двойное дополнение
, таким образом, является самим
В предыдущем примере
и
, тогда
.
Дополнение
, что равно множеству
.
Закон для пустого множества и универсального множества
-
Дополнением универсального множества является пустое множество или нулевое множество (
), а дополнением пустого множества — универсальное множество -
Поскольку универсальное множество содержит все элементы, а пустое множество не содержит никаких элементов, следовательно, их дополнения прямо противоположны друг другу, что представляется как
И
В примере выше, множество
содержит все элементы множества
, а множество
как универсальное множество содержит все элементы, поэтому
(пустое множество) и
.
Выводы
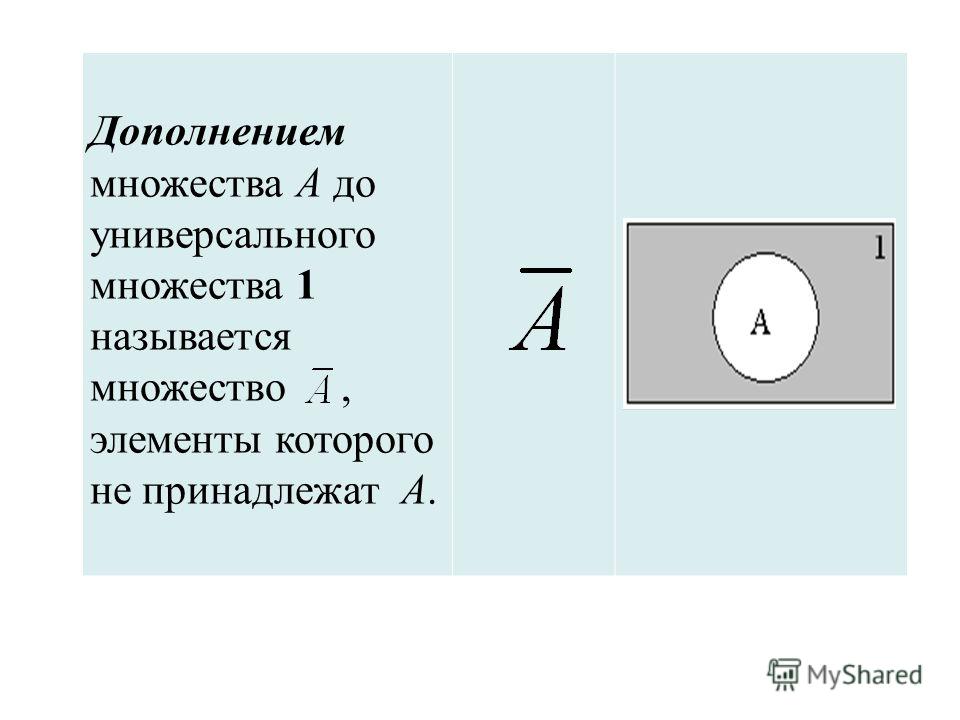
Универсальное множество. Дополнение множества до универсального множества.
В
конкретных математических областях
бывает полезно ввести в рассмотрение
столь обширное множество I,
что все рассматриваемые множества
окажутся его подмножествами. Такое
множество I
принято называть универсальным
множеством или универсумом.
Если выбрано некоторое универсальное
множество I,
то возникает новая теоретико-множественная
операция — дополнение. Для всякого
множества М (при этом подразумевается,
что М — подмножество универсального
множества I его
дополнение, обозначаемое через М,
— это множество всех элементов
универсума, которые не принадлежат
множеству М:
М
= {х | х
I и
x
M}
Таким
образом, дополнение — это частный
случай разности:
M
= I
M,
все отличие здесь состоит в том,
что разность берется относительно
фиксированного множества, содержащего
все множества, которые в данной связи
рассматриваются.
-
Объединение,
пересечение и вычитание множеств.
а) Пересечением
множеств М и N называют
множество тех объектов, которые
принадлежат множествам М и N одновременно.
Обозначение:
М
N
= {х|х
М
и х
N}.
б) Объединением
множеств М и N называют
множество тех элементов, которые
содержатся по крайней мере в одном из
множеств М или N. Обозначение: M
N
= {х | х
М
или х
N}.
в) Разностью
множеств М и N называют
множество тех элементов, которые
принадлежат множеству М и не принадлежат
множеству N. Обозначение: М N. = {х | х
М
и х
N}.
Свойства
операций над множествами.
1.
A U B = B U A — коммутативность . A
n B = B n A
2.
(A U B) U C = A U (B U C), A n (B n C) = (A n B) n C —
ассоциативность.
3.
(A U B) n C = (A n C) u (B n C), (AnB) U C = (A U C) n (B U C) —
дистрибутивность.
4.
Поглощение A U A = A, A n A = A.
5.
Существование универсальных границ.
А
U 0 = A A n 0 = 0 A u U = U A n U = A
6.
Двойное
дополнение A =
A
7.
A
U A =
U A n A =
0
8.
Законы двойственности или закон Де —
Моргана
(AUB) = A n B
(AnB) = A U B
Пусть
и
—
множества. Выражение вида
,
где
и
,
называется упорядоченной
парой.
Равенство вида
означает,
что
и
.
В общем случае, можно рассматриватьупорядоченную
n-ку
из
элементов
.
Упорядоченные n-ки иначе
называютнаборы или кортежи.
Определение
4. Декартовым
(прямым) произведением множеств
называется
множество упорядоченных n-ок (наборов,
кортежей) вида
Определение
5. Степенью
декартового произведения
называется
число множеств n, входящих в это декартово
произведение.
Замечание.
Если все множества
одинаковы,
то используют обозначение
-
Бинарные
отношения между элементами множеств.
Граф и график отношения.
Способы задания
отношения.
Для
строгого математического описания
любых связей между элементами двух
множеств вводится понятие бинарного
отношения, которое часто появляется
как в математике, так и в информатике.
Отношения между элементами нескольких
множеств (n-арные
отношения) применяются для описания
простой системы управления базами
данных.
Отношением (бинарным
отношением, двуместным отношением) из
множества A в
множество B называется
некоторое подмножество декартового
произведения
Отношения
в
дальнейшем
будем обозначать
(читается
отношение
из A в B)
Если
,
и
,
то говорят, что a находится
в отношении с b
.
Используется также запись
.
Есть два способа задания отношения –
перечиление всех пар и задание
характеристического свойства отношения.
граф-рисунок,
график с осью х и у
-
Отношении,
обратное и противоположное к данному
отношению.
Обратное
отношение
(отношение, обратное к R) — это
двухместное отношение, состоящее из
пар элементов (у, х), полученных
перестановкой пар элементов (х, у)
данного отношения R. Обозначается: R−1.
Для данного отношения и обратного ему
верно равенство: (R−1)−1 = R.
Взаимо-обратные
отношения (взаимообратные отношения)
— отношения, являющиеся обратными друг
по отношению к другу. Область значений
одного из них служит областью определения
другого, а область определения первого
— областью значений другого.
9.Основные
свойства отношений на множестве.
Пусть
,
т.е.
—
бинарное отношение на множестве A.
1) рефлексивное
отношение, если для
всякого элемента из
множества А пара (а,а) принадлежит
отношению
,
что означает что всякий элемент из
множества А находится в отношении сам
с собой.2)
симметричное отношение,
если для всяких элементов из множества
А, если одна пара принадлежит
отношению , то и другая
пара принадлежит отношению ,
что означает что если элемент a находится
в отношении c b,
то и элемент b находится
в отношении c a.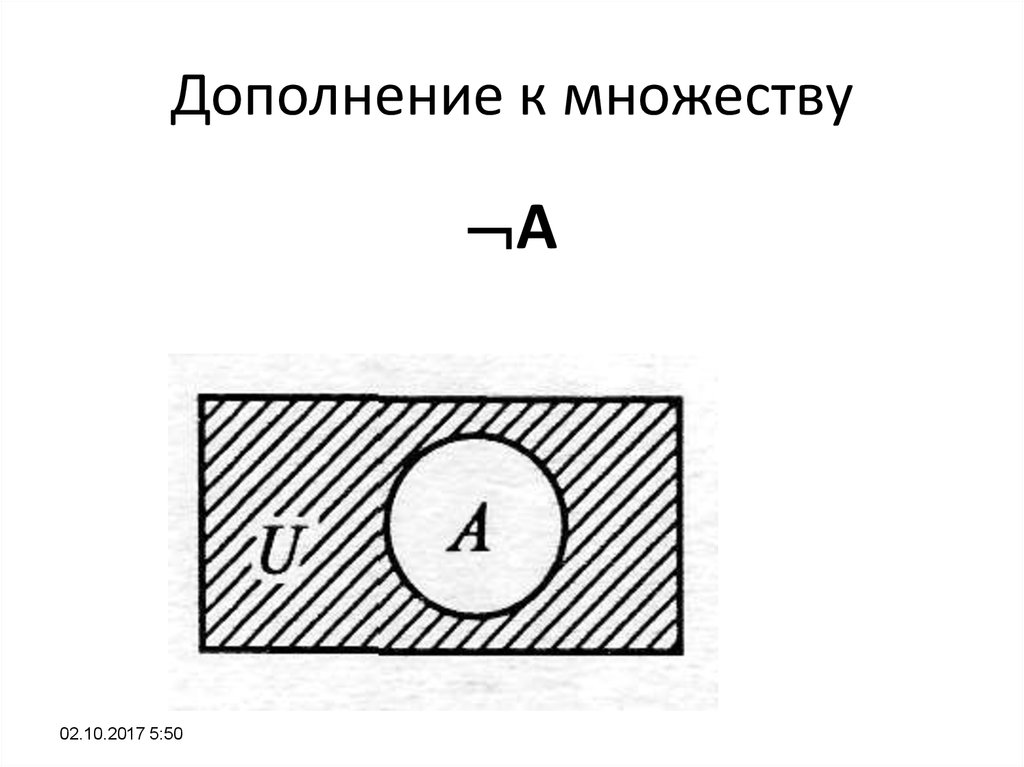
антисимметричное отношение,
если для всяких элементов из
множества А, если
пара принадлежит
отношению и пара принадлежит
отношению , то , что означает
что отношение не может содержать
пару одновременно с парой ,
если элемент
a отличен
от элемента b.4)
транзитивное отношение,
если для всяких элементов из множества
А, если пара принадлежит отношению и
пара принадлежит отношению ,
то и пара принадлежит отношению ,
что означает что если элемент a находится
в отношении c b и
элемент b находится
в отношении c с,
то и элемент a находится
в отношении c с.5)
полное или линейное отношение,
если для всяких элементов из множества А,
если , то пара принадлежит
отношению или пара принадлежит
отношению , что означает что для
любых двух различных элементов a находится
в отношении c b или
элемент b находится
в отношении c a .
Универсальный набор — определение и примеры
На предыдущих уроках мы узнали, что набор — это набор объектов и что можно использовать диаграммы Венна для объяснения как отношений наборов, так и логических отношений. Мы также узнали о различных типах наборов. В математике все эти различные типы множеств имеют свою ценность. Но набор, который, как известно, создает основу для любых двух или более наборов, — это универсальный набор .
В этой статье мы будем развивать понимание универсального набора.
Универсальное множество (обычно обозначаемое U) — это множество, состоящее из элементов всех родственных множеств без повторения элементов.
В этой статье мы рассмотрим следующие темы:
- Что такое универсальный набор?
- Как представлять универсальный набор?
- Разница между универсальным набором и объединением набора.
- Примеры
- Практические задачи
Что такое универсальный набор?
Универсальный набор является отражением его названия. Универсальное множество в общих чертах определяется как множество всех рассматриваемых объектов. Универсальное множество — это множество, содержащее все элементы или объекты других множеств, включая его элементы. Обычно обозначается буквой «U».
Точное определение U основано на рассматриваемом контексте или теории. Элементы, содержащиеся в U, могут варьироваться в зависимости от контекста формулируемых множеств. Например, мы можем описать U как совокупность всех живых существ на планете Земля. В этом случае множество всех млекопитающих, множество всех рептилий и множество всех птиц становятся подмножеством U. Точно так же мы можем сказать, что множество всех стран мира является универсальным.
С точки зрения математики универсальный набор — это набор целых чисел. В зависимости от контекста этот набор может также быть набором всех форм, набором всех многочленов второй степени и многими другими.
Поскольку набор представляет собой набор различных сущностей с общим свойством, универсальный набор представляет собой набор всех элементов, относящихся к конкретному предмету.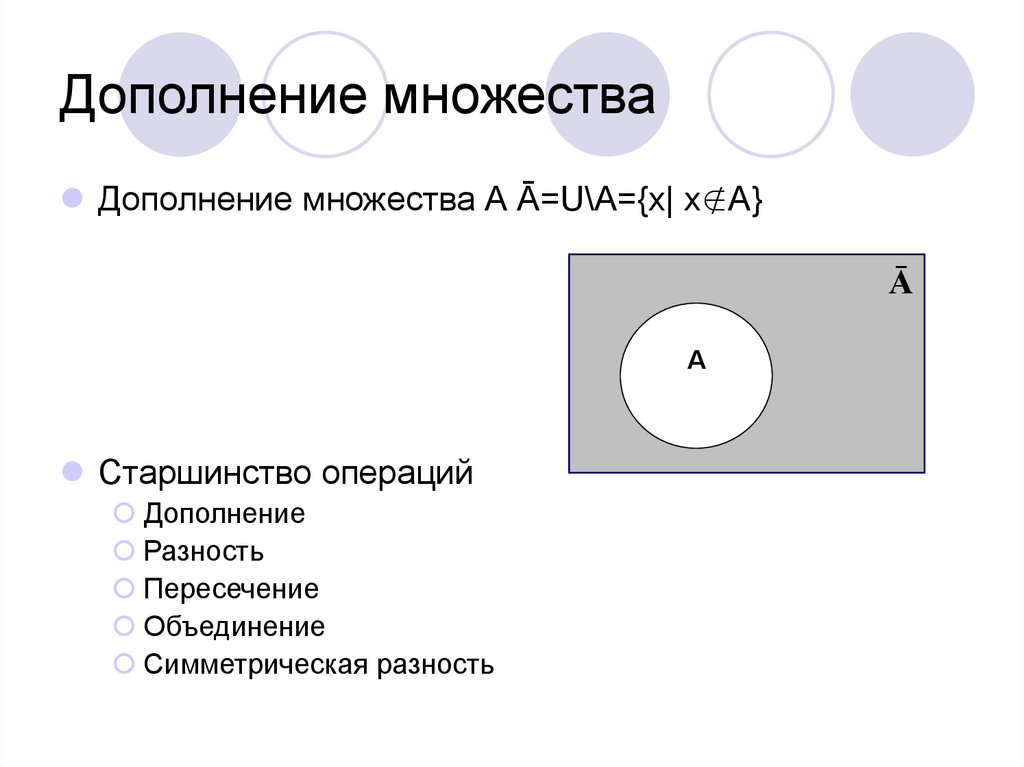
Давайте решим пример, чтобы лучше понять универсальные множества.
Пример 1
Рассмотрим три набора, а именно X, Y и Z. Элементы каждого набора приведены ниже:
X={2, 4, 6, 8}
Y ={3, 7, 9, 11}
Z={4, 8, 11}
Найдите универсальное множество для всех трех множеств X, Y и Z.
Решение
Мы знаем, что универсальное множество содержит все элементы заданных множеств; таким образом, универсальное множество X, Y и Z определяется как:
U={2, 3, 4, 6, 7, 8, 9, 11}
Из приведенного выше решения видно, что элементы множеств X, Y и Z полностью доступны в универсальном множестве ‘U ‘. Также в универсальном наборе нет повторяющихся элементов, и все элементы уникальны.
Как представить универсальный набор?
Теперь, когда мы знаем, что такое универсальное множество, следующая тема посвящена его представлению.
Универсальное множество может быть как конечным, так и бесконечным. Если универсальное множество бесконечно или даже если оно конечно с огромным количеством элементов, то эллипсы, три точки (…) используются для представления универсального множества. Пример показан ниже:
U = {1, 2, 3, …}
Или,
U = {1, 2, 3, …, 4000}
В математических терминах универсальное множество представляет собой набор чисел. Таким образом, мы также можем использовать жирные заглавные буквы для его представления. Специального обозначения универсального набора символов не существует.
Рассмотрим универсальный набор натуральных чисел, который представлен N. Обозначения этого универсального набора примерно такие:
N = {1, 2, 3, 4, …}
Некоторые примеры универсального набора приведены ниже.
Пример 2
Пусть A равно множеству нечетных чисел, а B равно множеству четных чисел. Что такое универсальное множество A и B?
Решение
Наборы A и B можно записать как:
A = {1, 3, 5, 7, 9…}
And,
B = {2, 4, 6, 8, 10…}
Итак, универсальный набор:
U = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10…}
Из приведенного выше примера видно, что универсальное множество U множеств A и B приводит к множеству натуральных чисел.
Разница между универсальным набором и объединением множества
Студенты чаще всего путаются между универсальным набором и объединением множества. Некоторые совершают распространенную ошибку, думая, что наборы похожи. Но это не тот случай. Мы можем лучше понять это, проанализировав определения этих двух множеств.
Универсальный набор, включая его элементы, представляет собой набор, состоящий из всех элементов или объектов. Принимая во внимание, что объединение множеств — это операция над двумя множествами, скажем, A и B, в результате чего получается множество со всеми элементами, принадлежащими обоим множествам A и B.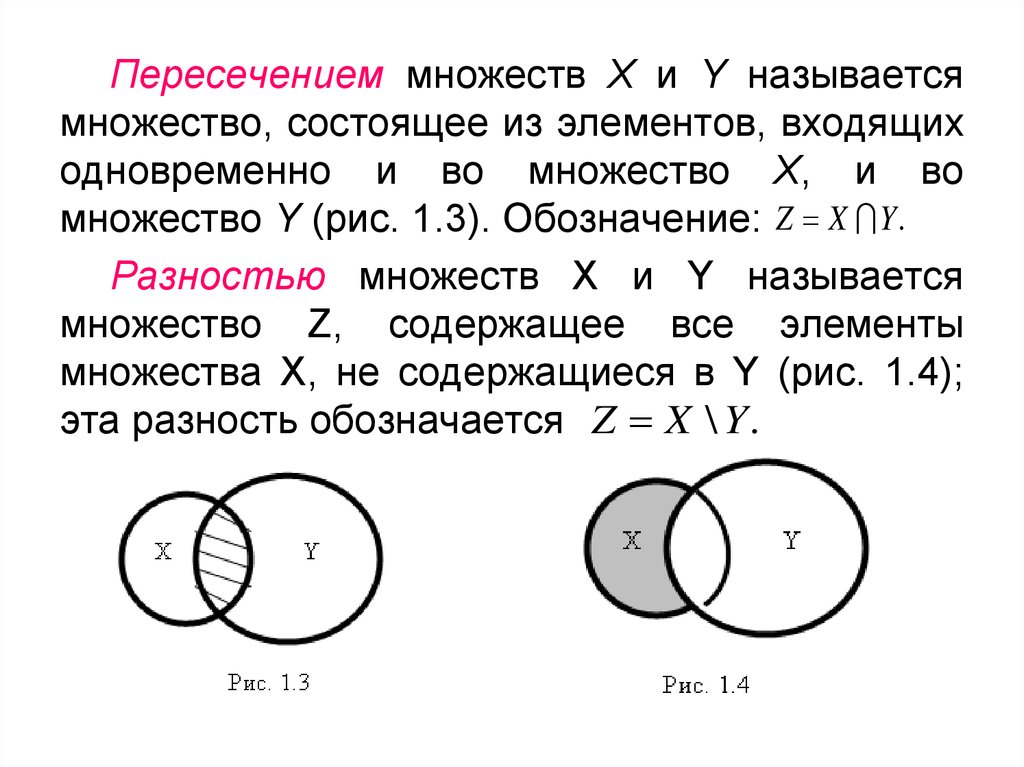
Следующий пример поможет нам лучше понять эту разницу.
Пример 3
Рассмотрим три множества с элементами U = {3, 5}, множеством X = {a, s, d} и множеством Y = {e, f, g}. Найдите универсальное множество U и объединение множеств X и Y?
Решение
Универсальный набор из трех наборов задается следующим образом:
U = { a, s, d, e, f, g, 3, 5}
Теперь найдем объединение. Объединение между X и Y задается как:
X U Y = {a, s, d, e, h, g}
Таким образом, универсальный набор представляет собой комбинацию X, Y и самого U, тогда как объединение X и Y содержат только элементы X и Y.
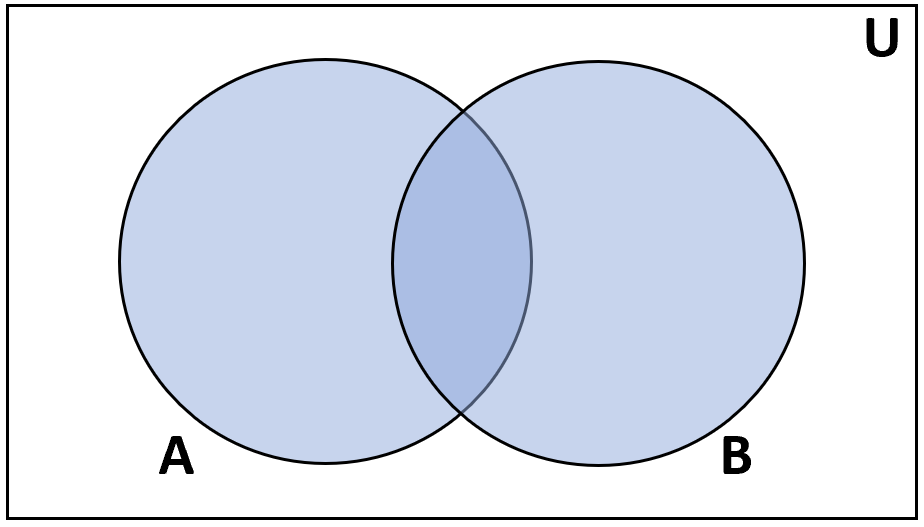
Представление универсального множества с помощью диаграммы Венна
Диаграмма Венна представляет собой две или более окружностей, используемых для иллюстрации взаимосвязей между различными множествами конечных объектов. Поскольку представление набора полностью визуальное, для изображения диаграмм Венна используются разные формы.
На диаграмме Венна кружки используются для обозначения множеств. Эти круги или наборы содержатся в универсальном наборе, представленном прямоугольником.
Универсальное множество изображается прямоугольником на диаграмме Венна и обозначается буквой U. Рассмотрим пример. Предположим, что набор, кратный 2, задан как A = {2, 4, 20, 22}. Теперь рассмотрим другое множество B, представляющее собой множество четных чисел, заданное как B = {2, 4, 6, 8, 10}. Универсальным множеством в этом случае является множество чисел U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Диаграммы Венна выглядят следующим образом:
Давайте решим пример, чтобы лучше понять это.
Пример 4
Пусть множество A = {1, 3, 5, 7, 9, 11} и множество B = {x : x — первичное число и 2
Решение
Чтобы решить этот пример, давайте сначала упростим наборы.
Набор B можно переписать как:
B = {3, 5, 7, 11, 13}
Аналогично множество U можно переписать как:
U = {1, 2, 3, 4, 5, …, 20}
Их взаимосвязь через диаграмму Венна следующая:
Универсальное множество и его подмножества
Поскольку универсальное множество — это множество, все элементы которого относятся к любому заданному контексту множеств, все остальные множества в нем являются подмножествами универсального множества.
Прежде чем мы займемся универсальным набором и его подмножествами, давайте рассмотрим подмножества. Множество A является подмножеством B, если все элементы A также являются элементами B. Символ представляет подмножество ⊆.
Таким образом, мы представляем A как подмножество B как:
X⊆Y
Поскольку все множества являются подмножествами самих себя, следовательно, универсальное множество также является подмножеством самого себя, которое может быть представлено как:
U ⊆ U.
Рассмотрим приведенный ниже пример, чтобы оценить эту концепцию.
Пример 5
Рассмотрим три набора U = {0,1, 2, 3, 4, 5…}, X = {1, 3, 5} и Y = {2, 4, 6} . Перечислите возможные подмножества.
Решение
Очевидно, что множества X и Y являются подмножествами U, поэтому:
X ⊂ U
X — собственное подмножество универсального множества U.
Аналогично, для множества Y:
Y ⊂ U
Y является правильным подмножеством универсального множества U.
Некоторые другие возможные подмножества, полученные из универсального множества, могут быть:
O = {1, 3, 5, 7,…}, т. е. множество всех нечетных чисел.
E = {2, 4, 6, 8,…} т.е. набор всех четных чисел.
Чтобы еще больше укрепить концепцию диаграмм Венна, рассмотрите следующие практические задачи.
Практические задачи
- Если X = {Азия, Африка, Северная Америка}, а Y = {Южная Америка, Антарктида, Европа, Австралия}, какой может быть универсальный набор?
- Учитывая, что U = {5, 6, 7, 8, 9, 10, 11, 12}, перечислите элементы следующих множеств.
(a) A = {x : x является коэффициентом 60} (b) B = {x : x является простым числом}
3. Если U = {2, 4, 6, 8, 10, 12, 14}, то какие из следующих являются подмножествами U.
X = {2, 4}, Y = {0}, Z = {1, 10, 5, 12}, A = {5, 14, 1} , B = {2, 4, 6, 8}
4. Если A = {x : x = 2n+1, n ∈ N}
B = { x : x = 2n, n ∈ N}
C = { x : x = n, n ∈ N}
Определите универсальное множество среди A, B и C.
5. Рассмотрим четыре множества:
U = {1, 3, 5, 7, 9, 13…}
Что из следующего является подмножеством U?
X = {1, 3, 5}
Y = {2, 4, 6}
Z = { 1, 8, 13}
Ответы
- U = {Континенты} 1, 5 =
- ; б) B = {5, 7, 11}
- X, B
- C
- X
) A
Предыдущий урок | Главная страница | Next Lesson
Съемочная площадка Nope становится постоянным аттракционом Universal Studios
Когда в конце этого месяца выйдет грядущий фильм ужасов Джордана Пила «Nope», в нем будет то, чего нет ни в одном другом фильме: аттракцион, являющийся частью всемирно известной студии Universal Studios Backlot Tour, открытие в тот же день .
Набор «Притязания Юпитера» из фильма будет доступен с 22 июля, в тот же день, когда «Нет» появится в кинотеатрах по всей стране. Впервые достопримечательность Studio Tour открылась одновременно с выходом фильма и теперь станет частью легендарного тура, наряду с разбившимся самолетом из «Войны миров» Стивена Спилберга, мотелем Бейтса из Альфреда. «Психо» Хичкока и площадь перед зданием суда из «Назад в будущее» Роберта Земекиса (и многих других фильмов). Это хорошая компания.
Декорации «Притязания Юпитера», деревенский городок Старого Запада (изначально снятый недалеко от Санта-Клариты, Калифорния), был разработан художником-постановщиком Рут ДеДжонг («Мы», «Йеллоустоун» Пила). Он был разобран во время постпродакшна и отправлен в Universal Studios Hollywood. Затем декорации были «тщательно реконструированы на месте с использованием оригинального реквизита и деталей из фильма» (согласно официальному пресс-релизу).
Читайте также:
Джордан Пил раскрывает, что «Нет» о «нашей зависимости от зрелищ и коварной природе внимания»
На официальном веб-сайте во вселенной «Притязания Юпитера» описываются как «лучший чертов тематический парк Калифорнийской золотой лихорадки в районе Санта-Кларита/Ланкастер! Идеально подходит для семейных прогулок, школьных групп и вечеринок по случаю дня рождения!» Jupiter’s Claim принадлежит и управляется бывшим ребенком-актером («Кид Шериф») и звездой реалити-шоу Рики «Юпитер» Паком (которого играет великий Стивен Юн).
В «Нет» Кеке Палмер и Дэниел Калуя играют братьев и сестер, которые унаследовали ранчо своего отца после его смерти при загадочных обстоятельствах. После того, как они захватывают ранчо, их вскоре терроризируют пришельцы из потустороннего мира. Он был описан как «эпопея ужасов» от оскароносного режиссера фильмов «Мы» и «Прочь».
Сам Пил очень взволнован открытием съемочной площадки в рамках Backlot Tour. «Я помню, как посетил Universal Studios, когда мне было 12 лет, и был загипнотизирован. Этот опыт укрепил мою страсть и стремление когда-нибудь присоединиться к метамагии «закулисной жизни». С тех пор мне посчастливилось снять три фильма для Universal», — сказал Пил в официальном заявлении. «Для меня большая честь отметить это сотрудничество с моими партнерами по студии, членами съемочной группы и актерами, а также иметь возможность поделиться «Притязаниями Юпитера» с фанатами».
Операции над множествами: объединение, пересечение, дополнение и различие
17 авг. 2022 г.
читать 2 мин
Набор — это набор предметов.
Мы обозначаем набор с помощью заглавной буквы, а элементы в наборе определяем с помощью фигурных скобок. Например, предположим, что у нас есть некоторый набор под названием «A» с элементами 1, 2, 3. Мы запишем это так:
А = {1, 2, 3}
В этом руководстве объясняются наиболее распространенные операции с множествами, используемые в теории вероятностей и статистике.
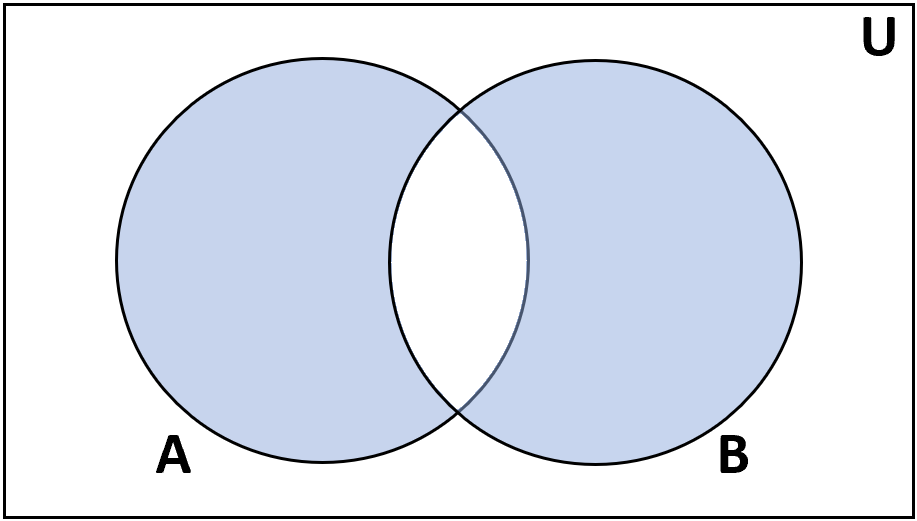
Союз
Определение: Объединение множеств A и B — это множество элементов, которые находятся либо в A, либо в B.
Обозначение: А ∪ В
Примеры:
- {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
- {1, 2} ∪ {1, 2} = {1, 2}
- {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
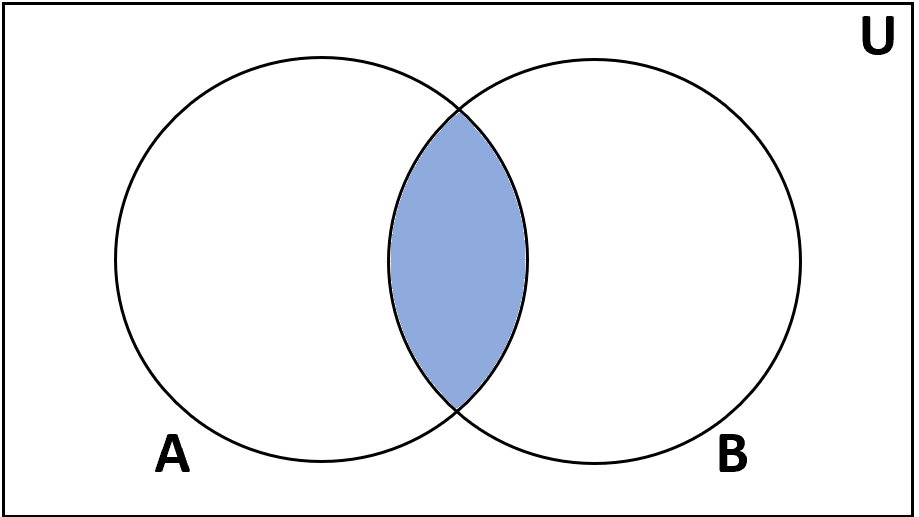
Перекресток
Определение: Пересечение множеств A и B — это множество элементов, которые находятся как в A, так и в B.
Обозначение: А ∩ В
Примеры:
- {1, 2, 3} ∩ {4, 5, 6} = {∅}
- {1, 2} ∩ {1, 2} = {1, 2}
- {1, 2, 3} ∩ {3, 4} = {3}
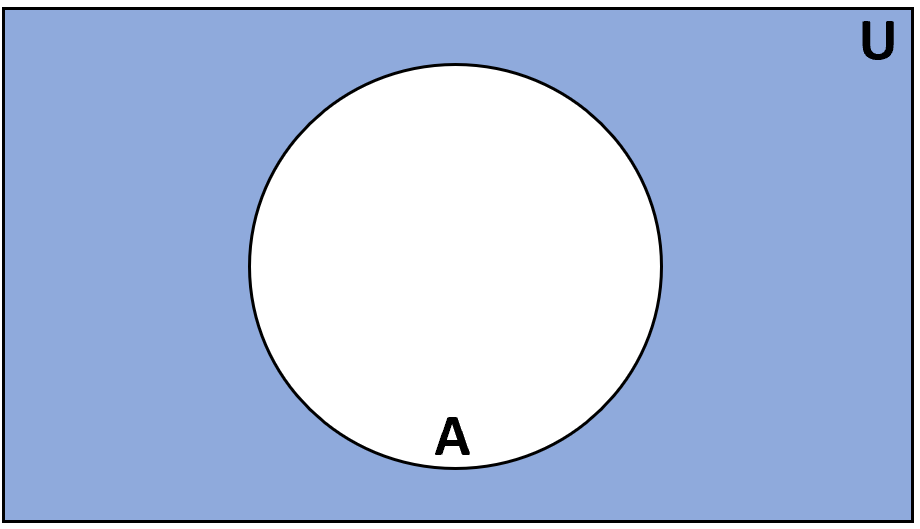
Дополнение
Определение: Дополнением множества A называется множество элементов, которые входят в универсальное множество U, но не входят в A.
Обозначение: A’ или A c
Примеры:
- Если U = {1, 2, 3, 4, 5, 6} и A = {1, 2}, то A c = {3, 4, 5, 6}
- Если U = {1, 2, 3} и A = {1, 2}, то A c = {3}
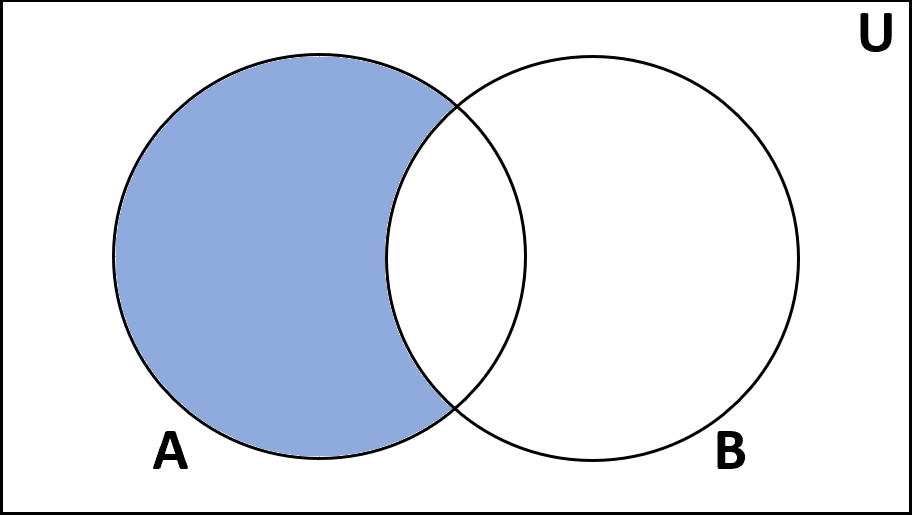
Разница
Определение: Разность множеств А и В — это множество элементов, которые есть в А, но отсутствуют в В.
Обозначение: А – Б
Примеры:
- {1, 2, 3} – {2, 3, 4} = {1}
- {1, 2} – {1, 2} = {∅}
- {1, 2, 3} – {4, 5} = {1, 2, 3}
Симметричная разница
Определение: Симметричная разность множеств A и B — это множество элементов, которые находятся либо в A, либо в B, но не в обоих.
Обозначение: А Δ В
Примеры:
- {1, 2, 3} ∆ {2, 3, 4} = {1, 4}
- {1, 2} ∆ {1, 2} = {∅}
- {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}
Декартово произведение
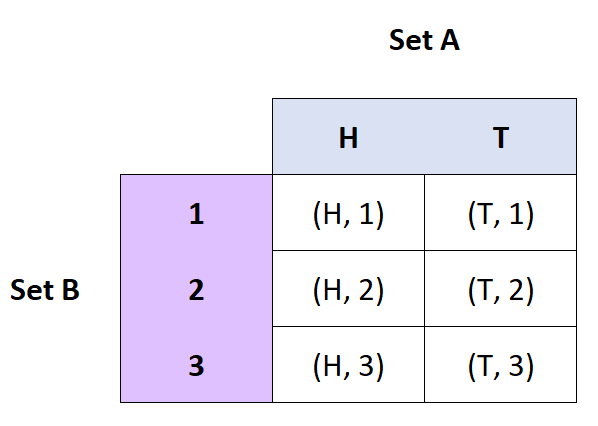
Определение: Декартово произведение множеств A и B — это множество упорядоченных пар из A и B.
Обозначение: А х В
Примеры:
- Если A = {H, T} и B = {1, 2, 3}, то A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( Т, 2), (Т, 3)}
- Если A = {T, H} и B = {1, 2, 3}, то A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( Н, 2), (Н, 3)}
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Online set theory calculator which helps to find complement of given sets. Complement of set A is the set of all elements in the universal set U which are not in A. It refers as Ac , A’, A—
Complement Set Theory
Online set theory calculator which helps to find complement of given sets. Complement of set A is the set of all elements in the universal set U which are not in A. It refers as Ac , A’, A—
Code to add this calci to your website 
Formula:
A— or A’ or Ac = U — A
Where,
A = Set A
U = Universal Set
A— or A’ or Ac = Complement of Set A


 Поэтому объединение
Поэтому объединение