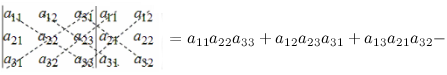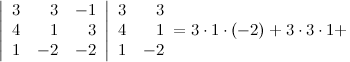Понятие минора и алгебраического дополнения было рассмотрено нами в теме «Как вычислить определитель матрицы третьего порядка». В данной статье разберем тему более подробно, а также научимся вычислять миноры и алгебраические дополнения матриц высших порядков.
Сначала рекомендуется повторить вычисление определителей второго, третьего и высших порядков.
Минор
Минором MijM_{ij} к элементу aija_{ij} определителя nn-го порядка называется определитель (n−1)(n-1)-го порядка, который получается из исходного определителя вычеркиванием ii-той строки и jj-того столбца.
Таким образом, минор — это определитель, который остается после вычеркивания определенной строки и определенного столбца. Например, M12M_{12} получается вычеркиванием 1-й строки и 2-го столбца, M34M_{34} — вычеркиванием 3-й строки и 4-го столбца.
Алгоритм нахождения миноров
- вычеркиваем i-ю строку;
- вычеркиваем j-й столбец;
- записываем определитель, который получили в результате действий 1 и 2.
Пример 1
Найти минор M34M_{34} к элементу a34a_{34} определителя ∣21−23−121213−1543−31∣begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}.
Те строки и столбцы, которые будем вычеркивать, выделим зеленым цветом.
M34=∣21−23−121213−1543−31∣=∣21−2−12143−3∣=2⋅2⋅(−3)+1⋅1⋅4+(−2)⋅3⋅(−1)−(−2)⋅2⋅4−1⋅(−3)⋅(−1)−2⋅1⋅3=−12+4+6+16−3−6=5M_{34}=begin{vmatrix}2&1&-2&color{green}3\-1&2&1&color{green}2\color{green}1&color{green}3&color{green}-1&color{green}5\4&3&-3&color{green}1end{vmatrix}=begin{vmatrix}2&1&-2\-1&2&1\4&3&-3end{vmatrix}=2cdot2cdot(-3)+1cdot1cdot4+(-2)cdot3cdot(-1)-(-2)cdot2cdot4-1cdot(-3)cdot(-1)-2cdot1cdot3=-12+4+6+16-3-6=5.
Пример 2
Найти миноры матрицы K=(03−122100−2−102−5711)K= begin{pmatrix}0&3&-1&2\2&1&0&0\-2&-1&0&2\-5&7&1&1end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, выделим зеленым цветом.
M11=(03−122100−2−102−5711)=∣100−102711∣=1⋅(−1)1+1∣0211∣=1⋅(−1)2∣0211∣=∣0211∣=1⋅(−1)2+1⋅2=1⋅(−1)3⋅2=−2M_{11}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\color{green}2&1&0&0\color{green}-2&-1&0&2\color{green}-5&7&1&1end{pmatrix}=begin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=1cdot(-1)^{1+1}begin{vmatrix}0&2\1&1end{vmatrix}=1cdot(-1)^{2}begin{vmatrix}0&2\1&1end{vmatrix}=begin{vmatrix}0&2\1&1end{vmatrix}=1cdot(-1)^{2+1}cdot2=1cdot(-1)^{3}cdot2=-2,
M12=(03−122100−2−102−5711)=∣200−202−511∣=2⋅(−1)1+1∣0211∣=2⋅(−1)2∣0211∣=2∣0211∣=2⋅(−1)2+1⋅2=2⋅(−1)3⋅2=−4M_{12}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\2&color{green}1&0&0\-2&color{green}-1&0&2\-5&color{green}7&1&1end{pmatrix}=begin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=2cdot(-1)^{1+1}begin{vmatrix}0&2\1&1end{vmatrix}=2cdot(-1)^{2}begin{vmatrix}0&2\1&1end{vmatrix}=2begin{vmatrix}0&2\1&1end{vmatrix}=2cdot(-1)^{2+1}cdot2=2cdot(-1)^{3}cdot2=-4,
M13=(03−122100−2−102−5711)=∣210−2−12−571∣=2⋅(−1)⋅1+0⋅7⋅(−2)+1⋅2⋅(−5)−0⋅(−1)⋅(−5)−2⋅2⋅7−1⋅1⋅(−2)=−2−10−28+2=−38M_{13}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\2&1&color{green}0&0\-2&-1&color{green}0&2\-5&7&color{green}1&1end{pmatrix}=begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=2cdot(-1)cdot1+0cdot7cdot(-2)+1cdot2cdot(-5)-0cdot(-1)cdot(-5)-2cdot2cdot7-1cdot1cdot(-2)=-2-10-28+2=-38,
M14=(03−122100−2−102−5711)=∣210−2−10−571∣=1⋅(−1)3+3∣21−2−1∣=0M_{14}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\2&1&0&color{green}0\-2&-1&0&color{green}2\-5&7&1&color{green}1end{pmatrix}=begin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=1cdot(-1)^{3+3}begin{vmatrix}2&1\-2&-1end{vmatrix}=0,
M21=(03−122100−2−102−5711)=∣3−12−102711∣=3⋅0⋅1+2⋅1⋅(−1)+(−1)⋅2⋅7−2⋅0⋅7−(−1)⋅1⋅(−1)−3⋅2⋅1=−2−14−1−6=−23M_{21}= begin{pmatrix}color{green}0&3&-1&2\color{green}2&color{green}1&color{green}0&color{green}0\color{green}-2&-1&0&2\color{green}-5&7&1&1end{pmatrix}=begin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=3cdot0cdot1+2cdot1cdot(-1)+(-1)cdot2cdot7-2cdot0cdot7-(-1)cdot1cdot(-1)-3cdot2cdot1=-2-14-1-6=-23,
M22=(03−122100−2−102−5711)=∣0−12−202−511∣=0⋅0⋅1+(−1)⋅2⋅(−5)+2⋅1⋅(−2)−2⋅0⋅(−5)−(−1)⋅1⋅(−2)−0⋅2⋅1=10−4−2=4M_{22}= begin{pmatrix}0&color{green}3&-1&2\color{green}2&color{green}1&color{green}0&color{green}0\-2&color{green}-1&0&2\-5&color{green}7&1&1end{pmatrix}=begin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=0cdot0cdot1+(-1)cdot2cdot(-5)+2cdot1cdot(-2)-2cdot0cdot(-5)-(-1)cdot1cdot(-2)-0cdot2cdot1=10-4-2=4,
M23=(03−122100−2−102−5711)=∣032−2−12−571∣=0⋅(−1)⋅1+3⋅2⋅(−5)+2⋅7⋅(−2)−2⋅(−1)⋅(−5)−3⋅1⋅(−2)−0⋅2⋅7=−30−28−10+6=−62M_{23}= begin{pmatrix}0&3&color{green}-1&2\color{green}2&color{green}1&color{green}0&color{green}0\-2&-1&color{green}0&2\-5&7&color{green}1&1end{pmatrix}=begin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=0cdot(-1)cdot1+3cdot2cdot(-5)+2cdot7cdot(-2)-2cdot(-1)cdot(-5)-3cdot1cdot(-2)-0cdot2cdot7=-30-28-10+6=-62,
M24=(03−122100−2−102−5711)=∣03−1−2−10−571∣=0⋅(−1)⋅1+3⋅0⋅(−5)+(−1)⋅7⋅(−2)−(−1)⋅(−1)⋅(−5)−3⋅1⋅(−2)−0⋅0⋅7=14+5+6=25M_{24}= begin{pmatrix}0&3&-1&color{green}2\color{green}2&color{green}1&color{green}0&color{green}0\-2&-1&0&color{green}2\-5&7&1&color{green}1end{pmatrix}=begin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=0cdot(-1)cdot1+3cdot0cdot(-5)+(-1)cdot7cdot(-2)-(-1)cdot(-1)cdot(-5)-3cdot1cdot(-2)-0cdot0cdot7=14+5+6=25,
M31=(03−122100−2−102−5711)=∣3−12100711∣=1⋅(−1)2+1∣−1211∣=1⋅(−1)3∣−1211∣=−∣−1211∣=−(−1−2)=3M_{31}= begin{pmatrix}color{green}0&3&-1&2\color{green}2&1&0&0\color{green}-2&color{green}-1&color{green}0&color{green}2\color{green}-5&7&1&1end{pmatrix}=begin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=1cdot(-1)^{2+1}begin{vmatrix}-1&2\1&1end{vmatrix}=1cdot(-1)^{3}begin{vmatrix}-1&2\1&1end{vmatrix}=-begin{vmatrix}-1&2\1&1end{vmatrix}=-(-1-2)=3,
M32=(03−122100−2−102−5711)=∣0−12200−511∣=2⋅(−1)2+1∣−1211∣=2⋅(−1)3∣−1211∣=−2∣−1211∣=−2(−1−2)=6M_{32}= begin{pmatrix}0&color{green}3&-1&2\2&color{green}1&0&0\color{green}-2&color{green}-1&color{green}0&color{green}2\-5&color{green}7&1&1end{pmatrix}=begin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=2cdot(-1)^{2+1}begin{vmatrix}-1&2\1&1end{vmatrix}=2cdot(-1)^{3}begin{vmatrix}-1&2\1&1end{vmatrix}=-2begin{vmatrix}-1&2\1&1end{vmatrix}=-2(-1-2)=6,
M33=(03−122100−2−102−5711)=∣032210−571∣=0⋅1⋅1+3⋅0⋅(−5)+2⋅7⋅2−2⋅1⋅(−5)−0⋅0⋅7−3⋅1⋅2=28+10−6=32M_{33}= begin{pmatrix}0&3&color{green}-1&2\2&1&color{green}0&0\color{green}-2&color{green}-1&color{green}0&color{green}2\-5&7&color{green}1&1end{pmatrix}=begin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=0cdot1cdot1+3cdot0cdot(-5)+2cdot7cdot2-2cdot1cdot(-5)-0cdot0cdot7-3cdot1cdot2=28+10-6=32,
M34=(03−122100−2−102−5711)=∣03−1210−571∣=0⋅1⋅1+3⋅0⋅(−5)+(−1)⋅7⋅2−(−1)⋅1⋅(−5)−3⋅1⋅2−0⋅0⋅7=−14−5−6=−25M_{34}= begin{pmatrix}0&3&-1&color{green}2\2&1&0&color{green}0\color{green}-2&color{green}-1&color{green}0&color{green}2\-5&7&1&color{green}1end{pmatrix}=begin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=0cdot1cdot1+3cdot0cdot(-5)+(-1)cdot7cdot2-(-1)cdot1cdot(-5)-3cdot1cdot2-0cdot0cdot7=-14-5-6=-25,
M41=(03−122100−2−102−5711)=∣3−12100−102∣=1⋅(−1)2+1∣−1202∣=1⋅(−1)3∣−1202∣=−∣−1202∣=−(−1)⋅(−1)1+1⋅2=1⋅(−1)2⋅2=2M_{41}= begin{pmatrix}color{green}0&3&-1&2\color{green}2&1&0&0\color{green}-2&-1&0&2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=1cdot(-1)^{2+1}begin{vmatrix}-1&2\0&2end{vmatrix}=1cdot(-1)^{3}begin{vmatrix}-1&2\0&2end{vmatrix}=-begin{vmatrix}-1&2\0&2end{vmatrix}=-(-1)cdot(-1)^{1+1}cdot2=1cdot(-1)^{2}cdot2=2,
M42=(03−122100−2−102−5711)=∣0−12200−202∣=2⋅(−1)2+1∣−1202∣=2⋅(−1)3∣−1202∣=−2∣−1202∣=−2⋅(−1)⋅(−1)1+1⋅2=2⋅(−1)2⋅2=4M_{42}= begin{pmatrix}0&color{green}3&-1&2\2&color{green}1&0&0\-2&color{green}-1&0&2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=2cdot(-1)^{2+1}begin{vmatrix}-1&2\0&2end{vmatrix}=2cdot(-1)^{3}begin{vmatrix}-1&2\0&2end{vmatrix}=-2begin{vmatrix}-1&2\0&2end{vmatrix}=-2cdot(-1)cdot(-1)^{1+1}cdot2=2cdot(-1)^{2}cdot2=4,
M43=(03−122100−2−102−5711)=∣032210−2−12∣=0⋅1⋅2+3⋅0⋅(−2)+2⋅(−1)⋅2−2⋅1⋅(−2)−3⋅2⋅2−0⋅0⋅(−1)=−4+4−12=−12M_{43}= begin{pmatrix}0&3&color{green}-1&2\2&1&color{green}0&0\-2&-1&color{green}0&2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=0cdot1cdot2+3cdot0cdot(-2)+2cdot(-1)cdot2-2cdot1cdot(-2)-3cdot2cdot2-0cdot0cdot(-1)=-4+4-12=-12,
M44=(03−122100−2−102−5711)=∣03−1210−2−10∣=0M_{44}= begin{pmatrix}0&3&-1&color{green}2\2&1&0&color{green}0\-2&-1&0&color{green}2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0.
Алгебраическое дополнение
Алгебраическим дополнением AijA_{ij} к элементу aija_{ij} определителя n-го порядка называется число Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij}, где i,ji, j — соответствующие строка и столбец, а MijM_{ij} — минор к элементу aija_{ij}.
Алгоритм нахождения алгебраических дополнений
- найти сумму номеров строки (i)(i) и столбца (j)(j);
- найти минор MijM_{ij} по алгоритму нахождения миноров, который представлен выше;
- подставить значения, полученные на шагах 1 и 2, в формулу Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij}.
Пример 1
Найти алгебраическое дополнение A34A_{34} к элементу a34a_{34} определителя
∣21−23−121213−1543−31∣begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}.
A34=(−1)3+4⋅M34=(−1)7⋅∣21−23−121213−1543−31∣=−∣21−2−12143−3∣=−(2⋅2⋅(−3)+1⋅1⋅4+(−2)⋅3⋅(−1)−(−2)⋅2⋅4−1⋅(−3)⋅(−1)−2⋅1⋅3)=−(−12+4+6+16−3−6)=−5A_{34}=(-1)^{3+4}cdot M_{34}=(-1)^{7}cdot
begin{vmatrix}2&1&-2&color{green}3\-1&2&1&color{green}2\color{green}1&color{green}3&color{green}-1&color{green}5\4&3&-3&color{green}1end{vmatrix}=-begin{vmatrix}2&1&-2\-1&2&1\4&3&-3end{vmatrix}=-(2cdot2cdot(-3)+1cdot1cdot4+(-2)cdot3cdot(-1)-(-2)cdot2cdot4-1cdot(-3)cdot(-1)-2cdot1cdot3)=-(-12+4+6+16-3-6)=-5.
Пример 2
Найти алгебраические дополнения матрицы K=(03−122100−2−102−5711)K= begin{pmatrix}0&3&-1&2\2&1&0&0\-2&-1&0&2\-5&7&1&1end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, выделим зеленым цветом.
A11=(−1)1+1⋅M11=(−1)1+1⋅∣100−102711∣=(−1)2∣100−102711∣=∣100−102711∣=−2A_{11}=(-1)^{1+1}cdot M_{11}=(-1)^{1+1}cdotbegin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=(-1)^{2}begin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=begin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=-2,
A12=(−1)1+2⋅M12=(−1)1+2⋅∣200−202−511∣=(−1)3⋅∣200−202−511∣=−∣200−202−511∣=−(−4)=4A_{12}=(-1)^{1+2}cdot M_{12}=(-1)^{1+2}cdotbegin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=(-1)^{3}cdotbegin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=-begin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=-(-4)=4,
A13=(−1)1+3⋅M13=(−1)1+3⋅∣210−2−12−571∣=(−1)4⋅∣210−2−12−571∣=∣210−2−12−571∣=−38A_{13}=(-1)^{1+3}cdot M_{13}=(-1)^{1+3}cdot begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=(-1)^{4}cdot begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=-38,
A14=(−1)1+4⋅M14=(−1)1+4⋅∣210−2−10−571∣=(−1)5⋅∣210−2−10−571∣=−∣210−2−10−571∣=0A_{14}=(-1)^{1+4}cdot M_{14}=(-1)^{1+4}cdotbegin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=(-1)^{5}cdot begin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=-begin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=0,
A21=(−1)2+1⋅M21=(−1)2+1⋅∣3−12−102711∣=(−1)3⋅∣3−12−102711∣=−∣3−12−102711∣=−(−23)=23A_{21}=(-1)^{2+1}cdot M_{21}=(-1)^{2+1}cdotbegin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=(-1)^{3}cdotbegin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=-begin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=-(-23)=23,
A22=(−1)2+2⋅M22=(−1)2+2⋅∣0−12−202−511∣=(−1)4⋅∣0−12−202−511∣=∣0−12−202−511∣=4A_{22}=(-1)^{2+2}cdot M_{22}=(-1)^{2+2}cdotbegin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=(-1)^{4}cdotbegin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=begin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=4,
A23=(−1)2+3⋅M23=(−1)2+3⋅∣032−2−12−571∣=(−1)5⋅∣032−2−12−571∣=−∣032−2−12−571∣=−(−62)=62A_{23}=(-1)^{2+3}cdot M_{23}=(-1)^{2+3}cdotbegin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=(-1)^{5}cdotbegin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=-begin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=-(-62)=62,
A24=(−1)2+4⋅M24=(−1)2+4⋅∣03−1−2−10−571∣=(−1)6⋅∣03−1−2−10−571∣=∣03−1−2−10−571∣=25A_{24}=(-1)^{2+4}cdot M_{24}=(-1)^{2+4}cdotbegin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=(-1)^{6}cdotbegin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=begin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=25,
A31=(−1)3+1⋅M31=(−1)3+1⋅∣3−12100711∣=(−1)4⋅∣3−12100711∣=∣3−12100711∣=3A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{3+1}cdotbegin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=(-1)^{4}cdotbegin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=begin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=3,
A32=(−1)3+2⋅M32=(−1)3+2⋅∣0−12200−511∣=(−1)5⋅∣0−12200−511∣=−∣0−12200−511∣=−6A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{3+2}cdotbegin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=(-1)^{5}cdotbegin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=-begin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=-6,
A33=(−1)3+3⋅M33=(−1)3+3⋅∣032210−571∣=(−1)6⋅∣032210−571∣=∣032210−571∣=32A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{3+3}cdotbegin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=(-1)^{6}cdotbegin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=begin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=32,
A34=(−1)3+4⋅M34=(−1)3+4⋅∣03−1210−571∣=(−1)7⋅∣03−1210−571∣=−∣03−1210−571∣=−(−25)=25A_{34}=(-1)^{3+4}cdot M_{34}=(-1)^{3+4}cdotbegin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=(-1)^{7}cdotbegin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=-begin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=-(-25)=25,
A41=(−1)4+1⋅M41=(−1)4+1⋅∣3−12100−102∣=(−1)5⋅∣3−12100−102∣=−∣3−12100−102∣=−2A_{41}=(-1)^{4+1}cdot M_{41}=(-1)^{4+1}cdotbegin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=(-1)^{5}cdotbegin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=-begin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=-2,
A42=(−1)4+2⋅M42=(−1)4+2⋅∣0−12200−202∣=(−1)6⋅∣0−12200−202∣=∣0−12200−202∣=4A_{42}=(-1)^{4+2}cdot M_{42}=(-1)^{4+2}cdotbegin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=(-1)^{6}cdotbegin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=begin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=4,
A43=(−1)4+3⋅M43=(−1)4+3⋅∣032210−2−12∣=(−1)7⋅∣032210−2−12∣=−∣032210−2−12∣=−(−12)=12A_{43}=(-1)^{4+3}cdot M_{43}=(-1)^{4+3}cdotbegin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=(-1)^{7}cdotbegin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=-begin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=-(-12)=12,
A44=(−1)4+4⋅M44=(−1)4+4⋅∣03−1210−2−10∣=(−1)8⋅∣03−1210−2−10∣=∣03−1210−2−10∣=0A_{44}=(-1)^{4+4}cdot M_{44}=(-1)^{4+4}cdotbegin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=(-1)^{8}cdotbegin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0.
Задачи на заказ недорого по любому предмету от наших экспертов!
Тест по теме «Минор матрицы и алгебраическое дополнение матрицы»
Методы вычисления определителей
При вычислении определителей высокого порядка (больше 3-го) определение, как правило, не используется, так как это приводит к громоздким выражениям и требует большого количества арифметических операций. Гораздо эффективнее использовать свойства определителей. Наиболее важными для вычисления определителей являются свойства 3, 6, 9. Эти свойства можно назвать элементарными преобразованиями определителя, что соответствует элементарным преобразованиям матрицы.
I. Перестановка двух столбцов (строк) определителя приводит к изменению его знака на противоположный.
II. Умножение всех элементов одного столбца (строки) определителя на одно и то же число, отличное от нуля, приводит к умножению определителя на это число.
III. Прибавление к элементам одного столбца (строки) определителя соответствующих элементов другого столбца, умноженных на одно и то же число, не изменяет определитель.
При помощи элементарных преобразований можно упростить определитель, т.е. привести его к виду, удобному для вычислений.
Метод приведения определителя к треугольному виду
При помощи элементарных преобразований любую матрицу можно привести к верхнему (или нижнему) треугольному виду (метод Гаусса). Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.
Итак, метод состоит из двух шагов.
1. При помощи элементарных преобразований привести определитель к треугольному виду.
2. Вычислить определитель треугольного вида, перемножая его элементы, стоящие на главной диагонали.
Пример 2.12. Вычислить определитель четвёртого порядка
приводя его к треугольному виду.
Решение. 1. При помощи элементарных преобразований приведем матрицу к треугольному виду. Взяв элемент первой строки в качестве ведущего, все остальные элементы первого столбца сделаем равными нулю. Для этого ко второй строке прибавим первую, умноженную на (-2), к третьей строке прибавим первую, умноженную на (-3), а к четвертой строке прибавим первую, умноженную на (-4):
Заметим, что при использовании этих элементарных преобразований III типа определитель не изменяется.
Умножим элементы второй строки на (-1), а элементы третьей строки — на 0,5, при этом, чтобы не нарушить равенство, надо полученный определитель разделить на , т.е. умножить на (-2):
В полученной матрице нужно сделать равными нулю элементы и
второго столбца, стоящие ниже главной диагонали. Для этого берем в качестве ведущего элемента
и прибавляем к третьей и четвертой строкам вторую строку, умноженную на 1 и на 7 соответственно:
Осталось сделать равным нулю элемент . К четвертой строке прибавим третью, умноженную на 2 (определитель при этом не изменится):
Получили определитель треугольного вида.
2. Вычислим определитель верхней треугольной матрицы, перемножая элементы, стоящие на главной диагонали:
Метод понижения порядка определителя
Этот метод также основан на элементарных преобразованиях определителя.
1. При помощи элементарного преобразования III типа нужно в одном столбце (или одной строке) сделать равными нулю все элементы, за исключением одного.
2. Разложить определитель по этому столбцу (строке) и получить определитель меньшего порядка, чем исходный. Если его порядок больше 1, то следует перейти к п. 1, иначе вычисления закончить.
Пример 2.13. Вычислить определитель четвёртого порядка методом понижения порядка.
Решение. 1. В качестве ведущего элемента возьмем , а все остальные элементы второй строки при помощи элементарных преобразований сделаем равными нулю. Для этого ко второму столбцу прибавим четвертый, умноженный на (-3):
2. Разложим определитель по второй строке
Получили определитель третьего порядка.
Вынесем за знак определителя множитель (2) из второго столбца (точнее все элементы второго столбца умножим на 0,5 , а получившийся определитель умножим на 2):
Прибавим ко второму столбцу первый
Полученный определитель разложим по второму столбцу
Получили определитель 2-го порядка.
Прибавим ко второй строке первую, умноженную на (-2)
Разложим определитель по второй строке и заменим определитель первого порядка единственным его элементом
Результат совпадает с полученным в примере 2.7.
Метод изменения всех элементов определителя
При вычислении определителей бывает полезно изменить все его элементы, умножив их на одно и то же число, не равное нулю, либо прибавить к каждому элементу одно и то же число. Найдем формулы изменения определителя при этих преобразованиях.
Пусть дана квадратная матрица n-го порядка. Из свойства 6 следует, что при умножении всех элементов определителя n-го порядка на число
определитель умножается на число
.
Рассмотрим теперь определитель матрицы , элементы которой
получены из соответствующих элементов матрицы
прибавлением числа
Применяя свойство 7 к первому столбцу этого определителя, получаем сумму определителей
То же свойство применяем к каждому определителю («раскладывая» второй столбец) и т.д. В итоге получим сумму определителей n-го порядка, причем определители, имеющие по два и более столбцов из элементов, равных
, равны нулю (по свойству 4). Поэтому в сумме остаются только
слагаемых: определитель матрицы
и
определителей вида
отличающихся от определителя матрицы только j-м столбцом. Раскладывая этот определитель по j-му столбцу, получаем сумму алгебраических дополнений элементов этого столбца, умноженную на
Следовательно, сумма всех таких определителей равна сумме алгебраических дополнений всех элементов матрицы
, умноженной на
Окончательно получаем, что при увеличении всех элементов определителя на число , определитель увеличивается на сумму всех алгебраических дополнений, умноженную на число
Пример 2.14. Вычислить определитель n-го порядка
Решение. Рассмотрим определитель диагональной матрицы
Искомый определитель получается прибавлением к каждому элементу определителя матрицы
числа
. Поэтому
Определитель диагональной матрицы равен произведению диагональных элементов:
Осталось вычислить сумму алгебраических дополнений всех элементов матрицы . Заметим, что алгебраическое дополнение недиагонального элемента равно нулю (
при
, так как дополнительный минор содержит нулевой столбец). Дополнительный минор диагонального элемента — это определитель диагональной матрицы, т.е.
Поэтому
Вычисление определителей с помощью рекуррентных уравнений
Этот метод заключается в том, что исходный определитель n-го порядка выражается через определители
того же вида, но меньшего порядка. Получается рекуррентное уравнение
Решая это уравнение, находим формулу, выражающую определитель через определители
и порядок
В последнюю формулу подставляем определители невысокого
порядка, которые нетрудно вычислить каким-либо другим способом.
Замечание 2.6. Рекуррентным уравнением называется равенство вида , выражающее n-й член
искомой числовой последовательности
через
её предыдущих членов
. Методы решения таких уравнений рассматриваются в разд.
Пример 2.15. Вычислить определитель n-го порядка
Решение. Разложим определитель по первой строке
Первый из полученных определителей (n-l)-ro порядка обозначим , так как он имеет такой же вид, что и
. Разложив последний определитель по первому столбцу, получим определитель того же вида, что и
, но (n-2)-го порядка
Следовательно, искомый определитель удовлетворяет рекуррентному уравнению
Решение этого уравнения будем искать в виде , где
и
— неизвестные коэффициенты. Заметим, что эта формула дает решение рекуррентного уравнения при любых коэффициентах
и
. В самом деле, подставляя
в уравнение, получаем тождество
Подберем теперь коэффициенты и
в формуле
так, чтобы при
и
она давала правильные результаты, т.е.
Решая систему уравнений получаем
. Следовательно, искомый определитель равен
Пример 2.16. Вычислить определитель Вандермонда
где
— действительные числа.
Решение. Рассмотрим определитель
который отличается от определителя Вандермонда последним столбцом, но совпадает с ним при . Раскладывая определитель
по последнему столбцу, получаем многочлен (n-1)-й степени действительной переменной
где старший коэффициент равен алгебраическому дополнению элемента
т.е. определителю — определителю Вандермонда (n-l)-ro порядка. Заметим, что при
определитель
равен нулю, так как он имеет два одинаковых столбца (свойство 4). Следовательно,
— корень многочлена
. То же самое можно сказать про числа
. Все они являются корнями многочлена
. Следовательно, этот многочлен имеет вид:
Подставляя в это равенство и учитывая, что
, получаем рекуррентное уравнение
Записывая аналогичным образом и учитывая, что
, получаем
Таким образом, определитель Вандермонда равен произведению всех разностей при
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Для любой квадратной
матрицы А существует число
илиdet
A,
называемое определителем, характеризующее
эту матрицу.
Опр.
Определителем квадратной матрицы п-го
порядка называется число, равное сумме
п!
слагаемых, каждое из которых является
произведением п
элементов матрицы, взятых по одному из
каждой строки и каждого столбца матрицы
со знаком “+”или “—” .
Так, определителем
первого порядка называется само число
а11.
Определителем
квадратной матрицы А второго порядка
называется число, определяемое по
формуле:
Правило вычисления
этого определителя легко запомнить
визуально: из произведения элементов
главной диагонали вычитается произведение
элементов побочной диагонали матрицы.
Определителем
квадратной матрицы А третьего порядка
называется число, определяемое по
формуле:

число представляет собой сумму 3!=6
слагаемых, в которые входят по одному
элементу из каждой строки и столбца.
Запомнить правило вычисления этого
определителя можно, пользуясь схемой,
называемой правилом треугольников или
правилом Сарруса.
Вычисление
определителей порядка больше 3 основано
на применении свойств определителей.
Опр.
Минором порядка к
матрицы Аm×n
называется
определитель к-го
порядка, полученный из матрицы А
вычеркиванием (т-к)
строк и (п-к)
столбцов ().
Опр.
Дополнительным минором Мij
элемента
aij
квадратной матрицы А п-го
порядка называется определитель порядка
(п-1),
полученный из матрицы А вычеркиванием
строки и столбца, на пересечении которых
стоит элемент aij.
Опр. Алгебраическим
дополнением Aij
элемента
aij
квадратной матрицы А п-го
порядка называется число
.
§4. Свойства определителей.
1. При транспонировании
величина определителя не меняется.
Следствие.
Строки и столбцы в определителе обладают
одинаковыми свойствами.
2. Если все элементы
строки определителя умножить на одно
число, то значение определителя умножится
на это число.
Следствие.
Постоянный множитель строки можно
вынести за знак определителя.
3. При перестановке
двух строк определитель меняет знак на
противоположный.
Следствие.
Определитель, имеющий равные или
пропорциональные строки, равен нулю.
4. Если каждый
элемент строки определителя представлен
в виде суммы, то определитель равен
сумме определителей, у которых в данной
строке стоят слагаемые.
5. Определитель
произведения двух квадратных матриц
равен произведению определителей этих
матриц.
6. Определитель
треугольной (в т.ч. диагональной) матрицы
равен произведению элементов главной
диагонали.
7. Определитель
равен сумме произведений элементов
любой строки на их алгебраические
дополнения (т. Лапласа):
—
разложение по i-й
строке,
—
разложение по j-му
столбцу.
8. Сумма произведений
элементов какой-либо строки определителя
на алгебраические дополнения элементов
другой строки равна нулю.
при
.
9. Определитель
матрицы не изменится, если к элементам
одной его строки прибавить элементы
другой строки, умноженной на одно и то
же число.
§5. Обратная матрица.
Вспомним свойство
чисел:
.
Аналог существует
для матриц.
Опр.
Квадратная матрица называется
невырожденной, если ее определитель не
равен нулю. В противном случае матрица
называется вырожденной.
Опр.
Матрица А-1
называется обратной к квадратной матрице
А, если их произведение равно единичной
матрице:
А·А-1=А-1·А=Е.
Теорема (необходимое
и достаточное условие существования
обратной матрицы). Обратная матрица А-1
существует и единственна тогда и только
тогда, когда матрица А невырожденная.
Док-во. Необходимость.
Дано: А-1.
Докажем, что
.
Имеем по определению:
А·А-1=А-1·А=Е.
Тогда
.
Следовательно,и
.
Достаточность.
Дано:
.
Докажем, что существует А-1.
Построим ее с помощью следующих действий.
1. Транспонируем
матрицу А: АТ.
2. Заменим каждый
элемент матрицы АТ
его алгебраическим дополнением, получим
так называемую присоединенную матрицу
А*:
3. Разделим все
элементы А*
на
:

Покажем, что
полученная таким способом матрица
является обратной к А.

.
.
Таким образом,
матрица С является единичной матрицей,
а значит матрица

Аналогично
доказывается, что А-1А=Е.
Единственность.
От противного.
Предположим, что у матрицы А есть две
различные обратные матрицы А-1
и
.
Имеем:А
А-1=Е.
Умножим это равенство слева на
.
А А-1=
Е,
ЕА-1=,
А-1=А.
Получили противоречие, доказывающее
теорему.▲
Замечание.
Теорема не только решает вопрос о
существовании обратной матрицы, но и
дает алгоритм ее нахождения:
-
Найти определитель
матрицы, убедиться, что она невырожденная. -
Транспонировать
матрицу:
.
-
Составить матрицу
алгебраических дополнений к
АТ(присоединенную
матрицу) А*
. -
Найти обратную
матрицу по формуле
.
Существует и другой
способ нахождения обратной матрицы,
связанный с выполнением над матрицей
так называемых элементарных преобразований.
К ним относятся:
— умножение любой
строки на число, отличное от нуля;
— сложение строк;
— перестановка
строк.
Опр.
Две матрицы называются эквивалентными,
если от одной можно перейти к другой с
помощью конечного числа элементарных
преобразований.
Любую невырожденную
квадратную матрицу с помощью элементарных
преобразований можно привести к единичной
матрице. Применяя ту же последовательность
преобразований к единичной матрице,
можно получить обратную матрицу к
данной. Обычно элементарные преобразования
проводят над данной матрицей и единичной
одновременно. Для этого составляют
расширенную матрицу, в левой части
которой записана данная матрица, а в
правой – единичная. С помощью элементарных
преобразований в левой части создают
единичную матрицу, а в правой автоматически
создается обратная матрица.
Пример.
Найти обратную матрицу для матрицы
Решение. Составим
расширенную матрицу:

строк

первую строку на (-3) и сложим со второй

вторую строку на 8
у

вторую строку на 2 и сложим с первой

.
Обратные матрицы
находят применение, например, в решении
матричных уравнений.
Пример.
Решить матричное уравнение
,
где А, В, С, Х —
квадратные матрицы одинакового порядка,
А – невырожденная.
Решение.
;
Умножим это
уравнение слева на А-1:
.
Получим:
;
.
Соседние файлы в предмете Линейная алгебра
- #
- #
- #
Определитель матрицы и его свойства
8 февраля 2018
В этом уроке мы детально рассмотрим несколько ключевые вопросов и определений, благодаря чему вы раз и навсегда разберётесь и с матрицами, и с определителями, и со всеми их свойствами.
Определители — центральное понятие в алгебре матриц. Подобно формулам сокращённого умножения, они будут преследовать вас на протяжении всего курса высшей математики. Поэтому читаем, смотрим и разбираемся досконально.:)
И начнём мы с самого сокровенного — а что такое матрица? И как правильно с ней работать.
Правильная расстановка индексов в матрице
Матрица — это просто таблица, заполненная числами. Нео тут ни при чём.
Одна из ключевых характеристик матрицы — это её размерность, т.е. количество строк и столбцов, из которых она состоит. Обычно говорят, что некая матрица $A$ имеет размер $left[ mtimes n right]$, если в ней имеется $m$ строк и $n$ столбцов. Записывают это так:
[A=left[ mtimes n right]]
Или вот так:
[A=left( {{a}_{ij}} right),quad 1le ile m;quad 1le jle n.]
Бывают и другие обозначения — тут всё зависит от предпочтений лектора/ семинариста/ автора учебника. Но в любом случае со всеми этими $left[ mtimes n right]$ и ${{a}_{ij}}$ возникает одна и та же проблема:
Какой индекс за что отвечает? Сначала идёт номер строки, затем — столбца? Или наоборот?
При чтении лекций и учебников ответ будет казаться очевидным. Но когда на экзамене перед вами — только листик с задачей, можно переволноваться и внезапно запутаться.
Поэтому давайте разберёмся с этим вопросом раз и навсегда. Для начала вспомним обычную систему координат из школьного курса математики:
Помните её? У неё есть начало координат (точка $O=left( 0;0 right)$) оси $x$и $y$, а каждая точка на плоскости однозначно определяется по координатам: $A=left( 1;2 right)$, $B=left( 3;1 right)$ и т.д.
А теперь давайте возьмём эту конструкцию и поставим её рядом с матрицей так, чтобы начало координат находилось в левом верхнем углу. Почему именно там? Да потому что открывая книгу, мы начинаем читать именно с левого верхнего угла страницы — запомнить это легче лёгкого.
Но куда направить оси? Мы направим их так, чтобы вся наша виртуальная «страница» была охвачена этими осями. Правда, для этого придётся повернуть нашу систему координат. Единственно возможный вариант такого расположения:
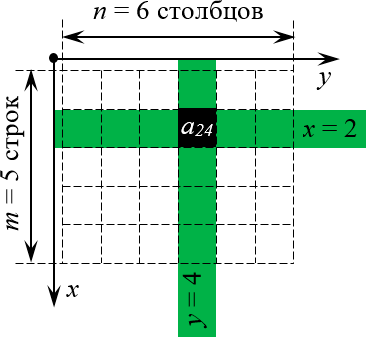
Теперь всякая клетка матрицы имеет однозначные координаты $x$ и $y$. Например запись ${{a}_{24}}$ означает, что мы обращаемся к элементу с координатами $x=2$ и $y=4$. Размеры матрицы тоже однозначно задаются парой чисел:
Просто всмотритесь в эту картинку внимательно. Поиграйтесь с координатами (особенно когда будете работать с настоящими матрицами и определителями) — и очень скоро поймёте, что даже в самых сложных теоремах и определениях вы прекрасно понимаете, о чём идёт речь.
Разобрались? Что ж, переходим к первому шагу просветления — геометрическому определению определителя.:)
Геометрическое определение
Прежде всего хотел бы отметить, что определитель существует только для квадратных матриц вида $left[ ntimes n right]$. Определитель — это число, которое cчитается по определённым правилам и является одной из характеристик этой матрицы (есть другие характеристики: ранг, собственные вектора, но об этом в других уроках).
Ну и что это за характеристика? Что он означает? Всё просто:
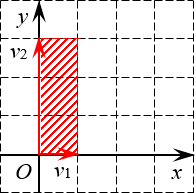
Определитель квадратной матрицы $A=left[ ntimes n right]$ — это объём $n$-мерного параллелепипеда, который образуется, если рассмотреть строки матрицы в качестве векторов, образующих рёбра этого параллелепипеда.
Например, определитель матрицы размера 2×2 — это просто площадь параллелограмма, а для матрицы 3×3 это уже объём 3-мерного параллелепипеда — того самого, который так бесит всех старшеклассников на уроках стереометрии.
На первый взгляд это определение может показаться совершенно неадекватным. Но давайте не будем спешить с выводами — глянем на примеры. На самом деле всё элементарно, Ватсон:
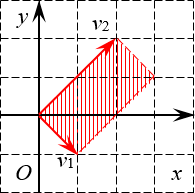
Задача. Найдите определители матриц:
[left| begin{matrix} 1 & 0 \ 0 & 3 \end{matrix} right|quad left| begin{matrix} 1 & -1 \ 2 & 2 \end{matrix} right|quad left| begin{matrix}2 & 0 & 0 \ 1 & 3 & 0 \ 1 & 1 & 4 \end{matrix} right|]
Решение. Первые два определителя имеют размер 2×2. Значит, это просто площади параллелограммов. Начертим их и посчитаем площадь.
Первый параллелограмм построен на векторах ${{v}_{1}}=left( 1;0 right)$ и ${{v}_{2}}=left( 0;3 right)$:
Определитель 2×2 — это площадь параллелограмма Очевидно, это не просто параллелограмм, а вполне себе прямоугольник. Его площадь равна
[S=1cdot 3=3]
Второй параллелограмм построен на векторах ${{v}_{1}}=left( 1;-1 right)$ и ${{v}_{2}}=left( 2;2 right)$. Ну и что с того? Это тоже прямоугольник:
Ещё один определитель 2×2 Стороны этого прямоугольника (по сути — длины векторов) легко считаются по теореме Пифагора:
[begin{align} & left| {{v}_{1}} right|=sqrt{{{1}^{2}}+{{left( -1 right)}^{2}}}=sqrt{2}; \ & left| {{v}_{2}} right|=sqrt{{{2}^{2}}+{{2}^{2}}}=sqrt{8}=2sqrt{2}; \ & S=left| {{v}_{1}} right|cdot left| {{v}_{2}} right|=sqrt{2}cdot 2sqrt{2}=4. \end{align}]
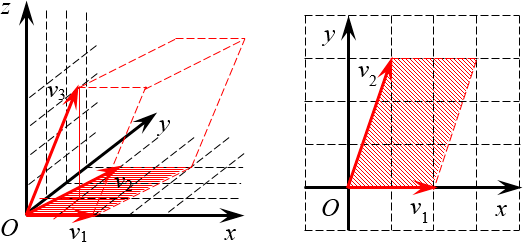
Осталось разобраться с последним определителем — там уже матрица 3×3. Придётся вспоминать стереометрию:
Определитель 3×3 — это объём параллелепипеда Выглядит мозговыносяще, но по факту достаточно вспомнить формулу объёма параллелепипеда:
[V=Scdot h]
где $S$ — площадь основания (в нашем случае это площадь параллелограмма на плоскости $OXY$), $h$ — высота, проведённая к этому основанию (по сути, $z$-координата вектора ${{v}_{3}}$).
Площадь параллелограмма (мы начертили его отдельно) тоже считается легко:
[begin{align} & S=2cdot 3=6; \ & V=Scdot h=6cdot 4=24. \end{align}]
Вот и всё! Записываем ответы.
Ответ: 3; 4; 24.
Небольшое замечание по поводу системы обозначений. Кому-то наверняка не понравится, что я игнорирую «стрелочки» над векторами. Якобы так можно спутать вектор с точкой или ещё с чем.
Но давайте серьёзно: мы с вами уже взрослые мальчики и девочки, поэтому из контекста прекрасно понимаем, когда речь идёт о векторе, а когда — о точке. Стрелки лишь засоряют повествование, и без того под завязку напичканное математическими формулами.
И ещё. В принципе, ничто не мешает рассмотреть и определитель матрицы 1×1 — такая матрица представляет собой просто одну клетку, а число, записанное в этой клетке, и будет определителем. Но тут есть важное замечание:
В отличие от классического объёма, определитель даст нам так называемый «ориентированный объём», т.е. объём с учётом последовательности рассмотрения векторов-строк.
И если вы хотите получить объём в классическом смысле этого слова, придётся взять модуль определителя, но сейчас не стоит париться об этом — всё равно через несколько секунд мы научимся считать любой определитель с любыми знаками, размерами и т.д.:)
Алгебраическое определение
При всей красоте и наглядности геометрического подхода у него есть серьёзный недостаток: он ничего не говорит нам о том, как этот самый определитель считать.
Поэтому сейчас мы разберём альтернативное определение — алгебраическое. Для этого нам потребуется краткая теоретическая подготовка, зато на выходе мы получим инструмент, позволяющий считать в матрицах что и как угодно.
Правда, там появится новая проблема… но обо всём по порядку.
Перестановки и инверсии
Давайте выпишем в строчку числа от 1 до $n$. Получится что-то типа этого:
[1;2;3;4;5;…;n-1;n]
Теперь (чисто по приколу) поменяем парочку чисел местами. Можно поменять соседние:
[1;3;2;4;5;…;n-1;n]
А можно — не особо соседние:
[n;2;3;4;5;…;n-1;1]
И знаете, что? А ничего! В алгебре эта хрень называется перестановкой. И у неё есть куча свойств.
Определение. Перестановка длины $n$ — строка из $n$ различных чисел, записанных в любой последовательности. Обычно рассматриваются первые $n$ натуральных чисел (т.е. как раз числа 1, 2, …, $n$), а затем их перемешивают для получения нужной перестановки.
Обозначаются перестановки так же, как и векторы — просто буквой и последовательным перечислением своих элементов в скобках. Например: $p=left( 1;3;2 right)$ или $p=left( 2;5;1;4;3 right)$. Буква может быть любой, но пусть будет $p$.:)
Далее для простоты изложения будем работать с перестановками длины 5 — они уже достаточно серьёзны для наблюдения всяких подозрительных эффектов, но ещё не настолько суровы для неокрепшего мозга, как перестановки длины 6 и более. Вот примеры таких перестановок:
[begin{align} & {{p}_{1}}=left( 1;2;3;4;5 right) \ & {{p}_{2}}=left( 1;3;2;5;4 right) \ & {{p}_{3}}=left( 5;4;3;2;1 right) \end{align}]
Естественно, перестановку длины $n$ можно рассматривать как функцию, которая определена на множестве $left{ 1;2;…;n right}$ и биективно отображает это множество на себя же. Возвращаясь к только что записанным перестановкам ${{p}_{1}}$, ${{p}_{2}}$ и ${{p}_{3}}$, мы вполне законно можем написать:
[{{p}_{1}}left( 1 right)=1;{{p}_{2}}left( 3 right)=2;{{p}_{3}}left( 2 right)=4;]
Количество различных перестановок длины $n$ всегда ограничено и равно $n!$ — это легко доказуемый факт из комбинаторики. Например, если мы захотим выписать все перестановки длины 5, то мы весьма заколебёмся, поскольку таких перестановок будет
[n!=5!=1cdot 2cdot 3cdot 4cdot 5=120]
Одной из ключевых характеристик всякой перестановки является количество инверсий в ней.
Определение. Инверсия в перестановке $p=left( {{a}_{1}};{{a}_{2}};…;{{a}_{n}} right)$ — всякая пара $left( {{a}_{i}};{{a}_{j}} right)$ такая, что $i lt j$, но ${{a}_{i}} gt {{a}_{j}}$. Проще говоря, инверсия — это когда большее число стоит левее меньшего (не обязательно соседнего).
Мы будем обозначать через $Nleft( p right)$ количество инверсий в перестановке $p$, но будьте готовы встретиться и с другими обозначениями в разных учебниках и у разных авторов — единых стандартов тут нет. Тема инверсий весьма обширна, и ей будет посвящён отдельный урок. Сейчас же наша задача — просто научиться считать их в реальных задачах.
Например, посчитаем количество инверсий в перестановке $p=left( 1;4;5;3;2 right)$:
[left( 4;3 right);left( 4;2 right);left( 5;3 right);left( 5;2 right);left( 3;2 right).]
Таким образом, $Nleft( p right)=5$. Как видите, ничего страшного в этом нет. Сразу скажу: дальше нас будет интересовать не столько само число $Nleft( p right)$, сколько его чётность/ нечётность. И тут мы плавно переходим к ключевому термину сегодняшнего урока.
Что такое определитель
Пусть дана квадратная матрица $A=left[ ntimes n right]$. Тогда:
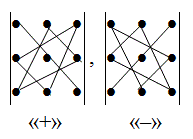
Определение. Определитель матрицы $A=left[ ntimes n right]$ — это алгебраическая сумма $n!$ слагаемых, составленных следующим образом. Каждое слагаемое — это произведение $n$ элементов матрицы, взятых по одному из каждой строки и каждого столбца, умноженное на (−1) в степени количество инверсий:
[left| A right|=sumlimits_{n!}{{{left( -1 right)}^{Nleft( p right)}}cdot {{a}_{1;pleft( 1 right)}}cdot {{a}_{2;pleft( 2 right)}}cdot …cdot {{a}_{n;pleft( n right)}}}]
Принципиальным моментом при выборе множителей для каждого слагаемого в определителе является тот факт, что никакие два множителя не стоят в одной строчке или в одном столбце.
Благодаря этому можно без ограничения общности считать, что индексы $i$ множителей ${{a}_{i;j}}$ «пробегают» значения 1, …, $n$, а индексы $j$ являются некоторой перестановкой от первых:
[j=pleft( i right),quad i=1,2,…,n]
А когда есть перестановка $p$, мы легко посчитаем инверсии $Nleft( p right)$ — и очередное слагаемое определителя готово.
Естественно, никто не запрещает поменять местами множители в каком-либо слагаемом (или во всех сразу — чего мелочиться-то?), и тогда первые индексы тоже будут представлять собой некоторую перестановку. Но в итоге ничего не поменяется: суммарное количество инверсий в индексах $i$ и $j$ сохраняет чётность при подобных извращениях, что вполне соответствует старому-доброму правилу:
От перестановки множителей произведение чисел не меняется.
Вот только не надо приплетать это правило к умножению матриц — в отличие от умножения чисел, оно не коммутативно. Но это я отвлёкся.:)
Матрица 2×2
Вообще-то можно рассмотреть и матрицу 1×1 — это будет одна клетка, и её определитель, как нетрудно догадаться, равен числу, записанному в этой клетке. Ничего интересного.
Поэтому давайте рассмотрим квадратную матрицу размером 2×2:
[left[ begin{matrix} {{a}_{11}} & {{a}_{12}} \ {{a}_{21}} & {{a}_{22}} \end{matrix} right]]
Поскольку количество строк в ней $n=2$, то определитель будет содержать $n!=2!=1cdot 2=2$ слагаемых. Выпишем их:
[begin{align} & {{left( -1 right)}^{Nleft( 1;2 right)}}cdot {{a}_{11}}cdot {{a}_{22}}={{left( -1 right)}^{0}}cdot {{a}_{11}}cdot {{a}_{22}}={{a}_{11}}{{a}_{22}}; \ & {{left( -1 right)}^{Nleft( 2;1 right)}}cdot {{a}_{12}}cdot {{a}_{21}}={{left( -1 right)}^{1}}cdot {{a}_{12}}cdot {{a}_{21}}={{a}_{12}}{{a}_{21}}. \end{align}]
Очевидно, что в перестановке $left( 1;2 right)$, состоящей из двух элементов, нет инверсий, поэтому $Nleft( 1;2 right)=0$. А вот в перестановке $left( 2;1 right)$ одна инверсия имеется (собственно, 2 < 1), поэтому $Nleft( 2;1 right)=1.$
Итого универсальная формула вычисления определителя для матрицы 2×2 выглядит так:
[left| begin{matrix} {{a}_{11}} & {{a}_{12}} \ {{a}_{21}} & {{a}_{22}} \end{matrix} right|={{a}_{11}}{{a}_{22}}-{{a}_{12}}{{a}_{21}}]
Графически это можно представить как произведение элементов, стоящих на главной диагонали, минус произведение элементов на побочной:
Рассмотрим пару примеров:
Задача. Вычислите определитель:
[left| begin{matrix} 5 & 6 \ 8 & 9 \end{matrix} right|;quad left| begin{matrix} 7 & 12 \ 14 & 1 \end{matrix} right|.]
Решение. Всё считается в одну строчку. Первая матрица:
[5cdot 9-8cdot 6=45-48=-3]
И вторая:
[7cdot 1-14cdot 12=7-168=-161]
Ответ: −3; −161.
Впрочем, это было слишком просто. Давайте рассмотрим матрицы 3×3 — там уже интересно.
Матрица 3×3
Теперь рассмотрим квадратную матрицу размера 3×3:
[left[ begin{matrix} {{a}_{11}} & {{a}_{12}} & {{a}_{13}} \ {{a}_{21}} & {{a}_{22}} & {{a}_{23}} \ {{a}_{31}} & {{a}_{32}} & {{a}_{33}} \end{matrix} right]]
При вычислении её определителя мы получим $3!=1cdot 2cdot 3=6$ слагаемых — ещё не слишком много для паники, но уже достаточно, чтобы начать искать какие-то закономерности. Для начала выпишем все перестановки из трёх элементов и посчитаем инверсии в каждой из них:
[begin{align} & {{p}_{1}}=left( 1;2;3 right)Rightarrow Nleft( {{p}_{1}} right)=Nleft( 1;2;3 right)=0; \ & {{p}_{2}}=left( 1;3;2 right)Rightarrow Nleft( {{p}_{2}} right)=Nleft( 1;3;2 right)=1; \ & {{p}_{3}}=left( 2;1;3 right)Rightarrow Nleft( {{p}_{3}} right)=Nleft( 2;1;3 right)=1; \ & {{p}_{4}}=left( 2;3;1 right)Rightarrow Nleft( {{p}_{4}} right)=Nleft( 2;3;1 right)=2; \ & {{p}_{5}}=left( 3;1;2 right)Rightarrow Nleft( {{p}_{5}} right)=Nleft( 3;1;2 right)=2; \ & {{p}_{6}}=left( 3;2;1 right)Rightarrow Nleft( {{p}_{6}} right)=Nleft( 3;2;1 right)=3. \end{align}]
Как и предполагалось, всего выписано 6 перестановок ${{p}_{1}}$, … ${{p}_{6}}$ (естественно, можно было бы выписать их в другой последовательности — суть от этого не изменится), а количество инверсий в них меняется от 0 до 3.
В общем, у нас будет три слагаемых с «плюсом» (там, где $Nleft( p right)$ — чётное) и ещё три с «минусом». А в целом определитель будет считаться по формуле:
[left| begin{matrix} {{a}_{11}} & {{a}_{12}} & {{a}_{13}} \ {{a}_{21}} & {{a}_{22}} & {{a}_{23}} \ {{a}_{31}} & {{a}_{32}} & {{a}_{33}} \end{matrix} right|=begin{matrix} {{a}_{11}}{{a}_{22}}{{a}_{33}}+{{a}_{12}}{{a}_{23}}{{a}_{31}}+{{a}_{13}}{{a}_{21}}{{a}_{32}}- \ -{{a}_{13}}{{a}_{22}}{{a}_{31}}-{{a}_{12}}{{a}_{21}}{{a}_{33}}-{{a}_{11}}{{a}_{23}}{{a}_{32}} \end{matrix}]
Вот только не надо сейчас садиться и яростно зубрить все эти индексы! Вместо непонятных цифр лучше запомните следующее мнемоническое правило:
Правило треугольника. Для нахождения определителя матрицы 3×3 нужно сложить три произведения элементов, стоящих на главной диагонали и в вершинах равнобедренных треугольников со стороной, параллельной этой диагонали, а затем вычесть такие же три произведения, но на побочной диагонали. Схематически это выглядит так:
Определитель матрицы 3×3: правило треугольников
Именно эти треугольники (или пентаграммы — кому как больше нравится) любят рисовать во всяких учебниках и методичках по алгебре. Впрочем, не будем о грустном. Давайте лучше посчитаем один такой определитель — для разминки перед настоящей жестью.:)
Задача. Вычислите определитель:
[left| begin{matrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 1 \end{matrix} right|]
Решение. Работаем по правилу треугольников. Сначала посчитаем три слагаемых, составленных из элементов на главной диагонали и параллельно ей:
[begin{align} & 1cdot 5cdot 1+2cdot 6cdot 7+3cdot 4cdot 8= \ & =5+84+96=185 \end{align}]
Теперь разбираемся с побочной диагональю:
[begin{align} & 3cdot 5cdot 7+2cdot 4cdot 1+1cdot 6cdot 8= \ & =105+8+48=161 \end{align}]
Осталось лишь вычесть из первого числа второе — и мы получим ответ:
[185-161=24]
Вот и всё!
Ответ: 24.
Тем не менее, определители матриц 3×3 — это ещё не вершина мастерства. Самое интересное ждёт нас дальше.:)
Общая схема вычисления определителей
Как мы знаем, с ростом размерности матрицы $n$ количество слагаемых в определителе составляет $n!$ и быстро растёт. Всё-таки факториал — это вам не хрен собачий довольно быстро растущая функция.
Уже для матриц 4×4 считать определители напролом (т.е. через перестановки) становится как-то не оч. Про 5×5 и более вообще молчу. Поэтому к делу подключаются некоторые свойства определителя, но для их понимания нужна небольшая теоретическая подготовка.
Готовы? Поехали!
Что такое минор матрицы
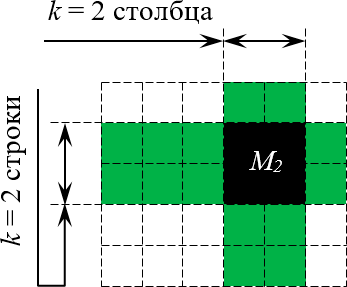
Пусть дана произвольная матрица $A=left[ mtimes n right]$. Заметьте: не обязательно квадратная. В отличие от определителей, миноры — это такие няшки, которые существуют не только в суровых квадратных матрицах. Выберем в этой матрице несколько (например, $k$) строк и столбцов, причём $1le kle m$ и $1le kle n$. Тогда:
Определение. Минор порядка $k$ — определитель квадратной матрицы, возникающей на пересечении выбранных $k$ столбцов и строк. Также минором мы будем называть и саму эту новую матрицу.
Обозначается такой минор ${{M}_{k}}$. Естественно, у одной матрицы может быть целая куча миноров порядка $k$. Вот пример минора порядка 2 для матрицы $left[ 5times 6 right]$:
Выбор $k = 2$ столбцов и строк для формирования минора
Совершенно необязательно, чтобы выбранные строки и столбцы стояли рядом, как в рассмотренном примере. Главное, чтобы количество выбранных строк и столбцов было одинаковым (это и есть число $k$).
Есть и другое определение. Возможно, кому-то оно больше придётся по душе:
Определение. Пусть дана прямоугольная матрица $A=left[ mtimes n right]$. Если после вычеркивания в ней одного или нескольких столбцов и одной или нескольких строк образуется квадратная матрица размера $left[ ktimes k right]$, то её определитель — это и есть минор ${{M}_{k}}$. Саму матрицу мы тоже иногда будем называть минором — это будет ясно из контекста.
Как говорил мой кот, иногда лучше один раз навернуться с 11-го этажа есть корм, чем мяукать, сидя на балконе.
Пример. Пусть дана матрица
[A=left[ begin{matrix} begin{matrix} 1 \ 2 \ 3 \end{matrix} & begin{matrix} 7 \ 4 \ 0 \end{matrix} & begin{matrix} 9 \ 5 \ 6 \end{matrix} & begin{matrix} 0 \ 3 \ 1 \end{matrix} \end{matrix} right]]
Выбирая строку 1 и столбец 2, получаем минор первого порядка:
[{{M}_{1}}=left| 7 right|=7]
Выбирая строки 2, 3 и столбцы 3, 4, получаем минор второго порядка:
[{{M}_{2}}=left| begin{matrix} 5 & 3 \ 6 & 1 \end{matrix} right|=5-18=-13]
А если выбрать все три строки, а также столбцы 1, 2, 4, будет минор третьего порядка:
[{{M}_{3}}=left| begin{matrix} 1 & 7 & 0 \ 2 & 4 & 3 \ 3 & 0 & 1 \end{matrix} right|]
Считать этот определитель мне уже в лом. Но он равен 53.:)
Читателю не составит труда найти и другие миноры порядков 1, 2 или 3. Поэтому идём дальше.
Алгебраические дополнения
«Ну ok, и что дают нам эти миньоны миноры?» — наверняка спросите вы. Сами по себе — ничего. Но в квадратных матрицах у каждого минора появляется «компаньон» — дополнительный минор, а также алгебраическое дополнение. И вместе эти два ушлёпка позволят нам щёлкать определители как орешки.
Определение. Пусть дана квадратная матрица $A=left[ ntimes n right]$, в которой выбран минор ${{M}_{k}}$. Тогда дополнительный минор для минора ${{M}_{k}}$ — это кусок исходной матрицы $A$, который останется при вычёркивании всех строк и столбцов, задействованных при составлении минора ${{M}_{k}}$:
Дополнительный минор к минору ${{M}_{2}}$ Уточним один момент: дополнительный минор — это не просто «кусок матрицы», а определитель этого куска.
Обозначаются дополнительные миноры с помощью «звёздочки»: $M_{k}^{*}$:
[M_{k}^{*}=left| Anabla {{M}_{k}} right|]
где операция $Anabla {{M}_{k}}$ буквально означает «вычеркнуть из $A$ строки и столбцы, входящие в ${{M}_{k}}$». Эта операция не является общепринятой в математике — я её сам только что придумал для красоты повествования.:)
Дополнительные миноры редко используются сами по себе. Они являются частью более сложной конструкции — алгебраического дополнения.
Определение. Алгебраическое дополнение минора ${{M}_{k}}$ — это дополнительный минор $M_{k}^{*}$, умноженный на величину ${{left( -1 right)}^{S}}$, где $S$ — сумма номеров всех строк и столбцов, задействованных в исходном миноре ${{M}_{k}}$.
Как правило, алгебраическое дополнение минора ${{M}_{k}}$ обозначается через ${{A}_{k}}$. Поэтому:
[{{A}_{k}}={{left( -1 right)}^{S}}cdot M_{k}^{*}]
Сложно? На первый взгляд — да. Но это не точно. Потому что на самом деле всё легко. Рассмотрим пример:
Пример. Дана матрица 4×4:
[A=left[ begin{matrix} 1 & 2 & 3 & 4 \ 5 & 6 & 7 & 8 \ 9 & 10 & 11 & 12 \ 13 & 14 & 15 & 16 \end{matrix} right]]
Выберем минор второго порядка
[{{M}_{2}}=left| begin{matrix} 3 & 4 \ 15 & 16 \end{matrix} right|]
Капитан Очевидность как бы намекает нам, что при составлении этого минора были задействованы строки 1 и 4, а также столбцы 3 и 4. Вычёркиваем их — получим дополнительный минор:
[M_{2}^{*}=left| begin{matrix} 5 & 6 \ 9 & 10 \end{matrix} right|=50-54=-4]
Осталось найти число $S$ и получить алгебраическое дополнение. Поскольку мы знаем номера задействованных строк (1 и 4) и столбцов (3 и 4), всё просто:
[begin{align} & S=1+4+3+4=12; \ & {{A}_{2}}={{left( -1 right)}^{S}}cdot M_{2}^{*}={{left( -1 right)}^{12}}cdot left( -4 right)=-4end{align}]
Ответ: ${{A}_{2}}=-4$
Вот и всё! По сути, всё различие между дополнительным минором и алгебраическим дополнением — только в минусе спереди, да и то не всегда.
Наша задача сейчас — научиться быстро считать алгебраические дополнения, потому что они являются составной частью «Теоремы, Которую Нельзя Называть». Но мы всё же назовём. Встречайте:
Теорема Лапласа
И вот мы пришли к тому, зачем, собственно, все эти миноры и алгебраические дополнения были нужны.
Теорема Лапласа о разложении определителя. Пусть в матрице размера $left[ ntimes n right]$ выбрано $k$ строк (столбцов), причём $1le kle n-1$. Тогда определитель этой матрицы равен сумме всех произведений миноров порядка $k$, содержащихся в выбранных строках (столбцах), на их алгебраические дополнения:
[left| A right|=sum{{{M}_{k}}cdot {{A}_{k}}}]
Причём таких слагаемых будет ровно $C_{n}^{k}$.
Ладно, ладно: про $C_{n}^{k}$ — это я уже понтуюсь, в оригинальной теореме Лапласа ничего такого не было. Но комбинаторику никто не отменял, и буквально беглый взгляд на условие позволит вам самостоятельно убедиться, что слагаемых будет именно столько.:)
Мы не будем её доказывать, хоть это и не представляет особой трудности — все выкладки сводятся к старым-добрым перестановкам и чётности/ нечётности инверсий. Тем не менее, доказательство будет представлено в отдельном параграфе, а сегодня у нас сугубо практический урок.
Поэтому переходим к частному случаю этой теоремы, когда миноры представляют собой отдельные клетки матрицы.
Разложение определителя по строке и столбцу
То, о чём сейчас пойдёт речь — как раз и есть основной инструмент работы с определителями, ради которого затевались вся эта дичь с перестановками, минорами и алгебраическими дополнениями.
Читайте и наслаждайтесь:
Следствие из Теоремы Лапласа (разложение определителя по строке/столбцу). Пусть в матрице размера $left[ ntimes n right]$ выбрана одна строка. Минорами в этой строке будут $n$ отдельных клеток:
[{{M}_{1}}={{a}_{ij}},quad j=1,…,n]
Дополнительные миноры тоже легко считаются: просто берём исходную матрицу и вычёркиваем строку и столбец, содержащие ${{a}_{ij}}$. Назовём такие миноры $M_{ij}^{*}$.
Для алгебраического дополнения ещё нужно число $S$, но в случае с минором порядка 1 это просто сумма «координат» клетки ${{a}_{ij}}$:
[S=i+j]
И тогда исходный определитель можно расписать через ${{a}_{ij}}$ и $M_{ij}^{*}$ согласно теореме Лапласа:
[left| A right|=sumlimits_{j=1}^{n}{{{a}_{ij}}cdot {{left( -1 right)}^{i+j}}cdot {{M}_{ij}}}]
Это и есть формула разложения определителя по строке. Но то же верно и для столбцов.
Из этого следствия можно сразу сформулировать несколько выводов:
- Эта схема одинаково хорошо работает как для строк, так и для столбцов. На самом деле чаще всего разложение будет идти именно по столбцам, нежели по строкам.
- Количество слагаемых в разложении всегда ровно $n$. Это существенно меньше $C_{n}^{k}$ и уж тем более $n!$.
- Вместо одного определителя $left[ ntimes n right]$ придётся считать несколько определителей размера на единицу меньше: $left[ left( n-1 right)times left( n-1 right) right]$.
Последний факт особенно важен. Например, вместо зверского определителя 4×4 теперь достаточно будет посчитать несколько определителей 3×3 — с ними мы уж как-нибудь справимся.:)
Что ж, попробуем посчитать одну такую задачку?
Задача. Найдите определитель:
[left| begin{matrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 9 \end{matrix} right|]
Решение. Разложим этот определитель по первой строке:
[begin{align} left| A right|=1cdot {{left( -1 right)}^{1+1}}cdot left| begin{matrix} 5 & 6 \ 8 & 9 \end{matrix} right|+ & \ 2cdot {{left( -1 right)}^{1+2}}cdot left| begin{matrix} 4 & 6 \ 7 & 9 \end{matrix} right|+ & \ 3cdot {{left( -1 right)}^{1+3}}cdot left| begin{matrix} 4 & 5 \ 7 & 8 \end{matrix} right|= & \end{align}]
[begin{align} & =1cdot left( 45-48 right)-2cdot left( 36-42 right)+3cdot left( 32-35 right)= \ & =1cdot left( -3 right)-2cdot left( -6 right)+3cdot left( -3 right)=0. \end{align}]
Ответ: 0.
Задача. Найдите определитель:
[left| begin{matrix} 0 & 1 & 1 & 0 \ 1 & 0 & 1 & 1 \ 1 & 1 & 0 & 1 \ 1 & 1 & 1 & 0 \end{matrix} right|]
Решение. Для разнообразия давайте в этот раз работать со столбцами. Например, в последнем столбце присутствуют сразу два нуля — очевидно, это значительно сократит вычисления. Сейчас увидите почему.
Итак, раскладываем определитель по четвёртому столбцу:
[begin{align} left| begin{matrix} 0 & 1 & 1 & 0 \ 1 & 0 & 1 & 1 \ 1 & 1 & 0 & 1 \ 1 & 1 & 1 & 0 \end{matrix} right|=0cdot {{left( -1 right)}^{1+4}}cdot left| begin{matrix} 1 & 0 & 1 \ 1 & 1 & 0 \ 1 & 1 & 1 \end{matrix} right|+ & \ +1cdot {{left( -1 right)}^{2+4}}cdot left| begin{matrix} 0 & 1 & 1 \ 1 & 1 & 0 \ 1 & 1 & 1 \end{matrix} right|+ & \ +1cdot {{left( -1 right)}^{3+4}}cdot left| begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 1 \end{matrix} right|+ & \ +0cdot {{left( -1 right)}^{4+4}}cdot left| begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right| & \end{align}]
И тут — о, чудо! — два слагаемых сразу улетают коту под хвост, поскольку в них есть множитель «0». Остаётся ещё два определителя 3×3, с которыми мы легко разберёмся:
[begin{align} & left| begin{matrix} 0 & 1 & 1 \ 1 & 1 & 0 \ 1 & 1 & 1 \end{matrix} right|=0+0+1-1-1-0=-1; \ & left| begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 1 \end{matrix} right|=0+1+1-0-0-1=1. \end{align}]
Возвращаемся к исходнику и находим ответ:
[left| begin{matrix} 0 & 1 & 1 & 0 \ 1 & 0 & 1 & 1 \ 1 & 1 & 0 & 1 \ 1 & 1 & 1 & 0 \end{matrix} right|=1cdot left( -1 right)+left( -1 right)cdot 1=-2]
Ну вот и всё. И никаких 4! = 24 слагаемых считать не пришлось.:)
Ответ: −2
Основные свойства определителя
В последней задаче мы видели, как наличие нулей в строках (столбцах) матрицы резко упрощает разложение определителя и вообще все вычисления. Возникает естественный вопрос: а нельзя ли сделать так, чтобы эти нули появились даже в той матрице, где их изначально не было?
Ответ однозначен: можно. И здесь нам на помощь приходят свойства определителя:
- Если поменять две строчки (столбца) местами, определитель поменяет знак;
- Если одну строку (столбец) умножить на число $k$, то весь определитель тоже умножится на число $k$;
- Если взять одну строку и прибавить (вычесть) её сколько угодно раз из другой, определитель не изменится;
- Если две строки определителя одинаковы, либо пропорциональны, либо одна из строк заполнена нулями, то весь определитель равен нулю;
- Все указанные выше свойства верны и для столбцов.
- При транспонировании матрицы определитель не меняется;
- Определитель произведения матриц равен произведению определителей.
Особую ценность представляет третье свойство: мы можем вычитать из одной строки (столбца) другую до тех пор, пока в нужных местах не появятся нули.
Чаще всего расчёты сводится к тому, чтобы «обнулить» весь столбец везде, кроме одного элемента, а затем разложить определитель по этому столбцу, получив матрицу размером на 1 меньше.
Давайте посмотрим, как это работает на практике:
Задача. Найдите определитель:
[left| begin{matrix} 1 & 2 & 3 & 4 \ 4 & 1 & 2 & 3 \ 3 & 4 & 1 & 2 \ 2 & 3 & 4 & 1 \end{matrix} right|]
Решение. Нулей тут как бы вообще не наблюдается, поэтому можно «долбить» по любой строке или столбцу — объём вычислений будет примерно одинаковым. Давайте не будем мелочиться и «обнулим» первый столбец: в нём уже есть клетка с единицей, поэтому просто возьмём первую строчку и вычтем её 4 раза из второй, 3 раза из третьей и 2 раза из последней.
В результате мы получим новую матрицу, но её определитель будет тем же:
[begin{matrix} left| begin{matrix} 1 & 2 & 3 & 4 \ 4 & 1 & 2 & 3 \ 3 & 4 & 1 & 2 \ 2 & 3 & 4 & 1 \end{matrix} right|begin{matrix} downarrow \ -4 \ -3 \ -2 \end{matrix}= \ =left| begin{matrix} 1 & 2 & 3 & 4 \ 4-4cdot 1 & 1-4cdot 2 & 2-4cdot 3 & 3-4cdot 4 \ 3-3cdot 1 & 4-3cdot 2 & 1-3cdot 3 & 2-3cdot 4 \ 2-2cdot 1 & 3-2cdot 2 & 4-2cdot 3 & 1-2cdot 4 \end{matrix} right|= \ =left| begin{matrix} 1 & 2 & 3 & 4 \ 0 & -7 & -10 & -13 \ 0 & -2 & -8 & -10 \ 0 & -1 & -2 & -7 \end{matrix} right| \end{matrix}]
Теперь с невозмутимостью Пятачка раскладываем этот определитель по первому столбцу:
[begin{matrix} 1cdot {{left( -1 right)}^{1+1}}cdot left| begin{matrix} -7 & -10 & -13 \ -2 & -8 & -10 \ -1 & -2 & -7 \end{matrix} right|+0cdot {{left( -1 right)}^{2+1}}cdot left| … right|+ \ +0cdot {{left( -1 right)}^{3+1}}cdot left| … right|+0cdot {{left( -1 right)}^{4+1}}cdot left| … right| \end{matrix}]
Понятно, что «выживет» только первое слагаемое — в остальных я даже определители не выписывал, поскольку они всё равно умножаются на ноль. Коэффициент перед определителем равен единице, т.е. его можно не записывать.
Зато можно вынести «минусы» из всех трёх строк определителя. По сути, мы трижды вынесли множитель (−1):
[left| begin{matrix} -7 & -10 & -13 \ -2 & -8 & -10 \ -1 & -2 & -7 \end{matrix} right|=cdot left| begin{matrix} 7 & 10 & 13 \ 2 & 8 & 10 \ 1 & 2 & 7 \end{matrix} right|]
Получили мелкий определитель 3×3, который уже можно посчитать по правилу треугольников. Но мы попробуем разложить и его по первому столбцу — благо в последней строчке гордо стоит единица:
[begin{align} & left( -1 right)cdot left| begin{matrix} 7 & 10 & 13 \ 2 & 8 & 10 \ 1 & 2 & 7 \end{matrix} right|begin{matrix} -7 \ -2 \ uparrow \end{matrix}=left( -1 right)cdot left| begin{matrix} 0 & -4 & -36 \ 0 & 4 & -4 \ 1 & 2 & 7 \end{matrix} right|= \ & =cdot left| begin{matrix} -4 & -36 \ 4 & -4 \end{matrix} right|=left( -1 right)cdot left| begin{matrix} -4 & -36 \ 4 & -4 \end{matrix} right| \end{align}]
Можно, конечно, ещё поприкалываться и разложить матрицу 2×2 по строке (столбцу), но мы же с вами адекватны, поэтому просто посчитаем ответ:
[left( -1 right)cdot left| begin{matrix} -4 & -36 \ 4 & -4 \end{matrix} right|=left( -1 right)cdot left( 16+144 right)=-160]
Вот так и разбиваются мечты. Всего-то −160 в ответе.:)
Ответ: −160.
Парочка замечаний перед тем, как мы перейдём к последней задаче:
- Исходная матрица была симметрична относительно побочной диагонали. Все миноры в разложении тоже симметричны относительно той же побочной диагонали.
- Строго говоря, мы могли вообще ничего не раскладывать, а просто привести матрицу к верхнетреугольному виду, когда под главной диагональю стоят сплошные нули. Тогда (в точном соответствии с геометрической интерпретацией, кстати) определитель равен произведению ${{a}_{ii}}$ — чисел на главной диагонали.
Идём дальше. Последняя задача в сегодняшнем уроке.
Задача. Найдите определитель:
[left| begin{matrix} 1 & 1 & 1 & 1 \ 2 & 4 & 8 & 16 \ 3 & 9 & 27 & 81 \ 5 & 25 & 125 & 625 \end{matrix} right|]
Решение. Ну, тут первая строка прямо-таки напрашивается на «обнуление». Берём первый столбец и вычитаем ровно один раз из всех остальных:
[begin{align} & left| begin{matrix} 1 & 1 & 1 & 1 \ 2 & 4 & 8 & 16 \ 3 & 9 & 27 & 81 \ 5 & 25 & 125 & 625 \end{matrix} right|= \ & =left| begin{matrix} 1 & 1-1 & 1-1 & 1-1 \ 2 & 4-2 & 8-2 & 16-2 \ 3 & 9-3 & 27-3 & 81-3 \ 5 & 25-5 & 125-5 & 625-5 \end{matrix} right|= \ & =left| begin{matrix} 1 & 0 & 0 & 0 \ 2 & 2 & 6 & 14 \ 3 & 6 & 24 & 78 \ 5 & 20 & 120 & 620 \end{matrix} right| \end{align}]
Раскладываем по первой строке, а затем выносим общие множители из оставшихся строк:
[cdot left| begin{matrix} 2 & 6 & 14 \ 6 & 24 & 78 \ 20 & 120 & 620 \end{matrix} right|=cdot left| begin{matrix} 1 & 3 & 7 \ 1 & 4 & 13 \ 1 & 6 & 31 \end{matrix} right|]
Снова наблюдаем «красивые» числа, но уже в первом столбце — раскладываем определитель по нему:
[begin{align} & 240cdot left| begin{matrix} 1 & 3 & 7 \ 1 & 4 & 13 \ 1 & 6 & 31 \end{matrix} right|begin{matrix} downarrow \ -1 \ -1 \end{matrix}=240cdot left| begin{matrix} 1 & 3 & 7 \ 0 & 1 & 6 \ 0 & 3 & 24 \end{matrix} right|= \ & =240cdot {{left( -1 right)}^{1+1}}cdot left| begin{matrix} 1 & 6 \ 3 & 24 \end{matrix} right|= \ & =240cdot 1cdot left( 24-18 right)=1440 \end{align}]
Порядок. Задача решена.
Ответ: 1440
Всё. Хорош читать этот бред.:)
Смотрите также:
- Обратная матрица
- Умножение матриц
- Геометрическая вероятность
- Решение задач B12: №448—455
- Задачи на проценты: формула, упрощающая вычисления
- Задача B4 про три дороги — стандартная задача на движение
Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 
элементов главной диагонали отнять произведение
элементов побочной диагонали:
$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком «минус»:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.
Решение.
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$
$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$
$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй — пять третьих и от четвертой — три третьих строки, получаем:
$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$
Полученный определитель разложим по элементам первого столбца:
$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$
$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$
Ответ. $Delta=-80$
Теорема Лапласа
Теорема
Пусть $Delta$ — определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$
Решение. Выберем в данном определителе пятого порядка две строки —
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$
$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$
$$=-23+128+90=195$$
Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$
Читать дальше: обратная матрица.


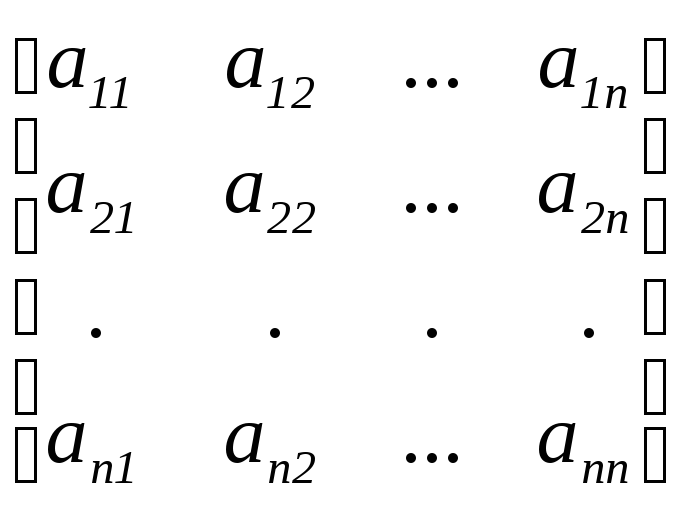

 .
.