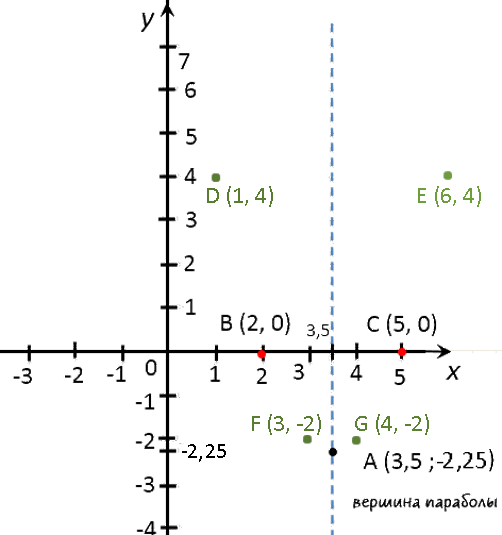Как найти дополнительные точки для построения параболы - Исправление недочетов и поиск решений вместе с Examum.ru

Home » 8 класс » Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?

Урок: как построить параболу или квадратичную функцию?

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Парабола — это график функции описанный формулой ax²+bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:

1 ) Формула параболы y=ax²+bx+c,
если а>0 то ветви параболы направленны вверх,
а<0 то ветви параболы направлены вниз.
Свободный член c эта точке пересекается параболы с осью OY;

2 ) Вершина параболы, ее находят по формуле x=(-b)/2a, найденный x подставляем в уравнение параболы и находим y;

3) Нули функции или по другому точки пересечения параболы с осью OX они еще называются корнями уравнения. Чтобы найти корни мы уравнение приравниваем к 0 ax²+bx+c=0;

Виды уравнений:

a) Полное квадратное уравнение имеет вид ax²+bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax²+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax²+bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax²+c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);

Как решать квадратные уравнения посмотреть тут.

4) Найти несколько дополнительных точек для построения функции.

ПРАКТИЧЕСКАЯ ЧАСТЬ

И так теперь на примере разберем все по действиям:
Пример №1:
y=x²+4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2)²+4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x²+4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b²-4ac=16-12=4
x=(-b±√(D))/2a
x₁=(-4+2)/2=-1
x₂=(-4-2)/2=-3

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2

х -4 -3 -1 0
у 3 0 0 3

Подставляем вместо х в уравнение y=x²+4x+3 значения
y=(-4)²+4*(-4)+3=16-16+3=3
y=(-3)²+4*(-3)+3=9-12+3=0
y=(-1)²+4*(-1)+3=1-4+3=0
y=(0)²+4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2

Пример №2:
y=-x²+4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1<0.
a=-1 b=4 c=0 x=(-b)/2a=(-4)/(2*(-1))=2 y=-(2)²+4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x²+4x=0
Неполное квадратное уравнение вида ax²+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x²+4x значения
y=0²+4*0=0
y=-(1)²+4*1=-1+4=3
y=-(3)²+4*3=-9+13=3
y=-(4)²+4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2

Пример №3
y=x²-4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0)²-4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x²-4=0
Неполное квадратное уравнение вида ax² +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x²=4
x₁=2
x₂=-2

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x²-4 значения
y=(-2)²-4=4-4=0
y=(-1)²-4=1-4=-3
y=1²-4=1-4=-3
y=2²-4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0

Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.

Источник

Свершилось! Она самая. Готовая раскрыть немало тайн. Каноническое уравнение параболы имеет вид , где – действительное число. Нетрудно понять,

что в своём стандартном положении парабола «лежит на боку» и её вершина находится в начале координат. При этом функция задаёт верхнюю ветвь данной линии, а функция –

нижнюю ветвь. Очевидно, что парабола симметрична относительно оси . Собственно, чего

париться, разберём всё в одной задаче:

Задача 101

Построить параболу

Решение: вершина параболы очевидна, найдём дополнительные точки. Уравнение определяет верхнюю дугу параболы, уравнение –

нижнюю дугу. Вычисления удобно провести «под одной гребёнкой» :

Отмечаем найденные точки на чертеже и аккуратно соединяем их линией:
Параболой называется множество всех точек плоскости,

равноудалённых от данной точки и данной прямой , не проходящей через точку .

Определение параболы понимается ещё проще, чем определения эллипса и гиперболы. Для любой точки параболы

длина отрезка (расстояние от точки до фокуса) равна длине перпендикуляра (расстоянию от точки до директрисы):

Точка называется фокусом параболы, а прямая – директрисой параболы (пишется с одной «эс»).

Константа «пэ» канонического уравнения называется фокальным параметром параболы, в данном случае . При этом фокус имеет координаты , а директриса задаётся уравнением .

В нашем примере: .

Поздравляю! Многие из вас сегодня сделали самое настоящие открытие!

Оказывается, гипербола и парабола вовсе не являются графиками «рядовых» функций, а имеют ярко выраженное геометрическое происхождение.

Очевидно, что при увеличении фокального параметра ветви графика будут

«раздаваться» вверх и вниз, бесконечно близко приближаясь к оси . При

уменьшении же значения «пэ» они начнут сжиматься и вытягиваться вдоль оси

Эксцентриситет любой параболы равен единице:

3.5.2. Поворот и параллельный перенос параболы

3.4.5. Поворот и параллельный перенос гиперболы

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

График квадратичной функции

График квадратичной функции y=ax²+bx+c, (где a, b, c — числа, причём a≠0) — парабола. При a>0 ветви параболы направлены вверх, при a<0 — вниз.

Как и в частном случае — y=±x²+bx+c — существуют различные способы построения графика функции y=ax²+bx+c. Рассмотрим два из них.

I способ — по точкам.

1) Ищем координаты вершины параболы.

2) Находим точки пересечения графика с осями координат.

3) Для более точного изображения графика подбираем дополнительные точки. Прямая, проходящая через вершину параболы параллельно оси Ox, является осью симметрии параболы. Поэтому в качестве дополнительных точек можно взять несколько точек либо справа, либо слева от вершины (где проще находить y), после чего построить симметричные им точки.

Примеры.

1) Построить график функции y=0,25x²+0,5x-4,75.

Решение:

y=0,25x²+0,5x-4,75 — квадратичная функция. График — парабола ветвями вверх (так как a=0,25>0). Координаты вершины параболы

$[{x_o} = frac{{ - b}}{{2a}} = frac{{ - 0,5}}{{2 cdot 0,25}} = - 1,]$

$[{y_o} = 0,25cdot{( - 1)^2} + 0,5cdot( - 1) - 4,75 = - 5.]$

Первая точка графика — (-1; -5).

Ищем точки пересечения параболы с осями координат. В точке пересечения с осью Ox y=0, то есть нужно решить уравнение 0,25x²+0,5x-4,75=0. Его дискриминант равен 5, искать корни смысла нет, поскольку положение точек в этом случае можно найти только приближенно.

В точках пересечения с осью Oy x=0, поэтому y(0)=0,25∙0²+0,5∙0-4,75=-4,75.

Вторая точка графика — (0; -4,75).

Прямая x= -1, проходящая через вершину параболы параллельно оси Ox, является осью симметрии параболы.

В качестве дополнительных берем точки справа от оси симметрии (проще вычислять y).

Найдём значение функции при x=1, x=3, x=5 и x=7 (удобнее брать нечётные значения x, поскольку в этом случае получаем целые значения y).

y(1)=0,25∙1²+0,5∙1-4,75=-4, точка (1; -4);

y(3)=0,25∙3²+0,5∙3-4,75=-1, точка (3; -1);

y(5)=0,25∙5²+0,5∙5-4,75=4, точка (5; 4);

y(7)=0,25∙7²+0,5∙7-4,75=11, точка (7; 11).

Найденные точки отмечаем на координатной плоскости. Строим точки, симметричные отмеченным относительно прямой x= -1. Через полученные точки проводим параболу:

График квадратичной функции y=0,25x²+0,5x-4,75

2) Построить график функции y= -2x²+12x-10.

Решение:

y= -2x²+12x-10 — квадратичная функция. График — парабола ветвями вверх (так как a=-2<0).

Координаты вершины параболы

$[{x_o} = frac{{ - b}}{{2a}} = frac{{ - 12}}{{2 cdot ( - 2)}} = 3,]$

$[{y_o} = - 2 cdot {3^2} + 12 cdot 3 - 10 = 8.]$

(3; — вершина, x=3 — ось симметрии параболы.

В точках пересечения графика с осью Ox y=0, то есть решаем уравнение -2x²+12x-10=0. Его корни — x=1 и x=5. Получили точки графика (1; 0) и (5; 0).

В точке пересечения графика с осью Oy x=0:

y= -2∙0²+12∙0-10= -10. Точка графика — (0; -10).

Дополнительную точку возьмём справа от оси симметрии: x=2.

y= -2∙2²+12∙2-10= 6, (2; 6).

Найденные 5 точек отмечаем на координатной плоскости. Находим еще две точки, симметричные относительно прямой x=3 точкам (0; -10) и (2; 6). Через эти семь точек проводим параболу:

График квадратичной функции y=-2x²+12x-10

3) Построить график функции

$[y = frac{1}{3}{x^2} - x + 2]$

Решение:

$[y = frac{1}{3}{x^2} - x + 2]$

— квадратичная функции. Её графиком является парабола, ветви которой направлены вверх (так как a=1/3>0). Координаты вершины параболы

$[{x_o} = frac{{ - b}}{{2a}} = frac{{ - ( - 1)}}{{2 cdot frac{1}{3}}} = frac{3}{2} = 1,5,]$

$[{y_o} = frac{1}{3} cdot {(frac{3}{2})^2} - frac{3}{2} + 2 = frac{5}{4} = 1,25.]$

Первая точка графика — вершина (1,5; 1,25) — найдена.

Чтобы найти точки пересечения графика с осью Ox, надо решить уравнение

$[frac{1}{3}{x^2} - x + 2 = 0]$

Его дискриминант — число отрицательное. Значит, уравнение не имеет корней, а график функции не пересекает ось абсцисс.

Чтобы найти точку пересечения графика с осью Oy, находим значение функции при x=0:

$[y(0) = frac{1}{3} cdot {0^2} - 0 + 2 = 2.]$

Вторая точка графика — (0; 2).

Прямая x=1,5, проходящая через вершину параболы — её ось симметрии. Найдем пару точек графика слева от оси симметрии.

$[y( - 1) = frac{1}{3} cdot {( - 1)^2} - ( - 1) + 2 = 3frac{1}{3},]$

$[y( - 3) = frac{1}{3} cdot {( - 3)^2} - ( - 3) + 2 = 8.]$

Таким образом, получили ещё две точки

$[( - 1;3frac{1}{3});( - 3;8).]$

На координатной плоскости отмечаем найденные точки, затем — точки, симметричные им относительно оси симметрии, и проводим через них параболу:

График квадратичной функции y=(1/3) x²-x+2

В алгебре с построением графиков, в том числе, графиков квадратичных функций, приходится иметь дело при решении заданий из самых разных разделов. Вот почему важно вовремя успешно овладеть навыками построения квадратичной параболы.

Другой способ построения графика квадратичной функции рассмотрим в следующий раз.

Источник

Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.

Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.

Что называют квадратичной функцией

Запомните!

Квадратичная функция — это функция вида

y = ax² + bx + c,

где a,
b и с — заданные числа.

Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.

Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».

Квадратичная функция	Коэффициенты
y = 2x² − 7x + 9	a = 2 b = −7 с = 9
y = 3x² − 1	a = 3 b = 0 с = −1
y = −3x² + 2x	a = −3 b = 2 с = 0

Как построить график квадратичной функции

Запомните!

График квадратичной функции называют параболой.

Парабола выглядит следующим образом.

Также парабола может быть перевернутой.

Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.

Чтобы было проще понять этот алгоритм, сразу разберем его на примере.

Построим график квадратичной функции «y = x² −7x + 10».

Направление ветвей параболы

Запомните!

Если «a > 0», то ветви направлены вверх.

Если «a < 0», то ветви направлены вниз.

В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
Координаты вершины параболы

Запомните!

Чтобы найти «x₀»
(координата вершины по оси «Ox»)
нужно использовать формулу:

Найдем «x₀» для нашей функции «y = x² −7x + 10».

Теперь нам нужно найти «y₀»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x₀» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».

y₀(3,5) =
(3,5)² − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =

−12,25 + 10 = −2,25

Выпишем полученные координаты вершины параболы.

(·) A (3,5; −2,25) — вершина параболы.

Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy».

Нули функции

Для начала давайте разберемся, что называют нулями функции.

Запомните!

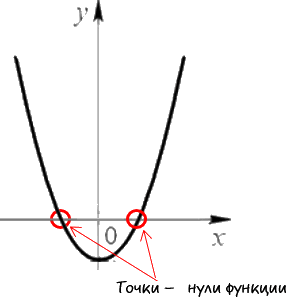
Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).

Наглядно нули функции на графике выглядят так:

Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.

Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.

Запомните!

Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».

Подставим в заданную функцию «y = x² −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .

0 = x² −7x + 10
x² −7x + 10 = 0

x_1;2 =

7 ±
√49 − 4 · 1 · 10

2 · 1

x_1;2 =

x₁ =	x₂ =
x₁ =	x₂ =
x₁ = 5	x₂ = 2

Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.

(·) B (5; 0)
(·) C (2; 0)

Отметим полученные точки («нули функции») на системе координат.

Дополнительные точки для построения графика

Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.

x	1	3	4	6
y

Для каждого выбранного значения «x»
рассчитаем «y».

y(1) = 1² − 7 · 1 + 10 = 1 − 7 + 10 =
4
y(3) = 3² − 7 · 3 + 10 = 9 − 21 + 10 =
−2
y(4) = 4² − 7 · 4 + 10 = 16 − 28 + 10 =
−2
y(6) = 6² − 7 · 6 + 10 = 36 − 42 + 10 =
4

Запишем полученные результаты в таблицу.

x	1	3	4	6
y	4	−2	−2	4

Отметим полученные точки графика на системе координат (зеленые точки).

Теперь мы готовы построить график.
На забудьте после построения подписать график функции.

Краткий пример построения параболы

Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.

Пусть требуется построить график функции
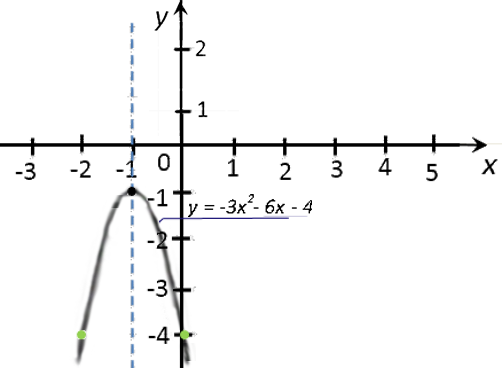
«y = −3x² − 6x − 4».

Направление ветвей параболы

«a = −3» — ветви параболы направлены вниз.

Координаты вершины параболы

x₀ =
x₀ = =

= −1

y₀(−1) = (−3) · (−1)² − 6 · (−1) − 4 =
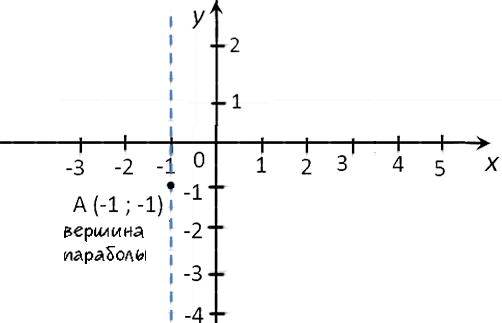
−3 · 1 + 6 − 4 = −1

(·) A (−1; −1)

— вершина параболы.
Нули функции
Точки пересечения с осью «Ox» (y = 0).

0 = −3x² − 6x − 4

−3x² − 6x − 4 = 0 |·(−1)

3x² + 6x + 4 = 0

x_1;2 =

−6 ±
√6² − 4 · 3 · 4

2 · 1

x_1;2 =

x_1;2 =

Ответ: нет действительных корней.

Так как корней нет, значит, график функции не пересекает ось
«Ox».

Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x² − 6x − 4».

y(−3) = −3 · (−3)² − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13

y(−2) = −3 · (−2)² − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4

y(0) = −3 · 0² − 6 · 0 − 4
= −4

y(1) = −3 · 1² − 6 · 1 − 4
= −3 −6 − 4 = −13

x	−3	−2	0	1
y	−13	−4	−4	−13

Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Графиком
любой квадратичной функции является парабола.
У каждой параболы есть вершина, при изображении графика важно знать её
координаты. Вершина параболы имеет
координаты (m,n).

Определите
координаты вершин для парабол:

Определим
координаты вершины параболы, которая является графиком квадратичной функции
записанной в виде .

Преобразуем
квадратный трёхчлен, выделим из него квадрат двучлена:

Второе
слагаемое представим в виде удвоенного произведения:

Выделим
квадрат суммы:

После
сокращения получаем:

Отсюда
запишем, что:

Вывод.

Графиком функции
является
парабола, которую можно получить из
параболы с помощью двух параллельных переносов: сдвига относительно оси x и сдвига относительно оси y. Данная парабола имеет вершину с
координатами (m,n), где ,
.
Осью симметрии является прямая x=m.

Пример.

Найти
координаты вершины параболы .

Вершина
будет иметь координаты (m,n), каждую из которых можно получить
по формуле. Подставим коэффициенты квадратичной функции в формулу и найдём эти
значения:

Вершина
параболы имеет координаты (-2,-5).

Воспользуемся
наиболее простым способом: сначала найдём m вершины по формуле. И учитывая,
что вершина принадлежит графику функции, подставим m вместо
аргумента в функцию:

Получили
вершину, которая имеет координаты (-2,-5).

Алгоритм
построения графика квадратичной функции:

1.
Определить
направление ветвей парабола. Если a>0, то ветви
направлены вверх, если a<0,
то — вниз.

2.
Найти
координаты вершины параболы и отметить её на координатной плоскости. Применив
формулу ,
найдём абсциссу вершины параболы, и, подставив это значение в формулу, задающую
функцию, найдем ординату этой точки.

3.
Определить
ось симметрии x=m.

4.
Построить
ещё несколько точек принадлежащих параболе, составив таблицу значений функции с
учётом оси симметрии.

5.
Соединить
отмеченные точки плавной линией.

Пример.

Изобразить
график функции .

1.
Определим
направление ветвей параболы:

2.
Найдём
координаты вершины:

Получили
вершину с координатами (-2, -3).

3.
Определим
ось симметрии:

4.
Составим
таблицу значений:

Выбранные
значения симметричны относительно оси симметрии.

5.
Отметим
и соединим полученные точки на координатной плоскости:

Получили
параболу, которая является графиком функции.

Пример.

Изобразить
график функции и
описать её свойства.

Изобразим
график функции:

1.
Определим
направление ветвей параболы:

2.
Найдём
координаты вершины параболы:

Вершина
имеет координаты (-2,-4).

3.
Определим
ось симметрии:

4.
Составим
таблицу значения функции:

5.
Соединив
эти точки, получаем:

Определим
свойства функции.

Областью
определения и областью значений являются:

Определим
нули функции:

Перечислим
промежутки знакопостоянства функции:

Опишем
промежутки монотонности:

Источник