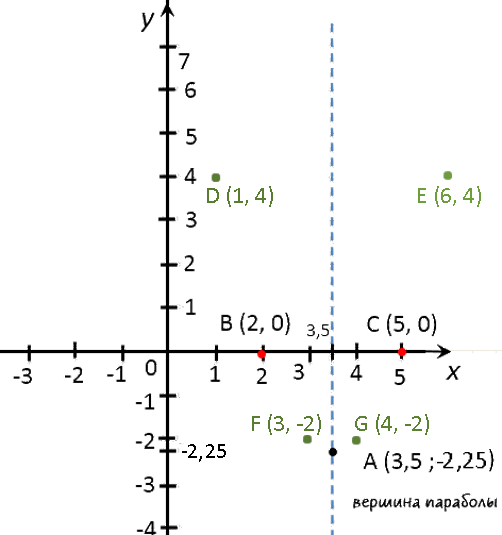Как найти дополнительные точки квадратичной функции - Исправление недочетов и поиск решений вместе с Examum.ru

Home » 8 класс » Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?

Урок: как построить параболу или квадратичную функцию?

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Парабола — это график функции описанный формулой ax²+bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:

1 ) Формула параболы y=ax²+bx+c,
если а>0 то ветви параболы направленны вверх,
а<0 то ветви параболы направлены вниз.
Свободный член c эта точке пересекается параболы с осью OY;

2 ) Вершина параболы, ее находят по формуле x=(-b)/2a, найденный x подставляем в уравнение параболы и находим y;

3) Нули функции или по другому точки пересечения параболы с осью OX они еще называются корнями уравнения. Чтобы найти корни мы уравнение приравниваем к 0 ax²+bx+c=0;

Виды уравнений:

a) Полное квадратное уравнение имеет вид ax²+bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax²+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax²+bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax²+c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);

Как решать квадратные уравнения посмотреть тут.

4) Найти несколько дополнительных точек для построения функции.

ПРАКТИЧЕСКАЯ ЧАСТЬ

И так теперь на примере разберем все по действиям:
Пример №1:
y=x²+4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2)²+4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x²+4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b²-4ac=16-12=4
x=(-b±√(D))/2a
x₁=(-4+2)/2=-1
x₂=(-4-2)/2=-3

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2

х -4 -3 -1 0
у 3 0 0 3

Подставляем вместо х в уравнение y=x²+4x+3 значения
y=(-4)²+4*(-4)+3=16-16+3=3
y=(-3)²+4*(-3)+3=9-12+3=0
y=(-1)²+4*(-1)+3=1-4+3=0
y=(0)²+4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2

Пример №2:
y=-x²+4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1<0.
a=-1 b=4 c=0 x=(-b)/2a=(-4)/(2*(-1))=2 y=-(2)²+4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x²+4x=0
Неполное квадратное уравнение вида ax²+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x²+4x значения
y=0²+4*0=0
y=-(1)²+4*1=-1+4=3
y=-(3)²+4*3=-9+13=3
y=-(4)²+4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2

Пример №3
y=x²-4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0)²-4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x²-4=0
Неполное квадратное уравнение вида ax² +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x²=4
x₁=2
x₂=-2

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x²-4 значения
y=(-2)²-4=4-4=0
y=(-1)²-4=1-4=-3
y=1²-4=1-4=-3
y=2²-4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0

Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.

Источник

Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.

Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.

Что называют квадратичной функцией

Запомните!

Квадратичная функция — это функция вида

y = ax² + bx + c,

где a,
b и с — заданные числа.

Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.

Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».

Квадратичная функция	Коэффициенты
y = 2x² − 7x + 9	a = 2 b = −7 с = 9
y = 3x² − 1	a = 3 b = 0 с = −1
y = −3x² + 2x	a = −3 b = 2 с = 0

Как построить график квадратичной функции

Запомните!

График квадратичной функции называют параболой.

Парабола выглядит следующим образом.

Также парабола может быть перевернутой.

Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.

Чтобы было проще понять этот алгоритм, сразу разберем его на примере.

Построим график квадратичной функции «y = x² −7x + 10».

Направление ветвей параболы

Запомните!

Если «a > 0», то ветви направлены вверх.

Если «a < 0», то ветви направлены вниз.

В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
Координаты вершины параболы

Запомните!

Чтобы найти «x₀»
(координата вершины по оси «Ox»)
нужно использовать формулу:

Найдем «x₀» для нашей функции «y = x² −7x + 10».

Теперь нам нужно найти «y₀»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x₀» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».

y₀(3,5) =
(3,5)² − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =

−12,25 + 10 = −2,25

Выпишем полученные координаты вершины параболы.

(·) A (3,5; −2,25) — вершина параболы.

Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy».

Нули функции

Для начала давайте разберемся, что называют нулями функции.

Запомните!

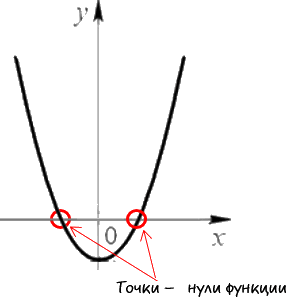
Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).

Наглядно нули функции на графике выглядят так:

Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.

Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.

Запомните!

Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».

Подставим в заданную функцию «y = x² −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .

0 = x² −7x + 10
x² −7x + 10 = 0

x_1;2 =

7 ±
√49 − 4 · 1 · 10

2 · 1

x_1;2 =

x₁ =	x₂ =
x₁ =	x₂ =
x₁ = 5	x₂ = 2

Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.

(·) B (5; 0)
(·) C (2; 0)

Отметим полученные точки («нули функции») на системе координат.

Дополнительные точки для построения графика

Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.

x	1	3	4	6
y

Для каждого выбранного значения «x»
рассчитаем «y».

y(1) = 1² − 7 · 1 + 10 = 1 − 7 + 10 =
4
y(3) = 3² − 7 · 3 + 10 = 9 − 21 + 10 =
−2
y(4) = 4² − 7 · 4 + 10 = 16 − 28 + 10 =
−2
y(6) = 6² − 7 · 6 + 10 = 36 − 42 + 10 =
4

Запишем полученные результаты в таблицу.

x	1	3	4	6
y	4	−2	−2	4

Отметим полученные точки графика на системе координат (зеленые точки).

Теперь мы готовы построить график.
На забудьте после построения подписать график функции.

Краткий пример построения параболы

Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.

Пусть требуется построить график функции
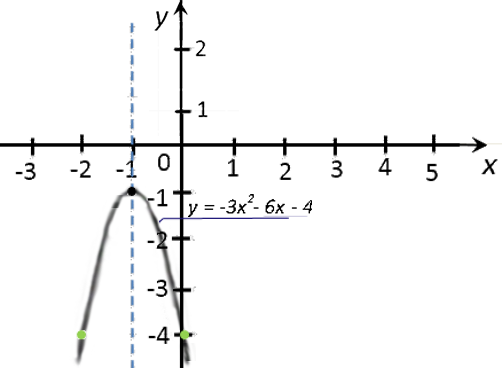
«y = −3x² − 6x − 4».

Направление ветвей параболы

«a = −3» — ветви параболы направлены вниз.

Координаты вершины параболы

x₀ =
x₀ = =

= −1

y₀(−1) = (−3) · (−1)² − 6 · (−1) − 4 =
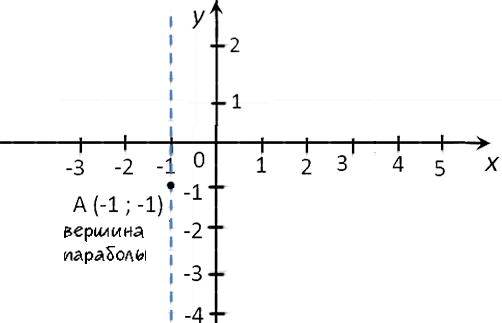
−3 · 1 + 6 − 4 = −1

(·) A (−1; −1)

— вершина параболы.
Нули функции
Точки пересечения с осью «Ox» (y = 0).

0 = −3x² − 6x − 4

−3x² − 6x − 4 = 0 |·(−1)

3x² + 6x + 4 = 0

x_1;2 =

−6 ±
√6² − 4 · 3 · 4

2 · 1

x_1;2 =

x_1;2 =

Ответ: нет действительных корней.

Так как корней нет, значит, график функции не пересекает ось
«Ox».

Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x² − 6x − 4».

y(−3) = −3 · (−3)² − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13

y(−2) = −3 · (−2)² − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4

y(0) = −3 · 0² − 6 · 0 − 4
= −4

y(1) = −3 · 1² − 6 · 1 − 4
= −3 −6 − 4 = −13

x	−3	−2	0	1
y	−13	−4	−4	−13

Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Как построить график параболы

Парабола является графиком квадратичной функции вида y=A·x²+B·x+C. Перед построением графика необходимо провести аналитическое исследование функции. Обычно параболу рисуют в декартовой прямоугольной системе координат, которая представлена двумя перпендикулярными осями Ox и Oy.

Инструкция

Первым пунктом запишите область определения функции D(y). Парабола определена на всей числовой прямой, если не задано никаких дополнительных условий. Обычно это указывается записью D(y)=R, где R – множество всех действительных чисел.

Найдите вершину параболы. Координата по оси абсцисс x0=-B/2A. Подставьте x0 в уравнение параболы и сосчитайте координату вершины по оси ординат Oy. Итак, вторым пунктом должна появится запись: (x0;y0) – координаты вершины параболы. Естественно, вместо x0 и y0 у вас должны быть конкретные числа. Отметьте эту точку на чертеже.

Сравнивая старший коэффициент A при x² с нулем, сделайте вывод о направлении ветвей параболы. Если A>0, то ветви параболы направлены вверх. При отрицательном значении числа A ветви параболы направлены вниз.

Теперь вы можете найти множество значений функции E(y). Если ветви направлены вверх, функция y принимает все значения выше y0. При направлении ветвей вниз функция принимает значения ниже y0. Для первого случая запишите: E(y)=[y0,+∞), для второго – E(y)=(-∞;y0]. Квадратная скобка говорит о том, что крайнее число включается в промежуток.

Напишите уравнение для оси симметрии параболы. Оно будет иметь вид: x=x0 и проходить через вершину. Начертите эту ось строго перпендикулярно оси Ox.

Найдите «нули» функции. Эти точки будут пересекать координатные оси. Приравняйте x нулю и посчитайте y для этого случая. Затем найдите, при каких значениях аргумента функция y обратится в нуль. Для этого решите квадратное уравнение A·x²+B·x+C=0. Отметьте точки на графике.

Найдите дополнительные точки для построения параболы. Оформите в виде таблицы. Первой строкой записывайте аргумент x, второй – функцию y. Лучше подбирать такие числа, для которых x и y будут целыми, т.к. дробные числа изображать неудобно. Полученные точки отметьте на графике.

Полезный совет

Иногда требуется начертить график функции x=A·y²+B·y+C. В этом случае не надо пытаться выразить y через x. Просто мысленно поменяйте местами функцию и аргумент и проведите аналогичное исследование. Парабола «ляжет» боком.

Источники:

как решать параболы

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Квадратичная функция – это функция вида (y=ax^2+bx+c). График квадратичной функции – парабола.

Примеры:

(y= x^2+6x+5)		(y=x^2-4x+5)
(y=-2x^2-4x+4)		(y=-3x^2+21x-34)

«Анатомия» квадратичной функции:

(x_в) и (y_в) – координаты вершины параболы. (x_в) можно найти с помощью формулы: (x_в=frac{-b}{2a}). (y_в) можно найти подставив в формулу квадратичной функции вместо (x) значение (x_в: y_в=ax_в^2+bx_в+с)
Ось симметрии проходит через вершину параболы и параллельна оси (y) (ординат). (x_1) и (x_2) – нули функции. Их можно найти, приравняв формулу функции к нулю и решив соответствующее квадратное уравнение.

3 параметра позволяющих сопоставить формулу квадратичной функции и график:

1.	(a>0) — ветви параболы направлены вверх
(a<0) — ветви параболы направлены вниз
2.	(c) равна ординате точки пересечения графика с осью (y)
3.	координата вершины параболы (x_в=-frac{b}{2a})

Пример (задание из ОГЭ). На рисунке изображён график квадратичной функции (y=ax^2+bx+c)

Какие знаки параметров (a) и (c)?

Решение:

Ветви параболы направлены вниз, значит (a<0)
График функции пересекает ось (y) в точке лежащий ниже оси (x), значит (c<0)

Ответ: (a<0),(c<0)

Пример (задание из ОГЭ). Установите соответствие между квадратичными функциями и их графиками:

Решение:
Во втором графике ветви параболы направлены вниз, значит (a<0). Под этот график подходит только функция под буквой В.
Во втором и третьем графике (a>0,c=1) – по этим параметрам нам определить их функции. Тогда найдем (x_в) функций под буквой А и Б:

А. (y=x^2-5x+1) (x_в=frac{5}{2}=2,5) так же как на графике 1
Б. (y=x^2+5x+1) (x_в= frac{-5}{2}=-2,5) так же как на графике 3

Ответ:

Как построить график квадратичной функции (параболу)?

Квадратичную функцию можно строить, как и все остальные, выбирая точки наугад (подробнее можно прочитать здесь). Но есть способ позволяющий строить параболу быстрее, выбирая точки осмысленно.

Найдите координаты вершины параболы. Поставьте точку вершины на координатной плоскости и проведите через неё ось симметрии параболы.
Найдите точку пересечения графика с осью (y): (x=0;y=c). Постройте точку симметричную точке ((0;c)) относительно оси параболы.
Найдите координату целой точки, лежащей вблизи оси параболы. Отметьте симметричную ей точку на плоскости.

Соедините точки плавной линией.

(a=2), (b=8), (c=2) 1. (x_в=frac{-b}{2a}=frac{-8}{2 cdot 2}=-2) (y_в=2 cdot (-2)^2+8 cdot (-2)+2=2 cdot 4-16+2=-6)
2. (x=0, y=2)
3. При (x=-3), (y=2 cdot (-3)^2+8 cdot (-3)+2=2 cdot 9-24+2=20-24=-4)
Готово!

Связь квадратичной функции и квадратных уравнений:

Давайте сравним общий вид квадратичной функции и общий вид квадратного уравнения:

(y=ax^2+bx+c)

(ax^2+bx+c=0)

И там, и там есть квадратный трехчлен (ax^2+bx+c). Разница в том, что в функции мы исследуем все возможные значения трехчлена, а в уравнении мы ищем (x), при которых значение трехчлена будет равно нулю или при каких (x), (y=0). Поэтому по графику функции (y=ax^2+bx+c) легко определить корни уравнения (ax^2+bx+c=0).

Пример:

(y=x^2+6x+5)

(y=x^2-4x+5)

Судя по графику, корнями уравне-
ния (x^2+6x+5=0) будут (x_1=-5) и (x_2=-1)

У уравнения (x^2-4x+5=0) нет корней, т.к. нету (x) при которых y будет равен нулю (функция не пересекает ось (x))

Смотрите также:
Линейная функция
Виды графиков функций
Квадратные неравенства

Источник

Как построить параболу

Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.

Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.

График квадратичной функции y=x²+bx+c — парабола, ветви которой направлены вверх. Для построения графика достаточно найти координаты вершины параболы. Абсцисса вершины параболы находится по формуле

$[{x_o} = frac{{ - b}}{{2a}},]$

для нахождения ординаты можно подставить в формулу y=x²+bx+c вместо каждого x найденное значение хₒ: yₒ=xₒ²+bxₒ+c. От вершины (хₒ; yₒ ) строим параболу y=x².

Пример.

Построить график функции y=x²+2x-3.

Решение:

y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы

$[{x_o} = frac{{ - b}}{{2a}} = frac{{ - 2}}{{2 cdot 1}} = - 1,]$

$[{y_o} = {( - 1)^2} + 2 cdot ( - 1) - 3 = - 4.]$

От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).

y=x²+2x-3

График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².

Пример.

Построить график функции y= -x²+2x+8.

Решение:

y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы

$[{x_o} = frac{{ - b}}{{2a}} = frac{{ - 2}}{{2cdot( - 1)}} = 1,]$

$[{y_o} = - {1^2} + 2cdot1 + 8 = 9.]$

От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):

y= -x²+2x+8

Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.

Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.

Примеры.

Построить график функции y=x²+5x+4.

Решение:

y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы

$[{x_o} = frac{{ - b}}{{2a}} = frac{{ - 5}}{{2 cdot 1}} = - 2,5;]$

$[{y_o} = {( - 2,5)^2} + 5 cdot ( - 2,5) + 4 = - 2,25,]$

то есть вершина параболы — точка (-2,5; -2,25).

Ищем точки пересечения графика с осями координат. В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).

В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).

Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:

y=x²+5x+4

Построить график функции y= -x²-3x.

Решение:

y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы

$[{x_o} = frac{{ - b}}{{2a}} = frac{{ - ( - 3)}}{{2 cdot 1}} = - 1,5;]$

$[{y_o} = - {( - 1,5)^2} - 3 cdot ( - 1,5) = 2,25.]$

Вершина (-1,5; 2,25) — первая точка параболы.

В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.

При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.

y= -x²-3x

Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.

Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.

Источник