Содержание материала
- Сложение дробей с одинаковыми знаменателями
- Видео
- НОЗ и НОК
- Как устроена десятичная дробь
- Как привести десятичную дробь к новому знаменателю
- Чтобы найти общий знаменатель, перемножим знаменатели:
- Вычитание дробей с разными знаменателями
Сложение дробей с одинаковыми знаменателями
Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают числители, а знаменатель оставляют тот же.
Пример.
C помощью букв это правило сложения можно записать так:

Записывая ответ, проверьте нельзя ли полученную дробь сократить.
Видео
НОЗ и НОК
При работе с дробями используются наименьший общий знаменатель (НОЗ) — это наименьшее натуральное число среди всех ОЗ ряда дробных чисел и наименьшее общее кратное (НОК) — это самый меньший общий делитель данного ряда чисел.
Наименьшее общее кратное — это НОЗ этого ряда. К нему можно прийти поиском НОК.
Например, необходимо провести следующую операцию для двух дробных значений: 7/16, 19/6. Нужно узнать, какой НОК у 16 и 6. Простые множители этих чисел:
16=8*2; 6= 3*2
НОК (16, 6) =8*2*3= 48.
Число 48 и есть искомый НОЗ.
Существует простое правило о том, как перевести дробное число к НОЗ. Вычисления проводятся по порядку:
- Найти НОК.
- Для каждого дробного числа из ряда определить дополнительный множитель. Определить его можно с помощью деления НОЗ на знаменатель каждой из дробей.
- Умножить обе части каждой дроби на их дополнительные множители.
Пример. Есть 2 дробных значения: 3/14 и 18/30. Теперь можно воспользоваться правилом, для того чтобы найти НОЗ:
- Найти НОК: 14 = 2*7; 30 = 5*2*3; НОК (14,32) = 5*2*7*3 = 210;
- Найти дополнительные множители: 210/14 = 15; 210/30 = 7;
- Перемножить верхнюю и нижнюю части с дополнительными множителями: 3*15/14*15 = 45/210; 18*7/30*7 = 126/210.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,3
- 4,23
- 9,939
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Как привести десятичную дробь к новому знаменателю
Для приведения десятичной дроби к новому знаменателю, необходимо десятичную дробь преобразовать в обыкновенную дробь. Затем числитель и знаменатель дроби домножить на дополнительный множитель.
Разберём пример. Приведём десятичную дробь 2.5 к знаменателю 4.Преобразуем десятичную дробь в обыкновенную дробь. 2.5 =5/2 Найдём дополнительный множитель — для этого разделим 4 на 2 получится 4 / 2 = 2. Домножим числитель и знаменатель дроби на 2 получится дробь 10/4
2.5
=
2.5 × 101 × 10
=
2510
=
5 × 5 2 × 5
=
52
=
5 × 22 × 2
=
104
Чтобы найти общий знаменатель, перемножим знаменатели:
Дополнительный множитель к первой дроби:
Дробь примет вид:
Дополнительный множитель ко второй дроби:
Дробь примет вид:
Дополнительный множитель к третьей дроби:
Дробь примет вид:
Итак, были дроби:
Запишем полученные дроби с общим знаменателем:
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби 



Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям 
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от 


Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей 



Первый рисунок изображает дробь 


Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь 
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби 
Получили ответ
Теги
Чтобы понять, как складывать дроби с разными знаменателями, сначала изучим правило, а затем рассмотрим конкретные примеры.
Чтобы сложить или вычесть дроби с разными знаменателями, надо:
1) Найти(НОЗ) данных дробей.
2) Найти дополнительный множитель к каждой дроби. Для этого новый знаменатель нужно разделить на старый.
3) Умножить числитель и знаменатель каждой дроби на дополнительный множитель и сложить или вычесть дроби с одинаковыми знаменателями.
4) Проверить, является ли полученная в результате дробь правильной и несократимой.
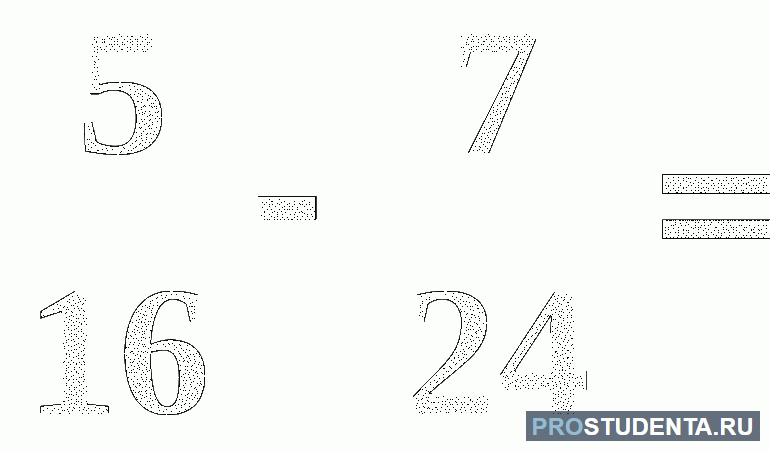
В следующих примерах надо сложить или вычесть дроби с разными знаменателями:
1) Чтобы вычесть дроби с разными знаменателями, сначала ищем наименьший общий знаменатель данных дробей. Выбираем большее из чисел и проверяем, делится ли оно на меньшее. 25 на 20 не делится. Умножаем 25 на 2. 50 на 20 не делится. Умножаем 25 на 3. 75 на 20 не делится. Умножаем 25 на 4. 100 на 20 делится. Значит, наименьший общий знаменатель равен 100.
2) Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый. 100:25=4, 100:20=5. Соответственно, к первой дроби дополнительный множитель 4, ко второй — 5.
3) Умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем дроби по правилу вычитания дробей с одинаковыми знаменателями.
4) Полученная дробь — правильная и несократимая. Значит, это — ответ.
1) Чтобы сложить дроби с разными знаменателями, сначала ищем наименьший общий знаменатель. 16 на 12 не делится. 16∙2=32 на 12 не делится. 16∙3=48 на 12 делится. Значит, 48 — НОЗ.
2) 48:16=3, 48:12=4. Это — дополнительные множители к каждой дроби.
3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и складываем новые дроби.
4)Полученная в результате дробь — правильная и несократимая.
1) 30 на 20 не делится. 30∙2=60 на 20 делится. Значит, 60 — наименьший общий знаменатель этих дробей.
2) чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель поделить на старый: 60:20=3, 60:30=2.
3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем новые дроби.
4) полученную дробьна 5.
1) 8 на 6 не делится. 8∙2=16 на 6 не делится. 8∙3=24 делится и на 4, и на 6. Значит, 24 — это и есть НОЗ.
2) чтобы найти дополнительный множитель к каждой дроби, нужно новый знаменатель разделить на старый. 24:8=3, 24:4=6, 24:6=4. Значит, 3, 6 и 4 — дополнительные множители к первой, второй и третьей дроби.
3) умножаем числитель и знаменатель каждой долби на дополнительный множитель. Складываем и вычитаем. Полученная дробь — неправильная, поэтому необходимо выделить целую часть.
На этом уроке мы рассмотрим приведение дробей к общему знаменателю и решим задачи по этой теме. Дадим определение понятию общего знаменателя и дополнительного множителя, вспомним о взаимно простых числах. Дадим определение понятию наименьший общий знаменатель (НОЗ) и решим ряд задач на его нахождение.
Тема: Сложение и вычитание дробей с разными знаменателями
Урок: Приведение дробей к общему знаменателю
Повторение. Основное свойство дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Например, числитель и знаменатель дроби можно разделить на 2. Получим дробь . Эту операцию называют сокращением дроби. Можно выполнить и обратное преобразование, умножив числитель и знаменатель дроби на 2. В этом случае говорят, что мы привели дробь к новому знаменателю. Число 2 называют дополнительным множителем.
Вывод.
Дробь можно привести к любому знаменателю кратному знаменателю данной дроби. Для того чтобы привести дробь к новому знаменателю, ее числитель и знаменатель умножают на дополнительный множитель.
1. Приведите дробь к знаменателю 35.
Число 35 кратно 7, то есть 35 делится на 7 без остатка. Значит, это преобразование возможно. Найдем дополнительный множитель. Для этого разделим 35 на 7. Получим 5. Умножим на 5 числитель и знаменатель исходной дроби.
2. Приведите дробь к знаменателю 18.
Найдем дополнительный множитель. Для этого разделим новый знаменатель на исходный. Получим 3. Умножим на 3 числитель и знаменатель данной дроби.
3. Приведите дробь к знаменателю 60.
Разделив 60 на 15, получим дополнительный множитель. Он равен 4. Умножим числитель и знаменатель на 4.
4. Приведите дробь к знаменателю 24
В несложных случаях приведение к новому знаменателю выполняют в уме. Принято только указывать дополнительный множитель за скобочкой чуть правее и выше исходной дроби.
Дробь можно привести к знаменателю 15 и дробь можно привести к знаменателю 15. У дробей и общий знаменатель 15.
Общим знаменателем дробей может быть любое общее кратное их знаменателей. Для простоты дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Пример. Привести к наименьшему общему знаменателю дроби и .
Сначала найдем наименьшее общее кратное знаменателей данных дробей. Это число 12. Найдем дополнительный множитель для первой и для второй дроби. Для этого 12 разделим на 4 и на 6. Три — это дополнительный множитель для первой дроби, а два — для второй. Приведем дроби к знаменателю 12.
Мы привели дроби и к общему знаменателю, то есть мы нашли равные им дроби, у которых один и тот же знаменатель.
Правило.
Чтобы привести дроби к наименьшему общему знаменателю, надо
Во-первых, найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
Во-вторых, разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель.
В-третьих, умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
а) Привести к общему знаменателю дроби и .
Наименьший общий знаменатель равен 12. Дополнительный множитель для первой дроби — 4, для второй — 3. Приводим дроби к знаменателю 24.
б) Привести к общему знаменателю дроби и .
Наименьший общий знаменатель равен 45. Разделив 45 на 9 на 15, получим, соответственно, 5 и 3. Приводим дроби к знаменателю 45.
в) Привести к общему знаменателю дроби и .
Общий знаменатель — 24. Дополнительные множители, соответственно, — 2 и 3.
Иногда бывает трудно подобрать устно наименьшее общее кратное для знаменателей данных дробей. Тогда общий знаменатель и дополнительные множители находят с помощью разложения на простые множители.
Привести к общему знаменателю дроби и .
Разложим числа 60 и 168 на простые множители. Выпишем разложение числа 60 и добавим недостающие множители 2 и 7 из второго разложения. Умножим 60 на 14 и получим общий знаменатель 840. Дополнительный множитель для первой дроби — это 14. Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. — М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. — ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О. и др. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.
Можно скачать книги, указанные в п.1.2. данного урока.
Домашнее задание
Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. — М.: Мнемозина, 2012. (ссылка см. 1.2)
Домашнее задание: №297, №298, №300.
Другие задания: №270, №290
В данном материале мы разберем, как правильно приводить дроби к новому знаменателю, что такое дополнительный множитель и как его найти. После этого сформулируем основное правило приведения дробей к новым знаменателям и проиллюстрируем его примерами задач.
Понятие приведения дроби к другому знаменателю
Вспомним основное свойство дроби. Согласно ему, обыкновенная дробь a b (где a и b – любые числа) имеет бесконечное количество дробей, которые равны ей. Такие дроби можно получить, умножив числитель и знаменатель на одинаковое число m (натуральное). Иными словами, все обыкновенные дроби могут быть заменены другими вида a · m b · m . Это и есть приведение исходного значения к дроби с нужным знаменателем.
Привести дробь к другому знаменателю можно, умножив ее числитель и знаменатель на любое натуральное число. Главное условие – множитель должен быть одинаков для обоих частей дроби. В итоге получится дробь, равная исходной.
Проиллюстрируем это примером.
Пример 1
Привести дробь 11 25 к новому знаменателю.
Решение
Возьмем произвольное натуральное число 4 и умножим обе части исходной дроби на него. Считаем: 11 · 4 = 44 и 25 · 4 = 100 . В итоге получилась дробь 44 100 .
Все подсчеты можно записать в таком виде: 11 25 = 11 · 4 25 · 4 = 44 100
Выходит, любую дробь можно привести к огромному количеству разных знаменателей. Вместо четверки мы могли бы взять другое натуральное число и получить еще одну дробь, эквивалентную исходной.
Но не любое число может стать знаменателем новой дроби. Так, для a b в знаменателе могут стоять только числа b · m , кратные числу b . Вспомните основные понятия деления – кратные числа и делители. Если число не кратно b , но делителем новой дроби оно быть не может. Поясним нашу мысль примером решения задачи.
Пример 2
Вычислить, возможно ли приведение дроби 5 9 к знаменателям 54 и 21 .
Решение
54 кратно девятке, которая стоит в знаменателе новой дроби (т.е. 54 можно разделить на 9). Значит, такое приведение возможно. А 21 мы разделить на 9 не можем, поэтому такое действие для данной дроби выполнить нельзя.
Понятие дополнительного множителя
Сформулируем, что такое дополнительный множитель.
Определение 1
Дополнительный множитель
представляет собой такое натуральное число, на которое умножают обе части дроби для приведения ее к новому знаменателю.
Т.е. когда мы выполняем это действие с дробью, мы берем для нее дополнительный множитель. Например, для приведения дроби 7 10 к виду 21 30 нам потребуется дополнительный множитель 3 . А получить дробь 15 40 из 3 8 можно с помощью множителя 5 .
Соответственно, если мы знаем знаменатель, к которому необходимо привести дробь, то мы можем вычислить для нее и дополнительный множитель. Разберем, как это сделать.
У нас есть дробь a b , которую можно привести к некоторому знаменателю c ; вычислим дополнительный множитель m . Нам надо произвести умножение знаменателя исходной дроби на m . У нас получится b · m , а по условию задачи b · m = c . Вспомним, как связаны между собой умножение и деление. Эта связь подскажет нам следующий вывод: дополнительный множитель есть не что иное, как частное от деления c на b , иначе говоря, m = c: b .
Таким образом, для нахождения дополнительного множителя нам нужно разделить требуемый знаменатель на исходный.
Пример 3
Найдите дополнительный множитель, с помощью которого дробь 17 4 была приведена к знаменателю 124 .
Решение
Используя правило выше, мы просто разделим 124 на знаменатель первоначальной дроби – четверку.
Считаем: 124: 4 = 31 .
Выполнять расчеты такого типа часто требуется при приведении дробей к общему знаменателю.
Правило приведения дробей к указанному знаменателю
Перейдем к определению основного правила, с помощью которого можно привести дроби к указанному знаменателю. Итак,
Определение 2
Для приведения дроби к указанному знаменателю нужно:
- определить дополнительный множитель;
- умножить на него и числитель, и знаменатель исходной дроби.
Как применить это правило на практике? Приведем пример решения задачи.
Пример 4
Выполните приведение дроби 7 16 к знаменателю 336 .
Решение
Начнем с вычисления дополнительного множителя. Разделим: 336: 16 = 21 .
Полученный ответ умножаем на обе части исходной дроби: 7 16 = 7 · 21 16 · 21 = 147 336 . Так мы привели исходную дробь к нужному знаменателю 336 .
Ответ: 7 16 = 147 336 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется приведением к общему знаменателю. А искомые числа, «выравнивающие» знаменатели, называются дополнительными множителями.
Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.
Задача. Найдите значения выражений:
Заметим, что 84: 21 = 4; 72: 12 = 6 . Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2 . Это число намного меньше произведения 8 · 12 = 96 .
Наименьшее число, которое делится на каждый из знаменателей, называется их наименьшим общим кратным (НОК).
Обозначение: наименьшее общее кратное чисел a
и b
обозначается НОК(a
; b
) . Например, НОК(16; 24) = 48 ; НОК(8; 12) = 24 .
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Задача. Найдите значения выражений:
Заметим, что 234 = 117 · 2; 351 = 117 · 3 . Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 · 4 . Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
- Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702 , следовательно, для первой дроби дополнительный множитель равен 3.
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Вычитание алгебраических дробей
Рассмотрим вычитание алгебраических (рациональных) дробей в теории и на практике.
Чтобы вычесть алгебраические дроби, нужно:
1) Найти наименьший общий знаменатель этих дробей.
2) Найти дополнительный множитель к каждой дроби.
3) Дополнительный множитель умножить на числитель и знаменатель.
4) Выполнить вычитание дробей с одинаковыми знаменателями (при вычитании дробей с одинаковыми знаменателями числители вычитают, а знаменатель оставляют тем же).
Примеры вычитания алгебраических дробей.
Наименьший общий знаменатель для чисел равен 18. Из степеней в общий знаменатель включаем каждый множитель, взяв его с наибольшим показателем. Таким образом, наименьший общий знаменатель данных дробей равен 18m²n².
Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый.
18m²n²:( 9mn²)=2m, 18m²n²:( 6mn²)=3m.
В знаменателях дробей стоят многочлены. Раскладываем их на множители. Для этого выносим за скобки общий множитель: в первом знаменателе — y, во втором — 5:
Наименьший общий знаменатель состоит из всех множителей и равен 5y(5x-y). Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый:
5y(5x-y):(y(5x-y))=5, 5y(5x-y):(5(5x-y))=y,
то есть, дополнительный множитель к первой дроби равен 5, ко второй — y. Затем умножаем числитель и знаменатель каждой дроби на дополнительный множитель.
Числитель раскладываем по формуле разности квадратов, после чего сокращаем дробь на (5x-y):
Многочлены, стоящие в знаменателях, раскладываем на множители по формулам сокращенного умножения. В знаменателе первой дроби — квадрат разности, в знаменателе второй дроби — разность квадратов:
Выражения (x-2) и (2-x), стоящие в знаменателях, отличаются только знаками. Изменим знаменатель второй дроби.
(2-x)= -(x-2). «Минус» вынесем перед дробью, соответственно, знак изменится на «+»:
Наименьший общий знаменатель состоит из всех входящих в знаменатели множителей, взятых в наибольшей степени. Он равен (x-2)²(2+x). Умножаем числитель и знаменатель каждой дроби на дополнительный множитель и складываем дроби с одинаковыми знаменателями.
В знаменателе второй дроби — формула разности кубов:
Приводим дроби к общему знаменателю и упрощаем:
Выносим из знаменателя «минус» и сокращаем дробь на (1+x+x):
В алгебре складывать и вычитать дроби с разными знаменателями сложнее, чем их умножать и делить (при умножении и делении дроби не нужно приводить к общему знаменателю).
Умножение и деление алгебраических (рациональных) дробей — следующие темы для изучения.
Пожалуй, одной из самых популярных арифметических операций в алгебре является вычитание дробей с разными знаменателями. Алгоритм выполнения этого действия несложен и ничем не отличается, по сути, от сложения.
Оглавление:
- Общие сведения
- Нахождение общего знаменателя
- Алгоритм вычитания
- Решение примеров
Базируется он на основном свойстве отношений, позволяющем домножить числитель и знаменатель на одно и то же число. Следует отметить, что знание операции позволяет в дальнейшем приводить сложные выражения к простому виду, упрощая вычисления.
Общие сведения
Для того чтобы успешно научиться вычитать дроби, нужно понимать суть термина. В математике под ним понимают число, которое состоит из одной или нескольких долей единицы. Простыми словами, это отношение чего-то к целому. Например, пусть имеется арбуз. Его можно разрезать на равные части, то есть как бы подробить. По факту количество ягоды не изменится. Но если съесть один кусочек, то на тарелке останется три. Количественно в математике это действие можно описать дробью. Для рассматриваемого примера запись будет иметь вид: ¾.
В верхней части цифра обозначает долю от целого, а в нижней — на сколько равных кусков было разделено целое.
Делимое, то есть число, которое изменяется, называют числителем, а делитель — знаменателем. Дробь всегда будет меньше целой части.
В зависимости от соотношения частей, дробные выражения принято разделять на следующие типы:
- Правильные. Рациональные числа, в которых делимое количественно меньше делителя.
- Неправильные. Простые выражения, у которых значение знаменателя меньше величины числителя или совпадает с ним по численности.
- Смешанные. Отношения, состоящие из натурального числа и правильной дроби. Практически они представляют собой их сумму.
Кроме этого, существует ещё отдельный класс выражений, называемый десятичным. К нему относят отношения, в которых знаменатель — это число десять в степени с любым натуральным числом.
Записывают десятичные выражения, используя в качестве разделителя запятую. Например, 1/10 = 0,1.
С дробями, так как по факту это числа, разрешено выполнять любые математические действия. Самые простые из них — это умножение и деление, немного сложнее сложение и вычитание. Чтобы вычитать обыкновенные дроби, нужно знать их основное свойство. Сформулировать его можно следующим образом: если делитель и делимое умножить или разделить на одну и ту же величину, то результат отношения не изменится. Причём такую операцию можно выполнять сколько угодно раз.
Естественно, это не должен быть ноль, иначе выражение потеряет смысл. Например, ¾ = (3 * n)/(4 * n). Это свойство позволяет не только преобразовывать выражение, делая вычисления проще и удобнее, но и выполнять вычитание.
Всё дело в том, что при выполнении действия находят так называемые дополнительные множители, которые можно определить, опираясь на основное свойство.
Нахождение общего знаменателя
Основная сложность, которая может возникнуть при нахождении разности дробей, — это правильное определение общего знаменателя.
В качестве него выступает положительное число, делящееся на делители вычитаемых выражений без остатка. Искомый параметр можно находить как для двух дробей, так и сразу для нескольких.
В простейшем понимании такое число можно получить простым перемножением знаменателей.
Но такой подход будет нерациональным, хотя назвать его в корне неправильным нельзя.
Общее правило для вычисления наименьшего общего знаменателя (НОЗ):
- Из чисел, стоящих в делимых, выбрать наибольшее и исследовать его на возможность деления с оставшимися. Если такое действие возможно, то выбранное значение и будет НОЗ. В ином случае переходят ко второму пункту.
- Наибольший знаменатель умножают на два и проверяют делимость полученного числа на все остальные.
- На этом шаге наибольший знаменатель умножают на три и повторяют проверку.
- Если НОЗ не найден, делители раскладывают на простые множители. В результате повторяющиеся числа убирают, а оставшиеся перемножают. Получившееся произведение и будет НОЗ.
Таким образом, чтобы найти нужный знаменатель, необходимо уметь раскладывать простые числа на множители. Эта операция является тождественным преобразованием. Выполняется она в несколько этапов.
Сначала ищется наименьшее число, на которое можно разделить исходное без остатка. Затем выполняют деление и повторяют действие, но уже для полученного значения. Операцию повторяют до тех пор, пока в ответе не получится единица.
Понять процедуру проще на примере. Пусть нужно выполнить вычитание двух дробей, у которых в знаменателях стоит 15 и 40. Следуя алгоритму, нужно наибольшее из этих чисел умножить на два и попробовать выполнить деление. В ответе получится число 80, которое на 15 разделить без остатка невозможно. Поэтому можно попробовать выполнить умножение на три: 40 * 3 = 120. Полученное произведение можно разделить на 15, в ответе будет восемь. Значит, 120 и будет искомым общим знаменателем.
Это значение можно было найти и пойдя путём разложения. Так, 15 можно представить как 5 * 3, а 40 в виде произведения 2 * 2 * 2 * 5. При сравнении записей видно, что и в первой, и во второй стоит цифра пять. Поэтому в одной из них её нужно убрать, а оставшиеся члены перемножить: 3 * 2 * 2 * 2 * 5 = 120. Ответ идентичен.
Алгоритм вычитания
Следует отметить, что сложение и вычитание дробей выполняется по одинаковому алгоритму. Единственное отличие в арифметическом знаке действия. Если нужно из одного дробного выражения вычесть другое, рекомендуется придерживаться следующего алгоритма:
- если в многочлене стоит смешанная дробь, то преобразовать её в неправильную;
- исследовать вычитаемое и уменьшаемое на возможность упрощения;
- найти наименьшее общее кратное среди знаменателей;
- вычислить дополнительные множители;
- домножить числители на найденные для них значения;
- записать в знаменатель НОЗ, а в числитель разницу произведений делимых;
- при возможности сократить дробь;
- привести ответ к виду смешанного числа в случае получения неправильной дроби.
Как можно заметить, алгоритм простой. Но может возникнуть вопрос по нахождению дополнительных множителей, несмотря на то что действие относят к простым операциям. После того как найден общий знаменатель, нужно делитель вычитаемого и уменьшаемого разделить на это число. Полученные значения и будут являться искомыми аргументами, предназначенными для домножения.
Кроме этого, необходимо обратить внимание на вычитание дробей разного типа. Чтобы правильно их вычесть, желательно вначале выполнить преобразование. Смешанное выражение можно довольно просто представить в виде неправильного числа. Для этого следует умножить целую часть на знаменатель и к полученному произведению добавить делимое. Затем результат сложения записать в числитель, а знаменатель оставить неизменным.
Существует и другой путь, обратный, то есть неправильную дробь превратить в смешанное число. Для этого числитель нужно разделить на знаменатель. По результату операции остаток записывают в делимое, а делитель оставляют без изменения. Целую же часть прибавляют к дробной. После того как два числа будут смешанными, алгоритм вычитания немного изменяется. Так, целые части вычитают отдельно от дробных чисел, а затем результаты просто складывают.
Какой алгоритм использовать для того, чтобы отнять дроби друг от друга, не принципиально. Всё дело в привычке и навыках решающего.
Но, пожалуй, способ, заключающийся в переводе смешанного числа в неправильное выражение, проще. Другой же метод лучше использовать, когда надо вычесть из целого числа дробное или же наоборот.
Решение примеров
Чтобы научиться правильно вычитать дроби с разными знаменателями, нужно самостоятельно решить несколько задач. Обычно хватает проработать порядка пяти примеров, чтобы получить необходимый опыт. Вот некоторые наиболее интересные задания:
- Вычислить разницу: (4 / 7) — (2 / 21). Придерживаясь алгоритма, вначале нужно найти общий знаменатель. Число в вычитаемом можно разделить на делитель уменьшаемого без остатка. Поэтому оно и будет искомым выражением. Далее, для первого члена дополнительным множителем будет 21: 7 = 3, а для второго 21: 21 = 1. Значит, решение примет следующий вид: (4 / 7) — (2 / 21) = ((3 * 4) — 2) / 21 = 10 / 21.
- Определить результат действия: 4 (1 / 3) — 1 / 7. Перед началом выполнения вычитания нужно смешанную дробь привести к неправильному виду, а уже после действовать по алгоритму. Итак, 4 (1 / 3) = ((4 * 3) + 1) / 3 = 13 / 3. Отсюда (13 / 3) — 1 / 7 = ((7 * 13) — (3 * 1)) / 21 = (91 — 3) / 21 = 88 / 21. Полученный ответ нужно представить в виде смешанного выражения: 88 / 21 = (4 + 4 * 21) / 21 = 4 (4 / 21).
- Сравнить два выражения по модулю: 4 / 5 — 12 / 4 — 4 (5 / 6) и 11 — 3 (1 / 3) + 8 / 7. Чтобы определить, какое из них больше, необходимо выполнить действия. Первый многочлен будет равен: 4 / 5 — 25 / 4 — 4 (5/6) = 4 / 5 — 12/ 4 — (4 * 6 + 5) / 6 = 4 / 5 — 25 / 4 — 29 / 6 = ((12*4) — (15 * 25) — (29 * 10)) / 60 = (48 — 375 — 290) / 60 = — 617 / 60 = -(17 + 10 * 60) / 60 = -10 (17 / 60). Второе выражение можно вычислить так: 11 — 3 (1 / 3) — 8 / 7 = 11 — 3 + 1 / 3 — 8 / 7 = 8 + 1 /3 — 8 / 7 = 8 + ((1*7) — (8 * 3)) / 21 = 8 + (7 — 24) / 21 = 8 — 17 / 21 = (8 / 1) — (17 / 21) = (168 — 17) / 21 = 151 / 21 = 74 / 21. Полученные ответы нужно сравнить без учёта знака. Поэтому можно утверждать, что первое выражение будет больше второго.
Таким образом, отнимать дроби с разными знаменателями не так уж и сложно. Нужно просто найти общий знаменатель, дополнительные множители и выполнить вычитание. При этом следует упомянуть так называемые онлайн-калькуляторы. Это веб-сервисы, которые в автоматическом режиме выполняют вычитание.
Их довольно удобно использовать не только для проверки самостоятельно решённых примеров, но и на стадии обучения.
Всё дело в том, что, кроме быстрого решения, эти сайты могут предоставить пользователям подробные решения того или иного примера.
«Человек подобен дроби: в знаменателе – то, что он о себе думает, в числителе – то, что есть на самом деле. Чем больше знаменатель, тем меньше дробь».
Лев Толстой
Изучая математику, мы, несомненно, увеличиваем свой «числитель». Продолжим же постигать истину и осваивать действия с рациональными числами. Сегодня мы рассмотрим, как выполняют вычитание дробей любого знака.