Коэффициент
достоверности аппроксимации
это значение которое характеризует
точность аппроксимации, т. е. показывает
на сколько точно теоретическое
распределение описывает реальное
распределение.
Коэффициент
достоверности аппроксимации R2 показывает
степень соответствия трендовой модели
исходным данным. Его значение может
лежать в диапазоне от 0 до 1. Чем ближе
R2 к
1, тем точнее модель описывает имеющиеся
данные.
Критерий
Фишера
используется для оценки значимости
модели в целом.
Для
оценки используется уравнение следующего
вида:
где – коэффициент
детерминации, n – количество наблюдений,
k – число объясняющих переменных.
Вычисленное
по этой формуле значение сравнивается
с критическим значением критерия Фишера
из таблиц распределения Фишера:
где –
уровень значимости,и
–
степени свободы.
Если
в результате сравнения оказывается,
что ,
то при заданном уровне значимостипринимается
гипотеза о надежности модели в целом.
Если в результате сравнения оказывается,
что,
то при заданном уровне значимостигипотеза
о надежности модели в целом отвергается.
52. Понятие экстраполяции (прогнозирование результатов измерений)
Экстраполяция—
это метод прогнозирования, который
предполагает, что закономерность
развития, действовавшая в прошлом,
сохранится и в прогнозируемом будущем.
53. Фундаментальная теорема переноса ошибок имеет вид:
где —
корреляционная матрица, –
матрица производных функций .
Эта формула применяется при оценке
функций.
–
это
дисперсия DY.
Если
оценивается несколько функций, то
матрица f будет являться матрицей Якоби
(используем формулу ).
Получим
ковариационную матрицу, диагональные
элементы которой соответствуют дисперсии,
корень из дисперсии будет соответствовать
СКО функций.
Если
мы имеем функцию суммы или разности
двух независимых величин
,
то квадрат
средней квадратической ошибки
функции выразится формулой
mz2=mx2+my2
При
Если
функция имеет вид
,
то (14)
т.
е. квадрат средней квадратической ошибки
алгебраической суммы аргументов равен
сумме квадратов средних квадратических
ошибок слагаемых.
Если m1=m2=m3=…=mn=m,то
формула(14) примет вид
т.
е. средняя квадратическая ошибка
алгебраической суммы (разности) измеренных
с одинаковой точностью величин
в раз
больше средней квадратической ошибки
одного слагаемого.
Если
функция имеет вид
То
где k1,
k2,
kз,
…, kп —
постоянные числа; m1,m2,m3,…,
тп —
средние квадратические ошибки
соответствующих аргументов. Если имеем
функцию многих независимых переменных
общего вида
то .
(15)
Из
формулы (15) следует, что квадрат средней
квадратической ошибки функции общего
вида равен сумме квадратов произведений
частных производных по каждому аргументу
на среднюю квадратическую ошибку
соответствующего аргумента
54. Оценка точности функций зависимых результатов измерений.
Формулы
для вычислений средних квадратических
ошибок функции u=f(x1,x2,….xn)
имеют
вид:
а)
в случае некоррелированных аргументов
:
mu2=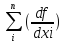
mxi2
б)
для коррелированных аргументов
mu2=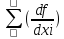
mxi2+2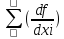
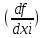
rxi
xj
mxi
mxj
Для
системы функций (вектор-функции) u = f(X)
Mu2=
AM2xAT
где Mu2
и M2x
—
соответственно эмпирическне корреляционные
матрицы вектор-функции и вектора
измерений. А — Матрица
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Корреляция и регрессия
Когда вы исследуете закономерности в своих данных, как вы можете определить, насколько тесно связаны между собой две переменные? Можете ли вы использовать одну переменную для предсказания другой?
В этом модуле вы познакомитесь с концепциями корреляции и регрессии, которые могут помочь вам в дальнейшем изучении, понимании и обмене данными.
Видео 1
Видео 2
Цели
По завершении этого модуля вы сможете:
- Различать сильную и слабую корреляцию.
- Различать характеристики корреляции и линейной регрессии.
Раздел 1. Корреляция
В этом модуле вы познакомитесь с двумя концепциями, которые помогут вам в изучении взаимосвязей между переменными: корреляция и регрессия. Начнем с корреляции.
Что такое корреляция?
Корреляция – это техника, которая может показать, насколько сильно связаны пары количественных переменных. Например, количество ежедневно потребляемых калорий и масса тела взаимосвязаны, но эта связь не абсолютная.
Многие из нас знают кого-то, кто очень худой, несмотря на то, что он/она регулярно потребляет большое количество калорий, и мы также знаем кого-то, у кого есть проблемы с лишним весом, даже когда он/она сидит на диете с пониженным содержанием калорий.
Однако средний вес людей, потребляющих 2000 калорий в день, будет меньшим, чем средний вес людей, потребляющих 2500, а их средний вес будет еще меньше, чем у людей, потребляющих 3000, и так далее.
Корреляция может сказать вам, насколько тесно разница в весе людей связана с количеством потребляемых калорий.
Корреляция между весом и потреблением калорий – это простой пример, но иногда данные, с которыми вы работаете, могут содержать корреляции, которых вы никак не ожидаете. А иногда вы можете подозревать корреляции, не зная, какие из них самые сильные. Корреляционный анализ помогает лучше понять связи в ваших данных.
Диаграммы разброса или Точечные диаграммы используются для графического представления взаимосвязей между количественными показателями. Диаграмма показывает данные и позволяет нам проверить свои предположения, прежде чем устанавливать корреляции. Глядя на взаимосвязь между продажами и маркетингом, можно предположить наличие в них корреляции. По мере того, как одна переменная растет, другая, похоже, тоже увеличивается.
Диаграмма, указывающая на корреляцию между двумя количественными переменными
Корреляция против причинно-следственной связи
Теперь вы знаете, как определяется корреляция и как ее можно представить графически. Теперь давайте посмотрим, как понимать корреляцию.
Во-первых, важно понимать, что корреляция никогда не доказывает наличие причинно-следственной связи.
Корреляция говорит нам только о том, насколько сильно пара количественных переменных линейно связана. Она не объясняет, как и почему.
Например, продажи кондиционеров коррелируют с продажами солнцезащитных кремов. Люди покупают кондиционеры, потому что они купили солнцезащитный крем, или наоборот? Нет. Причина обеих покупок явно в чем-то другом, в данном случае – в жаркой погоде.
Измерение корреляции
Корреляция Пирсона, также называемая коэффициентом корреляции, используется для измерения силы и направления (положительного или отрицательного) линейной связи между двумя количественными переменными. Когда корреляция измеряется в выборке данных, используется буква r. Критерий Пирсона r может находиться в диапазоне от –1 до 1.
Когда r = 1, существует идеальная положительная линейная связь между переменными, это означает, что обе переменные идеально коррелируют с увеличением значений. Когда r = –1, существует идеальная отрицательная линейная связь между переменными, это означает, что обе переменные идеально коррелируют при уменьшении значений. Когда r = 0, линейная связь между переменными не наблюдается.
На графиках разброса ниже показаны корреляции, где r = 1, r = –1 и r = 0.
Переверните каждую карту ниже, чтобы увидеть значение для этой совокупности.
Идеальная положительная корреляция
Когда r = 1, есть идеальная положительная линейная связь между переменными, и это означает, что обе переменные идеально коррелируют с увеличением значений.
Идеальная отрицательная корреляция
Когда r = –1, существует идеальная отрицательная линейная связь между переменными, и это означает, что обе переменные идеально коррелируют при уменьшении значений.
Нет линейной корреляции
Когда r = 0, линейная зависимость между переменными не наблюдается.
С реальными данными вы никогда не увидите значений r «–1», «0» или «1».
Как правило, чем ближе r к 1 или –1, тем сильнее корреляция, это показано в следующей таблице.
|
r = |
Сила корреляции |
|---|---|
|
От 0.90 до 1 |
Очень сильная корреляция |
|
От 0.70 до 0.89 |
Сильная корреляция |
|
От 0.40 до 0.69 |
Умеренная корреляция |
|
От 0.20 до 0.39 |
Слабая корреляция |
|
От 0 to 0.19 |
Очень слабая корреляция или ее нет вообще |
Условие корреляции
Чтобы корреляции были значимыми, они должны использовать количественные переменные, и описывать линейные отношения, при этом не может быть выбросов.
В 1973 году статистик по имени Фрэнсис Анскомб разработал показатель «квартет Анскомба», он показывает важность визуального представления данных в виде графиков, а не простого выполнения статистических тестов.
Выделенный график разброса в верхнем левом углу – единственный, который удовлетворяет условиям корреляции.
Четыре визуализации в его квартете показывают одну и ту же линию тренда, поэтому значение r будет одинаковым для всех четырех.
Что вы заметили? Только один из графиков рассеяния соответствует критериям линейности и отсутствия выбросов.
Другими словами, мы не должны проводить корреляции на трех из четырех примерах, потому что не имеет смысла устанавливать сильные отношения.
Проверка знаний
Силу корреляции при значении r, равному –0,52, лучше всего можно описать как:
- Очень сильная отрицательная корреляция
- Очень сильная положительная корреляция
- Умеренная отрицательная корреляция
- Умеренная положительная корреляция
Резюме
Итак, вы ознакомились с концепциями статистической техники корреляции. На следующем уроке вы узнаете о линейной регрессии.
Раздел 2. Линейная регрессия
На предыдущем уроке вы узнали, что корреляция относится к направлению (положительному или отрицательному) и силе связи (от очень сильной до очень слабой) между двумя количественными переменными.
Линейная регрессия также показывает направление и силу взаимосвязи между двумя числовыми переменными, но регрессия использует наиболее подходящую прямую линию, проходящую через точки на диаграмме рассеяния, чтобы предсказать, как X вызывает изменение Y. При корреляции значения X и Y взаимозаменяемы. При регрессии результаты анализа изменятся, если поменять местами X и Y.
Диаграмма рассеяния с линией регрессии
Видео 1
Видео 2
Линия регрессии
Как и в случае с корреляциями, для того, чтобы регрессии были значимыми, они должны:
- Использовать количественные переменные
- Быть линейными
- Не содержать выбросов
Как и корреляция, линейная регрессия отображается на диаграмме рассеяния
Линия регрессии на диаграмме рассеяния – это наиболее подходящая прямая линия, которая проходит через точки на диаграмме рассеяния. Другими словами, это линия, которая проходит через точки с наименьшим расстоянием от каждой из них до линии (поэтому в некоторых учебниках вы можете встретить название «регрессия наименьших квадратов»).
Почему эта линия так полезна? Мы можем использовать вычисление линейной регрессии для вычисления или прогнозирования нашего значения Y, если у нас есть известное значение X.
Чтобы было понятнее, давайте рассмотрим пример.
Пример регрессии
Представьте, что вы хотите предсказать, сколько вам нужно будет заплатить, чтобы купить дом площадью 1,500 квадратных футов.
Давайте используем для этого линейную регрессию.
- Поместите переменную, которую вы хотите прогнозировать, цену на жилье, на ось Y (зависимая переменная).
- Поместите переменную, на которой вы основываете свои прогнозы, квадратные метры, на ось x (независимая переменная).
Вот диаграмма рассеяния, показывающая цены на жилье (ось Y) и площадь в квадратных футах (ось x).
Вы можете видеть, что дома с большим количеством квадратных футов, как правило, стоят дороже, но сколько именно вам придется потратить на дом размером 1500 квадратных футов?
Диаграмма рассеяния цен на дома и квадратных метров
Чтобы помочь вам ответить на этот вопрос, проведите линию через точки. Это и будет линия регрессии. Линия регрессии поможет вам предсказать, сколько будет стоить типовой дом определенной площади в квадратных метрах. В этом примере вы можете видеть уравнение для линии регрессии.
Уравнение линии регрессии
Уравнение линии регрессии: Y = 113x + 98,653 (с округлением).
Что означает это уравнение? Если вы купили просто место без площади (пустой участок), цена составит 98,653 доллара. Вот как можно решить это уравнение:
Чтобы найти Y, умножьте значение X на 113, а затем добавьте 98,653. В этом случае мы не смотрим на квадратные метры, поэтому значение X равно «0».
- Y = (113 * 0) + 98,653
- Y = 0 + 98,653
- Y = 98,653
Значение 98,653 называется точкой пересечения по оси Y, потому что здесь линия пересекает ось Y. Это – значение Y, когда X равно «0».
Но что такое 113? Число «113» – это наклон линии. Наклон – это число, которое описывает как направление, так и крутизну линии. В этом случае наклон говорит нам, что за каждый квадратный фут цена дома будет расти на 113 долларов.
Итак, сколько вам нужно будет потратить на дом площадью 1500 квадратных футов?
Y = (113 * 1500) + 98,653 = $268,153
Взгляните еще раз на эту диаграмму рассеяния. Синие отметки – это фактические данные. Вы можете видеть, что у вас есть данные для домов площадью от 1100 до 2450 квадратных футов.
Насколько можно быть уверенным в результате, используя приведенное выше уравнение, чтобы спрогнозировать цену дома площадью в 500 квадратных футов? Насколько можно быть уверенным в результате, используя приведенное выше уравнение, чтобы предсказать цену дома площадью 10,000 квадратных футов?
Поскольку оба этих измерения находятся за пределами диапазона фактических данных, вам следует быть осторожными при прогнозировании этих значений.
Величина достоверности аппроксимации
Наведите курсор на линию регрессии, чтобы увидеть значение величины достоверности аппроксимации r.
В дополнение к уравнению в этом примере мы также видим значение величины достоверности аппроксимации r (также известная как коэффициент детерминации).
Это значение является статистической мерой того, насколько близки данные к линии регрессии или насколько хорошо модель соответствует вашим наблюдениям. Если данные находятся точно на линии, значение величины достоверности аппроксимации будет 1 или 100%, и это означает, что ваша модель идеально подходит (все наблюдаемые точки данных находятся на линии).
Для наших данных о ценах на жилье значение величины достоверности аппроксимации составляет 0,70, или 70%.
Корреляция против причинно-следственной связи
Теперь давайте рассмотрим, как отличить линейную регрессию от корреляции.
Линейная регрессия
- Показывает линейную модель и прогноз, прогнозируя Y из X.
- Использует величину достоверности аппроксимации для измерения процента вариации, которая объясняется моделью.
- Не использует X и Y как взаимозаменяемые значения (поскольку Y предсказывается из X).
Корреляция
- Показывает линейную зависимость между двумя значениями.
- Использует r для измерения силы и направления корреляции.
- Использует X и Y как взаимозаменяемые значения.
Готовы проверить свои знания? В следующем упражнении определите, чему соответствует каждое из описаний: корреляции или регрессии.
Варианты для категорий: «корреляция» или «регрессия».
Измеряется величиной достоверности аппроксимации
Прогнозирует значения Y на основе значений X.
Не предсказывает значения Y из значений X, только показывает взаимосвязь.
Переменные оси X и Y взаимозаменяемы.
Измеряется r
Если поменять местами X и Y, результаты анализа изменятся.
Резюме
Итак, здесь вы познакомились со статистическими концепциями корреляции и регрессии. Это поможет вам лучше исследовать и понимать данные, с которыми вы работаете, путем изучения взаимосвязей в них.
#dataliteracy, #информационная грамотность, #DataLiteracyProject
Следующая статья: Дополнительно
Михаил Витер
Эксперт по предмету «Информационные технологии»
Задать вопрос автору статьи
Определение 1
Аппроксимация табличных функций в Excel — это определение аппроксимирующей функции, которая является близкой к заданной.
Понятие аппроксимации
Среди разных методик прогнозирования следует отдельно выделить метод аппроксимации. С его помощью имеется возможность осуществления приблизительных подсчетов и вычисления планируемых показателей, за счёт подмены исходных объектов на более простые. В Excel также присутствует возможность применения этого метода с целью выполнения прогнозов и анализа.
Название этого метода произошло от латинского слова “proxima”, то есть, «ближайшая». Как раз приближение за счет упрощения и сглаживания некоторых показателей, формирование из них тенденции и считается его основой. Но эту методику можно применять не только для прогнозирования, но и для изучения уже полученных результатов. Поскольку аппроксимация выступает, по существу, как упрощение исходных данных, а упрощенную версию легче изучать.
Аппроксимация табличных функций в Excel
Основным инструментом, при помощи которого реализуется сглаживание в Excel, является формирование линии тренда. Суть заключается в том, что на базе уже существующих показателей выполняется достраивание графика функции на будущие периоды. Основным предназначением линии тренда очевидно является формирование прогнозов или определение общей тенденции.
Эта линия может быть построена с использованием одного из следующих типов аппроксимации:
линейная,
экспоненциальная,
логарифмическая,
полиномиальная,
* степенная.
Рассмотрим некоторые из этих вариантов более подробно, и начнем с линейной аппроксимации, которая фактически является линейным сглаживанием. Прежде всего, следует рассмотреть наиболее простую версию аппроксимации, то есть, при помощи линейной функции.
Замечание 1
Сначала необходимо построить график, на базе которого будет осуществляться процедура сглаживания.
«Аппроксимация табличных функций в Excel » 👇
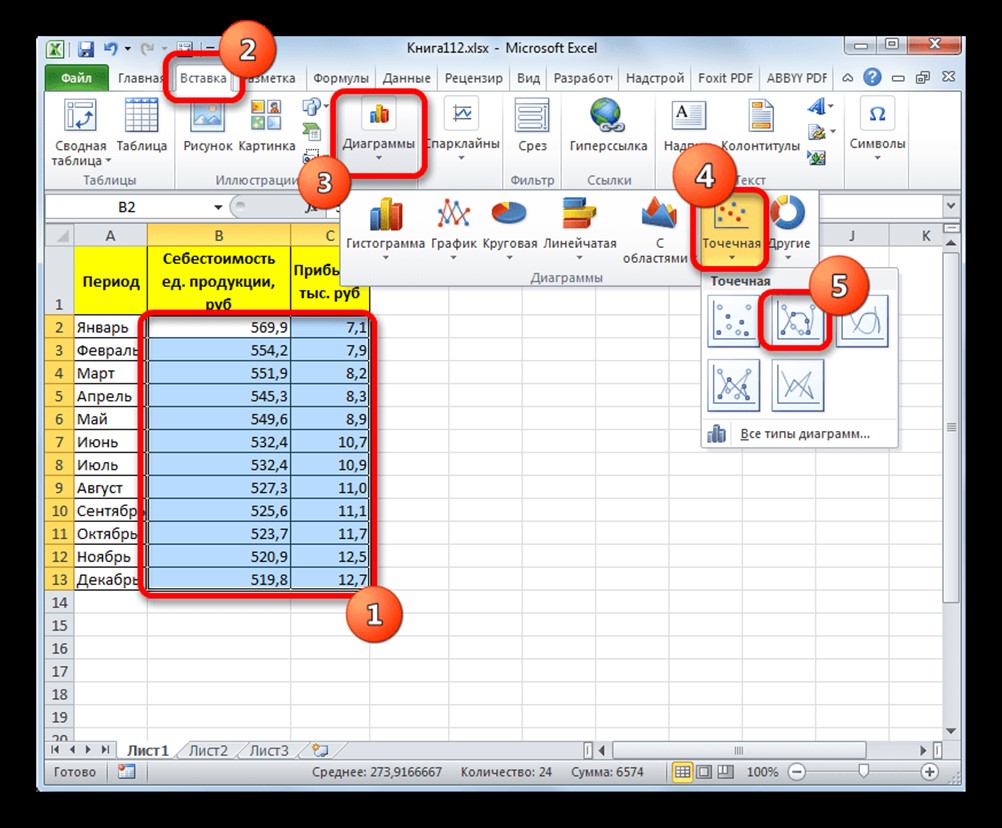
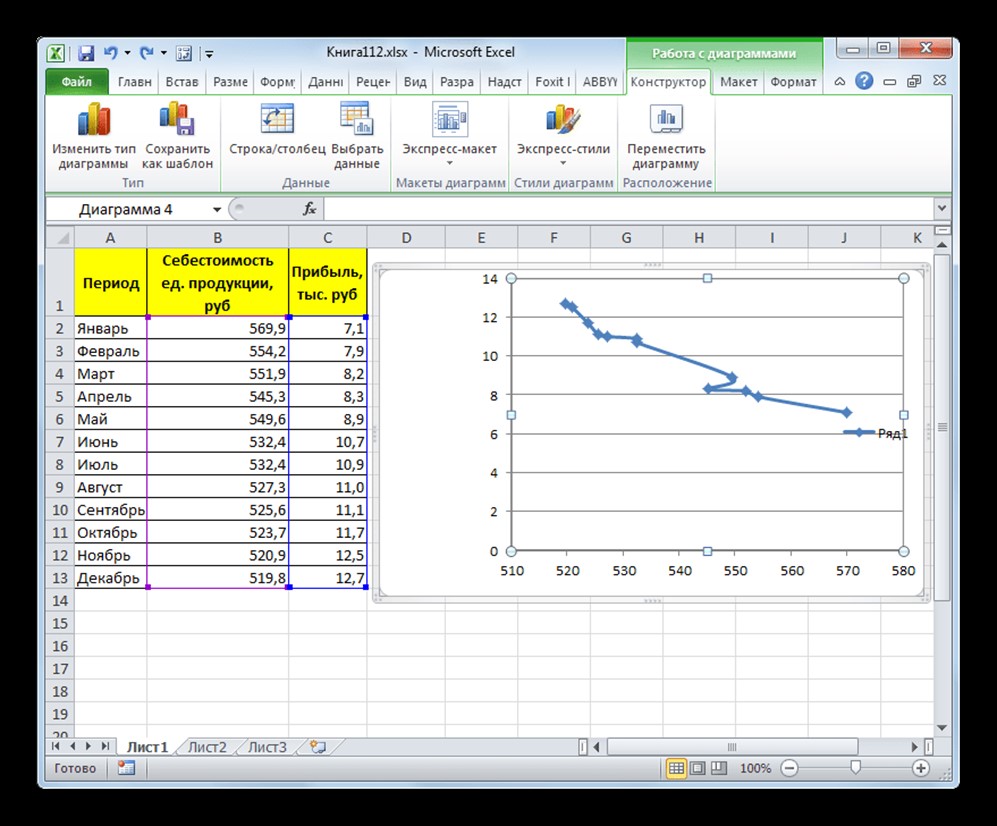
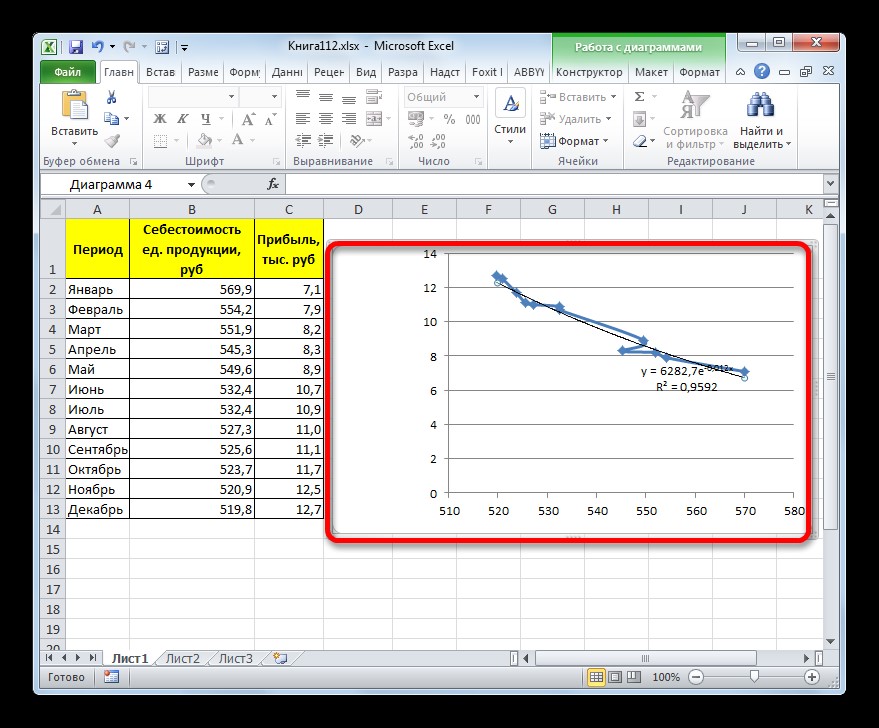
Чтобы построить график, необходимо взять таблицу, в которой, например, помесячно указывается себестоимость единицы продукции, выпускаемой организацией, и соответствующая прибыль за данный период. Графическая функция, которую необходимо построить, будет отображать зависимость роста прибыли от уменьшения себестоимости продукции. При построении графика сначала надо выделить столбцы «Себестоимость единицы продукции» и «Прибыль». После этого следует переместиться на вкладку «Вставка». Затем на ленте в блоке инструментов «Диаграммы» выполнить щелчок указателем мыши по кнопке «Точечная». В открывшемся списке нужно выбрать наименование «Точечная с гладкими кривыми и маркерами». Как раз такой вид диаграмм больше всего подходит для работы с линией тренда, а, следовательно, и для использования метода аппроксимации в Excel.
Рисунок 1. Параметры для построения графика. Автор24 — интернет-биржа студенческих работ
Затем будет построен следующий график:
Рисунок 2. Точечная с гладкими кривыми и маркерами. Автор24 — интернет-биржа студенческих работ
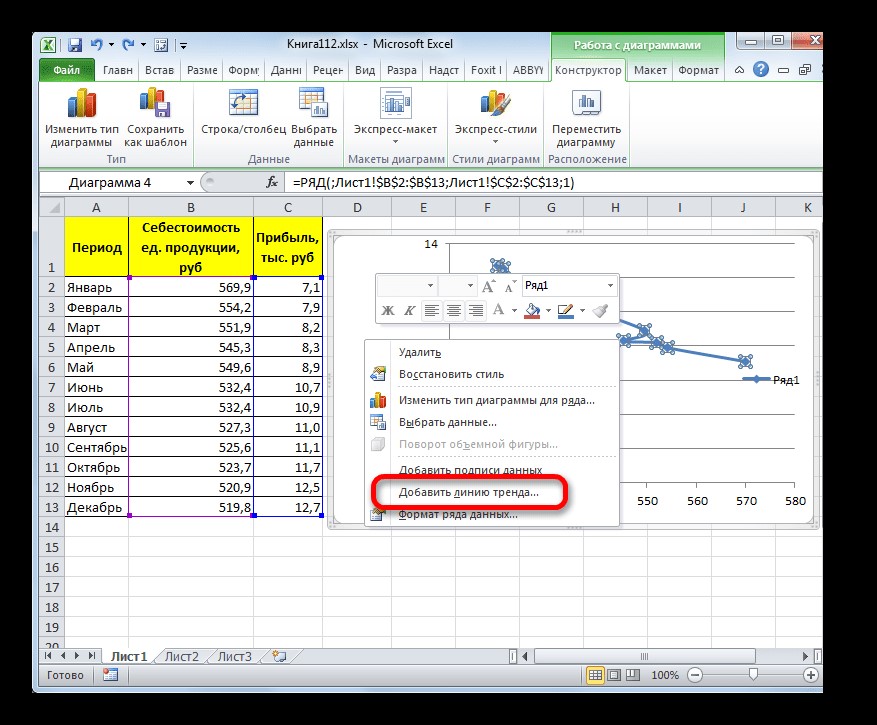
Чтобы добавить линию тренда, необходимо выделить график кликом правой кнопки мыши, после чего появится контекстное меню. Следует осуществить выбор в нем пункта «Добавить линию тренда…».
Рисунок 3. Добавить линию тренда на график. Автор24 — интернет-биржа студенческих работ
Имеется и другой вариант добавления линии тренда. В дополнительной группе вкладок на ленте «Работа с диаграммами» следует переместиться во вкладку «Макет». Затем в блоке инструментов «Анализ» необходимо сделать щелчок по кнопке «Линия тренда», после чего откроется список. Поскольку в нашем случае рассматривается применение линейной аппроксимации, то из предложенных позиций следует выбрать «Линейное приближение».
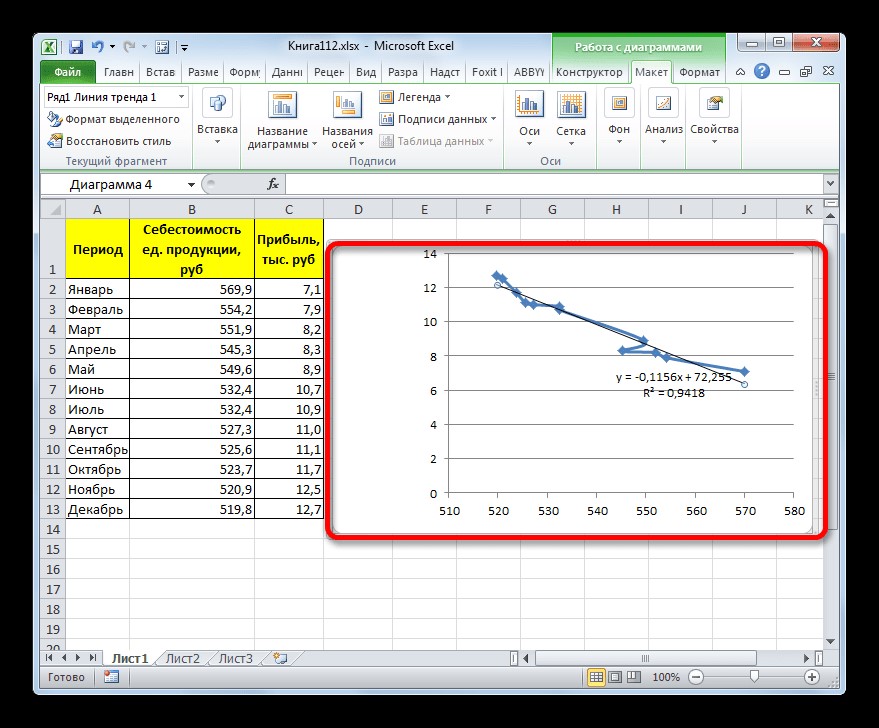
Если же был выбран первый вариант действий с добавлением через контекстное меню, то далее будет открыто окно формата. В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» необходимо установить переключатель в позицию «Линейная». Если это необходимо, то следует поставить галочку около позиции «Показывать уравнение на диаграмме». После данных действий на диаграмме будет отображено уравнение сглаживающей функции.
Кроме того, для сравнения разных вариантов аппроксимации можно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Этот показатель варьируется в диапазоне от нуля до единицы. Чем его значение больше, тем точнее выполнена аппроксимация. Считается, что если величина данного показателя равна 0,85 и выше, то сглаживание может считаться достоверным, а если показатель ниже, то его достоверность ниже допустимой. После проведения всех вышеуказанных настроек, следует нажать на кнопку «Закрыть», размещенную в нижней части окна. Появится линия тренда.
Рисунок 4. Отображение линии тренда. Автор24 — интернет-биржа студенческих работ
При выполнении линейной аппроксимации линия тренда обозначается черной прямой линией. Приведенный тип сглаживания может быть использован в самых простых случаях, когда данные меняются достаточно быстро и зависимость величины функции от аргумента является очевидной. Сглаживание, которое применяется в этом варианте, может быть описано следующей формулой:
y = ax + b.
Для конкретного варианта, приведенного выше, формула будет иметь следующий вид:
y = ‒ 0,1156x + 72,255.
Значение достоверности аппроксимации в рассмотренном случае равняется 0,9418, что считается достаточно приемлемым результатом, который характеризует сглаживание как достоверное.
Далее рассмотрим экспоненциальный тип аппроксимации в Excel. Для изменения типа линии тренда, следует выделить ее кликом правой кнопки мыши и в открывшемся меню нужно выбрать пункт «Формат линии тренда…». После этого будет запущено уже применявшееся ранее окно формата. В блоке выбора типа аппроксимации необходимо установить переключатель в положение «Экспоненциальная». Остальные настройки следует оставить такими же, как и в первом варианте, и затем выполнить щелчок по кнопке «Закрыть». После этого линия тренда будет построена на графике, как показано на рисунке ниже:
Рисунок 5. Экспоненциальный тип аппроксимации. Автор24 — интернет-биржа студенческих работ
При использовании этого метода линия тренда обладает несколько изогнутой формой. Причем уровень достоверности равняется 0,9592, что выше, чем при использовании линейной аппроксимации.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Когда научный руководитель сказал мне о необходимости указать на графике R² (р квадрат), я растерялся. В тот момент я не знал о трендах в диаграммах и графиках Excel. Этот материал поможет сориентироваться начинающим.
Что такое R² в Экселе
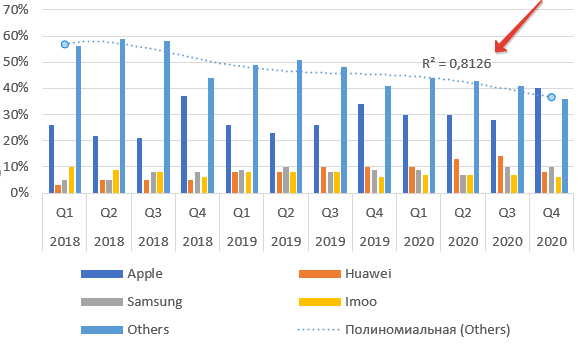
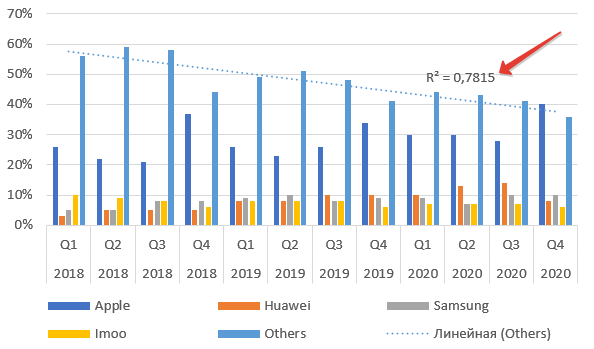
Для примера возьмем данные о продажах умных часов по брендам. Саму таблицу и график можно найти по этой ссылке на сайте CounterPointResearch. Там много подобной информации.
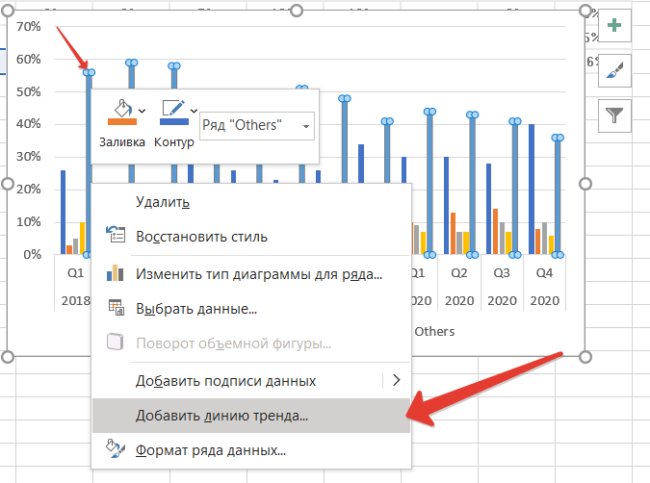
Выделяем диапазон данных и добавляем диаграмму. Теперь наводим мышь на столбцы бренда Others — «остальные», нажимаем правую клавишу мыши. Выбираем пункт Добавить линию тренда.
По умолчанию тренд линейный. Чуть позднее расскажу, как выбрать иную функцию, и стоит ли это делать. Теперь подводим курсор мыши к тренду и снова нажимаем правую кнопку.
Добавляем на график R².
Как видим из названия пункта, это величина достоверности апроксимации. Максимальное значение параметра Р-квадрат единица. Но получить ее можно только на специально подогнанных данных в реальной жизни приемлемое значение 0,8-0,9. В нашем случае — 0,78, что неплохо.
Стоит ли добиваться максимального значения R²
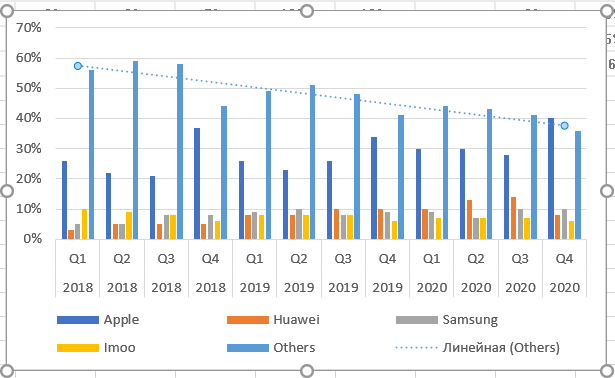
Улучшить достоверность апроксимации можно меняя вид кривой. Это можно сделать в открывающемся справа окошке Формат линии тренда.
Если использовать полиноминальную функцию, то апроксимацию можно улучшить значительно. Но вот смысла это не имеет. Экономические показатели обычно укладываются в линейный (рост/падение) или экспоненциальный тренд. Экспоненциально, например, растет число клиентов быстрорастущей фирмы.
Выбор полиноминальной функции может и улучшит показатель достоверности, а вот прогноз сделает менее точным.
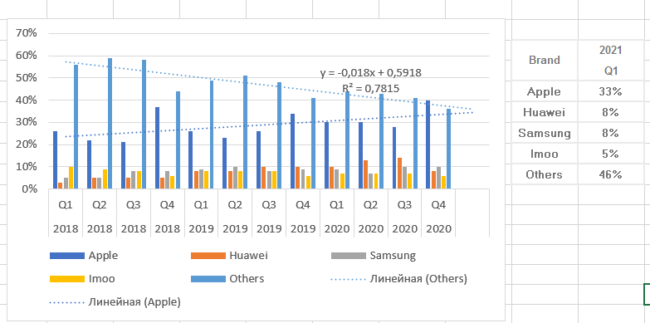
Как использовать тренд для прогноза
Кроме определения общего положения дел (рост/снижение), тренд может предсказать значения показателей в будущем. Это делается в окошке Формата линии тренда.
Попробуем предсказать продажи умных часов в первом квартале 2021 году и сравним их с фактом. Добавим два линейных тренда для Apple и Остальных.
Как видим, по яблочным часа прогноз построен верно, по остальным функция прогнозирует значение около 35%, а в реальности 46%. Возможно, это связано с выходом новых игроков на рынок или снижением доли Huawei. Мы имеем дело с относительными показателями (доля), а не с натуральными. Кстати, полиноминальный прогноз для категории Остальные дал бы еще менее точный прогноз, хотя R² и выше, что подтверждает необходимость осторожно выбирать функцию.
Почитайте и другие статьи про работу с таблицами Excel на нашем сайте. Например, у нас есть полезный материал об условном оформлении ячеек в таблице.
Понравилась статья? Поделитесь!
Решить задачу аппроксимации
экспериментальных данных – значит построить уравнение регрессии. Задача аппроксимации возникает в случае необходимости аналитически, то есть в виде математической зависимости, описать реальные явления, наблюдения за которыми заданы в виде таблицы, содержащей значения показателя в разные моменты времени или при разных значениях независимого аргумента. Например,
Известны показатели прибыли (их можно обозначить Y
) в зависимости от размера капиталовложений (X
);
Известны объемы реализации фирмы (Y
) за шесть недель ее работы. В этом случае, X
– это последовательность недель.
Иногда говорят, что требуется построить эмпирическую модель
. Эмпирической
называется модель, построенная на основе реальных наблюдений. Если модель удается найти, можно сделать прогноз о поведении исследуемого явления и процесса в будущем и, возможно, выбрать оптимальное направление ее развития.
В общем случае задача аппроксимации
экспериментальных данных имеет следующую постановку
:
Пусть известны данные, полученные практическим путем (в ходе
n
экспериментов или наблюдений), которые можно представить парами чисел (х
i ; у i)
. Зависимость между ними отражает таблица:
| X | х 1 | х 2 | х 3 | … | х n |
| Y |
y 1 |
y 2 |
y 3 |
… | y n |
Имеется класс разнообразных функций
F
. Требуется найти аналитическое (т.е. математическое) выражение зависимости между этими показателями, то есть надо подобрать из множества функций F функцию
f
, такую что . которая наилучшим образом сглаживала бы экспериментальную зависимость между переменными и по возможности точно отражала общую тенденцию зависимости между
X
и Y
, исключая погрешности измерения и случайные отклонения.
Выяснить вид функции можно либо из теоретических соображений, либо анализируя расположение точек (х i ; у i)
на координатной плоскости.
Графически решить задачу аппроксимации
означает, провести такую кривую , точки которой (х i ; ŷ i)
находились бы как можно ближе к исходным точкам (х i ; у i)
, отображающим экспериментальные данные.
Для решения задачи аппроксимации
используют метод наименьших квадратов
.
При этом функция считается наилучшим приближением к , если для нее сумма квадратов отклонений «теоретических» значений , найденных по эмпирической формуле, от соответствующих опытных значений , имеет наименьшее значение по сравнению с другими функциями, из числа которых выбирается искомое приближение.
Математическая запись метода наименьших квадратов имеет вид:
где n
— количество наблюдений показателей.
Таким образом, задача аппроксимации распадается на две части.
Сначала устанавливают вид зависимости и, соответственно, вид эмпирической формулы, то есть решают, является ли она линейной, квадратичной, логарифмической или какой-либо другой. Если нет каких-либо теоретических соображений для подбора вида формулы, обычно выбирают функциональную зависимость из числа наиболее простых, сравнивая их графики с графиком заданной функции.
После этого определяются численные значения неизвестных параметров выбранной эмпирической формулы, для которых приближение к заданной функции оказывается наилучшим.
Простейшим видом эмпирической модели с двумя параметрами, используемой для аппроксимации результатов экспериментов, является линейная регрессия, описываемая линейной функцией:
где а, b
— искомые параметры.
Для модели линейной регрессии метод наименьших квадратов (1) запишется:
Для решения (2) относительно а и b приравнивают к нулю частные производные:
В итоге для нахождения a и b надо решить систему линейных алгебраических уравнений вида:

Реализовать метод наименьших квадратов в случае линейной регрессии в Excel можно различными способами.
1 способ.
Построить систему линейных алгебраических уравнений, подставив в (3) все известные значения, и решить ее, например, матричным методом (см. зад. 4).
В формульном виде элемент расчетной таблицы приведен на рис. 26.
2 способ.
Решить в Excel задачу оптимизации (2), применив для этого Поиск решения
(см. зад. 5).
Замечание 1.
Следует обратить внимание, что для целевой функции S удобно применить встроенную математическую функцию СУММКВРАЗН(массив1;массив2)
, в результате которой как раз и вычисляется сумма квадратов разностей двух массивов. В нашем случае следует в качестве массива1 указать диапазон исходных значений , а в качестве массива2 – «теоретические» значения , рассчитанные по формуле , где a
и b
– это адреса ячеек с искомыми значениями.
Замечание 2.
В диалоговом окне команды Поиск решения следует задать целевую ячейку, направление цели – на минимум и изменяемые ячейки (рис. 28). Данная задача ограничений не содержит.
Замечание3.
В качестве эмпирических моделей с двумя параметрами могут использоваться и нелинейные модели вида:
Описанный способ решения метода наименьших квадратов применим и для нелинейных зависимостей.
3 способ.
Для нахождения значений параметров a
и b
в случае линейной регрессии можно использовать следующие встроенные в Excel статистические функции:
НАКЛОН(известные_значения_У; известные_значения_Х)
ОТРЕЗОК(известные_значения_У; известные_значения_Х)
ЛИНЕЙН (известные_значения_У; известные_значения_Х)
Причем, функция НАКЛОН () возвращает значение параметра а
, функция ОТРЕЗОК() возвращает значение параметра b.
Функция ЛИНЕЙН() возвращает одновременно оба параметра линейной зависимости, так как является функцией массива. Поэтому для ввода функции ЛИНЕЙН() в таблицу надо соблюдать следующие правила:
· выделить две рядом стоящие ячейки
· ввести формулу
· по окончании нажать одновременно комбинацию клавиш Ctrl+ Shift+Enter.
В результате в левой ячейке получится значение параметра а
, а в правой – значение параметра b.
Для решения задачи аппроксимации графическим способом
в Excel надо построить по исходным данным график, например, точечную диаграмму
со значениями, соединенными сглаживающими линиями (см.зад.1). На эту диаграмму Excel может нанести Линию тренда
. Линию тренда можно добавить к любому ряду данных, использующему следующие типы диаграмм: диаграммы с областями, графики, гистограммы, линейчатые или точечные диаграммы.
При создании линии тренда в Excel на основе данных диаграммы применяется та или иная аппроксимация. Excel позволяет выбрать один из пяти аппроксимирующих линий или вычислить линию, показывающую скользящее среднее.
Кроме того, Excel предоставляет возможность выбирать значения пересечения линии тренда с осью Y, а также добавлять к диаграмме уравнение аппроксимации и величину достоверности аппроксимации (R 2). Также, можно определять будущие и прошлые значения данных, исходя из линии тренда и связанного с ней уравнения аппроксимации.
Для наглядной иллюстрации тенденций изменения цены применяется линия тренда. Элемент технического анализа представляет собой геометрическое изображение средних значений анализируемого показателя.
Рассмотрим, как добавить линию тренда на график в Excel.
Добавление линии тренда на график
Для примера возьмем средние цены на нефть с 2000 года из открытых источников. Данные для анализа внесем в таблицу:
Линия тренда в Excel – это график аппроксимирующей функции. Для чего он нужен – для составления прогнозов на основе статистических данных. С этой целью необходимо продлить линию и определить ее значения.
Если R2 = 1, то ошибка аппроксимации равняется нулю. В нашем примере выбор линейной аппроксимации дал низкую достоверность и плохой результат. Прогноз будет неточным.
Внимание!!!
Линию тренда нельзя добавить следующим типам графиков и диаграмм:
- лепестковый;
- круговой;
- поверхностный;
- кольцевой;
- объемный;
- с накоплением.
Уравнение линии тренда в Excel
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:
На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):
Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).
Получаем результат:
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:
Строим график. Добавляем экспоненциальную линию.
Уравнение имеет следующий вид:
y = 7,6403е^-0,084x
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
Например:
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
Полиномиальная линия тренда в Excel
Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.
Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).
Чтобы получить такую величину достоверности аппроксимации (0,9256), пришлось поставить 6 степень.
Зато такой тренд позволяет составлять более-менее точные прогнозы.
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами
как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН
.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций
: в главном меню выберете Формулы / Вставить функцию
.
4) В окне Категория
выберете Статистические
, в окне функция — ЛИНЕЙН
. Щёлкните по кнопке ОК
как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у
Известные значения х
Константа
— логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика
— логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК
;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу
, а затем на комбинацию клавиш ++
.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Стандартная ошибка y | |
| F-статистика | |
| Регрессионная сумма квадратов
|
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
Означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: .
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее
, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия
можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа
. В главном меню последовательно выберите: Файл/Параметры/Надстройки
.
2) В раскрывающемся списке Управление
выберите пункт Надстройки Excel
и нажмите кнопку Перейти.
3) В окне Надстройки
установите флажок Пакет анализа
, а затем нажмите кнопку ОК
.
Если Пакет анализа
отсутствует в списке поля Доступные надстройки
, нажмите кнопку Обзор
, чтобы выполнить поиск.
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да
, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия
, а затем нажмите кнопку ОК
.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y
— диапазон, содержащий данные результативного признака;
Входной интервал X
— диапазон, содержащий данные факторного признака;
Метки
— флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа — ноль
— флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал
— достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист — можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК
.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как не превышает 8 — 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н 0 о статистически незначимом отличии показателей от нуля:
.
для числа степеней свободы
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ:
где 
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н 0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций
: в главном меню выберете Формулы / Вставить функцию
.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК
.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2003. — 192 с.: ил.
ЗАВИСИМОСТЕЙ
Excel
располагает средствами, позволяющими прогнозировать процессы. Задача
аппроксимации возникает в случае необходимости аналитически описать явления,
имеющие место в жизни и заданные в виде таблиц, содержащих значения аргумента
(аргументов) и функции. Если зависимость удается найти, можно сделать прогноз о
поведении исследуемой системы в будущем и, возможно, выбрать оптимальное
направление ее развития. Такая аналитическая функция (называемая еще трендом)
может иметь разный вид и разный уровень сложности в зависимости от сложности
системы и желаемой точности представления.
10.1. Линейная регрессия
Самый
простой и популярной является аппроксимация прямой линией – линейная регрессия.
Пусть мы
имеем фактическую информацию об уровнях прибыли Y в зависимости от размера X
капиталовложений – Y(X). На рис. 10.1-1 показаны четыре такие точки М(Y,X).
Пусть также у нас имеются основания предполагать, что зависимость эта линейная,
т.е. имеет вид Y=А+ВX.
Если бы нам удалось найти коэффициенты A и B и
по ним построить прямую (например, такую, как на рисунке), в дальнейшем мы
могли бы сделать осознанные предположения о динамике бизнеса и возможном
коммерческом состоянии предприятия в будущем. Очевидно, что нас бы устроила
прямая, находящаяся как можно ближе к известным точкам М(Y,X), т.е. имеющая
минимальную сумму отклонений или сумму ошибок (на рисунке отклонения показаны
пунктирными линиями). Известно, что существует только одна такая прямая.
Для решения этой задачи используют метод наименьших
квадратов ошибок. Разность (ошибка) между известным значением Y1 точки М1(Y1,X1) и значением Y(X1), вычисленным по уравнению прямой для того же
значения X1, составит
D1 = Y1 – A – B X1.
Такая же разность
для X=X2 составит D2 = Y2 – A – B X2;
для X=X3 D3 = Y3 – A – B X3;
и для X=X4 D4 = Y4 – A – B X4.
Запишем
выражение для суммы квадратов этих ошибок
Ф(A,В)=(Y1–A–B X1) 2 +(Y2–A–B X2) 2 +(Y3–A–B X3) 2 +(Y4–A–B X4) 2
или
сокращенно Ф(B,A) = å(Yi – A – BXi) 2 .
Здесь нам
известны все X и Y и неизвестны коэффициенты A и B. Проведем искомую прямую так
(т.е. выберем A и B такими), чтобы эта сумма квадратов ошибок Ф(A,B) была
минимальной. Условиями минимальности являются известные соотношения
¶Ф(A,B)/¶A=0 и ¶Ф(A,B)/¶B=0.
Выведем эти выражения (индексы при знаке суммы опускаем):
¶[å(Yi–A–B Xi) 2 ]/¶A = å(Yi–A–B Xi)(–1)
¶[å(Yi–A–B Xi) 2 ]/¶B = å(Yi–A–B Xi)(–Xi).
Преобразуем полученные формулы и приравняем их нулю
Решение задач аппроксимации средствами Excel
доктор физ.– мат. наук, профессор Гавриленко В.В. ассистент Парохненко Л.М.
(Национальный транспортный университет)
Теоретическая справка.
На практике при моделировании различных про-
цессов, в частности, экономических, физических, технических, социальных,
широко используются те или иные способы вычисления приближенных значе-
ний функций по известным их значениям в некоторых фиксированных точках.
Такого рода задачи приближения функций часто возникают:
∙
при построении приближенных формул для вычисления значений характер-
ных величин исследуемого процесса по данным таблиц, полученным в ре-
зультате физического или вычислительного эксперимента;
∙
при численном интегрировании, численном дифференцировании, числен-
ном решении дифференциальных уравнений и т.д.;
∙
при необходимости вычисления значений функций в промежуточных точ-
ках рассматриваемого интервала;
∙
при определении значений характерных величин процесса за пределами рас-
сматриваемого интервала, в частности, при необходимости заглянуть в
“ прошлое”), то есть при определении значений показателей процесса до на-
чала наблюдения;
∙
в прогнозировании, то есть при получении предварительных оценок буду-
щих значений интересуемых показателей процесса (возможность заглянуть
в
“ будущее”).
Если для моделирования некоторого процесса, заданного таблицей, по-
строить приближенно описывающую данный процесс функцию на основе ме-
тода наименьших квадратов, то она называется аппроксимирующей функцией
(регрессией), а сама задача построения аппроксимирующих функций называет-
ся задачей аппроксимации.
В данной статье рассмотрены возможности пакета Excel
при реше-
нии задач аппроксимации, а именно, приведены методы и приемы построения
(создания) регрессий для таблично заданных функций, что является основой регрессионного анализа.
В
Excel
для построения регрессий имеются такие возможности, как:
1)
добавление выбранных регрессий (линий тренда) в диаграмму, построенную на основе таблицы данных для исследуемой характеристики процесса (этим инструментом можно воспользоваться лишь при наличии построенной диа-
2)
использование встроенных статистических функций рабочего листа
Excel
,
позволяющих получать регрессии (линии тренда) на основе таблицы исход-
ных данных (использование данного инструмента предварительно не связы-
вается с наличием соответствующей диаграммы).
Добавление линий тренда в диаграмму
Для таблицы данных, описывающих некоторый процесс и представленных диаграммой, в Excel
имеется эффективный инструмент регрессионного анали-
за, позволяющий:
∙ строить на основе метода наименьших квадратов и добавлять в диаграмму пять типов регрессий (линий тренда), которые с той или иной степенью точно-
сти моделируют исследуемый процесс;
∙
добавлять к диаграмме уравнение построенной регрессии;
∙
определять степень соответствия выбранной регрессии отображаемым на диаграмме данным.
Построенные модели процесса – линии тренда (trendlines) показывают
тенденцию изменения данных, дают возможность определять значения иссле-
дуемой характеристики в промежуточных точках, прогнозировать поведение данного процесса в будущем (задача экстраполяции), а также заглянуть в его прошлое.
На основе данных диаграммы Excel
позволяет получать такие типы регрес-
сий или линий тренда, как линейный, полиномиальный, логарифмический, сте-
пенной, экспоненциальный, которые задаются уравнением y = y(x)
, где x – неза-
висимая переменная, которая часто принимает значения последовательности натурального ряда чисел (1; 2; 3; …) и производит, например, отсчет времени протекания исследуемого процесса.
1. Линейная
регрессия хороша при моделировании характеристик, значения которых увеличиваются или убывают с постоянной скоростью. Это наиболее простая в построении, но наименее точная модель исследуемого процесса.
y = m x + b ,
где m – угол наклона линейной регрессии к оси абсцисс; b – координата точки пересечения линейной регрессии с осью ординат.
2. Полиномиальная
линия тренда полезна для описания характеристик,
имеющих несколько ярко выраженных экстремумов (максимумов и миниму-
мов). Выбор степени полиномиальной линии тренда (полинома) определяется количеством экстремумов исследуемой характеристики. Так, полином второй степени может хорошо описать характеристику, имеющую только один макси-
мум или минимум; полином третьей степени – не более двух экстремумов; по-
лином четвертой степени – не более трех экстремумов и т.д.
Строится в соответствии с уравнением
y = c0
+ c1
x + c2
x2
+ c3
x3
+ c4
x4
+ c5
x5
+ c6
x6
,
где коэффициенты c
0
, c
1
, c
2
,…c
6
– константы.
3.
Логарифмическая
линия тренда с успехом применяется при моделирова-
нии характеристик, значения которых вначале быстро растут или убывают по величине, а затем постепенно стабилизируются.
Строится в соответствии с уравнением
y =
c×
ln(x)+
b,
4. Степенная
линия тренда дает хорошие результаты, если значения иссле-
дуемой зависимости характеризуются постоянным изменением скорости роста.
Примером такой зависимости может служить график равноускоренного движе-
ния автомобиля. При наличии в данных нулевых или отрицательных значений использовать степенную линию тренда нельзя.
Строится в соответствии с уравнением
y =
c×
xb
,
где коэффициенты b, с – константы.
5. Экспоненциальная
линия тренда следует использовать в том случае, если скорость изменения данных непрерывно возрастает. Для данных, содержащих нулевые или отрицательные значения, этот вид приближения неприменим.
Строится в соответствии с уравнением
y =
c×
eb
×
x
,
где коэффициенты b, с – константы.
При подборе линии тренда Excel
автоматически рассчитывает значение величиныR
2
, которая характеризует достоверность аппроксимации: чем ближе значениеR
2
к единице, тем надежнее линия тренда аппроксимирует исследуе-
мый процесс. При необходимости значение R
2
всегда можно отобразить на
диаграмме.
Определяется по формуле
|
R 2 |
Σ1 |
S2 |
× |
||||||
Для добавления линии тренда к ряду данных следует:
1. Активизировать построенную на основе ряда данных диаграмму, т.е. щелк-
нуть в пределах области диаграммы. В главном меню появится пункт Диа-
2. После щелчка на этом пункте на экране появится меню, в котором следует выбрать команду Добавить линию тренда.
затель мыши к графику, построенного на ряде данных, и щелкнуть правой кла-
вишей мыши, и в появившемся контекстном меню выбрать команду Добавить
линию тренда. На экране появится диалоговое окно Линия тренда с раскры-
той вкладкой Тип (рис.1).
Рис.1. Вкладка Тип диалогового окна Формат линии тренда
3. Выбрать на вкладке Тип необходимый тип линии тренда (по умолчанию выбирается тип Линейный). Для типа Полиномиальная в поле Степень сле-
дует задать степень выбранного полинома.
4. В поле Построен на ряде перечислены все ряды данных рассматриваемой диаграммы. Для добавления линии тренда к конкретному ряду данных следует в поле Построен на ряде выбрать его имя.
5. При необходимости, перейдя на вкладку Параметры (рис.2), можно для ли-
нии тренда задать следующие параметры:
∙ Изменить название линии тренда в поле Название аппроксимирующей
(сглаженной)
кривой;
∙ Задать количество периодов (вперед или назад) для прогноза в поле Про-
∙ Вывести в область диаграммы уравнение линии тренда, для чего следует ус-
тановить флажок для опции «показать уравнение на диаграмме».
∙ Вывести в область диаграммы значение достоверности аппроксимации R
2
,
для чего следует установить флажок для опции «поместить на диаграмму ве-
личину достоверности аппроксимации (R^2)
».
∙ Задать точку пересечения линии тренда с осью Y, для чего следует устано-
вить флажок для опции «пересечение кривой с осью Y
в точке:
». 6. Нажать клавишуOK
.
Рис.2. Вкладка Параметры диалогового окна Линия тренда
Для редактирования
уже построенной линии тренда следует:
1. Щелкнуть левой клавишей мыши по той линии тренда, которую требуется
изменить.
2. Нажать в главном меню клавишу Формат, а появившемся контекстном ме-
ню выбрать команду Выделенная линия тренда.
Пункты 1–2 легко реализуются также следующим приемом: направить ука-
затель мыши к графику линии тренда, щелкнуть правой клавишей мыши, и в появившемся контекстном меню выбрать команду Формат линии тренда.
Еще легче реализуются пункты 1–2: двойным щелчком левой клавишей мыши по графику линии тренда.
3. На экране появится диалоговое окно Формат линии тренда (рис.3), содер-
жащее три вкладки: Вид, Тип, Параметры, причем содержимое вкладок Тип,
Параметры полностью совпадает с аналогичными вкладками диалогового ок-
на Линия тренда (рис.1–2).
4.
При необходимости, перейдя на вкладку Вид (рис.3), можно для линии тренда задать тип линии, ее цвет и толщину.
5.
Нажать клавишу
OK
.
Для удаления
уже построенной линии тренда следует выбрать удаляемую линию тренда и нажать клавишуDelete
.
Достоинствами
этого инструмента регрессионного анализа являются:
∙ относительная легкость построения на диаграммах линии тренда без созда-
ния для нее таблицы данных;
∙
достаточно широкий перечень типов предложенных линий трендов, причем в этот перечень входят наиболее часто используемые регрессии;
∙
возможность прогнозирования поведения исследуемого процесса на произ-
вольное (в пределах здравого смысла) количество шагов вперед, а также назад;
∙
возможность получения уравнения линии тренда в аналитическом виде;
∙
возможность, при необходимости, получения оценки достоверности прове-
денной аппроксимации.
К
недостаткам
можно отнести следующие моменты:
∙
построение линии тренда осуществляется лишь при наличии построенной на ряде данных диаграммы;
∙
несколько загроможден процесс формирования рядов данных для исследуе-
мой характеристики на основании полученных для нее уравнений линий трен-
да, так как коэффициенты этих уравнений при каждом изменении значений ря-
да данных пересчитываются, но лишь в пределах области диаграммы;
∙ в отчетах сводных диаграмм при изменении представления диаграммы или связанного отчета сводной таблицы имеющиеся линии тренда не сохраняются,
то есть до проведения линий тренда или другого форматирования отчета свод-
ных диаграмм следует убедиться, что макет отчета удовлетворяет необходи-
мым требованиям.
Рис.3. Вкладка Вид диалогового окна Формат линии тренда
Линиями тренда можно дополнить ряды данных, представленные на гра-
фиках, гистограммах, плоских ненормированных диаграммах с областями, ли-
нейчатых, точечных, пузырьковых и биржевых диаграммах.
Нельзя дополнить линиями тренда ряды данных на объемных, нормиро-
ванных, лепестковых, круговых и кольцевых диаграммах. При замене типа диа-
граммы на один из вышеперечисленных, а также при изменении представления отчета сводной диаграммы или связанного отчета сводной таблицы соответст-
вующие данным линии тренда будут утеряны.
Использование встроенных функций Excel
В
Excel
имеется также инструмент регрессионного анализа для построения линий тренда вне области диаграммы. Для этой цели можно использовать ряд статистических функций рабочего листа, однако все они позволяют строить лишь линейные или экспоненциальные регрессии.
В
Excel
имеется несколько вариантов построения линейной регрессии (ли-
нейного тренда), в частности:
∙
с помощью функции ТЕНДЕНЦИЯ;
∙
с помощью функции ЛИНЕЙН;
∙
с помощью функций НАКЛОН и ОТРЕЗОК
.
В
Excel
имеется также несколько вариантов построения экспоненциальной линии тренда, в частности:
∙
с помощью функции РОСТ;
∙
с помощью функции ЛГРФПРИБЛ.
Следует отметить, что приемы построения регрессий с помощью функций
ТЕНДЕНЦИЯ и РОСТ практически совпадают. То же самое можно сказать и о паре функций ЛИНЕЙН и ЛГРФПРИБЛ. Для всех этих четырех функций при создании таблицы значений используются такие возможности Excel
, как формулы массивов, что несколько загромождает процесс построения регрес-
сий. Заметим также, что построение (создание) линейной регрессии, на наш взгляд, легче всего осуществить с помощью функций НАКЛОН и ОТРЕЗОК,
где первая из них определяет угловой коэффициент линейной регрессии, а вто-
рая – отрезок, отсекаемый регрессией на оси ординат.
Достоинствами
данного инструмента регрессионного анализа являются:
∙ достаточно простой однотипный процесс формирования рядов данных ис-
следуемой характеристики для всех встроенных статистических функций, за-
дающих линии тренда;
∙ стандартная методика построения линий тренда на основе сформированных рядов данных;
∙ возможность прогнозирования поведения исследуемого процесса на необ-
ходимое количество шагов вперед или назад.
К недостаткам
данного инструмента можно отнести то, что вExcel
нет встроенных функций для создания других (кроме линейного и экспоненциаль-
ного) типов линий тренда. Это обстоятельство часто не позволяет подобрать с помощью выше перечисленных встроенных функций достаточно точную мо-
дель исследуемого процесса, а также получать близкие к реальности прогнозы.
Кроме того, при использовании функций ТЕНДЕНЦИЯ и РОСТ не известны уравнения линий тренда.
тьи – на конкретных примерах показать возможности пакета Excel
при реше-
нии задач аппроксимации; продемонстрировать, каким эффективными инстру-
ментами для построения регрессий и прогнозирования обладает Excel
; проил-
люстрировать, как относительно легко такие задачи могут быть решены даже пользователем, не владеющим глубокими знаниями регрессионного анализа.
Предложенная в статье методика по овладению навыков решения средства-
ми Excel
такого рода задач (см. также , где приведены методики решения вExcel
систем линейных алгебраических уравнений, нелинейных уравнений,
задач оптимизации, транспортных задач) может быть полезна и интересна пользователям. Это связано с тем, что пакет Excel
установлен практически на каждом современном компьютере, в то время как такие известные специализи-
рованные математические пакеты, как Mathematica
,Maple
,Matlab
,Mathcad
,
обладающие более мощными возможностями для построения регрессий и про-
гнозирования, используются значительно меньшей пользовательской аудито-
Ниже приводятся решения конкретных задач с помощью перечисленных инструментов пакета Excel
.
Задача
1
.
Для таблицы данных о прибыли автотранспортного предприятия за 1995–2002 г.г. необходимо выполнить следующие действия.