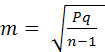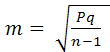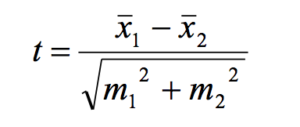-
Проверка статистических гипотез, критерий Стьюдента
В
научно-исследовательской практике
часто требуется сопоставить средние
арифметические, например, при сравнении
результатов в контрольной и экспериментальной
группах, при оценке показателей здоровья
населения в различных местностях за
несколько лет и т. д.
Методологической
основой любого исследования является
формулировка рабочей гипотезы. При этом
основной целью исследования является
получение данных, на основании которых
выдвинутую еще до начала исследования
(априори) гипотезу можно было бы принять,
т.е признать истинной, либо отвергнуть
— признать ложной.
Выдвинутую
гипотезу называют основной или нулевой
(H0).
Гипотезу,
которая противоречит нулевой и является
ее логическим отрицанием, называют
конкурирующей или альтернативной
(H1).
Гипотезы
H0
и Н1
предоставляют выбор только одного из
двух вариантов. Например, если нулевая
гипотеза предполагает, что среднее
арифметическое М = 15,
то логическим отрицанием будет М ≠ 15.
Коротко это записывается так: H0: М=15;
Н1:
М≠15.
В медико-биологических исследованиях
при сравнении регистрируемых признаков
в качестве нулевой гипотезы принимают
гипотезу об отсутствии различий.
Например,
при оценке токсичности какого-либо
вещества обычно берутся две группы
лабораторных животных. Подбираются
животные одинакового возраста, пола,
одинакового содержания и т. п. Таким
образом, делается все, чтобы эти группы
животных представляли собой единую,
как можно более однородную статистическую
совокупность, с тем, чтобы максимально
снизить исходную вариабельность
анализируемых данных. Оптимальным с
этой точки зрения считается ситуация,
когда отличия сравниваемых групп
заключаются только в том, что одна из
групп (опытная) подвергается воздействию
токсического вещества, а другая
(контрольная) — нет. В любом случае,
произошли ли после воздействия
токсического вещества изменения в
опытной группе или нет, различия средних
показателей в обеих группах обязательно
будут. Вопрос состоит в следующем:
являются ли эти различия только следствием
выборочного исследования, или разница
возникла из-за того, что произошли
существенные сдвиги физиологических
функций животных опытной группы, которые
будут обнаруживаться всегда, т.е. в
генеральной совокупности. Значит,
проверяется вопрос: принадлежат ли
животные опытной и контрольной групп
к той же самой генеральной совокупности
или опытная группа принадлежит к другой
генеральной совокупности (совокупности
с измененными физиологическими
параметрами)?
Методы
оценки достоверности различий средних
величин позволяют установить, насколько
выявленные различия существенны (носят
ли они закономерный характер или являются
результатом действия случайных причин).
Эту оценку можно выполнить только с
определенной степенью вероятности,
когда после установленного уровня
вероятности допущение о наличии различий
могут считаться закономерными или,
наоборот, отвергаются.
Выдвинутая
гипотеза может оказаться правильной
или неправильной. При ее статистической
проверке может быть отвергнута правильная
гипотеза. Вероятность совершить такую
ошибку называют уровнем значимости.
Этот параметр принято обозначать через
α
или p.
В биологии и медицине уровень значимости,
как правило, принимают не выше 0,05. Это
означает, что в 5 случаях из 100 (в 5%) мы
рискуем отвергнуть правильную гипотезу.
Соответственно, вероятность принятия
такой гипотезы (P)
равняется (P = 1 ‑ p)
0,95 (или 95%.)
Таким
образом, статистическая значимость
выборочных характеристик представляет
собой меру уверенности в их «истинности».
Уровень значимости находится в убывающей
зависимости от надежности результата.
Более высокая статистическая значимость
соответствует более низкому уровню
доверия к найденной в выборке средней
величине. Именно уровень значимости
представляет собой вероятность ошибки,
связанной с распространением наблюдаемого
результата на всю генеральную совокупность.
Выбор
порога уровня значимости, выше которого
результаты отвергаются как статистически
не подтвержденные, во многом произвольный.
Как правило, окончательное решение
обычно зависит от традиций и накопленного
практического опыта в данной области
исследований. Верхняя граница p<0,05
статистической значимости содержит
довольно большую вероятность ошибки
(5%). Поэтому в тех случаях, когда требуется
особая уверенность в достоверности
полученных результатов, принимается
значимость p<0,01
или даже p<0,001.
В
практике медико-биологических исследований
наиболее часто используются следующие
значения показателей значимости: 0,1;
0,05; 0,01; 0,001. Традиционная интерпретация
уровней значимости, принятая в этих
исследованиях, представлена в таблице
21.
Таблица
21
Интерпретация
уровня значимости (p).
|
Величина уровня значимости |
Интерпретация |
|
≥0,1 |
Данные |
|
≥0,05 |
Есть |
|
<0,05 |
Нулевая |
|
≤0,01 |
Нулевая |
|
≤0,001 |
Нулевая |
Приблизительно
о наличии достоверных различий между
средними величинами можно судить по их
доверительным границам. Если они имеют
пересечение верхней границы одного из
интервалов и нижней границы 2-го, можно
предположить, что полученная разница
средних является случайной и может не
повториться в следующих экспериментах
с вероятностью, которая использовалась
при вычислении этих границ (как правило,
95%).
Если
изучаемый признак подчиняется закону
нормального распределения Гауса, может
использоваться расчет критерия
достоверности Стьюдента (t)
(коэффициента достоверности). Величина
этого коэффициента определяется модулем
отношения разности сравниваемых средних
величин к ошибке их разности. Ошибка
разности равна корню квадратному из
суммы квадратов средних ошибок
сравниваемых величин:
.
Таким
образом, коэффициент достоверности (t)
определяется по формуле:
,
где: M1
– средняя арифметическая 1-го вариационного
ряда,
M2
–
средняя арифметическая 2-го вариационного
ряда,
m1
–
ошибка репрезентативности 1-го
вариационного ряда,
m2
–
ошибка репрезентативности 2-го
вариационного ряда.
Для сравнения
относительных величин (показателей)
применяется модифицированная формула:
где: P1
– относительная величина (показатель)
1-й группы;
P2
– относительная величина (показатель)
2-й группы;
m1
– ошибка репрезентативности 1-го
показателя;
m2
– ошибка репрезентативности 2-го
показателя.
При
этом ошибка репрезентативности
относительной величины может быть
вычислена по формуле:
,
где:
Р – величина
относительного показателя;
q
– величина, обратная Р
и вычисленная как (1-Р),
(100-Р),
(100-Р)
и т. д., в зависимости от основания, на
которое рассчитан показатель;
n – число
наблюдений.
В
медико-биологических исследованиях,
где число наблюдений больше 30, допускается
использовать сравнение вычисленного
значения t
с критическим значением 2. Если t-критерий
больше 2, тогда выявленные различия
считаются закономерными (не случайными,
достоверными), т.е. они статистически
подтверждены с вероятностью более 95%.
Если значение критерия меньше 2, то
разница не доказана и носит случайный
характер, статистически не подтверждается
(вероятность менее 95%). При меньшем числе
наблюдений значение критического уровня
для сравнения с расчетным значением
t-критерия
необходимо искать в книгах с таблицами
Стьюдента или вычислять в статистической
компьютерной программе.
Пример
определения достоверности различий
между средними величинами по критерию
Стьюдента.
Условие
задачи:
сравнение средней частоты сердечных
сокращений (ЧСС) детей 1-го года жизни в
отделениях №1, №2 (см. раздел III).
Задание:
а) приблизительно оценить достоверность
различий между средним пульсом пациентов
1-го и 2-го отделений с помощью доверительных
границ;
б)
вычислить критерий Стьюдента для
сравнения ЧСС детей в этих отделениях,
сделать вывод о достоверности различий
средних величин.
Решение:
Запустите программу Excel,
откройте требуемый файл в папке своей
учебной группы под именем «Статистика–Фамилии
студентов». Создайте
НОВЫЙ лист,
переименуйте его, обозначив названием
«Крит_Стьюдента». На
этом листе
введите данные и решение задачи, как
показано ниже, сохраните изменения и
покажите результат работы преподавателю.
а)
доверительные
границы колебаний средних в каждом
отделении при уровне значимости p<0,05,
т.е. с вероятностью прогноза более 95%,
составляет M±2m,
где M –
средняя арифметическая, m
– ошибка репрезентативности.
По
условию задачи в 1-м отделении M1=121,9,
m1=1,64.
Т.е. 121,9 ± 2*1,64
= 121,9
± 3,28 уд/мин. В ячейке таблицы Excel
вводятся формулы =121,9+3,28 и =121,9-3,28. Получаем
доверительные границы колебаний средней
частоты пульса в 1-м отделении от 118,62
до 125,18
уд/мин.
Аналогично
определяем доверительные границы
средней ЧСС во 2-м отделении. По условию
задачи M2=126,2,
m2=2,04.
Т.е. 126,29
± 2 * 2,04
=
126,2 ± 4,08
уд/мин. Формулы вычисления =126,29+4,08 и
=126,29-4,08. Получаем доверительные границы
колебаний средней частоты пульса в 2-м
отделении от 122,21
до 130,37
уд/мин.
Величина
доверительных границ частоты пульса в
2-х отделениях больницы позволяют
утверждать, что при повторных экспериментах
в 95% случаях будут получены средние
величины, укладывающиеся в пределах
вычисленных значений границ в 1-м
отделении от 118,62
до 125,18
уд/мин, во 2-ом — от 122,21
до 130,37
уд/мин. Поскольку доверительные границы
этих отделений имеют пересечение верхней
границы 1-го и нижней границы 2-го
отделений, можно предположить, что
полученная разница средних является
случайной и может не повториться в
следующих экспериментах.
б)
оценка достоверности различий средней
частоты пульса детей, поступающих в 1‑е
и 2-е отделение больницы по критерию
Стьюдента.
Ф
ормула
вычисления критерия Стьюдента: ,
где: M1
– средняя арифметическая 1-го вариационного
ряда — 121,8,
M2
– средняя арифметическая 2-го вариационного
ряда — 126,2,
m1
– ошибка репрезентативности 1-го
вариационного ряда — 1,64,
m2
– ошибка репрезентативности 2-го
вариационного ряда — 2,04.
В
программе Excel
эта формула принимает вид:
=(121,8
– 126,2)/КОРЕНЬ(1,64^2+2,04^2) = -1,64667.
Модуль
числа может быть получен с помощью
функции =ABS(Число) = ABS(-1,64667) = 1,64667. Округление
числа выполняется функцией =ОКРУГЛ(Число;
Разрядность) = ОКРУГЛ(1,64667;2) = 1,65)
Вычисленное
значение t-критерия
(-1,65) оценивается по
модулю
числа (1,65) в сравнении с критическим
значением, которое при числе наблюдений
n>30
составляет 2. При числе наблюдений n<30
критическое значение находят по таблицам
Стьюдента при степенях свободы df
= n1
+ n2
– 2 = 16 + 17 – 2 = 31.
В программе Excel
критическое значение критерия Стьюдента
вычисляется функцией = СТЬЮДРАСПОБР(Уровень
значимости p;
Степени свободы
df)
=
=
СТЬЮДРАСПОБР(0,05;(16+17-2)) = 2,04.
Если
t>2,04
– статистическая гипотеза о равенстве
средних с уровнем значимости p<0,05
опровергается, следовательно, истинной
будет являться гипотеза об их различии.
Если t<2,04
– гипотеза равенства средних
подтверждается.
В
нашем примере получаем: t
=
1,65 < 2,04.
Если
в сравниваемых вариационных рядах
равное число наблюдений (n1=n2),
программа Excel
позволяет выполнить вычисления при
помощи функции =ТТЕСТ(массив1;массив2;2;3),
где:
Массив1 —
первый вариационный ряд (множество
данных);
Массив2 —
второй вариационный ряд (множество
данных).
Функция
ТТЕСТ возвращает уровень значимости
основной гипотезы при сравнении 2-х
числовых массивов, вычисленный по
критерию Стьюдента. Он выражает
вероятность того, что две выборки взяты
из генеральных совокупностей, которые
имеют одно и то же среднее.
В
нашем случае можно выполнить вычисление
этой функцией на основе данных 16-и
человек в каждой группе. Получаем опытный
уровень значимости 0,12. Это означает,
что выдвинутая гипотеза о равенстве
средних в генеральной совокупности
подтверждается с вероятностью 12%.
Поскольку значение опытного уровня
значимости больше принятого критического
уровня (p=0,05
или 5%), то альтернативная гипотеза о
различии средних величин не может быть
принята, и значит, различия не подтверждены.
В такой ситуации можно провести
дополнительное исследование с теми же
условиями опыта, но с увеличенным числом
единиц наблюдения, что на более
качественном уровне подтвердит или
опровергнет рабочую гипотезу.
Вывод:
Различия средней частоты пульса пациентов
1-го и 2-го отделений НЕдостоверны. Значит,
более высокая средняя частота пульса
во 2-м отделении больницы (126,2 уд/мин) по
сравнению с ЧСС в 1-м отделении (121,9
уд/мин) не подтверждается при уровне
значимости p=0,05.
Пример
сравнения относительных
величин
и определения достоверности различий
между ними по критерию Стьюдента.
Условие
задачи:
группа животных в количестве 120 особей
получала препарат А. Из них у 98 животных
произошло восстановление функций
организма. Контрольная группа животных
в составе 50 особей содержалась в
аналогичных условиях без применения
этого препарата, из них восстановление
наблюдалось у 15 особей.
Задание:
а) вычислить показатели частоты
восстановления функций организма
животных (интенсивные относительные
величины) в 1-ой и 2-ой группах животных;
б)
вычислить ошибки репрезентативности
относительных величин;
в)
определить доверительные границы
колебаний относительной величины в
каждой группе;
г) вычислить
критерий Стьюдента для оценки достоверности
различий относительных величин в
изучаемых группах;
д)
сделать вывод о проявления эффекта
препарата в генеральной совокупности
с вероятностью более 95%.
Решение:
запустите программу Excel,
откройте файл в папке своей учебной
группы под именем «Статистика–Фамилии
студентов», на листе «Крит_Стьюдента»
этого файла выполните вычисления, как
показано ниже, сохраните изменения и
покажите результат работы преподавателю.
а
)
расчет относительных величин частоты
восстановления функций организма
животных в 2-х группах: ,
P1=
98/120*100 = 81,67% ;
P2=
15/98*100 = 15,31% .
б)
вычисление ошибок репрезентативности
относительных величин:
,
m1=
3,53%;
m2=
3,64%.
в)
определение доверительных границ
относительных величин в каждой группе:
при
уровне значимости p<0,05,
т.е. с вероятностью прогноза более 95%,
границы вычисляют по формуле P±2m,
где P –
относительная величина, m
– ошибка репрезентативности.
По
условию задачи в 1-й группе животных
P1=81,67,
m1=15,31.
Следовательно, 81,67 ± 2*3,53
= 81,67
± 7,06%. Получаем доверительные границы
колебаний относительных величин в 1-й
группе от 74,61%
до 88,73%,
во 2-й группе — от 8,03%
до 22,59%.
Поскольку доверительные границы не
пересекаются, можно предположить, что
полученная разница относительных
величин не случайна и будет обнаруживаться
в следующих экспериментах.
г)
вычисление критерия Стьюдента для
относительных величин:
t
= ABS((81,67
— 15,31) / КОРЕНЬ(3,53^2 + 3,64^2)) = 13,088901 > 2
Вывод:
восстановление функций организма
животных на фоне действия препарата А
проявляется в 81%. Этот показатель
достоверно выше, чем в контрольной
группе животных, не получавших препарат,
при уровне значимости p<0,05.
Т-критерий Стьюдента (t-тест) простым языком
Сегодня мы говорим о t-критерии. Т-критерий наиболее популярный статистический тест в биомедицинских исследованиях. Также его называют парный Т-критерий Стьюдента, t-test, two-sample unpaired t-test. Однако, при использовании этого статистического инструмента допускается достаточно много ошибок. Сегодня в этой статье мы постараемся разобраться, как избежать ошибок применения t-критерия Стьюдента, как интерпретировать его результаты и как рассчитывать t-критерий самостоятельно. Об этом обо всем читайте далее.
При описании любого статистического критерия, будь то t-критерий Стьюдента, либо какой-либо еще, нужно вспомнить о том, как же вообще используются статистические критерии. Для того, чтобы понять, как используется любой критерий, нужно перейти к нескольким достаточно логичным для понимания этапам:
Этапы статистического вывода (statistic inference)
- Первый из них – это вопрос, который мы хотим изучить с помощью статистических методов. То есть первый этап: что изучаем? И какие у нас есть предположения относительно результата? Этот этап называется этап статистических гипотез.
- Второй этап – нужно определиться с тем, какие у нас есть в реальности данные для того, чтобы ответить на первый вопрос. Этот этап – тип данных.
- Третий этап состоит в том, чтобы выбрать корректный для применения в данной ситуации статистический критерий.
- Четвертый этап это логичный этап применения интерпретации любой формулы, какие результаты мы получили.
- Пятый этап это создание, синтез выводов относительно первого, второго, третьего, четвертого, пятого этапа, то есть что же получили и что же это в реальности значит.
Предлагаю долго не ходить вокруг да около и посмотреть применение t-критерия Стьюдента на реальном примере.
Видео-версия статьи
Пример использования т-критерия Стьюдента
А пример будет достаточно простой: мне интересно, стали ли люди выше за последние 100 лет. Для этого нужно подобрать некоторые данные. Я обнаружил интересную информацию в достаточно известной статье The Guardian (Tall story’s men and women have grown taller over last century, Study Shows (The Guardian, July 2016), которая сравнивает средний возраст человека в разных странах в 1914 году и в аналогичных странах в 2014 году.
Там приведены данные практически по всем государствам. Однако, я взял лишь 5 стран для простоты вычислений: это Россия, Германия, Китай, США и ЮАР, соответственно 1914 год и 2014 год.
Общее количество наблюдений – 5 в 1914 году в группе 1914 года и общее значение также 5 в 2014 году. Будем думать опять же для простоты, что эти данные сопоставимы, и с ними можно работать.
Дальше нужно выбрать критерии – критерии, по которым мы будем давать ответ. Равны ли средние по росту в 1914 году x̅1914 и в 2014 году x̅2014. Я считаю, что нет. Поэтому моя гипотеза это то, что они не равны (x̅1914≠x̅2014). Соответственно альтернативная гипотеза моему предположению, так называемая нулевая гипотеза (нулевая гипотеза консервативна, обратная вашей, часто говорит об отсутствии статистически значимых связей/зависимостей) будет говорить о том, что они между собой на самом деле равны (x̅1914=x̅2014), то есть о том, что все эти находки случайны, и я, по сути, не прав.
Теперь нужно дать какой-то аргументированный ответ. Даем его с помощью статистического критерия. Соответственно теперь наступает самое важное: как выбрать статистический критерий? Я думаю, это будет темой отдельной статьи. Для корректности использования t-критерия Стьюдента лишь скажу, что нужно, чтобы:
Условия применения статистического критерия т-теста (критерия Стьюдента)
— данные распределялись по закону нормального распределения;
— данные были количественными;
— и это две независимые между собой выборки (независимые это значит, что в этих группах разные люди, а никак, например, до и после применения препарата у одной группы, люди должны быть разными, тогда группы являются несвязанными, либо независимыми), этот аспект стоит учитывать для выбора вида т-критерия Стьюдента, так как для парных выборок существует свой парный т-критерий (paired t-test).
В итоге Мы определились с тем, что это будет t-критерий Стьюдента.
Формула t-критерия Стьюдента достаточно простая. Она гласит о том, что в числителе у нас разница средних, в знаменателе у нас корень квадратный суммы ошибок репрезентативности по этим группам:
Ошибки репрезентативности были подробно объяснены мною в статье по доверительным интервалам. Поэтому я рекомендую вам ознакомиться с ней, чтобы лучше разобраться, что такое ошибки репрезентативности, что такое выборка, как она соотносится с генеральной совокупностью.
Для того, чтобы не тратить время, я в принципе все уже рассчитал по каждой из групп: средняя (x̅) ,стандартное отклонение (SD) и ошибка репрезентативности (mr).
Давайте остановимся на том, что же значат эти значения:
— средняя (x̅) это среднеарифметическое по 5 наблюдениям в каждой группе;
— если совсем упрощать значение стандартного отклонения (SD), то можно сказать, что оно представляет собой обобщенную среднюю отклонения каждого значения от среднего (стандартное отклонение показывает, насколько широко значения рассеяны (разбросаны) относительно средней). И дальше мы находим нечто среднее отклонений каждого варианта в группе от среднего;
— и ошибка репрезентативности она тоже находится достаточно просто: это как раз наше отклонение от средней некоторое стандартизованное, поэтому стандартное отклонение на размер выборки (mr=).
Итак, продолжаем. В ходе подстановки каждого значения в нашу формулу, мы находим, что t-критерий Стьюдента равен 3,78. Однако, я думаю, пока тем, кто не знаком со статистическими критериями, это мало о чем говорит.
Итак, теперь настает четвертый этап вопрос интерпретации. Ранее мы получили значение t-критерия в 3,78. Однако, что же это значит? Стоит отметить, что результаты статистических критериев и вообще их интерпретация не говорит о точном «да», либо «нет» в выводе, то есть рост отличается, либо рост не отличается. Всегда это вопрос определенной доли вероятности – доли вероятности ошибиться при констатации положительного результата (речь об ошибке первого рода (I type error, Alpha)). То есть, например, если мы скажем, что средний рост в начале ХХ и в начале XXI века отличаются с долей ошибкой меньше 5 %. Как раз эта величина в 5 % и фиксируется как достаточная для большинства биомедицинских исследований, помните, р больше, либо меньше 0,05.
Итак, как нам перейти от нашей t к р вероятности? Это сделать достаточно просто, стоит лишь воспользоваться табличными значениями t для определенных степеней свободы. Теперь вопрос: как найти эти степени свободы? Но это сделать достаточно просто. Для того, чтобы обнаружить степени свободы для наших групп, нужно лишь сложить количество наблюдений 5 и 5 в нашем случае и вычесть 2. В нашем случае степень свободы равна 8.
Итак, t=3,78, степень свободы равна 8. Переходим в табличное значение и получаем р вероятность – вероятность равна 0,005. То есть вероятность того, что мы ошибаемся при констатации факта различия роста ранее и сейчас, крайне мала – это 0,005 %, не 5 %, а 0,005 %. То есть мы можем говорить с высокой долей достоверности того, что наш рост сейчас в XXI веке и 100 лет назад отличаются.
Вот то, что касается расчета t-критерия Стьюдента и его интерпретации.
На этом наш разговор о t-критерии Стьюдента закончен. Спасибо, что ознакомились с этой статьей. Я очень надеюсь на вашу обратную связь. Пожалуйста, подписывайтесь на наш сайте, ставьте лайки, предлагайте свои темы для следующих выпусков. Спасибо большое за поддержку. С вами был Кирилл Мильчаков. Пока, до новых встреч!
Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях:
Предположим, что надо сравнить между собой результаты выполнения тестов на внимание в двух группах. Чтобы узнать различаются ли группы между собой необходимо вычислить t-критерий Стьюдента для независимых выборок.
1. Внесем данные по группам в таблицу:
| № | Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
| 1 | 30 | 46 |
| 2 | 45 | 49 |
| 3 | 41 | 52 |
| 4 | 38 | 55 |
| 5 | 34 | 56 |
| 6 | 36 | 40 |
| 7 | 31 | 47 |
| 8 | 30 | 51 |
| 9 | 49 | 58 |
| 10 | 50 | 46 |
| 11 | 51 | 46 |
| 12 | 46 | 56 |
| 13 | 41 | 53 |
| 14 | 37 | 57 |
| 15 | 36 | 44 |
| 16 | 34 | 42 |
| 17 | 33 | 40 |
| 18 | 49 | 58 |
| 19 | 32 | 54 |
| 20 | 46 | 53 |
| 21 | 41 | 51 |
| 22 | 44 | 57 |
| 23 | 38 | 56 |
| 24 | 50 | 44 |
| 25 | 37 | 42 |
| 26 | 39 | 49 |
| 27 | 40 | 50 |
| 28 | 46 | 55 |
| 29 | 42 | 43 |
Шаг 2. Проверить распределения на нормальность.
Шаг 3. Рассчитать среднее арифметическое, стандартное отклонение и количество человек в каждой группе.
Шаг 4. Вычисляем эмпирическое значения по формуле t-критерия Стьюдента для независимых выборок
Шаг 5. Вычисляем степени свободы.
Шаг 6. Определяем по таблице критических значений t-Стьюдента уровень значимости.
Значение 6,09 больше чем значение 3,473 следовательно уровень значимости меньше 0,001
Шаг 7. Если уровень значимости меньше 0,05 делается вывод о наличи различий между группами. Таким образом между двумя группами есть различия в скорости выполнения тестов на внимание.