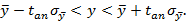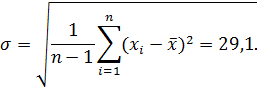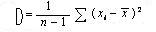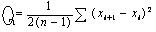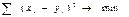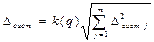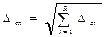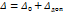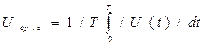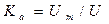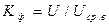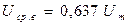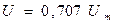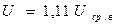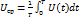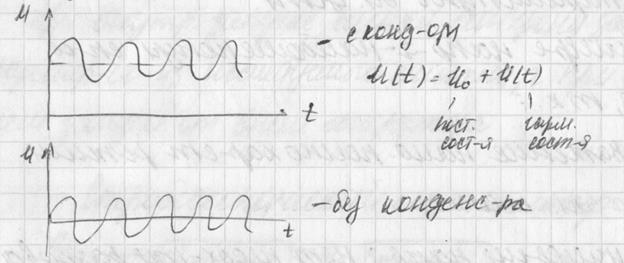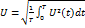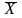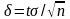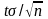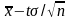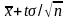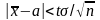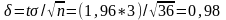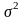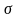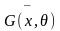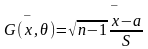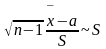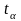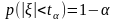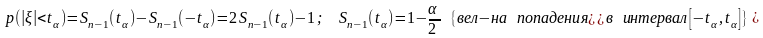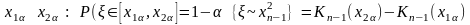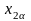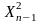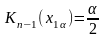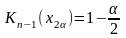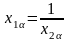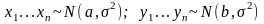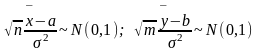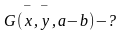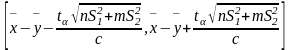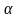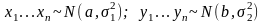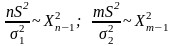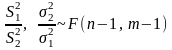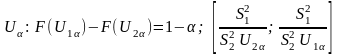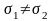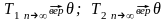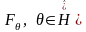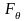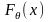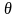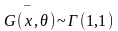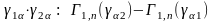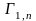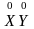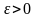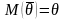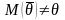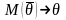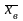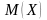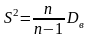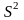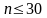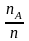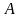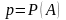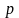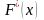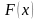Как найти доверительная вероятность попадания

Доверительная вероятность и доверительный интервал.

Вероятность того, что истинное значение измеряемой величины лежит внутри некоторого интервала, называется доверительной вероятностью, или коэффициентом надежности,а сам интервал — доверительным интервалом.

.

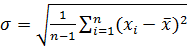
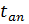
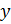
на так называемый коэффициент Стьюдента. Коэффициенты Стьюдента для ряда значений и n приведены в таблице.

Число измерений n	Доверительная вероятность y
0,67	0,90	0,95	0,99
2,0	6,3	12,7	63,7
1,3	2,4	3,2	5,8
1,2	2,1	2,8	4,6
1,2	2,0	2,6	4,0
1,1	1,8	2,3	3,3
1,0	1,7	2,0	2,6

Окончательно, для измеряемой величины y при заданной доверительной вероятности y и числе измерений n получается условие

Величину 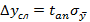мы будем называть случайной погрешностьювеличины y.

Пример: см. лекцию №5 – ряд чисел.

При числе измерений – 45 и доверительной вероятности – 0,95 получим, что коэффициент Стьюдента приблизительно равен 2,15. Тогда доверительный интервал для данного ряда измерений равен 62,6.

Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором:

— неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;

— неправильная запись результата наблюдений, значений отдельных мер использованного набора, например, гирь;

— хаотические изменения параметров напряжения, питающего средства измерения, например, его амплитуды или частоты.

Источник

Доверительный интервал — формула и примеры определения вероятности

В математической статистике при анализе и систематизации различных данных для подведения практических выводов часто используют метод доверительных интервалов. С его помощью выполняют определённую выборку среднего или доли с учётом стандартной ошибки. Благодаря этому достоверность вероятности увеличивается, так как оценка расширяется в обе стороны от исследуемой величины.

Общая схема построения

По сути, метод основан на модели классической математической статистики, подразумевающей бесконечно возможные выборки в генеральной совокупности. Пусть имеется главная выборка эпсилон с функцией распределения известной до некого параметра тау (Fe (x, τ)). Из этой генеральной совокупности получена выборка объёмом эн, включающая диапазон от x1 до xn. Этот параметр можно считать одномерным и принадлежащим диапазону от τ до R. Математически такое положение описывают как τ є T c R.

Если предположить, что для некоторого интервала йод, лежащего от нуля до единицы, существуют статистики S-(X|n|, J) и S+(X|n|, J), при этом им соответствует неравенство P< S-(X|n|, J) Свойство статистики и распределения

Таким образом, определить доверительную вероятность попадания тэта в интервал от S- до S+ можно от значения обратной функции в точках, равняющихся квантили статистики игрек порядка j/2 и 1 — j/2. При этом когда рассматриваемая функция монотонно убывает, знаки в неравенстве меняются на противоположные.

Пользуясь общим подходом расчёта доверительных интервалов, можно посчитать вероятность для нормальной генеральной совокупности, опираясь на ряд утверждений. Пусть известна выборка X|n,| взятая из совокупности E

N (j, ς 2 ), то есть имеющей нормальный закон распределения с математическим ожиданием j и дисперсией сигма в квадрате. Для такого состояния справедливо следующее:

Точный интервал

Существует ряд правил, позволяющих построить точные интервалы для математического ожидания и дисперсии нормально распределённой случайной величины. Есть два случая — при одном дисперсия может быть известной, а при другом нет. Следует обратить внимание, что точная доверительная вероятность строится с помощью общей схемы. Используют следующие правила для предоставления точных прогнозов:

Асимптотическое приближение

Однако не всегда можно рассчитать точный доверительный интервал. В этом случае строится приближённая вероятность — асимптотическая. Пусть для некоторого j Є (0,1) существует набор статистик S-(X|n|, j) и S-(X|n|, j), причём такие, что lim P< S-(X|n|, j) Примеры решения задач

Отсюда получают оценку: p = m / n. Теперь нужно убедиться, что p максимизирует функцию правдоподобия. То есть d2LnL / dp2 = — m / p2 — (n — m) / (1 — p)2 Использование онлайн-калькулятора

На практике довольно часто вычислить доверительную область не так уж и просто. Всё дело в том, что высокая вероятность часто находится в выборке большого объёма, поэтому приходится выполнять громоздкие вычисления. Учитывая, что доверительная вероятность определяет точность полученных результатов, другими словами, показывает, с какой вероятностью неправильное решение попадает в найденный интервал, обычно используют процент выборки от 95 до 99,9%.

Для высокой точности получения диапазона как раз и используют сервисы, которые в последнее время начали называться онлайн-калькуляторами. Это специализированные сайты, умеющие в автоматическом режиме решать различные математические задания. Особенность этих сайтов в том, что они предоставляют услуги бесплатно, при этом от их пользователей не требуется никаких знаний.

Всё что им нужно — это ввести в пролагаемую форму данные и нажать кнопку «Рассчитать». Система автоматически вычислит ответ и выведет его на экран. Из наиболее популярных можно отметить следующие сервисы:

Они доступны на русском языке, их интерфейс интуитивно понятен, поэтому воспользоваться их услугами сможет любой заинтересованный, имеющий доступ к интернету. Автоматический расчёт занимает буквально секунды, что составляет существенную разность по сравнению с затратой времени при самостоятельном вычислении.

Источник

Доверительная вероятность. Доверительный интервал.

Δr – доверительный интервал

Интервал значений случайной величины внутри которого с заданной вероятностью находится истинное значение измеряемой величины, называется доверительны интервалом, а соответствующая ей вероятность – доверительной вероятностью (Pд)

В соответствии со стандартом, принимают 4 градации доверительной вероятности

Рд	0.9	0.95	0.975	0.99
q	0.1	0.05	0.025	0.01

q – уровень значимости результата.

0,9;0,1 – для оценочных расчетов

0,95;0,05 – для технически расчетов

0,975 – для точных технических расчетов

0,99 – для особо ответственных расчетов

19. Статистические методы исключения грубых промахов.

Методика применяется к многократным измерениям

Оценка грубых промахов реш. методом мат. статистики.

Суть метода: выдвигается нулевая гипотеза, что сомнительных результат принадлежит к совокупности измерений, а затем пользуясь статистическими критериями опровергают данную гипотезу, и результат отбрасывается.

Методы подбора критериев:

1) Критерий позволяет отбросить результат резко отличающийся от среднего арифметического

— Критерий Гребса

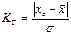
Z_Г(n,q) = f(q,n)– теор. знач. критер. Греббса

q – уровень значимости

К_Г>Z_Г – результат отбрасывается

Формулу f(q,n) придумал Гребс для больших n, Шарле и Шавене для малых

2) Критерий позволяет отбросить результат резко отличающийся от соседних результатов

— для n-ой точки

— для 1-ой точки

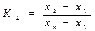
Если К_Δ>Z_Δ, то результат отбрасывается

20. Статистические методы исключения систематических погрешностей.

Есть случайные и систематические составляющие. Сначала надо определить есть ли систематическая составляющая

Критерий для оценки наличия систематической прогрессирующей погрешности (критерий Аббе)

Но это всё определяется не точно на 100%, а с некоторой доверительной вероятностью

Метод наименьших квадратов (исключение систематической составляющей)

Нужно, чтобы сумма квадратов разности была минимальной

21. Методика оценки погрешности при прямых измерениях с однократным наблюдением.

Для оценки точности при однократных измерениях надо иметь информацию об измерительном средстве, о методе измерения, об условиях измерения и об опыте оператора.

Расчёт погрешности на основе допустимых предельных погрешностей, без учёта разбиения погрешности на случайную и систематическую составляющие.

В основе методики – принцип наихудшего случая, т.е. что погрешность носит систематический характер и имеет один знак.

Методика даёт завышенный, но надёжный результат с вероятностью ≈ 1

Расчёт погрешности с учётом систематической и случайной составляющей

K – коэффициент, зависящий от уровня значимости результата и числа n.

n – число измерений

r – число интервалов

23. Правила округлений результатов измерений.

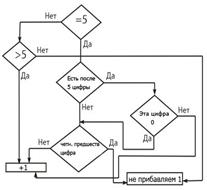
1) Погрешность результатов измерений указывается 2-мя значащими цифрами, если первая из них 1 или 2 и одной цифрой в остальных случаях.

2) Результат измерения округляют до того же десятичного знака, кот. оканчивается округленное значение абс. погрешности.

24. Средства измерений. Их классификация.

Средства измерений – техническое устройство предназначенное для измерений, имеющее нормированные метрологические характеристики воспроизвод. и хранящее ед. физ. вел, размер кот. принимается неизменным в теч. известного интервала времени.

1.по метролог. назначению

-метролог.(для работы метролог. служб)

2.по конструктивному исполнению

Мера – средство измерения, предназначенное для хранения и воспроизведения размера физ. вел.

Измерительный преобразователь – средство измерения, предназначенное для получения значения измеряемой величины в сигнал, удобный для передачи, хранения, обработки.

Он может быть отдельным прибором, тогда это датчик, но чаще он встроен в измерительный прибор

Измерительный прибор – средство измерения, предназначенное для измерения в заданном диапазоне, имеющее нормированные метролог. характеристики.

Измерительные системы – совокупность средств измерений и вычислительных средств, объединённых в единую систему.

3.по уровню автоматизации

ГОСТ дел. все приборы на 20 групп

М – измерит. мощности

У – измерит. усилители

Ц – комбинированные приборы

25. Основные метрологические характеристики электро-радиоизмерительных приборов.

Метрологическая хар-ка – это свойство средства измерения, влияющая на погрешность измерения.

1)Погрешность измеряемого средства

2)Диапазон показаний и измерений

Диапазон измерений – часть диапазона показаний, где обеспечивается нормированная точность.

3)Предел измерений – наим. и наиб. значение диапазона измерений

4)Градуированная характеристика – зависимость измерения показаний от измеряемой величины.

5)Чувствительность измерит. прибора- отношение измеренного сигнала на выходе к вызывающему его входному сигналу.

6)Разрешающая способность – min изменение входного сигнала, кот. различимо по показанию прибора

7)Быстродействие – число измерений в ед. времени

8)Внутреннее сопротивление (для приборов подключённых последовательно)

9)Входное сопротивление прибора (для приборов подключённых ||)

Может быть активным и реактивным

10)Вариация показаний – разница, показаний при плавном подходе к измеряемой точке при изменении измеряемой вел (Гистерезис). Характерно для динамических измерений

11)Мощность потребляемая от измерительной цепи

Она должна стремиться к 0.

26. Нормирование инструментальной погрешности

Нормировать можно в формах:

Основная и дополнительная погрешности нормируются отдельно

Типовые метрологические характеристики:

Обычно нормирование производится первой партии выпускаемых приборов (испытание на точность)

Измерение производятся в нормальных условиях

Измерения повторить для точек диапазона и некоторых точек в диапазоне.

Дополнительная погрешность измеряется так же, как и основная, но измеряются условия измерения (по каждому параметру измеряется отдельно)

27. Классы точности средств измерений.

Класс точности прибора- это основная метрологическая характеристика.

Класс точности количественно выражается в форме предела допустимой абс., относит. или приведенной погрешности.

Для радиоизмерит. приборов класс точности выражается пределом относит. или приведенной погрешности. Формулу для расчета погрешности приводят в паспорте на прибор. Используются одночленные формулы (погрешность имеет аддитивную составляющую) и двучленные (аддитивная составл. + мультипликативная)

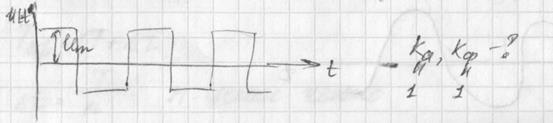
28. Измерение напряжения и других параметров электрической цепи. Измеряемые значения переменного напряжения.

Напряжения и токи могут быть постоянными и переменными. При измерении постоянного напряжения прибор будет указывать на его действительное значение. При измерении переменного напряжения в зависимости от применяемого прибора для измерений может быть получена одна из следующих величин:

-амплитудное значение переменного напряжения,

-среднеквадратичное значение (действительное значение).

Мгновенное значение напряжения переменного тока является функцией времени и определяется следующей формулой:

Где:

ω- круговая частота,

Среднее значение напряжения определяется по формуле:

Для симметричного синусоидального переменного (гармонического) напряжения это значение будет равно нулю. Поэтому для оценки гармонического переменного напряжения эта характеристика не применяется. Она может быть применена для выделения постоянной составляющей негармонического переменного напряжения.

Средневыпрямленное значение напряжения определяется по формуле:

Выпрямление может быть однополупериодное и двухполупериодное. При однополупериодном выпрямлении в формулу ( 3 ) надо добавить коэффициент 0,5.

Среднеквадратичное значение напряжения определяется по формуле:

ния называют также действующим значением переменного напряжения или тока.

Амплитудное, средневыпрямленное и среднеквадратичное значения напряжения связаны между собой коэффициентами амплитуды и формы.

Для гармонического напряжения Ка = 1,41, а Кф =1,11. То есть различные значения напряжения для гармонического сигнала связаны соотношениями:

29. Приборы для измерения напряжения и других параметров электрической цепи.

Измерение напряжения – наиболее популярный способ измерения так как :

1) Напряжение наиболее полно характеризует режим работы электрической схемы

2) При измерении напряжения не необходимости разрыва электрической цепи

3) Измеряя напряжение, косвенным методом можно измерить другие параметры (I,R)

Токи и напряжение могут быть постоянными и переменными. Когда напряжение постоянное, то прибор показывает его действующее значение, когда переменное – прибор может измерять разные значения. В этом случае надо знать какой прибор как работает

— мгновенное значение напряжения

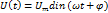
Характеристики переменного напряжения :

1) Амплитудное значение

2) Среднее значение

4) Действующее значение среднеквадратичное

Для гармонического сигнала Uср в = 0,637 Um

Для оценки формы сигнала:

Коэффициент амплитуды : Ка = Um / U =1,41

Коэффициент формы : Кф = U/ Uср в = 1,11

Классификация приборов для измерения напряжения

По виду измеряемого параметра приборы могут быть:

-измерители ёмкости, индуктивности

Если прибор измеряет несколько параметров он называется мультиметром

Все измеряющие приборы

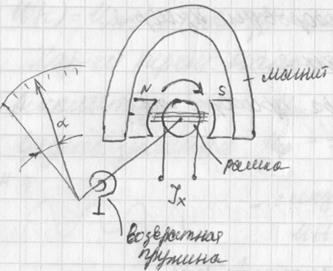
Электромагнитные приборы относятся к приборам непосредственной оценки. Обычно в таких приборах электрическая энергия преобразуется в механическую энергии. (?в част.? Во вращательное движение стрелочного механизма)

Они строятся по следующим измерительным схемам: машинно-электрическая, электромагнитная, электростатичесая, электродинамическая, магнитноэлектрическая

Высокая точность, высокая чувствительность (класс 0,1; 0,5)

Все остальные измеряемые системы более грубые

Используется для точных механических приборов

Недостатки: Большое потребление энергии от источника

Электростатические системы используются для высокочастотных измерений (используется конденсатор)

Электродинамические системы потребляют много энергии, для измерителей мощности, счётчиков электрической энергии

Электронноаналоговые приборы – используются те же принципы как и в электромеханических

Основной недостаток электрических систем – большое ….

Потребление мощности от измеряемой цепи, что ведет к методической погрешности

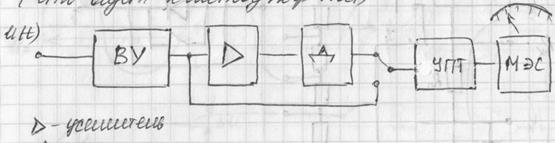
Треугольник-усилитель переменного напряжения

УПТ-усилитель постоянного тока

Достоинство: за счет усилителей данный прибор не отнимает энергию от измеряемой цепи. Имеет высокую чувствительность и точность. В основном используется для измерения малых величин.

Цифровые приборы:

ЦОУ-цифровое отсчетное устройство

30. Осциллографы. Назначение и классификация осциллографов.

Для измерения параметров динамических сигналов используют специальные приборы. Для детерминированных сигналов используют осциллографы, для случайных сигналов –измерители параметров случайных сигналов. (Измерение математического ожидания, дисперсии, среднего квадратичного отклонения, корреляционных характеристик и др.).

Электронный осциллограф предназначен для визуального отображения формы и приближенного измерения параметров периодических сигналов сложной формы.

Наряду с тестерами, цифровыми вольтметрами и импульсными генераторами осциллографы являются наиболее распространенными измерительными приборами и очень широко применяются на всех стадиях проектирования, производства и обслуживания ЭВМ.

Осциллограф позволяет получить на экране электронно-лучевой трубки график одного или нескольких периодов входного сигнала в координатах «время – напряжение», т.е. график функции y=f(t). Пример такого графика показан на рис.

1. Универсальные О. 100МГц

2. Стробоскопические О. – Они используются для измерения высокочастотных сигналов, либо кратковременных повторений сигналов до 10МГц работ.

3. Запоминающие О. для исследования однократных, редко повторяющихся процессов.

4. Специальные О. – О. Целевого назначения, снятие видеосигнала; для переходных процессов.

2) многоканальные (2,4…)

Осциллографы делятся по исполнению:

1) аналоговые на ЭЛТ

2) цифровые с использованием матричных экранов

3) виртуальные приборы

31. Назначение и классификация измерительных генераторов.

Измерительные генераторы подразделяются на несколько групп (см. рис. 2.1).

Наиболее распространенными являются генераторы звуковой частоты ГЗ, высокой частоты Г4, прямоугольных импульсов Г5, качающейся частоты Г2.

Источник сигналов разнообразных форм и частот, предназначенные для регулирования, настройки и измерений в электронных схемах.

Они должны обладать:

1) возможностью регулировки выходных параметров

2) высокую стабильность

3) стандартные средства связи с др. измерительными устройствами

В зависимости от формы сигнала, генераторы делятся:

— генератор сигналов произвольной формы

— генератор случайных сигналов

— генератор стандартной частоты

По принципу пострения:

Практические рекомендации по работе с измерительными генераторами сводятся к следующему:

а) перед подключением генератора к нагрузке следует убедиться, что её сопротивление не меньше, чем минимально-допустимое по «Техническое описанию»,

б) соединять выход генератора с нагрузкой следует только входящими в комплект коаксиальными радиочастотными кабелями,

в) генераторы импульсов обеспечивают гарантированную по «Техническому описанию» форму только при работе на согласованную нагрузку.

г) прежде чем устанавливать длительность импульса и его задержку, необходимо приближенно вычислить длительность периода».

32. Измерение частоты и интервалов времени.

Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычис­лить, когда этот.

Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем.

ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.

ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Источник

1. Доверительный интервал и доверитель­ная вероятность (надежность). Построение доверительного интервала для математического ожидания случайной величины, распределенной по нормальному закону.

§14. Точность оценки, доверительная вероятность (надежность). Доверительный интервал

Точечной
называют
оценку, которая определяется одним
числом. Все оценки, рассмотренные выше,-
точечные. При выборке малого объема
точечная оценка может значительно
отличаться от оцениваемого параметра,
т. е. приводить к грубым ошибкам. По этой
причине при небольшом объеме выборки
следует пользоваться интервальными
оценками.

Интервальной
называют
оценку, которая определяется двумя
числами — концами интервала. Интервальные
оценки позволяют установить точность
и надежность оценок (смысл этих понятий
выясняется ниже).

Пусть
найденная по данным выборки статистическая
характеристика Θ* служит оценкой
неизвестного параметра Θ. Будем считать
Θ постоянным числом (Θ может быть и
случайной величиной). Ясно, что Θ* тем
точнее определяет параметр Θ, чем меньше
абсолютная величина разности |Θ — Θ*|.
Другими словами, если δ>0
и |Θ — Θ*|<δ,
то чем меньше δ,
тем оценка точнее. Таким образом,
положительное число δ
характеризует точность
оценки.

Однако
статистические методы не позволяют
категорически утверждать, что оценка
Θ * удовлетворяет неравенству |Θ — Θ*|<δ;
можно лишь говорить о вероятности γ, с
которой это неравенство осуществляется.

Надежностью
(доверительной
вероятностью)
оценки
Θ по Θ* называют вероятность
γ,
с
которой осуществляется неравенство |Θ
— Θ*|<δ.
Обычно надежность оценки задается
наперед, причем в качестве γ берут число,
близкое к единице. Наиболее часто задают
надежность, равную 0,95; 0,99 и 0,999.

Пусть
вероятность того, что |Θ — Θ*|<δ,
равна γ:

Р[|Θ
— Θ*|<δ]=
γ.

Заменив
неравенство |Θ — Θ*|<δ
равносильным ему двойным неравенством
-δ
<Θ
— Θ*< δ,
или Θ*-
δ <Θ<
Θ* + δ,
имеем

Р[Θ*
— δ
<Θ< Θ* + δ]
= γ.

Это
соотношение следует понимать так:
вероятность того, что интервал(Θ*-δ,
Θ*+δ)
заключает в себе (покрывает) неизвестный
параметр Θ, равна γ.

Доверительным
называют
интервал (Θ*-δ,
Θ*+δ),
который покрывает неизвестный параметр
с заданной надежностью γ.

Замечание.
Интервал (Θ*-δ,
Θ*+δ)
имеет случайные концы (их называют
доверительными границами). Действительно,
в разных выборках получаются различные
значения Θ*. Следовательно, от выборки
к выборке будут изменяться и концы
доверительного интервала, т. е.
доверительные границы сами являются
случайными величинами — функциями от
х₁,
x₂,
…, х_n.

Так
как случайной величиной является не
оцениваемый параметр Θ, а доверительный
интервал, то более правильно говорить
не о вероятности попадания Θ в доверительный
интервал, а о вероятности того, что
доверительный интервал покроет Θ.

Метод
доверительных интервалов разработал
американский статистик Ю. Нейман, исходя
из идей английского статистика Р. Фишера.

§ 15. Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ

Пусть
количественный признак X
генеральной
совокупности распределен нормально,
причем среднее квадратическое отклонение
σ
этого распределения известно. Требуется
оценить неизвестное математическое
ожидание а
по выборочной средней

.
Поставим
своей задачей найти доверительные
интервалы, покрывающие параметр а
с
надежностью
γ.

Будем
рассматривать выборочную среднюю

как
случайную величину

(

изменяется от выборки к выборке) и
выборочные значения признака х₁,
x₂,
…,х_n
— как одинаково распределенные независимые
случайные величины Х₁,
Х₂,
…,Х_n
(эти
числа также изменяются от выборки к
выборке). Другими словами, математическое
ожидание каждой из этих величин равно
а
и
среднее квадратическое отклонение — σ.

Примем
без доказательства, что если случайная
величина X
распределена
нормально, то выборочная средняя

,
найденная
по независимым наблюдениям, также
распределена нормально. Параметры
распределения

таковы
(см. гл. VIII,
§ 9):

M(
)=a,


.

Потребуем,
чтобы выполнялось соотношение

Р(|Х
— а| <
δ)
= γ,

где γ
—
заданная надежность.

Пользуясь
формулой (см. гл. XII,
§ 6)

Р(|Х-а|
<
δ)
= 2Ф(δ/σ),

заменив
X
на

и
σ
на

,
получим

Р(|Х-а|)
<δ)
= 2Ф(δ
)
= 2Ф
(t),

где t
=
δ
.

Найдя
из последнего равенства

, можем написать

Р
(|
—а
|
<

)
= 2Ф(t).

Приняв
во внимание, что вероятность P
задана и равна γ,
окончательно
имеем (чтобы получить рабочую формулу,
выборочную среднюю вновь обозначим
через

)

Смысл
полученного соотношения таков: с
надежностью γ можно утверждать, что
доверительный интервал (
,

) покрывает неизвестный параметр а;
точность оценки

.

Итак,
поставленная выше задача полностью
решена. Укажем еще, что число
t
определяется из равенства 2Ф(t)
=
γ. или Ф(t)=
γ /2;
по таблице функции Лапласа (см. приложение
2) находят аргумент
t,
которому
соответствует значение функции Лапласа,
равное γ
/2.

Замечание
1.
Оценку


называют
классической. Из формулы

,
определяющей
точность классической оценки, можно
сделать следующие выводы:

1) при
возрастании объема выборки п
число
δ
убывает
и, следовательно, точность оценки
увеличивается;

2)
увеличение надежности оценки γ
= 2Ф(t)
приводит к увеличению t(Ф
(t)
— возрастающая функция), следовательно,
и к возрастанию δ;
другими словами, увеличение надежности
классической оценки влечет за собой
уменьшение ее точности.

Пример.
Случайная величина X
имеет
нормальное распределение с известным
средним квадратическим отклонением σ
= 3. Найти доверительные интервалы для
оценки неизвестного математического
ожидания а
по
выборочным средним

,
если
объем выборки n
= 36 и задана надежность оценки
γ= 0,95.

Решение.
Найдем
t.
Из
соотношения 2Ф(t)=0,95
получим Ф(t)
= 0,475. По таблице приложения 2 находим
t=1,96.

Найдем
точность оценки:

.

Доверительный
интервал таков: (
-0,98;

+ 0,98). Например, если

= 4,1, то доверительный интервал имеет
следующие доверительные границы:

—
0,98
= 4,1- 0,98 = 3,12;

+
0,98 = 4,1 + 0,98 = 5,08.

Таким
образом, значения неизвестного параметра
а,
согласующиеся
с данными выборки, удовлетворяют
неравенству 3,12 < а
< 5,08.
Подчеркнем, что было бы ошибочным
написать Р(3,12
<
а < 5,08) = 0,95. Действительно, так как а
—
постоянная величина, то либо она заключена
в найденном интервале (тогда событие
3,12 < а
< 5,08
достоверно и его вероятность равна
единице), либо в нем не заключена (в
этом
случае событие 3,12 < а
<
5,08 невозможно и его вероятность равна
нулю). Другими словами, доверительную
вероятность не следует связывать с
оцениваемым параметром; она связана
лишь с границами доверительного
интервала, которые, как уже было указано,
изменяются от выборки к выборке.

Поясним
смысл, который имеет заданная надежность.
Надежность γ = 0,95 указывает, что если
произведено достаточно большое число
выборок, то 95% из них определяет такие
доверительные интервалы, в которых
параметр действительно заключен; лишь
в 5% случаев он может выйти за границы
доверительного интервала.

Замечание
2.
Если требуется оценить математическое
ожидание с наперед заданной точностью
δ
и
надежностью γ, то минимальный объем
выборки, который обеспечит эту точность,
находят по формуле

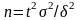
(следствие
равенства

).

Примеры построения
доверительных интервалов для параметров
нормального закона (случай одной и двух
выборок).

Пример: Нормальное
распределение. Пусть х₁…х_n
– выборка из N(a,
)
распределения. Построить ДИ для а, если

—
неизв. Выберем

,
не зависящую от второго параметра.

Решение:

.
По лемме Фишера имеет распределение
Стьюдента:

.
Выберем

:

(используя таблицу,

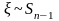
Находим

.
Т.о.

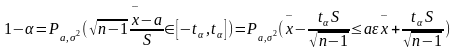
S-выб.дисперсия.
ДИ

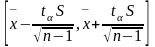
2. Строим ДИ для

(а – неизв); по п.3 лемме Фишера:

.
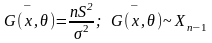
Очевидно, что

,

может быть выбраны неоднозначно. Решение
Х²
{рисунок}

Длина ДИ характеризует
точность оценки. В случае Стьюдента
построенный доверительный интервал
кратчайший. Для

— более сложная задача, поэтому находят
ДИ из условий

;

.
Решение задачи

.
{Если нет априорной информации, нужно
брать 2-сторонний интервал, если есть –
односторонний}

1. Пусть

   

   — независимые.

   — неизвестна (мешающий параметр). Построим
   ДИ для a-b.
   Согласно лемме Фишера:

Т.о.

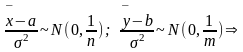
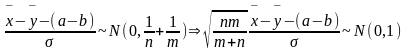
По лемме Фишера
п.3

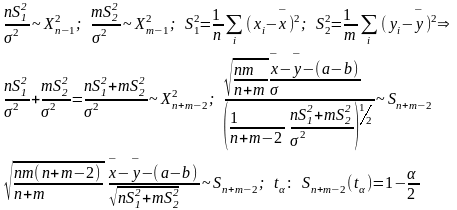
ДИ:

для параметра (a-b)
{считается что

задано}

Построим ДИ.

4.

ДИ для

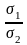
П.3 леммы Фишера :

;
По замечанию к лемме Фишера получим

— распределение Снедекора

— ДИ для

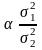
Примечание к
примеру 3: мешающий параметр

— одномерный, если

,
т.е. могут быть разные, т.е. мешающий –
двумерный, то задача не решена, проблема
Беренса-Фишера

{рисунок}

Доверительная
оценка Ĥ называется состоятельной, если
она стягивается в точку.

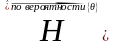
Если Ĥ- ДИ, то
состоятельность равносильна тому, что

.

В примерах 1-4 ДИ –
состоятельные (т.к. в нормальных законах)

Пример5:
Пусть x₁…x_n
– выборка из

;

— функция распределения х_1.
Пусть

при фиксиров. х – монотонная функция
от

.
Тогда в качестве

.
Отметим

;

,
где

— функция распределения

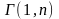
1. Корреляционный
   момент. Проверить обладает ли свой­ствами
   состоятельности и несмещенности оценка
   корреляционного момента. Функциональная,
   статистическая и корреляционная
   зависимости. Условные средние. Выборочное
   уравнение регрессии.

Для
описания системы двух случайных величин
кроме математических ожиданий и дисперсий
составляющих используют и другие
характеристики; к их числу относятся
корреляционный момент и коэффициент
корреляции.

Корреляционным
моментом μ_ху
случайных
величин X
и
Y
называют
математическое ожидание произведения
отклонений этих величин:

μ_ху={M[X—M(X)][Y—M(Y)]},

Для
вычисления корреляционного момента
дискретных величин используют формулу

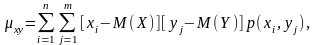
а для
непрерывных величин
— формулу

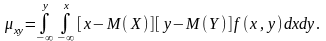
Корреляционный
момент служит для характеристики связи
между величинами X
и
Y.
Как будет показано ниже, корреляционный
момент равен нулю, если X
и Y
независимы; следовательно, если
корреляционный момент не равен нулю,
то X
и
Y
— зависимые случайные величины.

Замечание
1.
Учитывая, что отклонения есть центрированные
случайные величины (см. гл. VIII,
§ 2), корреляционный момент можно
определить как математическое ожидание
произведения центрированных случайных
величин:

μ_ху=M[
].

3амечание
2. Легко
убедиться, что корреляционный момент
можно записать в виде

μ_ху=M(XY)
—M(X)M(Y).

Статистические
оценки могут быть точечными
и интервальными.

Точечные оценки
представляют собой число или точку на
числовой оси. Чтобы оценка

была близка к значению параметра

,
она должна обладать свойствами
состоятельности, несмещенности и
эффективности.

Определение.
Оценка

параметра

называется состоятельной,
если она сходится по вероятности к
оцениваемому параметру, то есть для
любого

:

.

Поясним смысл
этого равенства.

Пусть

—
очень малое положительное число. Тогда
данное равенство означает, что чем
больше объем выборки

,
тем ближе оценка

приближается к оцениваемому параметру

.

Свойство
состоятельности нужно проверять в
первую очередь. Оно обязательно
для любого
правила оценивания. Несостоятельные
оценки не используются.

Определение.
Оценка

параметра

называется несмещенной,
если

,
то есть математическое ожидание оценки
равно оцениваемому параметру. Если
,
то оценка

называется смещенной.

Это свойство оценки
желательно, но не обязательно. Часто
полученная оценка бывает смещенной, но
ее можно поправить так, чтобы она стала
несмещенной.

Иногда, оценка
бывает асимптотически
несмещенной ,

то есть

.

Требования
несмещенности особенно важно при малом
числе опытов.

Определение.
Несмещенная
оценка

параметра

называется эффективной,
если она среди всех несмещенных оценок,
в определенном классе оценок данного
параметра, обладает наименьшей дисперсией.

Можно показать,
что:

—

является состоятельной, несмещенной и
эффективной оценкой

в классе линейных оценок;

—

является состоятельной, смещенной
оценкой

;

—

является состоятельной, несмещенной
оценкой

;

(при больших

разница между

и

мала.

используется при
малых выборках, обычно при

)
;

— относительная
частота

появления события

в

независимых испытаниях является
состоятельной, несмещенной и эффективной
оценкой, в классе линейных оценок,
неизвестной вероятности

(
—
вероятность появления события

в каждом испытании);

— эмпирическая
функция распределения выборки

является состоятельной, несмещенной
оценкой функции распределения

случайной величины

.

Для нахождения
оценок неизвестных параметров используют
различные методы. Наиболее распространенными
являются: метод моментов, метод
максимального правдоподобия (ММП), метод
наименьших квадратов (МНК).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вероятность попадания средней или относительной величины в доверительный интервал называется доверительной вероятностью.

Доверительные границы средней арифметической генеральной совокупности определяют по формуле:

М_ген = М_выб ± t · m_M

Доверительные границы относительной величины в генеральной совокупности определяют по следующей формуле:

Р_ген = Рвыб ± t · m_р

Где: М_ген и Р_ген — значения средней и относительной величин, полученных для генеральной совокупности;

М_выб и Р_выб — значения средней и относительной величин, полученных для выборочной совокупности;

m_M и m_р— ошибки репрезентативности выборочных величин;

t — доверительный критерий, который зависит от величины безошибочного прогноза, устанавливаемого при планировании исследования.

Произведение t · m (Δ) — предельная ошибка показателя, полученного при данном выборочном исследовании.

Размеры предельной ошибки зависят от коэффициента t, который избирает сам исследователь, исходя из заданной вероятности безошибочного прогноза.

Величина критерия t связана с вероятностью безошибочного прогноза (Р) и числом наблюдений в выборочной совокупности (табл. 4.1).

Таблица 4.1. Зависимость доверительного критерия t от степени вероятности безошибочного прогноза Р (при n > 30)

Степень вероятности безошибочного прогноза (Р %)	Доверительный критерий t
95,0
99,0	2,6
99,9	3,3

Для большинства медико-биологических и социальных исследований
достоверными считаются доверительные границы, установленные с
вероятностью безошибочного прогноза = 95% и более.

Чтобы найти критерий t при числе наблюдений (n) < 30, необходимо
пользоваться специальной таблицей Н.А.Плохинского (табл. 4.2), в которой
слева показано число наблюдений — единица (n — 1), а сверху (Р) —
степень вероятности безошибочного прогноза.

При определении доверительных границ сначала надо решить вопрос о
том, с какой степенью вероятности безошибочного прогноза необходимо
представить доверительные границы средней или относительной величины.
Избрав определенную степень вероятности, соответственно этому находят
величину доверительного критерия t при данном числе наблюдений. Таким
образом, доверительный критерий устанавливается заранее, при
планировании исследования.

Таблица 4.2. Значение критерия t для трех степеней вероятности (по Н.А.Плохинскому)

Р n = n-1	95%	99%	99,9%
12,7	63,7	37,0
4,3	9,9	31,6
3,2	5,8	12,9
2,8	4,6	8,6
2,6	4,0	6,9
2,4	3,7	6,0
2,4	3,5	5,3
2,3	3,4	5,0
2,3	3,3	4,8
2,2	3,2	4,6
2,2	3,1	4,4
2,2	3,1	4,3
2,3	3,0	4,1
14-15	2,1	3,0	4,1
16-17	2,1	2,9	4,0
18-20	2,1	2,9	3,9
21-24	2,1	2,8	3,8
25-29	2,0	2,8	3,7

Любой параметр (средняя или относительная величина) может оцениваться с учетом доверительных границ, полученных при расчете.

Например: требуется определить
доверительные границы среднего уровня пепсина у больных гипертериозом с
95% вероятностью безошибочного прогноза. Если известно, что:

n = 49;

М_выб =1г%;

m_м = ± 0,05г%

1. Определение доверительных границ средней величины в генеральной совокупности:

М_ген = М_выб ± t · m_M = 1г% ± 2 · 0,05г%

1г% + 0,1г% = 1,1 г%

М_{ген =}

1г% — 0,1г% = 0,9 г%

Заключение: установлено с вероятностью
безошибочного прогноза 95%, что средний уровень пепсина в генеральной
совокупности у больных гипертериозом находится в пределах от 1,1 г% до
0,9 г%.

Как видно, доверительные границы зависят от размера доверительного интервала.

Анализ доверительных интервалов указывает, что при заданных степенях
вероятности и n > 30 — t имеет неизменную величину и при этом
доверительный интервал зависит от величины ошибки репрезентативности.

С уменьшением величины ошибки суживаются доверительные границы
средних и относительных величин, полученных на выборочной совокупности,
т.е. уточняются результаты исследования, которые приближаются к
соответствующим величинам генеральной совокупности. Если ошибка большая,
то получают для выборочной величины большие доверительные границы,
которые могут противоречить логической оценке искомой величины в
генеральной совокупности. В подобном случае надо искать резервы
сокращения размаха доверительных границ в размере величины ошибки
репрезентативности.

Доверительные границы М_выб и Р_выб
зависят не только от средних ошибок этих величин, но и от избранной
исследователем степени вероятности безошибочного прогноза. При большой
степени вероятности размах доверительных границ увеличивается.

3. Определение достоверности разности средних (или относительных) величин (по критерию t — Стъюдента).

В медицине и здравоохранении по разности параметров оценивают
средние и относительные величины, полученные для разных групп населения
по полу, возрасту, а также групп больных и здоровых и т.д. Во всех
случаях при сопоставлении двух сравниваемых величин возникает
необходимость не только определить их разность, но и оценить ее
достоверность.

Достоверность разности величин, полученных при выборочных
исследованиях, означает, что вывод об их различии может быть перенесен
на соответствующие генеральные совокупности.

Достоверность разности выборочной совокупности измеряется доверительным критерием, который рассчитывается по специальным формулам для средних и относительных величин.

Формула оценки достоверности разности сравниваемых средних величин:

M₁ — M₂

m₁² + m₂²

Для относительных величин:

Р₁ — Р₂

m₁² + m₂²

Где: M₁; M₂ ; Р₁; Р₂ — параметры, полученные при выборочных исследованиях;

m₁; m₂ — их средние ошибки;

t — критерий достоверности (Стъюдента).

Разность статистически достоверна при t ≥ 2, что соответствует вероятности безошибочного прогноза, равной 95% и более.

Для большинства исследований, проводимых в медицине и здравоохранении, такая степень вероятности является вполне достаточной.

При величине критерия достоверности t < 2 степень вероятности
безошибочного прогноза составляет Р < 95%. При такой степени
вероятности нельзя утверждать, что полученная разность показателей
достоверна с достаточной степенью вероятности. В этом случае необходимо
получить дополнительные данные, увеличив число наблюдений.

Иногда при увеличении численности выборки разность продолжает
оставаться не достоверной. Если при повторных исследованиях разность
остается недостоверной, можно считать доказанным, что между
сравниваемыми совокупностями не обнаружено различий по изучаемому
признаку.

Например: требуется определить, достоверны ли
различия в уровне пепсина в желудочном соке больных гипертериозом и
здоровых лиц. Обследуются на пепсин две группы: 49 больных гипертериозом
и 50 здоровых людей (контрольная группа). Результаты представлены в
таблице 4.3.

Таблица 4.3. Сравнение среднего уровня пепсина в желудочном соке больных гипертериозом и здоровых лиц

Сравниваемые группы	N	М (г%)	m (г%)	t	Уровень вероятности безошибочного прогноза (Р)
Больные гипертериозом	1,0	± 0,3	10,0	< 99,9
Здоровые (контрольная группа)	4,0	± 0,1

M₁ — M₂

m₁² + m₂²

4 — 1

t = —————- = 10,0

0,3² + 0,1²