Как найти доверительный интервал для генеральной дисперсии

Доверительный интервал для математического ожидания нормальной случайной
величины при неизвестной дисперсии

Пусть

, причем

 и

 неизвестны.  Необходимо построить доверительный интервал,
накрывающий с надежностью

 истинное значение параметра

.

Для этого из генеральной
совокупности СВ

 извлекается
выборка объема

:

.

1) В качестве точечной
оценки математического ожидания

 используется
выборочное среднее

, а в
качестве оценки дисперсии

 –
исправленная выборочная дисперсия

которой соответствует стандартное отклонение

.

2) Для нахождения
доверительного интервала строится статистика

имеющая в этом случае распределение Стьюдента с
числом степеней свободы

 независимо
от значений параметров

 и

.

3) Задается требуемый
уровень значимости

.

4) Применяется следующая
формула расчета вероятности:

где

 –
критическая точка распределения Стьюдента, которая находится по таблице критических точек распределения Стьюдента (односторонняя критическая область).

Тогда:

Это означает, что
интервал:

накрывает неизвестный
параметр

 с
надежностью

Доверительный интервал для математического ожидания
нормальной случайной величины при известной дисперсии

Пусть количественный
признак

 генеральной
совокупности имеет нормальное распределение

 с
заданной дисперсией

 и
неизвестным математическим ожиданием

.  Построим
доверительный интервал для

.

1) Пусть для оценки

 извлечена
выборка

 объема

. Тогда

2) Составим случайную
величину:

Нетрудно показать, что случайная величина

имеет стандартизированное нормальное распределение, то есть:

3) Зададим уровень
значимости

.

4) Применяя формулу нахождения
вероятности отклонения нормальной величины от математического ожидания, имеем:

Это означает, что
доверительный интервал

накрывает неизвестный
параметр

 с надежностью

. Точность оценки определяется величиной:

Число

 определяется
по таблице значений функции Лапласа из равенства

Окончательно получаем:

Доверительный интервал для
дисперсии нормальной случайной величины при неизвестном математическом ожидании

Пусть

, причем

 и

 –
неизвестны. Пусть для оценки

 извлечена выборка объема

:

.

1) В качестве точечной оценки дисперсии

 используется
исправленная выборочная дисперсия
:

которой соответствует стандартное отклонение

.

2) При нахождении
доверительного интервала для дисперсии в этом случае вводится статистика

имеющая

 –
распределение с числом степеней свободы

 независимо
от значения параметра

.

3) Задается требуемый
уровень значимости

.

4) Тогда, используя таблицу критических точек хи-квадрат распределения, нетрудно указать критические
точки

, для которых будет выполняться следующее
равенство:

Подставив вместо

 соответствующее значение, получим:

Получаем доверительный
интервал для неизвестной дисперсии:

Доверительный интервал для
дисперсии нормальной случайной величины при известном математическом ожидании

Пусть

, причем

 –
известна, а

 –
неизвестна. Пусть для оценки

 извлечена выборка объема

:

.

1) В качестве точечной оценки дисперсии

 используется выборочная дисперсия:

2) При нахождении
доверительного интервала для дисперсии в этом случае вводится статистика

имеющая

 –
распределение с числом степеней свободы

 независимо
от значения параметра

.

3) Задается требуемый
уровень значимости

.

4) Тогда, используя таблицу критических точек хи-квадрат распределения,
нетрудно указать критические точки

, для которых будет выполняться следующее
равенство:

Подставив вместо

 соответствующее значение, получим:

Получаем доверительный
интервал для неизвестной дисперсии:

Доверительный интервал для
среднего квадратического отклонения

Извлекая квадратный корень:

Положив:

Получим следующий
доверительный интервал для среднего квадратического
отклонения:

Для отыскания

 по заданным

 и

 пользуются специальными таблицами.

Для проверки на нормальность заданного распределения случайной величины можно использовать

правило трех сигм.

Задача

Имеется
три независимых реализации нормальной случайной величины: 0.8, 3.2, 2.0.

Построить
доверительные интервалы для среднего и дисперсии с надежностью  

Указание:
воспользоваться таблицами Стьюдента и хи-квадрат.

Решение

Вычисление средней и дисперсии

Вычислим среднее и
исправленную дисперсию
:

Нахождение доверительных интервалов для средней и дисперсии

Найдем доверительный интервал для оценки
неизвестного среднего. Он считается по формуле:

По таблице критических точек t-критерия Стьюдента, для уровня значимости

 (односторонняя критическая область):

 Искомый
доверительный интервал для среднего:

Найдем доверительный интервал для оценки дисперсии.
Он считается по формуле:

Для уровня значимости

 и

 получаем по таблице значений хи-квадрат:

Искомый доверительный интервал для дисперсии:

Ответ

---

Кроме этой задачи на другой странице сайта есть

пример расчета доверительного интервала математического ожидания и среднего квадратического отклонения для интервального вариационного ряда

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Для помощи во время экзамена/зачета в онлайн режиме необходимо договариваться заранее.

Пусть из некоторой
генеральной совокупности значений X,
распределенной по нормальному закону
N(m;),
взята случайная выборка объемом n,
для которой вычислены выборочные
дисперсии: смещеннаяи несмещенная (исправленная).
Найдем с заданной надежностью
интервальные оценки для генеральной
дисперсии D
и среднеквадратичного отклонения .

Случайная величина
(3.22)

имеет распределение
Пирсона ()
сn-1
степенями свободы, поскольку:

а) все величины
распределены стандартно нормально,
т.е.A_iN(0;1),

б)
,

в) существует
уравнение линейной связи:
.

Это означает
(см.[1, п.2.1.1.])
.

Т.к. распределение
неотрицательное, то можно построить
как односторонние (и),
так и двусторонниедоверительные интервалы.

Построим
односторонние доверительные интервалы
для дисперсии по заданной надежности
=1-.
Заметим, что правостороннему по
интервалу соответствует левосторонний
поa
интервал, и наоборот. Тогда для определения
правостороннего по
интервала имеем:

или
,

где
– функция распределения Пирсона сn-1
степенями свободы. Из этого уравнения
находится критическое значение
.
Также значения «Хи – квадрат» при
заданном уровне значимости
и объеме выборки n
можно найти в таблице 8 приложения 1.
Тогда с вероятностью 
имеем

.
(3.23)

Соответственно,
для среднеквадратичного отклонения 
получится правосторонний
интервал
.

Для
определения левостороннего по
интервала имеем:

.

Из
этого уравнения находится критическое
значение
.

.
(3.24)

Соответственно,
получаем левосторонний
интервал
.

Видно,
что корни интегральных уравнений связаны
соотношением
,
поэтому в таблицах критических показателей
распределения Пирсона (Таблица 8,
приложение 1) дается общая границакак решение уравнения,
но для значений уровня значимости,
близких как к 0, так и к 1. Часто встречается
обозначениедля корней распределениясk
степенями свободы.

Построим двусторонние
доверительные интервалы для дисперсии
по заданной надежности =1-.

Итак,
.

Заметим,
что т.к. распределение Пирсона
асимметрично, то правая и левая критические
области могут быть взяты с произвольным
соотношением вероятностей, поскольку
определена только полная вероятность
попадания в них:.
Обычно берут обе критические области
с одинаковой вероятностью/2,
тогда границы доверительного интервала
надо искать отдельно:

.
(3.25)

Тем
самым, задача сведена к двум односторонним
интервалам с половинным уровнем
значимости :

,
.
(3.26)

Отсюда
можно получить двойной интервал для
среднеквадратического отклонения:
.

(3.27)

Очевидно, что
границы доверительного интервала не
симметричны относительно исправленного
значения дисперсии.

По
формуле (3.25) можно решить также и обратную
задачу – по заданному доверительному
интервалу генеральной дисперсии
определить доверительную вероятность
.

Существует
и другой способ найти границы доверительного
интервала для дисперсии, в основе
которого лежит выбор доверительного
интервала, симметричного относительно
.
Доверительный интервал для
среднеквадратического значения
в таком случае можно найти, зная
вероятность 
и
число степеней свободы, n
по формуле

s(1-q)<

<s(1+q),

(3.28)

где
q=q(,n)
– некоторое число, которое затабулировано
(Таблица 4, приложение 1). Причем, если 1-
q
<0, то
интервал имеет вид 0< 
<s(1+q).

Задача
13. Осуществляя
контроль качества выпускаемых болтов,
было проверено 15 штук. Предполагая, что
ошибка при их изготовлении подчинена
нормальному закону распределения,
причем выборочное среднее

квадратичное
отклонение _B
равно 5мм, определить с надежностью
=0.95
доверительный интервал для неизвестного
параметра .

Решение.
Т.к. по условию задачи n=15<30,
то воспользуемся полученными формулами.
Найдем пограничные значения вероятности
для =1-=0.05.
Тогда имеем

.

По
таблицам
-распределения
найдем пограничные значенияпри
заданной вероятности для=n-1=14
числа степеней свободы:
и,
тогда.
Отсюда границы интервала представим в
виде двойного неравенства:

или
3.78 
8.17 (мм).

Если решать эту
задачу по формулам (3.28), то

1. найдем
   исправленную дисперсию
   ,
   отсюдаs=5.17;

2. по
   таблицам (Таблицы 4 «Приложение» 1)
   найдем значение q
   по надежности =0.95
   и числу степеней свободы n=15:
   q_15,0.95=0.46;

3. доверительный
   интервал для 
   построим по формулам (3.28):

5.17(1-0.46)<
<5.17(1+0.46)
или 2.79< <7.58.

Как видно из
вычислений, величина доверительного
интервала зависит от способа его
построения и дает близкие между собой,
но не одинаковые ответы.

Задача
14. По данным
Гидрометцентра за последние 25 лет
средняя температура в середине октября
в нашем регионе имеет среднеквадратичное
отклонение _B=8
градусов. Учитывая, что ошибка подчинена
нормальному закону распределения,
определить с надежностью =0.9
доверительный интервал для неизвестного
параметра .

Решение.
Т.к. по условию задачи n<30,
то воспользуемся формулами
.

1)Найдем
пограничные значения вероятности для
=1-=0.1:
.

1. по
   таблицам
   —
   распределения (Таблица 7, приложение
   1) найдем пограничные значениядля=n-1=24
   числа степеней свободы: зная, что
   иимееми.

1. Найдем
   значения для :
   .

2. Найдем
   границы интервала
   или 6.63 <<
   12.73.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Построим доверительный интервал для оценки дисперсии случайной величины, распределенной по нормальному закону, в

MS

EXCEL

.

Построение

доверительного интервала

для оценки

среднего

приведено в статье

Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL

. Процедура построения

доверительного интервала

для оценки

дисперсии

имеет много общего с процедурой для оценки

среднего

, поэтому в этой статье она изложена менее подробно, чем в указанной статье.

Формулировка задачи.

Предположим, что из

генеральной совокупности

имеющей

нормальное распределение

с неизвестным

средним значением

μ и неизвестной

дисперсией

σ

²

взята

выборка

размера n. Необходимо на основании этой

выборки

оценить

дисперсию распределения

и построить

доверительный интервал

.

Примечание

: Построение

доверительного интервала для оценки среднего

относительно нечувствительно к отклонению

генеральной совокупности

от

нормального закона

. А вот при построении

доверительного интервала для оценки

дисперсии

требование

нормальности

является строгим.

СОВЕТ

: Для построения

Доверительного интервала

нам потребуется знание следующих понятий:

• дисперсия и стандартное отклонение

  ,

• доверительный интервал для оценки среднего

  ,

• выборочное распределение статистики

  ,

• уровень доверия/ уровень значимости

  ,

• нормальное распределение

  и

  распределение ХИ-квадрат

  .

В качестве

точечной оценкой дисперсии распределения,

из которого взята

выборка

, используют

Дисперсию выборки

s

²

.

Также, перед

процедурой проверки гипотезы

, исследователь устанавливает требуемый

уровень значимости

– это допустимая для данной задачи

ошибка первого рода

, т.е. вероятность отклонить

нулевую гипотезу

, когда она верна (

уровень значимости

обозначают буквой α (альфа) и чаще всего выбирают равным 0,1; 0,05 или 0,01)

В статье про

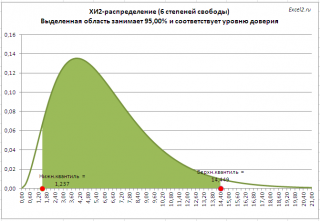
ХИ2-распределение

показано, что

выборочное распределение статистики

y=(n-1)

s

²

/σ

²

, имеет

ХИ2-распределение

с n-1 степенью свободы.

Воспользуемся этим свойством и построим

двухсторонний доверительный интервал

для оценки

дисперсии

:

где χ

²

_α/2,n-1

–

верхний α/2-квантиль

распределения ХИ-квадрат с

n

-1 степенью свободы (

такое значение случайной величины

χ

²

_n-1

,

что

P

(

χ

²

_n-1

>=

χ

²

_α/2,n-1

)=α/2)

. Чтобы найти этот

квантиль

в MS EXCEL используйте формулу

=ХИ2.ОБР.ПХ(α; n-1)

.

χ

²

_1-α/2,n-1

– верхний 1-α/2-квантиль

, который равен

нижнему α/2-

квантилю.

Чтобы найти этот

квантиль

в MS EXCEL используйте формулу

=ХИ2.ОБР(α; n-1)

.

Примечание

: В

файле примера на листе Квантили

показан расчет

квантилей

для

распределения ХИ2

. На рисунке выделена область соответствующая уровню доверия 95%, которая ограничена верхним и нижним

квантилем

. Обратите внимание, что в отличие от

нормального

и

t-распределения

распределение

ХИ2

несимметрично, поэтому для двустороннего

доверительного интервала

потребуется вычислить два

квантиля

, значения которых будут отличаться.

Примечание

:

Доверительный интервал

для

стандартного отклонения

может быть получен путем извлечения квадратного корня из вышеуказанного выражения.

В

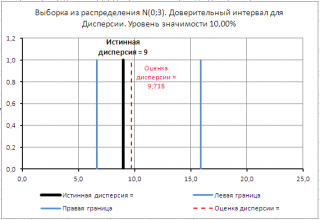
файле примера на листе 2х сторонний

создана форма для расчета и построения двухстороннего

доверительного интервала

.

Для построения

односторонних доверительных интервалов

используйте нижеследующие выражения:

Задача

В следующей задаче найдем

верхний односторонний доверительный интервал

для

дисперсии

.

Автоматический аппарат заполняет емкости с растворителем. Предполагается, что объемы налитой жидкости в емкостях распределены по

нормальному закону

. Если разброс значений объемов будет слишком велик, то значительная часть емкостей будет существенно переполнена или не заполнена. Для оценки

дисперсии

в качестве выборки взято 20 наполненных жидкостью емкостей. На основе выборки была вычислена

дисперсия выборки

s

²

, которая составила 0,0153 (литров

²

). Принято решение оценить верхний уровень

дисперсии

с

уровнем доверия

95%.

Для решения задачи воспользуемся выражением

Сначала найдем

верхний (1-α)-квантиль

(или равный ему

нижний α-квантиль

)

ХИ2-распределения

с n-1

степенью свободы

при у

ровне значимости

α равном 1-0,95=0,05. Это можно сделать в MS EXCEL по формулам:

=ХИ2.ОБР.ПХ(1-0,05; 20-1)

или

=ХИ2.ОБР(0,05; 20-1)

В результате получим

верхний доверительный интервал для дисперсии:

σ

²

<=0,0287

Или тоже, но словами и для

стандартного отклонения:

«Значения

выборки

показывают, что с вероятностью 95%,

стандартное отклонение

процесса наполнения емкости растворителем меньше или равно 0,17 литров».

Ход решения приведен в

файле примера на листе 1 сторонний

.

СОВЕТ

: О построении других

доверительных интервалов

см. статью

Доверительные интервалы в MS EXCEL

.

В статистике существует два вида оценок: точечные и интервальные. Точечная оценка представляет собой отдельную выборочную статистику, которая используется для оценки параметра генеральной совокупности.[1] Например, выборочное среднее — это точечная оценка математического ожидания генеральной совокупности, а выборочная дисперсия S² — точечная оценка дисперсии генеральной совокупности σ². Ранее было показано, что выборочное среднее является несмещенной оценкой математического ожидания генеральной совокупности. Выборочное среднее называется несмещенным, поскольку среднее значение всех выборочных средних (при одном и том же объеме выборки n) равно математическому ожиданию генеральной совокупности.

Для того чтобы выборочная дисперсия S² стала несмещенной оценкой дисперсии генеральной совокупности σ², знаменатель выборочной дисперсии следует положить равным n – 1, а не n. Иначе говоря, дисперсия генеральной совокупности является средним значением всевозможных выборочных дисперсий.

При оценке параметров генеральной совокупности следует иметь в виду, что выборочные статистики, такие как , зависят от конкретных выборок. Чтобы учесть этот факт, для получения интервальной оценки математического ожидания генеральной совокупности анализируют распределение выборочных средних (подробнее см. Выборочные распределения). Построенный интервал характеризуется определенным доверительным уровнем, который представляет собой вероятность того, что истинный параметр генеральной совокупности оценен правильно. Аналогичные доверительные интервалы можно применять для оценки доли признака р и основной распределенной массы генеральной совокупности.

Скачать заметку в формате Word или pdf, примеры в формате Excel2013

Построение доверительного интервала для математического ожидания генеральной совокупности при известном стандартном отклонении

Ранее мы применили информацию о распределении и центральную предельную теорему, [2] чтобы вычислить процентную долю выборочных средних, лежащих в окрестности математического ожидания генеральной совокупности на расстоянии, не превышающем заданное. Например, при анализе веса коробок с кукурузными хлопьями, 95% всех выборочных средних лежат в интервале от 362,12 до 373,88 г. Это утверждение получено с помощью дедукции, поскольку свойства выборки определялись на основе данных о генеральной совокупности. Однако теперь нам необходимо применить противоположный способ рассуждения — индуктивный, так как в теории статистического вывода, наоборот, свойства генеральной совокупности определяются на основе параметров отдельной выборки. На практике математическое ожидание генеральной совокупности, как правило, не известно и должно быть оценено. Вернемся к примеру с коробками. Допустим теперь, что математическое ожидание генеральной совокупности μ не известно, а истинное стандартное отклонение генеральной совокупности σ равно 15 г. Тогда в формулах для определения границ интервала  μ ± 1,96σ/√n математическое ожидание генеральной совокупности μ следует заменить выборочным средним . Следовательно, для оценки неизвестного математического ожидания генеральной совокупности можно применить интервал ± 1,96σ/√n. На практике, как правило, из генеральной совокупности извлекают выборку фиксированного объема n и вычисляют выборочное среднее . Однако, чтобы понять смысл интервальной оценки, необходимо рассмотреть гипотетическое множество всех возможных выборок данного объема.

Допустим, например, что математическое ожидание генеральной совокупности μ равно 368 г. Предположим, что из генеральной совокупности коробок извлекается выборка, состоящая из 25 коробок, средний вес которых равен 362,3 г. Интервал, предложенный для оценки математического ожидания μ, имеет границы: 362,3 ± 1,96×15/√25 = 362,3 ± 5,88. Таким образом, 356,42 < μ < 368,18.

Поскольку математическое ожидание генеральной совокупности μ равно 368, оно попадает в этот интервал, и, следовательно, данная выборка позволяет правильно ее оценить (рис. 1).

Рис. 1. Доверительные интервальные оценки математического ожидания генеральной совокупности, полученные по пяти разным выборкам объема n = 25, извлеченным из генеральной совокупности с параметрами μ = 368 и σ = 15

Допустим, что выборочное среднее некоей выборки объема n = 25, равно 369,5. Доверительный интервал, построенный по этой выборке, имеет границы, равные 369,5 ± 1,96×15/√25 , т.е. 369,5 ± 5,9. Таким образом, 363,62 < μ < 375,38. Поскольку математическое ожидание генеральной совокупности μ равно 368, оно попадает в этот интервал, и, следовательно, данная оценка является правильной. Возникает впечатление, что выборки, имеющие объем n = 25, всегда приводят к правильным оценкам математического ожидания генеральной совокупности μ. Чтобы опровергнуть это, рассмотрим третий гипотетический пример. Допустим, что средний вес коробок равен 360 г. Интервал, предложенный для оценки математического ожидания μ, имеет границы: 360 ± 1,96×15/√25 , т.е. 360 ± 5,88. Таким образом, в данном случае 354,12 < μ < 365,88. Эта оценка неверна, поскольку математическое ожидание генеральной совокупности μ равно 368 и не попадает в этот интервал (см. рис. 1). Таким образом, для некоторых выборок эта оценка верна, а для некоторых — нет. Кроме того, на практике, из генеральной совокупности извлекается только одна выборка. Следовательно, поскольку математическое ожидание генеральной совокупности μ не известно, невозможно сказать, верна полученная интервальная оценка или нет.

Чтобы разрешить эту дилемму, необходимо определить долю выборок, позволяющих правильно оценить математическое ожидание генеральной совокупности μ. Для этого следует исследовать еще две гипотетические выборки, средние значения которых равны 362,12 и 373,88 г соответственно. Если = 362,12, мы получаем интервал 362,12 ±1,96×15/√25 , т.е. 362,12 ± 5,88. Это приводит к оценке 356,24 < μ < 368,00. Поскольку математическое ожидание генеральной совокупности μ, равное 368, является верхней границей интервала, эта оценка верна. Если = 373,88, мы получаем интервал 373,88 ± 1,96×15/√25 , т.е. 373,88 ± 5,88. Это приводит к оценке 368,00 < μ < 379,76. Поскольку математическое ожидание генеральной совокупности μ, равное 368, является нижней границей интервала, эта оценка верна.

Таким образом, если выборочное среднее изменяется в диапазоне от 362,12 до 373,88 г, математическое ожидание генеральной совокупности лежит где-то внутри этого соответствующего доверительного интервала. Вероятность того, что это значение лежит в интервале с границами 362,12 и 373,88, равна 95% (об этом говорилось в начале раздела). Следовательно, 95% средних значений всех выборок, имеющих объем n = 25, позволяют правильно оценить математическое ожидание генеральной совокупности, а 5% — нет.

Интервальная оценка, доверительный уровень которой равен 95%, интерпретируется следующим образом: если из генеральной совокупности извлечь все выборки, имеющие объем n, и вычислить их выборочные средние, то 95% доверительных интервалов, построенных на их основе, будут содержать математическое ожидание генеральной совокупности, а 5% — нет. На практике, как правило, из генеральной совокупности извлекается только одна выборка, а математическое ожидание генеральной совокупности μ не известно. По этой причине невозможно гарантировать, что некий конкретный доверительный интервал содержит величину μ. Можно лишь утверждать, что вероятность этого события равна 95%.

В некоторых ситуациях желательно иметь более высокий доверительный уровень, а следовательно, точность оценки величины μ (например, 99%). Но иногда можно ограничиться и менее точной оценкой (например, 90%).

Как правило, доверительный уровень обозначают следующим образом: (1 – α)х100%, где величина α представляет собой площадь, ограниченную хвостом распределения, выходящим за пределы доверительного интервала. (Величину α называют уровнем значимости доверительного интервала. Кроме того, в качестве синонима для доверительного уровня иногда употребляется выражение «доверительная вероятность».) Площади, ограниченные как левым, так и правым хвостами распределения, выходящими за пределы доверительного интервала, равны α/2.

Построение доверительного интервала для математического ожидания генеральной совокупности при известном стандартном отклонении

где Z — значение стандартизованной нормально распределенной случайной величины, соответствующее интегральной вероятности, равной 1 – α/2, σ — стандартное отклонение генеральной совокупности.

Величина Z, выбранная для построения доверительного интервала, называется критическим значением распределения. Чтобы построить интервал, имеющий 95%-ный доверительный уровень, необходимо выбрать α = 0,05. Половина площади симметричной фигуры, ограниченной концами доверительного интервала и кривой стандартизованного нормального распределения, равна 0,95/2=0,475. Величина Z, соответствующая площади 0,4750, равна 1,96, поскольку площадь фигуры, ограниченной правым хвостом распределения, равна 0,025, а суммарная площадь фигуры, лежащей левее значения Z = 1,96, равна 0,975.

Каждому доверительному уровню 1 – α соответствует свое критическое значение. Например, доверительному уровню, равному 95%, соответствует Z = ±1,96 (рис. 2а). Если требуется построить интервал, доверительный уровень которого равен 99%, следует выбрать α = 0,01. В этом случае величина Z приближенно равна 2,58, поскольку площадь, ограниченная правым хвостом распределения, выходящим за пределы доверительного интервала, равна 0,005, а суммарная площадь фигуры, лежащей левее значения Z, равна 0,995 (рис. 2б).

Рис. 2. Гауссова кривая для определения критического значения Z, соответствующего доверительному уровню, равному: (а) 95%; (б) 99%

Возникает вопрос, почему бы не построить интервал, доверительный уровень которого был бы очень близок к 100%. Это нецелесообразно, поскольку такой доверительный интервал оказался бы слишком широким, а оценка математического ожидания — слишком неточной. Разумеется, вероятность того, что математическое ожидание лежит в этом интервале, очень высока, однако для принятия решения этот факт практически бесполезен.

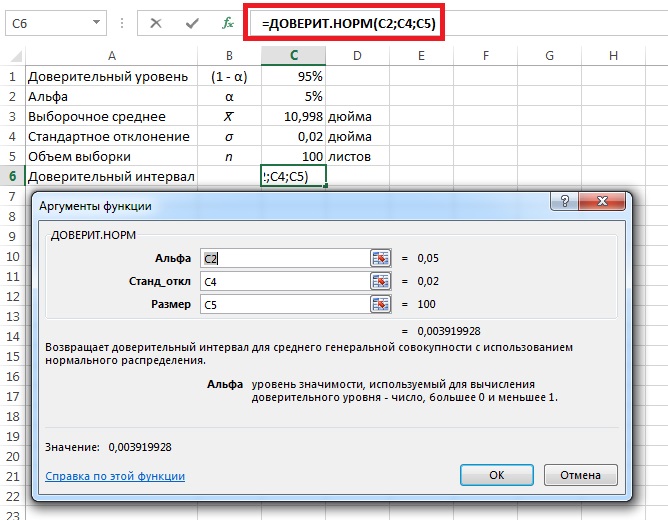
Пример 1. При производстве бумаги средняя длина листа должна быть равной 11 дюймам, а ее стандартное отклонение — 0,02 дюйма. Периодически из произведенной продукции, чтобы оценить ее качество, извлекаются выборки. Допустим, выборка состоит из 100 листов, а ее выборочное среднее — 10,998 дюйма. Постройте интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 95%.

Решение. Подставим в формулу (1) величину Z = 1,96, соответствующую доверительному уровню, равному 95%:

Таким образом, вероятность того, что математическое ожидание генеральной совокупности лежит в интервале от 10,99408 до 11,00192, равна 95%. [3] Поскольку номинальная длина бумаги — 11 дюймов, она попадает в построенный интервал. Следовательно, производственный процесс выполняется правильно.

В Excel до версии 2007 используется функция =ДОВЕРИТ(), начиная с версии 2010 =ДОВЕРИТ.НОРМ(), возвращающая доверительный интервал для среднего генеральной совокупности с использованием нормального распределения. Для приведенного выше примера 1 вычисления в Excel показаны на рис. 3.

Рис. 3. Расчет доверительного интервал для среднего генеральной совокупности в Excel

Построение доверительного интервала для математического ожидания генеральной совокупности при неизвестной дисперсии

На практике как математическое значение генеральной совокупности, так и его стандартное отклонение часто бывают неизвестными. Следовательно, необходимо построить доверительный интервал, содержащий математическое значение генеральной совокупности, используя лишь выборочные статистики и S.

В начале 20-го века статистик Уильям С. Госсет, сотрудник ирландского отделения пивоваренной компании Guinness, заинтересовался проблемой оценки математического ожидания при неизвестном стандартном отклонении. Поскольку компания Guinness запрещала своим сотрудникам публиковать работы под собственными именами, Госсет взял псевдоним Стьюдент. По этой причине распределение, предложенное Госсетом, называется t-распределением Стьюдента. Если случайная величина является нормально распределенной, то следующая статистика имеет t-распределение с n – 1 степенями свободы (о степенях свободы см. ниже):

Обратите внимание на то, что это выражение почти совпадает с формулой (3) определения величины Z для выборочного распределения средних, только вместо величины σ в нем стоит выборочное стандартное отклонение S:

Внешне распределение Стьюдента очень напоминает стандартизованное нормальное распределение (рис. 4).

Рис. 4. Стандартизованное нормальное распределение и t-распределение Стьюдента с различным числом степеней свободы

Оба распределения имеют колоколообразную форму и являются симметричными. Однако хвосты t-распределения «тяжелее» (т.е. ограничивают большую площадь), а площадь фигуры в центре определения меньше, чем у стандартизованного нормального распределения. Это происходит потому, что стандартное отклонение σ не известно, а вместо него используется его выборочная оценка S. Неопределенность значения σ порождает большую изменчивость переменной t по сравнению с величиной Z. Однако при увеличении количества степеней свободы t-распределение становится все ближе к стандартизованному нормальному распределению. Это происходит потому, что при увеличении объема выборки оценка S становится все точнее. При объеме выборки, равном 120 и более, величина S довольно точно аппроксимирует стандартное отклонение σ, так что разница между t-распределением и стандартизованным нормальным отклонением становится минимальной. По этой причине, если объем выборки превышает 120, многие статистики вместо величины t используют переменную Z.

Для построения в Excel графиков t-распределения Стьюдента, начиная с версии 2010 используется функция =СТЬЮДЕНТ.РАСП() (рис. 5). В Excel более ранних версий используется функция =СТЬЮДРАСП(). При этом следует иметь ввиду, что только начиная с версии 2010 с использованием функции =СТЬЮДЕНТ.РАСП() можно построить t-распределения Стьюдента, как для положительных, так и отрицательных значений без дополнительных не вполне очевидных манипуляций…

Рис. 5. Функция Excel =СТЬЮДЕНТ.РАСП() для построения плотности вероятности

Проверка предположений. Напомним, что t-распределение основано на предположении, что изучаемая случайная величина X является нормально распределенной. Однако на практике t-распределение можно применять для оценки неизвестного математического ожидания генеральной совокупности при неизвестном стандартном отклонении при достаточно большом объеме выборки и не слишком асимметричном распределении. При работе с небольшими выборками эти условия уже не выполняются автоматически, поэтому их следует проверять. Для этого необходимо строить гистограмму, диаграмму «ствол и листья», блочную диаграмму или график нормального распределения.

Критические значения для t-распределения с соответствующими степенями свободы можно найти в таблице (рис. 6). В заголовке каждого столбца этой таблицы указана площадь фигуры, ограниченной хвостом t-распределения (поскольку для переменной t указаны только положительные значения, эта площадь ограничена правым хвостом распределения). В заголовке каждой строки указано количество степеней свободы.

Рис. 6. Определение площади фигуры, ограниченной t-распределением, имеющим 99 степеней свободы, и соответствующим значением переменной t

Например, на рис. 6 показано, как найти площадь фигуры, ограниченной t-распределением, имеющим 99 степеней свободы, и соответствующим значением переменной t, если необходимо построить интервал, доверительный уровень которого равен 95%. Этот доверительный уровень означает, что площадь каждой фигуры, ограниченной хвостами t-распределения, равна 0,025. Найдем пересечение столбца, соответствующего величине 0,025, и строки, соответствующей 99 степеням свободы. В этой ячейке записано критическое значение, равное 1,9842. Поскольку t-распределение является симметричным и его математическое ожидание равно 0, площади, ограниченной правым хвостом, соответствует величина +1,9842, а площади, ограниченной левым хвостом, соответствует величина –1,9842. Величина 1,9842 означает следующее: вероятность того, что величина t превосходит +1,9842, равна 0,025, т.е. 2,5% (рис. 7).

Рис. 7. Распределение Стьюдента с 99 степенями свободы

Вместо таблиц удобнее и проще использовать функции Excel (к сожалению, эти функции вуалируют суть расчетов, так что иметь представление о механике расчета всё же полезно). Начиная с версии 2010 вместо таблиц используется функция =СТЬЮДЕНТ.ОБР.2Х() (рис.

Рис. 8. Использование функции =СТЬЮДЕНТ.ОБР.2Х() для определения t-параметра по известной вероятности (обратная задача построению плотности распределения)

Степени свободы. Для вычисления выборочной дисперсии S² необходимо вычислить величину

Таким образом, для вычисления выборочной дисперсии необходимо знать . Следовательно, мы можем варьировать лишь n – 1 выборочное значение. Это означает, что величина обладает n – 1 степенями свободы. Допустим, например, что выборка состоит из 5 чисел, а ее выборочное среднее равно 20. Сколько разных значений необходимо знать для того, чтобы однозначно определить остальные? Если n = 5 и = 20, то

поскольку

Таким образом, если известны четыре величины, пятое значение уже не свободно, поскольку сумма должна быть равна 100. Например, если нам известны величины 18, 24, 19 и 16, пятая величина должна быть равной 23, поскольку сумма равна 100.

Доверительный интервал. Рассмотрим формулу для вычисления интервала, содержащего математическое ожидание при неизвестном стандартном отклонении с вероятностью (1 – α)х100%.

где t_{n – 1} — критическое значение t-распределения с n – 1 степенями свободы, соответствующее площади, ограниченной правым хвостом и равной α/2.

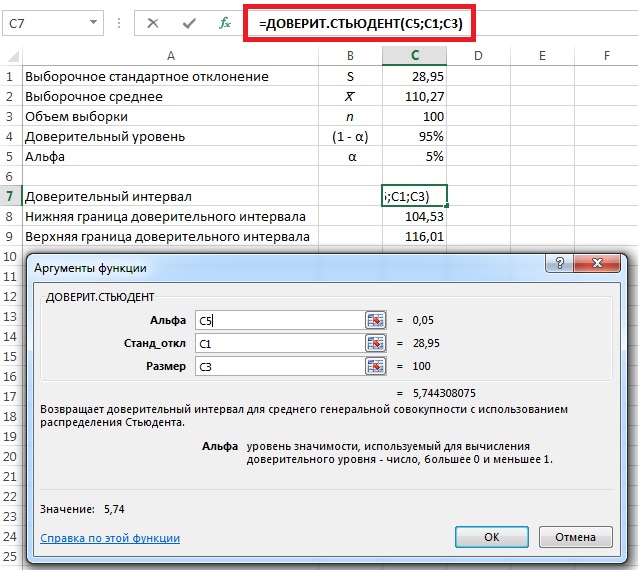
Проиллюстрируем применение этой формулы. Предположим, что при аудиторской проверки из информационной системы извлечена выборка, состоящая из 100 накладных, заполненных в течение последнего месяца. Допустим, что выборочное среднее равно 110,27долл., а выборочное стандартное отклонение — 28,95 долл. Если компания желает построить интервал, имеющий доверительный уровень, равный 95%, критическое значение t-распределения равно 1,9842 (см. табл. 7.1). Используя формулу доверительного интервала получаем:

Кроме уже перечисленных в Excel есть еще целый ряд функций, работающих с t-распределением Стьюдента. Например, вычисление доверительного интервала, содержащего среднюю сумму накладных, с помощью Excel продемонстрировано на рис. 9. Заметим, что до версии 2010 Excel не содержит функции, непосредственно рассчитывающей доверительный интервал для t-распределения Стьюдента.

Рис. 9. Вычисление доверительного интервала, содержащего среднюю сумму накладных, с помощью функции Excel =ДОВЕРИТ.СТЬЮДЕНТ()

Таким образом, вероятность того, что средняя сумма накладных находится в интервале от 104,53 до 116,01, равна 95%.

Рассмотрим пример 2. Некая промышленная компания на Среднем Западе производит электрические изоляторы. Если во время работы изолятор выходит из строя, происходит короткое замыкание. Чтобы проверить прочность изолятора, компания проводит испытания, в ходе которых определяется максимальная сила, необходимая для разрушения изолятора. Сила измеряется в фунтах нагрузки, приводящей к разрушению изолятора (рис. 10, столбец А). Постройте интервал, содержащий математическое ожидание генеральной совокупности величин силы, необходимой для разрушения изолятора, доверительный уровень которого равен 95%.

Решение. Как показано на рис. 10, выборочное среднее равно =1723,4 фунта, а выборочное стандартное отклонение равно S = 89,55 фунта.

Рис. 10. Результаты экспериментов и расчет доверительного интервала

Вероятность того, что средняя величина силы разрушения изолятора находится в интервале от 1689,96 до 1756,84, равна 95%. Корректность этих доверительных интервалов зависит от того, насколько распределение генеральной совокупности близко к нормальному. Напомним, что требование о большом объеме выборки можно ослабить. Таким образом, если объем выборки равен 30, предположение о нормальном распределении остается правдоподобным, даже если распределение силы разрушения слегка асимметрично. График нормального распределения (рис. 11а) и блочная диаграмма (рис. 11б) свидетельствуют о том, что распределение силы разрушения имеет легкую асимметрию, следовательно, для решения задачи можно применять t-распределение.

Рис 11. Средняя величины силы, необходимой для разрушения изолятора: (а) график нормального распределения (подробнее о том, как построить такой график см. Проверка гипотезы о нормальном распределении); (б) блочная диаграмма (подробнее о построении таких диаграмм см. Excel. Биржевая диаграмма, она же блочная, она же ящичная)

Построение доверительного интервала для доли признака в генеральной совокупности

В этом разделе понятие доверительного интервала распространяется на категорийные данные. Это позволяет оценить долю признака в генеральной совокупности р с помощью выборочной доли р_S = Х/n. Как указывалось ранее, если величины nр и n(1 – р) превышают число 5, биномиальное распределение можно аппроксимировать нормальным. Следовательно, для оценки доли признака в генеральной совокупности р можно построить интервал, доверительный уровень которого равен (1 – α)х100%.

где p_S — выборочная доля признака, равная Х/n, т.е. количеству успехов, деленному на объем выборки, р — доля признака в генеральной совокупности, Z — критическое значение стандартизованного нормального распределения, n — объем выборки.

Пример 3. Предположим, что из информационной системы извлечена выборка, состоящая из 100 накладных, заполненных в течение последнего месяца. Допустим, что 10 из этих накладных составлены с ошибками. Таким образом, р = 10/100 = 0,1. Доверительному уровню 95% соответствует критическое значение Z = 1,96.

Таким образом, вероятность того, что от 4,12% до 15,88% накладных содержат ошибки, равна 95%.

Для заданного объема выборки доверительный интервал, содержащий долю признака в генеральной совокупности, кажется более широким, чем для непрерывной случайной величины. Это объясняется тем, что измерения непрерывной случайной величины содержат больше информации, чем измерения категорийных данных. Иначе говоря, категорийные данные, принимающие лишь два значения, содержат недостаточно информации для оценки параметров их распределения.

Вычисление оценок, извлеченных из конечной генеральной совокупности

Оценка математического ожидания. Поправочный коэффициент для конечной генеральной совокупности (fpc) ранее использовался для уменьшения стандартной ошибки в раз. При вычислении доверительных интервалов для оценок параметров генеральной совокупности поправочный коэффициент применяется в ситуациях, когда выборки извлекаются без возвращения. Таким образом, доверительный интервал для математического ожидания, имеющий доверительный уровень, равный (1 – α)х100%, вычисляется по формуле:

Пример 4. Чтобы проиллюстрировать применение поправочного коэффициента для конечной генеральной совокупности, вернемся к задаче о вычислении доверительного интервала для средней суммы накладных, рассмотренной выше в примере 3. Предположим, что за месяц в компании выписываются 5000 накладных, причем X̅ =110,27долл., S = 28,95 долл., N = 5000, n = 100, α = 0,05, t₉₉ = 1,9842. По формуле (6) получаем:

Оценка доли признака. При выборе без возвращения доверительный интервал для доли признака, имеющий доверительный уровень, равный (1 – α)х100%, вычисляется по формуле:

Доверительные интервалы и этические проблемы

При выборочном исследовании генеральной совокупности и формулировании статистических выводов часто возникают этические проблемы. Основная из них — как согласуются доверительные интервалы и точечные оценки выборочных статистик. Публикация точечных оценок без указания соответствующих доверительных интервалов (как правило, имеющих 95%-ный доверительный уровень) и объема выборки, на основе которых они получены, может породить недоразумения. Это может создать у пользователя впечатление, что точечная оценка — именно то, что ему необходимо, чтобы предсказать свойства всей генеральной совокупности. Таким образом, необходимо понимать, что в любых исследованиях во главу угла должны быть поставлены не точечные, а интервальные оценки. Кроме того, особое внимание следует уделять правильному выбору объемов выборки.

Чаще всего объектами статистических манипуляций становятся результаты социологических опросов населения по тем или иным политическим проблемам. При этом результаты опроса выносят на первые страницы газет, а ошибку выборочного исследования и методологию статистического анализа печатают где-нибудь в середине. Чтобы доказать обоснованность полученных точечных оценок, необходимо указывать объем выборки, на основе которой они получены, границы доверительного интервала и его уровень значимости.

Предыдущая заметка Выборочные распределения

Следующая заметка

К оглавлению Статистика для менеджеров с использованием Microsoft Excel

---

[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 448–462

[2] Центральная предельная теорема утверждает, что при достаточно большом объеме выборок выборочное распределение средних можно аппроксимировать нормальным распределением. Это свойство не зависит от вида распределения генеральной совокупности.

[3] На мой взгляд авторы некорректно используют такую точность; если измерения ведутся с точностью до тысячной дюйма, то и вычисления следует округлять до той же точности. Я бы записал = 10,998 ± 0,004; 10,994 < μ < 11,002

Когда нам нужно получить одно число в качестве оценки параметра совокупности, мы используем точечную оценку. Тем не менее, из-за ошибки выборки, точечная оценка не будет в точности равняться параметру совокупности при любом размере данной выборки.

Часто, вместо точечной оценки, более полезным подходом будет найти диапазон значений, в рамках которого, как мы ожидаем, может находится значение искомого параметра с заданным уровнем вероятности.

Этот подход называется интервальной оценкой параметра (англ. ‘interval estimate of parameter’), а доверительный интервал выполняет роль этого диапазона значений.

Определение доверительного интервала.

Доверительный интервал (англ. ‘confidence interval’) представляет собой диапазон, для которого можно утверждать, с заданной вероятностью (1 — alpha ), называемой степенью доверия (или степенью уверенности, англ. ‘degree of confidence’), что он будет содержать оцениваемый параметр.

Этот интервал часто упоминается как (100 (1 — alpha)% ) доверительный интервал для параметра.

Конечные значения доверительного интервала называются нижним и верхним доверительными пределами (или доверительными границами или предельной погрешностью, англ. ‘lower/upper confidence limits’).

В этом чтении, мы имеем дело только с двусторонними доверительными интервалами — доверительные интервалами, для которых мы вычисляем и нижние и верхние пределы.

Доверительные интервалы часто дают либо вероятностную интерпретацию, либо практическую интерпретацию.

При вероятностной интерпретации, мы интерпретируем 95%-ный доверительный интервал для среднего значения совокупности следующим образом.

При повторяющейся выборке, 95% таких доверительных интервалов будут, в конечном счете, включать в себя среднее значение совокупности.

Например, предположим, что мы делаем выборку из совокупности 1000 раз, и на основании каждой выборки мы построим 95%-ный доверительный интервал, используя вычисленное выборочное среднее.

Из-за случайного характера выборок, эти доверительные интервалы отличаются друг от друга, но мы ожидаем, что 95% (или 950) этих интервалов включают неизвестное значение среднего по совокупности.

На практике мы обычно не делаем такие повторяющиеся выборки. Поэтому в практической интерпретации, мы утверждаем, что мы 95% уверены в том, что один 95%-ный доверительный интервал содержит среднее по совокупности.

Мы вправе сделать это заявление, потому что мы знаем, что 95% всех возможных доверительных интервалов, построенных аналогичным образом, будут содержать среднее по совокупности.

Доверительные интервалы, которые мы обсудим в этом чтении, имеют структуры, подобные описанной ниже базовой структуре.

Построение доверительных интервалов.

Доверительный интервал (100 (1 — alpha)% ) для параметра имеет следующую структуру.

Величину (Фактор надежности) (times) (Cтандартная ошибка) иногда называют точностью оценки (англ. ‘precision of estimator’). Большие значения этой величины подразумевают более низкую точность оценки параметра совокупности.

Самый базовый доверительный интервал для среднего значения по совокупности появляется тогда, когда мы делаем выборку из нормального распределения с известной дисперсией. Фактор надежности в данном случае на основан стандартном нормальном распределении, которое имеет среднее значение, равное 0 и дисперсию 1.

Стандартная нормальная случайная величина обычно обозначается как (Z). Обозначение (z_alpha ) обозначает такую точку стандартного нормального распределения, в которой (alpha) вероятности остается в правом хвосте.

Например, 0.05 или 5% возможных значений стандартной нормальной случайной величины больше, чем ( z_{0.05} = 1.65 ).

Предположим, что мы хотим построить 95%-ный доверительный интервал для среднего по совокупности, и для этой цели, мы сделали выборку размером 100 из нормально распределенной совокупности с известной дисперсией (sigma^2) = 400 (значит, (sigma) = 20).

Мы рассчитываем выборочное среднее как ( overline X = 25 ). Наша точечная оценка среднего по совокупности, таким образом, 25.

Если мы перемещаем 1.96 стандартных отклонений выше среднего значения нормального распределения, то 0.025 или 2.5% вероятности остается в правом хвосте. В силу симметрии нормального распределения, если мы перемещаем 1.96 стандартных отклонений ниже среднего, то 0.025 или 2.5% вероятности остается в левом хвосте.

В общей сложности, 0.05 или 5% вероятности лежит в двух хвостах и 0.95 или 95% вероятности лежит между ними.

---

Таким образом, ( z_{0.025} = 1.96) является фактором надежности для этого 95%-ного доверительного интервала. Обратите внимание на связь (100 (1 — alpha)% ) для доверительного интервала и (z_{alpha/2}) для фактора надежности.

Стандартная ошибка среднего значения выборки, заданная Формулой 1, равна:

( sigma_{overline X} = 20 Big / sqrt{100} = 2 )

Доверительный интервал, таким образом, имеет нижний предел:

( overline X — 1.96 sigma_{overline X} ) = 25 — 1.96(2) = 25 — 3.92 = 21.08.

Верхний предел доверительного интервала равен:

( overline X + 1.96sigma_{overline X} ) = 25 + 1.96(2) = 25 + 3.92 = 28.92

95%-ный доверительный интервал для среднего по совокупности охватывает значения от 21.08 до 28.92.

Доверительные интервалы для среднего по совокупности (нормально распределенная совокупность с известной дисперсией).

Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ), когда мы делаем выборку из нормального распределения с известной дисперсией ( sigma^2 ) задается формулой:

( Large dst overline X pm z_{alpha /2}{sigma over sqrt n}  ) (Формула 4)

Факторы надежности для наиболее часто используемых доверительных интервалов приведены ниже.

Факторы надежности для доверительных интервалов на основе стандартного нормального распределения.

Мы используем следующие факторы надежности при построении доверительных интервалов на основе стандартного нормального распределения:

Эти факторы надежности подчеркивают важный факт о всех доверительных интервалах. По мере того, как мы повышаем степень доверия, доверительный интервал становится все шире и дает нам менее точную информацию о величине, которую мы хотим оценить.

«Чем уверенней мы хотим быть, тем меньше мы должны быть уверены»

см. Freund и Williams (1977), стр. 266.

На практике, допущение о том, что выборочное распределение выборочного среднего, по меньшей мере, приблизительно нормальное, часто является обоснованным, либо потому, что исходное распределение приблизительно нормальное, либо потому что мы имеем большую выборку и поэтому к ней применима центральная предельная теорема.

Однако, на практике, мы редко знаем дисперсию совокупности. Когда дисперсия генеральной совокупности неизвестна, но выборочное среднее, по меньшей мере, приблизительно нормально распределено, у нас есть два приемлемых пути чтобы вычислить доверительные интервалы для среднего значения совокупности.

---

Вскоре мы обсудим более консервативный подход, который основан на t-распределении Стьюдента (t-распределение, для краткости).

Распределение статистики (t) называется t-распределением Стьюдента (англ. «Student’s t-distribution») из-за псевдонима «Студент» (Student), использованного британским математиком Уильямом Сили Госсеттом, который опубликовал свою работу в 1908 году.

В финансовой литературе, это наиболее часто используемый подход для статистической оценки и проверки статистических гипотез, касающихся среднего значения, когда дисперсия генеральной совокупности не известна, как для малого, так и для большого размер выборки.

Второй подход к доверительным интервалам для среднего по совокупности, основанного на стандартном нормальном распределении, — это z-альтернатива (англ. ‘z-alternative’). Он может быть использован только тогда, когда размер выборки является большим (в общем случае, размер выборки 30 или больше, можно считать большим).

В отличии от доверительного интервала, приведенного в Формуле 4, этот доверительный интервал использует стандартное отклонение выборки (s) при вычислении стандартной ошибки выборочного среднего (по Формуле 2).

Доверительные интервалы для среднего по совокупности — z-альтернатива (большая выборка, дисперсия совокупности неизвестна).

Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ) при выборке из любого распределения с неизвестной дисперсией, когда размер выборки большой, задается формулой:

( Large dst overline X pm z_{alpha /2}{s over sqrt n} ) (Формула 5)

Поскольку этот тип доверительного интервала применяется довольно часто, мы проиллюстрируем его вычисление в Примере 4.

Пример (4) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием z-статистики.

Предположим, что инвестиционный аналитик делает случайную выборку акций взаимных фондов США и рассчитывает средний коэффициент Шарпа.

[см. также: CFA — Коэффициент Шарпа]

Размер выборки равен 100, а средний коэффициент Шарпа составляет 0.45. Выборка имеет стандартное отклонение 0.30.

Рассчитайте и интерпретируйте 90-процентный доверительный интервал для среднего по совокупности всех акций взаимных фондов США с использованием фактора надежности на основе стандартного нормального распределения.

---

Фактор надежности для 90-процентного доверительного интервала, как указано ранее, составляет ( z_{0.05} = 1.65 ).

Доверительный интервал будет равен:

( begin{aligned} & overline X pm z_{0.05}{s over sqrt n } \ &= 0.45 pm 1.65{0.30 over sqrt {100}} \ &= 0.45 pm 1.65(0.03) = 0.45 pm 0.0495   end{aligned} )

Доверительный интервал охватывает значения 0.4005 до 0.4995, или от 0.40 до 0.50, с округлением до двух знаков после запятой. Аналитик может сказать с 90-процентной уверенностью, что интервал включает среднее по совокупности.

В этом примере аналитик не делает никаких конкретных предположений о распределении вероятностей, характеризующем совокупность. Скорее всего, аналитик опирается на центральную предельную теорему для получения приближенного нормального распределения для выборочного среднего.

Как показывает Пример 4, даже если мы не уверены в характере распределения совокупности, мы все еще можем построить доверительные интервалы для среднего по совокупности, если размер выборки достаточно большой, поскольку можем применить центральную предельную теорему.

Концепция степеней свободы.

Обратимся теперь к консервативной альтернативе и используем t-распределение Стьюдента, чтобы построить доверительные интервалы для среднего по совокупности, когда дисперсия генеральной совокупности не известна.

Для доверительных интервалов на основе выборок из нормально распределенных совокупностей с неизвестной дисперсией, теоретически правильный фактор надежности основан на t-распределении. Использование фактора надежности, основанного на t-распределении, имеет важное значение для выборок небольшого размера.

Применение фактора надежности (t) уместно, когда дисперсия генеральной совокупности неизвестна, даже если у нас есть большая выборка и мы можем использовать центральную предельную теорему для обоснования использования фактора надежности (z). В этом случае большой выборки, t-распределение обеспечивает более консервативные (широкие) доверительные интервалы.

t-распределение является симметричным распределением вероятностей и определяется одним параметром, известным как степени свободы (DF, от англ. ‘degrees of freedom’). Каждое значение для числа степеней свободы определяет одно распределение в этом семействе распределений.

Далее мы сравним t-распределения со стандартным нормальным распределением, но сначала мы должны понять концепцию степеней свободы. Мы можем сделать это путем изучения расчета выборочной дисперсии.

Формула 3 дает несмещенную оценку выборочной дисперсии, которую мы используем. Выражение в знаменателе, ( n — 1 ), означающее размер выборки минус 1, это число степеней свободы при расчете дисперсии совокупности с использованием Формулы 3.

Мы также используем ( n — 1 ) как число степеней свободы для определения факторов надежности на основе распределения Стьюдента. Термин «степени свободы» используются, так как мы предполагаем, что в случайной выборке наблюдения отобраны независимо друг от друга. Числитель выборочной дисперсии, однако, использует выборочное среднее.

---

Каким образом использование выборочного среднего влияет на количество наблюдений, отобранных независимо, для формулы выборочной дисперсии?

При выборке размера 10 и среднем значении в 10%, к примеру, мы можем свободно отобрать только 9 наблюдений. Независимо от отобранных 9 наблюдений, мы всегда можем найти значение для 10-го наблюдения, которое дает среднее значение, равное 10%. С точки зрения формулы выборочной дисперсии, здесь есть 9 степеней свободы.

Учитывая, что мы должны сначала вычислить выборочное среднее от общего числа (n) независимых наблюдений, только (n — 1) наблюдений могут быть отобраны независимо друг от друга для расчета выборочной дисперсии.

Концепция степеней свободы часто применяется в финансовой статистике, и вы встретите ее в последующих чтениях.

t-распределение Стьюдента.

Предположим, что мы делаем выборку из нормального распределения.

Коэффициент (z = (overline X — mu) Big / (sigma big / sqrt n) ) нормально распределен со средним значением 0 и стандартным отклонением 1, однако, коэффициент (t = (overline X — mu) Big / (s big / sqrt n) ) следует t-распределению со средним 0 и (n — 1) степеней свободы.

Коэффициент (t) не является нормальным, поскольку представляет собой отношение двух случайных величин, выборочного среднего и стандартного отклонения выборки.

Определение стандартной нормальной случайной величины включает в себя только одну случайную величину, выборочное среднее. По мере увеличения степеней свободы, однако, t-распределение приближается к стандартному нормальному распределению.

На Рисунке 1 показано стандартное нормальное распределение и два t-распределения, одно с DF = 2 и одно с DF = 8.

Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.

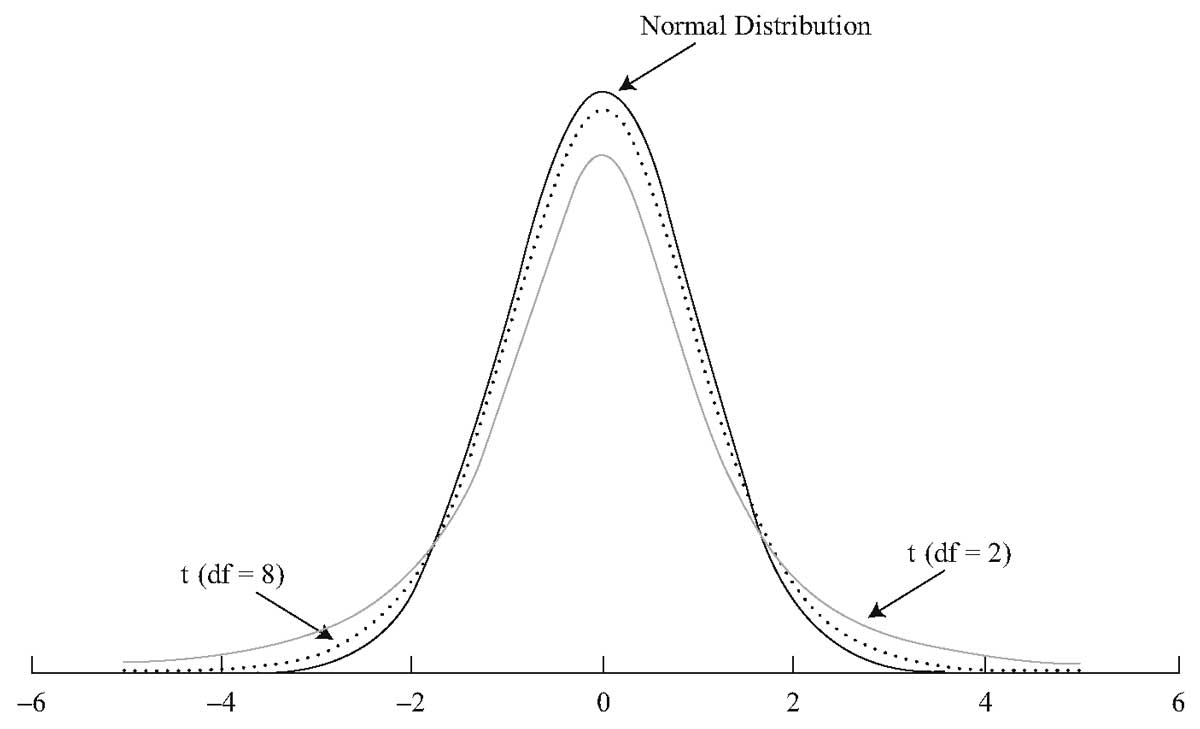
Из трех распределений, показанных на Рисунке 1, стандартное нормальное распределение имеет хвосты, которые стремятся к нулю быстрее, чем хвосты двух t-распределений. t-распределение симметрично распределено вокруг среднего нулевого значения, так же как и нормальное распределение.

По мере увеличения степеней свободы, t-распределение приближается к стандартному нормальному распределению. t-распределение с DF = 8 ближе к стандартному нормальному, чем t-распределение с DF = 2.

Помимо области плюс и минус четырех стандартных отклонений от среднего значения, остальная область под стандартным нормальным распределением, как представляется, близка к 0. Однако, оба t-распределения содержать некоторую площадь под каждой кривой за пределом четырех стандартных отклонений.

t-распределения имеют более толстые хвосты, но хвосты t-распределения Стьюдента с DF = 8 сильнее напоминают хвосты нормального распределения. По мере увеличения степеней свободы, хвосты распределения Стьюдента становятся менее толстыми.

Для часто используемых значений распределения Стьюдента составлены таблицы. Например, для каждой степени свободы (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) значения будут такими, что соответственно, 0.10, 0.05, 0.025, 0.01 и 0.005 вероятности останется в правом хвосте для заданного числа степеней свободы.

Значения (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) также называют односторонними критическими значениями t на значимых уровнях 0.10, 0.05, 0.025, 0.01 и 0.005, для указанного числа степеней свободы.

Например,

Приведем форму доверительных интервалов для среднего по совокупности, используя распределение Стьюдента.

Доверительные интервалы для среднего по совокупности (дисперсия совокупности неизвестна) — t-распределение.

Если мы делаем выборку из генеральной совокупности с неизвестной дисперсией и соблюдается одно из перечисленных ниже условий:

• выборка является большой, или
• выборка небольшая, но совокупность имеет нормальное распределение, или приблизительно нормально распределена,

то доверительный интервал (100 (1 — alpha)% ) для среднего совокупности ( mu ) задается формулой:

Пример 5 использует данные Примера 4, но применяет t-статистику, а не z-статистику, чтобы рассчитать доверительный интервал для среднего значения совокупности коэффициентов Шарпа.

Пример (5) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием t-статистики.

Как и в Примере 4, инвестиционный аналитик стремится вычислить 90-процентный доверительный интервал для среднего по совокупности коэффициентов Шарпа, основанных на случайной выборке из 100 взаимных фондов США.

Выборочное среднее коэффициентов Шарпа составляет 0.45, а выборочное стандартное отклонение — 0.30.

Теперь, признав, что дисперсия генеральной совокупности распределения коэффициентов Шарпа неизвестна, аналитик решает вычислить доверительный интервал, используя теоретически правильную t-статистику.

Поскольку размер выборки равен 100, DF = 99. Используя таблицу степеней свободы, мы находим, что (t_{0.05}) = 1.66.

Этот фактор надежности немного больше, чем фактор надежности (z_{0.05}) = 1.65, который был использован в Примере 4.

Доверительный интервал будет:

( begin{aligned} & overline X pm t_{0.05}{s over sqrt n } \  &= 0.45 pm 1.66{0.30 over sqrt {100}} \ &= 0.45 pm 1.66(0.03) = 0.45 pm 0.0498   end{aligned} )

Доверительный интервал охватывает значения 0.4002 до 0.4998, или 0.40 до 0.50, с двумя знаками после запятой. При округлении до двух знаков после запятой, доверительный интервал не изменился по сравнению с Примером 4.

В Таблице 3 приведены различные факторы надежности, которые мы использовали.

Таблица 3. Основы для расчета факторов надежности.

Выборка из:	Статистика для выборки малого размера	Статистика для выборки большого размера
Нормальное распределение с известной дисперсией	(z)	(z)
Нормальное распределение с неизвестной дисперсией	(t)	(t)*
Ненормальное распределение с известной дисперсией	недоступно	(z)
Ненормальное распределение с неизвестной дисперсией	недоступно	(t)*

* Использование (z) также приемлемо.