Загрузить PDF
Загрузить PDF
Доверительный интервал является показателем точности измерений. Это также показатель того, насколько стабильна полученная величина, то есть насколько близкую величину (к первоначальной величине) вы получите при повторении измерений (эксперимента). Выполните следующие действия, чтобы вычислить доверительный интервал для нужных величин.
Шаги
-
1
Запишите задачу. Например: средний вес студента мужского пола в университете АВС составляет 90 кг. Вы будете тестировать точность предсказания веса студентов мужского пола в университете АВС в пределах данного доверительного интервала.
-
2
Составьте подходящую выборку. Вы будете использовать ее для сбора данных для тестирования гипотезы. Допустим, вы уже случайно выбрали 1000 студентов мужского пола.
-
3
Рассчитайте среднее значение и стандартное отклонение этой выборки. Выберите статистические величины (например, среднее значение и стандартное отклонение), которые вы хотите использовать для анализа вашей выборки. Вот как вычислить среднее значение и стандартное отклонение:
- Для расчета среднего значения выборки сложите значения весов 1000 выбранных мужчин и разделите результат на 1000 (число мужчин). Допустим, получили средний вес, равный 93 кг.
- Для расчета стандартного отклонения выборки необходимо найти среднее значение. Затем нужно вычислить дисперсию данных или среднее значение квадратов разностей от среднего. Найдя это число, просто возьмите квадратный корень из него. Допустим, в нашем примере стандартное отклонение равно 15 кг (заметим, что иногда эта информация может быть дана вместе с условием статистической задачи).
-
4
Выберите нужный доверительный уровень. Наиболее часто используемые доверительные уровни: 90 %, 95 % и 99 %. Он также может быть дан вместе с условием задачи. Допустим, вы выбрали 95 %.
-
5
Рассчитайте предел погрешности. Вы можете найти предел погрешности с помощью следующей формулы: Za/2 * σ/√(n). Za/2 = коэффициент доверия (где а = доверительный уровень), σ = стандартное отклонение, а n = размер выборки. Это формула показывает, что вы должны умножить критическое значение на стандартную ошибку. Вот как вы можете решить эту формулу, разбив ее на части:
- Вычислите критическое значение или Za/2. Доверительный уровень равен 95 %. Преобразуйте проценты в десятичную дробь: 0,95 и разделите ее на 2, чтобы получить 0,475. Затем посмотрите в таблицу Z-оценок, чтобы найти соответствующее значение для 0,475. Вы найдете значение 1,96 (на пересечении строки 1,9 и столбца 0,06).
- Возьмите стандартную ошибку (стандартное отклонение): 15 и разделите ее на квадратный корень из размера выборки: 1000. Вы получите: 15/31,6 или 0,47 кг.
- Умножьте 1,96 на 0,47 (критическое значение на стандартную ошибку), чтобы получить 0,92 — предел погрешности.
-
6
Запишите доверительный интервал. Чтобы сформулировать доверительный интервал, просто запишите среднее значение (93) ± погрешность. Ответ: 93 ± 0,92. Вы можете найти верхнюю и нижнюю границы доверительного интервала, прибавляя и вычитая погрешность к/от средней величины. Итак, нижняя граница составляет 93 — 0,92 или 92,08, а верхняя граница составляет 93 + 0,92 или 93,92.
- Вы можете использовать следующую формулу для вычисления доверительного интервала: x̅ ± Za/2 * σ/√(n), где x̅ — среднее значение.
Реклама
Советы
- И t-оценки и z-оценки можно рассчитать вручную, а также с помощью графического калькулятора или статистических таблиц, которые часто встречаются в учебниках по статистике. Также доступны онлайн-инструменты.
- Критическое значение, используемое для расчета погрешности, является постоянным и выражается либо через t-оценку, либо через z-оценку. T-оценка обычно более предпочтительна в условиях, когда стандартное отклонение выборки неизвестно или когда используется маленькая выборка.
- Ваша выборка должна быть достаточной (по размеру) для того, чтобы вычислить правильный доверительный интервал.
- Доверительный интервал не указывает на вероятность получения того или иного результата. Например, если вы на 95 % уверены, что среднее значение вашей выборки лежит между 75 и 100, то доверительный интервал в 95 % не означает, что среднее значение попадает в ваш диапазон.
- Есть много методов, таких как простая случайная выборка, систематический отбор и стратифицированная выборка, с помощью которых вы можете собрать репрезентативную выборку для тестирования.
Реклама
Что вам понадобится
- Выборка
- Компьютер
- Доступ в интернет
- Учебник статистики
- Графический калькулятор
Об этой статье
Эту страницу просматривали 264 906 раз.
Была ли эта статья полезной?
Часто в статистике нас интересует измерение параметров населения — чисел, описывающих некоторые характеристики всего населения.
Двумя наиболее распространенными параметрами населения являются:
1. Среднее значение населения: среднее значение некоторой переменной в популяции (например, средний рост мужчин в США).
2. Доля населения: доля некоторой переменной в населении (например, доля жителей округа, которые поддерживают определенный закон).
Хотя мы заинтересованы в измерении этих параметров, обычно слишком дорого и долго собирать данные о каждом человеке в популяции, чтобы вычислить параметр популяции.
Вместо этого мы обычно берем случайную выборку из общей совокупности и используем данные из выборки для оценки параметра совокупности.
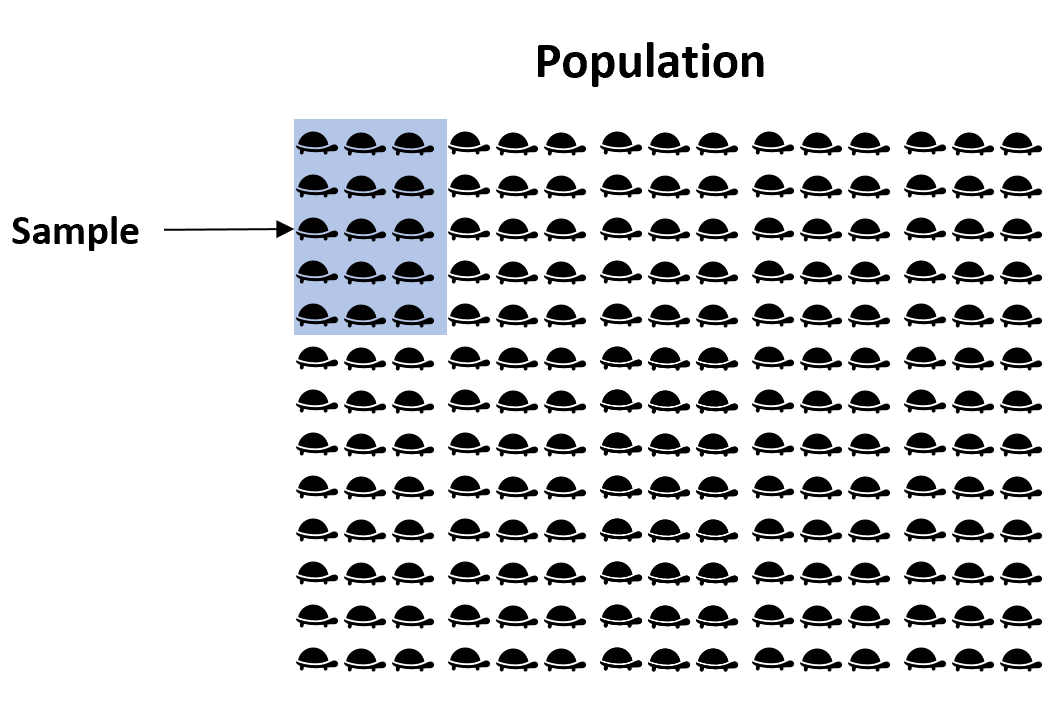
Например, предположим, что мы хотим оценить средний вес определенного вида черепах во Флориде. Поскольку во Флориде тысячи черепах, было бы очень много времени и денег, чтобы обойти и взвесить каждую отдельную черепаху.
Вместо этого мы могли бы взять простую случайную выборку из 50 черепах и использовать средний вес черепах в этой выборке для оценки истинного среднего значения популяции:
Проблема в том, что средний вес черепах в выборке не обязательно точно соответствует среднему весу черепах во всей популяции. Например, мы можем просто случайно выбрать образец, полный черепах с низким весом, или, возможно, образец, полный тяжелых черепах.
Чтобы зафиксировать эту неопределенность, мы можем создать доверительный интервал. Доверительный интервал — это диапазон значений, который может содержать параметр генеральной совокупности с определенным уровнем достоверности. Он рассчитывается по следующей общей формуле:
Доверительный интервал = (точечная оценка) +/- (критическое значение) * (стандартная ошибка)
Эта формула создает интервал с нижней границей и верхней границей, который, вероятно, содержит параметр совокупности с определенным уровнем достоверности.
Доверительный интервал = [нижняя граница, верхняя граница]
Например, формула для расчета доверительного интервала для среднего значения генеральной совокупности выглядит следующим образом:
Доверительный интервал = x +/- z*(s/ √n )
куда:
- x : выборочное среднее
- z: выбранное значение z
- s: стандартное отклонение выборки
- n: размер выборки
Z-значение, которое вы будете использовать, зависит от выбранного вами уровня достоверности. В следующей таблице показано значение z, которое соответствует популярным вариантам выбора уровня достоверности:
| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |
Например, предположим, что мы собираем случайную выборку черепах со следующей информацией:
- Размер выборки n = 25
- Средний вес выборки x = 300
- Стандартное отклонение выборки s = 18,5
Вот как найти вычислить 90% доверительный интервал для истинного среднего веса населения:
90% доверительный интервал: 300 +/- 1,645*(18,5/√25) = [293,91, 306,09]
Мы интерпретируем этот доверительный интервал следующим образом:
Вероятность того, что доверительный интервал [293,91, 306,09] содержит истинный средний вес популяции черепах, составляет 90%.
Другой способ сказать то же самое состоит в том, что существует только 10-процентная вероятность того, что истинное среднее значение генеральной совокупности лежит за пределами 90-процентного доверительного интервала. То есть существует только 10%-ная вероятность того, что истинный средний вес популяции черепах больше 306,09 фунтов или меньше 293,91 фунтов.
Ничего не стоит, что есть два числа, которые могут повлиять на размер доверительного интервала:
1. Размер выборки: чем больше размер выборки, тем уже доверительный интервал.
2. Уровень достоверности: чем выше уровень достоверности, тем шире доверительный интервал.
Типы доверительных интервалов
Существует много типов доверительных интервалов. Вот наиболее часто используемые:
Доверительный интервал для среднего
Доверительный интервал для среднего значения — это диапазон значений, который может содержать среднее значение генеральной совокупности с определенным уровнем достоверности. Формула для расчета этого интервала:
Доверительный интервал = x +/- z*(s/ √n )
куда:
- x : выборочное среднее
- z: выбранное значение z
- s: стандартное отклонение выборки
- n: размер выборки
Ресурсы: Как рассчитать доверительный интервал для среднего
Доверительный интервал для среднего калькулятора
Доверительный интервал для разницы между средними значениями
Доверительный интервал (ДИ) для разницы между средними значениями представляет собой диапазон значений, который, вероятно, содержит истинное различие между двумя средними значениями генеральной совокупности с определенным уровнем достоверности. Формула для расчета этого интервала:
Доверительный интервал = ( x 1 – x 2 ) +/- t * √ ((s p 2 /n 1 ) + (s p 2 /n 2 ))
куда:
- x 1 , x 2 : среднее значение для образца 1, среднее значение для образца 2
- t: t-критическое значение, основанное на доверительном уровне и (n 1 +n 2 -2) степенях свободы
- s p 2 : объединенная дисперсия
- n 1 , n 2 : размер выборки 1, размер выборки 2
куда:
- Объединенная дисперсия рассчитывается как: s p 2 = ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
- Критическое значение t можно найти с помощью калькулятора обратного t-распределения .
Ресурсы: Как рассчитать доверительный интервал для разницы между средними
Доверительный интервал для калькулятора разницы между средними значениями
Доверительный интервал для пропорции
Доверительный интервал для доли — это диапазон значений, который может содержать долю населения с определенным уровнем достоверности. Формула для расчета этого интервала:
Доверительный интервал = p +/- z * (√ p (1-p) / n )
куда:
- p: доля выборки
- z: выбранное значение z
- n: размер выборки
Ресурсы: Как рассчитать доверительный интервал для пропорции
Доверительный интервал для калькулятора пропорций
Доверительный интервал для разницы в пропорциях
Доверительный интервал для разницы в пропорциях — это диапазон значений, который может содержать истинную разницу между двумя пропорциями населения с определенным уровнем достоверности. Формула для расчета этого интервала:
Доверительный интервал = (p 1 –p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )
куда:
- p 1 , p 2 : доля образца 1, доля образца 2
- z: z-критическое значение, основанное на доверительном уровне
- n 1 , n 2 : размер выборки 1, размер выборки 2
Ресурсы: Как рассчитать доверительный интервал для разницы пропорций
Доверительный интервал для калькулятора разницы пропорций
Когда нам нужно получить одно число в качестве оценки параметра совокупности, мы используем точечную оценку. Тем не менее, из-за ошибки выборки, точечная оценка не будет в точности равняться параметру совокупности при любом размере данной выборки.
Часто, вместо точечной оценки, более полезным подходом будет найти диапазон значений, в рамках которого, как мы ожидаем, может находится значение искомого параметра с заданным уровнем вероятности.
Этот подход называется интервальной оценкой параметра (англ. ‘interval estimate of parameter’), а доверительный интервал выполняет роль этого диапазона значений.
Определение доверительного интервала.
Доверительный интервал (англ. ‘confidence interval’) представляет собой диапазон, для которого можно утверждать, с заданной вероятностью (1 — alpha ), называемой степенью доверия (или степенью уверенности, англ. ‘degree of confidence’), что он будет содержать оцениваемый параметр.
Этот интервал часто упоминается как (100 (1 — alpha)% ) доверительный интервал для параметра.
Конечные значения доверительного интервала называются нижним и верхним доверительными пределами (или доверительными границами или предельной погрешностью, англ. ‘lower/upper confidence limits’).
В этом чтении, мы имеем дело только с двусторонними доверительными интервалами — доверительные интервалами, для которых мы вычисляем и нижние и верхние пределы.
Кроме того, можно определить два типа односторонних доверительных интервалов для параметра совокупности.
Нижний односторонний доверительный интервал устанавливает только нижний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности равен или превышает нижний предел.
Верхний односторонний доверительный интервал устанавливает только верхний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности меньше или равен верхнему пределу.
Инвестиционные аналитики редко используют односторонние доверительные интервалы.
Доверительные интервалы часто дают либо вероятностную интерпретацию, либо практическую интерпретацию.
При вероятностной интерпретации, мы интерпретируем 95%-ный доверительный интервал для среднего значения совокупности следующим образом.
При повторяющейся выборке, 95% таких доверительных интервалов будут, в конечном счете, включать в себя среднее значение совокупности.
Например, предположим, что мы делаем выборку из совокупности 1000 раз, и на основании каждой выборки мы построим 95%-ный доверительный интервал, используя вычисленное выборочное среднее.
Из-за случайного характера выборок, эти доверительные интервалы отличаются друг от друга, но мы ожидаем, что 95% (или 950) этих интервалов включают неизвестное значение среднего по совокупности.
На практике мы обычно не делаем такие повторяющиеся выборки. Поэтому в практической интерпретации, мы утверждаем, что мы 95% уверены в том, что один 95%-ный доверительный интервал содержит среднее по совокупности.
Мы вправе сделать это заявление, потому что мы знаем, что 95% всех возможных доверительных интервалов, построенных аналогичным образом, будут содержать среднее по совокупности.
Доверительные интервалы, которые мы обсудим в этом чтении, имеют структуры, подобные описанной ниже базовой структуре.
Построение доверительных интервалов.
Доверительный интервал (100 (1 — alpha)% ) для параметра имеет следующую структуру.
Точечная оценка (pm) Фактор надежности (times) Стандартная ошибка
где
- Точечная оценка = точечная оценка параметра (значение выборочной статистики).
- Фактор надежности (англ. ‘reliability factor’) = коэффициент, основанный на предполагаемом распределении точечной оценки и степени доверия ((1 — alpha)) для доверительного интервала.
- Стандартная ошибка = стандартная ошибка выборочной статистики, значение которой получено с помощью точечной оценки.
Величину (Фактор надежности) (times) (Cтандартная ошибка) иногда называют точностью оценки (англ. ‘precision of estimator’). Большие значения этой величины подразумевают более низкую точность оценки параметра совокупности.
Самый базовый доверительный интервал для среднего значения по совокупности появляется тогда, когда мы делаем выборку из нормального распределения с известной дисперсией. Фактор надежности в данном случае на основан стандартном нормальном распределении, которое имеет среднее значение, равное 0 и дисперсию 1.
Стандартная нормальная случайная величина обычно обозначается как (Z). Обозначение (z_alpha ) обозначает такую точку стандартного нормального распределения, в которой (alpha) вероятности остается в правом хвосте.
Например, 0.05 или 5% возможных значений стандартной нормальной случайной величины больше, чем ( z_{0.05} = 1.65 ).
Предположим, что мы хотим построить 95%-ный доверительный интервал для среднего по совокупности, и для этой цели, мы сделали выборку размером 100 из нормально распределенной совокупности с известной дисперсией (sigma^2) = 400 (значит, (sigma) = 20).
Мы рассчитываем выборочное среднее как ( overline X = 25 ). Наша точечная оценка среднего по совокупности, таким образом, 25.
Если мы перемещаем 1.96 стандартных отклонений выше среднего значения нормального распределения, то 0.025 или 2.5% вероятности остается в правом хвосте. В силу симметрии нормального распределения, если мы перемещаем 1.96 стандартных отклонений ниже среднего, то 0.025 или 2.5% вероятности остается в левом хвосте.
В общей сложности, 0.05 или 5% вероятности лежит в двух хвостах и 0.95 или 95% вероятности лежит между ними.
Таким образом, ( z_{0.025} = 1.96) является фактором надежности для этого 95%-ного доверительного интервала. Обратите внимание на связь (100 (1 — alpha)% ) для доверительного интервала и (z_{alpha/2}) для фактора надежности.
Стандартная ошибка среднего значения выборки, заданная Формулой 1, равна:
( sigma_{overline X} = 20 Big / sqrt{100} = 2 )
Доверительный интервал, таким образом, имеет нижний предел:
( overline X — 1.96 sigma_{overline X} ) = 25 — 1.96(2) = 25 — 3.92 = 21.08.
Верхний предел доверительного интервала равен:
( overline X + 1.96sigma_{overline X} ) = 25 + 1.96(2) = 25 + 3.92 = 28.92
95%-ный доверительный интервал для среднего по совокупности охватывает значения от 21.08 до 28.92.
Доверительные интервалы для среднего по совокупности (нормально распределенная совокупность с известной дисперсией).
Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ), когда мы делаем выборку из нормального распределения с известной дисперсией ( sigma^2 ) задается формулой:
( Large dst overline X pm z_{alpha /2}{sigma over sqrt n} ) (Формула 4)
Факторы надежности для наиболее часто используемых доверительных интервалов приведены ниже.
Факторы надежности для доверительных интервалов на основе стандартного нормального распределения.
Мы используем следующие факторы надежности при построении доверительных интервалов на основе стандартного нормального распределения:
- 90%-ные доверительные интервалы: используется (z_{0.05}) = 1.65
- 95%-ные доверительные интервалы: используется (z_{0.025}) = 1.96
- 99%-ные доверительные интервалы: используется (z_{0.005}) = 2.58
На практике, большинство финансовых аналитиков используют значения для (z_{0.05}) и (z_{0.005}), округленные до двух знаков после запятой.
Для справки, более точными значениями для (z_{0.05}) и (z_{0.005}) являются 1.645 и 2.575, соответственно.
Для быстрого расчета 95%-ного доверительного интервала (z_{0.025}) иногда округляют 1.96 до 2.
Эти факторы надежности подчеркивают важный факт о всех доверительных интервалах. По мере того, как мы повышаем степень доверия, доверительный интервал становится все шире и дает нам менее точную информацию о величине, которую мы хотим оценить.
«Чем уверенней мы хотим быть, тем меньше мы должны быть уверены»
см. Freund и Williams (1977), стр. 266.
На практике, допущение о том, что выборочное распределение выборочного среднего, по меньшей мере, приблизительно нормальное, часто является обоснованным, либо потому, что исходное распределение приблизительно нормальное, либо потому что мы имеем большую выборку и поэтому к ней применима центральная предельная теорема.
Однако, на практике, мы редко знаем дисперсию совокупности. Когда дисперсия генеральной совокупности неизвестна, но выборочное среднее, по меньшей мере, приблизительно нормально распределено, у нас есть два приемлемых пути чтобы вычислить доверительные интервалы для среднего значения совокупности.
Вскоре мы обсудим более консервативный подход, который основан на t-распределении Стьюдента (t-распределение, для краткости).
Распределение статистики (t) называется t-распределением Стьюдента (англ. «Student’s t-distribution») из-за псевдонима «Студент» (Student), использованного британским математиком Уильямом Сили Госсеттом, который опубликовал свою работу в 1908 году.
В финансовой литературе, это наиболее часто используемый подход для статистической оценки и проверки статистических гипотез, касающихся среднего значения, когда дисперсия генеральной совокупности не известна, как для малого, так и для большого размер выборки.
Второй подход к доверительным интервалам для среднего по совокупности, основанного на стандартном нормальном распределении, — это z-альтернатива (англ. ‘z-alternative’). Он может быть использован только тогда, когда размер выборки является большим (в общем случае, размер выборки 30 или больше, можно считать большим).
В отличии от доверительного интервала, приведенного в Формуле 4, этот доверительный интервал использует стандартное отклонение выборки (s) при вычислении стандартной ошибки выборочного среднего (по Формуле 2).
Доверительные интервалы для среднего по совокупности — z-альтернатива (большая выборка, дисперсия совокупности неизвестна).
Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ) при выборке из любого распределения с неизвестной дисперсией, когда размер выборки большой, задается формулой:
( Large dst overline X pm z_{alpha /2}{s over sqrt n} ) (Формула 5)
Поскольку этот тип доверительного интервала применяется довольно часто, мы проиллюстрируем его вычисление в Примере 4.
Пример (4) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием z-статистики.
Предположим, что инвестиционный аналитик делает случайную выборку акций взаимных фондов США и рассчитывает средний коэффициент Шарпа.
[см. также: CFA — Коэффициент Шарпа]
Размер выборки равен 100, а средний коэффициент Шарпа составляет 0.45. Выборка имеет стандартное отклонение 0.30.
Рассчитайте и интерпретируйте 90-процентный доверительный интервал для среднего по совокупности всех акций взаимных фондов США с использованием фактора надежности на основе стандартного нормального распределения.
Фактор надежности для 90-процентного доверительного интервала, как указано ранее, составляет ( z_{0.05} = 1.65 ).
Доверительный интервал будет равен:
( begin{aligned} & overline X pm z_{0.05}{s over sqrt n } \ &= 0.45 pm 1.65{0.30 over sqrt {100}} \ &= 0.45 pm 1.65(0.03) = 0.45 pm 0.0495 end{aligned} )
Доверительный интервал охватывает значения 0.4005 до 0.4995, или от 0.40 до 0.50, с округлением до двух знаков после запятой. Аналитик может сказать с 90-процентной уверенностью, что интервал включает среднее по совокупности.
В этом примере аналитик не делает никаких конкретных предположений о распределении вероятностей, характеризующем совокупность. Скорее всего, аналитик опирается на центральную предельную теорему для получения приближенного нормального распределения для выборочного среднего.
Как показывает Пример 4, даже если мы не уверены в характере распределения совокупности, мы все еще можем построить доверительные интервалы для среднего по совокупности, если размер выборки достаточно большой, поскольку можем применить центральную предельную теорему.
Концепция степеней свободы.
Обратимся теперь к консервативной альтернативе и используем t-распределение Стьюдента, чтобы построить доверительные интервалы для среднего по совокупности, когда дисперсия генеральной совокупности не известна.
Для доверительных интервалов на основе выборок из нормально распределенных совокупностей с неизвестной дисперсией, теоретически правильный фактор надежности основан на t-распределении. Использование фактора надежности, основанного на t-распределении, имеет важное значение для выборок небольшого размера.
Применение фактора надежности (t) уместно, когда дисперсия генеральной совокупности неизвестна, даже если у нас есть большая выборка и мы можем использовать центральную предельную теорему для обоснования использования фактора надежности (z). В этом случае большой выборки, t-распределение обеспечивает более консервативные (широкие) доверительные интервалы.
t-распределение является симметричным распределением вероятностей и определяется одним параметром, известным как степени свободы (DF, от англ. ‘degrees of freedom’). Каждое значение для числа степеней свободы определяет одно распределение в этом семействе распределений.
Далее мы сравним t-распределения со стандартным нормальным распределением, но сначала мы должны понять концепцию степеней свободы. Мы можем сделать это путем изучения расчета выборочной дисперсии.
Формула 3 дает несмещенную оценку выборочной дисперсии, которую мы используем. Выражение в знаменателе, ( n — 1 ), означающее размер выборки минус 1, это число степеней свободы при расчете дисперсии совокупности с использованием Формулы 3.
Мы также используем ( n — 1 ) как число степеней свободы для определения факторов надежности на основе распределения Стьюдента. Термин «степени свободы» используются, так как мы предполагаем, что в случайной выборке наблюдения отобраны независимо друг от друга. Числитель выборочной дисперсии, однако, использует выборочное среднее.
Каким образом использование выборочного среднего влияет на количество наблюдений, отобранных независимо, для формулы выборочной дисперсии?
При выборке размера 10 и среднем значении в 10%, к примеру, мы можем свободно отобрать только 9 наблюдений. Независимо от отобранных 9 наблюдений, мы всегда можем найти значение для 10-го наблюдения, которое дает среднее значение, равное 10%. С точки зрения формулы выборочной дисперсии, здесь есть 9 степеней свободы.
Учитывая, что мы должны сначала вычислить выборочное среднее от общего числа (n) независимых наблюдений, только (n — 1) наблюдений могут быть отобраны независимо друг от друга для расчета выборочной дисперсии.
Концепция степеней свободы часто применяется в финансовой статистике, и вы встретите ее в последующих чтениях.
t-распределение Стьюдента.
Предположим, что мы делаем выборку из нормального распределения.
Коэффициент (z = (overline X — mu) Big / (sigma big / sqrt n) ) нормально распределен со средним значением 0 и стандартным отклонением 1, однако, коэффициент (t = (overline X — mu) Big / (s big / sqrt n) ) следует t-распределению со средним 0 и (n — 1) степеней свободы.
Коэффициент (t) не является нормальным, поскольку представляет собой отношение двух случайных величин, выборочного среднего и стандартного отклонения выборки.
Определение стандартной нормальной случайной величины включает в себя только одну случайную величину, выборочное среднее. По мере увеличения степеней свободы, однако, t-распределение приближается к стандартному нормальному распределению.
На Рисунке 1 показано стандартное нормальное распределение и два t-распределения, одно с DF = 2 и одно с DF = 8.
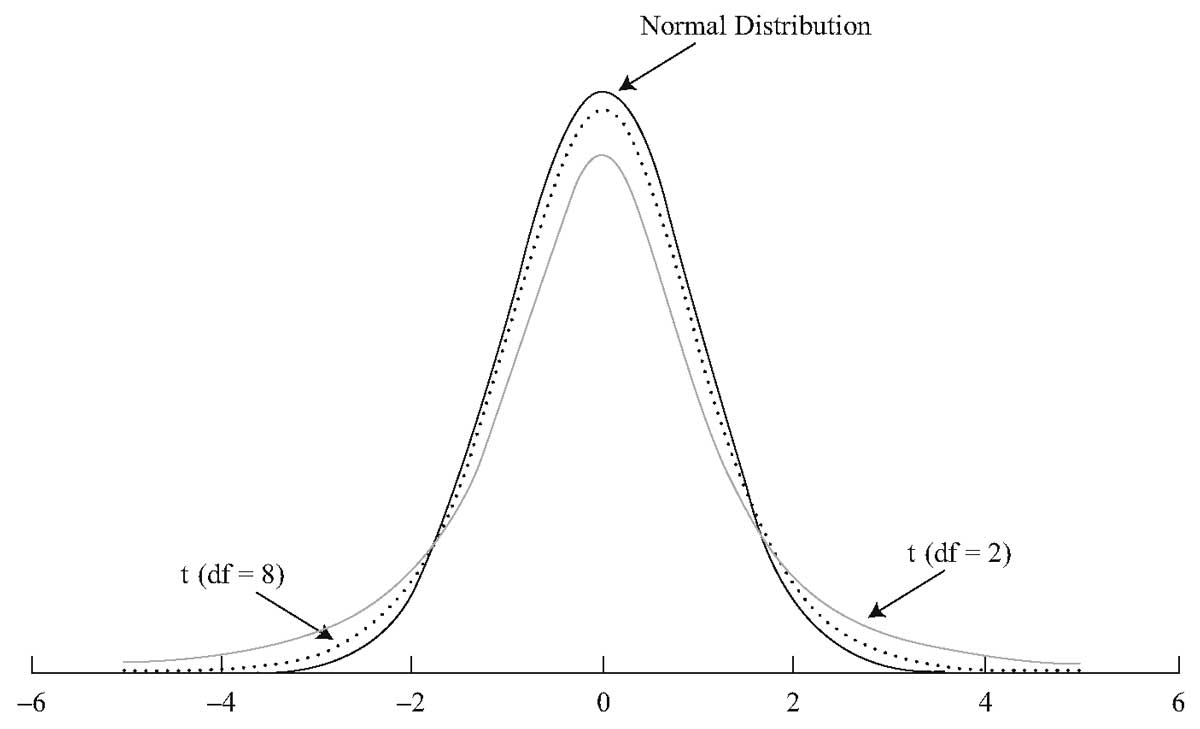
Из трех распределений, показанных на Рисунке 1, стандартное нормальное распределение имеет хвосты, которые стремятся к нулю быстрее, чем хвосты двух t-распределений. t-распределение симметрично распределено вокруг среднего нулевого значения, так же как и нормальное распределение.
По мере увеличения степеней свободы, t-распределение приближается к стандартному нормальному распределению. t-распределение с DF = 8 ближе к стандартному нормальному, чем t-распределение с DF = 2.
Помимо области плюс и минус четырех стандартных отклонений от среднего значения, остальная область под стандартным нормальным распределением, как представляется, близка к 0. Однако, оба t-распределения содержать некоторую площадь под каждой кривой за пределом четырех стандартных отклонений.
t-распределения имеют более толстые хвосты, но хвосты t-распределения Стьюдента с DF = 8 сильнее напоминают хвосты нормального распределения. По мере увеличения степеней свободы, хвосты распределения Стьюдента становятся менее толстыми.
Для часто используемых значений распределения Стьюдента составлены таблицы. Например, для каждой степени свободы (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) значения будут такими, что соответственно, 0.10, 0.05, 0.025, 0.01 и 0.005 вероятности останется в правом хвосте для заданного числа степеней свободы.
Значения (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) также называют односторонними критическими значениями t на значимых уровнях 0.10, 0.05, 0.025, 0.01 и 0.005, для указанного числа степеней свободы.
Например,
для DF = 30,
(t_{0.10}) = 1.310,
(t_{0.05}) = 1.697,
(t_{0.025}) = 2.042,
(t_{0.01}) = 2.457,
(t_{0.005}) = 2.750.
Приведем форму доверительных интервалов для среднего по совокупности, используя распределение Стьюдента.
Доверительные интервалы для среднего по совокупности (дисперсия совокупности неизвестна) — t-распределение.
Если мы делаем выборку из генеральной совокупности с неизвестной дисперсией и соблюдается одно из перечисленных ниже условий:
- выборка является большой, или
- выборка небольшая, но совокупность имеет нормальное распределение, или приблизительно нормально распределена,
то доверительный интервал (100 (1 — alpha)% ) для среднего совокупности ( mu ) задается формулой:
( Large dst overline X pm t_{alpha /2}{s over sqrt n} ) (Формула 6)
где число степеней свободы для ( t_{alpha /2}) равно ( n-1 ), а ( n ) — это размер выборки.
Пример 5 использует данные Примера 4, но применяет t-статистику, а не z-статистику, чтобы рассчитать доверительный интервал для среднего значения совокупности коэффициентов Шарпа.
Пример (5) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием t-статистики.
Как и в Примере 4, инвестиционный аналитик стремится вычислить 90-процентный доверительный интервал для среднего по совокупности коэффициентов Шарпа, основанных на случайной выборке из 100 взаимных фондов США.
Выборочное среднее коэффициентов Шарпа составляет 0.45, а выборочное стандартное отклонение — 0.30.
Теперь, признав, что дисперсия генеральной совокупности распределения коэффициентов Шарпа неизвестна, аналитик решает вычислить доверительный интервал, используя теоретически правильную t-статистику.
Поскольку размер выборки равен 100, DF = 99. Используя таблицу степеней свободы, мы находим, что (t_{0.05}) = 1.66.
Этот фактор надежности немного больше, чем фактор надежности (z_{0.05}) = 1.65, который был использован в Примере 4.
Доверительный интервал будет:
( begin{aligned} & overline X pm t_{0.05}{s over sqrt n } \ &= 0.45 pm 1.66{0.30 over sqrt {100}} \ &= 0.45 pm 1.66(0.03) = 0.45 pm 0.0498 end{aligned} )
Доверительный интервал охватывает значения 0.4002 до 0.4998, или 0.40 до 0.50, с двумя знаками после запятой. При округлении до двух знаков после запятой, доверительный интервал не изменился по сравнению с Примером 4.
В Таблице 3 приведены различные факторы надежности, которые мы использовали.
|
Выборка из: |
Статистика для выборки малого размера |
Статистика для выборки большого размера |
|---|---|---|
|
Нормальное распределение с известной дисперсией |
(z) |
(z) |
|
Нормальное распределение с неизвестной дисперсией |
(t) |
(t)* |
|
Ненормальное распределение с известной дисперсией |
недоступно |
(z) |
|
Ненормальное распределение с неизвестной дисперсией |
недоступно |
(t)* |
* Использование (z) также приемлемо.
Как определить размер выборки?
Время на прочтение
4 мин
Количество просмотров 56K
Статистика знает все. И Ильф и Е. Петров, «12 Стульев»
Представьте себе, что вы строите крупный торговый центр и желаете оценить автомобильный поток въезда на территорию парковки. Нет, давайте другой пример… они все равно этого никогда не будут делать. Вам необходимо оценить вкусовые предпочтения посетителей вашего портала, для чего необходимо провести среди них опрос. Как увязать количество данных и возможную погрешность? Ничего сложного — чем больше ваша выборка, тем меньше погрешность. Однако и здесь есть нюансы.
Теоретический минимум
Не будет лишним освежить память, эти термины нам пригодятся далее.
- Популяция – Множество всех объектов, среди которых проводится исследования.
- Выборка – Подмножество, часть объектов из всей популяции, которая непосредственно участвует в исследовании.
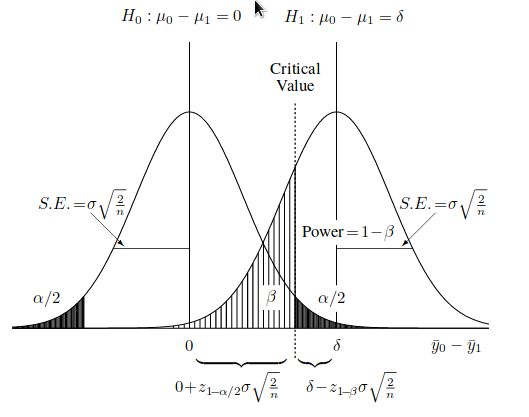
- Ошибка первого рода — (α) Вероятность отвергнуть нулевую гипотезу, в то время как она верна.
- Ошибка второго рода — (β) Вероятность не отвергнуть нулевую гипотезу, в то время как она ложна.
- 1 — β — Статистическая мощность критерия.
- μ0 и μ1 — Средние значения при нулевой и альтернативной гипотезе.
Уже в самих определениях ошибки первого и второго рода имеется простор для дебатов и толкований. Как с ними определиться и какую выбрать в качестве нулевой? Если вы исследуете уровень загрязнения почвы или вод, то как сформулируете нулевую гипотезу: загрязнение присутствует, или нет загрязнения? А ведь от этого зависит объем выборки из общей популяции объектов.
Исходная популяция, также как и выборка может иметь любое распределение, однако среднее значение имеет нормальное или гауссово распределение благодаря Центральной Предельной Теореме.
Относительно параметров распределения и среднего значения в частности возможно несколько типов умозаключений. Первое из них называется доверительным интервалом. Он указывает на интервал возможных значений параметра, с указанным коэффициентом доверия. Так например 100(1-α)% доверительный интервал для μ будет таким (Ур. 1).
- df — Степень свободы = n — 1, от английского «degrees of freedom».
— Двусторонняя критическая величина,
t-критерий Стьюдента.
Второе из умозаключений — проверка гипотезы. Оно может быть примерно таким.
- H0: μ = h
- H1: μ > h
- H2: μ < h
С доверительным интервалом 100(1-α) для μ можно сделать выбор в пользу H1 и H2 :
- Если нижний предел доверительного интервала
100(1-α) < h, то тогда отвергаем H0 в пользу H2. - Если верхний предел доверительного интервала
100(1-α)> h, то тогда отвергаем H0 в пользу H1. - Если доверительного интервала
100(1-α)включает в себя h, то тогда мы не может отвергнуть H0 и такой результат считается неопределенным.
Если нам нужно проверить значение μ для одной выборки из общей совокупности, то критерий обретет вид.
Где .
Доверительный интервал, погрешность и размер выборки
Возьмем самое первое уравнение и выразим оттуда ширину доверительного интервала (Ур. 2).
В некоторых случаях мы можем заменить t-статистику Стьюдента на z стандартного нормального распределения. Еще одним упрощением заменим половину от w на погрешность измерения E. Тогда наше уравнения примет вид (Ур. 3).
Как видим погрешность действительно уменьшается вместе с ростом количества входных данных. Откуда легко вывести искомое (Ур. 4).
Практика — считаем с R
Проверим гипотезу о том, что среднее значение данной выборки количества насекомых в ловушке равно 1.
- H0: μ = 1
- H1: μ > 1
| Насекомые | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Ловушки | 10 | 9 | 5 | 5 | 1 | 2 | 1 |
> x <- read.table("/tmp/tcounts.txt")
> y = unlist(x, use.names="false")
> mean(z);sd(z)
[1] 1.636364
[1] 1.654883Обратите внимание, что среднее и стандартное отклонение практически равны, что естественно для распределения Пуассона. Доверительный интервал 95% для t-статистики Стьюдента и df=32.
> qt(.975, 32)
[1] 2.036933и наконец получаем критический интервал для среднего значения: 1.05 — 2.22.
> μ=mean(z)
> st = qt(.975, 32)
> μ + st * sd(z)/sqrt(33)
[1] 2.223159
> μ - st * sd(z)/sqrt(33)
[1] 1.049568В итоге, следует отбраковать H0 и принять H1 так как с вероятностью 95%, μ > 1.
В том же самом примере, если принять, что нам известно действительное стандартное отклонение — σ, а не ее оценка полученная с помощью случайной выборки, можно рассчитать необходимое n для данной погрешности. Посчитаем для E=0.5.
> za2 = qnorm(.975)
> (za2*sd(z)/.5)^2
[1] 42.08144Поправка на ветер
На самом деле нет никаких причин, полагать, что нам будет известна σ (дисперсия), в то время как μ (среднее) нам еще только предстоит оценить. Из-за этого уравнение 4 имеет мало практической пользы, кроме особо рафинированных примеров из области комбинаторики, а реалистичное уравнение для n несколько сложнее при неизвестной σ (Ур. 5).
Обратите внимание, что σ в последнем уравнении не с шапкой (^), а тильдой (~). Это следствие того, что в самом начале у нас нет даже оценочного стандартного отклонения случайной выборки — , и вместо нее мы используем запланированное —
. Откуда же мы берем последнее? Можно сказать, что с потолка: экспертная оценка, грубые прикидки, прошлый опыт и т. д.
А что на счет второго слагаемого правой стороны 5-го уравнения, откуда оно взялось? Так как , необходима поправка Гюнтера.
Помимо уравнений 4 и 5 есть еще несколько приблизительно-оценочных формул, но это уже заслуживает отдельного поста.
Использованные материалы
- Sample sizes
- Hypothesis testing
Точечные оценки
параметров не дают информации о степени
близости к соответствующему теоретическому
параметру. Если объем выборки мал, то
точечная оценка может значительно
отличаться от оцениваемого параметра,
т.е. приводить к грубым ошибкам. Вычисленная
точечная оценка может быть близка к
оцениваемому параметру, а может и очень
сильно отличаться от него. Точечная
оценка не несет информацию о точности
процедуры оценивания.
Интервальная
оценка –
это числовой интервал, который определяется
двумя числами – границами интервала —
и содержащий неизвестный параметр
генеральной совокупности.
Пусть имеется
выборка объема
и
— статистическая оценка неизвестного
параметра(
— случайная величина, т.к. найдена по
выборочным данным).
Доверительным
интервалом
называется интервал со случайными
границами (,
),
в котором с заданной вероятностьюнаходится оцениваемый параметр
Вероятность
называетсядоверительной
вероятностью.
Доверительная
вероятность задается априорно. Чем
ближе
к единице, тем точнее оценка. Для
практических целей обычно выбирают;
0,99 или 0,9973. Доверительная вероятность,
например, 0,95 означает, что мы пренебрегаем
возможностью появления события (считаем
его невозможным), вероятность которого
меньше 1-0,95=0,05.
Т.к. при различных
выборках получаются различные значения
оценки
,
то и доверительные границы изменяются
от выборки к выборке. Поэтому лучше
говорить не о вероятности попадания
параметра в доверительный интервал, а
о вероятности того, что доверительный
интервал накроет параметр.
Доверительный
интервал применяется в случае сравнительно
небольшого объема выборки, когда
предполагается, что надежность точечной
оценки может быть невысокой.
Доверительный
интервал для оценки математического
ожидания случайной величины
с заданной надежностью
в случае
нормального закона распределения
определяется на основе неравенств
,
где
—
значение аргумента функции Лапласа,
получаемое из таблиц (см. Приложение
1), с учетом того, что;
—известное среднее
квадратичное отклонение или его оценка;
—объем выборки.
Пример 1.
Найти доверительный интервал с надежностью
0,95 для оценки математического ожидания
нормально распределенной случайной
величины
,
если известны
ее среднее квадратическое отклонение
,
выборочное среднее
и объем выборки
.
Решение.
По надежности
из соотношения
находим значение функции Лапласа:
.
По таблице значений
функции Лапласа (см. Приложение 1) находим
.
Используя неравенства для интервальной
оценки математического ожидания,
получаем
или
.
Задачи для самостоятельного решения
-
Найти доверительный
интервал с надежностью 0,8 для оценки
математического ожидания нормально
распределенной случайной величины
со средне квадратическим отклонением
,
выборочным средним
и объемом выборки
.
-
На овцеводческой
ферме из стада произведена выборка для
взвешивания 36 овец. Их средний вес
оказался равным 50 кг. Предположив
распределение веса нормальным и
определив несмещенную оценку выборочной
дисперсии
,
найти доверительный интервал для оценки
математического ожидания с надежностью
а)0,8; б) 0,9; в)
0,95. -
Из генеральной
совокупности извлечена выборка объемом
и найдено выборочное среднее, равное
30. Получено также несмещенное значение
выборочной дисперсии.
Предположив распределение случайной
величины
нормальным,
найти доверительный интервал для оценки
математического ожидания с надежностью
а) 0,8 и б) 0,9. -
Случайная величина
распределена
по нормальному закону. Статистическое
распределение выборки представлено в
таблице
|
|
3 |
5 |
7 |
8 |
10 |
12 |
14 |
|
|
3 |
7 |
4 |
6 |
7 |
5 |
8 |
Найти с надежностью
0,97 доверительный интервал для оценки
математического ожидания.
-
Случайная величина
распределена по нормальному закону.
Статистическое распределение выборки
представлено в таблице:
|
|
1 |
3 |
5 |
7 |
9 |
|
|
2 |
5 |
4 |
6 |
3 |
Найти с надежностью
0,95 доверительный интервал для оценки
математического ожидания.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #