Как найти дрейфовую скорость электрона

From Wikipedia, the free encyclopedia

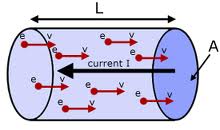
In physics, drift velocity is the average velocity attained by charged particles, such as electrons, in a material due to an electric field. In general, an electron in a conductor will propagate randomly at the Fermi velocity, resulting in an average velocity of zero. Applying an electric field adds to this random motion a small net flow in one direction; this is the drift.

Drift velocity is proportional to current. In a resistive material, it is also proportional to the magnitude of an external electric field. Thus Ohm’s law can be explained in terms of drift velocity. The law’s most elementary expression is:

where u is drift velocity, μ is the material’s electron mobility, and E is the electric field. In the MKS system, drift velocity has units of m/s, electron mobility, m²/(V·s), and electric field, V/m.

When a potential difference is applied across a conductor, free electrons gain velocity in the direction, opposite to the electric field between successive collisions (and lose velocity when traveling in the direction of the field), thus acquiring a velocity component in that direction in addition to its random thermal velocity. As a result, there is a definite small drift velocity of electrons, which is superimposed on the random motion of free electrons. Due to this drift velocity, there is a net flow of electrons opposite to the direction of the field.

Experimental measure[edit]

The formula for evaluating the drift velocity of charge carriers in a material of constant cross-sectional area is given by:^[1]

where u is the drift velocity of electrons, j is the current density flowing through the material, n is the charge-carrier number density, and q is the charge on the charge-carrier.

This can also be written as:

But the current density and drift velocity, j and u, are in fact vectors, so this relationship is often written as:

where

is the charge density (SI unit: coulombs per cubic metre).

In terms of the basic properties of the right-cylindrical current-carrying metallic ohmic conductor, where the charge-carriers are electrons, this expression can be rewritten as:^{[citation needed]}

where

• u is again the drift velocity of the electrons, in m⋅s⁻¹
• m is the molecular mass of the metal, in kg
• σ is the electric conductivity of the medium at the temperature considered, in S/m.
• ΔV is the voltage applied across the conductor, in V
• ρ is the density (mass per unit volume) of the conductor, in kg⋅m⁻³
• e is the elementary charge, in C
• f is the number of free electrons per atom
• ℓ is the length of the conductor, in m

Numerical example[edit]

Electricity is most commonly conducted through copper wires. Copper has a density of 8.94 g/cm³ and an atomic weight of 63.546 g/mol, so there are 140685.5 mol/m³. In one mole of any element, there are 6.022×10²³ atoms (the Avogadro number). Therefore, in 1 m³ of copper, there are about 8.5×10²⁸ atoms (6.022×10²³ × 140685.5 mol/m³). Copper has one free electron per atom, so n is equal to 8.5×10²⁸ electrons per cubic metre.

Assume a current I = 1 ampere, and a wire of 2 mm diameter (radius = 0.001 m). This wire has a cross sectional area A of π × (0.001 m)² = 3.14×10⁻⁶ m² = 3.14 mm². The charge of one electron is q = −1.6×10⁻¹⁹ C. The drift velocity therefore can be calculated:

Dimensional analysis:

Therefore, in this wire, the electrons are flowing at the rate of 23 μm/s. At 60 Hz alternating current, this means that, within half a cycle, on average the electrons drift less than 0.2 μm. In context, at one ampere around 3×10¹⁶ electrons will flow across the contact point twice per cycle. But out of around 1×10²² movable electrons per meter of wire, this is an insignificant fraction.

By comparison, the Fermi flow velocity of these electrons (which, at room temperature, can be thought of as their approximate velocity in the absence of electric current) is around 1570 km/s.^[2]

See also[edit]

• Flow velocity
• Electron mobility
• Speed of electricity
• Drift chamber
• Guiding center

References[edit]

External links[edit]

• Ohm’s Law: Microscopic View at Hyperphysics

Подвижность. Дрейф
носителей заряда

Если в полупроводнике создано электрическое поле величины Е, то помимо хаотического появляется
направленное перемещение носителей заряда, называемое дрейфом. Скорость дрейфа,
v_др,
– это скорость, направленная вдоль вектора напряженности электрического поля,
усредненная по всем носителям заряда одного знака (электронами или дырками).

Оценить среднюю скорость дрейфа можно исходя из формулы v_др=a t_п, где а
– ускорение, приобретаемое электроном между столкновениями. Среднее ускорение
электрона можно рассчитать, используя второй закон Ньютона

 ,

где qE=F – сила, действующая на
электрон со стороны поля.

Подставив это выражение в формулу для скорости дрейфа, получаем

.                                           (3.1)

В формуле (3.1)  величина называется подвижностью
носителей заряда. Таким образом, под­ви­­ж­ность носителей заряда обратно
про­пор­циональна эф­фек­ти­­в­­ной массе носителей m и прямо про­по­р­ци­ональна
времени свободного пробега t_п.

Поскольку скорость дрейфа v_др=μЕ,
то значение подвижности можно рассчитать по формуле

, м²/В·с.                                       (3.2)

Иначе говоря, подвижность носителей заряда – это скорость дрейфа,
приобретаемая свободными носителями в электрическом поле напряженности Е=1 В/м.

Оценка величины подвижности электрона
μ в кристаллической решетке по формуле (3.1)
дает следующее значение:

м²/В·с.

Поскольку в полу­про­водниках су­ще­ст­ву­­­ют два вида носи­­те­лей
заряда с различными эффективными мас­­­­сами, то раз­личают под­вижность электронов
m_n и подвиж­ность дырок
m_p. Под­виж­ность
электронов в кремнии по различным данным со­ста­в­ля­ет  (0,14…0,19) м²/(В×с),
а в арсениде галлия – (0,93…1,1) м²/(В×с). Под­ви­ж­ность дырок ока­­зывается
значительно меньшей и ра­в­ной (0,04…0,05) м²/(В×с) для
кремния и германия и 0,045 м²/(В×с) для арсенида галлия, что объясняется
меньшим временем свободного пробега ды­рок в этих полупроводниковых ма­териалах.

Температурная зависимость величины подвижности но­сите­лей заряда в
полупроводниках определяется механизмами рас­се­я­ния но­сителей заряда.

В слабых электрических полях дрейфовая скорость значительно меньше
средней скорости теплового хаотического движения. Длина свободного пробега
определяется в основном рассеянием
свободных носителей на колеблющихся атомах полупроводника (фононах) и ионизированных атомах при­месей. Фононное рассеяние преобладает при малых концентрациях при­месей
(10²⁰…10²³ м^-3), в этом случае длина свободного
пробега, следо­ва­тельно и подвижность, уменьшаются с
ростом температуры (рис. 3.1, а).

Подвижность
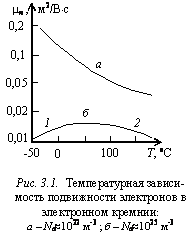
носителей заряда в полупроводнике становится значи­тель­но меньшей при высокой
концентрации примесей, 10²⁴…10²⁵ м^-3. В
этом случае при сравнительно низких температурах преоб­ла­дает рас­се­я­ние
носителей за­ряда на примесях, находящихся в ионизи­ро­ван­ном или ней­т­раль­ном
состоянии. При нагреве полупроводника вследствие увеличения тепловой
скорости электронов и уменьшения их времени взаимодействия с ионами,
подвижность но­си­­телей заряда m_и  ра­стет с тем­пературой по закону m_и~T^3/2/N_и, где N_и — кон­це­н­т­ра­ция ионизированных
примесей (доноров или ак­­­цепторов). При высоких температурах преобладает рас­се­яние
но­си­те­лей заряда на тепловых колебаниях атомов или ио­нов кри­стал­ли­чес­кой
ре­ше­тки полупроводника. При этом по­­­д­ви­ж­ность m_т уме­нь­­ша­е­тся с ростом
температуры по закону m_т ~T ^-3/2.

График зависимости m=f(T) в сильно легированом
полупроводнике представлен на рис. 3.1, б.
Видно, что температурная зависимость по­д­­вижности носителей заряда в при­мес­ном полупроводнике со­с­то­ит из двух участков.
Участок 1 ха­ра­кте­рен для низких
тем­пе­ра­тур, ко­гда пре­обладает рассеяние на ио­ни­зи­ро­ванных примесях; на
уча­с­­т­ке 2 по­д­вижность но­си­те­лей
умень­ша­­е­т­ся вследствие рассеяния на теп­ло­вых колебаниях ато­мов и ионов.

 Результирующая подвижность m определяется с помощью соотношения

.                                         (3.3)

Подвижность и дрейфовая скорость
носителей заряда за­ви­­сят не только от темпе­ра­ту­ры, но и от напряженности
элек­три­че­с­­­­ко­­го по­ля в по­лу­про­во­д­ни­ке.

В слабых электрических полях v_др<<v_т,
тогда полная средняя скорость не зависит от напряженности поля Е и подвижность m=m_o постоян­на. Дополнительная,
приобретаемая электронами на длине свободного пробега, энергия много меньше kT, она теряется при рассеянии
на возбуждение низкочастотных акустических фононов (п. 1.5.7).

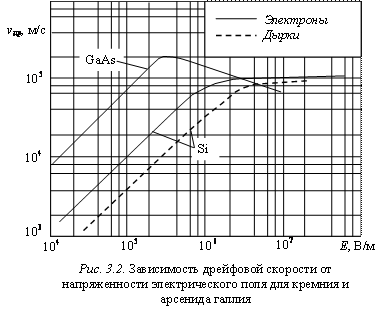
С ростом напряженности электрического поля скорость дрейфа электронов
возрастает (рис. 3.2), приобретаемая электронами энергия увеличивается и начинает
превышать потери при рассеянии, поскольку энергия возбуждаемых акустических
фононов по-прежнему мала по сравнению с kT. Это вытекает из условия сохранения
импульса — импульс возбуждаемого фонона должен быть равен изменению импульса
электрона. Однако импульс акустического фонона p_фон== =(h/v_фон)f_фон с энергией W_фонkT значительно превышает импульс электрона из-за невысокой скорости
фонона v_фон5·10³ м/с и энергия электрона не может быть
передана фононам с такой энергией.

Вследствие увеличения средней скорости электронов уменьшается время свободного
пробега t_п электрона
между двумя столкновениями и, согласно соотношению (3.1), подвижность
уменьшается.  Известно, что подвижность
снижается на 10%, когда напряженность электрического поля достигает критического
значения E_кр=1,4v_фон/m₀, где m₀
— значение подвижности в слабом электрическом поле. Таким образом, значение
критического поля обратно пропорционально величине подвижности носителей заряда
в конкретном полупроводниковом материале. В кремнии для электронов E_кр=7,5·10⁴ В/м, а для дырок E_кр=2·10⁵ В/м при Т=300 К. Следовательно, в кремнии
величина критического поля для дырок примерно в 2,5 раза выше, чем для
электронов, характеризующихся более высокой подвижностью.

 Величина подвижности носителей
заряда, в свою очередь, зависит от напряженности электрического поля. При E>>v_фон/m₀
подвижность уменьшается с ростом напряженности поля Е по закону m~1/, а дрейфовая скорость увеличивается: v_др~.

В сильных электрических полях (Е=10⁶…10⁷ В/м), когда скорость дрейфа приближается к средней тепловой
скорости, средняя энергия электронов становится достаточной для возбуждения
оптических фононов. В отличие от акустических оптические фононы при
сравнительно небольших импульсах того же порядка что и у электрона, обладают
большими энергиями (2…3)kТ при Т=300 K. В процессе рассеяния электроны отдают почти всю
свою кинетическую энергию на образование фононов, поскольку как только она
достигает величины W_{фон. опт}, возбуждается фонон и энергия электрона снижается. В этих условиях
время свободного пробега t_п и подвижность обратно пропорциональны напряженности электрического
поля: m~1/Е, а дрейфовая скорость перестает
зависеть от Е и достигает предельного
значения — скорости насыщения v_нас. В кремнии при Т=300 К для электронов v_нас=10⁵ м/c, а для
дырок v_нас=8×10⁴ м/c.

Скорость
насыщения v_нас является важнейшим электрофизическим
параметром полупроводника. При Т=300 К она имеет значение близкое к тепловой скорости, однако в
отличие от последней v_нас
может уменьшаться с ростом температуры. Например, в кремнии n-типа в диапазоне температур от минус 50 до +120 ^оС скорость насыщения v_нас уменьшается в
диапазоне (1,1…0,8)×10⁵,
а тепловая скорость v_т
– возрастает в диапазоне (1,7…2)×10⁵
м/с.

Для кремния и германия  зависимость дрейфовой скорости от напряженности
электрического поля может быть аппроксимирована формулой

,                        
                     (3.4)

где m₀ —
значение подвижности в слабом электрическом поле.

Таким образом, дрейфовая скорость в
полупроводниках возрастает с ростом напряженности электрического поля, достигая
своего максимального значения – скорости насыщения, близкого к тепловой
скорости.

Зависимость подвижности носителей заряда
(электронов или дырок) от напряженности электрического поля в кремнии аппроксимируется выражением

.                                        (3.5)

Подвижность носителей заряда в средних и
сильных электрических полях уменьшается с ростом напряженности электрического
поля.

Дрейфовый ток

Создание в од­­но­­­ро­дном полупроводнике электрического поля с
напря­жен­но­с­тью E, в результате
подключения внешнего ис­точ­ника ЭДС или тока, при­во­­дит к по­явлению дре­й­фа
носителей тока (электронов и ды­рок).

Поскольку знаки зарядов электронов и дырок противоположны, то носители
дрейфуют со скорос­тью v_др в
про­ти­воположных на­правлениях в со­от­ве­­тствии с си­ла­ми,  дей­с­т­ву­ю­щи­ми со сто­ро­ны эле­к­т­ри­ческого
поля. Поэтому соответствующие дрейфовые токи складываются, как показано на рис.
3.3.

 Плот­ность дрейфового тока j_др в соб­ст­­вен­ном по­лу­про­вод­нике
складывается из плотностей токов эле­к­т­­ро­нов j_{n др}
и ды­рок j_{p др} и определяется из выра­же­ни­я

j_др= j_{n др+} j_{p др=}(qn_iv_{n др}+qp_iv_{p др})= qn_i(m_n+m_p)E, А/м²,           
(3.6)

где q — заряды; n_i=p_i— концентрации; v_{n др} и v_{p др} — 
скорости дрейфа; m_n и m_p — подвижности эле­к­т­ро­нов и дырок.

В примесных полупроводниках общая
плотность дрейфового тока электронов и дырок

j_др= j_{n др+} j_{p др=q}(nm_n+pm_p)E, А/м²,                              (3.7)

В рабочей области температур плотность дрейфового то­ка определяется,
преимущественно, ос­но­в­­­ными носителями тока и рассчитывается по формулам j_{n др=qnnmnE}
и j_{p др=qppmpE}, где n_n и p_p —
концентрации основных но­си­те­­лей тока в электронном и ды­­рочном полу­про­вод­ни­ках.

Приложим
к проводнику внешнее поле

и в нем, естественно, возникнет ток

,
(4.1)

где
коэффициент пропорциональности

— удельная проводимость [
]=ом.м
(Сименс).У металлов

=10⁷
См. То же уравнение можно записать через
удельное сопротивление

.

Все
это свидетельствует о том, что в этих
условиях существует направленное
движение электронов и естественно
происходит изменение в функции
распределения по энергии или скорости
(см. рис.4.1). Такое направленное движение
электронов называют дрейфом, а средняя
скорость их движения — скоростью дрейфа
V_д
. Вычислим ее.

Сила,
действующая на электрон со стороны поля

равна

.
(4.2)

Если
бы не было сопротивления движению
электронов, то последние под действием
F_д
двигались бы ускоренно (F = ma). Поэтому
формально можно ввести силу сопротивления
F_с

, (4.3)

m_e—
эффективная масса электрона, V_Д
– скорость дрейфа электрона.

Это
уравнение можно переписать как уравнение
направленного движения электрона по
2-му закону Ньютона

,

общий
баланс сил запишем F
= F_Д
– F_c,
подставляя соответствующее значение
F_Д

и F_c
из уравнений (4.2) и (4.3) получим

.
(4.4)

Из
уравнения (4.4) видно, что электроны будут
ускоряться ,т.к. действует внешняя сила
F, но до тех пор, пока F_Д
>
F_с,
когда же F_Д
=
F_c,
то результирующая сила исчезнет и
движение электронов будет продолжаться
по инерции с некоторой затухающей
скоростью.

Из
уравнения (4.4) при F = 0 имеем

,

откуда

.
(4.5)

В
связи с тем, что заряд отрицателен, то
движение электронов будет происходить
навстречу вектору напряженности
электрического поля.

Отношение
скорости дрейфа к напряженности поля
называют подвижностью (носителей). В
случае классических частиц

(4.6)

для
квантовых частиц

,
(4.6 а)

где

—
время релаксации электронов на поверхности
Ферми,

Вообще
проводимость можно записать

,

где

.

Подставляя
сюда значения для U
из (4.6) и

из (4.11) запишем проводимость в классической
теории

,
(4.7)

по
аналогии с ней для квантовых частиц
используя (4.6) и (4.11) запишем

,
(4.7 а)

для
электронов U_e<О,
для дырок U_p>О.

Таким
образом, еще раз отметим, что причиной
появления электрического сопротивления
является реальная кристаллическая
решетка и тепловые возбуждения.

4.2. Время релаксации

Для
этого положим, что при некотором условии
Fс = F_Д,
когда U_Д
—
сonst
выключим внешнее поле

тогда движущая сила F_Д
=
0. На движущиеся по инерции электроны
будет действовать только сила сопротивления
Fс и, следовательно, газ электронов будет
переходить из ранее возбужденного в
равновесное состояние. Такие процессы
перехода в равновесное состояние в
системе, ранее выведенной из нее,
называются релаксацией.

Уравнение, описывающее этот процесс,
можно записать из уравнения (4.4):

.
(4.8)

Интегрируя
(4.8) найдем

.
(4.9)

Параметр

характеризует время установления в
системе равновесного состояния: чем
меньше

,
тем быстрее система переходит в
равновесное состояние и за время t=

скорость дрейфа уменьшится в e
раз. Время

называется временем релаксации. Для
чистых металлов

=10^-14
с.

При
описании движения электрона в рамках
кинетической теории газов, нам потребуется
ввести длину свободного пробега электрона

.
(4.10)

Это
выражение справедливо, в случае если
скорость движения гасилась бы за один
акт рассеяния. В реальных условиях это
происходит не так. Требуется некоторое
число столкновений

и естественно средний путь, который
пройдет электрон за время

,
будет уже не

,
а некоторая суммарная величина

,
(4.10 а)

где
_ср

— некоторая средняя за время движения
скорость.

Величину
L
называют транспортной длиной свободного
пробега. Из уравнения (4.10, а) найдем

.
(4.11)

Под
действием электрического поля

возникает дрейф, приводящий к появлению
электрического тока, что говорит о
перераспределении электронов проводимости
по состояниям, как это показано на
(рис.4.1) кривые, представленные штриховыми
линиями, сдвинуты против направления
вектора напряженности поля.

Плотность
электрического тока j
пропорциональна градиенту потенциала,
что следует из (4.1) при

.
(4.12)

В
отсутствии электрического поля также
возможно движение электронов за счет
температурного поля. Плотность теплового
тока j_T
пропорциональна градиенту температуры

,
где коэффициент пропорциональности К,
есть коэффициент теплопроводности,
т.е.

.
(4.13)

Поток
тепла, переносимый электронами, также
направлен навстречу градиенту, но уже
температуры.

Отметим,
что классическая и квантовая теории
приводят к различным результатам. Так,
в обоих теориях электроны участвуют в
тепловом движении и взаимодействуют с
остовами ионов, которые в свою очередь
совершают тепловые колебания около
положений равновесия. Чем выше температура,
тем больше амплитуда этих колебаний. В
соответствии с квантовой теорией
колебания существуют и при Т=0. При
отсутствии внешнего электрического
поля электроны между взаимодействиями
движутся равномерно, при наличии же
электрического поля, т.е. с появлением
силы возникает ускорение, а следовательно,
и кинетическая энергия. Таково
происхождение одной из причин возникновения
активного сопротивления и, следовательно,
джоулева тепла, которое выделяется при
протекании тока. Однако здесь существуют
и различия в теориях. В классической —
сопротивление обусловлено взаимодействием
решетки с электронами, а в квантовой
теории, решетка не создает препятствий
движению, т.е. она прозрачна для электронов,
а сопротивление обусловлено тепловыми
колебаниями решетки, т.е. фононами,
которые взаимодействуют с электронами.
Средняя длина свободного пробега (
)
электрона уменьшается с ростом
температуры.

Классическая
и квантовая теория приводят к следующим
результатам. В классической теории
имеем

;
(4.14)

. (4.15)

В
случае квантовой же теории запишем

;
(4.16)

,
(4.17)

где
h
и k-
универсальные постоянные.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В физика а скорость дрейфа это Средняя скорость достигается заряженными частицами, такими как электроны, в материале благодаря электрическое поле. В общем, электрон в дирижер будет распространяться случайным образом в Скорость Ферми, в результате чего средняя скорость равна нулю. Приложение электрического поля добавляет к этому случайному движению небольшой чистый поток в одном направлении; это дрейф.

Скорость дрейфа пропорциональна Текущий. В резистивный материала он также пропорционален величине внешнего электрического поля. Таким образом Закон Ома можно объяснить с точки зрения скорости дрейфа. Наиболее элементарное выражение закона:

куда ты скорость дрейфа, μ материал подвижность электронов, и E это электрическое поле. в Система МКС единицами измерения этих величин являются м / с, м²/(V · С) и В / м соответственно.

Когда к проводнику приложена разность потенциалов, свободные электроны между последовательными столкновениями приобретают скорость в направлении, противоположном электрическому полю (и теряют скорость при движении в направлении поля), таким образом приобретая компонент скорости в этом направлении в дополнение к его случайная тепловая скорость. В результате возникает определенная малая дрейфовая скорость электронов, которая накладывается на беспорядочное движение свободных электронов. Из-за этой скорости дрейфа возникает чистый поток электронов, противоположный направлению поля.

Экспериментальная мера

Формула для оценки скорости дрейфа носителей заряда в материале постоянного поперечный площадь определяется по:^[1]

куда ты — скорость дрейфа электронов, j это плотность тока протекает через материал, п является носителем заряда числовая плотность, и q это обвинять на носителе.

Это также можно записать как:

Но плотность тока и скорость дрейфа j и u на самом деле являются векторами, поэтому это соотношение часто записывается как:

куда

это плотность заряда (Единица СИ: кулоны на кубический метр ).

По основным свойствам право-цилиндрический Текущий -перенос металлический омический проводник, где носителями заряда являются электроны, это выражение можно переписать как:^{[нужна цитата ]}

куда

• ты — снова дрейфовая скорость электронов в м ⋅s⁻¹
• м это молекулярная масса металла, в кг
• σ это электропроводность среды при рассматриваемой температуре, в S /м.
• ΔV это Напряжение применяется поперек проводника, в V
• ρ это плотность (масса за единицу объем ) проводника, в кг ⋅м⁻³
• е это элементарный заряд, в C
• ж это количество свободные электроны на атом
• ℓ это длина проводника, в м

Числовой пример

Электричество чаще всего проводится по медным проводам. Медь имеет плотность 8,94 г / см³, и атомный вес из 63,546 г / моль, так что есть 1406850,5 моль / м³. В одной крот любого элемента есть 6.022×10²³ атомы ( Число Авогадро ). Поэтому в 1 мес.³ меди есть около 8.5×10²⁸ атомы (6.022×10²³ × 1406850,5 моль / м³). Медь имеет один свободный электрон на атом, поэтому п равно 8.5×10²⁸ электронов на кубический метр.

Предположим, что ток я = 1 ампер, и провод 2 мм диаметр (радиус = 0,001 м). Этот провод имеет площадь поперечного сечения А из π × (0,001 м)² = 3.14×10⁻⁶ м² = 3,14 мм². Заряд одного электрон является q = −1.6×10⁻¹⁹ C. Таким образом, скорость дрейфа можно рассчитать:

Размерный анализ:

Следовательно, в этом проводе электроны текут со скоростью 23 мкм / с. При переменном токе 60 Гц это означает, что за половину цикла электроны дрейфуют менее чем на 0,2 мкм. Другими словами, электроны, протекающие через точку контакта в переключателе, никогда не покинут переключатель.

Для сравнения, скорость потока Ферми этих электронов (которую при комнатной температуре можно рассматривать как их приблизительную скорость в отсутствие электрического тока) составляет около 1570 км / с.^[2]

Смотрите также

• Скорость потока
• Электронная подвижность
• Скорость электричества
• Камера дрейфа
• Гид-центр

Рекомендации

внешняя ссылка

• Закон Ома: вид под микроскопом в Гиперфизике