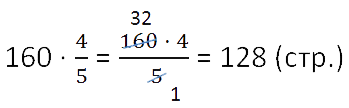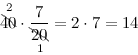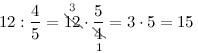Как найти дробь от числа выраженного дробью

 «Методика обучения решению задач на нахождение дроби

от числа и числа по его дроби»                                                            

Большинство применений математики связано с измерением величин. Однако на множестве целых чисел не всегда возможно выполнить деление: не всегда единица величины укладывается целое число раз в измеряемой величине. Чтобы в такой ситуации точно выразить результат измерения, необходимо расширить множество целых чисел, введя  дробные  числа.  К этому выводу люди пришли еще в глубокой древности: необходимость измерения  длин, площадей, масс и других величин привела к возникновению дробных чисел.    

     Знакомство учащихся с дробными числами происходит  в начальных классах. Затем понятие дроби уточняется и расширяется в средней школе. И одной из самых сложных тем  математики курса средней школы является решение задач на дроби.  Дроби проходят в школе не один год, в изучении   темы выделяется несколько этапов. Связано это с различными ограничениями в использовании чисел.  Поэтому программа пятого класса тесно  переплетается с программой шестого. Задачи, на которых формируются представление о дробях,  достаточно сложны для восприятия учениками, поэтому  при решении задач на дроби  учителю математики приходится действовать нестандартно, опираясь не только на  традиционные объяснения.  

Методика обучения решению задач на нахождение дроби от числа и числа по его дроби.

В пятом  классе  учащиеся уже  научились решать задачи на нахождение части от числа и на нахождение числа по его дроби. Для решения этих задач они применяли следующие правила:

1) Чтобы найти часть от числа, выраженную дробью, нужно это число разделить на знаменатель и умножить на числитель;

2) Чтобы найти число по его части, выраженной дробью, нужно  эту часть разделить на знаменатель и умножить на числитель.

В шестом классе  учащиеся узнают, что часть от числа находится умножением на дробь, а  число по его части – делением на дробь. Поэтому    учитель имеет возможность устранить пробелы в знаниях учащихся по этой теме  на материале для закрепления новых способов решения задач на нахождение части от числа и числа по его части.

        При решении задач на дроби основные затруднения у учащихся вызывает определение типа задач. В объяснительном тексте учебников часто  нет краткой записи условий данных задач, и  это  приводит  учащихся к непониманию того, почему  в одном случае они должны выполнять   умножение числа на дробь,  а в другом деление числа на данную  дробь. Поэтому при решении задач на нахождение дроби от числа и числа по его дроби необходимо, чтобы ученики   видели, что в условии задачи является целым, а что его частью.

1.Задачи на нахождение дроби от числа.

Задача 1.

        На пришкольном участке должны посадить    20 деревьев. В первый день ученики посадили    . Сколько деревьев они посадили в первый день?

 Решение:

20 деревьев — это 1 (целое).

       — эта та часть деревьев (часть от целого),

     которую  посадили  в первый день.  

        20 : 4 = 5,  а всех деревьев равна  

5 · 3 = 15, то есть 15 деревьев посадили на участке в первый день.

        Ответ:15 деревьев посадили на пришкольном участке в первый день.

Записываем  решение задачи выражением:  20 : 4· 3 = 15.

        20 разделили на знаменатель дроби и полученный результат умножили на числитель.

        Тот же результат получится, если 20 умножить на   .

             (20·3) : 4 = 20 · .

Вывод: для нахождения дроби от числа, нужно число умножить на данную дробь.

        Далее решаем еще  задачи на нахождение дроби от числа.

Задача 2.

        За два дня заасфальтировали   20 км. В первый день заасфальтировали   0,75 этого расстояния. Сколько километров дороги заасфальтировали  в первый день?

Решение.

20 км-это 1 (целое).

   0,75 —  эта та часть дороги (часть от целого),

 которую заасфальтировали в первый день

        Так как 0,6 = то для решения задачи надо умножить 20 на .

Получим  20==  =15. Значит,  в первый день заасфальтировали 15 километров.

Тот же ответ получится, если 20 умножить на 0,75.

Имеем: 200,75=15. 

Так как проценты можно записать в виде дроби, то задачи на нахождение процентов от числа решаются аналогично.

 Задача 3.

        За два дня заасфальтировали   20 км. В первый день заасфальтировали  75% этого расстояния. Сколько километров дороги заасфальтировали  в первый день?

        Решение

 20 км-это 100%

75% —   заасфальтировали в первый день

        Так как  75%=0,75, то для решения задачи надо  умножить 20 на 0,75. Получим  200,75=15. Значит,  в первый день заасфальтировали 15 километров.

 Задача 4.

        Сад  занимает  всего земельного участка. Яблони занимают   сада. Какую часть всего земельного участка занимают яблони?

Решение.

                                                                В                                  С

                                                                     А                                 D

Изобразим весь земельный участок в виде прямоугольника АВСD. Из рисунка видно, что участок, занятый  яблонями занимает  земельного участка. Тот же ответ можно получит, если умножить   на  :

  = =.

Ответ:  всего земельного участка занимают яблони.

         Материал для закрепления  новых способов решения задач на нахождение дроби от числа лучше всего  распределить  по разделам, в первом из которых  выполняются задания на прямое выполнение нового правила, затем разбираются задачи на нахождение дроби от числа,  после чего учащиеся переходят к решению комбинированных задач, этапом решения которых является решение простой задачи на дроби.

 №1.

       Найдите:

а)   от    128;   б)   от    245;   в)    от    104;   г) от ;  

        д) 0,4  от  30;    е) 0,55  от  40;     ж) 0,4  от  0,9;     з) 0,7  от  4,2;  

        и) 30%  от  60;   к)  35%  от  11,5; л) 42%  от   ; м) 65% от 2 .

 №2.  

1. В школьную столовую привезли 120 кг картофеля. В первый день  израсходовали   всего привезенного картофеля. Сколько килограммов картофеля израсходовали в первый день?                                                                                          

2. Длина  прямоугольника  56 см.  Ширина  составляет    длины.  Найти  ширину  прямоугольника.

3. Пришкольный  участок занимает площадь 600 м2.  Ученики шестого класса в первый день вскопали  0,3  всего участка. Какую площадь вскопали ученики в первый день?

 4.  В  драматическом  кружке  занимаются  25   человек.  Девочки  составляют  60 %  всех  участников  кружка.  Сколько  девочек  занимается  в  кружке?

5. Площадь огорода     га. Картофелем  засажено   огорода. Сколько гектаров засажено картофелем?

№ 3

1. В один пакет насыпали  2   кг пшена, а в другой  –     этого количества.

    На сколько меньше пшена насыпали во второй пакет, чем в первый?

2. С одного участка собрали  2,7   т моркови, а с другого  –     этого       количества. Сколько всего собрали овощей с двух участков?

3. Пекарня выпекает в день 450 кг хлеба. 40 % всего хлеба идет в торговую сеть,    оставшегося – в столовые. Сколько кг хлеба каждый день идет в столовые?

4. В овощехранилище привезли 320 т овощей. 75 % привезенных овощей составлял картофель, а    остатка – капуста. Сколько тонн капусты привезли в овощехранилище?

5. Глубина горного озера к началу лета была  60м. За июнь его уровень понизился на 15%, а в июле оно обмелело на 12% от уровня июня. Какова стала глубина озера к началу августа?

6.  До обеда путник прошел 0,75 намеченного пути, а после обеда он прошел  пути,  пройденного до обеда. Прошел ли путник за день весь намеченный путь?  

7. На ремонт тракторов в зимнее время было затрачено 39 дней, а на ремонт комбайнов  — на 7 дней меньше. Время ремонта прицепного инвентаря составило  того времени, которое ушло на ремонт комбайнов. На сколько дней больше  длился ремонт тракторов, чем ремонт прицепного инвентаря?

8. В первую неделю бригадой было выполнено 30% месячной нормы, во    вторую – 0,8 того, что было выполнено в первую неделю, а в третью неделю —   того, что выполнили во вторую неделю. Сколько процентов месячной нормы осталось выполнить бригаде в четвертую неделю?

2.Нахождение числа по его дроби .

         Задачи на нахождение числа по его дроби являются обратными по  отношению к задачам на нахождение дроби данного числа. Если в задачах по нахождению дроби от числа  давалось число и требовалось найти некоторую дробь от этого числа, то в этих задачах  даётся дробь от числа и требуется найти само это число.

Обратимся к решению задач такого типа.

Задача 1.

  В первый день путешественник прошел 15 км, что составило 5/8 всего пути. Какое расстояние должен был пройти путешественник?

Запишем краткое условие:

Все расстояние- это 1 (целое).

  – это 15км

        15км — это 5 долей. Сколько километров  в одной доле?

     15 : 5 = 3(км)

Так как  все расстояние содержит 8 таких долей, то найдем его:  

      3 · 8 = 24 (км).

Ответ: путешественник должен пройти  24 км.

Запишем решение задачи  выражением: 15 : 5 ·  8 = 24(км) или 15 : 5 · 8 = · 8 = = 15=  15 :.

Вывод: чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.

Задача 2.

На  капитана  баскетбольной  команды  приходится  0,25 всех  полученных  очков  в  игре.  Сколько  всего  очков  получено  этой  командой  в  игре,  если  капитан  принес  команде  24  очка?

Решение.

Все количество очков, полученное командой – это 1 (целое).

0,25  — это 24 очка.

Так как 24: 0,25= 2400 : 25 = 96, то команда получила 96 очков .

Ответ: 96 очков.

Задача 3.

Тетради  в  клетку  составляют  45 %  купленных  тетрадей.  Сколько  всего  купили  тетрадей,  если  среди  них  было  9  тетрадей  в  клетку?

Решение.

 Общее количество купленных тетрадей – это 100%

45% — это 9 тетрадей в клетку

Так как  45% =0,45, а 9: 0,45= 20, то всего купли 20 тетрадей.

        Материал для закрепления для закрепления новых способов решения задач на нахождение числа по его дроби так же  целесообразно распределить  по разделам. В первом разделе выполняются задания на  закрепление  нового правила, во втором — разбираются задачи на нахождение числа по его дроби,  а в третьем  учащиеся разбирают  решение более сложных задач, частью которых являются  задачи на нахождение числа по его дроби.

№1

1) Найдите число:

а)  которого равны 12;  б) 1 которого равны 0,88; в) 0,7 которого равны 112;

г)  которого равны 4,5;     д) 12% которого равны 156;     е) 12 %  которого

равны 4,588.

№2

 1) Мальчик прошел на лыжах 200 метров, что составило  всей дистанции. Какова длина дистанции?

2)        За    кг печенья заплатили 6 руб. Сколько стоит 1 кг?

3)  За   кг  конфет  заплатили  15 р.  Сколько  стоит  1 кг  этих  конфет?

4) В фотоальбоме 45 черно-белых  фотографий, что составляет   всех снимков. Сколько снимков в фотоальбоме?

5) На полке стоит 12 книг в мягком переплете, что составляет  0,6 всех книг, стоящих на полке. Сколько  книг стоит на полке?

6) После замены двигателя средняя скорость самолета увеличилась на 18 %? Что составляет 68,4 км/ч. Какова была средняя скорость самолета с прежним двигателем?

№3

1)  Длина прямоугольника составляет   его ширины. Найдите его площадь, если длина равна 28 дм.

2) В первый час автомашина проехала 12% всего пути, после чего ей осталось проехать  440 км. Какова длина всего пути?

3) В  первый  день  магазин  продал  32%  имевшегося  ситца,  а  во  второй  день  7%  имевшегося  ситца.  После  этого  осталось  274,5 м.  Сколько  ситца  поступило  в  магазин?

4) Собранную в саду вишню разложили  в три корзины . В первую вошло  всей вишни, во вторую 0,4 , а в третью – остальные 20 кг. Сколько всего килограммов вишни было собрано?

5) Трое рабочих  изготовили некоторое число деталей. Первый рабочий изготовил 0,3 всех деталей, второй – 0,6 остатка, а третий остальные  84 детали. Сколько всего деталей изготовили рабочие?

6) На опытном участке капуста занимала   участка, картофель  оставшейся площади, а остальные 42 га были засеяны кукурузой. Найдите площадь всего опытного участка.

7) Автомобиль прошел в первый час  всего пути, во второй час —  оставшегося пути, а в третий час – остальной путь. Известно, что в третий час он прошел  на 40 км меньше, чем во второй час. Сколько километров прошел автомобиль за эти три часа?

Задачи  на дроби являются важным средством обучения математике. С их помощью учащиеся получают опыт работы с  дробными  и целыми величинами, постигают взаимосвязи между ними, получают опыт применения математики к решению практических задач. Решение  задач  на дроби развивает смекалку и сообразительность, умение ставить вопросы, отвечать на них,  и готовит школьников к дальнейшему обучению.

учитель математики

 МБОУ лицей №1 п.Нахабино        

Первушкина  Ольга   Викторовна

Литература:

1.Математика. 5 класс: учеб. для общеобразоват. учреждений   / Н.Я. Виленкин, В.И.  Жохов, А.С. Чесноков, С.И. Шварцбурд.  –  М. : Мнемозина, 2009г.

2. Математика. 6 класс: учеб. для общеобразоват. учреждений / Н.Я. Виленкин, В.И.  Жохов, А.С. Чесноков, С.И. Шварцбурд.  –  М. : Мнемозина, 2009г.

3. Дидактические материалы по математике: 5 класс: практикум/ А.С. Чесноков, К.И. Нешков. – М.: Академкнига / Учебник, 2012.

4. Дидактические материалы по математике: 6класс: практикум/ А.С. Чесноков, К.И. Нешков. – М.: Академкнига/ Учебник, 2012.

5. Самостоятельные и контрольные работы по математике для 6 класса. / А.П. Ершова, В.В. Голобородько. – М.: ИЛЕКСА, 2011.

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Нахождение дроби от числа

Поддержать сайт

Существует ряд задач, в которых необходимо найти часть или дробь
некоторого числа. Такие задачи решаются умножением на основании следующего правила:

Чтобы найти дробь от заданного числа, нужно это число умножить на дробь.

Иногда требуется по известной части числа и дроби, которая выражает эту часть, определить все число. Подобные задачи решаются делением.

Чтобы найти число, по известной величине его дроби, надо заданную величину поделить на дробь.

Читать следующую тему: десятичные дроби.