Как найти дробь под корнем

В примерах по извлечению квадратного корня из дроби требуется работать с обыкновенными дробями.
Поэтому рекомендуем перед решением примеров освежить знания по действиям с
обыкновенными дробями:

• правильные и неправильные дроби;
• сложение дробей;
• вычитание дробей;
• умножение дробей;
• деление дробей.

Свойство квадратного корня из дроби

Как найти квадратный корень из дроби

По традиции от теории переходим к практике. Разберем пример вычисления квадратного корня из дроби.

Разбор примера

Вычислить:

1)

=

…

Используем правило квадратного корня из дроби. Извлечем квадратный корень отдельно из числителя и знаменателя.

=

=

Разбор примера

Вычислить:

1)

=

=

√9

=

3

Как извлечь квадратный корень из смешанного числа

Разбор примера

Вычислить:

4)

5

= …

Избавимся от целой части дроби и превратим ее в неправильную.

5

=

=

=

=

= …

Используем свойство квадратного корня из дроби.

5

=

=

=

=

=

=

= …

Для завершения примера не забудем выделить целую часть.

5

=

=

=

=

=

=

=
2

Разбор примера

Вычислить:

4)

+

= …

Перед тем как работать с дробями требуется выполнить действие извлечения квадратного корня из дробей.

 

+

=

 

+

= …

Вспомним, что квадратный корень из единицы равен единице (
√1 = 1
) и используем правило сложения дробей.

 
+

=

 
+

=

+

=

=

=
1

Примеры извлечения квадратного корня из дроби

Разбор примера

2)    5

−

3

= …

Вспомним, что в краткой записи между квадратным корнем и числом знак умножения «·» не пишут.
Для наглядности поставим его в пример и вычислим пример по правилу
умножения числа на дробь.

   5

−

3

=

=

  5
 
·

−

3
 
·

=

=

  5
 
·
 

−

3
 
·
 

=

=

  5

·

−

3

·

= …

Вспомним правило умножения дроби на число.

   5

−

3

=

=
  5
  ·

−

3
 
·

=

=

  5
 
·
 

−

3
 
·
 

=

=

  5

·

−

3

·

=

−

=

=
1 − 1 = 0

Разбор примера

Вычислить:

4)
= …

Чтобы вычислить квадратный корень, используем правило умножения дробей
и правило квадратного корня из дроби.

=

·

=

4  

·

=

=

4 · √9 =
4 · 3 = 12

Разбор примера

Вычислить:

2)

5 · 11

= …

Избавимся от целой части
в смешанных числах, чтобы можно было использовать свойство квадратного корня из дроби.

5 · 11

=

=

·

=

=

·

=

·

=

=

·

= …

Вспомним таблицу квадратов, чтобы вычислить
√289.

5 · 11

=

=

·

=

=

·

=

·

=

=

·

=

·

=

=

=

=

…

Выделим целую часть смешанного числа для того, чтобы дать окончательный ответ.

5 · 11

=

=

·

=

=

·

=

·

=

=

·

=

·

=

=

=

=

7

---

Ваши комментарии

Оставить комментарий:

---

Как извлечь корень из дроби

Результатом выполнения операции извлечения корня должно быть число, которое при возведении его в степень, равную степени корня, даст значение, указанное под знаком корня. Это значение называется «подкоренным выражением» и может быть задано формулой, целым или дробным числом. Извлечение корня из дробного числа имеет некоторые правила, предназначенные для упрощения этой операции.

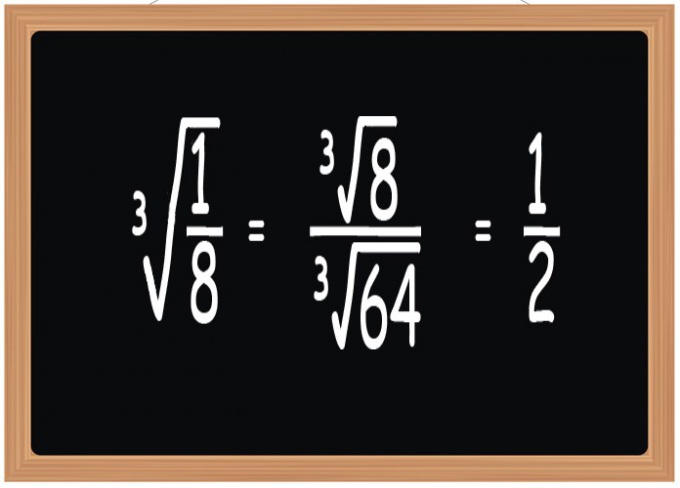
Инструкция

Если подкоренное выражение представлено в виде десятичной дроби, а результат надо получить в формате дроби обыкновенной, то начните с преобразования формата. Например, для извлечения кубического корня из числа 0,125 эта операция будет выглядеть так: 0,125 = 125/1000 = 1/8.

Если подкоренное выражение представляет собой обыкновенную дробь, то исходите из того, что корень из нее можно представить, как отношение корня той же степени из числителя к такому же корню из знаменателя. Например, операцию извлечения квадратного корня из дроби 4/9 можно записать так: √(4/9) = √4/√9 = 2/3.

Если числитель и знаменатель подкоренного выражения в его исходном виде не позволяет получить удобное для дальнейших вычислений значение, то попробуйте привести их к нужному виду. Подберите такой общий множитель, чтобы из обоих или хотя бы из одного из них можно было при извлечении корня получить целочисленного значение. Например, для вычисления кубического корня из дроби 1/8 будет удобнее предварительно увеличить ее числитель и знаменатель в 8 раз: ³√(1/8) = ³√(1*8/8*8) = ³√(8/64) = ³√8/³√64 = 2/4.

Полученную в результате этой математической операции обыкновенную дробь следует сократить, если это представляется возможным. Например, образец вычисления из последнего шага будет оставаться незаконченным, пока вы не разделите числитель и знаменатель результата на двойку: ³√(1/8) = ³√(1*8/8*8) = ³√(8/64) = ³√8/³√64 = 2/4 = 1/2.

Если вам важен только результат операции извлечения корня из дроби, а формат полученного числа и ход вычислений значения не имеют, то воспользуйтесь каким-либо калькулятором. Например, это может быть стандартная программа операционной системы Windows. Она запускается из главного меню на кнопке «Пуск» — соответствующая ссылка в разделе «Все программы» помещена в подраздел «Стандартные».

Источники:

• как извлечь корень из корня
• квадратный корень из 0,

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Для
начала давайте вспомним определение арифметического квадратного корня. Итак, арифметическим
квадратным корнем из числа а называется неотрицательное число,
квадрат которого равен а.

Пример 1:

Пример 2:

Следует обратить внимание, что

Заметим, что

Видно, что квадратный корень из
произведения двух неотрицательных чисел равен произведению квадратных корней из
этих чисел.

Этим свойством обладает квадратный
корень из произведения любых двух неотрицательных чисел.

Чтобы извлечь квадратный корень из
произведения неотрицательных чисел, можно извлечь его из каждого сомножителя
отдельно и результаты перемножить.

Следует заметить, что это свойство
распространяется и на тот случай, когда подкоренное выражение
представляет собой произведение трёх, четырёх и т.д. неотрицательных
множителей.

Например:

Корень из неотрицательных множителей
равен произведению корней из этих множителей.

Верно и обратное утверждение: произведение
корней из неотрицательных чисел равно корню из произведения этих чисел.

Задание: вычислите значение выражения.

Решение:

Рассмотрим теперь арифметический
квадратный корень из дроби.

Пример 1:  

Видим, что квадратный корень из дроби
равен корню из числителя, делённому на корень из знаменателя.

Этим свойством обладает квадратный
корень из дроби, числитель которой неотрицательное число, а знаменатель положителен.

Чтобы извлечь квадратный корень из
дроби, можно извлечь корень отдельно из числителя и знаменателя и первый
результат разделить на второй.

Вывод: корень из дроби, числитель
которой неотрицателен, а знаменатель положителен, равен корню из числителя,
деленному на корень из знаменателя.

Верно и обратное утверждение: частное
корней равно корню из частного этих чисел.

Выполнить задание: вычислите значение
выражения.

Решение:

Итоги:

Корень из неотрицательных множителей равен
произведению корней из этих множителей.

Корень из дроби, числитель которой
неотрицателен, а знаменатель положителен, равен корню из числителя, деленному
на корень из знаменателя.

Извлечение корня

• Извлечение корня из произведения, степени и дроби
• Вынесение множителя из-под знака корня
• Внесение множителя под корень

Извлечь из данного числа корень какой-нибудь степени значит найти такое число, которое при возведении в эту степень, будет равно данному числу.

Из правил знаков при возведении в степень следует, что:

1. Корень нечётной степени из положительного числа есть число положительное, а из отрицательного – отрицательное.

   Примеры:

   ³√+27 = +3,   так как   (+3)³ = 27;

   ³√-27 = -3,   так как   (-3)³ = -27.

2. Корень чётной степени из положительного числа может быть как положительным, так и отрицательным числом.

   Примеры:

   √+9 = ±3,   так как   (+3)² = +9   и   (-3)² = +9;

   ⁴√+256 = ±4,   так как   (+4)⁴ = +256   и   (-4)⁴ = +256.

3. Корень чётной степени из отрицательного числа является невозможным выражением, потому что любое положительное или отрицательное число при возведении в чётную степень даёт только положительный результат. Таким образом,

   √-49 ,   ⁴√-256 ,   ⁶√-64   — это невозможные выражения.

   Невозможные выражения иначе называют мнимыми.

Извлечение корня из произведения, степени и дроби

Чтобы извлечь корень из произведения, надо извлечь его из каждого множителя отдельно.

Так же можно сказать, что корень произведения равен произведению корней всех его множителей:

Чтобы извлечь корень из степени, следует показатель степени разделить на показатель корня:

Чтобы извлечь корень из дроби, следует извлечь его отдельно из числителя и из знаменателя:

Вынесение множителя из-под знака корня

Когда нельзя извлечь корень из всего подкоренного числа или выражения, то подкоренное число или выражение раскладывают на множители и извлекают корень только из тех множителей, из которых это возможно сделать.

Внесение множителя под корень

Если нужно внести множитель под знак корня, то его следует возвести в степень, равную показателю корня.

Нахождение квадратного корня из дроби может показаться сложной задачей. Несмотря на это, разбиение уравнений на несколько простых шагов облегчает их решение. Изучение того, как вычислить квадратный корень из дроби, поможет вам понять, как работают различные части процесса и формула. В этой статье мы обсудим, что такое квадратный корень из дроби, как можно вычислить квадратный корень из дроби и приведем несколько примеров уравнений.

Что такое квадратный корень из дроби?

Квадратный корень из дроби предполагает нахождение квадратного корня из числителя и квадратного корня из знаменателя, чтобы разделить их друг на друга. Квадратный корень, в общем смысле, это число, которое при умножении на себя дает определенное количество.

Формула квадратного корня из дроби и части дроби

Чтобы вычислить квадратный корень из дроби, необходимо воспользоваться следующей формулой:

vfraction = vnumerator vdenominator

Имея в виду эту формулу, важно сначала понять различные компоненты, из которых состоит дробь, прежде чем приступать к вычислениям. Вот различные части дроби:

• Числитель: Это верхняя часть дроби, которая представляет собой определенное количество частей от целого.

• Знаменатель: Это нижняя часть дроби, которая представляет собой целое значение того, что представляет собой дробь.

• Дробная линейка: Это линия, которая проходит между числителем и знаменателем, разделяя их так, что они являются двумя частями одной дроби.

Советы по нахождению квадратного корня из дроби

Вот несколько советов, которые вы можете использовать при вычислении квадратного корня из дроби:

Обратитесь за помощью

Если вы испытываете трудности при вычислении квадратного корня из дроби, попробуйте обратиться за помощью к другу или коллеге. Нахождение квадратного корня из дроби может включать сложные шаги, поэтому если вы не знакомы с квадратными корнями или дробями, вам будет полезно обратиться за помощью.

Дважды проверьте свою работу

При вычислении квадратного корня из дроби важно перепроверить свои математические вычисления, чтобы убедиться, что вы получаете правильные ответы. Отличный способ проверить точность своей работы — воспользоваться калькулятором после завершения вычислений. Если вы получили другой ответ от калькулятора, значит, вы знаете, что нужно вернуться и попробовать выполнить вычисления еще раз.

Еще один способ проверить свою работу — выполнить одни и те же вычисления дважды. Если вы дважды получили один и тот же ответ, то можно предположить, что ваши математические вычисления верны. Если со второй попытки вы получили другой ответ, попробуйте выполнить расчеты еще несколько раз, чтобы получить больше практики в следующих вопросах.

Практика

Важно практиковать вычисления, чтобы вы могли расширить свои математические навыки и приобрести опыт в вычислении квадратного корня из дробей. Чтобы попрактиковаться в работе с квадратными корнями из дробей, вы можете использовать онлайн-ресурсы, чтобы найти практические задачи в Интернете, которые могут бросить вызов и развить ваши математические навыки. Для дальнейшего развития навыков вы также можете играть в математические онлайн игры, в которых используются основные математические приемы, включая дроби и умножение.

Когда нужно найти квадратный корень из дроби

Вот несколько примеров, когда вам может понадобиться найти квадратный корень из дроби:

• Работа: Вы можете работать на работе, которая требует от вас использования базовых или сложных математических навыков, которые могут включать нахождение квадратного корня из дроби. Вам может потребоваться находить квадратный корень из дроби в вашей профессии, если вы строитель, архитектор интерьера и экстерьера или электрик.

• Высшее образование: Многие программы высшего образования требуют от студентов всех специальностей пройти базовые курсы математики. Эти математические курсы могут включать статистику, геометрию и алгебру, все из которых используют вычисления для квадратных корней дробей.

Как вычислить квадратный корень из дроби

Выполните следующие действия, которые помогут вам вычислить квадратный корень из дроби:

1. Определите правильные числа

Для того чтобы найти квадратный корень из дроби, необходимо сначала определить правильные числа для использования в уравнении. Чтобы найти числитель, определите число в верхней части дроби. Затем, чтобы найти знаменатель, определите число под числителем, которое находится в нижней части дроби.

2. Найдите квадратный корень из числителя

Первое вычисление, которое необходимо выполнить, — это нахождение квадратного корня из числителя в дроби. Для этого найдите коэффициенты вычисляемого числа. Факторы — это числа, которые можно умножить вместе, чтобы получить число, от которого вы ведете расчет. Чтобы найти коэффициент, найдите два или более чисел, которые можно перемножить вместе, чтобы получить искомое число. Например, коэффициент 16 равен четырем, поэтому вы начнете с v16 = v(4×4).

3. Найдите квадратный корень из знаменателя

Следующий шаг в вычислениях — нахождение квадратного корня из знаменателя в дроби. Для этого вы можете еще раз найти коэффициенты вычисляемого числа. Например, если знаменатель равен 25, то коэффициент 25 равен пяти, поэтому в итоге получится v25 = (5×5).

4. Выполните деление

Следующий шаг — деление квадратного корня из числителя на квадратный корень из знаменателя. Например, если квадратный корень из числителя равен 4, а квадратный корень из знаменателя равен 5, то вы разделите 45, в результате чего квадратный корень дроби будет равен 0.08.

Примеры вычисления квадратного корня из дроби

Вот несколько примеров нахождения квадратного корня из дроби, включая объяснения:

v100625 = 1025 = 0.04

Здесь числитель равен 100, а знаменатель — 625. Сначала вычислите квадратный корень из 100, найдя его коэффициенты. Коэффициент 100 равен 10, поэтому v100 = (10×10). Затем найдите квадратный корень из 625 путем нахождения его коэффициентов. Коэффициент 625 равен 25, поэтому v625 = (25×25). Чтобы завершить вычисления, разделите квадратный корень из числителя на квадратный корень из знаменателя: 1025 = 0.04.

v9144 = 312 = 0.25

В этом уравнении числитель равен 9, а знаменатель — 144. Сначала вычислите квадратный корень из 9, найдя его коэффициенты. Коэффициент 9 равен 3, поэтому v9 = (3×3). Затем найдите квадратный корень из 144, найдя его коэффициенты. Коэффициент 144 равен 12, поэтому v144 = (12×12). Чтобы найти квадратный корень из дроби, разделите коэффициенты 312, чтобы вычислить произведение 0.25.

v3681 = 69 = 0.66

Чтобы вычислить квадратный корень из этой дроби, сначала определите числитель и знаменатель. Здесь числитель равен 36, а знаменатель — 81. Затем найдите квадратный корень из числителя, найдя его коэффициенты. Коэффициент 36 равен 6, поэтому v36 = (6×6). Затем найдите квадратный корень из 81, найдя его коэффициенты. Коэффициент 81 равен 9, поэтому v81 = (9×9). Затем разделите 69, что даст вам произведение 0.66.