При вычислении любой длины следует помнить, что это величина конечная, то есть просто число. Если имеется в виду длина дуги кривой, то такая задача решается с помощью определенного интеграла (в плоском случае) или криволинейного интеграла первого рода (по длине дуги). Дуга АВ будет обозначаться UАВ.
Первый случай (плоский). Пусть UАВ задана плоской кривой y = f(x). Аргумент функции изменятся в пределах от а до b и она непрерывно дифференцируема этом отрезке. Найдем длину L дуги UАВ (см. рис. 1а). Для решения этой задачи разбейте рассматриваемый отрезок на элементарные отрезки ∆xi, i=1,2,…,n. В результате UАВ разобьется на элементарные дуги ∆Ui, участков графика функции y=f(x) на каждом из элементарных отрезков. Найдете длину ∆Li элементарной дуги приближенно, заменив ее соответствующей хордой. При этом можно приращения заменить дифференциалами и использовать теорему Пифагора. После вынесения из квадратного корня дифференциала dx получите результат, приведенный на рисунке 1b.![1_5254fef39271a5254fef392758[1]](https://ic.pics.livejournal.com/wrtorr/66163308/11897/11897_900.png "1_5254fef39271a5254fef392758[1]")
Как вычислить длину кривой
Второй случай (дуга UАВ задана параметрически). x=x(t), y=y(t), tє[α,β]. Функции x(t) и y(t) имеют непрерывные производные на отрезке этом отрезке. Найдите их дифференциалы. dx=f’(t)dt, dy=f’(t)dt. Подставьте эти дифференциалы в формулу для вычисления длины дуги в первом случае. Вынесите dt из квадратного корня под интегралом, положите х(α)=а, x(β)=b и придете к формуле для вычисления длины дуги в данном случае (см. рис. 2а).
Третий случай. Дуга UАВ графика функции задана в полярных координатах ρ=ρ(φ) Полярный угол φ при прохождении дуги изменяется от α до β. Функция ρ(φ)) имеет непрерывную производную на отрезке ее рассмотрения. В такой ситуации проще всего использовать данные, полученные на предыдущем шаге. Выберите φ в качестве параметра и подставьте в уравнения связи полярных и декартовых координат x=ρcosφ y=ρsinφ. Продифференцируйте эти формулы и подставьте квадраты производных в выражение на рис. 2а. После небольших тождественных преобразований, основанных в основном, на применении тригонометрического тождества (cosφ)^2+(sinφ)^2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).
Четвертый случай (пространственная кривая, заданная параметрически). x=x(t), y=y(t), z=z(t) tє[α,β]. Строго говоря, здесь следует применить криволинейный интеграл первого рода (по длине дуги). Криволинейные интегралы вычисляют переводом их в обычные определенные. В результате ответ останется практическим таким же как и случае два, с тем лишь отличием, что под корнем появится добавочное слагаемое – квадрат производной z’(t) (см рис. 2с).
Примеры:
Пример 1. Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.
Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у’ = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную
Применим схему I (метод сумм).
1. Точками х0 = а, х1…, хn = b (х0 < x1 < …< хn) разобьем отрезок [а; b] на n частей (см. рис. 183). Пустьэтим точкам соответствуют точки М0 = А, M1,…,Mn =В на кривой АВ. Проведем хорды М0M1, M1M2,…, Мn-1Мn, длины которых обозначим соответственно через ΔL1, AL2,…, ΔLn. Получим ломаную M0M1M2 … Mn-ιMn, длина которой равна Ln=ΔL1 + ΔL2+…+ ΔLn = 
2. Длину хорды (или звена ломаной) ΔL1 можно найти по теореме Пифагора из треугольника с катетами Δxi и Δуi:
По теореме Лагранжа о конечном приращении функции Δуi=ƒ'(сi)•Δхi, где ci є (xi-1;xi). Поэтому
а длина всей ломаной M0M1… Мn равна
3.Длина l кривой АВ, по определению, равна
.
Заметим, что при ΔLi→0 также и Δxi →0 ΔLi =
и, следовательно, |Δxi|<ΔLi).
Функция
непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δxi→ 0:
Таким образом,
или в сокращенной записи l =
Если уравнение кривой АВ задано в параметрической форме
где x(t) и y(t) — непрерывныефункции с непрерывными производными и х(а) = а, х(β) = b, то длина l кривой АВ находится по формуле
Формула (41.5) может быть получена из формулы (41.3) подстановкой x = x(t),dx = x'(t)dt,
Пример 2. Определить длину окружности x2 + y2 = r2. Решение. Вычислим сначала длину четвертой части окружности, лежащей в первом квадранте. Тогда уравнение дуги AB будет
, откуда,следовательно,
Длина всей окружности L = 2πr.
Пример 3. Найти длину дуги кривой y2 = x3 от x = 0 до x = 1 (y > 0). Решение. Дифференцируя уравнение кривой, найдем y’ = (3/2)x1/2, откуда
Пример 4. Пусть кривая лежит в плоскости x0y и описывается уравнением y = f(x).
Для нахождения длины дуги этой кривой, заключенной между точками с абсциссами a и b, разобьем дугу на столь малые элементы, чтобы каждый из них можно было аппроксимируовать прямолинейным участком (см. рисунок 1).
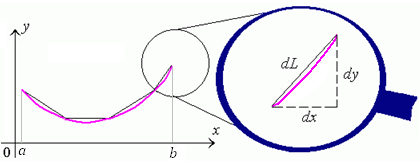
Рис. 1. Аппроксимация элемента дуги кривой прямолинейным участком.
Длину dL бесконечно малого участка можно выразить через dx и dy с помощью теоремы Пифагора:
 |
(1) |
где y ‘ – производная функции y = f(x) по переменной x.
Длина дуги равна сумме длин составляющих ее элементов:
 . |
Пример 5.
2 / 8820 — (10x) / 21 + 500, x = 0..4200
Таким образом, длина каждого троса составляет около 4354 футов в длину, чуть больше, чем расстояние между башнями. Обратите внимание, что Wolfram | Alpha показывает также интеграл, который нужно вычислить для нахождения длины дуги, а не только ответ.
Длина дуги пространственной кривой
Одно из обычных упражнений в стандартном курсе интегрального исчисления — найти длину дуги спирали. С прикладной точки зрения, это может быть, например, длина проволоки в катушке или количество ленты, которое потребуется, чтобы обернуть цилиндр, не оставляя промежутков.
Спираль может быть выражена как параметрическая кривая, в которой координаты х и у определяют круг, а координата z линейно возрастает. Например:
arc length (x, y, z) = (sin(t), cos(t), 2t), t =0..10
Длина дуги в полярных координатах
Можно также находить длину дуги кривых в полярных координатах. В приведенном ниже примере, использование переменных r, θ позволяет Wolfram | Alpha догадаться, что данная кривая задана уравнением в полярных координатах:
arc length r = theta*sin(theta), theta = 2.
2} from 0
На рисунке выше, Wolfram | Alpha автоматически выбрал второе значение значение t=2. Изменяя это значение, можно подобрать, что при t=3.571 получим такой результат:
1По материалам: by Peter Barendse
От себя
Просто запросу arc length Wolfram|Alpha выводит калькулятор для вычисления длины дуги, где можно задать произвольную функцию и указать пределы интегрирования:
Надеюсь, что вам понравилась функция arc length, и я с нетерпением ожидаю следующей возможности доставить вам удовольствием рассказом об интересных и полезных применениях Wolfram|Alpha.
Калькулятор длины дуги — примеры, Калькулятор длины дуги онлайн
Калькулятор длины дуги — это онлайн-инструмент, который вычисляет длину дуги, зная радиус окружности и центральный угол дуги. Дуга определяется как часть окружности окружности, которая лежит между любыми двумя точками.
Что такое калькулятор длины дуги?
Калькулятор длины дуги вычисляет длину дуги, используя различные формулы в зависимости от единицы измерения заданного центрального угла.
Центральный угол может быть выражен как в градусах, так и в радианах. Чтобы использовать Калькулятор длины дуги , введите значения в соответствующие поля ввода.
Калькулятор длины дуги
Как пользоваться калькулятором длины дуги?
Чтобы найти длину дуги с помощью калькулятора длины дуги, выполните указанные ниже действия.
- Шаг 1: Перейти к онлайн-калькулятору длины дуги Cuemath
- Шаг 2:
Введите значения в указанные поля ввода. - Шаг 3: Нажмите кнопку « Рассчитать », чтобы найти длину дуги.
- Шаг 4: Нажмите кнопку « Сброс », чтобы очистить поля и ввести новые значения.
Как работает калькулятор длины дуги?
Для расчета длины дуги нам нужно знать два параметра. Они следующие:
- Радиус круга — Расстояние от центра круга до любой точки на окружности известно как радиус круга
- Центральный угол — Угол, образуемый дугой в центре окружности, называется центральным углом.
Чтобы найти длину дуги, мы можем использовать две разные формулы в зависимости от единицы измерения центрального угла.
1. Центральный угол дается в радианах.
- Чтобы найти длину дуги, мы просто умножаем радиус на значение угла.
Формула дается как:
L = θ × r.
2. Центральный угол указывается в градусах.
- Сначала мы преобразуем угол из градусов в радианы. Это можно сделать, умножив угол на коэффициент (π/180).
- Далее мы берем произведение значения угла, полученного на шаге 1, и радиуса окружности. Это дает нам длину дуги.
Формула выглядит следующим образом:
L = θ × (π/180) × r
Здесь L — длина дуги, r — радиус окружности, θ — центральный угол, а π ( pi) — константа со значением 3,14 или 22/7.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы.
С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Решенные примеры длины дуги
Пример 1: Найдите длину дуги, радиус которой равен 5 единицам, а центральный угол равен 4 радианам. Проверьте результат с помощью калькулятора длины дуги.
Решение:
Поскольку центральный угол дается в радианах, мы используем формулу L = θ × r
L = 4 × 5
L = 20 единиц.
Таким образом, длина дуги составляет 20 единиц.
Пример 2: Найдите длину дуги, радиус которой равен 3,5 единицы, а центральный угол равен 6 градусам. Проверьте результат с помощью калькулятора длины дуги.
Решение:
Поскольку центральный угол дан в радианах, мы используем формулу L = θ × (π/180) × r
L = 6 × (3,14 / 180) × 3,5
л = 0,37 ед.
Таким образом, длина дуги составляет 0,37 единицы.
Теперь используйте калькулятор длины дуги, чтобы найти длину дуги с заданными размерами:
- Радиус = 20 единиц, Угол = 2 радиана
- Радиус = 14,3 единицы, Угол = 17 градусов
☛ Математические калькуляторы:
Калькулятор длины дуги
Выберите параметры и введите их значения.
Инструмент рассчитает длину дуги, диаметр, площадь, радиус, центральный угол, высоту сегмента и хорду заданного круга с отображением шагов.
РЕКЛАМА
Рассчитайте:
Центральный угол и радиусрадий и сегмент Heightradius и сектор ареарадиус и длина хорды и диаметр и диаметр угловой угол сектора (θ). * π рад
Радиус (r)
mmcmmkminftydminmi
Diameter
mmcmmkminftydminmi
Sector area (A)
mm²cm²dm²m²km²in²ft²yd²mi²adahaacsoccer fields
Chord length (c)
mmcmmkminftydminmi
Segment Height (h )
ммкммкминфтидминми
РЕКЛАМА
РЕКЛАМА
Содержание
| 1 | Что такое дощатый фут в пиломатериалах (BF)? |
| 2 | Бортовой фут Формула: |
| 3 | Подставка для досок Единицы: |
| 4 | Важно Толщина: |
| 5 | Как рассчитать доски? |
| 6 | Что вы подразумеваете под термином «Измерение поверхности»? |
| 7 | Что подразумевается под номинальным размером? |
| 8 | Как определить линейное измерение? |
Получите виджет!
Добавьте этот калькулятор на свой сайт, чтобы пользователи могли выполнять простые расчеты.
Получить код
Обратная связь
Насколько легко было пользоваться нашим калькулятором? Сталкивались ли вы с какой-либо проблемой, сообщите нам!
ОБРАТНАЯ СВЯЗЬ
Онлайн-калькулятор длины дуги помогает найти длину дуги, центральный угол, радиус, диаметр, площадь сектора, высоту сегмента и длину хорды окружности. Когда дело доходит до определения длины дуги окружности, этот калькулятор дуги сообщает нам значение длины дуги вместе с другими соответствующими измерениями только в соответствии с выбранным полем.
Что такое длина дуги?
Длину дуги можно определить как общее расстояние между двумя точками на участке любой кривой. Вычисление длины сегмента дуги неправильной формы называется выпрямлением кривой. Меру дуги можно рассчитать с помощью обоих:
• Уравнение длины дуги
• Калькулятор дуги
Дуга и центральный угол:
Вершина или вершина центрального ангела является центром (O ) любой круг.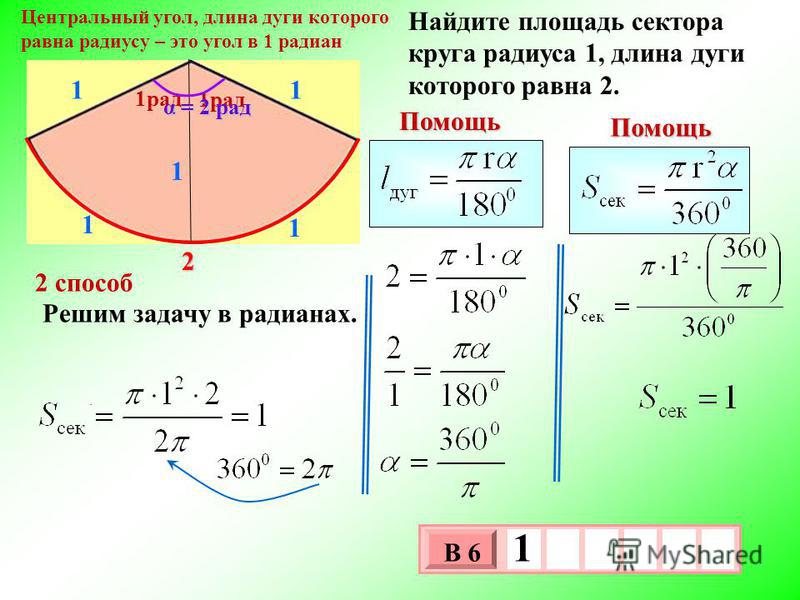
Его стороны представляют собой радиусы, пересекающие окружность в двух дискретных точках, скажем, A и B. Кроме того, она опирается на дугу между точками A и B.
Формула длины дуги:
Формулу длины дуги можно понять из следующего изображения:
Если угол равен (360) градусов или (2π), то длина дуги будет быть равным окружности. Кроме того, пропорция между углом и длиной дуги остается постоянной, поэтому уравнение длины дуги будет:
• (L / θ = C / 2π)
• В формуле для длины дуги длина окружности (C = 2πr )
• (L/θ = 2πr/2π)
• После деления останется только: (L / θ = r)
• Чтобы рассчитать формулу длины дуги, нужно умножить это уравнение на (θ: L = r * θ)
В радианах:
• Чтобы найти длину арки с радиусом, формула будет: (s = ϴ × r).
В градусах:
• Чтобы найти градусы длины арки, формула будет выглядеть так:( s = 2 π r (θ/360°)).
Как найти длину дуги (решенные примеры)?
Определение длины дуги больше не является сложным методом, так как вы можете использовать калькулятор длины дуги для быстрых вычислений. Кроме того, формула длины дуги является лучшим, но трудоемким способом определения длины дуги. Посмотрите приведенные примеры для лучшего понимания:
Пример:
Если радиус данного круга равен (50 см ), а его центральный угол равен (π/4 ), то какова будет площадь дуги?
• Поскольку даны две меры; радиус и центральный ангел. Поэтому мы применим формулу, чтобы найти длину дуги в радианах: ( s = ϴ × r ). просто поместите в него значения.
• ( S = 50 * π/4 = 25π/2см = 39см).
Как работает калькулятор длины дуги?
Этот онлайн-калькулятор дуги предлагает очень простой интерфейс, с помощью которого вы можете легко определить длину дуги и различные связанные параметры. Шаги:
Ввод:
Калькулятор поможет вам рассчитать длину дуги по:
1.
No related posts.
20)
Вычисление длины дуги плоской кривой
Пусть
известна функция 
и
требуется найти длину дуги, заданной
функцией 
,
где ![$ xin[a,,b]$](https://studfile.net/html/2706/39/html_aL1tHGr2Kq.YG82/img-IYCnLe.png){kind=small}
.
Для
определения длины дуги 
необходимо
вычислитьопределенный
интеграл:
Рассмотрим
случай параметрического задания кривой:
где ![$ tin[a,,b]$](https://studfile.net/html/2706/39/html_aL1tHGr2Kq.YG82/img-DBnYVc.png){kind=small}
.
В этом случае для определения длина
дуги 
вычисляется определенный
интеграл:
Рассмотрим
случай, когда кривая задается в полярных
координатах 
где![$ varphiin[alpha,,beta]$](https://studfile.net/html/2706/39/html_aL1tHGr2Kq.YG82/img-SZBr42.png){kind=small}
.
Тогда для определения длины
дуги
вычисляется
следующийопределенный
интеграл:
21)
Как вычислить объем тела вращения с помощью определенного интеграла?
Помимо нахождения
площади плоской фигуры с помощью
определенного интегралаважнейшим
приложением темы является вычисление
объема тела вращения.
Материал простой, но читатель должен
быть подготовленным: необходимо уметь
решатьнеопределенные
интегралы средней
сложности и применять формулу
Ньютона-Лейбница в определенном
интеграле.
Как и для задачи нахождения площади,
нужны уверенные навыки построения
чертежей – это чуть ли не самое важное
(поскольку интегралы сами по себе чаще
будут лёгкими). Освоить грамотную и
быструю технику построения графиков
можно с помощью методических
материалов Графики
и свойства Элементарных функций и Геометрические
преобразования графиков.
Но, собственно, о важности чертежей я
уже неоднократно говорил на
уроке Определенный
интеграл. Как вычислить площадь фигуры.
Вообще
в интегральном исчислении очень много
интересных приложений, с помощью
определенного интеграла можно вычислить
площадь фигуры, объем тела вращения,длину
дуги, площадь
поверхности вращения и
многое другое. Поэтому будет весело,
пожалуйста, настройтесь на оптимистичный
лад!
Представьте
некоторую плоскую фигуру на координатной
плоскости. Представили? … Интересно,
кто что представил… =))) Её площадь мы
уже находили. Но, кроме того, данную
фигуру можно ещё и вращать, причем
вращать двумя способами:
–
вокруг
оси абсцисс 
;
–
вокруг оси ординат 
.
В
данной статье будут разобраны оба
случая. Особенно интересен второй способ
вращения, он вызывает наибольшие
затруднения, но на самом деле решение
практически такое же, как и в более
распространенном вращении вокруг оси
абсцисс. В качестве бонуса я вернусь
к задаче
нахождения площади фигуры,
и расскажу вам, как находить площадь
вторым способом – по оси 
.
Даже не столько бонус, сколько материал
удачно вписывается в тему.
Начнем
с наиболее популярной разновидности
вращения.
Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
Пример
1
Вычислить
объем тела, полученного вращением
фигуры, ограниченной линиями 
,
вокруг
оси
.
Решение:
Как и в задаче на нахождение площади, решение
начинается с чертежа плоской фигуры.
То есть, на плоскости 
необходимо
построить фигуру, ограниченную
линиями
,
,
при этом не забываем, что уравнение
задаёт
ось
.
Как рациональнее и быстрее выполнить
чертёж, можно узнать на страницахГрафики
и свойства Элементарных функций и Определенный
интеграл. Как вычислить площадь фигуры.
Это китайское напоминание, и на данном
моменте я больше не останавливаюсь.
Чертёж
здесь довольно прост:
Искомая
плоская фигура заштрихована синим
цветом, именно она и вращается вокруг
оси 
В
результате вращения получается такая
немного яйцевидная летающая тарелка,
которая симметрична относительно оси
.
На самом деле у тела есть математическое
название, но по справочнику что-то лень
уточнять, поэтому едем дальше.
Соседние файлы в папке Матан
- #
- #
- #
- #
12.03.201538.36 Кб21экзамен матан 15-19.odt
- #
- #
12.03.2015195.13 Кб21Экзаменационные ответы матан 1-8.odt
Приложения определённого интеграла
Вычисление площадей плоских фигур
Пусть f(x)≥0 для ∀x∈[a,b]. Рассмотрим криволинейную трапецию, ограниченную кривыми y=0, x=a, x=b, y=f(x). Разобьём отрезок [a,b] на части точками a=x0<x1<…<xn=b, выберем внутри каждого элементарного отрезка [xi,i+1] по точке ξi∈[xi,i+1]. Заменим криволинейную трапецию, ограниченную линиями y=0,x=xi, x=xi+1, y=f(x), прямоугольником y=0, x=xi, x=i+1, y=f(ξ). Если f — непрерывная функция, то площадь этого прямоугольника равна f(ξ)·(xi+1-xi)=f(ξ)·Δxi и при достаточно малом Δxi близка площади заменяемой трапеции. Просуммировав, получим, с одной стороны, приближенное значение площади криволинейной трапеции, с другой стороны, интегральную сумму 
для интеграла 
. Переходя к пределу при увеличении числа точек разбиения, получаем площадь S исходной криволинейной трапеции 
Назовём трапецию простейшей областью, если она ограничена кривыми x = a, x = b, y = f1(x), y = f2(x), и для всех x∈[a,b] выполнено неравенство f1(x) ≤ f2(x). Нетрудно видеть, что для простейшей области 
Аналогично, если φ1(y)≤φ2(y) для всех y∈[c,d], то для криволинейной трапеции ограниченной кривыми y=c, y=d, x = φ1(y), x = φ2(y) (простейшей областью второго типа), имеем
В общем случае плоскую область разбивают на простейшие области рассмотренных выше типов.
Примеры
1. Найти площадь фигуры, ограниченной линиями y = x2 и x = y2.
Эти кривые пересекаются в точках A(0,0) и B(1,1). Поэтому
2. Найти площадь фигуры, ограниченной линиями y2 = 2x + 1 и x-y-1=0.
Эти кривые пересекаются в точках A(0,-1) и B(4,3). В данном случае лучше рассматривать простейшую область второго типа. Поэтому
см. также Площадь фигуры, ограниченной линиями:
Вычисление объёмов
Пусть область такова, что для ∀x∈[a,b] известна площадь S(x) сечения плоскостью x=const. Тогда, заменяя объём области заключенной между плоскостями x=xi, x=xi+1 на объём цилиндра S(ξ)·Δxi, получаем
Для тел, полученных вращением кривой y=f(x) вокруг оси OX, имеем . Если кривую y=f(x) вращать вокруг оси OY, то .
Примеры
1. Трапеция ограничена кривыми Вычислить объём тела, полученного вращением этой трапеции вокруг оси OX.
Подставляя в формулу, получаем
см. также Объем фигуры, образованной в результате вращения вокруг оси:
Вычисление длины дуги кривой
Рассмотрим кривую L. Разделим кривую на части точками (xi,yi), i = 1,..,n. Заменим дугу кривой между точками (xi, yi) и (xi+1, yi+1) хордой эти точки соединяющей. Тогда для длины дуги Δli имеем . Просуммировав по всем точкам деления, получаем
Пусть кривая задана параметрически или, что то же самое, в векторной форме . Тогда где ti — точка лежащая между ti и ti+1. Переходя к пределу при увеличении числа точек разбиения, имеем
(1)
Аналогично, для пространственной кривой, заданной параметрически или, что, то же самое, в векторной форме , длина кривой равна
(2)
Для кривой, заданной явно уравнением y=f(x), формула (1) приобретает вид
(3)
Если кривая задана в полярной системе координат, то
Поэтому
Подставляя в формулу для длины кривой, получаем
(4)
Примеры.
1. Найти длину дуги кривой y = ln(x), заключенной между точками Так как кривая задана явно, то . Делаем замену . Тогда x²=t²-1, 2x·dx=2t·dt и поэтому
2. Найти длину дуги кривой заключенной между точками t1 = 0 и t2 = 2π.
Так как кривая задана параметрически, то x′i=-3·a·cos²(t)·sin(t), y′t=3·a·sin²(t)·cos(t) и поэтому
.
Вычисление двойных интегралов (криволинейные интегралы). Также рассмотрен пример нахождения центра тяжести однородной плоской фигуры.
Также рекомендуется ознакомиться с возможностью решения интегралов онлайн.
Приложения криволинейных интегралов
Краткая теория
Длина дуги
Длину дуги
плоской или пространственной линии
определяют по формуле:
Масса дуги
Если
– линейная плотность вещества в точках дуги,
то массу
дуги
определяют по формуле:
Статистические моменты
Статистические
моменты
и
плоской дуги
относительно координатных осей
и
определяют по формулам:
Моменты инерции
Моменты
инерции
,
плоской дуги
относительно координатных осей
и
определяют по формулам:
Полярный момент инерции
Полярный
момент инерции
плоской дуги
относительно начала координат определяют по
формуле:
Площадь фигуры
Площадь
фигуры, расположенной в плоскости
и ограниченной замкнутой линией
, вычисляют по формуле:
Работа, приложенная к точке, при перемещении по дуге
Работу, совершаемую силой
приложенной в точке
при перемещении ее по дуге
, вычисляют по формуле:
Примеры решения задач
Задача 1
Найти
момент инерции относительно оси
четверти однородной окружности
, расположенной в первом
квадранте.
Решение
Окружность
однородна, следовательно
, следовательно искомый
момент инерции:
Для
удобства вычислений перейдем к параметрическим уравнениям окружности
Тогда:
Ответ:
Задача 2
Найти
массу дуги кривой
от точки
до
, если плотность в каждой точке
ее равна абсциссе точки;
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Плотность
дуги:
Искомая масса будет выражаться
криволинейным интегралом 1-го рода:
Производная:
Искомая масса:
Ответ:
.
Задача 3
Найти
массу дуги окружности
, лежащей в первой
четверти, если плотность в каждой ее точке равна абсциссе точки.
Решение
Плотность:
Искомая масса будет
выражаться криволинейным интегралом 1-го рода:
Параметрическое
уравнение окружности:
Окружность лежит в
первой четверти, поэтому
Ответ:
.
Задача 4
Вычислить
работу силы
при обходе точки ее приложения по границе
области
в положительном направлении, начиная от точки
.
Решение
Искомая
работа будет равна криволинейному интегралу 2-го рода:
Для
вычисления интеграла воспользуемся формулой Грина:
Ответ:
.
Задача 5
Вычислить
работу силового поля
при перемещении материальной точки вдоль пути
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Параметр
:
Перейдем к
определенному интегралу:
Искомая работа:
Ответ:
Задача 6
Вычислить
работу силы
при перемещении материальной точки вдоль линии
от точки
до точки
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Криволинейный
интеграл 2-го рода можно свести к определенному интегралу по следующей формуле:
Получаем:
Ответ: