Как найти дугу вписанного угла четырехугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Вписанный четырехугольник — это четырехугольник, все вершины которого лежат на одной окружности.

Центр окружности, описанной около четырехугольника — точка пересечения серединных перпендикуляров, проведенных к сторонам четырехугольника.

Признаки вписанного четырехугольника

Для того, чтобы четырехугольник был вписанным, необходимо и достаточно, чтобы выполнялось одно из следующих равенств:

Специальные случаи

Любые квадраты, прямоугольники, равнобедренные трапеции можно вписать в окружность.

Свойства вписанного четырехугольника

Произведение диагоналей вписанного четырехугольника равняется сумме произведений его противолежащих сторон.
Диагонали вписанного четырехугольника относятся как суммы, произведений сторон, сходящихся в концах диагоналей.
Диагонали вписанного четырехугольника разбивают его на две пары подобных треугольников.
Сумма квадратов противолежащих сторон четырехугольника равна квадрату диаметра описанной окружности.
Сумма противолежащих углов четырехугольника равна $180^{circ}$ .

Использование свойств и признаков вписанного четырехугольника при решении геометрических задач.

Задача 1. Высоты и остроугольного треугольника пересекаются в точке . Докажите, что .

Решение. Рассмотрим четырехугольник .

$angle ADF+angle AEF=90^{circ}+90^{circ}=180^{circ}$ .

Следовательно, вокруг четырехугольника можно описать окружность и по свойству вписанных углов, опирающихся на одну дугу .

Рассмотрим четырехугольник .

$angle BEC=angle CDB=90^{circ}$ .

Следовательно, вокруг четырехугольника можно описать окружность и по свойству вписанного четырехугольника $angle ECB+angle EDB =180^{circ}$ .

$angle EDB +angle ADE = 180^{circ}$ — свойство смежных углов.

Следовательно, $angle ECB+180^{circ}-angle ADE =180^{circ}$ .

ч.т.д.

Задача 2. В остроугольном треугольнике проведены высоты и . На них из точек и опущены перпендикуляры и соответственно. Докажите, что прямые и параллельны.

Решение. Рассмотрим четырехугольник .

$angle EFD=angle EGD=90^{circ}$ .

Рассмотрим четырехугольник .

$angle AEC=angle ADC=90^{circ}$ .

— соответственные углы, образованные при пересечении прямых и секущей .

Следовательно, прямые и параллельны.

ч.т.д.

Источник

Четырехугольники, вписанные в окружность. Теорема Птолемея

Вписанные четырёхугольники и их свойства

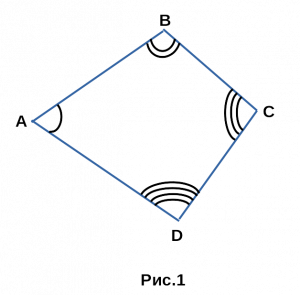
Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .

Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .

Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .

Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.

Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

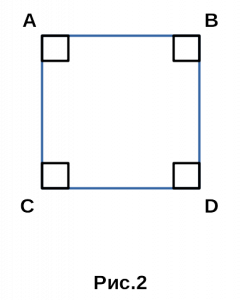
Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.

Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.

Теорема 2 доказана.

Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Фигура	Рисунок	Свойство
Окружность, описанная около параллелограмма		Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба		Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции		Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида		Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Окружность, описанная около параллелограмма
	Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
	Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
	Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
	Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Окружность, описанная около параллелограмма

Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность, описанная около ромба

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность, описанная около трапеции

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность, описанная около дельтоида

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Теорема Птолемея

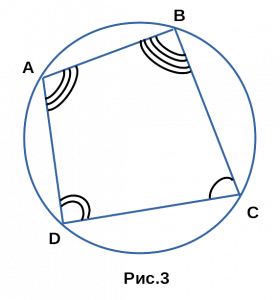
Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).

Докажем, что справедливо равенство:

Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

откуда вытекает равенство:

(1)

Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

Вписанный четырехугольник. Задание 6

При решении задач на нахождение углов вписанного четырехугольника нам нужно вспомнить, что

1. Четырехугольник называется вписанным в окружность, если все его вершины лежат на окружности:

2. Сумма противоположных углов вписанного четырехугольника равна 180°:

Рассмотрим решение задач из Открытого банка заданий по математике:

1 .Задание B7 (№ 27871)

Угол A четырехугольника ABCD, вписанного в окружность, равен 58°. Найдите угол C этого четырехугольника. Ответ дайте в градусах.

Сумма углов А и С равна 180°, поэтому угол С равен 180°-58°=122°

Ответ: 122°

2 . Задание B7 (№ 27927)

Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

Углы 82° и 58° не могут быть противоположными, так как их сумма не равна 180°. Значит, оставшиеся углы являются противоположными к этим. очевидно. что величина большего угла равна 180°-58°=122°

3 . Задание B7 (№ 27928)

Углы A, B и C четырехугольника ABCD относятся как 1:2:3. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.

Введем единичный угол. Тогда величины углов А, В и С можно записать так:

А=х, В=2х, С=3х. Суммы противоположных углов вписанного четырехугольника равны и равны 180°. Сумма углов А и С равна 4х и равна 180°. Отсюда х=45°.

Очевидно, что величина угла D равна 4х-2х=90°

Сумма углов четырехугольника

Свойства

Сумма углов четырехугольника равна 360°.
∠A + ∠B + ∠C + ∠D = 360°.
Если четырехугольник правильный, то каждый угол по 90°
и этот четырехугольник является квадратом.
∠A = ∠B = ∠C = ∠D, ⇒ ∠A = ∠B = ∠C = ∠D = 90°,
ABCD — квадрат.
Сумма противоположных углов четырехугольника равна 180°,
если около четырехугольника описана окружность.
∠A + ∠С = ∠В + ∠D = 180°.

Такие четырехугольники называют вписанными.

Это все виды четырехугольников,
которые изучаются в школьном
курсе по геометрии.

источники:

http://ege-ok.ru/2012/03/23/vpisannyiy-chetyirehugolnik-zadanie-6

http://colibrus.ru/summa-uglov-chetyrehugolnika/

Источник

Вписанный четырехугольник. Задание 6

При решении задач на нахождение углов вписанного четырехугольника нам нужно вспомнить, что

1. Четырехугольник называется вписанным в окружность, если все его вершины лежат на окружности:

2. Сумма противоположных углов вписанного четырехугольника равна 180°:

Рассмотрим решение задач из Открытого банка заданий по математике:

1 .Задание B7 (№ 27871)

Сумма углов А и С равна 180°, поэтому угол С равен 180°-58°=122°

Ответ: 122°

2 . Задание B7 (№ 27927)

3 . Задание B7 (№ 27928)

Введем единичный угол. Тогда величины углов А, В и С можно записать так:

Очевидно, что величина угла D равна 4х-2х=90°

Центральные и вписанные углы

О чем эта статья:

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

Сумма углов четырехугольника

Свойства

Сумма углов четырехугольника равна 360°.
∠A + ∠B + ∠C + ∠D = 360°.
Если четырехугольник правильный, то каждый угол по 90°
и этот четырехугольник является квадратом.
∠A = ∠B = ∠C = ∠D, ⇒ ∠A = ∠B = ∠C = ∠D = 90°,
ABCD — квадрат.
Сумма противоположных углов четырехугольника равна 180°,
если около четырехугольника описана окружность.
∠A + ∠С = ∠В + ∠D = 180°.

Такие четырехугольники называют вписанными.

Это все виды четырехугольников,
которые изучаются в школьном
курсе по геометрии.

источники:

http://skysmart.ru/articles/mathematic/centralnye-i-vpisannye-ugly

http://colibrus.ru/summa-uglov-chetyrehugolnika/

Источник

Геометрия

Окружность и четырехугольник

Определение

Четырехугольник называется вписанным в окружность, если окружность проходит через все вершины четырехугольника.

Очевидно, что окружность, в которую вписан четырехугольник, является описанной около любого из треугольников, на которые разбивается четырехугольник какой-либо диагональю.

Определение

Четырехугольник называется описанным около окружности, если окружность касается всех сторон четырехугольника.

Свойства и признаки вписанных и описанных четырехугольников

Напомним, что сумма внутренних углов выпуклого -угольника находится по формуле . Для четырехугольника n=4 и сумма углов выпуклого четырехугольника равна . Обращаем внимание, что ь далее будут рассматриваться именно выпуклые четырехугольники.

Теорема 1 (свойство и признак вписанного четырехугольника)

Если четырехугольник вписан в окружность, то сумма его противолежащих углов равна (свойство). И наоборот.
Если у четырехугольника сумма противолежащих углов равна , то около него можно описать окружность (признак).

Доказательство:

Пусть четырехугольник ABCD вписан в окружность (рис. 1). Тогда вписанные углы ABC и CDA , а также углы BCD и DAB опираются на дуги, дополняющие одна другую до окружности. А это и означает, что как , так и . Свойство вписанного четырехугольника доказано.

Рис. 1

Докажем признак вписанного четырехугольника.
Пусть у выпуклого четырехугольника ABCD сумма противолежащих углов и а значит, углов и равна . Через три вершины четырехугольника, например, через вершины проведем окружность (это можно сделать всегда). Тогда и четверая вершина принадлежит окружности так как в противном случае вершина лежала бы или внутри круга, ограниченного окружностью, или вне его. Следовательно, угол не измерялся бы половиной дуги ABC, и значит, сумма углов и не измерялась бы полусуммой дуг ABC и ADC и, таким образом, сумма углов и не равнялась бы Полученное противоречие и доказывает теорему.

Теорема доказана.

Теорема 2

Доказать, что если в выпуклом четырехугольнике ABCD углы ABD и ACD равны, то такой четырехугольник можно вписать в окружность. Верно и обратное.

Доказательство:

Пусть в четырехугольнике ABCD углы ABD и ACD равны. Проведем через точки A, B, C окружность и предположим, что вершина лежит, например, внутри круга (рис. 2), границей которого является проведенная окружность.

Рис. 2

Продолжим отрезки и до пересечения с окружностью в точках D_1 и D_2 соответственно.
Тогда $angle ABD = frac{1}{2} smile AD_2D_1$ , а $angle ACD = frac{1}{2} smile AD_2$ , что приводит к противоречию, так как по условию . Итак, точка должна лежать на окружности или находиться вне круга. Предположим, что она находится вне круга (рис. 3).

Рис. 3

Обозначим через D_1 и D_2 точки пересечения окружности с отрезками и соответственно. Тогда $angle ABD = frac{1}{2} smile AD_1$ , а $angle ACD = frac{1}{2} smile AD_1D_2$ , что, как и в первом случае, также вступает в противоречие с условием задачи. Вывод: точка является точкой окружности, описанной около четырехугольника ABCD .
Обратно, если четырехугольник ABCD вписан в окружность, то равенство углов ABD и ACD следует из того, что они являются вписанными углами, опирающимися на одну и ту же дугу.

Теорема доказана.

Замечание 1
Очевидно, что четырехугольник ABCD можно вписать в окружность и в случаях, когда или , или , или .

Теорема 3

Доказать, что если — точка пересечения диагоналей четырехугольника ABCD и , то около такого четырехугольника можно описать окружность. Верно и обратное.

Доказательство:

Пусть имеет место равенство , которое преобразуется в пропорцию $frac{AM}{BM} = frac{MD}{MC}$ . А тогда так как как вертикальные углы (рис. 4), то треугольники BMC и AMD подобны и, значит, .

Рис. 4

Последнее равенство и означает (замечание 1), что около четырехугольника ABCD можно описать окружность. Справедливость обратного утверждения очевидным образом следует из свойства хорд.

Теорема доказана.

Теорема 4 (Теорема Птолемея)

Если четырехугольник вписан в окружность, то сумма произведений его противолежащих сторон равна произведению его диагоналей.

Доказательство:

В четырехугольнике ABCD (рис. 5) построим угол ABE ( — точка диагонали ), равный углу DBC . Тогда треугольники ABE и DBC будут подобными, так как как вписанные углы, опирающиеся на одну и ту же дугу.

Рис. 5

Но в таком случае $frac{AB}{BD} = frac{AE}{DC}$ , т.е. Из подобия же треугольников BCE и ABD следует, что $frac{BC}{BD} = frac{EC}{AD}$ или Таким образом,, что и требовалось доказать.
Обратно. Пусть в четырехугольнике произведение его диагоналей равно сумме произведений его противолежащих сторон, то есть .
Через точки и проведем прямые так, чтобы в получившемся треугольнике ABK выполнялись равенства: , (рис. 6).

Рис. 6

Тогда по первому признаку подобия треугольников и, значит, $frac{AB}{AC} = frac{BK}{CD} = frac{AK}{AD}$ , откуда следует, что . Так как то по второму признаку подобия треугольников и, таким образом, $frac{KD}{BC} = frac{AD}{AC}$ , откуда . Но тогда или . Отсюда следует, что и, значит, точка принадлежит отрезку , откуда вытекает равенство . Полученное равенство углов означает, что точки , , и лежат на одной окружности (отрезок виден из точек и под одним углом), а это и требовалось доказать.

Теорема доказана.

Теорема 5 (свойство и признак описанного четырехугольника)

Если четырехугольник описан около окружности, то суммы его противолежащих сторон равны (свойство). И наоборот.
Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность (признак).

Доказательство:

Пусть четырехугольник ABCD описан около окружности и пусть , , , — точки касания окружности со сторонами четырехугольника (рис. 7). Тогда по свойству касательных имеем . Складывая полученные равенства, находим, что или .
Свойство описанного четырехугольника доказано.

Рис. 7

Докажем признак описанного четырехугольника.
Если четырехугольник ABCD ромб, то он является описанным около окружности с центром в точке пересечения его диагоналей.

Рассмотрим теперь случай, когда у выпуклого четырехугольника ABCD есть неравные соседние стороны. Допустим, что AB > BC , и, значит, AD > DC . Отложим на сторонах углов ABC и ADC отрезки BM = BC и DN=DC (рис. 8).

Рис. 8

Поскольку по условию имеем AM=AN , и поэтому треугольник AMN — равнобедренный с основанием . Треугольники CBM и CDN по построению также равнобедренные с основаниями и .
По свойству медианы равнобедренного треугольника медианы этих трех треугольников, проведенные к их основаниям, являются их высотами. Значит, прямые, содержащие эти медианы, — серединные перпендикуляры к сторонам треугольника CMN и поэтому пересекаются в одной точке .
Эти же медианы являются и биссектрисами равнобедренных треугольников AMN , CBM и CDN . Поэтому лучи , и — биссектрисы углов , и четырехугольника ABCD , которые образуют с его сторонами острые углы, так как по условию данный четырехугольник выпуклый. Значит, точка равноудалена от всех сторон четырехугольника ABCD , и поэтому он является описанным около окружности с центром в этой точке.
Теорема доказана.

Рассмотрим примеры.

Пример 1

В остроугольном треугольнике ABC проведены высоты $AA_{1}$ , $BB_{1}$ , $CC_{1}$ . Пусть — точка пересечения высот. Построить треугольник $A_{1}B_{1}C_{1}$ и перечислить все образовавшиеся четырехугольники, около которых можно описать окружность (рис. 9).

Рис. 9

Решение:
Рассмотрим четырёхугольник $BA_{1}HC_{1}$ : прямые углы $BA_{1}H$ и $BC_{1}H$ опираются на один и тот же отрезок , который и будет диаметром описанной окружности. Аналогично для четырёхугольников: $AC_{1}A_{1}C$ (диаметр ); $BC_{1}B_{1}C$ (диаметр ); $BA_{1}B_{1}A$ (диаметр ); $CA_{1}HB_{1}$ (диаметр ); $AB_{1}HC_{1}$ (диаметр ).

Ответ:

$BA_{1}HC_{1}$ , $CA_{1}HB_{1}$ , $AC_{1}HB_{1}$ , $AC_{1}A_{1}C$ , $BC_{1}B_{1}C$ , $BA_{1}B_{1}A$ .

Пример 2

В остроугольном треугольнике ABC проведены высоты $AA_{1}$ и $CC_{1}$ . Доказать, что треугольник $A_{1}BC_{1}$ подобен данному треугольнику ABC с коэффициентом подобия, равным cos B .

Решение:
На стороне треугольника ABC как на диаметре опишем полуокружность, которая пройдет через основания высот $A_{1}$ и $C_{1}$ (рис. 10).

Рис. 10

Так как четырехугольник $AC_{1}A_{1}C$ вписанный, то $angle BAC = 180^circ - angle C_{1}A_{1}C.$ Следовательно, $angle BAC = angle C_{1}A_{1}B$ и $triangle A_{1}BC_{1} sim triangle ABC$ . Так как стороны $A_{1}B$ и являются соответствующими сторонами в подобных треугольниках, то их отношение $A_{1}B : AB$ равно коэффициенту подобия. Но в прямоугольном треугольнике $ABA_{1}$ отношение сторон $A_{1}B : AB = cos B$ . Итак, $triangle A_{1}BC_{1} sim triangle ABC$ и . Что и требовалось доказать.

Пример 3

Доказать, что около параллелограмма можно описать окружность тогда и только тогда, когда параллелограмм является прямоугольником.

Решение:
Покажем, что если параллелограмм можно вписать в окружность, то такой параллелограмм будет прямоугольником.
Действительно, пусть параллелограмм ABCD вписан в окружность. Тогда по теореме 1 . Но в параллелограмме противолежащие углы равны, поэтому .
Аналогично показывается, что и , а это и доказывает требуемое. Обратное утверждение очевидно.

Пример 4

Доказать, что параллелограмм, в который можно вписать окружность, является ромбом.

Решение:
Так как в описанном около окружности четырехугольнике суммы противолежащих сторон равны (теорема 5), то в случае параллелограмма это условие равносильно равенству смежных сторон. Следовательно, такой параллелограмм — ромб. Что и требовалось доказать.

Следствие 1

Параллелограмм, в который можно вписать окружность и около которого можно описать окружность, является квадратом.

Пример 5

Доказать, что около трапеции можно описать окружность тогда и только тогда, когда она является равнобочной.

Решение:
Рассмотрим трапецию ABCD с параллельными сторонами и (рис. 11).

Рис. 11

Так как сумма внутренних односторонних углов при параллельных прямых равна , то
А поскольку около трапеции можно описать окружность тогда и только тогда, когда сумма ее противолежащих углов равна (теорема 1), то . Таким образом, . Но эти вписанные углы измеряются соответственно половинами дуг BCD и ABC . Поэтому, так как дуга у дуг BCD и ABC общая, то вписанные углы, опирающиеся на дуги и , равны. Но тогда равными будут и дуги и . Но равные дуги стягиваются равными хордами, что и требовалось доказать.

Пример 6

Доказать, что если выпуклый четырехугольник имеет ось симметрии, то либо около него можно описать окружность, либо в него можно вписать окружность.

Решение:
Если ось симметрии не проходит ни через одну вершину четырехугольника, он представляет собой равнобочную трапецию или прямоугольник и является вписанным.
Рассмотрим случай, когда ось симметрии выпуклого четырехугольника, например, ABCD проходит через его вершину, скажем, . Тогда очевидно, что эта ось будет проходить и через противолежащую вершине вершину . Но в таком случае вершина будет симметрична вершине и, значит, сторона окажется симметричной стороне , а сторона будет симметрична стороне . Поэтому AB=AD , BC=CD и, таким образом, . Полученное равенство означает, что четырехугольник ABCD является описанным около окружности и это есть или дельтоид (рис. 12), или ромб. Что и требовалось доказать.

Рис. 12

Пример 7

Трапеция описана около окружности. Доказать, что концы боковой стороны трапеции и центр окружности являются вершинами прямоугольного треугольника.

Решение:
Рассмотрим описанную трапецию с параллельными сторонами и (рис. 13).

Рис. 13

Так как сумма внутренних односторонних углов при параллельных прямых равна , то .
А поскольку лучи и , где — центр вписанной в трапецию окружности, являются биссектрисами углов BCD и CDA соответственно, то и, таким образом, в треугольнике DOC угол COD с вершиной является прямым.
Аналогично показывается, что треугольник BOA также является прямоугольным, а это и доказывает требуемое.

Пример 8

Равнобочная трапеция описана около окружности. Найти радиус окружности, если основания трапеции равны и .

Решение:
Пусть в описанной равнобочной трапеции ABCD основание AD = a , а основание (рис. 14).

Рис. 14

Тогда из равенства сторон и и того, что (теорема 5), следует, что $AB = CD = frac{(a + b)}{2}$ .
Пусть и — перпендикуляры к основанию . Очевидно, что и AE = FD , а значит, четырехугольник EBCF — прямоугольник, у которого . Поэтому $AE = frac{AD - EF}{2} = frac{a - b}{2}$ . Из прямоугольного же треугольника BEA находим $BE = sqrt{{AB^2} - {AE^2}} = sqrt{(frac{a+b}{2})^2 - (frac{a - b}{2})^2} = sqrt{ab}$ и, таким образом, радиус вписанной в трапецию окружности равен $frac{sqrt{ab}}{2}$

Ответ:

$dfrac{sqrt{ab}}{2}$

Пример 9

Около окружности описана равнобочная трапеция, у которой средняя линия равна Определить периметр трапеции и ее боковую сторону.

Решение:
Пусть K, L, N — точки касания окружности с описанной около нее равнобочной трапецией ABCD (рис. 15) и пусть , а — средняя линия трапеции.

Рис. 15

Тогда , а DN = DL . Поэтому DM = DC . Но поскольку отрезок $DM = frac{1}{2}(BC + AD) = EF = m$ , то DC = m . Отсюда периметр трапеции ABCD — это .

Ответ:

4 m; m

Пример 10

Доказать, что если центр вписанной в четырехугольник окружности совпадает с точкой пересечения диагоналей, то этот четырехугольник — ромб. Верно и обратное.

Решение:
Пусть точка — центр окружности, вписанной в четырехугольник ABCD (рис.16), — точки касания окружности с четырехугольником.

Рис. 16

Так как , то и, значит, Треугольники ABC и ADC — равнобедренные и — биссектриса, поэтому — равнобедренный и Тогда , т. е. четырехугольник ABCD — ромб. Наоборот, если — точка пересечения диагоналей ромба, которые по свойству ромба лежат на биссектрисах его углов, то расстояния от точки до каждой из сторон ромба равны. Отсюда и следует, что точка — центр вписанной в ромб окружности. Что и требовалось доказать.

Источник

Посмотри, углы ( displaystyle alpha ) и ( displaystyle beta ) лежат друг напротив друга, значит, они противоположные. А что же тогда с углами ( displaystyle varphi ) и ( displaystyle psi )? Они вроде бы тоже противоположные?

Можно ли вместо углов ( displaystyle alpha ) и ( displaystyle beta ) взять углы ( displaystyle varphi ) и ( displaystyle psi )?

Конечно, можно!

Главное, чтобы у четырехугольника нашлись какие-то два противоположных угла, сумма которых будет ( displaystyle 180{}^circ ).

Оставшиеся два угла тогда сами собой тоже дадут в сумме ( displaystyle 180{}^circ ). Не веришь? Давай убедимся.

Смотри:

Пусть ( displaystyle alpha +beta =180{}^circ ). Помнишь ли ты, чему равна сумма всех четырех углов любого четырехугольника? Конечно, ( displaystyle 360{}^circ ).

То есть ( displaystyle alpha +beta +varphi +psi =360{}^circ ) — всегда! ( displaystyle 180{}^circ )

Но ( displaystyle alpha +beta =180{}^circ ), →( displaystyle varphi +psi =360{}^circ -180{}^circ =180{}^circ).

Волшебство прямо!

Так что запомни крепко-накрепко:

Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна ( displaystyle 180{}^circ )

и наоборот:

Если у четырехугольника есть два противоположных угла, сумма которых равна ( displaystyle 180{}^circ ), то такой четырехугольник вписанный.

Доказательство смотри чуть дальше.

А пока давай посмотрим, к чему приводит этот замечательный факт о том, что у вписанного четырехугольника сумма противоположных углов равна ( displaystyle 180{}^circ ).

Вот, например, приходит в голову вопрос, а можно ли описать окружность вокруг параллелограмма?

Источник