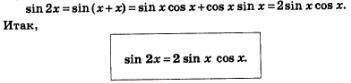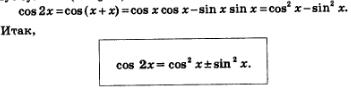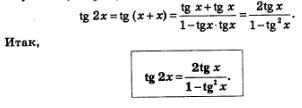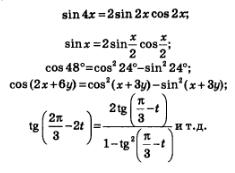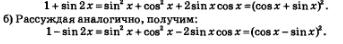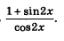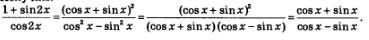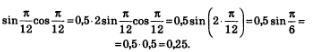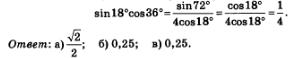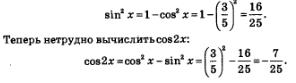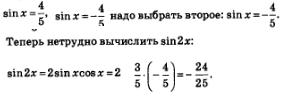Как найти два аргумента - Исправление недочетов и поиск решений вместе с Examum.ru

Формулы двойного и половинного аргумента. Универсальная подстановка

Формулы двойного аргумента
Формулы половинного аргумента
Формулы универсальной подстановки
Примеры

п.1. Формулы двойного аргумента

Выведем формулы двойного аргумента, исходя из формул суммы (см. §13 и §14 данного справочника)

begin{gather*} sin2alpha=sin(alpha+alpha)=sinalpha cosalpha+cosalpha sinalpha=2sinalpha cosalpha\ cos2alpha=cos(alpha+alpha)=cosalpha cosalpha-sinalpha sinalpha=cos^2alpha-sin^2alpha\ tg2alpha=tg(alpha+alpha)=frac{tgalpha+tgalpha}{1-tgalphacdot tgalpha}=frac{2tgalpha}{1-tg^2alpha} end{gather*}

Умножим полученное выражение на котангенс вверху и внизу дроби, и получим еще одно полезное выражение:

begin{gather*} tg2alpha=frac{2tgalpha}{1-tg^2alpha}=frac{2tgalpha}{1-tg^2alpha}cdot{ctgalpha}{ctgalpha}=frac{2}{ctgalpha-tgalpha}\ ctg2alpha=ctg(alpha+alpha)=frac{ctgalphacdot ctgalpha-1}{ctgalpha+ctgalpha}=frac{ctg^2alpha-1}{2ctgalpha}=frac{ctgalpha-tgalpha}{2} end{gather*}

begin{gather*} sin2alpha=2sinalpha cosalpha\ cos2alpha=cos^2alpha-sin^2alpha=2cos^alpha-1=1-2sin^2alpha\ tg2alpha=frac{2tgalpha}{1-tg^2alpha}=frac{2}{ctgalpha-tgalpha}\ ctg2alpha=frac{ctg^2alpha-1}{2ctgalpha}=frac{ctgalpha-tgalpha}{2} end{gather*}

Например:
Найдем (sin2alpha) и (tg2alpha), если (sinalpha=0,8, fracpi2ltalphaltpi)
Угол (alpha) во 2-й четверти, косинус отрицательный:
(cosalpha=-sqrt{1-sin^2alpha}=-sqrt{1-0,8^2}=-0,6)
(tgalpha=frac{sinalpha}{cosalpha}=frac{0,8}{-0,6}=-frac43)
Синус двойного угла: (sin2alpha=2sinalpha cosalpha=2cdot 0,8cdot(-0,6)=-0,96)
Тангенс двойного угла: (tg2alpha=frac{2tgalpha}{1-tg^2alpha}=frac{2cdot left(-frac43right)}{1-left(-frac43right)^2}=frac{-frac83}{1-frac{16}{9}}=frac83 : frac79=frac83cdotfrac97=frac{24}{7}=3frac37)

п.2. Формулы половинного аргумента

По формуле двойного аргумента для косинуса: (cos2alpha=2cos^2alpha-1)
Заменим слева угол (2alpharightarrow alpha), а справа угол (alpharightarrowfrac{alpha}{2}).
Получаем: begin{gather*} cosalpha=2cos^2frac{alpha}{2}-1Rightarrow 2cos^2frac{alpha}{2}=1+cosalphaRightarrow cos^2frac{alpha}{2}=frac{1+cosalpha}{2} end{gather*} Из другой формулы двойного аргумента для косинуса: (cos2alpha=1-2sin^2alpha), получаем: begin{gather*} cosalpha=1-2sin^2frac{alpha}{2}Rightarrow 2sin^2frac{alpha}{2}=1-cosalphaRightarrow sin^2frac{alpha}{2}=frac{1-cosalpha}{2} end{gather*} Для квадрата тангенса и котангенса половинного угла: begin{gather*} tg^2frac{alpha}{2}=frac{sin^2frac{alpha}{2}}{cos^2frac{alpha}{2}}=frac{1-cosalpha}{1+cosalpha}, ctg^2frac{alpha}{2}=frac{1}{tg^2frac{alpha}{2}}=frac{1+cosalpha}{1-cosalpha} end{gather*}

begin{gather*} sin^2frac{alpha}{2}=frac{1-cosalpha}{2}, cos^2frac{alpha}{2}=frac{1+cosalpha}{2}\ tg^2frac{alpha}{2}=frac{1-cosalpha}{1+cosalpha}, ctg^2frac{alpha}{2}=frac{1+cosalpha}{1-cosalpha} end{gather*}

Например:
Найдем (cosfrac{alpha}{2}) и (ctgfrac{alpha}{2}), если (sinalpha=-frac{-sqrt{3}}{2}, piltalphaltfrac{3pi}{2})
Угол (alpha) в 3-й четверти, косинус отрицательный: (cosalpha=-frac12)
Половинный угол (fracpi2ltfrac{alpha}{2}ltfrac{3pi}{4}) во 2-й четверти, косинус отрицательный:
(cosfrac{alpha}{2}=-sqrt{frac{1+cosalpha}{2}}=-sqrt{frac{1-frac12}{2}}=-frac12)
Котангенс тоже отрицательный:
(ctgfrac{alpha}{2}=-sqrt{frac{1+cosalpha}{1-cosalpha}}=-sqrt{frac{1-frac12}{1+frac12}}=-frac{1}{sqrt{3}})

п.3. Формулы универсальной подстановки

Любую тригонометрическую функцию можно выразить через тангенс половинного угла.

Для тангенса формула универсальной подстановки получается из формулы двойного угла: $$ tgalpha=frac{2tgfrac{alpha}{2}}{1-tg^2frac{alpha}{2}} $$ Тогда котангенс через тангенс половинного угла: $$ ctgalpha=frac{1-tg^2frac{alpha}{2}}{2tgfrac{alpha}{2}} $$ Для синуса: $$ sinalpha=2sinfrac{alpha}{2}cosfrac{alpha}{2}=2frac{sinfrac{alpha}{2}}{cosfrac{alpha}{2}}cos^2frac{alpha}{2}=2tgfrac{alpha}{2}cos^2frac{alpha}{2}=frac{2tgfrac{alpha}{2}}{1+tg^2frac{alpha}{2}} $$ Для косинуса: $$ cosalpha=frac{sinalpha}{tgalpha}=frac{2tgfrac{alpha}{2}}{1+tg^2frac{alpha}{2}} : frac{2tgfrac{alpha}{2}}{1-tg^2frac{alpha}{2}}=frac{1-tg^2frac{alpha}{2}}{1+tg^2frac{alpha}{2}} $$

begin{gather*} sinalpha=frac{2tgfrac{alpha}{2}}{1+tg^2frac{alpha}{2}}\ \ cosalpha=frac{1-tg^2frac{alpha}{2}}{1+tg^2frac{alpha}{2}}\ \ tgalpha=frac{2tgfrac{alpha}{2}}{1-tg^2frac{alpha}{2}}\ \ ctgalpha=frac{1-tg^2frac{alpha}{2}}{2tgfrac{alpha}{2}} end{gather*}

Универсальная подстановка эффективна при решении тригонометрических уравнений, а также интегрировании.

п.4. Примеры

Пример 1. Вычислите:
a) begin{gather*} 2cosfrac{pi}{8}sinfrac{7pi}{8}=2cosfrac{pi}{8}sinleft(pi-frac{pi}{8}right)=2cosfrac{pi}{8}sinfrac{pi}{8}=sinfrac{pi}{4}=frac{sqrt{2}}{2} end{gather*}
б) begin{gather*} 6cos^2frac{pi}{12}-3=3left(2cos^2frac{pi}{12}-1right)=3cdot cosfrac{pi}{6}=3cdot frac{sqrt{3}}{2}=frac{3sqrt{3}}{2} end{gather*}
в) begin{gather*} cos^4frac{23pi}{12}-sin^4frac{13pi}{12}=cos^4left(2pi-frac{pi}{12}right)-sin^4left(pi+frac{pi}{12}right)=cos^4frac{pi}{12}-sin^4frac{pi}{12}=\ =left(cos^2frac{pi}{12}-sin^2frac{pi}{12}right)underbrace{left(cos^2frac{pi}{12}+sin^2frac{pi}{12}right)}_{=1}=cos^2frac{pi}{12}-sin^2frac{pi}{12}=cosfrac{pi}{6}=frac{sqrt{3}}{2} end{gather*}
г) begin{gather*} ctgfrac{7pi}{8}+tgfrac{7pi}{8}=ctgleft(pi-frac{pi}{8}right)+tgleft(pi-frac{pi}{8}right)=-ctgfrac{pi}{8}-tgfrac{pi}{8}=\ =-left(frac{cosfrac{pi}{8}}{sinfrac{pi}{8}}+frac{sinfrac{pi}{8}}{cosfrac{pi}{8}}right)=-frac{cos^2frac{pi}{8}+sin^2frac{pi}{8}}{sinfrac{pi}{8}cdot cosfrac{pi}{8}}=-frac{1}{frac12 sinfrac{pi}{4}}=-frac{1}{frac12cdot frac{sqrt{2}}{2}}=-frac{4}{sqrt{2}}=-2sqrt{2} end{gather*}
д) begin{gather*} frac{1+ctg15^{circ}}{1-ctg15^{circ}}=frac{1+ctg15^{circ}}{1-ctg15^{circ}}cdot frac{sin15^{circ}}{sin15^{circ}}=frac{sin15^{circ}+cos15^{circ}}{sin15^{circ}-cos15^{circ}}=\ =frac{(sin15^{circ}+cos15^{circ})^2}{(sin15^{circ}-cos15^{circ})(sin15^{circ}+cos15^{circ})}=frac{sin^2 15^{circ}+2sin15^{circ}cos15^{circ}+cos^2 15^{circ}}{sin^2 15^{circ}-cos^2 15^{circ}}=\ =-frac{1+2sin15^{circ}cos15^{circ}}{cos^2 15^{circ}-sin^2 15^{circ}}=-frac{1+sin30^{circ}}{cos30^{circ}}=-frac{1+frac12}{frac{sqrt{3}}{2}}=-frac{3}{sqrt{3}}=-sqrt{3} end{gather*}
e*) begin{gather*} sinfrac{pi}{10}sinfrac{3pi}{10}=frac{2cosfrac{pi}{10}}{2cosfrac{pi}{10}}cdot sinfrac{pi}{10}sinfrac{3pi}{10}=frac{left(2cosfrac{pi}{10}sinfrac{pi}{10}right)}{2cosfrac{pi}{10}}sinfrac{3pi}{10}=\ =frac{sinfrac{pi}{5}}{2cosfrac{pi}{10}}sinleft(frac{pi}{2}-frac{pi}{5}right)=frac{sinfrac{pi}{5}cosfrac{pi}{5}}{2cosfrac{pi}{10}}=frac{sinfrac{2pi}{5}}{4cosleft(frac{pi}{2}-frac{2pi}{5}right)}=frac{sinfrac{2pi}{5}}{4sinfrac{2pi}{5}}=frac14 end{gather*}

Пример 2.Упростите выражение:
a) begin{gather*} frac{1-tg^2alpha}{1+tg^2alpha}=frac{1-tg^2alpha}{frac{1}{cos^2alpha}}=(1-tg^2alpha)cos^2alpha=cos^2alpha-sin^2alpha=cos2alpha end{gather*}
б) begin{gather*} cos^4left(2alpha+frac{5pi}{2}right)-sin^4left(2alpha-frac{3pi}{2}right)=cos^4left(2alpha+2pi+frac{pi}{2}right)-sin^4left(2alpha-2pi+frac{pi}{2}right)=\ =cos^4left(2alpha+frac{pi}{2}right)-sin^4left(2alpha+frac{pi}{2}right)=sin^4 2alpha-cos^4 2alpha=\ =(sin^2 2alpha-cos^2 2alpha)underbrace{(sin^2 2alpha+cos^2 2alpha)}_{=1}=sin^2 2alpha-cos^2 2alpha=-cos4alpha end{gather*}
в) begin{gather*} sin2alpha+2sin^2left(alpha-frac{5pi}{4}right)=sin2alpha+1-cosleft(2left(alpha-frac{5pi}{4}right)right)=\ =sin2alpha+1-cosleft(2alpha-frac{5pi}{2}right)=sin2alpha+1-cosleft(2alpha-2pi-fracpi2right)=\ =sin2alpha+1-cosleft(2alpha-fracpi2right)=sin2alpha+1-sin2alpha=1 end{gather*}
г) begin{gather*} frac{ctgalpha(sin2alpha-sinalpha)}{cos2alpha-cosalpha+1}=frac{frac{cosalpha}{sinalpha}(2sinalpha cosalpha-sinalpha)}{cos2alpha-cos alpha+1}=frac{cosalpha(2cosalpha-1)}{cos2alpha-cosalpha+1}=\ =frac{2cos^2alpha-cosalpha}{2cos^2alpha-1-cosalpha+1}=frac{2cos^2alpha-cosalpha}{2cos^2alpha-cosalpha}=1 end{gather*}
д) begin{gather*} frac{tg^2left(2alpha-fracpi4right)-1}{tg^2left(2alpha-frac{5pi}{4}right)+1}=frac{tg^2left(2alpha-fracpi4right)-1}{tg^2left(2alpha-fracpi4-piright)+1}=frac{tg^2left(2alpha-fracpi4right)-1}{tg^2left(2alpha-fracpi4right)+1}=\ =left(tg^2left(2alpha-fracpi4right)-1right)cos^2left(2alpha-fracpi4right)=sin^2left(2alpha-fracpi4right)-cos^2left(2alpha-fracpi4right)=\ =-cos2left(2alpha-fracpi4right)=-cosleft(4alpha-fracpi2right)=-sin4alpha end{gather*}

Пример 3.Найдите:
a) (sin2alpha) и (ctg2alpha), если (cosalpha=frac{12}{13}, -fracpi2ltalphalt 0)
Угол (alpha) в 4-й четверти, синус отрицательный: (sinalpha=-sqrt{1-cos^2alpha}=-sqrt{1-left(frac{12}{13}right)^2}=-frac{5}{13})
Котангенс: (ctgalpha=frac{cosalpha}{sinalpha}=frac{12}{13} : left(-frac{5}{13}right)=-frac{12}{5}=-2,4)
Синус двойного угла: (sin2alpha=2sinalpha cosalpha=2cdot left(-frac{5}{13}right)cdot frac{12}{13}=-frac{120}{169})
Котангенс двойного угла: (ctg2alpha=frac{ctg^2alpha-1}{2ctgalpha}=frac{left(-frac{12}{5}right)^2-1}{2cdotleft(-frac{12}{5}right)}=frac{144-25}{25} : left(-frac{24}{5}right)=-frac{119}{5cdot 24}=-frac{119}{120})
Ответ: (-frac{120}{169}) и (-frac{119}{120})

б) (tg^2left(fracpi4+alpharight)), если (sin2alpha=frac15) begin{gather*} tg^2left(fracpi4+alpharight)=left(tgleft(fracpi4+alpharight)right)^2=left(frac{tgfracpi4+tgalpha}{1-tgfracpi4cdot tgalpha}right)^2=left(frac{1+tgalpha}{1-tgalpha}right)^2=\ =left(frac{1+tgalpha}{1-tgalpha}cdot frac{cosalpha}{cosalpha}right)^2=left(frac{cosalpha+sinalpha}{cosalpha-sinalpha}right)^2=frac{cos^2alpha+2sinalpha cosalpha+sin^2alpha}{cos^2alpha-2sinalpha cosalpha+sin^2alpha}=\ =frac{1+2sinalpha cosalpha}{1-2sinalpha cosalpha}=frac{1+sin2alpha}{1-sin2alpha} end{gather*} Подставляем:
(tg^2left(fracpi4+alpharight)=frac{1+frac15}{1-frac15}=frac64=1,5)
Ответ: 1,5

в) ( frac{sin(60^{circ}+alpha)}{4sinleft(15^{circ}+fracalpha4right)sinleft(75^{circ}-fracalpha4right)}), если (sinleft(30^{circ}+fracalpha2right)=0,8, 0^{circ}ltalphalt 90^{circ}) begin{gather*} frac{sin(60^{circ}+alpha)}{4sinleft(15^{circ}+fracalpha4right)sinleft(75^{circ}-fracalpha4right)}=frac{sin(60^{circ}+alpha)}{4sinleft(15^{circ}+fracalpha4right)sinleft(90^{circ}-left(15^{circ}+fracalpha4right)right)}=\ =frac{sin(60^{circ}+alpha)}{4sinleft(15^{circ}+fracalpha4right)cosleft(15^{circ}+fracalpha4right)}=frac{sin(60^{circ}+alpha)}{2sinleft(2left(15^{circ}+fracalpha4right)right)}=frac{sin(60^{circ}+alpha)}{2sinleft(30^{circ}+fracalpha2right)}=\ =frac{2sinleft(30^{circ}+fracalpha2right)cosleft(30^{circ}+fracalpha2right)}{2sinleft(30^{circ}+fracalpha2right)}=cosleft(30^{circ}+fracalpha2right) end{gather*} Нужно найти косинус при известном синусе. $$ 0^{circ}ltalphalt 90^{circ}Rightarrow 0^{circ}ltfracalpha2lt 45^{circ}Rightarrow 30^{circ}+fracalpha2lt 75^{circ} $$ Угол (left(30^{circ}+fracalpha2right)) в 1-й четверти, косинус положительный:
$$ cosleft(30^{circ}+fracalpha2right)=sqrt{1-sin^2left(30^{circ}+fracalpha2right)}=sqrt{1-0,8^2}=0,6 $$ Ответ: 0,6

г) ( sin2alpha), если (frac{2cosalpha+3sinalpha}{3cosalpha-2sinalpha}=-2) begin{gather*} frac{2cosalpha+3sinalpha}{3cosalpha-2sinalpha}=frac{frac{2cosalpha+3sinalpha}{cosalpha}}{frac{3cosalpha-2sinalpha}{cosalpha}}=frac{2+3tgalpha}{3-2tgalpha}=-2\ 2+3tgalpha=-2(3-2tgalpha)\ 3tgalpha-4tgalpha=-6-2\ tgalpha=8\ sin2alpha=2sinalpha cosalpha=2frac{sinalpha}{cosalpha}cos^2alpha=2tgalphacdot cos^2alpha=frac{2tgalpha}{1+tg^2alpha} end{gather*} Подставляем: (sin2alpha=frac{2cdot 8}{1+8^2}=frac{16}{65})
Ответ: (frac{16}{65})

Пример 4*.Упростите:
a) ( cosfrac{pi}{33}cosfrac{2pi}{33}cosfrac{4pi}{33}cosfrac{8pi}{33}cosfrac{16pi}{33} )
Умножим и разделим на (sinfrac{pi}{33}): begin{gather*} frac{sinfrac{pi}{33}cosfrac{pi}{33}}{sinfrac{pi}{33}}cosfrac{2pi}{33}cosfrac{4pi}{33}cosfrac{8pi}{33}cosfrac{16pi}{33}=frac{sinfrac{2pi}{33}cosfrac{2pi}{33}}{2sinfrac{pi}{33}}cosfrac{4pi}{33}cosfrac{8pi}{33}cosfrac{16pi}{33}=\ =frac{sinfrac{4pi}{33}cosfrac{4pi}{33}}{4sinfrac{pi}{33}}cosfrac{8pi}{33}cosfrac{16pi}{33}=frac{sinfrac{8pi}{33}cosfrac{8pi}{33}}{8sinfrac{pi}{33}}cosfrac{16pi}{33}=frac{sinfrac{16pi}{33}cosfrac{16pi}{33}}{16sinfrac{pi}{33}}=\ =frac{sinfrac{32pi}{33}}{32sinfrac{pi}{33}}=frac{sinleft(pi-frac{pi}{33}right)}{32sinfrac{pi}{33}}=frac{sinfrac{pi}{33}}{32sinfrac{pi}{33}}=frac{1}{32} end{gather*} Ответ: (frac{1}{32})

б) ( sin18^{circ}sin54^{circ} ) begin{gather*} sin18^{circ}sin54^{circ}=sin18^{circ}sin(90^{circ}-36^{circ})=sin18^{circ}cos36^{circ}=frac{sin18^{circ}cos18^{circ}cos36^{circ}}{cos18^{circ}}=\ =frac{sin36^{circ}cos36^{circ}}{2cos18^{circ}}=frac{sin72^{circ}}{4cos18^{circ}}=frac{sin72^{circ}}{4cos18^{circ}}=frac{sin(90^{circ}-18^{circ})}{4cos18^{circ}}=frac{cos18^{circ}}{4cos18^{circ}}=frac14 end{gather*} Ответ: (frac14)

в) ( sqrt{2+sqrt{2+2cos4alpha}} ), где (0le alphalefracpi2) begin{gather*} sqrt{2+sqrt{2+2cos4alpha}}=sqrt{2+sqrt{2(1+cos4alpha)}}=sqrt{2+sqrt{2cdot 2cos^2 2alpha}}=\ =sqrt{2+2cdot |cos2alpha|}=sqrt{2(1+|cos2alpha|)}= left[ begin{array} {l l} sqrt{2(1+cos2alpha)}, cos2alphageq 0\ sqrt{2(1-cos2alpha)}, cos2alphalt 0 end{array} right. =\ = left[ begin{array} {l l} sqrt{2cdot 2cos^2alpha}, 0leq 2alphaleqfracpi2\ sqrt{2cdot 2sin^2alpha}, fracpi2lt 2alphaleq pi end{array} right. = left[ begin{array} {l l} 2cosalpha, 0leq alphaleqfracpi4\ 2sinalpha, fracpi4lt alphaleq fracpi2 end{array} right. end{gather*} Ответ: (2cosalpha) при (0leq alphaleqfracpi4; 2sinalpha) при (fracpi4lt alphaleq fracpi2)
г) ( 4(sin^4x+cos^4x)-4(sin^6x+cos^6x)-1 )
Основное тригонометрическое тождество: (sin^2x+cos^2x=1)
Возведём в квадрат: begin{gather*} (sin^2x+cos^2x)^2=sin^4x+cos^4x+2sin^2x cos^2x=1\ sin^4x+cos^4x=1-frac{(2sinx cosx)^2}{2}=1-frac{sin^2 2x}{2} end{gather*} Возведём в куб: begin{gather*} (sin^2x+cos^2x)^3=sin^6x+cos^6x+3sin2x cos^4x+3sin^4x cos^2x=1\ sin^6x+cos^6x = 1-3sin^2x cos^2xunderbrace{(cos^2x+sin^2x)}_{=1}=\ =1-frac34(2sinx cosx)^2=1-frac{3sin^2 2x}{4} end{gather*}

begin{gather*} sin^4x+cos^4x=1-frac{sin^2 2x}{2}\ \ sin^6x+cos^6x = 1-frac{3sin^2 2x}{4} end{gather*}

Подставляем: begin{gather*} 4left(1-frac{sin^2 2x}{2}right)-4left(1-frac{3sin^2 2x}{4}right)=1=4-2sin^2 2x-4+3sin^2 2x-1=\ =sin^2 2x-1=-cos^2 2x end{gather*} Ответ: (-cos^2 2x)

Источник

Формулы двойного аргумента позволяют представить тригонометрическую функцию удвоенного аргумента в виде выражения тригонометрических функций простого (одинарного) аргумента.

Эти формулы устанавливают соотношение между (sin 2 x), (cos 2 x), (tg 2 x) и (sin x), (cos x), (tg x).

Последовательно приведём и докажем формулы двойного аргумента для функций синуса, косинуса и тангенса.

1. Рассмотрим выражение (sin 2 x) — представим его аргумент в виде (2 x=x+x) и воспользуемся известной формулой синуса суммы аргументов:

sin(α+β)=sinα⋅cosβ+cosα⋅sinβ

Тогда получим:

sin2x=sin(x+x)=sinx⋅cosx+cosx⋅sinx=2sinx⋅cosx

Итак,

формула синуса двойного аргумента:

sin2x=2sinx⋅cosx

2. Рассмотрим выражение (cos 2 x) и аналогично представим его аргумент в виде (2 x=x+x), а также воспользуемся известной формулой косинуса суммы аргументов:

cos(α+β)=cosα⋅cosβ−sinα⋅sinβ

Тогда получим:

cos2x=cos(x+x)=cosx⋅cosx−sinx⋅sinx=cos2x−sin2x

Итак,

формула косинуса двойного аргумента:

cos2x=cos2x−sin2x

3. Теперь рассмотрим выражение ( tg 2 x) и вновь представим его аргумент в виде (2 x=x+x), что даст возможность воспользоваться известной формулой тангенса суммы аргументов:

tg(α+β)=tgα+tgβ1−tgα⋅tgβ

Тогда получим:

tg2x=tg(x+x)=tgx+tgx1−tgx⋅tgx=2tgx1−tg2x

;

формула тангенса двойного аргумента:

tg2x=2tgx1−tg2x

Обрати внимание!

Формулы синуса двойного аргумента и косинуса двойного аргумента верны для всех значений аргумента.

Формула тангенса двойного аргумента верна лишь для значений (x), входящих в область определения функций (tg x) и (tg 2 x), при выполнении условия

1−tg2x≠0

. То есть

x≠π2+πk,k∈ℤ

x≠π4+πn,n∈ℤ

Вместо аргумента (x) может стоять любое выражение, например:

sinx=2sinx2⋅cosx2

— эту формулу называют формулой половинного аргумента;

cos(2x+6y)=cos2(x+3y)=cos2(x+3y)−sin2(x+3y)

;

tg(2π3−2t)=tg(2(π3−t))=2tg(π3−t)1−tg2(π3−t)

и т. п.

Любую из рассмотренных формул двойного аргумента можно использовать в обе стороны.

Источник

17 декабря 2014

В закладки

Обсудить

Жалоба

Как найти второй аргумент к сочинению?

Несколько примеров того, как придумать второй аргумент в сочинении.

arg.docx

Источник

Гипермаркет знаний>>Математика>>Математика 10 класс>> Формулы двойного аргумента

§ 24. Формулы двойного аргумента

Здесь речь пойдет о формулах тригонометрии, позволяющих выразить Эти формулы обычно называют формулами двойного аргумента. Название, может быть, не очень удачно, как, впрочем, и такие названия, как «формулы приведения», «синус суммы», «косинус разности» и т.д., но это не суть важно: главное, что есть некий словесный символ, позволяющий посвященным понять, о чем идет речь.
Рассмотрим выражение sin2х, представив при этом 2х в виде х+х. Это позволит применить к выражению sin (х+ х)формулу «синус суммы» (см. § 21). Имеем:

Рассмотрим выражение соs2х, представив при этом 2х в виде х+х. Это позволит применить к выражению соs (х+х) формулу «косинус суммы» (см. § 21). Имеем:

Рассмотрим выражение tg 2х, представив при этом 2х в виде х+х. Это позволит применить к выражению tg (х+х) формулу «тангенс суммы» (см. § 23). Имеем:

Формулы «синус двойного аргумента» и «косинус двойного аргумента» справедливы для любых значений аргумента (никаких ограничений нет), тогда как формула «тангенс двойного аргумента» справедлива лишь для тех значений аргумента х, для которых определены tg х и tg 2 х, а также отличен от нуля знаменатель дроби, т.е.
Разумеется, формулы двойного аргумента можно применять и в тех случаях, когда место аргумента х занимает более сложное выражение. Так, справедливы следующие соотношения:

И, как всегда, любую из трех полученных в этом параграфе формул двойного аргумента можно использовать в написании как справа налево, так и слева направо. Например,

Пример 1. Доказать тождества:

Решение: а) Воспользуемся тем, что 1 = sin² х + соз² х, и формулой синуса двойного аргумента. Получим:

Пример 2. Сократить дробь
Решение. В числителе дроби воспользуемся доказанным в примере 1 а тождеством, а в знаменателе — формулой косинуса двойного аргумента. Получим:

Пример3.Вычислить:
Решение: а) Заданное выражение представляет собой правую часть формулы косинуса двойного аргумента. Заметив это, получим

б) Заданное выражение представляет собой правую часть формулы синуса двойного аргумента, но только не хватает множителя 2. Введя его, получим:

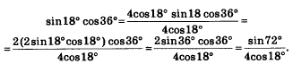
в) Этот пример значительно сложнее, но зато он красивее предыдущих: здесь нужно догадаться умножить и разделить заданное выражение на 4соs18°. Что это даст? Смотрите:

Как видите, мы дважды воспользовались формулой синуса двойного аргумента. Чтобы довести вычисления до конца, заметим, что 72°=90°-18°. Значит, sin 72⁰=sin (90°-18⁰)=соs18⁰. Таким образом,

Пример 4. Доказать тождество
Решение. Преобразуем левую часть доказываемого тождества:

Умножив и числитель, и знаменатель последней дроби на 2 («подгоняем» знаменатель под формулу синуса двойного аргумента), получим:

Итак, что и требовалось доказать.
Замечание. Еще раз обращаем ваше внимание на то, что тождество доказано лишь для допустимых значении х, конкретнее для
для значений х, при которых имеющиеся знаменатели отличны от нуля.
Пример 5. Зная, что

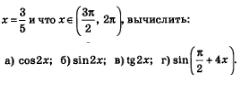
Решение: а) Воспользуемся формулой sin² х + соз² х = 1. Имеем:

б) Для вычисления sin2х воспользуемся формулой sin 2х = 2 sin хсоз x.
Значение соз х дано в условии, а значение sin х найдем следующим образом. Во-первых, мы уже знаем, что
Во-вторых, по условию аргумент х принадлежит четвертой четверти, а в ней синус отрицателен. Это значит, что из двух значении

в) tg2х вычислим, воспользовавшись определением тангенса:

г) Для вычисления 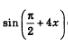сначала воспользуемся формулой приведения:
Применим к выражению соз4x формулу косинуса двойного аргумента: соз4х=соз² 2х — sin² 2х. Воспользуемся тем, что значения соз 2х и sin 2xуже найдены нами:

Пример 6. Решить уравнение sin4х-соз2х=0.
Решение. Если в левой части уравнения применить к выражению sin4x формулу синуса двойного аргумента, то удастся разложить левую часть на множители. Имеем последовательно:

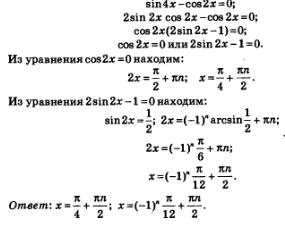
А.Г. Мордкович Алгебра 10 класс

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.

Разработка — Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email:

Источник

Функции одного и двух случайных аргументов

Краткая теория
Примеры решения задач

Краткая теория

Функция одного случайного аргумента

Если
каждому возможному значению случайной величины

соответствует одно возможное значение
случайной величины

, то

называют функцией случайного аргумента

Пусть
аргумент

– дискретная случайная величина.

Если
различным возможным значениям аргумента

соответствуют различные возможные значения
функции

, то вероятности
соответствующих значений

между собой равны.

Если
различным возможным значениям

соответствуют значения

, среди которых есть равные
между собой, то следует складывать вероятности повторяющихся значений

Математическое
ожидание такой функции:

Пусть
аргумент

– непрерывная случайная величина.

Если

– дифференцируемая строго возрастающая или
строго убывающая функция, обратная функция которой

, то плотность
распределения

случайной величины

находится с помощью равенства:

Математическое
ожидание такой функции:

или
непосредственно по формуле:

Функция двух случайных аргументов

Если
каждой паре возможных значений случайных величин

соответствует одно возможное значение
случайной величины

, то

называют функцией двух случайных аргументов

Пусть

– дискретные независимые случайные величины.
Для того, чтобы составить закон распределения функции

, надо найти все возможные
значения

и их вероятности.

Пусть

– непрерывные случайные величины. Если

независимы, то плотность распределения

суммы

(при условии, что плотность хотя бы одного из
аргументов задана на интервале

одной формулой) может быть найдена с помощью
равенства:

либо с
помощью равносильного равенства:

где

– плотности распределения аргументов

Если
возможные значения аргументов неотрицательны, то

находят по формуле:

либо с
помощью равносильного равенства:

Плотность
распределения суммы независимых случайных величин называют композицией.

Смежные темы решебника:

Плотность распределения вероятностей
Функции распределения случайных величин
Математическое ожидание и его свойства

Примеры решения задач

Пример 1

Дискретная
случайная величина

задана распределением:

Найти распределение функции

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Вероятность
возможного значения

равна сумме вероятностей несовместных событий

, то есть 0,4+0,5=0,9.
Вероятность возможного значения

равна 0,1.

Искомый
закон распределения

Пример 2

Случайная величина

распределена
равномерно на интервале

. Построить график случайной величины

и определить
плотность вероятности

Решение

Построим
график

В
зависимости от числа

обратных функций выделим следующие интервалы
для

На
интервалах

обратных функций не существует

Функция

на интервале

имеет две обратные функции:

На
интервале

, так как

Величина

распределена равномерно на интервале

, поэтому в этом интервале:

Искомая
плотность распределения может быть найдена по формуле:

Функция

на интервале

имеет одну обратную функцию:

На
интервале

, так как

Таким образом:

Проверка:

Пример 3

Случайная
величина

имеет плотность распределения

. Для случайной величины

найти плотность распределения

, вероятность

, математическое ожидание

и дисперсию

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Плотность
распределения

задается формулой:

где

-функция обратная к

Остальные величины можно вычислить с
помощью

или
непосредственно через

по формулам

Пример 4

Дискретные
независимые случайные величины заданы распределениями:

Составить
закон распределения случайной величины

Решение

Возможные
значения

есть суммы каждого возможного значения

со всеми возможными значениями

Найдем
вероятности этих возможных значений.

Для того,
чтобы

, достаточно, чтобы
величина

приняла значение

и величина

– значение

. Вероятности этих
возможных значений, как следует из данных законов распределения, соответственно
равны 0,4 и 0,2.

Аргументы

независимы, поэтому события

независимы, и, следовательно, вероятность их
совместного наступления (то есть вероятность события

) по теореме умножения
вероятностей равна

Аналогично
найдем:

Сложим
вероятности несовместных событий:

Искомое
распределение:

Проверка:

Пример 5

Независимые
случайные величины

заданы плотностями распределений:

Найти
композицию этих законов, то есть плотность распределения случайной величины

Решение

Так как
возможные значения аргументов неотрицательны, то применима формула:

Следовательно:

Здесь

, так как

и возможные значения

неотрицательны.

Итак:

Краткая теория
Примеры решения задач

Источник