-
Булевые функции и их представление. Двоичная запись целых чисел.
В курсе математического
анализа изучаются функции, определённые
на числовой прямой, на отрезке числовой
прямой, на плоскости и т.п. Так или
иначе, область определения – непрерывное
множество.
В курсе дискретной математики изучаются
функции, область определения которых
– дискретное
множество. Простейшим (но нетривиальным)
таким множеством является множество,
состоящее из двух элементов. Таким
образом, частным случаем функции
y=f(x1;x2;…;xn)
является функция, значения которой и
значения компонент её аргумента
принадлежат множеству {0;1}. Такую функцию
называют логической.
Аргумент логической функции (x1;x2;…;xn)
часто называют двоичным
(или булевым)
вектором, а его компоненты —двоичными(или
булевыми) переменными.
Логическую функцию
также называют логической
операцией,
т.к. значения функции и её аргументов
принадлежат одному множеству {0;1}.
Знаки логических
операций называют логическими связками.
Определение.
Алгебру,
носителем которой является множество
Х={х1, х2, …, хn,y},
элементы которого могут принимать
значения 0 или 1, а сигнатура которой
определена множеством логических связок
или логических операций, называют
алгеброй
логики (Булевой алгеброй).
Носитель –
переменный аргумент.
0 и 1 — не числа в
обычном понимании, а это логические
значения – истина и ложь.
Логическая функция
может быть задана несколькими способами:
–
словесно (описанием
ситуации),
–
алгебраическим
выражением,
–
таблицей истинности
–
электрической
схемой, состоящей из контактов
переключателей
Например:
1.Лифт
можно вызвать, если закрыты двери лифта
на первом этаже и на втором этаже и на
третьем этаже.
2.Если
закрытые двери на первом этаже обозначить
как А = 1, на втором – В = 1, на третьем –
С = 1, возможность вызвать лифт обозначить
как F = 1, а логическую функцию И обозначить
знаком умножения » × «, то алгебраическое
выражение будет иметь вид:
F =
A×B×С
3.
Таблица истинности, соответствующая
данному примеру будет иметь следующий
вид:
Таблица
25.1.
В
таблицу истинности заносятся все
возможные комбинации входных аргументов
и соответствующие этим комбинациям
значения выходной функции. Входные
комбинации записываются в порядке
возрастания их значений от всех нулей
до всех единиц сверху вниз. Число строк
полностью определённой функции от n
компонентов аргумента равно 2n,
где n
– число переменных (А,В,С).
4.
Электрическая контактная схема обладает
хорошей наглядностью, но может быть
легко построена лишь для самых простых
логических функций. Для нашего примера
эта схема может иметь следующий вид:

Описание логической функции одной и двух двоичных переменных.
Как уже было
отмечено, число логических функций для
n
компонентов аргумента определяется
выражением: 2p,
где p=2n.
Для n=1
число возможных значений логической
функции равно 4.
Таблица 25.2.
|
X |
y=f(x) |
|||
|
f0(x) |
f1(x) |
f2(x) |
f3(x) |
|
|
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
Анализ таблицы 25.2. позволяет
дать определение каждой из четырёх
логических функций:
-
f0(x)
— функция-константа “0”, т.к. она не
изменяет своего значения при изменении
аргумента, т.е. (y=0),
переменная x
для этой функции несущественна; -
f1(x)
— функция повторитель, т.к. она принимает
значения, равные значению аргумента,
т.е. (y=x); -
f2(x)
– функция отрицания, т.к. она принимает
значения противоположные значению
аргумента, т.е. (y=`x),
эта функция может еще обозначаться:
ùx,
¬x,
`x; -
f3(x)
— функция-константа “1”, т.к. она не
изменяет своего значения при изменении
аргумента, т.е. (y=1)
и, как для функции f0(x),
переменная x
для этой функции несущественна.
Все функции таблицы
2 – унарные, т.к. это функции от одной
переменной.
Для n=2
число возможных значений логической
функции равно 16.
Таблица 25.3.
|
Арг. |
Функция y=fi(x1,x2) |
||||||||||||||||
|
x1 |
x2 |
f0 |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
f8 |
f9 |
f10 |
f11 |
f12 |
f13 |
f14 |
f15 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
Перечислим
важнейшие функции, представленные в
таблице:
1) f1
— конъюнкция
(функция И),
конъюнкция – это фактически обычное
умножение
(нулей и
единиц). Конъюнкцией является функция,
которая принимает значение 1 только
тогда, когда все переменные равны 1, в
противном случае функция равна 0. Иногда
эту функцию обозначают x1&
x2
или x1
x2.
2)
f7
— дизъюнкция
(функция ИЛИ).
Дизъюнкцией (или логическим сложением)
n-переменных
называется функция, которая ровна 0
только тогда, когда все переменные равны
0. Иногда эту функцию обозначают (x1Úx2).
3)
f13
— импликация
(следование). (x1®x2)=`x1×x2
. Иногда
импликацию обозначают x1
x2,
это очень важная функция, особенно в
логике. Ее можно рассматривать следующим
образом: если x1
= 0 (т. е.
x1
“ложно”),
то из этого факта можно вывести и “ложь”,
и “истину” (и это будет правильно), если
x2=
1 (т. е. x2
“истинно”),
то истина выводится и из “лжи” и из
“истины”, и это тоже правильно. Только
вывод “из истины ложь” является
неверным.
4)
f9
—
эквивалентность или подобие. Эта функция
f9= 1
тогда и только тогда, когда x1 = x2.
Иногда эту функцию обозначают x1≡
x2
или x1~x2.
Любую
логическую
(булеву)
функцию
можно
выразить
через
три
логические
функции:
конъюнкцию,
дизъюнкцию
и
отрицание.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Загрузка…
Аннотация: Рассматривается принцип синтеза логических схем, реализующих заданную математическую формулу.
Преобразователь произвольных кодов — это логическая схема, реализующая определённую математическую формулу. На вход такой схемы подаётся двоичный код, соответствующий значению переменной 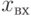

В качестве примера синтеза логической схемы рассмотрим 3-входовую схему [2], реализующую увеличение входного кода в три раза: 
- Определим максимально возможный код на выходе 3-входовой схемы:
— это пятиразрядное двоичное число. Поэтому количество выходов для данной схемы будет равно пяти.
- Заполним таблицу истинности для синтезируемой схемы (табл. 3.1). Поскольку количество выходов данной схемы больше одного, таблица включает в себя несколько (здесь пять ) столбцов, соответствующих двоичным разрядам выходного сигнала.
- Для каждого выхода найдем минимальное выражение с помощью карт Карно (рис. 3.1).
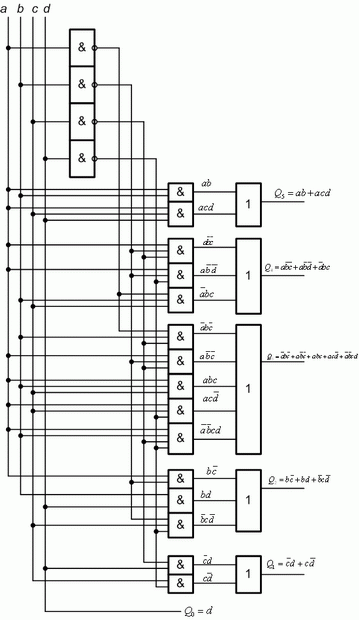
- По полученным выражениям построим логическую схему на пять выходов, каждый из которых соответствует двоичному разряду вычисляемого по заданной формуле числа (рис. 3.2).
увеличить изображение
Рис.
3.1.
Минимизация логических выражений для выходных сигналов преобразователя, реализующего формулу x_{вых}=3x_{вх}
увеличить изображение
Рис.
3.2.
Логическая схема преобразователя на 3 входа, реализующего формулу умножения на 3
Рассмотрим далее схему на 4 входа, реализующую ту же самую формулу 
- Определим максимально возможный код на выходе 4-входовой схемы:
— это шестиразрядное двоичное число. Поэтому количество выходов для данной схемы будет равно шести.
- Заполним таблицу истинности для синтезируемой схемы (табл. 3.2). Она включает в себя шесть столбцов, соответствующих двоичным разрядам выходного сигнала.
- Для каждого выхода найдем минимальное выражение с помощью карт Карно (рис. 3.3).
- По полученным выражениям построим логическую схему на шесть выходов, каждый из которых соответствует двоичному разряду вычисляемого по заданной формуле числа (рис. 3.4).
- Если весь столбец значений для выхода
, это означает, что независимо от состояния входных сигналов на выход
подаётся напряжение источника питания.
- Если весь столбец значений для выхода
, это означает, что независимо от состояния входных сигналов выход
подключен к общей точке («земле»).
увеличить изображение
Рис.
3.3.
Минимизация логических выражений для выходных сигналов 4-входового преобразователя, реализующего формулу x_{вых}=3x_{вх}
увеличить изображение
Рис.
3.4.
Логическая схема преобразователя на 4 входа, реализующего формулу умножения на 3
Определение 1.1. Двоичной функцией от N (N ³ 1) переменных называется функция , аргументы и значения которой выбираются из множеств
, т. е.
F: ,
Где
,
.
Замечание 1.2. Двоичные функции от N переменных также называют Булевыми (Булевскими) функциями от N переменных или N-местными булевыми функциями.
На множестве определим так называемый лексикографический порядок, т. е. для любого двоичного набора
определим его номер
.
Тогда двоичная функция однозначно может быть задана Табл.1.1 (называемой Таблицей истинности).
Таблица 1.1
|
Номер набора |
X1 … XN-1 Xn |
F(X1, …, XN) |
|
0 |
0 … 0 0 |
F(0, …, 0,0) |
|
1 |
0 … 0 1 |
F(0, …, 0,1) |
|
. . . |
. . . |
. . . |
|
2N – 2 |
1 … 1 0 |
F(1, …, 1,0) |
|
2N – 1 |
1 … 1 1 |
F(1, …, 1,1) |
При указанной договоренности о расположении наборов из функция однозначно определяется набором — столбцом значений. Отсюда непосредственно вытекает справедливость следующего утверждения.
Утверждение 1.3. Число двоичных функций от N переменных равно .
Перечислим все двоичные функции от одной и двух переменных. Имеется четыре функции от одной переменной (табл.1.2).
Таблица 1.2
|
X1 F |
F0 |
F1 |
F2 |
F3 |
|
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
Условное обозначение |
0 |
|
|
1 |
Функции и
не зависят от значения переменной
и называются Константными (
,
). Функция
называется Тождественной функцией, а функция
называется Отрицанием.
Функций от двух переменных — шестнадцать (табл.1.3).
Таблица 1.3
|
|
F0 |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
|
0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
Обозначение |
0 |
X1×X2 |
X1 |
X2 |
X1ÅX2 |
X1ÚX2 |
Продолжение табл.1.3
|
X1, X2 F |
F8 |
F9 |
F10 |
F11 |
F12 |
F13 |
F14 |
F15 |
|
0 0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
Обозначение |
X1¯X2 |
X1 ~ X2 |
|
|
X1 ® X2 |
X1½X2 |
1 |
Важнейшими из них являются: — конъюнкция (X1 X2, X1 & X2, X1
X2),
— сложение по модулю 2 (X1
X2),
— дизъюнкция (X1
X2),
— функция Пирса (X1
X2),
— импликация (X1
X2),
— функция Шеффера (X1| X2).
Определение 1.4. Переменная XI, или I-я переменная двоичной функции F(X1, …, XN) называется Существенной переменной функции F (т. е. функция F Существенно зависит от XI), если существует набор (A1, …, AI-1, AI+1, …, AN) Î, такой, что
F(A1, …, AI-1, 0, AI+1, …, AN) ¹ F(A1, …, AI-1, 1, AI+1, …, AN).
В противном случае переменная XI называется Несущественной (Фиктивной) переменной функции F.
Так, среди функций от двух переменных имеется ровно десять функций, существенно зависящих от всех своих переменных.
Число двоичных функций от N переменных растет с увеличением N чрезвычайно быстро. В табл.1.4 приведена зависимость функций от своих переменных при N £ 8.
Таблица 1.4
|
N |
Число функций от N переменных |
|
1 |
2 |
|
2 |
16 |
|
3 |
256 |
|
4 |
65536 |
|
5 |
4294967296 |
|
6 |
> 1.8 ×1019 |
|
7 |
> 3.4 ×1038 |
|
8 |
> 1.1 ×1077 |
С табличным заданием функции непосредственно связан такой ее параметр, как вес.
Определение 1.5. Множество двоичных наборов {(A1, …, AN) Î Î| F(A1, …, AN) = 1}, на которых функция F принимает значение 1, называется Областью истинности функции F. Мощность области истинности функции F называется Весом функции F и обозначается || F ||.
Очевидно, что 0 £ || F || £ 2N, причем равенства достигаются лишь для функций-констант 0 и 1. Если || F || = 2N-1, то функция F называется Равновероятной.
Для двоичных функций используются и другие способы задания, приспособленного для рассматриваемой в каждом конкретном случае задачи, которые будут рассмотрены далее.
| Следующая > |
|---|
Построение таблицы истинности. СДНФ. СКНФ. Полином Жегалкина.
Онлайн калькулятор позволяет быстро строить таблицу истинности для произвольной булевой функции или её вектора, рассчитывать совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы, находить представление функции в виде полинома Жегалкина, строить карту Карно и классифицировать функцию по классам Поста.
Калькулятор таблицы истинности, СКНФ, СДНФ, полинома Жегалкина
введите функцию или её вектор
Скрыть клавиатуру
∨
∧
¬
⊕
→
≡
↓
↑
0
1
a
b
c
x
y
z
(
)
X1
X2
X3
X4
X5
X6
Показать настройки
Таблица истинности
СКНФ
СДНФ
Полином Жегалкина
Классификация Поста
Минимизация, карта Карно
Фиктивные переменные
С решением
Построить
Построено таблиц, форм:
Как пользоваться калькулятором
- Введите в поле логическую функцию (например, x1 ∨ x2) или её вектор (например, 10110101)
- Укажите действия, которые необходимо выполнить с помощью переключателей
- Укажите, требуется ли вывод решения переключателем «С решением»
- Нажмите на кнопку «Построить»
Видеоинструкция к калькулятору
Используемые символы
В качестве переменных используются буквы латинского и русского алфавитов (большие и маленькие), а также цифры, написанные после буквы (индекс переменной). Таким образом, именами переменных будут: a, x, a1, B, X, X1, Y1, A123 и так далее.
Для записи логических операций можно использовать
как обычные символы клавиатуры (*, +, !, ^, ->, =), так и символы, устоявшиеся в литературе (∧, ∨, ¬, ⊕, →, ≡). Если на вашей клавиатуре отсутствует нужный символ операции, то используйте клавиатуру калькулятора (если она не видна, нажмите «Показать клавиатуру»), в которой доступны как все логические операции, так и набор наиболее часто используемых переменных.
Для смены порядка выполнения операций используются круглые скобки ().
Обозначения логических операций
- И (AND):
&•∧* - ИЛИ (OR):
∨+ - НЕ (NOT):
¬! - Исключающее ИЛИ (XOR):
⊕^ - Импликация:
->→=> - Эквивалентность:
=~≡<=> - Штрих Шеффера:
↑| - Стрелка Пирса:
↓
Что умеет калькулятор
- Строить таблицу истинности по функции
- Строить таблицу истинности по двоичному вектору
- Строить совершенную конъюнктивную нормальную форму (СКНФ)
- Строить совершенную дизъюнктивную нормальную форму (СДНФ)
- Строить полином Жегалкина (методами Паскаля, треугольника, неопределённых коэффициентов)
- Определять принадлежность функции к каждому из пяти классов Поста
- Строить карту Карно
- Минимизировать ДНФ и КНФ
- Искать фиктивные переменные
Что такое булева функция
Булева функция f(x1, x2, ... xn) — это любая функция от n переменных x1, x2, … xn, в которой её аргументы принимают одно из двух значений: либо 0, либо 1, и сама функция принимает значения 0 или 1. То есть это правило, по которому произвольному набору нулей и единиц ставится в соответствие значение 0 или 1. Подробнее про булевы функции можно посмотреть на Википедии.
Что такое таблица истинности?
Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов. Таблица состоит из n+1 столбцов и 2n строк, где n — число используемых переменных. В первых n столбцах записываются всевозможные значения аргументов (переменных) функции, а в n+1-ом столбце записываются значения функции, которые она принимает на данном наборе аргументов.
Довольно часто встречается вариант таблицы, в которой число столбцов равно n + число используемых логических операций. В такой таблице также первые n столбцов заполнены наборами аргументов, а оставшиеся столбцы заполняются значениями подфункций, входящих в запись функции, что позволяет упростить расчёт конечного значения функции за счёт уже промежуточных вычислений.
Логические операции
Логическая операция — операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых. В качестве основных операций обычно называют конъюнкцию (∧ или &), дизъюнкцию (∨ или |), импликацию (→), отрицание (¬), эквивалентность (=), исключающее ИЛИ (⊕).
Таблица истинности логических операций
Как задать логическую функцию
Есть множество способов задать булеву функцию:
- таблица истинности
- характеристические множества
- вектор значений
- матрица Грея
- формулы
Рассмотрим некоторые из них:
Чтобы задать функцию через вектор значений необходимо записать вектор из 2n нулей и единиц, где n — число аргументов, от которых зависит функция. Например, функцию двух аргументов можно задать так: 0001 (операция И), 0111 (операция ИЛИ).
Чтобы задать функцию в виде формулы, необходимо записать математическое выражение, состоящее из аргументов функции и логических операций. Например, можно задать такую функцию: a∧b ∨ b∧c ∨ a∧c
Способы представления булевой функции
С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:
- Совершенная дизъюнктивная нормальная форма (СДНФ)
- Совершенная конъюнктивная нормальная форма (СКНФ)
- Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Совершенная дизъюнктивная нормальная форма (ДНФ)
Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.
Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.
Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.
Например, ДНФ является функция ¬abc ∨ ¬a¬bc ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.
Совершенная конъюнктивная нормальная форма (КНФ)
Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.
Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.
Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.
Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.
Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.
Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1
Алгоритм построения СДНФ для булевой функции
- Построить таблицу истинности для функции
- Найти все наборы аргументов, на которых функция принимает значение 1
- Выписать простые конъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 0, то она входит в конъюнкцию с отрицанием, а иначе без отрицания
- Объединить все простые конъюнкции с помощью дизъюнкции
Алгоритм построения СКНФ для булевой функции
- Построить таблицу истинности для функции
- Найти все наборы аргументов, на которых функция принимает значение 0
- Выписать простые дизъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 1, то она входит в дизъюнкцию с отрицанием, а иначе без отрицания
- Объединить все простые дизъюнкции с помощью конъюнкции
Алгоритм построения полинома Жегалкина булевой функции
Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.
- Построить таблицу истинности для функции
- Добавить новый столбец к таблице истинности и записать в 1, 3, 5… ячейки значения из тех же строк предыдущего столбца таблицы истинности, а к значениям в строках 2, 4, 6… прибавить по модулю два значения из соответственно 1, 3, 5… строк.
- Добавить новый столбец к таблице истинности и переписать в новый столбец значения 1, 2, 5, 6, 9, 10… строк, а к 3, 4, 7, 8, 11, 12… строкам аналогично предыдущему пункту прибавить переписанные значения.
- Повторить действия каждый раз увеличивая в два раза количество переносимых и складываемых элементов до тех пор, пока длина не станет равна числу строк таблицы.
- Выписать булевы наборы, на которых значение последнего столбца равно единице
- Записать вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора записать единицу) и объединить их с помощью операции исключающего ИЛИ.
Примеры построения различных представлений логических функций
Построим совершенные дизъюнктивную и дизъюнктивную нормальные формы, а также полином Жегалкина для функции трёх переменных F = ¬ab∨¬bc∨ca
1. Построим таблицу истинности для функции
Построение совершенной дизъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает истинное значение: { 0, 0, 1 } { 0, 1, 0 } { 0, 1, 1 } { 1, 0, 1 } { 1, 1, 1 }
В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием:
K1: { 0, 0, 1 } — ¬a¬bc
K2: { 0, 1, 0 } — ¬ab¬c
K3: { 0, 1, 1 } — ¬abc
K4: { 1, 0, 1 } — a¬bc
K5: { 1, 1, 1 } — abc
Объединим конъюнкции с помощью дизъюнкции и получим совершенную дизъюнктивную нормальную форму:
K1 ∨ K2 ∨ K3 ∨ K4 ∨ K5 = ¬a¬bc ∨ ¬ab¬c ∨ ¬abc ∨ a¬bc ∨ abc
Построение совершенной конъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает ложное значение: { 0, 0, 0 } { 1, 0, 0 } { 1, 1, 0 }
В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием:
D1: { 0, 0, 0 } — a∨b∨c
D2: { 1, 0, 0 } — ¬a∨b∨c
D3: { 1, 1, 0 } — ¬a∨¬b∨c
Объединим дизъюнкции с помощью конъюнкции и получим совершенную конъюнктивную нормальную форму:
D1 ∧ D2 ∧ D3 = (a∨b∨c) ∧ (¬a∨b∨c) ∧ (¬a∨¬b∨c)
Построение полинома Жегалкина:
Добавим новый столбец к таблице истинности и запишем в 1, 3, 5 и 7 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 2, 4, 6 и 8 сложим по модулю два со значениями из соответственно 1, 3, 5 и 7 строк:
Добавим новый столбец к таблице истинности и запишем в 1 и 2, 5 и 6 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 3 и 4, 7 и 8 сложим по модулю два со значениями из соответственно 1 и 2, 5 и 6 строк:
Добавим новый столбец к таблице истинности и запишем в 1 2, 3 и 4 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 5, 6, 7 и 8 сложим по модулю два со значениями из соответственно 1, 2, 3 и 4 строк:
Окончательно получим такую таблицу:
Выпишем наборы, на которых получившийся вектор принимает единичное значение и запишем вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора следует записать единицу):
{ 0, 0, 1 } — c, { 0, 1, 0 } — b, { 0, 1, 1 } — bc, { 1, 1, 0 } — ab, { 1, 1, 1 } — abc
Объединяя полученные конъюнкции с помощью операции исключающего или, получим полином Жегалкина: c⊕b⊕bc⊕ab⊕abc


 — это пятиразрядное двоичное число. Поэтому количество выходов для данной схемы будет равно пяти.
— это пятиразрядное двоичное число. Поэтому количество выходов для данной схемы будет равно пяти.

 — это шестиразрядное двоичное число. Поэтому количество выходов для данной схемы будет равно шести.
— это шестиразрядное двоичное число. Поэтому количество выходов для данной схемы будет равно шести. , это означает, что независимо от состояния входных сигналов на выход
, это означает, что независимо от состояния входных сигналов на выход 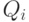 подаётся напряжение источника питания.
подаётся напряжение источника питания.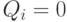 , это означает, что независимо от состояния входных сигналов выход
, это означает, что независимо от состояния входных сигналов выход