Как найти двойное векторное произведение - Исправление недочетов и поиск решений вместе с Examum.ru

Двойное векторное произведение трех векторов

Двойным векторным или векторно-векторным произведением трех векторов vec{a},vec{b},vec{c} называется выражение вида
(vec{a}times vec{b})times vec{c} или vec{a}times (vec{b}times vec{c}).
Для двойного векторного произведения надо сначала умножить векторно два вектора vec{a} и vec{b} , а затем полученное произведение еще раз умножают векторно на третий вектор vec{c} .
Двойное векторное произведение выражается формулами

(vec{a}times vec{b})times vec{c}=vec{b}left(vec{a}vec{c} right)-vec{a}left(vec{b}vec{c} right),

vec{a}times (vec{b}times vec{c})=vec{b}left(vec{a} vec{c}right)-vec{c}left(vec{a} vec{b}right); ; left(1 right)

Правило: Двойное векторное произведение равно произведению среднего вектора на скалярное произведение двух других, минус крайний вектор в скобке, умноженный на скалярное произведение двух других.
Если векторы vec{a},vec{b},vec{c} заданы своими проекциями

$vec{a}=x_{1}vec{i}+y_{1}vec{j}+z_{1}vec{k},; vec{b}=x_{2}vec{i}+y_{2}vec{j}+z_{2}vec{k},;vec{c}=x_{3}vec{i}+y_{3}vec{j}+z_{3}vec{k},;$

то двойное векторное произведение vec{a}times (vec{b}times vec{c}) будет равно:

$vec{a}times (vec{b}times vec{c})=begin{vmatrix} vec{i} & vec{j} &vec{k} \ x_{1} & y_{1} &z_{1} \ begin{vmatrix} y_{2} & z_{2}\ y_{3}& z_{3} end{vmatrix}&begin{vmatrix} z_{2} &x_{2} \ z_{3}& x_{3} end{vmatrix} & begin{vmatrix} x_{2} & y_{2}\ x_{3}& y_{3} end{vmatrix} end{vmatrix}=$

$=(y_{1}(x_{2}y_{3}-x_{3}y_{2})-z_{1}(x_{3}z_{2}-x_{2}z_{3}))vec{i}+$

$+(z_{1}(y_{2}z_{3}-y_{3}z_{2})-x_{1}(x_{2}y_{3}-x_{3}y_{2}))vec{j}+$

$+(x_{1}(x_{3}z_{2}-x_{2}z_{3})-y_{1}(y_{2}z_{3}-y_{3}z_{2}))vec{k}.$

Источник

Двойное векторное произведение и его свойства

Двойным векторным произведением векторов vec{a},vec{b},vec{c} называется вектор bigl[vec{a},[vec{b},vec{c}]bigr] , равный векторному произведению вектора vec{a} на векторное произведение векторов vec{b} и vec{c} . Произведение обозначается также vec{a}times(vec{b}timesvec{c}) .

Двойное векторное произведение обладает следующими свойствами, справедливыми для любых векторов vec{a},vec{b},vec{c} :

1. bigl[vec{a},[vec{b},vec{c}]bigr],=(vec{a},vec{c})cdotvec{b}-(vec{a},vec{b})cdotvec{c} ;

2. bigl[vec{a},[vec{b},vec{c}]bigr],+bigl[vec{b},[vec{c},vec{a}]bigr],+bigl[vec{c},[vec{a},vec{b}]bigr],=vec{o} ;

3. $vec{b}=frac{(vec{a},vec{b})}{|vec{a}|^2}cdotvec{a}+frac{1}{|vec{a}|^2}cdotbigl[vec{a},[vec{b},vec{a}]bigr],~vec{a}nevec{o}$ ;

4. Если $a=begin{pmatrix}x_a&y_a&z_aend{pmatrix}^T~b=begin{pmatrix}x_b&y_b&z_bend{pmatrix}^T,~c=begin{pmatrix}x_c&y_c&z_cend{pmatrix}^T$ — координатные столбцы векторов vec{a},vec{b},vec{c} в стандартном базисе, то координатный столбец $d=begin{pmatrix}x_d&y_d&z_dend{pmatrix}^T$ двойного векторного произведения vec{d}=bigl[vec{a},[vec{b},vec{c}]bigr] находится по формуле $vec{d}=bcdot a^Tcdot c-ccdot a^Tcdot b$ (мнемоническое правило: «бац» минус «цаб»).

Первое свойство доказывается, применяя формулы вычисления скалярного и векторного произведений в ортонормированном базисе.

Второе свойство следует из первого, если сделать циклическую перестановку векторов: bigl[vec{b},[vec{c},vec{a}]bigr],=(vec{b},vec{c})cdotvec{c}-(vec{b},vec{c})cdotvec{a} , bigl[vec{c},[vec{a},vec{b}]bigr],=(vec{c},vec{b})cdotvec{a}-(vec{c},vec{a})cdotvec{b} , а затем сложить эти равенства вместе с исходным (учитывая коммутативность скалярного произведения).

Третье свойство следует из первого (если положить vec{c}=vec{a} ). Это равенство дает разложение произвольного вектора vec{b} в виде суммы ортогональной проекции $vec{operatorname{pr}}_{vec{a}}vec{b}=frac{(vec{a},vec{b})}{|vec{a}|^2}cdotvec{a}$ и ортогональной составляющей $vec{b}_{perpvec{a}}=frac{1}{|vec{a}|^2}cdotbigl[vec{a},[vec{b},vec{a}]bigr]$ вектора vec{b} относительно оси, задаваемой вектором vec{a} (см. разд. 1.6).

Последнее свойство следует из первого с учетом п.2 замечаний 1.10. Заметим, что все произведения строк и столбцов согласованы, поэтому умножения можно производить в любом порядке, разумеется, не переставляя матрицы.

Пример 1.24. Даны векторы vec{a}=vec{i}+2{cdot}vec{j}+2{cdot}vec{k},~vec{b}=3{cdot}vec{i}-2{cdot}vec{j}+vec{k},~vec{c}=2{cdot}vec{i}-1{cdot}vec{j}+3{cdot}vec{k} . Требуется:

а) показать, что векторы vec{a},vec{b},vec{c} образуют базис, и найти векторы $vec{a},^{ast}, vec{b},^{ast}, vec{c},^{ast}$ взаимного базиса;
б) найти двойное векторное произведение bigl[vec{a},[vec{b},vec{c}]bigr] ;
в) найти ортогональную проекцию вектора vec{b} на ось, заданную вектором vec{a} , и ортогональную составляющую вектора vec{b}

относительно этой оси.

Решение. а) Поскольку смешанное произведение (vec{a},vec{b},vec{c})=-17 , найденное в примере 1.22, отлично от нуля, то векторы не компланарны (согласно второму геометрическому свойству смешанного произведения), т.е. образуют базис пространства. Найдем векторы взаимного базиса по формулам пункта 3 замечаний 1.13:

$begin{aligned} vec{a},^{ast}=&frac{[vec{b},vec{c}]}{(vec{a},vec{b},vec{c})}=frac{1}{-17}begin{vmatrix}vec{i}&vec{j}&vec{k}\3&-2&1\2&-1&3end{vmatrix}=-frac{1}{17}bigl(-5{cdot}vec{i}-7{cdot}vec{j}+1{cdot}vec{k}bigr);\ vec{b},^{ast}=&frac{[vec{c},vec{a}]}{(vec{a},vec{b},vec{c})}=frac{1}{-17}begin{vmatrix}vec{i}&vec{j}&vec{k}\2&-1&3\1&2&2end{vmatrix}=-frac{1}{17}bigl(-8{cdot}vec{i}-1{cdot}vec{j}+5{cdot}vec{k}bigr);\ vec{c},^{ast}=&frac{[vec{a},vec{b}]}{(vec{a},vec{b},vec{c})}=frac{1}{-17}begin{vmatrix}vec{i}&vec{j}&vec{k}\1&2&2\3&-2&1end{vmatrix}=-frac{1}{17}bigl(6{cdot}vec{i}+5{cdot}vec{j}-8{cdot}vec{k}bigr). end{aligned}$

б) По свойству 1 находим

$begin{aligned}bigl[vec{a},[vec{b},vec{c}]bigr],=,&(vec{a},vec{c})cdotvec{b}-(vec{a},vec{b})cdotvec{c}=\[3pt]=,&(1cdot2+2cdot(-1)+2cdot3)bigl(3cdotvec{i}-2cdotvec{j}+1cdotvec{k}bigr),-,(1cdot3+2cdot(-2)+2cdot1)bigl(2cdotvec{i}-1cdotvec{j}+3cdotvec{k}bigr),=\[2pt] =,&16cdotvec{i}-11cdotvec{j}+ 3cdotvec{k}.end{aligned}$

Для нахождения двойного векторного произведения можно использовать матричную форму записи (см. четвертое свойство). Векторам vec{a},vec{b},vec{c} соответствуют координатные столбцы

$a=begin{pmatrix}1\2\2end{pmatrix}!,qquad b=begin{pmatrix}3\-2\1end{pmatrix}!,qquad c=begin{pmatrix}2\-1\3end{pmatrix}!.$

По свойству 4 получаем координатный столбец vec{d} двойного векторного произведения vec{d}=bigl[vec{a},[vec{b},vec{c}]bigr] :

$begin{aligned} d=&begin{pmatrix}x_d\y_d\z_dend{pmatrix}= bcdot a^Tcdot c-ccdot a^Tcdot b= begin{pmatrix}3\-2\1end{pmatrix}!cdot! begin{pmatrix}1&2&2end{pmatrix}!cdot! begin{pmatrix}2\-1\3end{pmatrix}- begin{pmatrix}2\-1\3end{pmatrix}!cdot! begin{pmatrix}1&2&2end{pmatrix}!cdot! begin{pmatrix}3\-2\1end{pmatrix}\[2pt] =&begin{pmatrix}3\-2\1end{pmatrix}!cdot! begin{pmatrix}1cdot2+2cdot(-1)+2cdot3end{pmatrix}- left(!!!begin{array}{*{20}{r}}2&4&4\-1&-2&-1\3&6&6end{array}!!right)!cdot! begin{pmatrix}3\-2\1end{pmatrix}= begin{pmatrix}18\-12\6end{pmatrix}-begin{pmatrix}2\-1\3end{pmatrix}= begin{pmatrix}16\-11\3end{pmatrix}. end{aligned}$

то есть vec{d}=16cdotvec{i}-11cdotvec{j}+3cdotvec{k} .

в) Учитывая,что $|vec{a}|^2=langlevec{a},vec{a}rangle=1^2+2^2+2^2=9,~langlevec{a},vec{b}rangle=1$ и

$begin{aligned}bigl[vec{a},[vec{b},vec{c}]bigr],=,&langlevec{a},vec{a}ranglecdotvec{b}-langlevec{a},vec{b}ranglecdotvec{a}=9cdotvec{b}-1cdotvec{a}=\[2pt]=,&9cdotbigl(3cdotvec{i}-2cdotvec{j}+1cdotvec{k}bigr),-,1cdotbigl(1cdotvec{i}+2cdotvec{j}+2cdotvec{k}bigr),=\[2pt]=,&26cdotvec{i}-20cdotvec{j}+7cdotvec{k}.end{aligned}$

по свойству 3 находим

$begin{aligned}vec{b}&=frac{langlevec{a},vec{b}rangle}{|vec{a}|^2}cdotvec{a}+frac{1}{|vec{a}|^2}cdotbigl[vec{a},[vec{b},vec{a}]bigr],=frac{1}{9}cdotvec{a}+frac{1}{9}cdotbigl(9cdotvec{b}-1cdotvec{a}bigr),=\[3pt] &=frac{1}{9}cdotbigl(1cdotvec{i}+2cdotvec{j}+2cdotvec{k}bigr),+frac{1}{9}cdotbigl(26cdotvec{i}-20cdotvec{j}+7cdotvec{k}bigr),end{aligned}$

т.е. ортогональная проекция $vec{operatorname{pr}}_{vec{a}}vec{b}=frac{1}{9}cdotvec{a}=frac{1}{9}cdotvec{i}+frac{2}{9}cdotvec{j}+frac{2}{9}cdotvec{k}$ , а ортогональная составляющая равна

$vec{b}_{perpvec{a}}=vec{b}-vec{operatorname{pr}}_{vec{a}}vec{b}=vec{b}-frac{1}{9}cdotvec{a}=frac{26}{9}cdotvec{i}-frac{20}{9}cdotvec{j}+frac{7}{9}cdotvec{k}.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Лекция
4. Двойные произведения трех векторов

Из трех векторов
можно составить только три типа
произведений:

1). Двойное скалярное произведение
(простейшее).

Можно перемножить два вектора

и

скалярно и полученный скаляр

умножить на третий вектор
.
В результате получится вектор
,
называемый простейшим (или двойным
скалярным) произведением трех векторов.

Двойное векторное произведение.

Можно перемножить два вектора

и
векторно
и полученный вектор

умножить тоже векторно на третий вектор

.
В результате получится вектор
,
называемый двойным векторным
произведением трех векторов.

Смешанное произведение.

Можно перемножить два вектора

и

векторно и полученный вектор

умножить скалярно на третий вектор
.
В результате получится скаляр
(число)
,
называемый смешанным (векторно —
скалярным произведением) трех векторов.

Этими тремя произведениями и исчерпываются
все типы произведений трех векторов.

Изучим их подробно и установим два
замечательных факта. Во-первых, мы
покажем, что двойное векторное произведение

можно представить через двойные скалярные
произведения перемножаемых векторов.

Во-вторых, мы покажем, что смешанное
произведение

выражается через попарные скалярные
произведения своих множителей.

Двойное скалярное (простейшее)
произведение трех векторов по
нашему определению получается умножением
скалярного произведения двух векторов

на третий вектор
:
.
Мы видим, что в результате получается
вектор, коллинеарный с третьим вектором
.

Из этого свойства, в общем виде, вытекает
неравенство
,
(которое заменится равенством лишь в
том особом случае, когда векторы

и
коллинеарны).
Итак, в общем случае, простейшее
произведение трех векторов не подчиняется
закону ассоциативности.

Этими двумя замечаниями исчерпываются
все особенности простей-шего произведения
трех векторов, которые полезно иметь в
виду. Во всем остальном, так как простейшее
произведение есть ничто иное как
произве-дение вектора на скаляр, то оно
подчиняется законам этого произведения.

Двойное векторное произведение трех
векторов.

— вектор. Имеет место неравенство:.

Действительно, например:

Теорема. Двойное векторное
произведение

векторов
,
,

есть линейная комбинация векторов,
стоящих в скобках этого произведения.

Доказательство

Рассмотрим вектор
.
Вектор
.
Отсюда следует, что вектор

принадлежит плоскости векторов

и

и может быть разложен по этим векторам,
т.е.
.

Найдем
коэффициенты  и
.
Для этого введем прямоугольную декартову
систему координат Oxyz так,
чтобы ось Ох пошла по вектору
,
плоскость Oxy совпала с
плоскостью векторов

и

(рис. 3). Тогда

Рис. 3

Выразим теперь в координатной форме
:

Преобразуем правую часть полученного
равенства:

Но,

следовательно,

Аналогично можно доказать, что
.

Смешанное произведение трех векторов.

Смешанное произведение

трех векторов
,
,

есть число (скаляр), которое получается
в результате скалярного умножения
векторного произведения

векторов

и

на третий вектор
.

(4.1)

ыясним его

геометрический смысл

.
Пусть
тогда
обозначив
,
получим

Чтобы
истолковать полученный результат,
построим на векторах
,
,

параллелепипед, основанием которого
будем считать параллелограмм со сторонами

и
.
Площадь этого основания равна
.
Обозначим через Н высоту параллелепипеда,
опущенную на это основание. Тогда объем
V параллелепипеда определим
по известной из школы формуле
.

Теперь нам придется различать два
случая.

В первом случае, когда перемножаемые
векторы
,
,

образуют правую систему (рис. 4),
тогда угол
,
угол между векторами

и
,
будет острый и
.
Формула (4.1) примет вид:
.

Т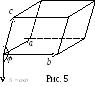аким
образом, смешанное произведение векторов,
образующих правую тройку, равно объему
параллелепипеда, построенного на этих
векторах.

Во втором случае, когда перемножаемые
векторы
,
,

образуют левую тройку векторов
(рис.5), тогда

и формула (4.1) примет вид:
.

Таким образом, смешанное произведение
трех векторов, образующих левую тройку
векторов, отличается только знаком от
объема параллелепипеда, построенного
на перемножаемых векторах.

Итак,
,
причем знак «+» получается, когда
перемножаемые векторы образуют правую
тройку, и знак «-», когда их тройка левая.

Отсюда следует, что объем параллелепипеда,
построенного на трех векторах, всегда
равен абсолютной величине их
векторно-скалярного произведения:

В этом и состоит геометрический смысл
смешанного проведения трех векторов.

Алгебраические
свойства смешанного произведения

1. Свойство
ассоциативности.

Смешанное
произведение трех векторов не зависит
от группировки его сомножителей, т.е.
.

Действительно,
оба эти произведения имеют одинаковые
абсолютные величины, равные объему
параллелепипеда, построенного на
перемножаемых векторах
,
,

(если эти векторы отличны от нуля).

Знаки этих
произведений также совпадают, так как,
если система (,
,
)
– правая, то и (,,)
– правая (проверить самостоятельно).
Следовательно, оба произведения

и

равны.

На основании
свойства ассоциативности в смешанном
произведении можно опускать знаки
векторного и скалярного умножения и
записывать

или (,
,
).

Итак,
.

2.
Свойство цикличности (круговой
переместительности).

Так
как знак векторного умножения можно
поставить между любой парой соседних
множителей смешанного произведения
трех векторов, то перестановка этих
множителей изменит только знак. На
основании этого последовательно получим
.

Чтобы сформулировать
полученное свойство, отметим на окружности
три точки, которые обозначим, как
множители, буквами a,b,c.
Будем считать положительным обход
окружности в направлении abca
(рис. 6). Мы видим, что при перестановке
множителей, не нарушающей их кругового
порядка, смешанное произведение не
меняется, при перестановке же множителей,
нарушающей круговой порядок, смешанное
произведение трех векторов
,
,

меняет только свой знак.

3.
Свойство однородности.

Числовой множитель
можно выносить за знак смешанного
произведения, т.е.

4.
Свойство дистрибутивности.

Векторно-скалярное
умножение суммы векторов на два других
вектора можно выполнить почленно, т.е.
.

Это свойство не
нуждается в доказательстве, так как оно
непосредственно вытекает из свойства
дистрибутивности скалярного и векторного
произведений двух векторов.

Замечание.
Однородность и дистрибутивность
выполняется не только относительно
первого множителя произведения.

5.
Критерий компланарности трех векторов.

(,
,

— компланарны).

Доказательство
следует непосредственно из определения.

Смешанное
произведение в координатной форме

Пусть векторы
,
,

разложены по ортам
,
т.е.

Согласно представлению

в координатной форме, имеем

Следовательно,
,
или, окончательно,
.

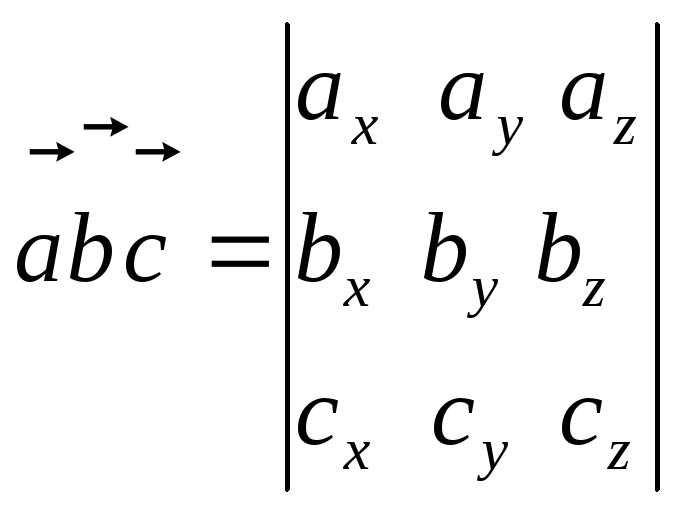
Пример.
Пусть

Найти
.

Решение

Знак минус в ответе
указывает на то, что векторы
,
,

составляют левую тройку.

Объем параллелепипеда,
построенного на указанных векторах,
равен V=13.

Соседние файлы в папке Лекции по АГиТДУ

Источник

Двойное векторное произведение.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Двойным векторным произведением называется вектор $[a, [b, c]],$ где $[a, b] -$ векторное произведение векторов $a$ и $b.$

2.123*. Вектор $[a, [b, c]]$ называется двойным векторным произведением. Доказать, что справедливо равенство $$[a, [b, c]]=b(a, c)-c(a, b).$$

Решение.

Пусть $a=(a_x, a_y, a_z), b=(b_x, b_y, b_z), c=(c_x, c_y, c_z).$ Тогда

$$[b, c]=begin{vmatrix}i&j&k\b_x&b_y&b_z\c_x&c_y&c_zend{vmatrix}=i(b_yc_z-b_zc_y)-j(b_xc_z-b_zc_x)+k(b_xc_y-b_yc_x).$$

$$[a, [b,c]]=begin{vmatrix}i&j&k\a_x&a_y&a_z\b_yc_z-b_zc_y&-b_xc_z+b_zc_x&b_xc_y-b_yc_xend{vmatrix}=$$ $$=i(a_y(b_xc_y-b_yc_x)-a_z(b_zc_x-b_xc_z))-$$ $$-j(a_x(b_xc_y-b_yc_x)-a_z(b_yc_z-b_zc_y))+$$ $$+k(a_x(b_zc_x-b_xc_z)-a_y(b_yc_z-b_zc_y))=$$ $$=i(a_yb_xc_y-a_yb_yc_x+a_zb_xc_z-a_zb_zc_x)-$$ $$-j(a_xb_xc_y-a_xb_yc_x-a_zb_yc_z+a_zb_zc_y)+$$ $$+k(a_xb_zc_x-a_xb_xc_z-a_yb_yc_z+a_yb_zc_y).$$

Далее найдем вектор $b(a, c)-c(a, b):$

$$b(a, c)=(b_x, b_y, b_z)(a_xc_x+a_yc_y+a_zc_z)=$$ $$=(a_xb_xc_x+a_yb_xc_y+a_zb_xc_z, a_xb_yc_x+a_yb_yc_y+a_zb_yc_z, $$ $$a_xb_zc_x+a_yb_zc_y+a_zb_zc_z);$$

$$c(a, b)=(c_x, c_y, c_z)(a_xb_x+a_yb_y+a_zb_z)=$$ $$=(a_xb_xc_x+a_yb_yc_x+a_zb_zc_x, a_xb_xc_y+a_yb_yc_y+a_zb_zc_y, $$ $$a_xb_xc_z+a_yb_yc_z+a_zb_zc_z);$$

Отсюда

$$b(a, c)-c(a, b)=i(a_yb_xc_y-a_yb_yc_x+a_zb_xc_z-a_zb_zc_x)-$$ $$-j(a_xb_xc_y-a_xb_yc_x-a_zb_yc_z+a_zb_zc_y)+$$ $$+k(a_xb_zc_x-a_xb_xc_z-a_yb_yc_z+a_yb_zc_y)=[a, [b, c]].$$

Что и требовалось доказать.

Источник

Авторы
Файлы
Ключевые слова
Литература

Савицкий И.В.

1

Матвеева Т.А.

1 Волжский политехнический институт, филиал Волгоградского государственного технического университета

1. Кочин Н.Е. Введение в векторный и тензорный анализ.

2. Клетеник Д.В. Сборник задач по аналитической геометрии.

3. Высшая математика для технических университетов. Линейная алгебра: учебное пособие / В.Н. Задорожный, В.Ф. Зальмеж, А.Ю. Трифонов, А.В. Шаповалов.

В разделе математики «Линейная алгебра и аналитическая геометрия» мы изучили скалярное, векторное и смешанное произведения векторов. Я случайно увидел в некоторых книгах информацию о двойном векторном произведении и решил подробнее узнать о нём и его свойствах.

Пусть вектор умножается векторно на вектор , после чего полученный вектор умножается снова векторно на вектор . В результате получается так называемое двойное векторное произведение (ясно, что в результате имеем -вектор).

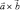
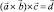
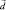
Двойное векторное произведение вычисляется по формуле

(1)

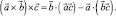
В общем случае, 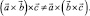Покажем это, используя свойства векторного и скалярного произведения двух векторов

(2)

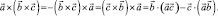
Из сопоставления формул (1) и (2) можно вывести следующее правило для запоминания: двойное векторное произведение равно произведению среднего вектора на скалярное произведение двух других, минус крайний вектор скобки, умноженный на скалярное произведение двух других или говорят 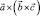равно «б а ц» минус «ц а б».

При круговой перестановке векторов 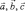формула (1) приводит к трем разным векторам:

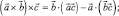
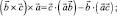
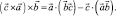
Складывая вместе эти три равенства, получим тождество

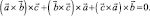
Одно из применений формулы (2) состоит в выводе разложения данного вектора , на две компоненты, из которых одна параллельна, а другая перпендикулярна к заданному вектору . В самом деле, положив в формуле (2) , найдем:

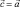
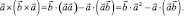
Решая это уравнение относительно , получим:

(3)

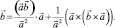
Первый из слагаемых векторов правой части, очевидно, параллелен вектору , а второй перпендикулярен к нему. Формула (3) для разложения упрощается, если есть единичный вектор. Тогда и формула (3) примет вид:

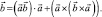
Рассмотрим следующий пример: показать, что если 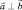то

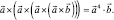
По формуле (2) имеем

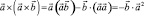
т.к. .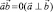

Умножая векторно слева на , получим:

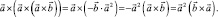
Повторяя ту же операцию, найдем:

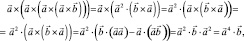
что и требовалось.

Таким образом, я познакомился с двумя случаями произведений трех векторов в трехмерном пространстве: скалярно-векторное (в результате получаем число) и двойное векторное произведение (в результате получаем вектор).

Библиографическая ссылка

Савицкий И.В., Матвеева Т.А. ДВОЙНОЕ ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ТРЕХ ВЕКТОРОВ // Современные наукоемкие технологии. – 2013. – № 6.
– С. 109-110;

URL: https://top-technologies.ru/ru/article/view?id=32013 (дата обращения: 26.05.2023).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Источник

Двойное векторное произведение и его свойства

Лекция 4. Двойные произведения трех векторов

Двойное векторное произведение.

Библиографическая ссылка

Лекция
4. Двойные произведения трех векторов