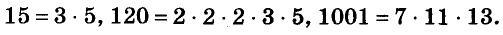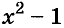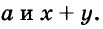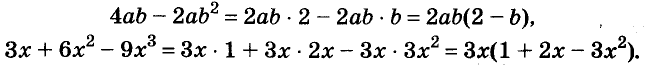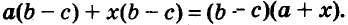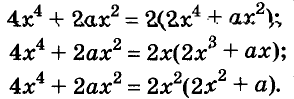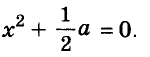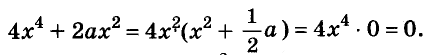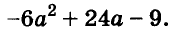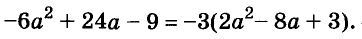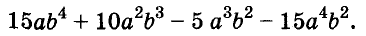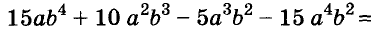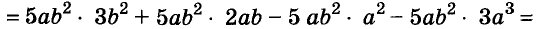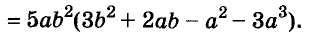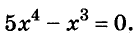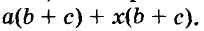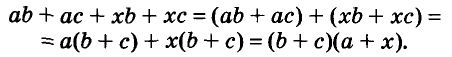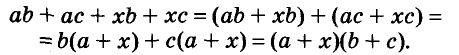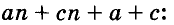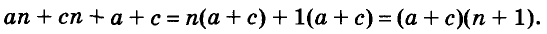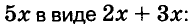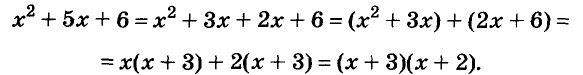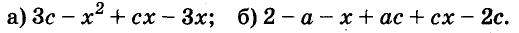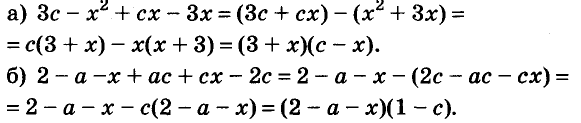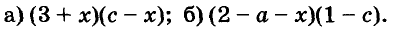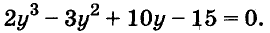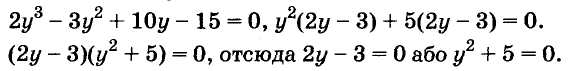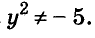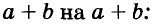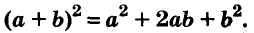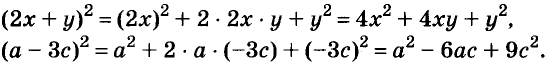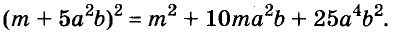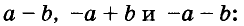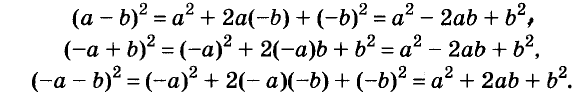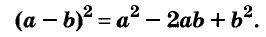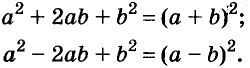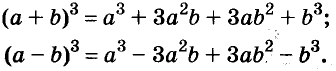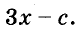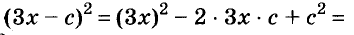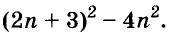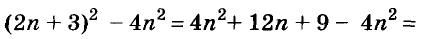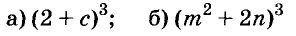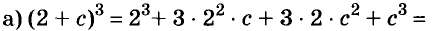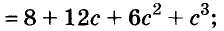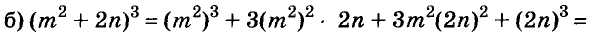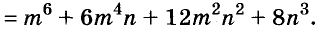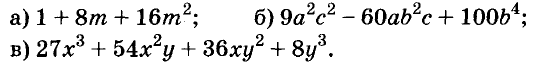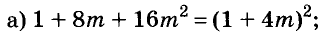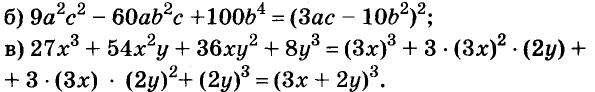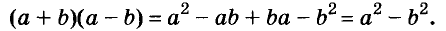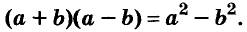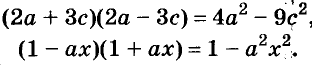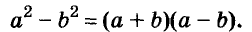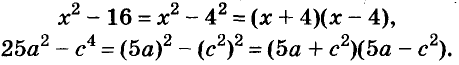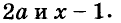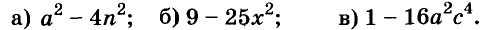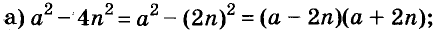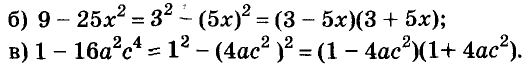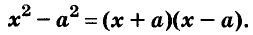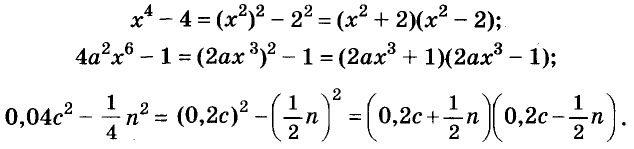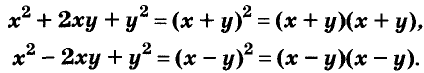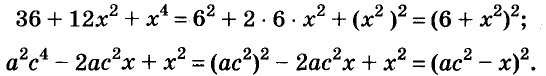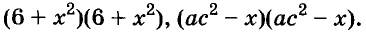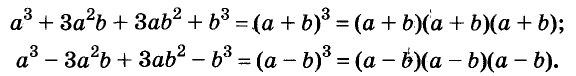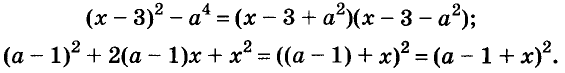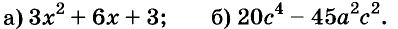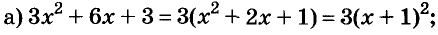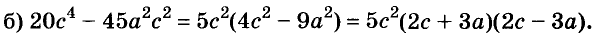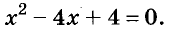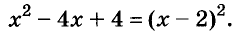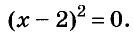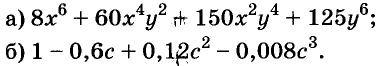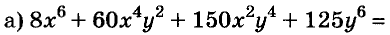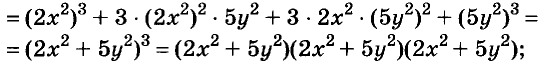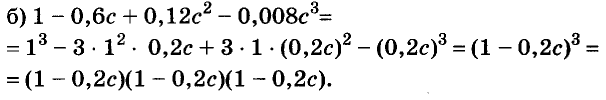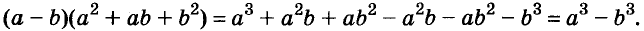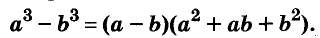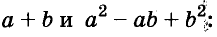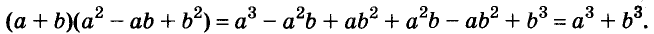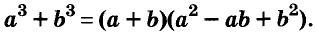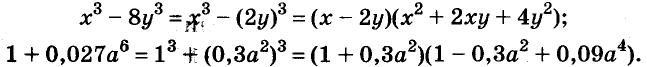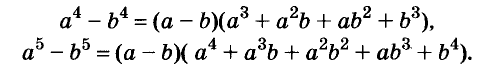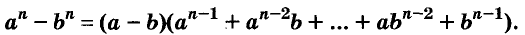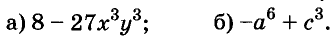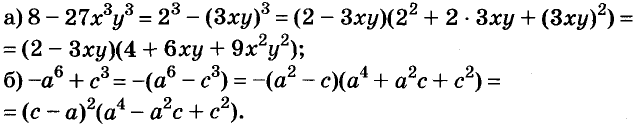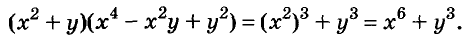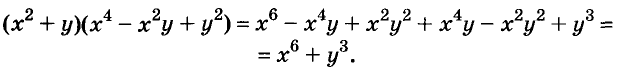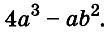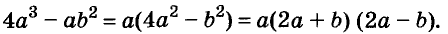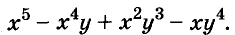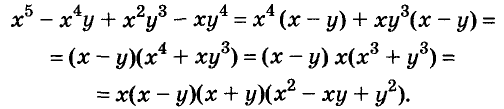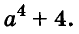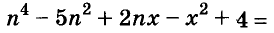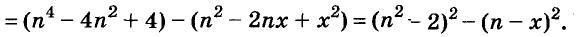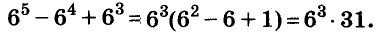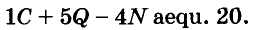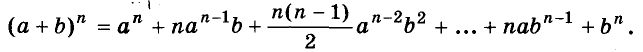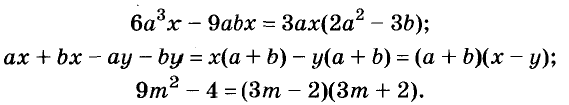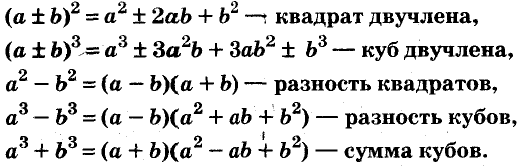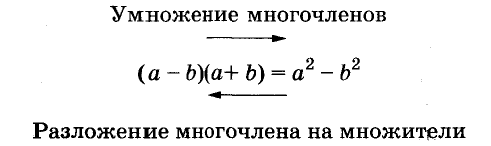Как найти двучлен в разложении на множители - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание:

Разложение многочленов на множители

Разложение многочленов на множители — операция, об-I ратная умножению многочленов. Как вы уже знаете, решая разные задачи, иногда умножают два или более чисел, а иногда — раскладывают данное число на множители. Подобные задачи возникают и при преобразовании целых алгебраических выражений. В этой главе вы узнаете о:

вынесении общего множителя за скобки;
способе группировки;
формулах сокращённого умножения;
применении разных способов разложения многочленов на множители.

Вынесение общего множителя за скобки

Вы уже умеете раскладывать на множители натуральные числа. Например,

На множители раскладывают и многочлены. Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену. Например, многочлен

Один из способов разложения многочленов на множители — вынесение общего множителя за скобки. Рассмотрим его.

Каждый член многочлена ах + ау имеет общий множитель а. На основании распределительного закона умножения 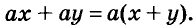Это означает, что данный многочлен ах + ау разложен на два множителя:

Другие примеры:

Чтобы убедиться, правильно ли разложен многочлен на множители, нужно выполнить умножение полученных множителей. Если всё верно, то в результате должен получиться данный многочлен.

Иногда приходится раскладывать на множители и выражения, имеющие общий многочленный множитель. Например, в выражении 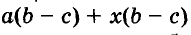общий множитель b — с. Его также можно выносить за скобки:

Один и тот же многочлен можно разложить на множители по-разному. Например,

Как правило, стараются вынести за скобки такой общий множитель, чтобы в скобках осталось простейшее выражение. Поэтому чаще всего в качестве коэффициента общего множителя берут наибольший общий делитель (НОД) коэффициентов всех членов данного многочлена или их модулей. Но не всегда. Все зависит от того, с какой целью раскладывают на множители многочлен.

Пусть, например, надо найти значение выражения 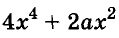при условии, когда

Чтобы использовать условие, это упражнение можно решить так:

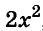
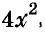
Здесь вынесено за скобки не , а тогда в скобках имеем выражение, значение которого известно из условия.

Пример:

Разложите на множители многочлен

Решение:

или

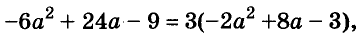
Пример:

Разложите на множители многочлен

Решение:

Пример:

Докажите, что число 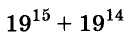делится на 20.

Доказательство:

Последнее произведение делится на 20, поэтому делится на 20 и данная сумма.

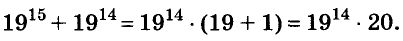
Пример:

Решите уравнение

Решение:

поэтому данное уравнение равносильно уравнению Произведение двух чисел равно нулю тогда, когда хотя бы одно из них равно нулю.

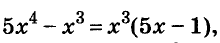
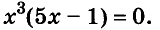
Значит, 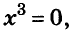отсюда х = 0, или 5х — 1 = 0, отсюда х = 0,2.

Ответ. Уравнение имеет два корня: 0 и 0,2.

Способ группировки

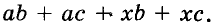
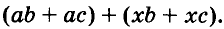
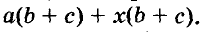
Разложим на множители многочлен Сгруппируем его члены так, чтобы слагаемые в каждой группе имели общий множитель Вынесем из первой группы за скобки общий множитель а, из второй — общий множитель х, получим выражение Слагаемые этого выражения имеют общий множитель b + с, вынесем его за скобки, получим выражение

Указанные преобразования можно записать цепочкой:

Такой способ разложения многочленов на множители называют способом группировки.

Замечание. Раскладывая на множители представленный выше многочлен, можно сгруппировать его члены иначе:

Получили такой же результат.

Разложим на множители многочлен

Записывать сумму а + с в виде 1 (а + с) необязательно, но сначала, чтобы не допускать ошибок, можно писать и так.

Чтобы воспользоваться способом группировки, иногда приходится один член данного многочлена представлять в виде суммы или разности одночленов. Чтобы разложить на множители трёхчлен 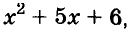• запишем одночлен

Подобные преобразования также можно выполнять, используя тождества.

Пример:

Разложите на множители многочлен:

Решение:

Ответ.

Пример:

Решите уравнение:

Решение:

Разложим левую часть уравнения на множители:

Корнем первого уравнения является у = 1,5, а второе уравнение корней не имеет, так как

Ответ. у = 1,5.

Квадрат двучлена

Решая различные задачи, часто приходится умножать двучлены вида 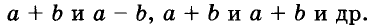Чтобы в таких случаях можно было сразу написать ответ, полезно запомнить тождества, которые называют формулами сокращённого умножения. Рассмотрим некоторые из них.

Умножим двучлен

Следовательно,

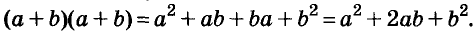
Квадрат двучлена равен квадрату первого его члена плюс удвоенное произведение первого на второй плюс квадрат второго члена.

Доказанное равенство — тождество, его называют формулой квадрата двучлена. Пользуясь ею, можно сразу записать:

Промежуточные преобразования желательно выполнять устно, тем самым сокращается запись:

По формуле квадрата двучлена можно возводить в квадрат любые двучлены, в том числе

Запомните формулу

Формулы квадрата двучлена используют и в «обратном направлении»:

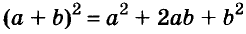
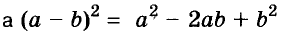
Формулу часто называют формулой квадрата суммы двух выражений, — квадрата разности двух выражений.

Для положительных чисел а и b формулу

можно доказать геометрически, как показано на рисунке 44. Так её доказывали ещё древние греки. Ведь площадь квадрата со стороной а + b равна сумме площадей квадратов а также прямоугольников ab и ab.

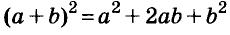
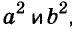
Существуют и другие формулы сокращённого умножения:

Пример:

Возведите в квадрат двучлен

Решение:

Пример:

Упростите выражение

Решение:

Пример:

Представьте в виде многочлена выражение:

Решение:

Пример:

Представьте выражение в виде степени двучлена:

Решение:

Заказать решение задач по высшей математике

Разность квадратов

Умножим сумму переменных а и b на их разность.

Значит,

Это равенство — тождество. Словами его читают так:

Произведение суммы двух выражений и их разности равно разности квадратов этих выражений.

Пользуясь доказанной формулой, можно сразу записать:

Левую и правую части доказанной формулы можно поменять местами. Получим формулу разности квадратов двух выражений:

Разность квадратов двух выражений равна произведению их суммы и разности.

Пример:

Формула разности квадратов очень удобна для разложения многочленов на множители.

Для положительных чисел а и b формулу 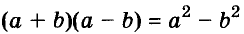можно проиллюстрировать геометрически (рис. 46). Но это тождество верно не только для положительных чисел, но и для любых других чисел и выражений.

Истинность формулы разности квадратов следует из правила умножения многочленов, а это правило — из законов действий сложения и умножения. Законы сложения и умножения чисел — это своеобразные аксиомы, следствиями которых являются алгебраические тождества.

Пример:

Напишите разность квадратов и квадрат разности выражений

Решение:

— разность квадратов; — квадрат разности данных выражений.

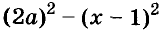
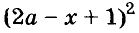
Пример:

Запишите в виде произведения двух двучленов выражение:

Решение:

Пример:

Представьте в виде двучлена выражение:

Решение:

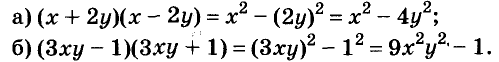
Используя формулу разности квадратов, промежуточные вычисления и преобразования можно выполнять устно, а записывать лишь конечный результат.

Использование формул сокращённого умножения

С помощью формул сокращённого умножения некоторые многочлены можно разложить на множители. Например, двучлен 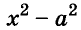можно представить в виде произведения по формуле разности квадратов:

Примеры:

Трёхчлены 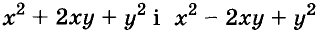раскладывают на множители по формуле квадрата двучлена:

Примеры:

Полученные, выражения можно разложить на множители и записать так:

Многочлен 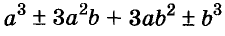можно разложить на множители по формуле куба двучлена:

Раскладывать на множители можно не только многочлены, но и некоторые другие целые выражения.

Например, 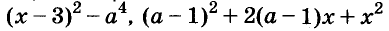— не многочлены, но и их можно представить в виде произведений многочленов:

Пример:

Разложите на множители многочлен:

Решение:

Пример:

Решите уравнение

Решение:

Значит, данное уравнение равносильно такому:

Квадрат числа равен нулю только тогда, когда это число равно 0. А х — 2 = 0, когда х = 2.

Ответ. х = 2.

Пример:

Разложите на множители многочлен:

Решение:

Разность и сумма кубов

Выполним умножение многочленов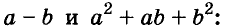

Следовательно, при любых значениях а и b

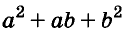
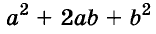
Трёхчлен называют неполным квадратом суммы выражений а и b (от он отличается только коэффициентом среднего члена). Поэтому доказанную формулу словами читают так:

разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

Выполним умножение многочленов

Следовательно,

Трёхчлен 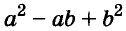называют неполным квадратом разности выражений а и b. Поэтому полученную формулу читаю так:

сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

С помощью доказанных формул можно раскладывать на множители многочлены, являющиеся разностями или суммами кубов.

Примеры:

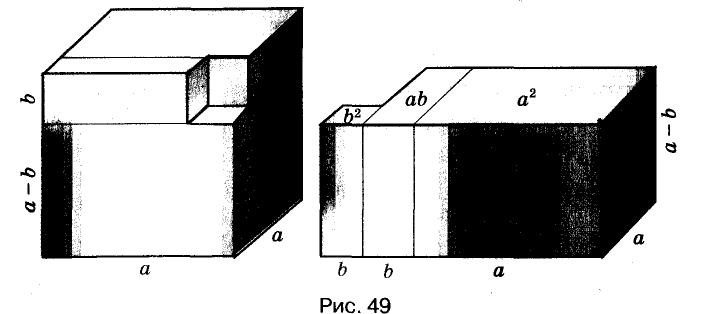
Формулу «разность кубов» для положительных значений а и b можно проиллюстрировать геометрически, как показано на рисунке 49.

Если умножить на а — b выражения то получим формулы:

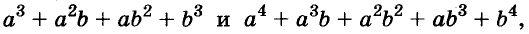
Можно доказать, что для каждого натурального значения n истинна формула:

Формулы «разность квадратов» и «разность кубов» — простейшие случаи этой общей формулы.

Пример:

Разложите на множители двучлен:

Решение:

Пример:

Найдите произведение многочленов: •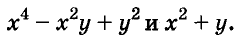

Решение:

Первый способ. По формуле суммы кубов:

Второй способ. По правилу умножения многочленов:

Применение разных способов разложения многочленов на множители

Чтобы разложить многочлен на множители, иногда приходится применять несколько способов.

Пример:

Разложите на множители многочлен

Решение:

Сначала за скобки вынесен общий множитель а, потом выражение в скобках разложено на множители по формуле разности квадратов.

Пример:

Разложите на множители выражение

Решение:

Здесь применены способ группировки, вынесение общего множителя за скобки и формула суммы кубов.

Чтобы разложить на множители более сложные многочлены, приходится применять несколько известных способов или искусственные приёмы.

В этом случае можно использовать такое правило-ориентир:

Вынести общий множитель (если он есть) за скобки.
Проверить, не является ли выражение в скобках разностью квадратов, разностью или суммой кубов.
Если это трёхчлен, то проверить, не является ли он квадратом двучлена.
Если многочлен содержит больше трёх членов, то надо попробовать группировать их и к каждой группе применить п. 1—3.

Иногда удаётся разложить многочлен на множители, прибавляя и вычитая из него одно и то же выражение.

Пример:

Разложите на множители двучлен

Решение:

Прибавим к данному двучлену выражение

Пример:

Разложите на множители выражение

Решение:

Пример:

Представьте многочлен 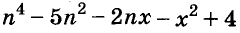в виде разности квадратов двух многочленов.

Решение:

Пример:

Докажите, что число 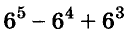делится на 31.

Доказательство:

Последнее произведение делится на 31, поэтому делится на 31 и равное ему данное числовое выражение.

Исторические сведения:

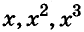
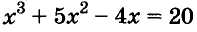
Наибольший вклад в развитие алгебраической символики внёс известный французский математик Ф. Виет, которого называли «отцом алгебры ». Он часто использовал буквенные обозначения. Вместо писал соответственно N,Q,C — первые буквы латинских слов Numerus (число), Quadratus (квадрат), Cubus (куб). Уравнение Ф. Виет записывал так:

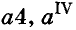
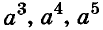
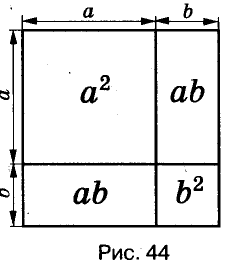
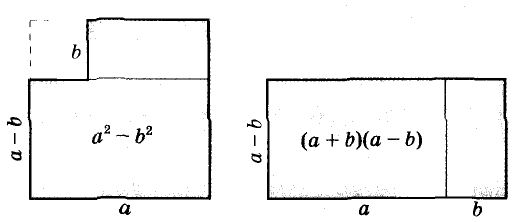
Степени чисел продолжительное время не имели специальных обозначений, четвёртую степень числа а записывали в виде произведения аааа. Позднее такое произведение начали записывать . Записи предложил Р. Декарт.

Формулы сокращённого умножения древним китайским и греческим математикам были известны за много веков до начала нашей эры. Записывали их тогда не с помощью букв, а словами и доказывали геометрически (только для положительных чисел). Пользуясь рисунком, объясняли, что для любых чисел а и b площадь квадрата со стороной а + b равна сумме площадей двух квадратов со сторонами а и b к двух прямоугольников со сторонами а, b. Итак, 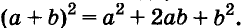Подобным способом обосновали и другие равенства, которые. мы теперь называем формулами сокращённого умножения.

В учебнике рассмотрены простейшие формулы сокращённого умножения.

Формулы квадрата и куба двучлена — простейшие случаи общей формулы бинома Ньютона:

Напомню:

Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену.

Простейшие способы разложения многочленов на множители:

вынесение общего множителя за скобки;
способ группировки;
использование формул сокращённого умножения.

Примеры:

Формулы сокращённого умножения

Разложение многочленов на множители — это преобразование, обратное умножению многочленов. Схематично эти две операции можно изобразить, например, так.

Системы линейных уравнений с двумя переменными
Рациональные выражения
Квадратные корни
Квадратные уравнения
Целые выражения
Одночлены
Многочлены
Формулы сокращенного умножения

Источник

Загрузить PDF

Двучлен (бином) – это математическое выражение с двумя членами, между которыми стоит знак «плюс» или «минус», например, ax+b . Первый член включает переменную, а второй включает или не включает ее. Разложение бинома на множители подразумевает нахождение таких членов, при перемножении которых получается исходный двучлен, чтобы решить или упростить его.

1
Уясните основы процесса разложения на множители. При разложении на множители двучлена за скобку выносится множитель, который является делителем каждого члена исходного бинома. Например, число 6 нацело делится на 1, 2, 3, 6. Таким образом, делителями числа 6 являются числа 1, 2, 3, 6.
- Делители 32: 1, 2, 4, 8, 16, 32.
- Делителями любого числа являются 1 и само число. Например, делители 3 – это 1 и 3.
- Делителями целого числа могут быть только целые числа. Число 32 можно разделить на 3,564 или 21,4952, но получится не целое число, а десятичная дробь.
2

Упорядочьте члены бинома, чтобы облегчить процесс разложения на множители. Двучлен – это сумма или разность двух членов, по крайней мере один из которых содержит переменную. Иногда переменные возведены в степень, например, $x^{2}$ или $5y^{4}$ . Лучше упорядочить члены бинома в порядке возрастания показателей степеней, то есть член с наименьшим показателем степени записывается первым, а с наибольшим – последним. Например:
3
Найдите наибольший общий делитель (НОД) обоих членов. НОД – это наибольшее число, на которое нацело делятся оба члена бинома. Для этого найдите делители каждого члена бинома, а затем выберите наибольший общий делитель. Например:
- Задача:.
  - Делители 3: 1, 3
  - Делители 6: 1, 2, 3, 6.
  - НОД = 3.
4

Разделите каждый член бинома на наибольший общий делитель (НОД). Сделайте это, чтобы вынести НОД за скобки. Обратите внимание, что каждый член бинома уменьшается (потому что делится), но если НОД вынести за скобку, конечное выражение будет равно исходному.
5

Вынесите делитель за скобки. Ранее вы разделили оба члена бинома на делитель 3 и получили . Но избавиться от 3 нельзя – чтобы значения исходного и конечного выражений были равны, нужно 3 вынести за скобки, а в скобках написать выражение, полученное в результате деления. Например:
6

Проверьте ответ. Для этого умножьте член перед скобками на каждый член внутри скобок. Если получился исходный бином, решение правильное. Теперь решите задачу :

Реклама

1
Разложите двучлен на множители, чтобы упростить его и решить уравнение. На первый взгляд решить некоторые уравнения (особенно со сложными биномами) не представляется возможным. Например, решите уравнение $5y-2y^{2}=-3y$ . В этом уравнении присутствуют степени, поэтому сначала разложите выражение на множители.
- Задача: $5y-2y^{2}=-3y$
- Помните, что бином состоит из двух членов. Если выражение включает большее количество членов, научитесь решать многочлены.
2

К обеим сторонам уравнения прибавьте или вычтите некоторый одночлен, чтобы на одной из сторон уравнения остался нуль. В случае разложения на множители решение уравнений основывается на непреложном факте, что любое выражение, умноженное на нуль, равно нулю. Поэтому если приравнять уравнение к нулю, то любой из его множителей должен быть равен нулю. Сделайте так, чтобы на одной из сторон уравнения остался 0.
3

Разложите на множители полученный бином. Сделайте это как описано в предыдущем разделе. Найдите наибольший общий делитель (НОД), разделите на него оба члена бинома, а затем вынесите делитель за скобки.
4

Приравняйте каждый множитель к нулю. В полученном выражении 2y умножается на 4 — у, и это произведение равно нулю. Так как любое выражение (или член), умноженное на нуль, равно нулю, то 2y или 4 — у равно 0. Приравняйте полученные одночлен и двучлен к нулю, чтобы найти «y».
5

Решите полученные уравнения, чтобы найти окончательный ответ (или ответы). Так как каждый множитель приравнивается к нулю, уравнение может иметь несколько решений. В нашем примере:
6

Проверьте ответ. Для этого найденные значения подставьте в исходное уравнение. Если равенство соблюдается, то решение правильное. Найденные значения подставьте вместо «у». В нашем примере у = 0 и у = 4:

Реклама

1

Запомните, что член с переменной тоже можно разложить на множители, даже если переменная возводится в степень. При разложении на множители нужно найти одночлен, которое делит каждый член бинома нацело. Например, одночлен $x^{4}$ можно разложить на множители . То есть если второй член бинома также содержит переменную «х», то «х» можно вынести за скобки. Таким образом, работайте с переменными как с целыми числами. Например:
2

Сложите или вычтите подобные члены, чтобы получить бином. Например, дано выражение . На первый взгляд это многочлен, но на самом деле это выражение можно преобразовать в бином. Сложите подобные члены: 6 и 14 (не содержат переменную), а также 2x и 3x (содержат одинаковую переменную «х»). В этом случае процесс разложения на множители упростится:
3
4

Разложите на множители разность полных кубов. Если бином представляет собой разность полных кубов, например, $a^{3}-b^{3}$ , то он раскладывается на множители по специальной формуле. В этом случае из каждого члена бинома нужно извлечь кубический корень, а найденные значения подставить в формулу.
5

Разложите на множители сумму полных кубов. В отличие от суммы полных квадратов сумму полных кубов, например, $a^{3}+b^{3}$ , можно разложить на множители по специальной формуле. Она похожа на формулу для разности кубов, но знаки меняются местами. Формула довольно проста – чтобы воспользоваться ею, в задаче найдите сумму полных кубов.

Реклама

Советы

Иногда члены бинома не имеют общего делителя. В некоторых задачах члены представлены в упрощенном виде.
Если сразу найти НОД не получается, начните с деления на небольшие числа. Например, если вы не видите, что НОД чисел 32 и 16 равен 16, разделите оба числа на 2. Вы получите 16 и 8; эти числа можно разделить на 8. Теперь вы получите 2 и 1; эти числа сократить нельзя. Таким образом, очевидно, что существует большее число (по сравнению с 8 и 2), которое является общим делителем двух данных чисел.
Обратите внимание, что члены шестого порядка (с показателем степени, равным 6, например, x⁶) являются как полным квадратами, так и полными кубами. Таким образом, к биномам с членами шестого порядка, например, x⁶ — 64, можно применить (в любом порядке) формулы разности квадратов и разности кубов. Но лучше сначала применить формулу разности квадратов, чтобы правильнее разложить бином.

Предупреждения

Бином, представляющий собой сумму полных квадратов, разложить на множители нельзя.

Об этой статье

Эту страницу просматривали 39 065 раз.

Была ли эта статья полезной?

Источник

Основные определения (разбираемся со «сложными» словами)

Одночлены

Одночленами могут быть числа, переменные, произведения чисел и переменных, а так же переменные в степени (если забыл, что такое степень, посмотри тему «Степень и ее свойства»)

Например:

( 4)
( x)
( 4x)
( 4{{x}^{2}})
( 4{{x}^{2}}y)

Все это – одночлены. Видишь у них нет знаков «+» или «-«, как бы нет других членов.

Многочлены

Многочлен – это выражение, состоящее из суммы (или разности) нескольких одночленов различного вида:

( 4{{x}^{2}}+9x)
( 2{{x}^{3}}-16{{x}^{2}}+4x)
( 8xcdot 4{{y}^{2}}-12+4{{x}^{2}}y-3{{y}^{2}}cdot {{x}^{4}}+6-5{{y}^{2}}{{x}^{4}})

Множители

Так, ну давай по порядку. Как нетрудно догадаться, слово «множитель» происходит от слова «умножать».

Возьмем, например, число ( 12), разложить его на множители означает расписать его в виде «умножения» или, как принято говорить в математике «произведения» множителей.

Так ( 12) мы можем получить, умножив ( 2) на ( 6).

А ( 6), в свою очередь, можно представить как произведение ( 2) и ( 3).

Чтоб было более наглядно, обратимся к картинке:

На картинке мы видим пошаговое разложение на множители, те которые подчеркнуты – это множители, которые дальше разложить уже нельзя.

То есть их нельзя уже представить в виде произведения (можно конечно представить каждое из них как единица, умноженная на само число, но это нам ничего не дает).

Я обещал, что картинка все разъяснит, ну разве из нее не понятно, что, ( 12=2cdot 6), а ( 6=2cdot 3)?

Вот и я говорю, что элементарно!

Иными словами, ( 2cdot 2cdot 3=12).

Тут ( 2), еще раз ( 2) и ( 3) – это и есть множители, на которые мы раскладываем.

Зачем нужно раскладывать многочлен на множители?

Это самый главный вопрос. Я уже говорил – чтобы облегчить тебе жизнь.

Раскладывая многочлен на множители, ты упрощаешь выражение! Ты как бы делишь одну большую и сложную проблему, на несколько маленьких и простых и потом разбираешься с каждой маленькой проблемой по отдельности.

А теперь «официальное» определение.

Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей. При этом каждый множитель может быть как многочленом, так и одночленом.

Для чего нужно знать все пять способов?

Потому что нет универсального способа, подходящего для всех многочленов.

Давай посмотрим на каждый из них…

5 способов разложения многочлена на множители

1. Вынесение общего множителя за скобки

( displaystyle ac+bc=c(a+b))

2. Формулы сокращенного умножения

( begin{array}{l}left[ 1 right] {{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\left[ 2 right] {{left( a-b right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\left[ 3 right] {{a}^{2}}-{{b}^{2}}=left( a-b right)left( a+b right)\left[ 4 right] {{left( a+b right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\left[ 5 right] {{left( a-b right)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\left[ 6 right] {{a}^{3}}+{{b}^{3}}=left( a+b right)left( {{a}^{2}}-ab+{{b}^{2}} right)\left[ 7 right] {{a}^{3}}-{{b}^{3}}=left( a-b right)left( {{a}^{2}}+ab+{{b}^{2}} right)end{array})

3. Метод группировки

Применяется если преобразование не очевидно. Здесь, например, можно переставить второй член на другое место:

( {{x}^{3}}-5{{x}^{2}}y-3xy+15{{y}^{2}})

Группируем члены парами, получаем:

( ({{x}^{3}}-5{{x}^{2}}y)-(3xy-15{{y}^{2}}))

( {{x}^{2}}(x-5y)-3y(x-5y))

( ({{x}^{2}}-3y)(x-5y))

4. Выделение полного квадрата

Можно преобразовать многочлен и привести к виду разности квадратов, например и применить формулу сокращенного умножения

( {{x}^{4}}-4{{x}^{2}}-1=underbrace{{{x}^{4}}-2cdot 2cdot {{x}^{2}}+4}_{text{ }{{left( {{x}^{2}}-2 right)}^{2}}}-4-1={{left( {{x}^{2}}-2 right)}^{2}}-5=left( {{x}^{2}}-2+sqrt{5} right)left( {{x}^{2}}-2-sqrt{5} right))

5. Разложение квадратного трехчлена на множители

Квадратный трехчлен – многочлен вида

( a{{x}^{2}}+bx+c=0)

Теорема. Если квадратное уравнение ( a{{x}^{2}}+bx+c=0) имеет корни ( {{x}_{1}},text{ }{{x}_{2}}), то его можно записать в виде:

( a{{x}^{2}}+bx+c=aleft( x-{{x}_{1}} right)left( x-{{x}_{2}} right)).

Подробнее о каждом из 5-ти способов разложения на множители

1. Вынесение общего множителя за скобки

Это один из самых элементарных способов упростить выражение. Для применения этого метода давай вспомним распределительный закон умножения относительно сложения (не пугайся этих слов, ты обязательно знаешь этот закон, просто мог забыть его название).

Закон гласит:

Чтобы сумму двух чисел умножить на третье число, нужно каждое слагаемое умножить на это число и полученные результаты сложить.

Иначе говоря, ( aleft( btext{ }+text{ }c right)text{ }=text{ }abtext{ }+text{ }ac).

Так же можно проделать и обратную операцию, ( abtext{ }+text{ }actext{ }=text{ }aleft( btext{ }+text{ }c right)).

Вот именно эта обратная операция нас и интересует. Как видно из образца, общий множитель а, можно вынести за скобку.

Подобную операцию можно проделывать как с переменными, такими как ( x) и ( y), например, так и с числами: ( 6text{ }+text{ }8text{ }=text{ }2left( 3text{ }+text{ }4 right)).

Да, это слишком элементарный пример, так же, как и приведенный ранее пример, с разложением числа ( 12), ведь все знают, что числа ( 6), ( и ( 12) делятся на ( 2).

А как быть, если вам досталось выражение посложнее:

( 3xy+123y)?

Как узнать на что, например, делится число ( 123).

Нееет! С калькулятором-то любой сможет, а без него слабо?

А для этого существуют признаки делимости, эти признаки действительно стоит знать, они помогут быстро понять, можно ли вынести за скобку общий множитель.

Что ж, вернемся к выражению ( 3xy+123y), может вынести за скобку ( y) да и хватит с него?

Нет, у математиков принято упрощать, так по полной, выносить ВСЕ, что выносится!

И так, с игреком все понятно, а что с числовой частью выражения? Оба числа нечетные, так что на ( 2) разделить не удастся.

Можно воспользоваться признаком делимости на ( 3), сумма цифр ( 1), ( 2) и ( 3), из которых состоит число ( 123), равна ( 6), а ( 6) делится на ( 3), значит и ( 123) делится на ( 3).

Зная это, можно смело делить в столбик, в результате деления ( 123) на ( 3) получаем ( 41) (признаки делимости пригодились!).

Таким образом, число ( 3) мы можем вынести за скобку, так же, как y и в результате имеем:

( 3xytext{ }+text{ }123ytext{ }=text{ }3ycdot left( xtext{ }+text{ }41 right)).

Чтобы удостовериться, что разложили все верно, можно проверить разложение, умножением!

Также общий множитель можно выносить и в степенных выражениях.

Вот тут, например, ( 2{{x}^{3}}-16{{x}^{2}}+4x), видишь общий множитель?

У всех членов этого выражения есть иксы – выносим, все делятся на ( 2) – снова выносим, смотрим что получилось: ( 2{{x}^{3}}-16{{x}^{2}}+4x=2x({{x}^{2}}-8x+2)).

3. Метод группировки

А вот тебе еще примерчик:

( displaystyle {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}})

Ну и что с ним делать будешь? Вроде бы и на ( displaystyle 3) что-то делится и на ( displaystyle 5), а что-то на ( displaystyle x) и на ( displaystyle y)

Но все вместе на что-то одно не разделишь, ну нет тут общего множителя, как не ищи, что, так и оставить, не раскладывая на множители?

Тут надо смекалку проявить, а имя этой смекалке – группировка!

Применяется она как раз, когда общие делители есть не у всех членов. Для группировки необходимо найти группки слагаемых, имеющих общие делители и переставить их так, чтобы из каждой группы можно было получить один и тот же множитель.

Переставлять местами конечно не обязательно, но это дает наглядность, для наглядности же можно взять отдельные части выражения в скобки, их ставить не запрещается сколько угодно, главное со знаками не напутать.

Не очень понятно все это? Объясню на примере:

В многочлене ( displaystyle {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}) ставим член – ( displaystyle 3xy) после члена – ( displaystyle 5x2y) получаем:

( displaystyle {{x}^{3}}-5{{x}^{2}}y-3xy+15{{y}^{2}})

Группируем первые два члена вместе в отдельной скобке и так же группируем третий и четвертый члены, вынеся за скобку знак «минус», получаем:

( displaystyle ({{x}^{3}}-5{{x}^{2}}y)-(3xy-15{{y}^{2}}))

А теперь смотрим по отдельности на каждую из двух «кучек», на которые мы разбили выражение скобками.

Хитрость в том, чтоб разбить на такие кучки, из которых можно будет вынести максимально большой множитель, либо, как в этом примере, постараться сгруппировать члены так, чтобы после вынесения из кучек множителей за скобку у нас внутри скобок оставались одинаковые выражения.

Из обеих скобок выносим за скобки общие множители членов, из первой скобки ( displaystyle {{x}^{2}}), а из второй ( displaystyle 3y), получаем:

( displaystyle {{x}^{2}}(x-5y)-3y(x-5y))

Но это же не разложение!

После разложения должно остаться только умножение, а пока у нас многочлен просто поделен на две части…

НО! Этот многочлен имеет общий множитель. Это ( displaystyle (x-5y))

( displaystyle (x-5y))за скобку и получаем финальное произведение ( displaystyle ({{x}^{2}}-3y)(x-5y))

Бинго! Как видишь, тут уже произведение и вне скобок нет ни сложения, ни вычитания, разложение завершено, т.к. вынести за скобки нам больше нечего.

Может показаться чудом, что после вынесения множителей за скобки у нас в скобках остались одинаковые выражения ( displaystyle (x-5y)), которые опять же мы и вынесли за скобку.

И вовсе это не чудо, дело в том, что примеры в учебниках и в ЕГЭ специально сделаны так, что большинство выражений в заданиях на упрощение или разложение на множители при правильном к ним подходе легко упрощаются и резко схлопываются как зонтик при нажатии на кнопку, вот и ищи в каждом выражении ту самую кнопку.

Что-то я отвлекся, что у нас там с упрощением? Замысловатый многочлен принял более простой вид: ( displaystyle {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}=({{x}^{2}}-3y)(x-5y)).

Согласись, уже не такой громоздкий, как был?

4. Выделение полного квадрата

Иногда для применения формул сокращенного умножения (повтори тему «Формулы сокращенного умножения») необходимо преобразовать имеющийся многочлен, представив одно из его слагаемых в виде суммы или разности двух членов.

В каком случае приходится это делать, узнаешь из примера:

Многочлен ( displaystyle {{x}^{2}}-4x+2) в таком виде не может быть разложен при помощи формул сокращенного умножения, поэтому его необходимо преобразовать.

Возможно, поначалу тебе будет не очевидно какой член на какие разбивать, но со временем ты научишься сразу видеть формулы сокращенного умножения, даже если они не присутствуют не целиком, и будешь довольно быстро определять, чего здесь не хватает до полной формулы, а пока – учись, студент, точнее школьник.

Для полной формулы квадрата разности здесь нужно ( displaystyle 4) вместо ( displaystyle 2).

Представим третий член ( displaystyle 2) как разность ( displaystyle 4-2), получим: ( displaystyle {{x}^{2}}-4x+4-2=({{x}^{2}}-4x+4)-2)

К выражению в скобках можно применить формулу квадрата разности (не путать с разностью квадратов!!!), имеем: ( displaystyle {{left( x-2 right)}^{2}}-2), к данному выражению можно применить формулу разности квадратов (не путать с квадратом разности!!!), представив ( displaystyle 2), как ( displaystyle sqrt{2}), получим: ( displaystyle (x-2-sqrt{2})(x-2+sqrt{2})).

Не всегда разложенное на множители выражение выглядит проще и меньше, чем было до разложения, но в таком виде оно становится более подвижным, в том плане, что можно не париться про смену знаков и прочую математическую ерунду.

Ну а вот тебе для самостоятельного решения, следующие выражения нужно разложить на множители.

Примеры:

( displaystyle 25{{m}^{2}}-49{{n}^{2}};)
( displaystyle {{b}^{2}}-{{(a+1)}^{2}};)
( displaystyle {{(x-y)}^{2}}-{{(x+y+1)}^{2}};)
( displaystyle {{x}^{2}}+2{x}-3)
( displaystyle {{x}^{2}}+6x+5;)

Решения:

Источник

Калькулятор онлайн.
Выделение квадрата двучлена и разложение на множители квадратного трехчлена.

Эта математическая программа выделяет квадрат двучлена из квадратного трехчлена, т.е. делает преобразование вида:

( ax^2+bx+c rightarrow a(x+p)^2+q )

и раскладывает на множители квадратный трехчлен:

( ax^2+bx+c rightarrow a(x+n)(x+m) )

Т.е. задачи сводятся к нахождению чисел ( p, q ) и ( n, m )

Программа не только даёт ответ задачи, но и отображает процесс решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода квадратного трехчлена, рекомендуем с ними ознакомиться.

Правила ввода квадратного многочлена

В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x — 3,5x^2

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &

Ввод: 3&1/3 — 5&6/5x +1/7x^2
Результат: ( 3frac{1}{3} — 5frac{6}{5} x + frac{1}{7}x^2 )

При вводе выражения можно использовать скобки. В этом случае при решении введённое выражение сначала упрощается.
Например: 1/2(x-1)(x+1)-(5x-10&1/2)

Пример подробного решения

Выделение квадрата двучлена.

$$ ax^2+bx+c rightarrow a(x+p)^2+q $$

$$2x^2+2x-4 = $$

$$2x^2 +2 cdot 2 cdotleft( frac{1}{2} right)cdot x+2 cdot left( frac{1}{2} right)^2-frac{9}{2} = $$

$$2left( x^2 + 2 cdotleft( frac{1}{2} right)cdot x + left( frac{1}{2} right)^2 right)-frac{9}{2} = $$

$$2left( x+frac{1}{2} right)^2-frac{9}{2} $$

Ответ: $$2x^2+2x-4 = 2left( x+frac{1}{2} right)^2-frac{9}{2} $$

Разложение на множители.

$$ ax^2+bx+c rightarrow a(x+n)(x+m) $$

$$2x^2+2x-4 = $$
$$ 2left( x^2+x-2 right) = $$
$$ 2 left( x^2+2x-1x-1 cdot 2 right) = $$

$$ 2 left( x left( x +2 right) -1 left( x +2 right) right) = $$

$$ 2 left( x -1 right) left( x +2 right) $$

Ответ: $$2x^2+2x-4 = 2 left( x -1 right) left( x +2 right) $$

Наши игры, головоломки, эмуляторы:

Немного теории.

Выделение квадрата двучлена из квадратного трехчлена

Если квадратный трехчлен aх²+bx+c представлен в виде a(х+p)²+q, где p и q — действительные числа, то
говорят, что из квадратного трехчлена выделен квадрат двучлена.

Покажем на примере как это преобразование делается.

Выделим из трехчлена 2x²+12x+14 квадрат двучлена.

Вынесем за скобки коэффициент a, т.е. 2:
( 2x^2+12x+14 = 2(x^2+6x+7) )

Преобразуем выражение в скобках.
Для этого представим 6х в виде произведения 2*3*х, а затем прибавим и вычтем 3². Получим:
$$ 2(x^2+2 cdot 3 cdot x + 3^2-3^2+7) = 2((x+3)^2-3^2+7) = $$
$$ = 2((x+3)^2-2) = 2(x+3)^2-4 $$

Т.о. мы выделили квадрат двучлена из квадратного трехчлена, и показоли, что:
$$ 2x^2+12x+14 = 2(x+3)^2-4 $$

Разложение на множители квадратного трехчлена

Если квадратный трехчлен aх²+bx+c представлен в виде a(х+n)(x+m), где n и m — действительные числа, то
говорят, что выполнена операция разложения на множители квадратного трехчлена.

Покажем на примере как это преобразование делается.

Разложим квадратный трехчлен 2x²+4x-6 на множители.

Вынесем за скобки коэффициент a, т.е. 2:
( 2x^2+4x-6 = 2(x^2+2x-3) )

Преобразуем выражение в скобках.
Для этого представим 2х в виде разности 3x-1x, а -3 в виде -1*3. Получим:
$$ = 2(x^2+3 cdot x -1 cdot x -1 cdot 3 ) = 2(x(x+3)-1 cdot (x+3) ) = $$
$$ = 2(x-1)(x+3) $$

Т.о. мы разложили на множители квадратный трехчлен, и показоли, что:
$$ 2x^2+4x-6 = 2(x-1)(x+3) $$

Заметим, что разложение на множители квадратного трехчлена возможно только тогда, когда, квадратное уравнение, соответсвующее этому
трехчлену имеет корни.
Т.е. в нашем случае разложить на множители трехчлен 2x²+4x-6 возможно, если квадратное уравнение 2x²+4x-6 =0
имеет корни. В процессе разложения на множители мы установили, что уравнение 2x²+4x-6 =0 имеет два корня 1 и -3,
т.к. при этих значениях уравнение 2(x-1)(x+3)=0 обращается в верное равенство.

Источник

План урока:

Вынесение общего множителя за скобки

Способ группировки

Применение разложение многочленов на множители

Вынесение общего множителя за скобки

В предыдущем уроке мы изучили умножение многочлена на одночлен. Например, произведение монома a и полинома b + c находится так:

a(b + c) = ab + bc

Однако в ряде случае удобнее выполнить обратную операцию, которую можно назвать вынесением общего множителя за скобки:

ab + bc = a(b + c)

Например, пусть нам надо вычислить значение полинома ab + bc при значениях переменных a = 15,6, b = 7,2, c = 2,8. Если подставить их напрямую в выражение, то получим

ab + bc = 15.6 * 7.2 + 15.6 * 2.8

что, скорее всего, не получится посчитать в уме. Если же вынести a за скобки, то получим иную запись:

ab + bc = a(b + c) = 15.6 * (7.2 + 2.8) = 15.6 * 10 = 156

В данном случае мы представили полином ab + bc как произведение двух множителей: a и b + с. Данное действие называют разложением многочлена на множители.

При этом каждый из множителей, на которые разложили многочлен, в свою очередь может быть многочленом или одночленом.

Рассмотрим полином 14ab – 63b². Каждый из входящих в него одночленов можно представить как произведение:

14ab = 7b * 2a

63b² = 7b * 9b

Видно, что у обоих многочленов есть общий множитель 7b. Значит, его можно вынести за скобки:

14ab — 63b² = 7b*2a — 7b*9b = 7b(2a-9b)

Проверить правильность вынесения множителя за скобки можно с помощью обратной операции – раскрытия скобки:

7b(2a — 9b) = 7b*2a — 7b*9b = 14ab — 63b²

Важно понимать, что часто полином можно разложить несколькими способами, например:

5abc + 6bcd = b(5ac + 6cd) = c(5ab + 6bd) = bc(5a + 6d)

Обычно стремятся вынести, грубо говоря, «наибольший» одночлен. То есть раскладывают полином так, чтобы из оставшегося полинома больше нечего нельзя было вынести. Так, при разложении

5abc + 6bcd = b(5ac + 6cd)

в скобках осталась сумма одночленов, у которых есть общий множитель с. Если же вынести и его, то общих множителей в скобках не останется:

b(5ac + 6cd) = bc(5a + 6d)

Разберем детальнее, как находить общие множители у одночленов. Пусть надо разложить сумму

8a³b⁴ + 12a²b⁵v + 16a⁴b³c¹⁰

Она состоит из трех слагаемых. Сначала посмотрим на числовые коэффициенты перед ними. Это 8, 12 и 16. В 3 уроке 6 класса рассматривалась тема НОД и алгоритм его нахождения.Это наибольший общий делитель.Почти всегда его можно подобрать устно. Числовым коэффициентом общего множителя как раз будет НОД числовых коэффициентов слагаемых полинома. В данном случае это число 4.

Далее рассмотрим буквенную часть. В ней должны быть переменные, которые есть во ВСЕХ слагаемых. В данном случае это a и b, а переменная c общей не является, так как не входит в первое слагаемое.

Далее смотрим на степени у этих переменных. В общем множителе у букв должны быть минимальные степени, которые встречаются в слагаемых. Так, у переменной a в многочлене степени 3, 2, и 4 (минимум 2), поэтому в общем множителе будет стоять a². У переменной b минимальная степень равна 3, поэтому в общем множителе будет стоять b³:

8a³b⁴ + 12a²b⁵v + 16a⁴b³c¹⁰= 4a²b³(2ab + 3b²c + 4a²c¹⁰)

В результате у оставшихся слагаемых 2ab, 3b²c, 4a²c¹⁰ нет ни одной общей буквенной переменной, а у их коэффициентов 2, 3 и 4 нет общих делителей.

Выносить за скобки можно не только одночлены, но и многочлены. Например:

x(a-5) + 2y(a-5) = (a-5)(x+2y)

Еще один пример. Необходимо разложить выражение

5t(8y — 3x) + 2s(3x — 8y)

Решение. Напомним, что знак минус меняет знаки в скобках на противоположные, поэтому

-(8y — 3x) = -8y + 3x = 3x — 8y

Значит, можно заменить (3x – 8y) на – (8y – 3x):

5t(8y — 3x) + 2s(3x — 8y) = 5t(8y — 3x) + 2*(-1)s(8y — 3x) = (8y — 3x)(5t — 2s)

Ответ: (8y – 3x)(5t – 2s).

Запомним, что вычитаемое и уменьшаемое можно поменять местами, если изменить знак перед скобками:

(a — b) = — (b — a)

Верно и обратное: минус, уже стоящий перед скобками, можно убрать, если одновременно переставить местами вычитаемое и уменьшаемое:

Этот прием часто используется при решении заданий.

Способ группировки

Рассмотрим ещё один способ разложения многочлена на множители, который помогает раскладывать полином. Пусть есть выражение

ab — 5a + bc — 5c

Вынести множитель, общий для всех четырех мономов, не получается. Однако можно представить этот полином как сумму двух многочленов, и в каждом из них вынести переменную за скобки:

ab — 5a + bc — 5c = (ab — 5a) + (bc — 5c) = a(b — 5) + c(b — 5)

Теперь можно вынести выражение b – 5:

a(b — 5) + c(b — 5) = (b — 5)(a + c)

Мы «сгруппировали» первое слагаемое со вторым, а третье с четвертым. Поэтому описанный метод называют способом группировки.

Пример. Разложим полином 6xy + ab– 2bx– 3ay.

Решение. Группировка 1-ого и 2-ого слагаемого невозможна, так как у них нет общего множителя. Поэтому поменяем местами мономы:

6xy + ab — 2bx — 3ay = 6xy — 2bx + ab — 3ay = (6xy — 2bx) + (ab — 3ay) = 2x(3y — b) + a(b — 3y)

Разности 3y – b и b – 3y отличаются только порядком переменных. В одной из скобок его можно изменить, вынеся знак минус за скобки:

(b — 3y) = — (3y — b)

Используем эту замену:

2x(3y — b) + a(b — 3y) = 2x(3y — b) — a(3y — b) = (3y — b)(2x — a)

В результате получили тождество:

6xy + ab — 2bx — 3ay = (3y – b)(2x – a)

Ответ: (3y – b)(2x – a)

Группировать можно не только два, а вообще любое количество слагаемых. Например, в полиноме

x² — 3xy + xz + 2x — 6y + 2z

можно сгруппировать первые три и последние 3 одночлена:

x² — 3xy + xz + 2x — 6y + 2z = (x² — 3xy + xz) + (2x — 6y + 2z) = x(x — 3y + z) + 2(x — 3y + z) = (x + 2)(x — 3y + z)

Теперь рассмотрим задание повышенной сложности

Пример. Разложите квадратный трехчлен x²– 8x +15.

Решение. Данный полином состоит всего из 3 одночленов, а потому, как кажется, группировку произвести не получится. Однако можно произвести такую замену:

-8x = -3x — 5x

Тогда исходный трехчлен можно представить следующим образом:

x² — 8x + 15 = x² — 3x — 5x + 15

Сгруппируем слагаемые:

x² — 3x — 5x + 15 = (x² — 3x) + (- 5x + 15) = x(x — 3) — 5(x — 3) = (x — 5)(x — 3)

Ответ: (x– 5)(х – 3).

Конечно, догадаться о замене – 8х = – 3х – 5х в приведенном примере нелегко. Покажем иной ход рассуждений. Нам надо разложить полином второй степени. Как мы помним, при перемножении многочленов их степени складываются. Это значит, что если мы и сможем разложить квадратный трехчлен на два множителя, то ими окажутся два полинома 1-ой степени. Запишем произведение двух многочленов первой степени, у которых старшие коэффициенты равны 1:

(x + a)(x + b) = x² + xa + xb + ab = x² + (a + b)x + ab

Здесь за a и b мы обозначили некие произвольные числа. Чтобы это произведение равнялось исходному трехчлену x²– 8x +15, надо подобрать подходящие коэффициенты при переменных:

С помощью подбора можно определить, что этому условию удовлетворяют числа a= – 3 и b = – 5. Тогда

(x — 3)(x — 5) = x² * 8x + 15

в чем можно убедиться, раскрыв скобки.

Для простоты мы рассмотрели только случай, когда у перемножаемых полиномов 1-ой степени старшие коэффициенты равны 1. Однако они могли равняться, например, 0,5 и 2. В этом случае разложение выглядело бы несколько иначе:

x² * 8x + 15 = (2x — 6)(0.5x — 2.5)

Однако, вынеся коэффициент 2 из первой скобки и умножив его на вторую, получили бы изначальное разложение:

(2x — 6)(0.5x — 2.5) = (x — 3) * 2 * (0.5x — 2.5) = (x — 3)(x — 5)

В рассмотренном примере мы разложили квадратный трехчлен на два полинома первой степени. В дальнейшем нам часто придется это делать. Однако стоит отметить, что некоторые квадратные трехчлены, например,

x² — x + 1

невозможно разложить таким образом на произведение полиномов. Доказано это будет позднее.

Применение разложение многочленов на множители

Разложение полинома на множители может упростить выполнение некоторых операций. Пусть необходимо выполнить вычисление значения выражения

2 + 2² + 2³ + 2⁴ + 2⁵ + 2⁶ + 2⁷ + 2⁸ + 2⁹

Вынесем число 2, при этом степень каждого слагаемого уменьшится на единицу:

2 + 2² + 2³ + 2⁴ + 2⁵ + 2⁶ + 2⁷ + 2⁸ + 2⁹= 2(1 + 2 + 2² + 2³ + 2⁴ + 2⁵ + 2⁶ + 2⁷ + 2⁸ )

Обозначим сумму

2 + 2² + 2³ + 2⁴ + 2⁵ + 2⁶ + 2⁷ + 2⁸

за х. Тогда записанное выше равенство можно переписать:

x + 2⁹ = 2(1 + x)

Получили уравнение, решим его (см. урок уравнения):

x + 2⁹ = 2(1 + x)

x + 2⁹ = 2 + 2x

2x — x = 2⁹— 2

x = 512 — 2 = 510

Теперь выразим искомую нами сумму через х:

2 + 2² + 2³ + 2⁴ + 2⁵ + 2⁶ + 2⁷ + 2⁸ + 2⁹= x + 2⁹= 510 + 512 = 1022

При решении этой задачи мы возводили число 2 только в 9-ую степень, а все остальные операции возведения в степень удалось исключить из вычислений за счет разложения многочлена на множители. Аналогично можно составить формулу вычисления и для других подобных сумм.

Теперь вычислим значение выражения

38.4² — 61.6 * 29.5 + 61.6 * 38.4 — 29.5 * 38.4

Посчитать это напрямую достаточно сложно. Однако можно применить метод группировки:

38.4² — 61.6 * 29.5 + 61.6 * 38.4 — 29.5 * 38.4 = 38.4² — 29.5 * 38.4 + 61.6 * 38.4 — 61.6 * 29.5 = 38.4(38.4 — 29.5) + 61.6(38.4 — 29.5) = (38.4 + 61.6)(38.4 — 29.5) = 8.9*100 = 890

Далее посмотрим, как можно использовать разложение полинома для доказательства делимости чисел. Пусть требуется доказать, что выражение

81⁴ — 9⁷ + 3¹²

делится на 73. Заметим, что числа 9 и 81 являются степенями тройки:

9 = 3²

81 = 9² = (3²)² = 3⁴

Зная это, произведем замену в исходном выражении:

81⁴ — 9⁷ + 3¹²= (3⁴)⁴ — (3²)⁷ + 3¹² = 3¹⁶ — 3¹⁴ + 3¹²

Вынесем 3¹²:

3¹⁶ — 3¹⁴ + 3¹²= 3¹²(3⁴ — 3² + 1) = 3¹² * (81 — 9 + 1) = 3¹² * 73

Произведение 3¹²•73 делится на 73 (так как на него делится один из множителей), поэтому и выражение 81⁴ – 9⁷ + 3¹² делится на это число.

Вынесение множителей может использоваться для доказательства тождеств. Например, докажем верность равенства

(a² + 3a)² + 2(a² + 3a) = a(a + 1)(a + 2)(a + 3)

Для решения тождества преобразуем левую часть равенства, вынеся общий множитель:

(a² + 3a)² + 2(a² + 3a) = (a² + 3a)(a² + 3a) + 2(a² + 3a) = (a² + 3a)(a² + 3a + 2)

Далее произведем замену 3a = 2a + a:

(a² + 3a)(a² + 3a + 2) = (a² + 3a)(a² + 2a + a + 2) = (a² + 3a)((a² + 2a) + (a + 2) = (a² + 3a)(a(a + 2) + (a + 2)) = (a² + 3a)(a + 1)(a + 2) = a(a + 3)(a + z)(a + 2) = a(a + 1)(a + 2)(a + 3)

Ещё один пример. Докажем, при любых значениях переменных x и у выражение

(x — y)(x + y) — 2x(x — y)

не является положительным числом.

Решение. Вынесем общий множитель х – у:

(x — y)(x + y) — 2x(x — y) = (x — y)(x + y — 2x) = (x — y)(y — x)

Обратим внимание, что мы получили произведение двух похожих двучленов, отличающихся лишь порядком букв x и y. Если бы мы поменяли местами в одной из скобок переменные, то получили бы произведение двух одинаковых выражений, то есть квадрат. Но для того, чтобы поменять местами x и y, нужно перед скобкой поставить знак минус:

(x — y) = -(y — x)

Тогда можно записать:

(x — y)(y — x) = -(y — x)(y — x) = -(y — x)²

Как известно, квадрат любого числа больше или равен нулю. Это относится и к выражению (у – х)². Если же перед выражением стоит минус, то оно должно быть меньше или равным нулю, то есть не является положительным числом.

Разложение полинома помогает решать некоторые уравнения. При этом используется следующее утверждение:

Если в одной части уравнения стоит ноль, а в другой произведение множителей, то каждый из них следует приравнять нулю.

Пример. Решите уравнение (s – 1)(s + 1) = 0.

Решение. В левой части записано произведение мономов s – 1 и s + 1, а в правой – ноль. Следовательно, нулю должно равняться или s – 1, или s + 1:

(s — 1)(s + 1) = 0

s — 1 = 0 или s + 1 = 0

s = 1 или s = -1

Каждое из двух полученных значений переменной s является корнем уравнения, то есть оно имеет два корня.

Ответ: –1; 1.

Пример. Решите уравнение 5w² – 15w = 0.

Решение. Вынесем 5w:

5w² – 15w = 0

5w(w — 3) = 0

Снова в левой части записано произведение, а в правой ноль. Продолжим решение:

5w = 0 или (w — 3) = 0

w = 0 или w = 3

Ответ: 0; 3.

Пример. Найдите корни уравнения k³– 8k² + 3k– 24 = 0.

Решение. Сгруппируем слагаемые:

k³– 8k² + 3k– 24 = 0

(k³– 8k²) + (3k– 24) = 0

k²(k — + 3(k — = 0

(k³ + 3)(k — = 0

k² + 3 = 0 или k — 8 = 0

k² = -3 или k = 8

Заметим, что уравнение k² = – 3 решения не имеет, так как любое число в квадрате не меньше нуля. Поэтому единственным корнем исходного уравнения является k = 8.

Ответ: 8.

Пример. Найдите корни уравнения

(2u — 5)(u + 3) = 7u + 21

Решение: Перенесем все слагаемые в левую часть, а после сгруппируем слагаемые:

(2u — 5)(u + 3) = 7u + 21

(2u — 5)(u + 3) — 7u — 21 = 0

(2u — 5)(u + 3) — 7(u + 3) = 0

(2u — 5 — 7)(u + 3) = 0

(2u — 12)(u + 3) = 0

2u — 12 = 0 или u + 3 = 0

u = 6 или u = -3

Ответ: – 3; 6.

Пример. Решите уравнение

(t² — 5t)² = 30t — 6t²

Решение:

(t² — 5t)² = 30t — 6t²

(t² — 5t)² — (30t — 6t²) = 0

(t² — 5t)(t² — 5t) + 6(t² — 5t) = 0

(t² — 5t)(t² — 5t + 6) = 0

t² — 5t = 0 или t² — 5t + 6 = 0

Далее решим по отдельности эти уравнения:

t² — 5t = 0

t(t — 5) = 0

t = 0 или t — 5 = 0

t = 0 или t = 5

Теперь займемся вторым уравнением. Перед нами снова квадратный трехчлен. Чтобы разложить его на множители методом группировки, нужно представить его в виде суммы 4 слагаемых. Если произвести замену – 5t = – 2t – 3t, то дальше удастся сгруппировать слагаемые:

t² — 5t + 6 = 0

t² — 2t — 3t + 6 = 0

t(t — 2) — 3(t — 2) = 0

(t — 3)(t — 2) = 0

T — 3 = 0 или t — 2 = 0

t = 3 или t = 2

В результате получили, что у исходного уравнения есть 4 корня.

Ответ: 0, 2, 3, 5

Источник