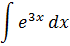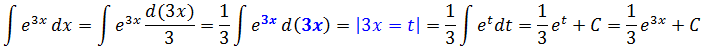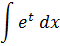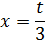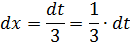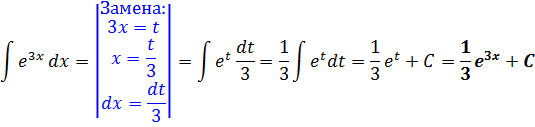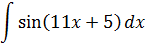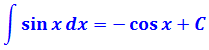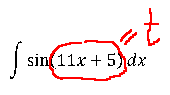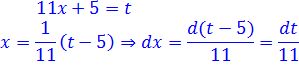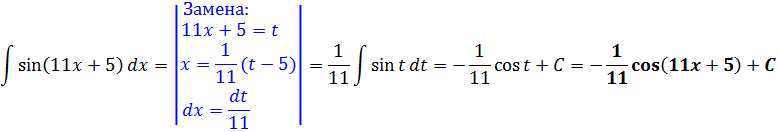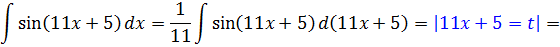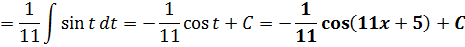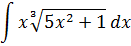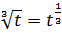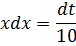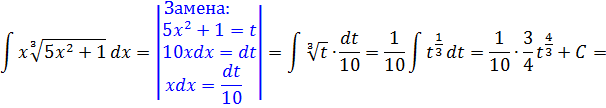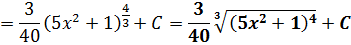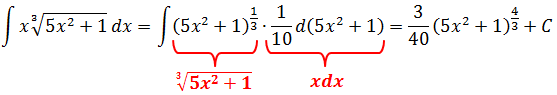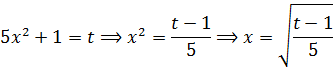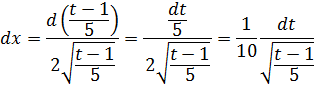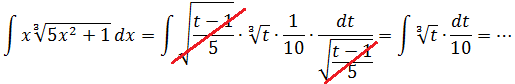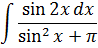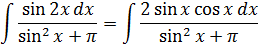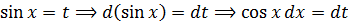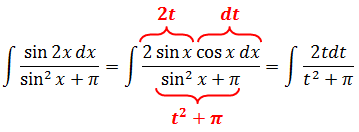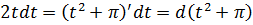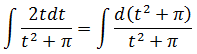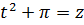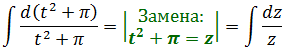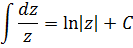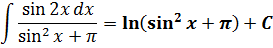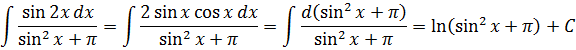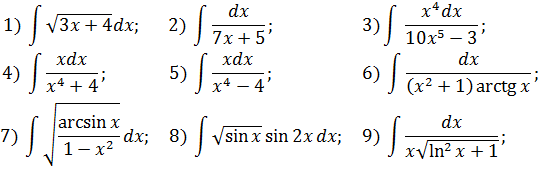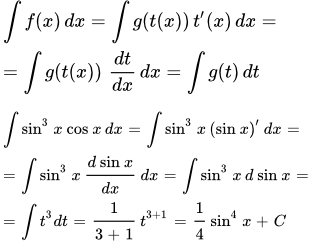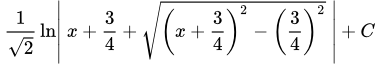Как найти dx при замене переменной - Исправление недочетов и поиск решений вместе с Examum.ru

Заказать задачи по любым предметам можно здесь от 10 минут

Замена переменной в неопределенном интеграле

Замена переменной в неопределенном интеграле используется при нахождении интегралов, в которых одна из функций является производной другой функции. Пусть есть интеграл $ int f(x) dx $, сделаем замену $ x=phi(t) $. Отметим, что функция $ phi(t) $ является дифференцируемой, поэтому можно найти $ dx = phi'(t) dt $.

Теперь подставляем $ begin{vmatrix} x = phi(t) \ dx = phi'(t) dt end{vmatrix} $ в интеграл и получаем, что:

$$ int f(x) dx = int f(phi(t)) cdot phi'(t) dt $$

Эта и есть формула замены переменной в неопределенном интеграле.

Алгоритм метода замены переменной

Таким образом, если в задаче задан интеграл вида: $$ int f(phi(x)) cdot phi'(x) dx $$ Целесообразно выполнить замену переменной на новую: $$ t = phi(x) $$ $$ dt = phi'(t) dt $$

После этого интеграл будет представлен в виде, который легко взять основными методами интегрирования: $$ int f(phi(x)) cdot phi'(x) dx = int f(t)dt $$

Не нужно забывать также вернуть замененную переменную назад к $ x $.

Примеры решений

Пример 1

Найти неопределенный интеграл методом замены переменной: $$ int e^{3x} dx $$

Решение

Выполняем замену переменной в интеграле на $ t = 3x, dt = 3dx $:

$$ int e^{3x} dx = int e^t frac{dt}{3} = frac{1}{3} int e^t dt = $$

Интеграл экспоненты всё такой же по таблице интегрирования, хоть вместо $ x $ написано $ t $:

$$ = frac{1}{3} e^t + C = frac{1}{3} e^{3x} + C $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ int e^{3x} dx = frac{1}{3} e^{3x} + C $$

Пример 2

Найти неопределенный интеграл методом замены переменной:

$$ int sin^5 x cos x dx $$

Решение

Замечаем, что $ (sin x)’ = cos x $, поэтому выгодно сделать замену переменной $$ t = sin x, dt = cos x dx $$

Тогда после подставления её в интеграл будем иметь:

$$ int t^5 dt = frac{t^6}{6} + C = frac{1}{6} sin^6 x + C $$

В самом конце очень важно не забывать возвращать замену назад, чтобы получить окончательный ответ.

Ответ

$$ int sin^5 x cos x dx =frac{1}{6}sin^6 x + C $$

Пример 3

Найти интеграл с помощью замены переменной: $$ int frac{cos sqrt{x}}{sqrt{x}} dx $$

Решение

Как обычно анализируем интеграл и замечаем, что в интеграле есть функция и её производная. А именно этой функцией является $ sqrt{x} $ и её производная $ frac{1}{2sqrt{x}} $. Поэтому замену переменной сделаем такой: $$ t = sqrt{x}, dt = frac{dx}{2sqrt{x}} $$

Подставляем в интеграл и решаем:

$$ int frac{cos sqrt{x}}{sqrt{x}} dx = 2int cos t = 2sin t + C = $$

Выполняем обратную замену:

$$ = 2sin sqrt{x} + C $$

Ответ

$$ int frac{cos sqrt{x}}{sqrt{x}} dx = 2sin sqrt{x} + C $$

Источник

Итак, друзья, продолжаем наше знакомство с базовыми методами интегрирования! В прошлых уроках мы порешали простенькие интегралы на прямое применение таблицы, а также познакомились с первым базовым методом интегрирования — подведением функции под знак дифференциала. С этого урока уже начнётся серьёзное интегрирование и не менее серьёзные примеры. Так что, у кого пока проблемы с простыми интегралами — читайте предыдущие темы, пока не поздно. Почему? А потому, что в этом уроке мы резко расширяем наши возможности! А именно — знакомимся с одним из самых мощных методов интегрирования — методом замены переменной.

И в чём же заключается могущество сего метода? А в том, что в подавляющем большинстве случаев именно он позволяет превращать многие ужасные, на первый взгляд, примеры в белые и пушистые.) Например, интеграл с каким-нибудь страшным корнем или арксинусом после удачной замены может свестись к безобидному многочлену. Или к рациональной функции, которая всяко проще для интегрирования. Имеет смысл разобраться!

Итак, начнём.)

Суть замены переменной. Простейшие примеры.

Процедура замены переменной знакома всем вам ещё со школы. Например, решая жуткое тригонометрическое уравнение

sin²x — 2sin x — 3 = 0,

что вы обычно делаете? Правильно! Вы заменяете выражение sin x новой буквой — y, z, t — какой хотите. И дальше работаете уже с более простым квадратным уравнением — дискриминант считаете, тыры-пыры…

Всё то же самое и с интегралами.) Принцип тот же. Основная идея любой замены состоит в том, чтобы выражение, которое нам не нравится, заменить новой буквой. И все остальные части примера также выразить через эту самую новую букву. Тогда, если после всех преобразований пример упрощается, то, значит, основная цель данной замены выполнена.

На прошлом уроке я уже говорил, что метод подведения функции под знак дифференциала — это простейший частный случай более общего метода замены переменной. Теперь настал черёд посмотреть, почему же это именно так и как работает сама процедура замены. Примеров в данном уроке будет не так много, но все они будут разобраны максимально подробно. Чтобы суть уловить.) Рассмотрим все проблемные места, исследуем каждую тонкость.

Начнём сразу с примера. Чтобы далеко не ходить, давайте вернёмся к нашему самому первому примеру из прошлого урока.

Пример 1

Что мы делали в прошлый раз, когда решали этот пример? Сначала мы добивались равенства выражений в показателе экспоненты и под дифференциалом. Для этого мы сначала выражали новый дифференциал d(3x) через старый dx, а уже в самом конце вводили новую переменную 3х = t и сводили наш интеграл к табличному.

Всё решение примера выглядело вот так:

d(3x) = (3x)’dx = 3dx

dx = d(3x)/3

Вспомнили? Отлично!

А теперь подойдём к данному примеру немного с другой стороны. Для начала вопрос: что вам больше всего не нравится в данном примере? 99 человек из 100 скажут: три икс! И будут правы. ) Вот и будем от этого самого 3х избавляться. Безопасно для самого примера.)

Для этого поступаем просто и элегантно. Нам ведь в примере не нравится 3х, верно? Вот и заменяем это самое 3х новой буквой! Да-да! Прямо сразу! Безо всяких дифференциалов. Дифференциалы будут потом.)

Так прямо и пишем:

3x = t

В результате данной замены наша подынтегральная функция превращается в простенькую табличную функцию e^t. И наш пример становится уже вот таким:

Но для применения табличной формулы этого пока мало. Почему? А потому, что, раз уж мы ввели новую переменную t, то, ясное дело, и весь пример целиком также должен быть выражен через t! А у нас в примере пока что торчит старый дифференциал dx. Надо бы его тоже как-то превратить в dt. Как? Очень просто!

Чтобы понять, во что же у нас превратится дифференциал dx, самым логичным было бы сначала выразить сам икс через новую переменную t. Здесь это проще простого. Для этого берём наше равенство 3x = t и выражаем из него икс через t. Вот так:

Отлично. Полдела сделано.) И теперь, чтобы выразить интересующий нас дифференциал dx через букву t, просто берём дифференциалы от обеих частей нашего равенства. Думаю, для этой процедуры комментарии уже излишни:

dx = d(t/3)

Вот и всё. Вставляем теперь в наш пример вместо dx выражение dt/3, выносим дробь 1/3 за знак интеграла и дорешиваем по таблице. Чистовое оформление примера теперь выглядит немного по-другому. Вот так:

Как видите, ответ получился тем же самым. Что вполне логично.)

Разберём ещё один пример с непосредственной заменой линейной конструкции. На закрепление.)

Пример 2

Напрашивается табличная формула с синусом:

Только э-э-э… в формуле стоит просто икс, а в нашем примере под синусом стоит сложный аргумент 11х+5. Неувязочка… А что, если заменить этот сложный аргумент 11х+5 новой буквой? Ведь именно это выражение нам и не нравится! Посмотрим…

На черновике так прямо и пишем вот такую заготовку:

Отлично! sin(11x+5) превращается в sin t, а dx превращается в dt/11. Жизнь налаживается.) Не пример, а сплошное удовольствие)

А теперь посмотрим на решение того же примера методом подведения выражения 11х+5 под дифференциал:

Получили тот же самый ответ, но оформление всё же немного другое. Почувствовали разницу?

В чём сходство этих двух способов? В том, что и там и тут мы заменяем новой буквой одно и то же выражение (в наших примерах это 3х и 11х+5). А отличие этих двух способов состоит лишь в том, на каком этапе решения вводится сама замена. Здесь мы сразу заменяем новой буквой то, что нам не нравится, потом связываем переменные старую с новой, а уж потом, в самом конце, находим связь и между их дифференциалами. А в методе подведения мы сначала связываем сами дифференциалы, а уже потом вводим замену. Или даже вообще не вводим, если уже «руку набили».:)

Как видите, и так и сяк решать можно. Тем, кто крепко дружит с дифференциалами, рекомендую сразу решать подобные интегралы методом подведения. Ибо такое решение гораздо короче. А этот способ, с изначальной заменой, хорош для тех студентов, кто с дифференциалами пока того… не очень…) Или если пример достаточно накрученный. Но зато этот способ более понятен, универсален и надёжен! Спасает в любой ситуации. Если, конечно, удачно выбрана сама замена.)

Это были самые простые примеры, где заменялась линейная конструкция — так, для разминки. Суть ясна, я думаю.)

А теперь разберём примеры посерьёзнее. Такие, где надо заменять не линейные, а более сложные выражения и подвести функцию под дифференциал уже не так-то просто, хоть и возможно. Как и в прошлом уроке, суть этой группы примеров будет заключаться в выделении из подынтегральной функции f(x) какой-то вспомогательной функции g(x) и её производной g’(x). И последующей замене g(x) = t. Здесь уже надо уметь чувствовать и узнавать в функциях производные других функций. В лицо! Зачем? А чтобы удачно подобрать замену! Ведь можно и неудачно подобрать, да. Особенно если плохо знать таблицу производных. Об этом мы уже подробно поговорили на прошлом уроке.)

Пример 3

Внимательно осматриваем пример и ищем в подынтегральной функции конструкцию, которая нам больше всего не нравится. Вот тут, в отличие от предыдущих примеров, уже возможны варианты. Кому-то не понравится корень, кому-то сам по себе корень будет по душе, но не понравится выражение 5х²+1, стоящее под корнем. Отдельным индивидуумам может не понравиться множитель x… Что именно заменять — пока не знаем. Всматриваемся дальше. У нас есть подкоренная конструкция 5х²+1 и есть множитель х, отдалённо похожий на её производную, так как

(5х²+1)’ = 10х

Именно это равенство и должно служить ключевой зацепкой!

А не попробовать ли заменить наше сложное подкоренное выражение 5х²+1 новой буквой? Что ж, попробуем и посмотрим, к чему это приведёт. Итак, делаем замену:

5х²+1 = t

Тогда наш корень после такой замены превратится в безобидную степенную конструкцию:

Так, с корнем расправились. Но, помимо корня, под интегралом у нас ещё осталось произведение xdx, которое тоже надо выразить через новую букву t, да.

Для этого немного схитрим. Не будем выражать «в лоб» икс через t, а затем искать dx. Это можно, но не нужно. Почему — объясню позже. Давайте сразу продифференцируем наше равенство для замены! Да-да! Целиком! Обе части. Вот так:

5х²+1 = t (это равенство — наша замена)

d(5х²+1) = dt (дифференцируем обе части)

(5х²+1)’dx = dt (раскрываем дифференциалы)

10xdx = dt

И что нам даёт эта запись? А то, что из неё теперь легко выражается нужная нам конструкция xdx:

Всё. Начинка интеграла теперь полностью выражена через t. Продолжаем наши игры.)

Подставляем теперь все данные в наш пример и получаем простенький табличный интеграл от степенной функции (n = 1/3, n+1 = 4/3):

Вот и все дела.) Пример разложили по полочкам. А можно ли решить данный интеграл через подведение под значок d? Можно! В одну строчку!

Другое дело, что догадаться, какую именно конструкцию надо подводить под дифференциал, уже гораздо сложнее: легко запутаться в коэффициентах. И под силу не каждому студенту. Поэтому те, кто пока не наловчился в подведении функции под дифференциал — решаем подобные примеры сразу через замену. Аккуратно. Чуть длиннее, зато надёжнее.)

А теперь ответ на вопрос, почему я не стал в явном виде выражать икс через t и затем находить dx. Не стал я этого делать по той причине, что наличие х² в подкоренном выражении резко усложняет эту процедуру из-за того, что возникают корни.

Смотрите сами:

Тогда для дифференциала этого самого икса мы получим:

И, если теперь подставить в наш пример отдельные выражения для x и dx, то наши нехорошие корни благополучно сократятся и мы придём к тому же самому интегралу:

Как видите, получили всё то же самое, только выкладки более громоздкие. Поэтому, по возможности, сокращаем объём работы: ошибок меньше будет.

Иногда встречаются и сюрпризы, когда замену переменной приходится проделывать более одного раза. Ничего страшного! Просто аккуратно заменяем неудобную конструкцию и последовательно упрощаем пример, шаг за шагом добираясь до табличного интеграла. И, конечно, после получения результата корректно осуществляем обратную замену. От новой переменной к предыдущей.)

Пример 4

Что, внушает? Минутку смотрим на пример, ужасаемся, после чего берём себя в руки и вспоминаем золотое правило всей математики:

Не знаешь, что нужно — делай, что можно!

И размышляем. Примерно так:

«Под интегралом нехорошая дробь. Сплошные синусы, аргументы разные — x и 2x. Да ещё и число «пи» затесалось… Кошмар! Но, очевидно, что чем больше одинаковых значков в примере и меньше разных, тем лучше. Поэтому первым делом упрощу-ка я синус двойного угла. По школьной формуле sin 2x = 2sin x·cos x. Поможет ли нам такое преобразование или нет — неясно. Но начинаем-то с самого простого! А там — видно будет.»

Если вы мыслите примерно так, то вы движетесь правильным курсом. Да! Сводим всё подынтегральное выражение к одному аргументу — к иксу. Два икс тут явно ни к чему.

Ну вот, уже лучше. В аргументах остались только иксы. А теперь снова пытаемся выявить родственные функции, опираясь на таблицу производных. Сразу же видно, что в получившейся дроби везде тусуются синусы, а в числителе в качестве множителя затесался косинус. Но косинус — ближайший родственник синуса! Родственник по производной. Ибо таблица производных гласит, что:

cos x = (sin x)’ .

Поэтому вводим напрашивающуюся замену sin x = t и продолжаем упрощать наш злой пример:

Отлично. Все синусы пропали напрочь, при этом суть примера не изменилась.

А дальше что делать с этой дробью? Таблица-то не катит! Нету пока подходящей формулы… Тупик? Вовсе нет! Опять внимательно осматриваем нашу дробь, выявляя родню по производной/дифференциалу, и… радостно замечаем, что в числителе стоит дифференциал знаменателя!

Вот так:

Мы же понимаем, что под дифференциал мы имеем право спрятать любую константу! В том числе и «пи».)

А вот теперь снова вводим замену! Да-да!

Тогда вообще красота получится!

Вот и всё. И нету больше никакого «пи»! Спряталось оно под дифференциал. Как и любая константа, да… А ведь как испугало в самом начале! Пример становится всё лучше и лучше:

Вот мы и свели ужасную дробь к безобидному табличному интегралу. По шагам, через две замены.) Но радоваться ещё рано, так как это ещё не ответ: нам икс нужен, а не z или t. Поэтому теперь последовательно проводим обратную замену. Тоже по шагам:

z = t²+π, где t = sin x

Итого z = sin²x + π.

Всё. Теперь со спокойной душой записываем окончательный ответ нашего злого примера:

Готово!

С опытом необходимость так подробно всё расписывать отпадёт сама собой. За ненадобностью. И особо продвинутые студенты этот интеграл легко вычислят в одну строчку вообще без замены! С помощью подведения под дифференциал, ага:

Быстро, правда? И вы тоже так сможете! Причём опыт нарабатывается достаточно скоро. Тренировка — залог успеха.)

Ну как, прониклись? Замена переменной (вкупе с подведением под дифференциал) — оч-чень мощный инструмент для интегрирования! И золотой ключик к успешному решению самых разнообразных примеров. Это было начальное знакомство с самой сутью замены, чтобы прочувствовать, как именно она работает.

А со следующего урока мы уже начнём копать глубже и познакомимся с отдельными специфическими видами замен — степенной заменой и тригонометрической заменой. И типовые примеры тоже обязательно порешаем. Посерьёзнее.)

А теперь несколько несложных примеров для тренировки.

Найти неопределённые интегралы

а) методом подведения функции под знак дифференциала,

б) непосредственной заменой переменной,

в) сравнить результаты и проверить ответ дифференцированием.

Ответов здесь тоже не дам. Не вижу смысла. Примеры довольно простые, и материала сегодняшнего и прошлого уроков вполне достаточно для успешной расправы с ними.) Проверяйте окончательный ответ обратным дифференцированием, не ленитесь! Выучите таблицу производных! Узнавайте в лицо производные популярных функций. Да-да! Обратное дифференцирование — самый надёжный помощник в интегрировании.

И тогда удача обязательно улыбнётся, поверьте! А у меня пока всё, продолжение следует!

Источник

Метод замены переменной или метод подстановки. Этот метод заключается во введении новой переменной интегрирования (то есть делается подстановка). При этом заданный интеграл приводится к новому интегралу, который является табличным или с помощью преобразований его можно свести к табличному.

Пусть требуется вычислить интеграл	. Сделаем подстановку	.
Тогда	и интеграл принимает вид:	∫ ( )	,
или
	, т.е в подынтегральном выражении должна находиться некоторая
функция		. После решения интеграла		делаем
	∫ ( ) и её производная

обратную подстановку t = x.

Общее правило: за t обозначаем саму функцию (а не её производную).

Находим dt следующим образом:

1)записываем формулу подстановки: ϕ(t) = f(x);

2)заключаем функции в скобки со знаком производной и домножаем на dx и dt

соответственно: (ϕ(t))’dt =(f(x))’dx;

3)берем производные и выражаем dx через dt.

Например подстановка: t2 = (2x-1) → ( t2)’ dt = (2x-1)’dx → 2tdt = 2dx →

→ dx = tdt Запомните это.

Пример 15.

Найти интеграл Сделаем замену переменной: , далее приведем интеграл к табличному виду и решим

его. В конце решения делаем обратную замену.

Пример 16

Найти интеграл .

Упростим подынтегральную функцию, а потом сделаем замену переменной:

Пример 17

Найти неопределенный интеграл 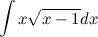Введем замену

Заменим интеграл суммы на сумму интегралов и вынесем постоянные коэффициенты.

Полученные интегралы находим как интегралы от степенной функции:

Делая обратную замену, окончательно получим

Пример 18

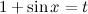
Найти неопределенный интеграл Введем замену и полученный интеграл находим как интеграл от степенной функции:

Сделаем обратную замену

Пример 19

Найти неопределенный интеграл Введем замену и полученный интеграл находим как интеграл от обратной функции:

Выполним обратную замену

Пример 20

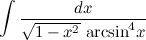
Выполним обратную замену и окончательно получим:

Источник

Теперь подставляем $ begin x = phi(t) \ dx = phi'(t) dt end $ в интеграл и получаем, что:

Эта и есть формула замены переменной в неопределенном интеграле.

Не нужно забывать также вернуть замененную переменную назад к $ x $.

= frac int e^t dt = $$

Интеграл экспоненты всё такой же по таблице интегрирования, хоть вместо $ x $ написано $ t $:

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Найти неопределенный интеграл методом замены переменной:

$$ int sin^5 x cos x dx $$

Замечаем, что $ (sin x)’ = cos x $, поэтому выгодно сделать замену переменной $$ t = sin x, dt = cos x dx $$

Тогда после подставления её в интеграл будем иметь:

$$ int t^5 dt = frac+ C = frac sin x + C $$

В самом конце очень важно не забывать возвращать замену назад, чтобы получить окончательный ответ.

Как обычно анализируем интеграл и замечаем, что в интеграле есть функция и её производная. А именно этой функцией является $ sqrt $ и её производная $ frac> $. Поэтому замену переменной сделаем такой: $$ t = sqrt, dt = frac> $$

Подставляем в интеграл и решаем:

$$ int frac>> dx = 2int cos t = 2sin t + C = $$

Метод замены переменной в неопределённом интеграле

Во многих случаях подынтегральное выражение не позволяет сразу же найти интеграл по таблице. Тогда введение новой переменной интегрирования помогает свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки или методом замены переменной.

Вводится новая переменная, назовём её t . Например,

в интеграле можем ввести новую переменную ;
в интеграле можем ввести новую переменную ;
в интеграле можем ввести новую переменную .

Далее dx определеяем как дифференциал по переменной t . После этого интеграл можно найти по таблице интегралов. Заменив обратно t на функцию от x , находим данный интеграл окончательно.

Прежде чем перейти к подробным решениям примеров, следует привести теорему, в которой обобщаются перечисленные выше действия.

Теорема. Пусть функция определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула

Формула (1) называется формулой замены переменной в неопределённом интеграле.

Метод замены переменной обычно применяется, когда подынтегральное выражение представляет собой независимую переменную, умноженную на многочлен от этой переменной, или на тригонометрическую функцию от этой переменной или на степенную функцию (в том числе корень) от этой переменной.

Применяем замену переменной вместе

Надо полагать, вы уже держите перед собой домашние задания и готовы применять к ним приёмы по аналогии с теми, которые мы ниже рассмотрим. При этом не обойтись без преобразований выражений. Для этого потребуется открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.

Пример 1. Найти неопределённый интеграл методом замены переменной:

Решение. Производим замену x − 1 = t ; тогда x = t + 1 . Отсюда dx = dt . По формуле (1)

Возвращаясь к переменной x , окончательно получаем

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Замечание. При замене переменной в неопределённом интеграле иногда более удобно задавать не х как функцию t, а, наоборот, задавать t как функцию от x.

Заметим, что удачный выбор подстановки обычно представляет известные трудности. Для их преодоления необходимо овладеть техникой дифференцирования и хорошо знать табличные интегралы.

Пример 2. Найти неопределённый интеграл методом замены переменной:

Решение. Положим . Отсюда
.
По формуле (1) и, пользуясь табличными интегралом 13, находим

Возвращаясь к переменной x, окончательно получаем

Если трудно уследить, куда в процессе решения примера 2 делись и , это признак того, что нужно повторить действия со степенями из элементарной (школьной) математики.

Пример 3. Найти неопределённый интеграл методом замены переменной:

Решение. Положим , откуда и .

Тогда , в свою очередь .

Заменяем переменную и получаем:

где степени при t складываются. Продолжаем преобразования и, пользуясь уже упомянутым табличным интегралом 7, получаем:

Приводим дроби к общему знаменателю и возвращаемся к переменной x. Решаем и получаем ответ:

Применить замену переменной самостоятельно, а затем посмотреть решение

Пример 4. Найти неопределённый интеграл методом замены переменной:

Пример 5. Найти неопределённый интеграл методом замены переменной:

Пример 6. Найти неопределённый интеграл методом замены переменной:

Снова применяем замену переменной вместе

Пример 7. Найти неопределённый интеграл методом замены переменной:

Решение. Положим , откуда , , .

Заменяем переменную и получаем:

Возвращаясь к переменной х, получаем ответ:

Пример 8. Найти неопределённый интеграл методом замены переменной:

Решение. Положим , откуда , .

Заменяем переменную и получаем:

Подставляя вместо t его выражение через x получаем ответ:

Кому лишь смутно понятно или совсем не понятно, как преобразуются выражения в примере 5, пожалуйста, повторите из курса элементарной (школьной) математики действия с корнями, степенями и дробями!

И если вы ещё не открыли в новых окнах пособия Действия со степенями и корнями и Действия с дробями, то сделайте это сейчас!

Пример 9. Найти неопределённый интеграл методом замены переменной:

Решение. Положим , тогда
.

Заменяем переменную и получаем:

Решение с переменной t получено с использованием формулы 21 из таблицы интегралов.

Подставляя вместо t его выражение через x получаем ответ:

Интегрирование методом замены переменной

С помощью замены переменной можно вычислить простые интегралы и, в некоторых случаях, упростить вычисление более сложных.

Метод замены переменной заключается в том, что мы от исходной переменной интегрирования, пусть это будет x , переходим к другой переменной, которую обозначим как t . При этом мы считаем, что переменные x и t связаны некоторым соотношением x = x ( t ) , или t = t ( x ) . Например, x = ln t , x = sin t , t = 2 x + 1 , и т.п. Нашей задачей является подобрать такую зависимость между x и t , чтобы исходный интеграл либо свелся к табличному, либо стал более простым.

Основная формула замены переменной

Рассмотрим выражение, которое стоит под знаком интеграла. Оно состоит из произведения подынтегральной функции, которую мы обозначим как f ( x ) и дифференциала dx : . Пусть мы переходим к новой переменной t , выбрав некоторое соотношение x = x ( t ) . Тогда мы должны выразить функцию f ( x ) и дифференциал dx через переменную t .

Чтобы выразить подынтегральную функцию f ( x ) через переменную t , нужно просто подставить вместо переменной x выбранное соотношение x = x ( t ) .

Преобразование дифференциала выполняется так:
.
То есть дифференциал dx равен произведению производной x по t на дифференциал dt .

На практике, чаще всего встречается случай, в котором мы выполняем замену, выбирая новую переменную как функцию от старой: t = t ( x ) . Если мы догадались, что подынтегральную функцию можно представить в виде
,
где t′ ( x ) – это производная t по x , то
.

Итак, основную формулу замены переменной можно представить в двух видах.
(1) ,
где x – это функция от t .
(2) ,
где t – это функция от x .

Важное замечание

В таблицах интегралов переменная интегрирования, чаще всего, обозначается как x . Однако стоит учесть, что переменная интегрирования может обозначаться любой буквой. И более того, в качестве переменной интегрирования может быть какое-либо выражение.

В качестве примера рассмотрим табличный интеграл
.

Здесь x можно заменить любой другой переменной или функцией от переменной. Вот примеры возможных вариантов:
;
;
.

В последнем примере нужно учитывать, что при переходе к переменной интегрирования x , дифференциал преобразуется следующим образом:
.
Тогда
.

В этом примере заключена суть интегрирования подстановкой. То есть мы должны догадаться, что
.
После чего интеграл сводится к табличному.
.

Можно вычислить этот интеграл с помощью замены переменной, применяя формулу (2). Положим t = x 2 + x . Тогда
;
;

Примеры интегрирования заменой переменной

1) Вычислим интеграл
.
Замечаем, что (sin x )′ = cos x . Тогда

.
Здесь мы применили подстановку t = sin x .

2) Вычислим интеграл
.
Замечаем, что . Тогда

.
Здесь мы выполнили интегрирование заменой переменной t = arctg x .

3) Проинтегрируем
.
Замечаем, что . Тогда

. Здесь, при интегрировании, произведена замена переменной t = x 2 + 1 .

Линейные подстановки

Пожалуй, самыми распространенными являются линейные подстановки. Это замена переменной вида
t = ax + b ,
где a и b – постоянные. При такой замене дифференциалы связаны соотношением
.

Примеры интегрирования линейными подстановками

A) Вычислить интеграл
.
Решение.
.

B) Найти интеграл
.
Решение.
Воспользуемся свойствами показательной функции.
.
ln 2 – это постоянная. Вычисляем интеграл.

C) Вычислить интеграл
.
Решение.
Приведем квадратный многочлен в знаменателе дроби к сумме квадратов.
.
Вычисляем интеграл.

D) Найти интеграл
.
Решение.
Преобразуем многочлен под корнем.

.
Интегрируем, применяя метод замены переменной .

$frac1<sqrt<2>> ln left| ; x + frac34 + sqrt <left( x + frac34 right)^2 - left( frac34 right)^2 >; right| + C» width=»375″ height=»64″ /> . Ранее мы получили формулу . Отсюда . Подставив это выражение, получим окончательный ответ. E) Вычислить интеграл . Решение. Применим формулу произведения синуса и косинуса. ; . Интегрируем и делаем подстановки. . Использованная литература: Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.$

Источник

Интегрирование методом замены переменной

Замена переменной в неопределенном интеграле

Одним из наиболее мощных методов интегрирования является замена переменной в интеграле. Поясним суть этого метода. Пусть F'(x)=f(x) , тогда

int f(x),dx= int F'(x),dx= int dbigl(F(x)bigr)=F(x)+C.

Но в силу инвариантности формы дифференциала равенство dbigl(F(x)bigr)=F'(x),dx= f(x),dx остается справедливым и в случае, когда {x} — промежуточный аргумент, т.е. x=varphi(t) . Это значит, что формула textstyle{int f(x),dx=F(x)+C} верна и при . Таким образом,

int fbigl(varphi(t)bigr),dbigl(varphi(t)bigr)= Fbigl(varphi(t)bigr)+C , или int fbigl(varphi(t)bigr)varphi'(t),dt= Fbigl(varphi(t)bigr)+C .

Итак, если F(t) является первообразной для f(x) на промежутке {X} , а x=varphi(t) — дифференцируемая на промежутке {T} функция, значения которой принадлежат {X} , то Fbigl(varphi(t)bigr) — первообразная для fbigl(varphi(t)bigr)varphi'(t),~tin T , и, следовательно,

int fbigl(varphi(t)bigr)varphi'(t),dt= int f(x),dx,.

Эта формула позволяет свести вычисление интеграла textstyle{int fbigl(varphi(t)bigr)varphi'(t),dt} к вычислению интеграла textstyle{int f(x),dx} . При этом мы подставляем вместо переменную {x} , а вместо дифференциал этой переменной, т. е. . Поэтому полученная формула называется формулой замены переменной под знаком неопределенного интеграла. Она используется на практике как «слева направо», так и «справа налево». Метод замены переменной позволяет сводить многие интегралы к табличным. После вычисления интеграла textstyle{int f(x),dx} надо снова заменить {x} на varphi(t) .

Пример 1. Вычислим intcos2t,dt .

Решение. Введем новую переменную {x} , положив 2t=x . Тогда $2,dt=dx,~dt=frac{1}{2},dx$ и, следовательно,

$intcos2t,dt= intcos{x},frac{1}{2},dx= frac{1}{2}intcos{x},dx= frac{1}{2}sin{x}+C= frac{1}{2}sin2t+C.$

Замечание. Вычисление короче записывают так:

$intcos2t,dt= frac{1}{2}intcos2t,d(2t)= frac{1}{2}sin2t+C.$

Аналогичными преобразованиями мы будем пользоваться и в дальнейшем.

Пусть известно, что textstyle{int f(t),dt=F(t)+C} . Тогда

$int f(ax+b),dx= frac{1}{a}int f(ax+b),d(ax+b)= frac{1}{a}F(ax+b)+C.$

Итак, если int f(t),dt=F(t)+C , то $int f(ax+b),dx=frac{1}{a}F(ax+b)+C.$ .

Например, $intfrac{dx}{x}=ln|x|+C$ и потому $intfrac{dx}{5x-3}=frac{1}{5}ln|5x-3|+C$ .

Пример 2. Вычислить неопределённый интеграл $intfrac{e^{operatorname{arctg}t}}{1+t^2},dt$ .

Решение. В состав данного подынтегрального выражения входит множитель $frac{dt}{1+t^2}$ , являющийся дифференциалом функции operatorname{arctg}t . Полагая operatorname{arctg}t=x , получим:

$intfrac{e^{operatorname{arctg}t}}{1+t^2},dt= int e^x,dx=e^x+C= e^{operatorname{arctg}t}+C.$

Пример 3. Вычислим $intfrac{x^2}{x^6+9},dx$ .

Решение. Числитель данного подынтегрального выражения напоминает дифференциал для x^3 : в самом деле, d(x^3)=3x^2,dx . Кроме того, знаменатель подынтегрального выражения легко выражается через x^3: x^6+9=(x^3)^2+9 .

Это наводит на мысль о целесообразности подстановки x^3=u . Тогда du=3x^2,dx , откуда $x^2,dx=frac{1}{3},du$ . Таким образом,

$intfrac{x^2}{x^6+9},dx= intfrac{1}{u^2+9}frac{1}{3},du= frac{1}{3}intfrac{du}{u^2+3^2}= frac{1}{9}operatorname{arctg}frac{u}{3}+C= frac{1}{9}operatorname{arctg}frac{x^3}{3}+C.$

В рассмотренных примерах новая переменная была функцией от переменной интегрирования. В ряде случаев бывает целесообразно переменную интегрирования в заданном интеграле заменить функцией от другой переменной. В частности, при интегрировании некоторых видов иррациональных функций оказываются удобными тригонометрические подстановки.

Пример 4. Вычислим $intsqrt{a^2-x^2},dx$ .

Решение. Положим $x=asin{t},,-frac{pi}{2}leqslant tleqslantfrac{pi}{2}~ (a>0)$ и выразим все множители, входящие в состав подынтегрального выражения, через новую переменную

$a^2-x^2=a^2-a^2sin^2t= a^2(1-sin^2t)= a^2cos^2t,quad dx=acos{t},dt$

При этом cos{t}geqslant0 , так как $-frac{pi}{2}leqslant tleqslantfrac{pi}{2}$ . Переходя к новой переменной под знаком неопределенного интеграла, учитывая, что и потому $sqrt{cos^2t}=|cos{t}|=cos{t}$ , получим:

$begin{aligned} intsqrt{a^2-x^2},dx&= intsqrt{a^2cos^2t},acos{t},dt= int acos{t},acos{t},dt= a^2intcos^2t,dt=\ &=a^2intfrac{1+cos2t}{2},dt= frac{a^2}{2}int dt+frac{a^2}{4}intcos2t,d(2t)= frac{a^2}{2},t+ frac{a^2}{4},sin2t+C=\ &=frac{a^2}{2},t+frac{a^2}{4}2sin{t}cos{t}+C= frac{a^2}{2}(t+ sin{t}cos{t})+C.end{aligned}$

Так как x=asin{t} , то $sin{t}=frac{x}{a}$ откуда $t=arcsinfrac{x}{a}$ (переход к обратной тригонометрической функции возможен, поскольку по условию $-frac{pi}{2}leqslant tleqslantfrac{pi}{2}$ ). Далее имеем:

$cos{t}=sqrt{1-sin^2t}= sqrt{1-frac{x^2}{a^2}}= frac{1}{a}sqrt{a^2-x^2}$

(перед радикалом берется знак «плюс», поскольку cos{t}geqslant0 ). Значит,

$int!sqrt{a^2-x^2},dx= frac{a^2}{2}!left(arcsinfrac{x}{a}+ frac{x}{a}cdot frac{sqrt{a^2-x^2}}{a}right)+C= frac{a^2}{2}arcsinfrac{x}{a}+ frac{x}{2}sqrt{a^2-x^2}+C.$

Замена переменной в определенном интеграле

Пусть F(x) является первообразной для f(x) на отрезке [a,b] и пусть x=varphi(t) — дифференцируемая функция на отрезке [a,b] , отображающая его в отрезок [a,b] , причем varphi(alpha)=a, varphi(beta)=b . В предыдущем пункте мы видели, что

int fbigl(varphi(t)bigr)varphi'(t),dt= Fbigl(varphi(t)bigr)+C.

Значит,

$intlimits_{alpha}^{beta}fbigl(varphi(t)bigr)varphi'(t),dt= Bigl.{Fbigl(varphi(t)bigr)}Bigr|_{alpha}^{beta}= Fbigl(varphi(beta)bigr)-Fbigl(varphi(alpha)bigr)= F(b)-F(a)= intlimits_{a}^{b}f(x),dx,.$

В результате мы приходим к следующему утверждению:

Пусть функция y=f(x) имеет первообразную на отрезке [a,b] , а функция x=varphi(t) определена на отрезке [alpha,beta] и дифференцируема внутри этого отрезка, причем varphi(alpha)=a,~ varphi(beta)=b и varphi([alpha,beta])=[a,b] . Тогда

$intlimits_{a}^{b}f(x),dx= intlimits_{alpha}^{beta} fbigl(varphi(t)bigr) varphi'(t),dt,.$

(1)

На этом утверждении и основан метод замены переменной под знаком определенного интеграла. Заметим, что на практике формула (1) используется как «слева направо», так и «справа налево».

Условие, что при varphi(alpha)=a,~ varphi(beta)=b имеем: varphi([alpha,beta])=[a,b] , заведомо выполняется, если функция x=varphi(t) монотонна на отрезке . Это имеет место, если ее производная сохраняет знак на .

Пример 5. Вычислим $intlimits_{0}^{a}sqrt{a^2-x^2},dx$ .

Решение. Воспользуемся тригонометрической подстановкой x=varphi(t)=asin{t} . Найдем пределы интегрирования alpha и beta для новой переменной {t} .

Функция x=asin{t} возрастает на отрезке $left[0;frac{pi}{2}right]$ и принимает на нем все значения от до {a} . Поэтому и $frac{pi}{2}$ соответственно нижний и верхний пределы интегрирования для новой переменной {t} .

Функция varphi(t)=asin{t} на отрезке $left[0;frac{pi}{2}right]$ определена и дифференцируема внутри него, причем $varphi(0)=0,~ varphi!left(frac{pi}{2}right)=a$ и $varphi!left(left[0;frac{pi}{2}right]right)=[0;a]$ . Значит, мы можем воспользоваться формулой (1). Используя решение примера 4, получаем:

$begin{aligned}intlimits_{0}^{a}sqrt{a^2-x^2},dx&= frac{a^2}{2} intlimits_{0}^{pi/2}dt+ frac{a^2}{2}intlimits_{0}^{pi/2}cos2t,dt= left.{frac{a^2}{2}, t}right|_{0}^{pi/2}+ left.{frac{a^2}{2}cdot frac{sin2t}{2}}right|_{0}^{pi/2}=\ &=frac{a^2}{2} !left(frac{pi}{2}-0right)+ frac{a^2}{2}(sinpi-sin0)= frac{pi}{4},a^2.end{aligned}$

Пример 6. Вычислим $intlimits_{1/2}^{3/2}frac{dx}{4x^2-4x+5}$ .

Решение. Выделим полный квадрат в знаменателе:

4x^2-4x+5=(4x^2-4x+1)+4= (2x-1)^2+4.

Положим u=2x-1 , тогда du=2,dx . Если x=1/2 , то u=2x-1=2cdot(1/2)-1=0 ; если x=3/2 , то u=2x-1=2cdot(3/2)-1=2 . Таким образом, 0 и 2 — новые пределы интегрирования. Функция u=2x-1 на отрезке $left[frac{1}{2};frac{3}{2}right]$ определена, дифференцируема и монотонно возрастает; значит, можно воспользоваться формулой (1) (но если в предыдущем примере мы использовали эту формулу «слева направо», то теперь будем идти «справа налево»). Получаем;

$begin{aligned}intlimits_{1/2}^{3/2}frac{dx}{4x^2-4x+5}&= frac{1}{2} intlimits_{1/2}^{3/2}frac{dx}{(2x-1)^2+4}= frac{1}{2}intlimits_{0}^{2} frac{du}{u^2+2^2}= left.{frac{1}{2}cdotfrac{1}{2}operatorname{arctg}frac{u}{2}}right|_{0}^{2}=\ &=frac{1}{4}bigl(operatorname{arctg}1-operatorname{arctg}0bigr)= frac{1}{4}!left( frac{pi}{4}-0right)=frac{pi}{16},.end{aligned}$

Метод неопределенных коэффициентов

В ряде случаев по виду подынтегральной функции можно предположить, что ее первообразная будет иметь ту же структуру, что и подынтегральная функция. Это бывает в тех случаях, когда, например, подынтегральная функция представляет собой произведение многочлена и показательной функции, произведение многочлена и синуса или косинуса или произведение показательной функции и синуса или косинуса. Тогда записывают искомую первообразную в предполагаемом виде с неопределенными буквенными коэффициентами. Задача в этом случае сводится к нахождению неопределенных буквенных коэффициентов, для чего, пользуясь свойствами неопределенного интеграла, сначала дифференцируют обе части равенства, а затем сравнивают левую часть полученного равенства с правой. Поясним сказанное на примерах.

Пример 1. Вычислим интеграл с экспонентой int(x^3+2x^2+5)e^x,dx .

Решение. Если вычислить этот интеграл с помощью трехкратного интегрирования по частям, то получим:

int(x^3+2x^2+5)e^x,dx=(x^3-x^2+2x+3)e^x+C.

Этот ответ имеет ту же структуру, что и подынтегральная функция, т.е. является (с точностью до произвольной постоянной) произведением многочлена третьей степени на показательную функцию e^x . Поэтому первообразную можно было сразу искать в следующем виде:

int(x^3+2x^2+5)e^x,dx=(Ax^3+Bx^2+Cx+D)e^x+E,

(1)

где — произвольная постоянная.

Чтобы найти неопределенные коэффициенты A,,B,,C,,D , продифференцируем обе части равенства (1), учитывая при этом, что производная неопределенного интеграла равна подынтегральной функции:

(x^3+2x^2+5)e^x= (3Ax^2+2Bx+C)e^x+ (Ax^3+Bx^2+Cx+D)e^x.

Разделив обе части этого равенства на e^x , получим:

x^3+2x^2+5= 3Ax^2+2Bx+C+ Ax^3+Bx^2+Cx+D,

откуда

x^3+2x^2+5= Ax^3+(3A+B)x^2+ (2B+C)x+(C+D).

(2)

Воспользуемся теперь тем, что два многочлена тождественно равны тогда и только тогда, когда они имеют одинаковую степень и равны их коэффициенты при одинаковых степенях переменной. Сравнив в тождестве (2) коэффициенты при одинаковых степенях переменной {x} , получим:

$begin{array}{lcl}x^3!&vline!&A=1,\ x^2!&vline!&3A+B=2,\ x^1!&vline!&2B+C=0,\ x^0!&vline!&C+D=5. end{array}$

Мы получили систему из четырех уравнений с четырьмя переменными A,,B,,C,,D . Решая ее, находим: A=1,~B=-1, C=2,~D=3 . Таким образом,

int(x^3+2x^2+5)e^x,dx= (x^3-x^2+2x+3)e^x+E.

Пример 2. Вычислим интеграл с экспонентой и синусом $int e^{3x}sin2x,dx$ .

Решение. Здесь подынтегральная функция является произведением показательной функции и синуса. Мы видели, что в этом случае ее первообразная равна произведению показательной функции и линейной комбинации синуса и косинуса того же аргумента:

$int e^{3x}sin2x,dx= e^{3x}(Acos2x+Bsin2x)+C.$

(3)

Для нахождения неопределенных коэффициентов и продифференцируем обе части равенства (3):

$e^{3x}sin2x= 3e^{3x}(Acos2x+Bsin2x)+ e^{3x}(-2Asin2x+2Bcos2x).$

Разделим обе части этого равенства на $e^{3x}:$

sin2x= 3Acos2x+3Bsin2x-2Asin2x+2Bcos2x.

Далее имеем:

sin2x= (3B-2A)sin2x+ (3A+2B)cos2x,.

Полученное равенство справедливо для любых значений {x} . Это имеет место тогда и только тогда, когда равны коэффициенты при sin2x и cos2x в левой и правой частях равенства. Приравняв друг другу указанные коэффициенты, получим:

$begin{array}{lcl}sin2x !&vline!& 3B-2A=1,\ cos2x !&vline!& 3A+2B=0.end{array}$

Из этой системы двух уравнении с двумя переменными и находим: $A=-frac{2}{13},$ $B=frac{3}{13}$ . Значит,

$int e^{3x}sin2x,dx= e^{3x}!left(-frac{2}{13}cos2x+frac{3}{13}sin2xright)+C= frac{e^{3x}}{13}(3sin2x-2cos2x)+C.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник