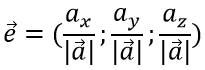1.5.5. Как найти единичный вектор?
Единичный вектор – это вектор, длина которого в ортонормированном базисе равна единице. Таковыми являются сами
координатные векторы и
,
и противоположно направленные им векторы, например:
То, что их длина равна единице, элементарно видно не только по чертежам, но и по формулам .
А теперь рассмотрим произвольный вектор либо
и поставим задачу найти
единичный вектор , коллинеарный исходному. Таких векторов будет два. Чтобы найти сонаправленный единичный вектор нужно каждую координату вектора
разделить на его длину:
либо
,
или, что то же самое – умножить каждую координату вектора на
. То
есть, деление – это частный случай умножения (осознаём и привыкаем). Противоположно направленный единичный
вектор очевиден:
либо
Задача 10
Найти единичные векторы, коллинеарные векторам а) , б)
. Выполнить проверку.
Решение: а) вычислим длину вектора и найдём
сонаправленный единичный вектор:
, от иррациональности в знаменателе (корня) тут
обычно не избавляются. Проверка состоит в нахождении длины полученного вектора:
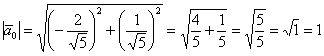
Второй вектор очевиден: , как очевидна и его
длина .
Ответ:
Потребность найти единичный вектор возникает не только в геометрических задачах, и поэтому обязательно прорешайте пункт б)
самостоятельно.


| Оглавление |
Автор: Aлeксaндр Eмeлин
Единичный вектор
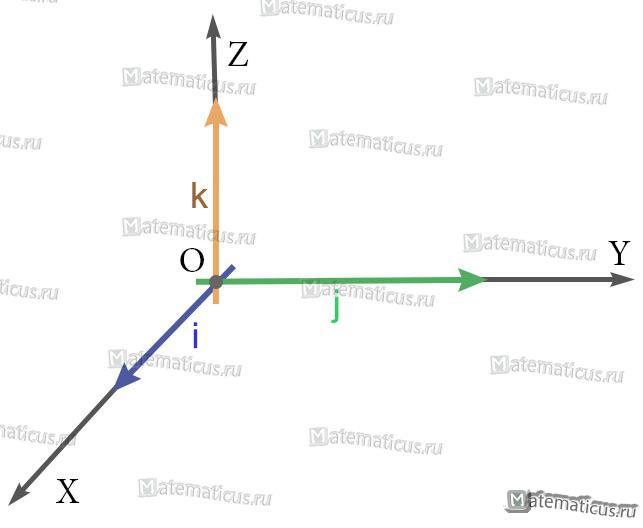
Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.
i — единичный вектор оси абсцисс;
j — единичный вектор оси ординат;
k — единичный вектор оси аппликат.
i⊥j⊥k, i=j=k=1
В прямоугольной системе координат в пространстве координаты векторов равны:
i(1;0;0), j(0;1;0), k(0;0;1)
Единичные векторы являются некомпланарными.
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.
a=xi+уj+zk
где x, y, z — координаты вектора проекции на соответствующие координатные оси.
Эта формула называется разложением вектора по ортам координатных осей.
Единичный вектор определяется по формуле:
Дан вектор а = (1; 2; -2)
Требуется найти длину (модуль) и единичный вектор e направления вектора а
Находим длину вектора a
затем вычисляем единичный вектор e
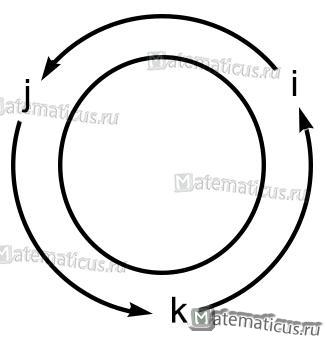
Векторное произведения единичных векторов
Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус» . Смотрите схему 1.
На основании схемы получаем таблицу векторного произведения единичных векторов
Пример 1
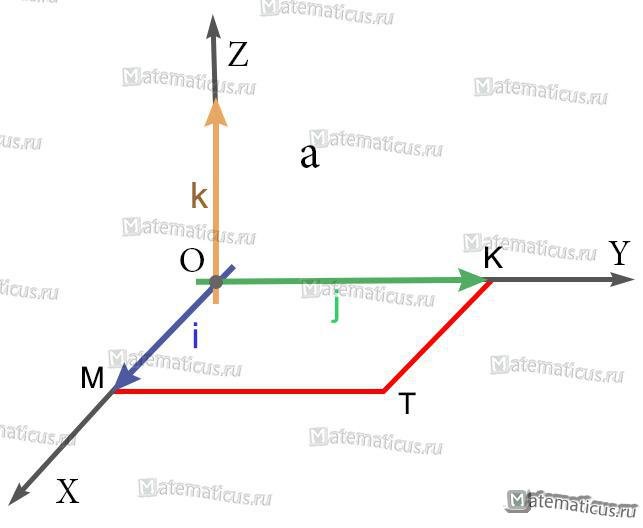
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.
Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).
iхj=k
Пример 2
Найти векторное произведение jхi.
Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.5 / 5. Количество оценок: 4
Вектор: определение и основные понятия
Определение вектора
 |
| рис. 1 |
Обозначение вектора
Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a .
Длина вектора
Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.
Нулевой вектор
Нулевой вектор обычно обозначается как 0 .
Длина нулевого вектора равна нулю.
Коллинеарные вектора
 |
| рис. 2 |
Сонаправленные вектора
 |
| рис. 3 |
Противоположно направленные вектора
 |
| рис. 4 |
Компланарные вектора
 |
| рис. 5 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Равные вектора
 |
| рис. 6 |
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b , если a ↑↑ b и | a | = | b |.
Единичный вектор
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Единичные векторы: характеристики, как получить, примеры
Содержание:
В единичные векторы — это те, модуль, величина или размер которых равны числовому значению. Единичные векторы полезны для указания направления других неединичных векторов.
Помните, что векторы — это математические объекты, которые математически представляют физические величины, зависящие от направления, такие как сила, скорость, ускорение и другие.
Независимо от физической величины, с которой они связаны, единичные векторы лишены единиц измерения, и их размер всегда равен 1, чистому числу.
Например, скорость частицы, движущейся со скоростью 3 м / с в положительном направлении декартовой оси X, обозначается: v = (3 м / с) я, где жирным шрифтом обозначены векторные величины. В этом примере модуль v составляет 3 м / с, а модуль единичного вектора я равно 1 (без единиц).
Модуль, направление и смысл
Учитывая, насколько важно установить ориентацию этих величин для того, чтобы узнать их влияние, векторы имеют три важные характеристики: величину или модуль, связанный с размером вектора, направление и смысл. При представлении векторной величины необходимо четко указать эти аспекты.
Теперь единичный вектор может иметь любое направление и любое значение, но величина всегда должна быть равна 1.
Единичные векторы используются для обозначения конкретного направления в пространстве или на плоскости. Если, например, нам нужно работать со всеми силами, которые действуют вдоль горизонтальной оси, то единичный вектор в этом направлении помогает нам отличать эти силы от других, направленных в другом направлении.
А чтобы отличить их от неединичных векторов, в печатных буквах обычно используется жирный шрифт, а сверху ставится каретка, например:
Характеристики единичного вектора
Математически единичный вектор:
Итак, мы можем установить, что:
-Модуль единичного вектора всегда равен 1, не имеет значения, является ли это силой, скоростью или другим вектором.
-Унитарные векторы имеют определенное направление, а также смысл, например единичный вектор в вертикальном направлении, который может иметь смысл вверх или вниз.
-Единичные векторы имеют точку происхождения. Когда она представлена декартовой системой координат, эта точка совпадает с началом системы: (0,0), если это плоскость, или (0,0,0), если вектор находится в трехмерном пространстве.
-Также с единичными векторами вы можете выполнять все операции сложения, вычитания и умножения векторов, которые выполняются с использованием обычных векторов. Следовательно, можно умножать единичный вектор на скаляр, а также выполнять точечное произведение и кросс-произведение.
-С помощью единичного вектора в определенном направлении могут быть выражены другие векторы, которые также ориентированы в этом направлении.
Единичные векторы в пространстве
Чтобы выразить любой вектор в пространстве или на плоскости, можно использовать набор единичных векторов, перпендикулярных друг другу, которые образуют ортонормированный базис. Каждое из трех предпочтительных направлений пространства имеет собственный единичный вектор.
Вернемся к примеру сил, направленных по горизонтальной оси. Это ось абсцисс, которая имеет две возможности: вправо и влево. Предположим, у нас есть единичный вектор на оси x, направленный вправо, который мы можем обозначить любым из следующих способов:
Любой из них действителен. Теперь предположим, что сила F1 величиной 5 Н вдоль этой оси и направленной вправо такую силу можно выразить как:
Если бы сила была направлена вдоль оси x, но в противоположном направлении, то есть влево, то для установления этой разницы можно было бы использовать отрицательный знак.
Например, сила величиной 8 Н, расположенная по оси x и направленная влево, будет выглядеть так:
А для векторов, которые не направлены вдоль декартовых осей, также есть способ представить их в терминах ортогональных единичных векторов, используя их декартовы компоненты.
Как получить / рассчитать единичный вектор?
Чтобы вычислить единичный вектор в направлении любого произвольного вектора v, применяется следующая формула:
Это модуль или величина вектора v, квадрат которого рассчитывается так:
Произвольный вектор через единичный вектор
В качестве альтернативы вектор v можно выразить так:
То есть произведение его модуля и соответствующего единичного вектора. Именно это и было сделано ранее, когда говорилось о силе величиной 5 Н, направленной вдоль положительной оси x.
Графическое представление
Графически это видно на этом изображении, где вектор v он синего цвета, а соответствующий единичный вектор в его направлении — красным.
В этом примере вектор v его величина больше, чем у единичного вектора, но объяснение справедливо, даже если это не так. Другими словами, у нас могут быть векторы, которые, например, в 0,25 раза больше единичного вектора.
Примеры единичных векторов
Перпендикулярные единичные векторы i, j и k
Как мы видели ранее, перпендикулярные единичные векторы я, j Y k они очень полезны для представления любого другого вектора на плоскости или в пространстве, а также для выполнения векторных операций. В терминах этих векторов произвольный вектор v представлен как:
v = vИкся + vYj + vzk
Где VИкс, vY и Vz — прямоугольные компоненты вектора v, которые являются скалярами — жирным шрифтом они не выделяются в печатном тексте.
Закон Кулона
Единичные векторы часто появляются в физике. Вот, например, закон Кулона, который количественно описывает взаимодействие двух точечных электрических зарядов.
В нем говорится, что сила F Притяжение или отталкивание между указанными зарядами пропорционально их произведению, обратно пропорционально квадрату расстояния, которое их разделяет, и направлено в направлении единичного вектора, соединяющего заряды.
Этот вектор обычно представлен:
А закон Кулона в векторной форме выглядит так:
Упражнение решено
Найдите единичный вектор в направлении вектора v = 5я + 4j -8kв условных единицах.
Решение
Применяется определение единичного вектора, данное выше:
Но сначала мы должны вычислить модуль вектора, который, поскольку он состоит из трех компонентов, определяется:
|v| 2 = (5) 2 + (4) 2 + (-8) 2 = 25 + 16 + 64 = 105
Поэтому модуль v это:
Искать единичный вектор просто:
Что в конечном итоге приводит нас к следующему:
v = 0.488 я + 0.390 j – 0.781 k
Ссылки
- Бауэр, В. 2011. Физика для инженерии и науки. Том 1. Мак Гроу Хилл.
- Бедфорд, 2000. А. Инженерная механика: Статика. Эддисон Уэсли.
- Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB).
- Джамбаттиста, А. 2010. Физика. 2-й. Эд. Макгроу Хилл.
- Резник, Р. (1999). Физический. Том 1. 3-е изд. На испанском языке. Compañía Editor Continental S.A. de C.V.
Кинезический язык: понятие, характеристики, типы, примеры
http://ru.onlinemschool.com/math/library/vector/vector-definition/
http://ru1.warbletoncouncil.org/vectores-unitarios-9631
Download Article
Learn how to calculate a unit vector and pass your math test with flying colors
Download Article
- Unit Vector Formula
- How to Calculate a Unit Vector
- Vectors
- Unit Vectors
- Magnitude
- Example Problems
- Solutions
|
|
|
|
|
|
At some point in your algebra course, you might have to learn about vectors, including unit vectors and magnitude. While your teacher or tutor may have taught a whole class on calculating a unit vector, you might still have some questions about the process. That’s why we’ve broken it down for you, below! Check out our guide to finding a unit vector, including a refresher on what vectors are and the formula for calculating magnitude, so you can ace your next pop quiz.
Things You Should Know
-
The formula to find unit vector is
. You can calculate the unit vector
of any vector by dividing the vector by its magnitude
. For instance, to calculate the unit vector of vector
, you would follow this equation:
.[1]
Advertisement
-
1
-
2
Divide the vector by its magnitude. Once you’ve determined the magnitude of the vector, take the vector and divide it by its magnitude. So if vector
is
, then
=
= (
,
). The unit vector, then, is (
).[3]
Advertisement
-
A vector is an object that contains both direction and magnitude. A vector is represented as a line on the Cartesian coordinate system, and it is denoted as a set of numbers representing its relationship to the x-axis (the vertical line on the graph) and the y-axis (the horizontal line). A vector’s magnitude refers to the size of the vector and is represented by a line with an arrow on the end. The length of the line denotes the length of the vector, while the direction of the arrow denotes the direction of the vector. Vectors possess both a starting point (the tail) and an ending point (the head, where the arrow is).[4]
-
A unit vector is a vector with a magnitude of 1. Unit vectors, also called direction vectors, are used to describe the direction of a given vector—or, the angle the vector makes on an x-axis. Unit vectors are marked with a cap symbol, which looks like a little arrow pointing upward: ^.[5]
Advertisement
-
The magnitude is the length or size of the vector. A vector’s magnitude, also called its norm, denotes its length on an x-axis (or the vertical line on the graph on which the vector appears), giving it numeric value. The magnitude on summarizes the length of the vector on the x-axis, y-axis (the horizontal line), and z-axis. Magnitude is denoted as 2 vertical lines, one on each side of the vector:
. To calculate the magnitude of a given vector with the direction of the x-axis, y-axis, or z-axis, follow the Pythagorean Theorem: add the squares of the vector’s direction ratios. Then, calculate the square root of that sum.[6]
- The magnitude of
would be
, the magnitude of
would be
, and the magnitude of
would be
.
- To find the magnitude of vector
, where
=
(and where
,
, and
represent the x-axis, y-axis, and z-axis, respectively), use the following equation:
= √
.
- For example, if
and
and
, then
, and
= √
= √
=
. Thus, the magnitude of vector
would be 3 units.
- The magnitude of
-
1
Given vector
=
+
+
, find
.
-
2
Given vector
=
+
, find
.
Advertisement
-
1
Answer #1:
=
. In this problem, we’re asked to find the unit vector of a 3-dimensional vector; hence, the inclusion of the z-axis in the equation. To find the unit vector, we identified the magnitude of the vector and then divided the vector by its magnitude:[7]
-
2
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
References
About This Article
Thanks to all authors for creating a page that has been read 1,588 times.
Did this article help you?
Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.
i — единичный вектор оси абсцисс;
j — единичный вектор оси ординат;
k — единичный вектор оси аппликат.
i⊥j⊥k, i=j=k=1
В прямоугольной системе координат в пространстве координаты векторов равны:
i(1;0;0);j(0;1;0); k(0;0;1);
Замечание 1
Единичные векторы являются некомпланарными.
Замечание 2
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.
a=xi+уj+zk
где x, y, z — координаты вектора проекции на соответствующие координатные оси.
Эта формула называется разложением вектора по ортам координатных осей.
Единичный вектор определяется по формуле:
Пример
Дан вектор а = (1; 2; -2)
Требуется найти длину (модуль) и единичный вектор e направления вектора а
Решение
Находим длину вектора a
$left| {vec a} right| = sqrt {{1^2} + {2^2} + {{left( { — 2} right)}^2}} = 3$
затем вычисляем единичный вектор e
$vec e = left( {frac{1}{3};frac{2}{3}; — frac{2}{3}} right)$
Векторное произведения единичных векторов
Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус». Смотрите схему 1.
Схема 1
На основании схемы получаем таблицу векторного произведения единичных векторов
i×i=0 i×j=k i×k=-j
j×i=-k j×j=0 j×k=i
k×i=j k×j=-i k×k=0
Пример 1
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.
Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).
iхj=k
Пример 2
Найти векторное произведение jхi.
Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k
20941
Все курсы > Линейная алгебра > Занятие 1
Материалы по линейной алгебре используют определения и примеры следующих курсов:
- 3Blue1Brown⧉
- Khan Academy: Linear Algebra⧉
- Linear Algebra⧉, PCA⧉, ICL
- Linear Algebra⧉, MIT
- Matrix Methods for Data Analysis and Machine Learning⧉, MIT
- Matrix Algebra for Engineers⧉
На первом занятии мы более подробно рассмотрим понятие вектора и векторного пространства.
Ноутбук к сегодняшнему занятию⧉
Понятие вектора
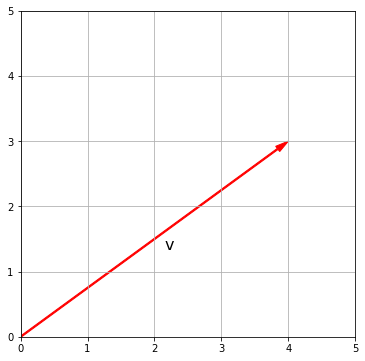
Вектор (vector) — это направленный отрезок, и для нас будет важно, что любой вектор обладает длиной (magnitude) и направлением (direction). Например, возьмем вот такой двумерный вектор $textbf{v}$
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix} $$
На курсе мы будем обозначать векторы полужирной строчной буквой, например $textbf{v}$, а матрицы заглавной буквой, например, А.
Вектор $textbf{v}$ удобно изобразить на координатной плоскости, исходящим из начала координат.
|
v = np.array([4, 3]) ax = plt.axes() plt.xlim([0, 5]) plt.ylim([0, 5]) plt.grid() ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0]/2, v[1]/2), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) plt.show() |
Добавлю, что вектор — частный случай матрицы. В случае вектор-столбца речь идет о матрице размерностью n x 1. В случае вектор-строки — 1 x n. Вектор $textbf{v}$ — это матрица 2 х 1.
Операции над векторами
Сложение векторов
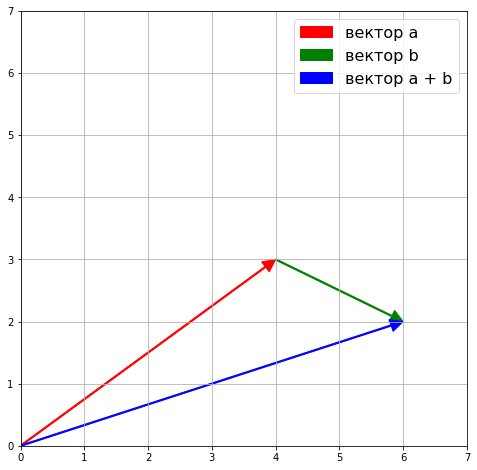
Складывать векторы очень несложно. Достаточно сложить их компоненты или координаты.
$$ begin{bmatrix} 4 \ 3 end{bmatrix} + begin{bmatrix} 2 \ -1 end{bmatrix} = begin{bmatrix} 6 \ 2 end{bmatrix} $$
|
a = np.array([4, 3]) b = np.array([2, —1]) a_plus_b = a + b a_plus_b |
Графически, если поставить начало второго вектора в конец первого, сложение можно представить как расстояние от начала первого вектора до конца второго. Своего рода путь, пройденный двумя векторами.
|
ax = plt.axes() plt.xlim([0, 7]) plt.ylim([0, 7]) plt.grid() arrow_a = ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) arrow_b = ax.arrow(a[0], a[1], b[0], b[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) arrow_a_plus_b = ax.arrow(0, 0, a_plus_b[0], a_plus_b[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.legend([arrow_a, arrow_b, arrow_a_plus_b], [‘вектор a’, ‘вектор b’, ‘вектор a + b’], prop = {‘size’: 16}) plt.show() |
Сложение векторов ассоциативно $textbf{a} + textbf{b} = textbf{b} + textbf{a}$.
Умножение на скаляр
Умножение на скаляр просто удлиняет или укорачивает вектор.
$$ 2 cdot textbf{v} = 2 cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} 8 \ 6 end{bmatrix} $$
|
v = np.array([4, 3]) double_v = 2 * v double_v |
|
ax = plt.axes() plt.xlim([0, 10]) plt.ylim([0, 10]) plt.grid() ax.arrow(0, 0, double_v[0], double_v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.annotate(‘2v’, xy=(double_v[0], double_v[1]), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0], v[1]), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) plt.show() |
Умножение на отрицательное число не только удлиняет или укорачивает вектор, но и переворачивает его направление.
$$ -0,5 cdot textbf{v} = -0,5 cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} -2 \ -1,5 end{bmatrix} $$
|
v = np.array([4, 3]) neg_half_v = —0.5 * v neg_half_v |
|
ax = plt.axes() plt.xlim([—5, 5]) plt.ylim([—5, 5]) plt.grid() ax.arrow(0, 0, neg_half_v[0], neg_half_v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.annotate(‘-0.5v’, xy=(neg_half_v[0], neg_half_v[1]), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0], v[1]), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) plt.show() |
Очевидно, что умножение на −1 просто переворачивает направление вектора, но не меняет его длины.
$$ -1 cdot textbf{v} = -1 cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} -4 \ -3 end{bmatrix} $$
|
v = np.array([4, 3]) neg_one_v = —1 * v neg_one_v |
|
ax = plt.axes() plt.xlim([—5, 5]) plt.ylim([—5, 5]) plt.grid() ax.arrow(0, 0, neg_one_v[0], neg_one_v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.annotate(‘-v’, xy=(neg_one_v[0], neg_one_v[1]), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0], v[1]), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) plt.show() |
Вычитание и деление на число
Вычитание векторов можно представить как сумму первого вектора со вторым вектором, умноженным на −1.
$$ begin{bmatrix} 4 \ 3 end{bmatrix} + left( -1 cdot begin{bmatrix} 2 \ -1 end{bmatrix} right) = begin{bmatrix} 2 \ 4 end{bmatrix} $$
|
a = np.array([4, 3]) b = np.array([2, —1]) b_neg = —1 * b a_minus_b = a + b_neg b_neg, a_minus_b |
|
(array([-2, 1]), array([2, 4])) |
Графически мы сначала находим вектор $textbf{-b}$ (зеленая стрелка), а затем прибавляем его к вектору $textbf{a}$ (красная стрелка).
|
plt.figure(figsize = (8, 8)) ax = plt.axes() plt.xlim([0, 7]) plt.ylim([0, 7]) plt.grid() arrow_a = ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) arrow_b_neg = ax.arrow(a[0], a[1], b_neg[0], b_neg[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) arrow_b = ax.arrow(a[0], a[1], b[0], b[1], width = 0.0001, head_width = 0.1, head_length = 0.1, length_includes_head = True, fc = ‘black’, ec = ‘black’, linestyle = ‘—‘) arrow_a_minus_b = ax.arrow(0, 0, a_minus_b[0], a_minus_b[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.legend([arrow_a, arrow_b_neg, arrow_b, arrow_a_minus_b], [‘вектор a’, ‘вектор -b’, ‘вектор b’, ‘вектор a+(-b)’], prop = {‘size’: 16}) plt.show() |
Остается добавить, что деление вектора на число, это всего лишь умножение на обратное число (multiplicative inverse). Разделим вектор $textbf{v}$ на семь.
$$ frac{textbf{v}}{7} = begin{bmatrix} 4 \ 3 end{bmatrix} cdot frac{1}{7} = begin{bmatrix} frac{4}{7} \ frac{3}{7} end{bmatrix} $$
|
v = np.array([4, 3]) v * (1/7) |
|
array([0.57142857, 0.42857143]) |
Тот факт, что мы выразили вычитание через сложение и умножение на скаляр, а деление через умножение на обратное число позволило нам остаться в пределах операций сложения и умножения на скаляр.
Видео про векторы⧉.
Длина вектора
Длину или норму вектора (norm, length, magnitude or size of a vector) рассчитать не сложно, достаточно вспомнить теорему Пифагора. Снова возьмем вектор $textbf{v}$
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix} $$
|
v = np.array([4, 3]) ax = plt.axes() plt.xlim([0, 5]) plt.ylim([—0.01, 5]) plt.grid() ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0]/2, v[1]/2), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) ax.hlines(y = 0, xmin = 0, xmax = 4, linewidth = 3, color = ‘b’, linestyles = ‘—‘) ax.vlines(x = 4, ymin = 0, ymax = 3, linewidth = 3, color = ‘g’, linestyles = ‘—‘) plt.show() |
Как видно на графике, вектор $textbf{v}$, смещение вдоль оси x и смещение вдоль оси y образуют прямоугольный треугольник. Значит, длина вектора (гипотенуза) равна квадратному корню из суммы квадратов смещений (катетов или в нашем случае координат).
$$ ||textbf{v}|| = sqrt{4^2 + 3^2} = sqrt{25} = 5 $$
Для n-мерного вектора ничего не меняется.
$$ ||textbf{v}|| = sqrt{v_1^2 + v_2^2 + dots + v_n^2} $$
Например, найдем длину трехмерного вектора $textbf{w}$.
$$ textbf{w} = begin{bmatrix} 6 \ 3 \ 2 end{bmatrix} rightarrow ||textbf{w}|| = sqrt{6^2 + 3^2 + 2^2} = sqrt{49} = 7 $$
Единичный вектор
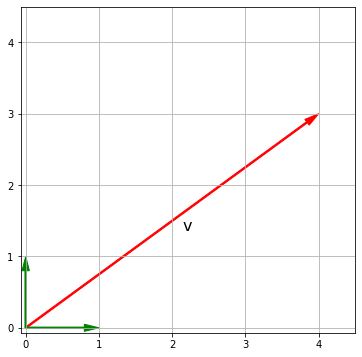
Вектор с длиной, равной единице, называют единичным вектором (unit vector). Примерами единичных векторов, с которыми мы будем часто встречаться в пространстве $ R^2 $, являются следующие два вектора
$$ hat{i} = begin{bmatrix} 1 \ 0 end{bmatrix}, hat{j} = begin{bmatrix} 0 \ 1 end{bmatrix} $$
Единичный вектор принято обозначать строчной буквой с знаком циркумфлекса, «крышечки» (hat).
Проверим, равна ли их длина единице.
$$ ||hat{i}|| = sqrt{1^2 + 0^2} = sqrt{1} = 1, ||hat{j}|| = sqrt{0^2 + 1^2} = sqrt{1} = 1 $$
Интересно, что с помощью векторов $ hat{i}, hat{j} $ можно выразить любой другой вектор в $ R^2 $. Например, вектор $textbf{v}$ можно представить как
$$ 4 begin{bmatrix} 1 \ 0 end{bmatrix} + 3 begin{bmatrix} 0 \ 1 end{bmatrix} = begin{bmatrix} 4 \ 3 end{bmatrix} rightarrow 4hat{i} + 3 hat{j} $$
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
v = np.array([4, 3]) i = np.array([1, 0]) j = np.array([0, 1]) ax = plt.axes() plt.xlim([—0.07, 4.5]) plt.ylim([—0.07, 4.5]) plt.grid() ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0]/2, v[1]/2), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) plt.show() |
Это обстоятельство нам пригодится в будущем.
Нормализация вектора
Длина нормализованного вектора равна единице. Для того чтобы нормализовать вектор, достаточно разделить вектор на его длину. Создадим единичный вектор $hat{v}$ для вектора $textbf{v}$.
$$ hat{v} = frac{textbf{v}}{||textbf{v}||} = frac{1}{5} cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} frac{4}{5} \ frac{3}{5} end{bmatrix} $$
|
v = np.array([4, 3]) v * (1/np.linalg.norm(v)) |
Скалярное произведение
Важной операцией над векторами является уже знакомое нам скалярное произведение (dot product). В качестве напоминания того, как работает скалярное произведение приведем несложный пример. Пусть даны два вектора $textbf{v}$ и $textbf{w}$.
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix}, textbf{w} = begin{bmatrix} 2 \ 1 end{bmatrix} $$
Найдем их скалярное произведение.
$$ textbf{v} cdot textbf{w} = 4 cdot 2 + 3 cdot 1 = 11 $$
Как вы видите, мы перемножаем компоненты векторов и складываем получившиеся произведения.
Скалярное произведение как длина вектора
Интересно, что корень из скалярного произведения вектора на самого себя есть его длина.
$$ sqrt{ textbf{v} cdot textbf{v} } = sqrt{4 cdot 4 + 3 cdot 3 } = sqrt{ 4^2 + 3^2 } = sqrt{25} = 5 $$
|
v = np.array([4, 3]) np.sqrt(v.dot(v)) |
Угол между векторами
Помимо этого скалярное произведение определяется как произведение длин векторов на косинус угла между ними.
$$ mathbf a cdot mathbf b = ||a|| cdot ||b|| cdot cos(theta) $$
Именно это свойство привело нас к расчету косинусного расстояния между векторами.
$$ cos(theta) = frac{mathbf a cdot mathbf b}{||a|| cdot ||b||} $$
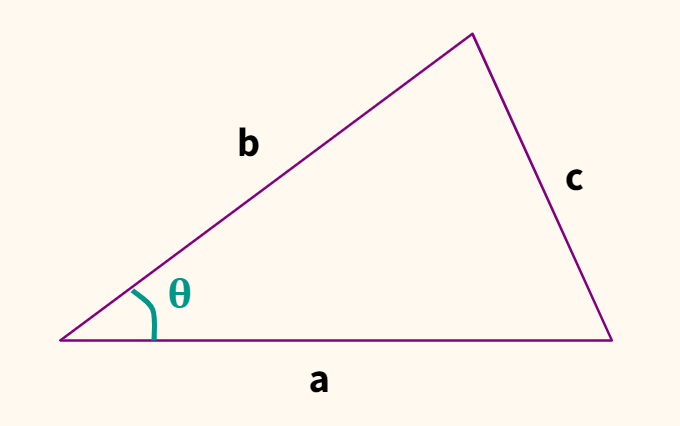
Выведем эту формулу. Для начала вспомним теорему косинусов.
$$ c^2 = a^2 + b^2-2ab cdot cos(theta) $$
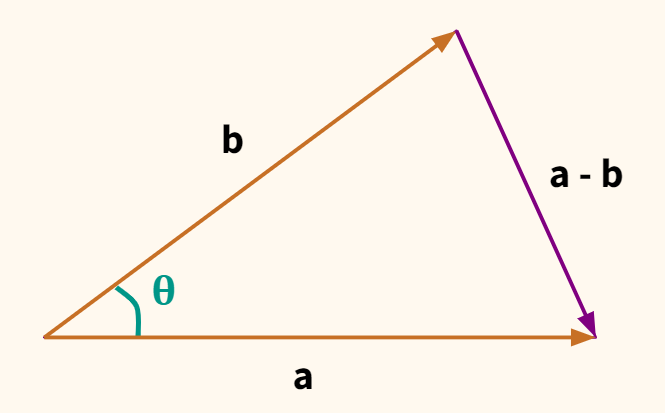
Теперь представим, что у нас не стороны треугольника, а векторы. Если сторону а обозначить как вектор $ textbf{a} $, сторону b — как вектор $ textbf{b} $, то сторона с станет разностью между $ textbf{a} $ и $ textbf{b} $. Чтобы убедиться в этом, найдите $ textbf{-b} $ и приставьте его к окончанию $ textbf{a} $.
Выразим теорему косинусов через длины векторов.
$$ || a-b ||^2 = ||a||^2 + ||b||^2-2 cdot ||a|| cdot ||b|| cdot cos(theta) $$
Помня, что длина есть скалярное произведение вектора на самого себя, мы можем выразить левую часть $ || a-b || $ как
$$ (a-b)(a-b) = a cdot a-a cdot b-b cdot a + (-b) cdot (-b) = ||a||^2-2ab + ||b||^2 $$
Поместим результат в исходное выражение.
$$ ||a||^2-2ab + ||b||^2 = ||a||^2 + ||b||^2-2 cdot ||a|| cdot ||b|| cdot cos(theta) $$
Сократив подобные члены получим
$$ a cdot b = ||a|| cdot ||b|| cdot cos(theta) $$
Выводы. Из тригонометрии мы помним, что косинус 90 градусов равен нулю. Как следствие, скалярное произведение перпендиклярных (правильнее сказать ортогональных (orthogonal)) векторов $ textbf{a} perp textbf{b} $ равно нулю.
$$ a cdot b = ||a|| cdot ||b|| cdot cos(90) = 0 $$
Очевидно, что если угол между двумерными векторами меньше 90 градусов, косинус, а значит и скалярное произведение положительны. В противном случае — отрицательны. Для n-мерных векторов положительное скалярное произведение говорит, что они в целом смотрят в одну строну, отрицательное — противоположные.
Для коллинеарных (сонаправленных) векторов скалярное произведение равно произведению их длин, потому что косинус нуля равен единице.
$$ a cdot b = ||a|| cdot ||b|| cdot cos(0) = ||a|| cdot ||b|| $$
Добавлю, что если $ textbf{a} $ и $ textbf{b} $ — единичные векторы, то косинус угла между векторами просто равен его их скалярному произведению.
$$ cos(theta) = a cdot b $$
Рассчитаем косинусное расстояние для векторов
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix}, textbf{w} = begin{bmatrix} 1 \ 7 end{bmatrix} $$
|
a = np.array([4, 3]) b = np.array([1, 7]) numerator = np.dot(a, b) aLen = np.linalg.norm(a) bLen = np.linalg.norm(b) denominator = aLen * bLen cosine = numerator / denominator angle = np.arccos(cosine) * 360/2/np.pi cosine, angle |
|
(0.7071067811865475, 45.00000000000001) |
|
from scipy.spatial import distance 1 — distance.cosine([4, 3], [1, 7]) |
Внешнее произведение
Под внешним произведением (outer product) понимается умножение вектор-столбца на вектор-строку по обычным правилам матричного умножения. Результатом такого произведения будет матрица, а не число, как в случае скалярного произведения.
Ортогональность векторов
Еще раз продемонстрируем, почему если векторы ортогональны, их скалярное произведение будет равно нулю. Возьмем три вектора, образовывающих прямоугольный треугольник.
Тогда, по теореме Пифагора,
$$ || mathbf x ||^2 + || mathbf y ||^2 = || mathbf x + mathbf y ||^2 $$
$$ mathbf x^T mathbf x + mathbf y^T mathbf y = (mathbf x + mathbf y)^T (mathbf x + mathbf y) $$
$$ mathbf x^T mathbf x + mathbf y^T mathbf y = mathbf x^T mathbf x + mathbf y^T mathbf y + mathbf x^T mathbf y + mathbf y^T mathbf x $$
$$ mathbf x^T mathbf x + mathbf y^T mathbf y = mathbf x^T mathbf x + mathbf y^T mathbf y + 2 mathbf x^T mathbf y $$
$$ mathbf 0 = 2 mathbf x^T mathbf y $$
$$ mathbf x^T mathbf y = mathbf 0 $$
Проекция вектора на вектор
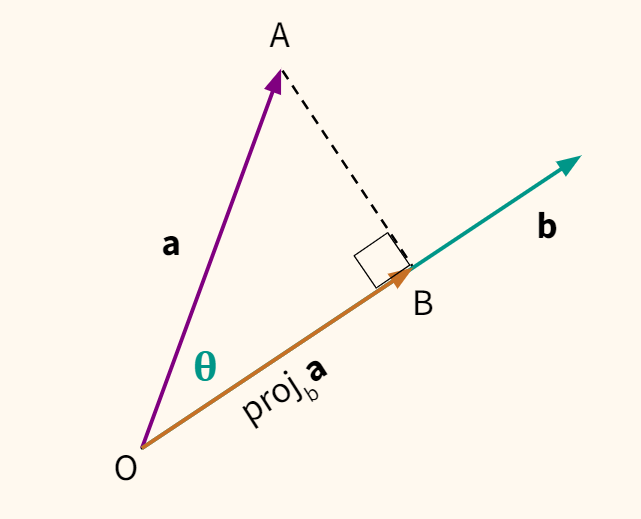
Подойдем к скалярному произведению с другой стороны. Рассмотрим два вектора $ textbf{a} $ и $ textbf{b} $ и найдем проекцию первого вектора на второй.
Проекция через угол между векторами
Говоря неформально, проекцией вектора $ textbf{a} $ на вектор $ textbf{b} $ будет такой участок вектора $ textbf{b} $, что расстояние от точки A до точки B минимально. Минимальным оно будет, если угол OAB будет равен 90 градусов. Получается прямоугольный треугольник. Найдем отрезок OB.
$$ cos(theta) = frac {OB}{OA} = frac {OB}{||a||} rightarrow OB = ||a|| cdot cos(theta) $$
Выразим то же самое через формулу скалярного произведения, заменив $||a|| cdot cos(theta) $ на OB.
$$ b cdot a = ||b|| cdot ||a|| cdot cos(theta) rightarrow b cdot a = ||b|| cdot OB $$
Так мы нашли длину проекции OB. Ее называют числовой или скалярной проекцией (scalar projection).
$$ frac{b cdot a}{||b||} = ||a|| cdot cos(theta) = OB $$
Более того, если длина вектора $ textbf{b} $ равна единице, то длина проекции OB просто равна скалярному произведению.
$$ ||b|| = 1 rightarrow b cdot a = OB $$
Это объясняет, почему скалярное произведение еще называют projection product.
Очевидное и тем не менее интересное примечание. Обратите внимание на связь понимания скалярного произведения как проекции одного вектора на другой и произведения длин векторов на косинус угла между ними. Если векторы перпендикулярны, проекция одного вектора на другой равна нулю, а значит и произведение проекции второго вектора на первый равно нулю.
Предположим, нас интересует не только длина проекции, но и ее направление. В этом случае говорят про векторную проекцию (vector projection).
Она выражается как произведение нормализованного вектора $ textbf{b} $ на длину проекции (то есть скалярную проекцию) OB.
$$ proj_mathbf{b} textbf{a} = OB cdot hat{b} $$
Перепишем OB через скалярное произведение, а $hat{b}$ через частное вектора $ textbf{b} $ на его длину.
$$ proj_mathbf{b} textbf{a} = frac{b cdot a}{||b||} cdot frac{b}{||b||} $$
Таким образом, можно сказать, что векторная проекция показывает, длину вектора $ textbf{a} $ в направлении вектора $ textbf{b} $.
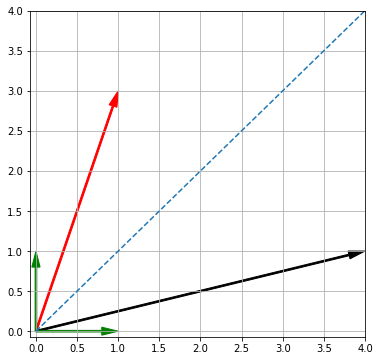
Пример. Возьмем два вектора a и b и найдем вначале скалярную, затем векторную проекцию вектора a на вектор b.
|
a = np.array([3, 4]) b = np.array([1, 1]) scalar_proj_a_on_b = np.dot(a, b) / np.linalg.norm(b) scalar_proj_a_on_b |
|
vector_proj_a_on_b = scalar_proj_a_on_b * (b / np.linalg.norm(b)) vector_proj_a_on_b |
|
a = np.array([3, 4]) b = np.array([1, 1]) proj = np.array([3.5, 3.5]) ax = plt.axes() plt.xlim([—0.07, 4.5]) plt.ylim([—0.07, 4.5]) plt.grid() ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, b[0], b[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, proj[0], proj[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) plt.show() |
Матрица проекции
Векторную проекцию можно выразить с помощью матрицы проекции $P$.
$$ proj_mathbf{b} textbf{a} = P cdot mathbf a = frac{mathbf b mathbf b^T}{mathbf b^T mathbf b} cdot mathbf a $$
В знаменателе находится скалярное произведение и результатом умножения будет число. В числителе — внешнее произведение и результатом будет матрица. Найдем внешнее произведение из примера выше.
|
b_bT = np.outer(b, b) b_bT |
Найдем скалярное произведение.
Создадим матрицу проекции $P$ и умножим ее на вектор $mathbf a$.
Симметрия скалярного произведения
Продемонстрируем с точки зрения проекции, почему $a cdot b = b cdot a $. Возьмем два вектора a и b.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
a = np.array([1, 3]) b = np.array([4, 1]) i = np.array([1, 0]) j = np.array([0, 1]) ax = plt.axes() plt.xlim([—0.07, 4]) plt.ylim([—0.07, 4]) plt.grid() ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, b[0], b[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.plot([0, 4], [0, 4], linestyle = ‘dashed’) plt.show() |
Выше мы сказали, что $ a cdot b = OB cdot ||b|| $. То есть скалярное произведение вектора a на вектор b равно произведению проекции a на b, умноженной на длину вектора b.
Продемонстрируем, что произведение проекции вектора a на вектор b, умноженное на длину вектора b, равно произведению проекции вектора b на вектор a, умноженному на длину вектора a.
$$ proj_ba times || b || = proj_ab times || a || $$
|
scalar_proj_a_on_b = np.dot(a, b) / np.linalg.norm(b) scalar_proj_a_on_b * np.linalg.norm(b) |
|
scalar_proj_b_on_a = np.dot(b, a) / np.linalg.norm(a) scalar_proj_b_on_a * np.linalg.norm(a) |
|
np.dot(a, b), np.dot(b, a) |
Видео про скалярное произведение векторов⧉.
Векторное произведение
Векторное произведение (cross product) задано только в трехмерном пространстве. Результатом такого произведения будет вектор, перпендикулярный каждому из исходных векторов. Приведем иллюстрацию из Википедии⧉.
Математически векторное произведение задается формулой
$$ a times b = || a || || b || sin(theta) $$
Геометрически — это площадь параллелограмма, сформированного из исходных векторов a и b.
Приведем пример.
|
a = [1, 2, 3] b = [4, 5, 6] np.cross(a, b) |
Подведем итог
Сегодня мы ввели понятие вектора, познакомились с базовыми операциями с векторами, в частности, изучили скалярное произведение векторов и научились находить скалярную и векторную проекцию одного вектора на другой.
Перейдем к рассмотрению векторного пространства.