Самый эффективный метод следующий: пока число (его надо интерпретировать как беззнаковое число, чтобы подсчитать все единицы), допустим n, не равно нулю выполнить следующую операцию
n &= n - 1;
и соответственно увеличить счетчик единиц на единицу.
Принцип следующий. Допустим в числе имеется одна 1
0b00100000
Если из этого числа вычесть 1, то получится
0b00011111
Теперь если применить бинарную операцию И, то получим
0b00100000
&
0b00011111
==========
0b00000000
Число стало равным 0, следовательно оно содержало только одну 1, так как данная операция была проделана только один раз.
Используя же те методы, которые вы указали, то придется сдвигать либо само число, либо единицу 6 раз, чтобы добраться до единицы в исходном числе, и 6 раз придется выполнить сравнение с единицей. А таблица просмотра совершенно не применима для чисел, которые занимают более одного байта. Тем более она еще занимает место в памяти для такой простой задачи.
Данная задачка судя по всему типовая в ЕГЭ по информатике, алгоритм ее решения в общем случае следующий: перевести число в двоичную форму (например, тут — http://floatingpoint.ru/online/dec2bin.php) и подсчитать количество единиц — калькулятор нулей и единиц в двоичной записи числа
Однако в некоторых простых случаях можно попробовать разложить искомое число на сумму или разность степеней двоек, и проделать вычисления в уме.
Для этого нужно помнить несколько первых степеней двойки и двоичные записи по крайней мере некоторых чисел от 1 до 15:
1024 = 2^10, 512 = 2^9, 256 = 2^8, 128 = 2^7, 64 = 2^6, 32 = 2^5, 16 = 2^4
15 = 1111, 14 = 1110, 13 = 1101, 12 = 1100, 11 = 1011, 10 = 1010, 9 = 1001, 8 = 1000, 7 = 111, 6 = 110, 5 = 101, 4 = 100, 3 = 11, 2 = 10, 1 = 1.
Так же могут оказаться полезны некоторые суммы, например:
192 = 128 + 64
160 = 128 + 32
320 = 256 + 64
640 = 512 + 128
Приведем некоторые типовые примеры.
Сколько единиц в двоичной записи числа 1025?
1025 = 1024 + 1 1024 = 2^10 это степень двойки, а единица так и будет единицей, следовательно,
всего в двоичной записи числа 1025 ровно 2 единицы.
10000000001
Сколько единиц в двоичной записи числа 519?
519 = 512 + 7 512 = 2^9 это степень двойки, а 7 записывается в двоичной системе как 111 и содержит три единицы,
следовательно, всего в двоичной записи числа 519 содержится ровно 4 единицы.
1000000111
Сколько единиц в двоичной записи числа 514?
514 = 512 + 2 Слагаемые 512 = 2^9 и 2 = 2^1 - это степени двойки, следовательно, в двоичной записи числа 514
ровно 2 единицы.
1000000010
Сколько единиц в двоичной записи числа 127?
127 = 128 - 1 Число 128 представляет собой целую степень двойки и равняется 2^7, требуя таким образом
для своей записи ровно 8 бит: 10000000 10000000-1 = 1111111 Следовательно, в записи числа 127 содержится 7 единиц.
1111111
Сколько единиц в двоичной записи числа 195?
195 = 192 + 3 = 128 + 64 + 3 128 = 2^7 64 = 2^6 3 = 11 в двоичной системе и содержит 2 единицы. Таким образом в двоичной записи числа 195
содержится 4 единицы.
11000011
Сколько единиц в двоичной записи числа 173?
173 = 160 + 13 160 = 128 + 32 = 2^7 + 2^5, а 13 = 1101 в двоичной системе. Тогда всего получим 5 единиц.
10101101
Сколько единиц в двоичной записи числа 3458?
3458 = 2048 + 1410 1410 = 1024 + 386 386 = 256 + 130 130 = 128 + 2 Таким образом 3458 = 2^11 + 2^10 + 2^8 + 2^7 + 2^1 и всего будет 5 единиц.
110110000010
|
266 / 71 / 11 Регистрация: 29.05.2011 Сообщений: 2,121 |
|
|
1 |
|
Сколько единиц в числе?13.02.2023, 23:29. Показов 859. Ответов 11
Задача. Сколько единиц в двоичной записи числа 42014+22015-9? Пытался осмыслить методику данную в учебнике: Только больше путаницы получил. Совсем ум за разум зашел. Иду по порядку. Далее. 9=23+1. Ответ: 2015 единиц. Правильно ли я понял?
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
13.02.2023, 23:29 |
|
Ответы с готовыми решениями:
Определить, сколько раз встречается разряд единиц и десятков в заданном числе
11 |
|
4712 / 3365 / 1074 Регистрация: 01.09.2014 Сообщений: 9,247 |
|
|
14.02.2023, 00:56 |
2 |
|
Правильно. Про 42014 можно было бы временно забыть, потому что это один разряд намного левее следующей по счету единицы. Затем к количеству единиц в 22015-9 прибавить 1. Для наглядности можно было посмотреть, как выглядят числа 2n — 9 для небольших n >= 5.
1 |
|
Платежеспособный зверь 8818 / 4245 / 1618 Регистрация: 28.10.2009 Сообщений: 11,385 |
|
|
14.02.2023, 01:14 |
3 |
|
Ваш способ имеет право на существование, но он не оптимален. Это Вам лёгкий пример достался. С более сложным Вы быстро запутаетесь. Предлагаю Вам свой способ, он достаточно прост и работает на любых сложных примерах: Примерчик для тренировки:
2 |
|
266 / 71 / 11 Регистрация: 29.05.2011 Сообщений: 2,121 |
|
|
14.02.2023, 01:30 [ТС] |
4 |
|
У нас есть два минуса подряд, избавляемся от большего: Не понял.
0 |
|
Платежеспособный зверь 8818 / 4245 / 1618 Регистрация: 28.10.2009 Сообщений: 11,385 |
|
|
14.02.2023, 01:34 |
5 |
|
А так и получается. Из соотношения 2n+1=2n+2n
1 |
|
266 / 71 / 11 Регистрация: 29.05.2011 Сообщений: 2,121 |
|
|
14.02.2023, 01:38 [ТС] |
6 |
|
2n+1=2n+2n Такое впечатление, что первый раз вижу.(
0 |
|
Платежеспособный зверь 8818 / 4245 / 1618 Регистрация: 28.10.2009 Сообщений: 11,385 |
|
|
14.02.2023, 01:39 |
7 |
|
Ну, проверьте на примерах
1 |
|
266 / 71 / 11 Регистрация: 29.05.2011 Сообщений: 2,121 |
|
|
14.02.2023, 01:40 [ТС] |
8 |
|
Это работает только с основанием 2?
0 |
|
Платежеспособный зверь 8818 / 4245 / 1618 Регистрация: 28.10.2009 Сообщений: 11,385 |
|
|
14.02.2023, 01:42 |
9 |
|
2n+1=2*2n=2n+2n
1 |
|
266 / 71 / 11 Регистрация: 29.05.2011 Сообщений: 2,121 |
|
|
14.02.2023, 01:44 [ТС] |
10 |
|
кот Бегемот, выходит только с двойкой такой фокус проходит? Не правомерно же х3=2х2
0 |
|
Модератор 9588 / 4908 / 3244 Регистрация: 17.08.2012 Сообщений: 15,334 |
|
|
19.02.2023, 00:40 |
11 |
|
Bazaroff, это не фокус, почитайте что-нибудь про свойства степени, Вы малость подзабыли школьную программу. Есть такое свойство xa+b=xaxb. В частности, При x=2, a=n, b=1 получается 2n+1=2n21=2*2n=2n+2n При x=3, a=n, b=1 тоже будет неплохо: 3n+1=3n31=3*3n=3n+3n+3n
1 |
|
Ушел с форума 15883 / 7459 / 1010 Регистрация: 11.11.2010 Сообщений: 13,441 |
|
|
19.02.2023, 02:09 |
12 |
|
Bazaroff, Кликните здесь для просмотра всего текста
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
19.02.2023, 02:09 |
|
Помогаю со студенческими работами здесь Подсчитать количество единиц в числе, кроме единиц в младших разрядах В длинном целом числе N все серии единиц, состоящие из трёх и более единиц, заменить на нули В числе подсчитали количество единиц, в получившемся числе опять подсчитали количество единиц и т.д. Определение единиц в числе
С клавиатуры вводится натуральное число, есть ли подряд шесть- 111111 ? Пример: если… Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 12 |
Решение задач 1 ЕГЭ по информатике 2015 года
Рассмотрим задачу №1 из демоверсии ФИПИ 2015 года:
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А – 0; Б – 100; В – 1010; Г – 111; Д – 110.Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны. Каким из указанных способов это можно сделать?
1) для буквы В – 101
2) это невозможно
3) для буквы В – 010
4) для буквы Б – 10
Давайте проанализируем текст задачи. Итак, нам известно, что используется неравномерный двоичный код. Что это такое? На самом деле все очень просто:
равномерное кодирование — каждый символ кодируется кодами равной длины
неравномерное кодирование — разные символы могут кодироваться кодами разной длины
Например, если у нас есть три символа А, Б, В и закодированы они так:
- А — 010
- Б — 011
- В — 111
, то это равномерное кодирование, так как длина кода одинаковая. Если же эти же символы мы закодируем вот так:
- А — 01
- Б — 110
- В — 1011
, то получим неравномерное кодирование.
Кроме этого, нам необходимо знать и понимать условие Фано
Никакое кодовое слово не может быть началом другого кодового слова
Также существует обратное условие Фано
Никакое кодовое слово не является окончанием другого кодового слова
Чтобы однозначно декодировать сообщение, достаточно того, чтобы условие Фано (или обратное условие) выполнялось.
Теперь, получив необходимые знания, можем перейти к решению задачи.
Рассмотрим первый вариант ответа. Если мы для буквы В сократим код до 101, то условие Фано нарушено не будет. Действительно, с кода 101 не начинается ни один из четырех оставшихся кодов для А, Б, Г и Д и все коды различны.
Второй вариант отпадает, так как мы только что убедились, что это возможно.
Третий вариант не подходит, так как в этом случае код буквы В — 010 будет начинаться с 0, а 0 — это код буквы А. Получается, что это нарушает условие Фано.
Вариант 4 тоже не подходит. В этом случае код буквы Б — 10 будет являться началом для кода буквы В, а это нарушение условия Фано.
Правильный ответ: 1.
Для успешного решения задач типа А1 ЕГЭ по информатике рекомендую ознакомиться со статьями “Системы счисления” и “Перевод чисел из двоичной системы счисления в десятичную”. Для контроля правильности перевода удобно использовать “Скрипт для перевода числа из десятичной системы счисления в любую другую”.
Задачи А1 предполагают проверку знаний о системах счисления и двоичном представлении информации в памяти компьютера.
Рассмотрим решение задачи А1 из демоверсии ЕГЭ 2012.
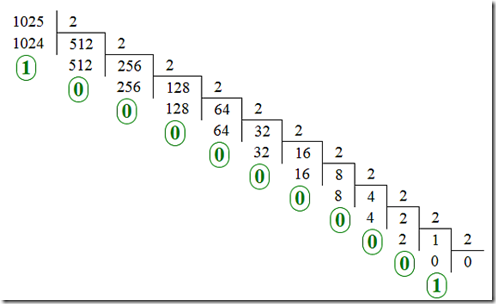
Сколько единиц в двоичной записи числа 1025?
1) 1
2) 2
3) 10
4) 11
Данную задачу можно решить простым переводом числа 1025 в двоичную систему счисления, а затем посчитать количество единиц.
Как видно, в полученном двоичном числе содержится 2 единицы.
Второй способ решения данной задачи рассчитан на тех, кто хорошо знает степени числа 2. Если посмотреть на число 1025 внимательно, можно заметить, что 1025=1024+1. Число 1024 – это 210. Отсюда следует, что 1025=210+1.
Если посмотреть как выглядят степени числа 2 записанные в двоичной системе счисления, то нетрудно представить число 1024 в двоичной системе счисления.
21=210=102
22=410=1002
23=810=10002
24=1610=100002
25=3210=1000002
…
210=102410=100000000002
Прибавив к получившемуся числу единицу получим число 100000000012, которое содержит 2 единицы.
Третий способ вытекает из предыдущего. Если посмотреть внимательно, то можно увидеть, что любое число, являющееся степенью двойки и записанное в двоичной системе счисления содержит одну единицу. Таким образом узнать количество единиц в двоичной записи любого числа очень просто — достаточно представить его как сумму степеней числа 2 — количество слагаемых и будет указывать число единиц.
Возьмем для примера число 73 и узнаем сколько единиц в его двоичной записи.
73=64+8+1=26+23+20. Так как слагаемых у нас получилось три, значит и единиц в двоичной записи числа 73 будет тоже 3.
Решение задачи А1 демонстрационной версии ЕГЭ 2013:
Сколько единиц в двоичной записи десятичного числа 255?
1) 1 2) 2 3) 7 4) 8
Первый способ:
Для успешного решения данной задачи необходимо знать, что 256 это 2 в восьмой степени или 10000 0000 в двоичной системе счисления — 256=28=1000000002. Соответственно, 255 — это 11111111 в двоичной системе счисления — 25510=111111112. Правильный ответ — 4 (8 единиц).
Второй способ:
Этот способ заключается в переводе числа 255 из десятичной системы счисления в двоичную и подсчете единиц:
Как видим, количество единиц восемь. Правильный ответ 4.
Автор:
В работе часто встречаются следующие проблемы: Для 32-битного целого числа n без знака найдите число 1 в двоичном представлении значения, например, когда значение = 0x05 (0b0101), возврат 2, значение = 0x8e (0b1000 1110 ) Когда, вернитесь к 4. Ниже приведены несколько часто используемых решений, а результаты сравнения этих нескольких методов приведены в конце статьи.
Метод первый: основной метод
Базовый метод является самым простым для понимания, он проходит напрямую через каждый бит, код выглядит следующим образом, идея обоих методов одинакова, но первый метод должен быть выполнен в цикле 32 раза, а второй метод может завершить цикл. рано и эффективнее. Немного выше. Окончательный тест рассчитывается с использованием метода цикла for.
uint8_t count_bits_1(uint32_t value)
{
uint8_t count = 0,i = 0;
for(i = 0; i < 32 ; i++)
{
if(value & 0x01)
{
count ++;
}
value >>= 1;
}
return count;
}
uint8_t count_bits_1(uint32_t value)
{
uint8_t count = 0,i = 0;
while(value)
{
if(value & 0x01)
{
count ++;
}
value >>= 1;
}
return count;
}Метод второй: быстрый метод
Этот метод относительно быстрый и зависит только от количества единиц в значении. Если в двоичном представлении значения n единиц, то этому методу нужно выполнить цикл только n раз. Принцип состоит в том, чтобы постоянно очищать крайнюю правую единицу в двоичном представлении значения и одновременно накапливать счетчик, пока значение не станет 0, код выглядит следующим образом.
Например, когда value = 0x0A (0b1010), после первого входа в цикл while значение = 0b1010 & 0b1001 = 0xb1000, count = 1; после второго входа в цикл while value = 0b1000 & 0b0111 = 0 , count = 2; В этот момент значение было 0, и функция возвращает 2.
uint8_t count_bits_2(uint32_t value)
{
uint8_t count = 0;
while(value)
{
value &= value - 1;
count ++;
}
return count;
}Метод 3: метод справочной таблицы
Принцип метода таблицы поиска относительно прост. Он напрямую основан на значении значения для запроса данных. Позиция бита установлена на 1. Идея состоит в том, чтобы изменить пространство на время. Таблица может быть 4-битной, 8-битной, 16-битной, 32-битной. По сравнению с 32-битной, 4-битная более экономит место, но время вычисления относительно велико. Вот компромисс между временем и пространством. Например, значение имеет тип uint32_t При использовании 4-битной таблицы для запроса ему необходимо запросить 8 раз, в то время как при использовании 32-битной таблицы для запроса ему потребуется только 1 раз. Метод запроса к 8-битной таблице — более скромный метод.
Примечание: если таблица изменена с помощью const, при запросе будет читаться FLASH.Если она не определена как const, таблица будет скопирована в RAM, а RAM будет прочитана при запросе. Скорость чтения RAM выше, чем чтения FLASH.
static uint8_t table[256] =
{
0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
4, 5, 5, 6, 5, 6, 6, 7, 5, 6, 6, 7, 6, 7, 7, 8,
};
uint8_t count_bits_3(uint32_t value)
{
uint8_t count = 0;
count = table[value & 0xff] +
table[(value >>8) & 0xff] +
table[(value >>16) & 0xff] +
table[(value >>24) & 0xff] ;
return count ;
}Метод 4: Расширенный метод (параллельный метод)
uint8_t count_bits_4(uint32_t value)
{
value = ( value & 0x55555555 ) + ( (value >>1) & 0x55555555 ) ;
value = ( value & 0x33333333 ) + ( (value >>2) & 0x33333333 ) ;
value = ( value & 0x0f0f0f0f ) + ( (value >>4) & 0x0f0f0f0f ) ;
value = ( value & 0x00ff00ff ) + ( (value >>8) & 0x00ff00ff ) ;
value = ( value & 0x0000ffff ) + ( (value >>16) & 0x0000ffff ) ;
return value ;
}Этот метод очень грубый, его нелегко понять на первый взгляд, на самом деле он заключается в сложении всех битов в значение. Каждый раз добавляется 1 соседняя группа битов, первый раз накапливаются 2 соседних бита, второй раз накапливаются 4 соседних бита и в третий раз накапливаются 8 смежных битов и так далее.
Чтобы облегчить объяснение, мы можем сначала упростить тему, предположив, что значение является типом данных uint2_t (тип uint2_t на самом деле не существует, это гипотетически, всего 2 бита), а затем сколько бит в значении значение 1 может быть вычислено напрямую. Используйте следующую строку кода, чтобы это сделать. Это нужно понимать с первого взгляда, правда? То есть выньте бит 1 и добавьте его к биту 0, и сумма сложения будет числом, установленным в 1.
/ * Когда значение имеет тип uint2_t * /
value = ( value & 0x01 ) +( (value >> 1) & 0x01 );
/ * Или так, в любом случае, только последние 2 бита в 0x05 участвуют в вычислении * /
value = ( value & 0x05 ) +( (value >> 1) & 0x05 );Хорошо, это немного сложнее. Предполагая, что значение является типом данных uint4_t, тогда код можно записать следующим образом:
/ * Если значение - тип uint4_t * /
value = ( value & 0x05 ) +( (value >> 1) & 0x05 );
value = ( value & 0x03 ) +( (value >> 2) & 0x03 );Наконец, возьмем пример, когда значение имеет тип uint8_t.
/ * Если значение - тип uint8_t * /
value = ( value & 0x55 ) + ( (value >> 1) & 0x55 ) ;
value = ( value & 0x33 ) + ( (value >> 2) & 0x33 ) ;
value = ( value & 0x0f ) + ( (value >> 4) & 0x0f ) ; Например, если значение равно 0x6D (0b01101101), результат будет 0 + 1 + 1 + 0 + 1 + 0 + 1 + 1 = 5. На рисунке ниже показан процесс вычисления: сначала сложите их соседние двоичные цифры, затем сложите две соседние цифры и, наконец, сложите соседние четыре цифры. При добавлении 0x6D в расчет первый шаг равен 0b01011001, второй шаг — 0b00100011, а третий шаг — 0b00000101, что равно 5. После выяснения ситуации с 2, 4 и 8 битами 32-битная ситуация является той же самой программой. Кроме того, можно отметить, что при вычислении типа uint2_t его нужно вычислять один раз; при вычислении типа uint4_t его нужно вычислять дважды; при вычислении типа uint8_t его нужно вычислять 3 раза. Тогда мы можем догадаться, что его нужно вычислить 5 раз при вычислении типа uint32_t и 6 раз при вычислении типа uint64_t, то есть
Метод 5: Восьмеричный метод
uint8_t count_bits_5(uint32_t value)
{
uint32_t temp= value - ((value >>1) & 033333333333) - ((value >>2) & 011111111111);
return ((temp+ (temp>>3)) &030707070707) % 63;
}Позвольте мне сначала пояснить один момент: число, начинающееся с 0, является восьмеричным числом, а число, начинающееся с 0x, является шестнадцатеричным числом.В приведенном выше коде используются три восьмеричных числа. Запишите двоичное представление значения, а затем разделите каждые 3 бита на группу, найдите число 1 в каждой группе и затем выразите его в двоичной форме. Например, значение = 50, его двоичное представление — 110010, после группирования — 110 и 010, число 1 в этих двух группах — 2 и 3. 2 соответствует 010, 3 соответствует 011, поэтому после окончания первого строка кода, tmp = 010011, как это реализовано? Поскольку каждая группа из 3 битов, десятичные числа, соответствующие этим 3 битам, могут быть выражены в форме 2 ^ 2 * a + 2 ^ 1 * b + c, то есть в форме 4a + 2b + c, где значения A, b и c равны 0 или 1, если это 0, это означает, что соответствующая двоичная цифра равна 0, если это 1, это означает, что соответствующая двоичная цифра равна 1, поэтому значение a + b + c также равно 1 в двоичном числе 4a + 2b + c Число вверху. Например, десятичное число 6 (0110) = 4 * 1 + 2 * 1 + 0, где a = 1, b = 1, c = 0, a + b + c = 2, поэтому в двоичном представлении их два из 6 Один. Теперь вопрос, как получить a + b + c? Обратите внимание, что в битовой операции сдвиг на один бит вправо эквивалентен делению на 2. Используйте это свойство!
4a + 2b + c сдвиг вправо равен 2a + b, 4a + 2b + c сдвиг вправо равен a, а затем вычитается, 4a + 2b + c — (2a + b) — a = a + b + c, Это то, что делает первая строка кода.
Функция второй строки кода: на основе первой строки накопить количество единиц в двух соседних группах в tmp. Поскольку некоторые группы были добавлены один раз в процессе накопления, эти дополнительные части должны быть отброшены., Это роль & 030707070707, потому что конечный результат может быть больше 63.
Следует отметить, что после первой строки кода с правой стороны есть только четыре возможности для каждого смежного 3 бита, а именно 000, 001, 010, 011, почему? Потому что количество единиц в каждых 3-х битах не больше трех. Следовательно, в следующем добавлении нет проблемы переноса, потому что 3 + 3 = 6, что меньше 8, и переноса не будет.
тест
Запустите указанные выше 5 методов на однокристальном микрокомпьютере, чтобы сравнить эффективность работы. Одночиповый компьютер — Pandora STM32L475, основная частота 80 МГц, метод тестирования следующий.
#define TEST_NUMBER 0xFFFFFFFF
start_tick = HAL_GetTick();
for(i = 0; i < 100000; i++)
{
count = count_bits_1(TEST_NUMBER);
}
end_tick = HAL_GetTick();
printf("Function 1 result:%d,takes %d ms.rn",count,end_tick - start_tick);Пять алгоритмов тестируются с использованием вышеуказанных методов.После того, как каждый алгоритм выполняется 100000 раз, рассчитывается время выполнения.Конечные результаты выглядят следующим образом.
|
способ 1 |
Способ 2 |
Способ 3 |
Метод 4 |
Метод 5 |
|
|
0x00000000 |
465ms |
22ms |
59ms |
42ms |
45ms |
|
0x00000001 |
465ms |
31ms |
59ms |
43ms |
46ms |
| 0x0000000F | 465ms | 57ms | 59ms | 42ms | 46ms |
| 0x0000001F | 465ms | 66ms | 59ms | 43ms | 46ms |
|
0x11111111 |
465ms |
92ms |
59ms |
42ms |
55ms |
|
0x33333333 |
465ms |
162ms |
59ms |
43ms |
55ms |
|
0x77777777 |
465ms |
232ms |
59ms |
43ms |
56ms |
|
0xFFFFFFFF |
465ms |
302ms |
59ms |
43ms |
56ms |
|
способ 1 |
Способ 2 |
Способ 3 |
Метод 4 |
Метод 5 |
|
|
0x00000000 |
375ms | 20ms | 33ms | 35ms | 31ms |
|
0x00000001 |
376ms | 29ms | 33ms | 35ms | 32ms |
| 0x0000000F | 380ms | 55ms | 33ms | 35ms | 32ms |
| 0x0000001F | 381ms | 64ms | 33ms | 35ms | 32ms |
|
0x11111111 |
385ms | 90ms | 33ms | 35ms | 41ms |
|
0x33333333 |
395ms | 160ms | 32ms | 35ms | 41ms |
|
0x77777777 |
405ms | 230ms | 32ms | 35ms | 43ms |
|
0xFFFFFFFF |
415ms | 300ms | 32ms | 35ms | 43ms |
Заключение (не считайте оптимизацию компилятора)
Метод 1 наименее эффективен и имеет фиксированное время выполнения.
На время выполнения метода 2 влияет вычисленное значение.Чем больше 1 в двоичной системе вычисленного значения, тем больше время выполнения.
Метод 3 — это метод поиска по таблице, и время выполнения фиксировано.
Метод 4 наиболее эффективен и имеет фиксированное время выполнения. Когда количество битов меньше или равно 4, эффективен метод 2, а когда больше 4, метод 4, очевидно, лучше, чем метод 2.
Метод 5 — второй эффективный метод, время выполнения относительно фиксировано, а его низкая эффективность должна быть вызвана остаточной операцией в алгоритме.
Таким образом, при выборе алгоритма предпочтительнее использовать метод 4.Но это не совсем так, лучшее для вашего проекта — лучшее. Например, в моем проекте есть модуль сенсорных кнопок. Бит используется, чтобы указать, сколько кнопок в данный момент нажато. Обычно нажимается только одна кнопка. Тогда метод 2 является наиболее эффективным.


 Сколько единиц в восьмеричной записи значения выражения
Сколько единиц в восьмеричной записи значения выражения