Как найти эдс если известно внутреннее сопротивление - Исправление недочетов и поиск решений вместе с Examum.ru

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
Сторонняя сила
Закон Ома для полной цепи
КПД электрической цепи
Закон Ома для неоднородного участка

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила $vec{F_E}$ , направленная против движения заряда (т.е. против направления тока).

к оглавлению ▴

Сторонняя сила

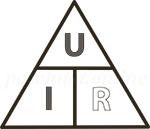
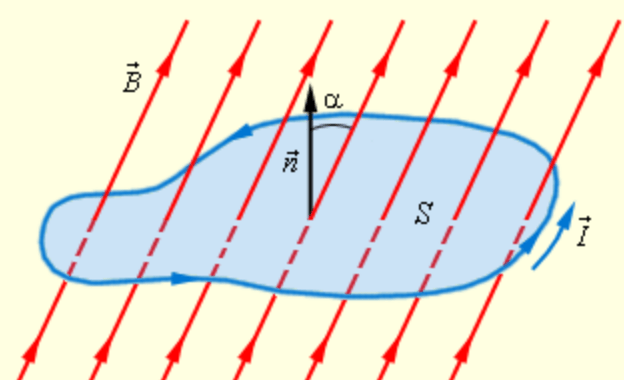
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила $vec{F_{CT}}$ не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через $A_{CT}$ работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы $A_{CT}$ называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, $A_{CT}$ — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа $A_{CT}$ прямо пропорциональна перемещаемому заряду . Поэтому отношение $A_{CT}/q$ уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :

$mathcal E = frac{displaystyle A_{CT}}{displaystyle q vphantom{1^a}}.$ (1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

к оглавлению ▴

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь

Наша задача — найти силу тока в цепи и напряжение на резисторе .

За время по цепи проходит заряд q = It . Согласно формуле (1) источник тока совершает при этом работу:

$A_{CT} = Eq = EIt.$ (2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:

(3)

Итак, $A_{CT} = Q$ , и мы приравниваем правые части формул (2) и (3):

После сокращения на получаем:

Вот мы и нашли ток в цепи:

$I = frac{displaystyle mathcal E}{displaystyle R + r vphantom{1^a}}.$ (4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления (R = 0) , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

$I_{K3} = frac{displaystyle mathcal E}{displaystyle r vphantom{1^a}}.$

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:

$U = IR = frac{displaystyle mathcal E R}{displaystyle R + r vphantom{1^a}}.$ (5)

Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При r = 0 формула (5) даёт .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина R + r неотличима от , и формула (5) снова даёт нам .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

к оглавлению ▴

КПД электрической цепи

Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим $Q_{polezn}$ .

Если сила тока в цепи равна , то

$Q_{polezn} = I^2Rt.$

Некоторое количество теплоты выделяется также на источнике тока:

$Q_{ist} = I^2rt.$

Полное количество теплоты, которое выделяется в цепи, равно:

$Q_{poln} = Q_{polezn} + Q_{ist} = I^2Rt + I^2rt = I^2(R + r)t.$

КПД электрической цепи — это отношение полезного тепла к полному:

$eta = frac{displaystyle Q_{polezn}}{displaystyle Q_{poln} vphantom{1^a}} = frac{displaystyle I^2Rt}{displaystyle I^2(R+r)t vphantom{1^a}} = frac{displaystyle R}{displaystyle R+r vphantom{1^a}}.$

КПД цепи равен единице лишь в том случае, если источник тока идеальный (r = 0) .

к оглавлению ▴

Закон Ома для неоднородного участка

Простой закон Ома U = IR справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно , можно просто заменить резистор на резистор R + r ).

Рис. 3. ЭДС «помогает» току:

Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: . За время через участок проходит заряд q = It , при этом стационарное электрическое поле совершает работу:

$A_{POL} = Uq = UIt.$

Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):

$A_{CT} = mathcal Eq = mathcal EIt.$

Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: $A_{POL} + A_{CT} = Q$ .

Подставляем сюда выражения для $A_{POL}$ , $A_{CT}$ и закон Джоуля–Ленца:

Сокращая на , получаем закон Ома для неоднородного участка цепи:

(6)

или, что то же самое:

(7)

Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то . Тогда из формулы (6) получаем U = IR — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на R + r :

Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

$A_{CT} = mathcal E q = mathcal EIt.$

Тогда закон Ома для неоднородного участка примет вид:

(8)

или:

где по-прежнему — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Повторим основные понятия и определения по теме «Закон Ома».

Напомним, что напряжение измеряется в вольтах.

Сила тока измеряется в амперах.

Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.

Основные определения, которые мы используем в решении задач:

Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.

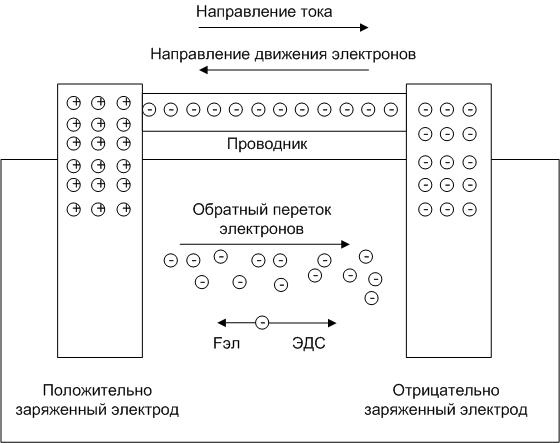
Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.

Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.

Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.

По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).

Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.

Сопротивление измеряют в омах (Ом).

Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).

Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:

Сопротивление проводника тем больше, чем больше его длина.
Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.

Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм²/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:

Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.

Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм² от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм²/м.

Решение:

Из закона Ома для проводника или участка цепи без источника следует:

$displaystyle I=frac{U}{R};$

$displaystyle R=frac{U}{I}.$

По графику: при

Из формулы сопротивления выражаем и находим длину проводника:

Ответ: 10.

Задача 2. Через поперечное сечение проводников за 8 с прошло 10²⁰ электронов. Какова сила тока в проводнике? Ответ дайте в амперах.

Решение:

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Заряд всех электронов: где е — модуль заряда электрона, $e=1,6cdot 10^{-19}$ Кл.

Тогда $displaystyle I=frac{Ncdot e}{t}=frac{10^{20}cdot 1,6cdot 10^{-19}}{8}=2 A.$

Ответ: 2.

Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)

Решение:

По закону Ома для полной цепи:

Тогда $displaystyle I=frac{5}{66+4}=0,07 A.$

Ответ: 0,07.

Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.

Решение:

Сила тока короткого замыкания определяется следующим образом:

Отсюда выражаем и находим внутреннее сопротивление источника:

При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:

Отсюда выражаем сопротивление резистора и находим его:

Ответ: 1,9.

Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.

Решение:

Выражаем время в секундах: t = 10 минут = 600 с.

Определяем силу тока по закону Ома для полной цепи:

Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Отсюда Кл.

Ответ: 1500.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Закон Ома

В 1826 величайший немецкий физик Георг Симон Ом публикует свою работу «Определение закона, по которому металлы проводят контактное электричество», где дает формулировку знаменитому закону. Ученые того времени встретили враждебно публикации великого физика. И лишь после того, как другой ученый – Клод Пулье, пришел к тем же выводам опытным путем, закон Ома признали во всем мире.

Закон Ома – физическая закономерность, которая определяет взаимосвязь между током, напряжением и сопротивлением проводника. Он имеет две основные формы.

Закон Ома для участка цепи

Формулировка закона Ома для участка цепи – сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению.

Это простое выражение помогает на практике решать широчайший круг вопросов. Для лучшего запоминания решим задачу.

Задача 1.1

Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм², если к концам провода приложено напряжение 12 B.

Задача простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.

Закон Ома для полной цепи

Формулировка закона Ома для полной цепи — сила тока прямо пропорциональна сумме ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи , где E – ЭДС, R- сопротивление цепи, r – внутреннее сопротивление источника.

Здесь могут возникнуть вопросы. Например, что такое ЭДС? Электродвижущая сила — это физическая величина, которая характеризует работу внешних сил в источнике ЭДС. К примеру, в обычной пальчиковой батарейке, ЭДС является химическая реакция, которая заставляет перемещаться заряды от одного полюса к другому. Само слово электродвижущая говорит о том, что эта сила двигает электричество, то есть заряд.

В каждом источнике присутствует внутреннее сопротивление r, оно зависит от параметров самого источника. В цепи также существует сопротивление R, оно зависит от параметров самой цепи.

Формулу закона Ома для полной цепи можно представить в другом виде. А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.

Для закрепления материала, решим две задачи на формулу закона Ома для полной цепи.

Задача 2.1

Найти силу тока в цепи, если известно что сопротивление цепи 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.

Теперь решим задачу посложнее.

Задача 2.2

Источник ЭДС подключен к резистору сопротивлением 10 Ом с помощью медного провода длиной 1 м и площадью поперечного сечения 1 мм². Найти силу тока, зная что ЭДС источника равно 12 В, а внутреннее сопротивление 1,9825 Ом.

Приступим.

Мнемоническая диаграмма

Для лучшего запоминания закона Ома существует мнемоническая диаграмма, благодаря которой можно всегда напомнить себе формулу. Пользоваться этой диаграммой очень просто. Достаточно закрыть искомую величину и две другие укажут, как её найти. Потренируйтесь, это может вам пригодится.

Успехов в изучении электричества! Рекомендуем прочесть статью — законы Кирхгофа.

Источник

Закон Ома

Главная
/
Физика
/
Закон Ома

Чтобы посчитать Закон Ома воспользуйтесь нашим очень удобным онлайн калькулятором:

Закон Ома для участка цепи

Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).

Онлайн калькулятор

Найти силу тока

Напряжение: U =В
Сопротивление: R =Ом

Сила тока: I =

Формула

I = ^U/_R

Пример

Если напряжение на концах участка цепи U = 12 В, а его электрическое сопротивление R = 2 Ом, то:

Сила тока на этом участке I = ¹²/₂= 6 А

Найти напряжение

Сила тока: I =A
Сопротивление: R =Ом

Напряжение: U =

Формула

U = I ⋅ R

Пример

Если сила тока на участке цепи I = 6 А, а электрическое сопротивление этого участка R = 2 Ом, то:

Напряжение на этом участке U = 6⋅2 = 12 В

Найти сопротивление

Напряжение: U =В
Сила тока: I =A

Сопротивление: R =

Ом

Формула

R = ^U/_I

Пример

Если напряжение на концах участка цепи U = 12 В, а сила тока на участке цепи I = 6 А, то:

Электрическое сопротивление на этом участке R = ¹²/₆ = 2 Ом

Закон Ома для полной цепи

Закон Ома для полной цепи гласит, что сила тока в цепи пропорциональна действующей в цепи электродвижущей силе (ЭДС) и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

Онлайн калькулятор

Найти силу тока

ЭДС: ε =В
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =Ом

Сила тока: I =

Формула

I = ^ε/_R+r

Пример

Если ЭДС источника напряжения ε = 12 В, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:

Сила тока I = ¹²/₄₊₂ = 2 А

Найти ЭДС

Сила тока: I =А
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =Ом

ЭДС: ε =

Формула

ε = I ⋅ (R+r)

Пример

Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:

ЭДС ε = 2 ⋅ (4+2) = 12 В

Найти внутреннее сопротивление источника напряжения

Сила тока: I =А
ЭДС: ε =В
Сопротивление всех внешних элементов цепи: R =Ом

Внутреннее сопротивление источника напряжения: r =

Ом

Формула

r = ^ε/_I — R

Пример

Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а ЭДС источника напряжения ε = 12 В, то:

Внутреннее сопротивление источника напряжения r = 12/2 — 4 = 2 Ом

Найти сопротивление всех внешних элементов цепи

Сила тока: I =А
ЭДС: ε =В
Внутреннее сопротивление источника напряжения: r =Ом

Сопротивление всех внешних элементов цепи: R =

Ом

Формула

R = ^ε/_I — r

Пример

Если сила тока в цепи I = 2A, внутреннее сопротивление источника напряжения r = 2 Ом, а ЭДС источника напряжения ε = 12 В, то:

Сопротивление всех внешних элементов цепи: R = 12/2 — 2 = 4 Ом

См. также

Источник

Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!

Идеальный источник ЭДС

Имеем источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

Или проще:

Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.

Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?

Внутреннее сопротивление источника ЭДС

Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.

Выглядит все это в аккумуляторе примерно вот так:

Цепляем лампочку

Итак, что у нас получается в чистом виде?

Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:

Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.

На резисторе R падает напряжение U_R , а на внутреннем резисторе r падает напряжение U_r .

Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.

Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Закон Ома для полной цепи

Итак, последнее выражение носит название «закон Ома для полной цепи»

где

Е — ЭДС источника питания, В

R — сопротивление всех внешних элементов в цепи, Ом

I — сила ток в цепи, А

r — внутреннее сопротивление источника питания, Ом

Просадка напряжения

Итак, знакомьтесь, автомобильный аккумулятор!

Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус

Наш подопечный готов к бою.

Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.

Первым делом давайте замеряем напряжение на клеммах аккумулятора

12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.

Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:

Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!

А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:

Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.

[quads id=1]

Смотрим на показания приборов:

Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.

Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла

Смотрим показания:

Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.

Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.

Как найти внутреннее сопротивление источника ЭДС

Давайте снова вернемся к этой фотографии

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе U_r тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.

Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение U_R=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило U_r=E-U_R=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r

Вывод

Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.

Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.

Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.

Источник

На чтение 9 мин Просмотров 2.1к. Опубликовано 11.09.2022 Обновлено 11.09.2022

Содержание

Понятие ЭДС и единица измерения
Где и как образуется электродвижущая сила
Виды ЭДС
Законы и формулы
ЭДС аккумуляторной батареи
ЭДС индукции
Внутреннее сопротивление источника ЭДС
Закон Ома для полной цепи
Как найти мощность ЭДС

Чтобы в какой-либо среде (металле, растворе, ионизированном газе и т.п.) протекал электрический ток в течение продолжительного времени, недостаточно наличия свободных носителей заряда и электрического поля. Еще потребуется сила, которая будет разделять заряды в направлении, противоположном направлению электрического поля.

Понятие ЭДС и единица измерения

Если имеется заряженный предмет и соединить его с электрически нейтральным (или противоположно заряженным предметом), некоторое время в цепи будет существовать ток. Как только все свободные электроны перейдут от одного тела к другому, и заряды уравняются, ток прекратится.

Опыт с двумя электроскопами

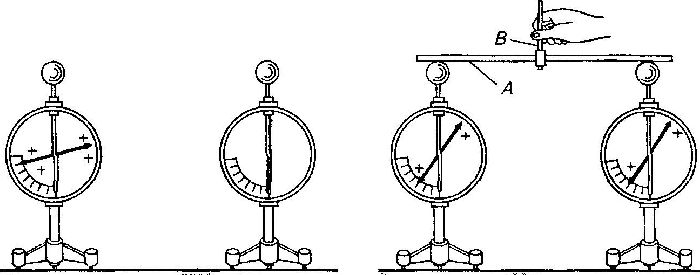
Это можно увидеть на примере школьного опыта с двумя электроскопами. Один из них заряжен (например, положительно), а другой заряда не имеет. Если их соединить металлическим стержнем, то заряды перейдут от одного прибора к другому. Количество зарядов уравновесится, потенциалы электроскопов станут равными, электрическое поле прекратит действие на электроны, и ток перестанет течь.

Чтобы ток продолжался, надо носители зарядов из второго электроскопа перенести обратно в первый. Для этого нужна сторонняя сила, действующая против направления электрического поля. Такая сила называется ЭДС. Расшифровка этого сокращения – электродвижущая сила.

Перенос зарядов посредством ЭДС

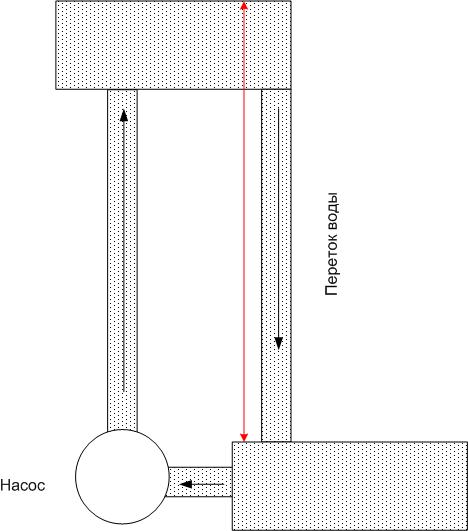
Можно провести аналогию с водой. Если есть два бассейна, один из которых находится выше другого, то вода может перетекать из верхнего водоема в нижний. Но как только запас воды закончится, переток прекратится. Чтобы он продолжался, надо воду из нижнего бассейна перекачивать обратно в верхний (например, с помощью насоса).

Необходимость наличия ЭДС на примере перетока воды

ЭДС обозначается греческой буквой ε (эпсилон), а иногда E. Измеряется ЭДС, как и напряжение, в вольтах (1 В). Понятие электродвижущей силы является не очень удачным – сила не измеряется в вольтах. Но этот термин укоренился и широко применяется.

Из-за сходства единиц измерения часто происходит путаница ЭДС и напряжения. Эти термины регулярно подменяются друг с другом. В некоторых случаях действительно принципиальной разницы нет, но в целом эти понятия различны.

В видео простыми словами объясняется чем отличаются ЭДС и напряжение

Где и как образуется электродвижущая сила

Электродвижущая сила образуется в источнике питания. Это необходимое условие существования разности потенциалов на выходных клеммах такого источника. Образовываться ЭДС может по-разному, в зависимости от устройства источника.

Виды ЭДС

Электродвижущая сила может быть различной природы (но всегда неэлектрической). В зависимости от типа источника питания ЭДС может быть:

фотоэлектрического характера – возникает в полупроводниковых переходах при облучении видимым светом или ультрафиолетом (на этом эффекте основана работа солнечных батарей);
электрохимической природы – всем известные гальванические элементы и аккумуляторы;
термоэлектрической ЭДС – возникает при разности температур между холодным и горячим спаем металлов (термопары для генерации электроэнергии и измерения температуры);
пьезоэлектрической природы (возникает при деформации некоторых материалов) – применяется в пьезозажигалках;
ЭДС электромагнитного характера – генераторы электростанций, автомобилей и т.п.

В технике встречаются и некоторые другие виды ЭДС, но реже.

Законы и формулы

Электродвижущая сила совершает работу по переносу заряда, а движущийся заряд представляет собой электрический ток/ Этот ток равен I=qt, где q – заряд, перенесенный полем за время t. За это время поле совершает работу A=ε*q= ε*I*t.

Можно определить ЭДС, как отношение работы по переносу заряда к величине этого заряда:

ε=A/q=A/(I*t)

ЭДС аккумуляторной батареи

ЭДС аккумуляторной батареи определяется типом электрохимических реакций, протекающих внутри элемента. Для различных технологий батарей наибольшая электродвижущая сила составит:

Свинцово-кислотные элементы – 2,17 вольта.
Никель-кадмиевые батареи – 1,37 вольта.
Никель-металлогидридные элементы – 1,37 вольта.
Щелочные аккумуляторы – 1,45 вольта.
Литий-ионные элементы – 4,2 вольта.

Электродвижущая сила химических источников тока не зависит от размеров и площади пластин. Чтобы повысить выходное напряжение, единичные аккумуляторы соединяют в батареи последовательно.

Последовательно соединенные элементы автомобильной батареи

ЭДС индукции

Основной источник получения электроэнергии на Земле – генераторы постоянного и переменного тока. Их принцип действия основан на создании ЭДС индукции.

Если замкнутый контур находится в магнитном поле, и его пронизывает магнитный поток Ф, и этот поток изменяется во времени (по направлению или по величине), то в контуре возникает ЭДС. Ее величина равна:

ε=∆Ф/∆t, где Ф – магнитный поток, а t – время его изменения.

Ток в замкнутом контуре, вызываемый ЭДС индукции под действием внешнего магнитного поля

В свою очередь магнитный поток зависит от величины магнитной индукции и площади поверхности, охватываемой контуром. Следовательно, чтобы увеличить ЭДС, надо усиливать магнитное поле (повышением тока возбуждения), или увеличивать площадь витка (при разработке или изготовлении генератора), или заставить магнитный поток изменяться быстрее (например, увеличивая скорость вращения ротора генератора). Каждый путь имеет определенные технические ограничения, поэтому в генераторах делают большое количество витков, соединяя их последовательно. При этом электродвижущие силы всех контуров складываются.

Статор автомобильного генератора – витки соединяются последовательно

Внутреннее сопротивление источника ЭДС

Пусть имеется источник тока — например, аккумулятор — с напряжением на разомкнутых клеммах (в отсутствие нагрузки) 12 вольт. Если его нагрузить на сопротивление в 5 Ом, напряжение на клеммах упадет (например, до 11,5 вольт). Если нагрузить аккумулятор на сопротивление 1 Ом, на его выходных терминалах напряжение снизится до 9,86 вольт.

Снижение выходного напряжения аккумулятора при уменьшении сопротивления нагрузки

Это явление легко объяснить, если ввести понятие внутреннего сопротивления источника питания. При разделении зарядов они движутся к соответствующим полюсам, но при этом взаимодействуют с кристаллической решеткой вещества, с ионами электролитов и отдают часть своей энергии. Движение носителей заряда замедляется, ток уменьшается, его ограничивает внутреннее сопротивление источника.

Это сопротивление включается последовательно с нагрузкой, и часть выходного напряжения падает на нем. Чем меньше сопротивление нагрузки, тем больше ток, тем больше потеря напряжения на внутреннем сопротивлении источника.

Внутреннее сопротивление определяется его конструкцией и типом ЭДС. Например, в аккумуляторе внутреннее сопротивление зависит от электрохимических реакций, протекающих в источнике тока.

Внутреннее сопротивление в виде резистора внутри источника тока

Для анализа электрических цепей внутреннее сопротивление рисуется на схеме в виде резистора, подключенного внутри источника параллельно его выходным клеммам. На самом деле, конечно, никакого резистора там нет, но это удобно для рассмотрения процессов, протекающих в цепи.

Для наглядности рекомендуем видео-урок.

Закон Ома для полной цепи

Один из фундаментальных законов электротехники – закон Ома для участка цепи. Согласно ему, ток на участке цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению.

Ток в полной цепи, в которую кроме нагрузки входит еще и источник, определяется величиной ЭДС, приложенной к внутреннему сопротивлению r и сопротивлению внешней нагрузки R, включенными последовательно. Общее значение сопротивления равно r+R. Следовательно, ток определяется соотношением I=ε/(R+r).

Как найти мощность ЭДС

Идеальный источник имеет нулевое внутреннее сопротивление. В нем напряжение под нагрузкой не уменьшается и всегда равно ЭДС. На практике таких источников не бывает.

Согласно закону Ома для полной цепи, формула ЭДС источника выглядит, как ε=I*R+I*r (в таком виде формулируется второй закон Кирхгофа). В этом выражении:

I*R=Uвнеш – напряжение на внешней нагрузке;
i*r=Uвнутр – падение напряжения на внутреннем сопротивлении источника.

Если источник идеален, то r=0 и вся ЭДС прикладывается к нагрузке. Чем выше r и выше ток, тем меньше напряжения достается потребителю, тем меньшая мощность выделяется на нем. Отсюда очевидно, что с ростом внутреннего сопротивления r, при равном токе, снижается напряжение на внешней нагрузке.

Внутреннее сопротивление источника можно рассчитать по результатам измерений напряжения на терминалах источника ЭДС по итогам двух замеров. Для этого надо воспользоваться законом Ома для полной цепи. Так, в рассмотренном примере, в первом случае падение напряжения на резисторе в 5 Ом составляет 11,5 вольт. Тогда можно найти ток в цепи по формуле:

I=U/R=11,5/5=2,3 А.

Выражение для ЭДС примет вид:

ε= 2,3*5+2,3*r=11,5+2,3*r.

Для второго замера на сопротивлении 1 Ом ток составит:

I=U/R=9,86/1=9,86 ампер

Следовательно,

ε= 9,86 *1+9,86 *r=9,86 +9,86 *r.

Левые части уравнений равны, тогда можно приравнять правые:

11,5+2,3*r=9,86 +9,86 *r

Путем несложных вычислений получается, что r=0,217 Ом. Если источник имеет меньшее внутреннее сопротивление, то при подключении той же нагрузки на ней будет большее напряжение. Напряжение на разомкнутых клеммах (на холостом ходу) в отсутствие ток будет примерно равно значению величины ЭДС. Таким образом, чем меньше внутреннее сопротивление, тем большее напряжение способен выдавать источник в нагрузку и тем больше мощность ЭДС.

Если же идеальный источник тока замкнуть накоротко, ток короткого замыкания будет бесконечным, так как R=r=0. На самом деле этого не происходит – в реальном источнике ток КЗ при R=0 ограничивается внутренним сопротивлением r.

Электродвижущая сила является одним из основополагающих понятий в физике. Ее суть и значение надо четко осознавать, в противном случае дальнейшее освоение электротехники будет затруднено.

Источник