Как найти эйлеров путь графа - Исправление недочетов и поиск решений вместе с Examum.ru

Определение. Эйлеров путь — это путь в графе, проходящий через все его рёбра.

Определение. Эйлеров цикл — это эйлеров путь, являющийся циклом.

Для простоты в обоих случаях будем считать, что граф неориентированный.

Граф на пяти вершинах и один из его эйлеровых циклов: CDCBBADEBC

Также существует понятие гамильтонова пути и цикла — они посещают все вершины по разу, а не рёбра. Нахождение гамильтонова цикла (задача коммивояжера, англ. travelling salesman problem) — одна из самых известных NP-полных задач, в то время как нахождение эйлерова цика решается за линейное время, и мы сейчас покажем, как.

#Нахождение эйлерова цикла

Теорема. Эйлеров цикл существует тогда и только тогда, когда граф связный и степени всех вершин чётны.

Доказательство. Необходимость показывается так: можно просто взять эйлеров цикл и ориентировать все его ребра в порядке обхода. Тогда из каждой вершины будет выходить столько же рёбер, сколько входить, а значит степень у всех вершин исходного неориентированного графа была четной.

Достаточность докажем конструктивно — предъявим алгоритм нахождения цикла:

void euler(int v) {
    while (!g[v].empty()) {
        u = *g[v].begin(); // берем любое ребро
        remove_edge(v, u); // удаляем его
        euler(u);            // запускаемся от противоположного конца
    }
    cout << v <<  " ";     // выписываем текущую вершину
}

Заметим, что:

выведется последовательность из ровно $(m + 1)$ вершин,
между каждой соседней парой выписанных вершин есть ребро,
каждое ребро будет выписано ровно один раз.

Значит, если условия на связность и четность степеней выполняются, то выведенная последовательность вершин действительно будет эйлеровым циклом, причём и в случае ориентированного графа тоже.

#Как удалять ребра

Проще всего хранить все списки смежности в set-подобной структуре и удалять их напрямую там:

const int maxn = 1e5;
set<int> g[maxn];

void euler(int v) {
    while (!g[v].empty()) {
        u = *g[v].begin();
        g[v].erase(u);
        g[u].erase(v); // если граф ориентированный, обратное ребро удалять не надо
        euler(u);
    }
    cout << v <<  " ";
}

Это будет работать за $O(m log n)$, однако просто заменив дерево на хеш-таблицу (unordered_set) можно уменьшить время до линейного.

Также можно использовать более общий подход, который часто применяется в задачах, где ребра как-то изменяются. Создадим отдельный массив с мета-информацией о ребрах и будем хранить в списках смежности не номера вершин, а номера рёбер:

struct edge {
    int to;
    bool deleted;
};

vector<edge> edges;
stack<int> g[maxn];

void add_edge(int u, int v) {
    g[u].push(edges.size());
    edges.add({v, false});
    g[u].push(edges.size());
    edges.add({u, false});
}

Если добавлять каждое ребро неориентированного графа через add_edge, то у получившейся нумерации ребер будет интересное свойство: чтобы получить обратное к ребру e, нужно вычислить e^1.

Тогда во время обхода можно поддерживать эту информацию вместо какой-то сложной модификации структур:

void euler(int v) {
    while (!g[v].empty()) {
        e = g[v].top();
        g[v].pop();
        if (!edges[e].deleted) {
            edges[e].deleted = edges[e^1].deleted = true;
            euler(e.to);
        }
    }
    cout << v <<  " ";
}

Во всех вариантах реализации нужно быть чуть аккуратнее в случае, когда в графе есть петли и кратные ребра.

#Эйлеров путь

Поговорим теперь про эйлеровы пути. Может, всё-таки можно что-нибудь сделать, даже если степени не всех вершин чётные?

Заметим, что, так как каждое ребро меняет четность степеней ровно двух вершин, и в пустом графе все степени изначально нулевые, то число вершин с нечетными степенями будет четным.

Если нечетных вершин ровно две, то можно сделать следующее: соединить их ребром, построить эйлеров цикл (ведь теперь степени всех вершин четные), а затем удалить это ребро из цикла. Если правильно сдвинуть этот цикл, мы получили эйлеров путь.

Альтернативно, можно просто запустить обход из одной из нечетных вершин и получить такой же результат.

Если нечетных вершин больше двух, то мы уже построить эйлеров путь не сможем, потому что любой эйлеров путь входит или покидает каждую вершину четное число раз, кроме, возможно двух своих концов.

Следствие. Эйлеров путь существует тогда и только тогда, когда граф связен и количество вершин с нечётными степенями не превосходит 2.

Упражнение. Дан связный неориентированный граф. Требуется покрыть его ребра наименьшим количеством непересекающихся путей. Асимптотика $O(n + m)$.

Упражнение. Сформулируйте и докажите аналогичные утверждения для случая ориентированного графа.

Источник

import java.util.ArrayList;

import java.util.Arrays;

import java.util.List;

// Класс для хранения ребра Graph

class Edge

{

int source, dest;

public Edge(int source, int dest)

{

this.source = source;

this.dest = dest;

}

// Класс для представления graphического объекта

class Graph

{

// Список списков для представления списка смежности

List<List<Integer>> adjList;

// Конструктор

Graph(List<Edge> edges, int n)

{

adjList = new ArrayList<>();

for (int i = 0; i < n; i++) {

adjList.add(new ArrayList<>());

}

// добавляем ребра в неориентированный graph

for (Edge edge: edges)

{

adjList.get(edge.source).add(edge.dest);

adjList.get(edge.dest).add(edge.source);

}

class Main

{

// Вспомогательная функция для обхода DFS на Graphе

public static void DFS(Graph graph, int v, boolean[] discovered)

{

// помечаем текущий узел как обнаруженный

discovered[v] = true;

// делаем для каждого ребра (v, u)

for (int u: graph.adjList.get(v))

{

// если `u` еще не обнаружен

if (!discovered[u]) {

DFS(graph, u, discovered);

}

// Функция для проверки, все ли вершины с ненулевой степенью в Graph

// принадлежат одному связанному компоненту

public static boolean isConnected(Graph graph, int n)

{

// чтобы отслеживать, посещена ли вершина или нет

boolean[] visited = new boolean[n];

// запускаем поиск в глубину с первой вершины с ненулевой степенью

for (int i = 0; i < n; i++)

{

if (graph.adjList.get(i).size() > 0)

{

DFS(graph, i, visited);

break;

}

// если один вызов DFS не может посетить все вершины с ненулевой степенью,

// graph содержит более одной компоненты связности

for (int i = 0; i < n; i++)

{

if (!visited[i] && graph.adjList.get(i).size() > 0) {

return false;

}

return true;

}

// Вспомогательная функция для возврата общего количества вершин в Graph

// с нечетной степенью

public static int countOddVertices(Graph graph)

{

int count = 0;

for (List<Integer> list: graph.adjList)

{

if ((list.size() & 1) == 1) {

count++;

}

return count;

}

public static void main(String[] args)

{

// Список ребер Graph согласно приведенной выше диаграмме

List<Edge> edges = Arrays.asList(new Edge(0, 1), new Edge(0, 3),

new Edge(1, 2), new Edge(1, 3), new Edge(1, 4),

new Edge(2, 3), new Edge(3, 4));

// общее количество узлов в Graph (от 0 до 4)

int n = 5;

// создаем неориентированный graph из заданных ребер

Graph graph = new Graph(edges, n);

// проверяем, все ли вершины с ненулевой степенью принадлежат

// одиночный связный компонент

boolean is_connected = isConnected(graph, n);

// находим общее количество вершин с нечетной степенью

int odd = countOddVertices(graph);

// Эйлеров путь существует, если все вершины не нулевой степени соединены,

// и ноль или две вершины имеют нечетную степень

if (is_connected && (odd == 0 || odd == 2))

{

System.out.println(«The graph has an Eulerian path»);

// Связный graph имеет эйлеров цикл, если каждая вершина имеет

// четная степень

if (odd == 0) {

System.out.println(«The graph has an Eulerian cycle»);

}

// В Graph есть эйлеров путь, но нет эйлерова цикла

else {

System.out.println(«The Graph is Semi–Eulerian»);

}

else {

System.out.println(«The Graph is not Eulerian»);

}

Источник

From Wikipedia, the free encyclopedia

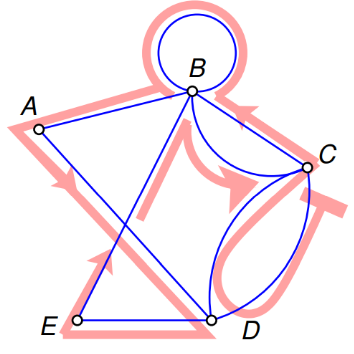
Every vertex of this graph has an even degree. Therefore, this is an Eulerian graph. Following the edges in alphabetical order gives an Eulerian circuit/cycle.

In graph theory, an Eulerian trail (or Eulerian path) is a trail in a finite graph that visits every edge exactly once (allowing for revisiting vertices). Similarly, an Eulerian circuit or Eulerian cycle is an Eulerian trail that starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of Königsberg problem in 1736. The problem can be stated mathematically like this:

Given the graph in the image, is it possible to construct a path (or a cycle; i.e., a path starting and ending on the same vertex) that visits each edge exactly once?

Euler proved that a necessary condition for the existence of Eulerian circuits is that all vertices in the graph have an even degree, and stated without proof that connected graphs with all vertices of even degree have an Eulerian circuit. The first complete proof of this latter claim was published posthumously in 1873 by Carl Hierholzer.^[1] This is known as Euler’s Theorem:

A connected graph has an Euler cycle if and only if every vertex has even degree.

The term Eulerian graph has two common meanings in graph theory. One meaning is a graph with an Eulerian circuit, and the other is a graph with every vertex of even degree. These definitions coincide for connected graphs.^[2]

For the existence of Eulerian trails it is necessary that zero or two vertices have an odd degree; this means the Königsberg graph is not Eulerian. If there are no vertices of odd degree, all Eulerian trails are circuits. If there are exactly two vertices of odd degree, all Eulerian trails start at one of them and end at the other. A graph that has an Eulerian trail but not an Eulerian circuit is called semi-Eulerian.

Definition[edit]

An Eulerian trail,^[3] or Euler walk, in an undirected graph is a walk that uses each edge exactly once. If such a walk exists, the graph is called traversable or semi-eulerian.^[4]

An Eulerian cycle,^[3] also called an Eulerian circuit or Euler tour, in an undirected graph is a cycle that uses each edge exactly once. If such a cycle exists, the graph is called Eulerian or unicursal.^[5] The term «Eulerian graph» is also sometimes used in a weaker sense to denote a graph where every vertex has even degree. For finite connected graphs the two definitions are equivalent, while a possibly unconnected graph is Eulerian in the weaker sense if and only if each connected component has an Eulerian cycle.

For directed graphs, «path» has to be replaced with directed path and «cycle» with directed cycle.

The definition and properties of Eulerian trails, cycles and graphs are valid for multigraphs as well.

An Eulerian orientation of an undirected graph G is an assignment of a direction to each edge of G such that, at each vertex v, the indegree of v equals the outdegree of v. Such an orientation exists for any undirected graph in which every vertex has even degree, and may be found by constructing an Euler tour in each connected component of G and then orienting the edges according to the tour.^[6] Every Eulerian orientation of a connected graph is a strong orientation, an orientation that makes the resulting directed graph strongly connected.

Properties[edit]

An undirected graph has an Eulerian cycle if and only if every vertex has even degree, and all of its vertices with nonzero degree belong to a single connected component.
An undirected graph can be decomposed into edge-disjoint cycles if and only if all of its vertices have even degree. So, a graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint cycles and its nonzero-degree vertices belong to a single connected component.
An undirected graph has an Eulerian trail if and only if exactly zero or two vertices have odd degree, and all of its vertices with nonzero degree belong to a single connected component
A directed graph has an Eulerian cycle if and only if every vertex has equal in degree and out degree, and all of its vertices with nonzero degree belong to a single strongly connected component. Equivalently, a directed graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint directed cycles and all of its vertices with nonzero degree belong to a single strongly connected component.
A directed graph has an Eulerian trail if and only if at most one vertex has (out-degree) − (in-degree) = 1, at most one vertex has (in-degree) − (out-degree) = 1, every other vertex has equal in-degree and out-degree, and all of its vertices with nonzero degree belong to a single connected component of the underlying undirected graph.^{[citation needed]}

Constructing Eulerian trails and circuits[edit]

Using Eulerian trails to solve puzzles involving drawing a shape with a continuous stroke:

As the Haus vom Nikolaus puzzle has two odd vertices (orange), the trail must start at one and end at the other.
Annie Pope’s with four odd vertices has no solution.
If there are no odd vertices, the trail can start anywhere and forms an Eulerian cycle.
Loose ends are considered vertices of degree 1.

Fleury’s algorithm[edit]

Fleury’s algorithm is an elegant but inefficient algorithm that dates to 1883.^[7] Consider a graph known to have all edges in the same component and at most two vertices of odd degree. The algorithm starts at a vertex of odd degree, or, if the graph has none, it starts with an arbitrarily chosen vertex. At each step it chooses the next edge in the path to be one whose deletion would not disconnect the graph, unless there is no such edge, in which case it picks the remaining edge left at the current vertex. It then moves to the other endpoint of that edge and deletes the edge. At the end of the algorithm there are no edges left, and the sequence from which the edges were chosen forms an Eulerian cycle if the graph has no vertices of odd degree, or an Eulerian trail if there are exactly two vertices of odd degree.

While the graph traversal in Fleury’s algorithm is linear in the number of edges, i.e. O(|E|) , we also need to factor in the complexity of detecting bridges. If we are to re-run Tarjan’s linear time bridge-finding algorithm^[8] after the removal of every edge, Fleury’s algorithm will have a time complexity of ${displaystyle O(|E|^{2})}$ . A dynamic bridge-finding algorithm of Thorup (2000) allows this to be improved to ${displaystyle O(|E|cdot log ^{3}|E|cdot log log |E|)}$ , but this is still significantly slower than alternative algorithms.

Hierholzer’s algorithm[edit]

Hierholzer’s 1873 paper provides a different method for finding Euler cycles that is more efficient than Fleury’s algorithm:

Choose any starting vertex v, and follow a trail of edges from that vertex until returning to v. It is not possible to get stuck at any vertex other than v, because the even degree of all vertices ensures that, when the trail enters another vertex w there must be an unused edge leaving w. The tour formed in this way is a closed tour, but may not cover all the vertices and edges of the initial graph.
As long as there exists a vertex u that belongs to the current tour but that has adjacent edges not part of the tour, start another trail from u, following unused edges until returning to u, and join the tour formed in this way to the previous tour.
Since we assume the original graph is connected, repeating the previous step will exhaust all edges of the graph.

By using a data structure such as a doubly linked list to maintain the set of unused edges incident to each vertex, to maintain the list of vertices on the current tour that have unused edges, and to maintain the tour itself, the individual operations of the algorithm (finding unused edges exiting each vertex, finding a new starting vertex for a tour, and connecting two tours that share a vertex) may be performed in constant time each, so the overall algorithm takes linear time, O(|E|) .^[9]

This algorithm may also be implemented with a deque. Because it is only possible to get stuck when the deque represents a closed tour, one should rotate the deque by removing edges from the tail and adding them to the head until unstuck, and then continue until all edges are accounted for. This also takes linear time, as the number of rotations performed is never larger than |E| (intuitively, any «bad» edges are moved to the head, while fresh edges are added to the tail)

Orthographic projections and Schlegel diagrams with Hamiltonian cycles of the vertices of the five platonic solids – only the octahedron has an Eulerian path or cycle, by extending its path with the dotted one

Counting Eulerian circuits[edit]

Complexity issues[edit]

The number of Eulerian circuits in digraphs can be calculated using the so-called BEST theorem, named after de Bruijn, van Aardenne-Ehrenfest, Smith and Tutte. The formula states that the number of Eulerian circuits in a digraph is the product of certain degree factorials and the number of rooted arborescences. The latter can be computed as a determinant, by the matrix tree theorem, giving a polynomial time algorithm.

BEST theorem is first stated in this form in a «note added in proof» to the Aardenne-Ehrenfest and de Bruijn paper (1951). The original proof was bijective and generalized the de Bruijn sequences. It is a variation on an earlier result by Smith and Tutte (1941).

Counting the number of Eulerian circuits on undirected graphs is much more difficult. This problem is known to be #P-complete.^[10] In a positive direction, a Markov chain Monte Carlo approach, via the Kotzig transformations (introduced by Anton Kotzig in 1968) is believed to give a sharp approximation for the number of Eulerian circuits in a graph, though as yet there is no proof of this fact (even for graphs of bounded degree).

Special cases[edit]

An asymptotic formula for the number of Eulerian circuits in the complete graphs was determined by McKay and Robinson (1995):^[11]

${displaystyle operatorname {ec} (K_{n})=2^{frac {(n+1)}{2}}pi ^{frac {1}{2}}e^{{frac {-n^{2}}{2}}+{frac {11}{12}}}n^{frac {(n-2)(n+1)}{2}}{bigl (}1+O(n^{-{frac {1}{2}}+epsilon }){bigr )}.}$

A similar formula was later obtained by M.I. Isaev (2009) for complete bipartite graphs:^[12]

${displaystyle operatorname {ec} (K_{n,n})=left({frac {n}{2}}-1right)!^{2n}2^{n^{2}-n+{frac {1}{2}}}pi ^{-n+{frac {1}{2}}}n^{n-1}{bigl (}1+O(n^{-{frac {1}{2}}+epsilon }){bigr )}.}$

Applications[edit]

Eulerian trails are used in bioinformatics to reconstruct the DNA sequence from its fragments.^[13] They are also used in CMOS circuit design to find an optimal logic gate ordering.^[14] There are some algorithms for processing trees that rely on an Euler tour of the tree (where each edge is treated as a pair of arcs).^[15]^[16] The de Bruijn sequences can be constructed as Eulerian trails of de Bruijn graphs.^[17]

In infinite graphs[edit]

An infinite graph with all vertex degrees equal to four but with no Eulerian line

In an infinite graph, the corresponding concept to an Eulerian trail or Eulerian cycle is an Eulerian line, a doubly-infinite trail that covers all of the edges of the graph. It is not sufficient for the existence of such a trail that the graph be connected and that all vertex degrees be even; for instance, the infinite Cayley graph shown, with all vertex degrees equal to four, has no Eulerian line. The infinite graphs that contain Eulerian lines were characterized by Erdõs, Grünwald & Weiszfeld (1936). For an infinite graph or multigraph G to have an Eulerian line, it is necessary and sufficient that all of the following conditions be met:^[18]^[19]

G is connected.
G has countable sets of vertices and edges.
G has no vertices of (finite) odd degree.
Removing any finite subgraph S from G leaves at most two infinite connected components in the remaining graph, and if S has even degree at each of its vertices then removing S leaves exactly one infinite connected component.

Undirected Eulerian graphs[edit]

Euler stated a necessary condition for a finite graph to be Eulerian as all vertices must have even degree. Hierholzer proved this is a sufficient condition in a paper published in 1873. This leads to the following necessary and sufficient statement for what a finite graph must have to be Eulerian: An undirected connected finite graph is Eulerian if and only if every vertex of G has even degree.^[20]

The following result was proved by Veblen in 1912: An undirected connected graph is Eulerian if and only if it is the disjoint union of some cycles.^[20]

A directed graph with all even degrees that is not Eulerian, serving as a counterexample to the statement that a sufficient condition for a directed graph to be Eulerian is that it has all even degrees

Hierholzer developed a linear time algorithm for constructing an Eulerian tour in an undirected graph.

Directed Eulerian graphs[edit]

It is possible to have a directed graph that has all even out-degrees but is not Eulerian. Since an Eulerian circuit leaves a vertex the same number of times as it enters that vertex, a necessary condition for an Eulerian circuit to exist is that the in-degree and out-degree are equal at each vertex. Obviously, connectivity is also necessary. König proved that these conditions are also sufficient. That is, a directed graph is Eulerian if and only if it is connected and the in-degree and out-degree are equal at each vertex.^[20]

In this theorem it doesn’t matter whether «connected» means «weakly connected» or «strongly connected» since they are equivalent for Eulerian graphs.

Hierholzer’s linear time algorithm for constructing an Eulerian tour is also applicable to directed graphs.^[20]

Mixed Eulerian graphs[edit]

This mixed graph is Eulerian. The graph is even but not symmetric which proves that evenness and symmetricness are not necessary and sufficient conditions for a mixed graph to be Eulerian.

If a mixed graph has even degrees only, it is not guaranteed to be an Eulerian graph. This means that evenness is a necessary but not sufficient condition for a mixed graph to be Eulerian. If a mixed graph is even and symmetric, it is guaranteed to be symmetric. This means that evenness and being symmetric is a necessary condition for a mixed graph to be Eulerian. This is not a necessary and sufficient condition however, because it is possible to construct a graph that is even and not symmetric that is still Eulerian.^[21]

Ford and Fulkerson proved in 1962 in their book Flows in Networks a necessary and sufficient condition for a graph to be Eulerian, viz., that every vertex must be even and satisfy the balance condition. For every subset of vertices S, the difference between the number of arcs leaving S and entering S must be less than or equal to the number of edges incident with S. This is the balanced set condition. A mixed and strongly connected graph is Eulerian if and only if G is even and balanced.^[21]

The process of checking if a mixed graph is Eulerian is harder than checking if an undirected or directed graph is Eulerian because the balanced set condition concerns every possible subset of vertices.

An even mixed graph that violates the balanced set condition and is therefore not Eulerian.

An even mixed graph that satisfies the balanced set condition and is therefore an Eulerian mixed graph.

Notes[edit]

^ N. L. Biggs, E. K. Lloyd and R. J. Wilson, Graph Theory, 1736–1936, Clarendon Press, Oxford, 1976, 8–9, ISBN 0-19-853901-0.
^ C. L. Mallows, N. J. A. Sloane (1975). «Two-graphs, switching classes and Euler graphs are equal in number» (PDF). SIAM Journal on Applied Mathematics. 28 (4): 876–880. doi:10.1137/0128070. JSTOR 2100368.
^ ^a ^b Some people reserve the terms path and cycle to mean non-self-intersecting path and cycle. A (potentially) self-intersecting path is known as a trail or an open walk; and a (potentially) self-intersecting cycle, a circuit or a closed walk. This ambiguity can be avoided by using the terms Eulerian trail and Eulerian circuit when self-intersection is allowed.
^ Jun-ichi Yamaguchi, Introduction of Graph Theory.
^ Schaum’s outline of theory and problems of graph theory By V. K. Balakrishnan [1].
^ Schrijver, A. (1983), «Bounds on the number of Eulerian orientations», Combinatorica, 3 (3–4): 375–380, doi:10.1007/BF02579193, MR 0729790, S2CID 13708977.
^ Fleury, Pierre-Henry (1883), «Deux problèmes de Géométrie de situation», Journal de mathématiques élémentaires, 2nd ser. (in French), 2: 257–261.
^ Tarjan, R. Endre (1974), «A note on finding the bridges of a graph», Information Processing Letters, 2 (6): 160–161, doi:10.1016/0020-0190(74)90003-9, MR 0349483.
^ Fleischner, Herbert (1991), «X.1 Algorithms for Eulerian Trails», Eulerian Graphs and Related Topics: Part 1, Volume 2, Annals of Discrete Mathematics, vol. 50, Elsevier, pp. X.1–13, ISBN 978-0-444-89110-5.
^ Brightwell and Winkler, «Note on Counting Eulerian Circuits», 2004.
^ Brendan McKay and Robert W. Robinson, Asymptotic enumeration of eulerian circuits in the complete graph, Combinatorica, 10 (1995), no. 4, 367–377.
^ M.I. Isaev (2009). «Asymptotic number of Eulerian circuits in complete bipartite graphs». Proc. 52-nd MFTI Conference (in Russian). Moscow: 111–114.
^ Pevzner, Pavel A.; Tang, Haixu; Waterman, Michael S. (2001). «An Eulerian trail approach to DNA fragment assembly». Proceedings of the National Academy of Sciences of the United States of America. 98 (17): 9748–9753. Bibcode:2001PNAS…98.9748P. doi:10.1073/pnas.171285098. PMC 55524. PMID 11504945.
^ Roy, Kuntal (2007). «Optimum Gate Ordering of CMOS Logic Gates Using Euler Path Approach: Some Insights and Explanations». Journal of Computing and Information Technology. 15 (1): 85–92. doi:10.2498/cit.1000731.
^ Tarjan, Robert E.; Vishkin, Uzi (1985). «An efficient parallel biconnectivity algorithm». SIAM Journal on Computing. 14 (4): 862–874. CiteSeerX 10.1.1.465.8898. doi:10.1137/0214061.
^ Berkman, Omer; Vishkin, Uzi (Apr 1994). «Finding level-ancestors in trees». J. Comput. Syst. Sci. 2. 48 (2): 214–230. doi:10.1016/S0022-0000(05)80002-9.
^ Savage, Carla (January 1997). «A Survey of Combinatorial Gray Codes». SIAM Review. 39 (4): 605–629. doi:10.1137/S0036144595295272. ISSN 0036-1445.
^ Komjáth, Peter (2013), «Erdős’s work on infinite graphs», Erdös centennial, Bolyai Soc. Math. Stud., vol. 25, János Bolyai Math. Soc., Budapest, pp. 325–345, doi:10.1007/978-3-642-39286-3_11, MR 3203602.
^ Bollobás, Béla (1998), Modern graph theory, Graduate Texts in Mathematics, vol. 184, Springer-Verlag, New York, p. 20, doi:10.1007/978-1-4612-0619-4, ISBN 0-387-98488-7, MR 1633290.
^ ^a ^b ^c ^d Corberán, Ángel; Laporte, Gilbert, eds. (2015). Arc Routing | SIAM Digital Library. MOS-SIAM Series on Optimization. doi:10.1137/1.9781611973679. ISBN 978-1-61197-366-2. Retrieved 2022-08-19.
^ ^a ^b Corberán, Ángel; Laporte, Gilbert, eds. (2015). Arc Routing | SIAM Digital Library. MOS-SIAM Series on Optimization. doi:10.1137/1.9781611973679. ISBN 978-1-61197-366-2. Retrieved 2022-08-19.

References[edit]

Erdõs, Pál; Grünwald, Tibor; Weiszfeld, Endre (1936), «Végtelen gráfok Euler vonalairól» [On Euler lines of infinite graphs] (PDF), Mat. Fix. Lapok (in Hungarian), 43: 129–140. Translated as Erdős, P.; Grünwald, T.; Vázsonyi, E. (1938), «Über Euler-Linien unendlicher Graphen» [On Eulerian lines in infinite graphs] (PDF), J. Math. Phys. (in German), 17 (1–4): 59–75, doi:10.1002/sapm193817159.
Euler, L., «Solutio problematis ad geometriam situs pertinentis», Comment. Academiae Sci. I. Petropolitanae 8 (1736), 128–140.
Hierholzer, Carl (1873), «Ueber die Möglichkeit, einen Linienzug ohne Wiederholung und ohne Unterbrechung zu umfahren», Mathematische Annalen, 6 (1): 30–32, doi:10.1007/BF01442866, S2CID 119885172.
Lucas, E., Récréations Mathématiques IV, Paris, 1921.
Fleury, «Deux problemes de geometrie de situation», Journal de mathematiques elementaires (1883), 257–261.
T. van Aardenne-Ehrenfest and N. G. de Bruijn (1951) «Circuits and trees in oriented linear graphs», Simon Stevin 28: 203–217.
Thorup, Mikkel (2000), «Near-optimal fully-dynamic graph connectivity», Proc. 32nd ACM Symposium on Theory of Computing, pp. 343–350, doi:10.1145/335305.335345, S2CID 128282
W. T. Tutte and C. A. B. Smith (1941) «On Unicursal Paths in a Network of Degree 4», American Mathematical Monthly 48: 233–237.

External links[edit]

Discussion of early mentions of Fleury’s algorithm.
Euler tour at Encyclopedia of Mathematics.

Источник

Определение эйлерового пути в графе

Одна из важных
задач теории графов заключается в
нахождении пути (маршрута), содержащего
по одному разу все ребра графа. Этот
путь называется эйлеровым
путем (ЭП) или
эйлеровой линией в графе, а задачу его
нахождения называют задачей Эйлера.
Графы, на которых существуют замкнутые
эйлеровы линии, называют эйлеровыми
графами.

На практике задача
нахождения ЭП на графе может встретиться,
например, при определении порядка
регламентных проверок исправности
каналов связи между звеньями какой-нибудь
достаточно сложной системы, обслуживаемой
одной ремонтной единицей.

Ответ
на вопрос о существовании ЭП на графах
дают теоремы Эйлера.

Теорема Эйлера
для неориентированных графов:
для того чтобы на графе существовал
замкнутый эйлеров путь (маршрут),
необходимо и достаточно, чтобы граф был
связным и степени всех его вершин были
четными [1, 8].

Теорема Эйлера
для ориентированных графов:
для того чтобы на ориентированном графе
существовал замкнутый ЭП, необходимо
и достаточно, чтобы граф был связным и
для каждой его вершины полустепень
исхода равнялась полустепени захода
[1, 8].

Для нахождения ЭП
на графе (если он существует — см. теорему
Эйлера) удобно воспользоваться следующим
алгоритмом (для неориентированного
графа):

0. Задается начальный
шаг итерации k
=0. Задается начальная (она же и конечная
в случае замкнутого ЭП) вершина ЭП V₀_. Если,
например, V₀= A₃,
то это означает, что начальной вершиной
ЭП на шаге k
= 0 выбрана третья вершина графа. Все
ребра графа считаются непомеченными.
Число непомеченных ребер S
равно числу
ребер графа.

1. k=k+1.
Определяются все вершины, непосредственно
связанные непомеченными ребрами с
вершиной V_k_-1.

2. Определяется
число S_k
непомеченных ребер, инцидентных вершине
V_k_-1.

Если S_k=
1, то вторая вершина, инцидентная этому
ребру, становится очередной вершиной
V_k
ЭП. Это ребро помечается. Возвращаемся
на п. 1.

Если S_k>1, то среди
вершин, смежных V_k_-1,
выбирается
вершина с наименьшим номером
k,
которая становится очередной вершиной
V_k
ЭП. Ребро, соединяющее эту вершину с
вершиной V_k_-1,
помечается.
Возвращаемся на п. 1.

3. S_k
= 0. Для вершины, принадлежащей полученному
таким образом пути и имеющей непомеченные
инцидентные ребра, строится цикл по
непомеченным ребрам. Определение новой
вершины этого цикла начинается с п. 1.

4. Построенный
таким образом новый цикл объединяется
с ранее построенным в вершине, с которой
начиналось построение нового цикла.

5. Если в цикле есть
еще вершины, имеющие непомеченные
инцидентные ребра, то возвращаемся на
п. 3. Если таких ребер нет, то ЭП найден.

Отметим, что выбор
вершины с наименьшим номером нужен для
того, чтобы была определенность при
выборе вершины на каждом шаге. Можно,
однако, предложить выбор вершин и с
наибольшим номером.

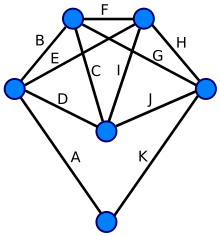
В
качестве примера рассмотрим задачу
нахождения ЭП для графа (рис. 4.3). ЭП
существует, так как степени всех вершин
четные.

Рис. 4.3

0.
k
= 0. Выберем начальную вершину с номером
3, т.е. V₀
= 3. Число
непомеченных ребер S
= 12.

1.
k
= 1. С вершиной V₀
= 3 связаны
вершины 1, 2.

2. Число непомеченных
ребер для 3-й вершины S₁
= 2. Следующей вершиной ЭП является
вершина с номером 1. Ребро 3-1 помечается.
Возвращаемся к п. 1.

1. k
= 2. С вершиной 1 связаны вершины 2, 4, 6.

2. S₂
= 3. Вершина 2. Помечается ребро 1-2.
Возвращаемся к п. 1.

1. k
= 3. С вершиной 2 связаны вершины 3, 5, 7.

2. S₃
= 3. Вершина 3. Помечается ребро 2-3.
Возвращаемся к п. 1.

1.
k
= 4. С вершиной 3 связаны вершины 1, 2.

2. S₄
= 0. Вершин таких нет. Следовательно,
получен цикл 3-1-2-3, который еще не является
ЭП.

3. Вершины 1 и 2,
входящие в этот цикл, имеют непомеченные
инцидентные ребра. Рассмотрим вершину
1 в качестве начальной точки следующего
цикла A₄
= 1.

1. k
= 5. Вершины 4, 6.

2. S₅= 2. Вершина
4. Ребро 1-4.

1. k
= 6. Вершина 5.

2. S₆= 1. Вершина
5. Ребро 4-5.

1. k
= 7. Вершины 2, 7, 8.

2. S₇= 3. Вершина
2. Ребро 5-2.

1. k
= 8. Вершина 7.

2. S₈= 1. Вершина
7. Ребро 2-7.

1. k
= 9. Вершины 5, 6, 8.

2. S₉=
3. Вершина 5. Ребро 7-5.

1. k
= 10. Вершина 8.

2. S₁₀= 1. Вершина
8. Ребро 5-8.

1. k
= 11. Вершина 7.

2. S₁₁= 1. Вершина
7. Ребро 8-7.

1. k
= 12. Вершина
6.

2. S₁₂= 1. Вершина
6. Ребро 7-6.

1. k
= 13. Вершина
1.

2. S₁₃= 1. Вершина
1. Ребро 6-1.

1. k
= 14. Вершин, связанных непомеченными
ребрами, нет.

3. S₁₄= 0. В найденных
циклах нет вершин, имеющих инцидентные
непомеченные ребра.

4. Для нахождения
ЭП необходимо объединить два найденных
цикла 3-1-2-3 и 1-4-5-2-7-5-8-7-6-1 в вершине 1.
Результатом объединения будет путь:
3-1-4-5-2-7-5-8-7-6-1-2-3.

5. Так как в этом
пути нет вершин с непомеченными ребрами,
то найденный путь является эйлеровым.

Нахождение
сильных компонент, базового и доминирующего
множеств

При определении
сильных компонент и базового множества
ориентированного графа
G
используется матрица
достижимости
L
и контрдостижимости
Q
графа [6]. Элементы l_ik
и q_ik
этих матриц определяются следующим
образом:

Матрица достижимости
L графа G,
имеющего n
вершин, может быть получена путем
последовательного
булевого
умножения матрицы R¹графа
(достижимости не более чем за один шаг)
саму на себя
N
раз.

Значение N
определяется из условия, при котором
R^N
= R^N^-1,причем N

n-1.

Матрица
контрдостижимости
Q
графа G
может быть
найдена из матрицы достижимости путем
ее транспонирования, то есть Q
= L^T
.

х₂

ример.

Рис. 4.4

,

,
.

Под сильной
компонентой
(СК)
графа G
будем понимать подграф G’
графа G
максимальной размерности (максимальное
число вершин), являющийся сильно связным
графом, который не содержится в любом
другом сильном подграфе графа G.
Ориентированный граф G=(X,F)
является сильно связным, если для любой
пары вершин (x_i,
x_j)существует
хотя бы один путь как из x_i
x_j,
так и наоборот из x_j
x_i.

Сильные компоненты
произвольного графа G
могут быть найдены в результате
поэлементного логического перемножения
матриц достижимости и контрдостижимости.
Номера столбцов в i-й
строке, для которых элемент матрицы
равен 1, соответствуют номерам вершин,
входящих в данную сильную компоненту.
В нашем случае получим

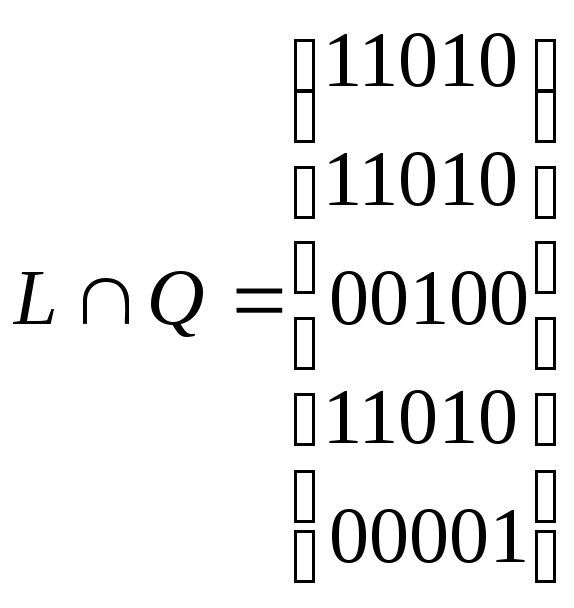
Для рассмотренного
выше графа (рис. 4.4) получим три сильные
компоненты: CK_x₁={x₁,
x₂,
x₄},
CK_x₂=
{x₃},
CK_x₃=
{x₅}.

На сильных
компонентах, как на вершинах, может быть
построен новый граф G*=(X*,
F*)
– который называется конденсацией
графа G.
Каждая его вершина отображает множество
вершин, соответствующих одной из сильных
компонент исходного графа G,
а дуга (x_^,x_^)
существует в G*
тогда и только тогда, когда в графе G
существует дуга (x_i,x_j)
такая, что х_iСКх_,
а х_j
СКх_.

Для исходного
графа конденсацией будет граф, состоящий
из 3-х вершин (рис. 4.5).

x₃^

x₅^

Рис. 4.5.

Базовым множеством
графа G
называется такое множество В
вершин этого графа, из которых достижима
любая вершина графа и которое является
минимальным в том смысле, что не существует
его подмножества, обладающего таким же
свойством достижимости.

Доминирующим
множеством
вершин SX
графа G=(X,F)
называется такое множество вершин, что
для каждой вершины х_jS
существует дуга (путь длиной 1), идущая
от некоторой вершины множества S
к данной вершине х_j.

Задача нахождения
базового и доминирующего множеств в
графе сводится к определению такого
множества вершин, из которых достижима
любая вершина графа (но за различное
число шагов). Для этого целесообразно
использовать матрицы достижимости и
смежности соответственно.

Задача определения
минимального
доминирующего множества
эквивалентна задаче нахождения
минимальной ДНФ на импликантной матрице
(см. работу №2 настоящего руководства),
т.е.
такого наименьшего множества строк,
что каждый столбец содержит единицу,
хотя бы в одной из этого множества строк.
Поиск минимального доминирующего
множества осуществляется на матрице
R¹достижимости
не более чем за один шаг.
Таким минимальным доминирующим множеством
для графа на рис. 4.4 является множество,
состоящее из вершин x₁,
x₃ или
x₁,
x₄
.

Базовое множество
определяется аналогично. Но, при этом,
в отличие от определения доминирующего
множества, задача решается не на матрице
R¹,
а на матрице достижимости L.

В случае графа
большой размерности для поиска базового
множества целесообразно сначала найти
конденсацию графа, затем базу конденсации,
и только затем базу исходного графа,
выбирая по одной вершине из каждой
сильной компоненты, входящей в базу
конденсации. Размерность задачи в этом
случае существенно снижается.

Для графа на рис.
4.4 базовым множеством будут вершины или
x₁,
или
x₂,
или x₄,
(одна из вершин, входящих в сильную
компоненту CK_x₁={x₁,
x₂,
x₄},
соответствующую базе конденсации графа
G*
– вершине x₁^).

Для нахождения
базовых и доминирующих множеств могут
использоваться алгоритмы нахождения
ТДНФ и МДНФ из работы №2 настоящего
руководства.

Варианты заданий
для поиска гамильтонова и эйлерова пути
в графе, а также компонент связности
графа приведены в Приложении. Для
нахождения сильных компонент, базового
и доминирующего множеств использовать
варианты заданий для поиска ГП в графе.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Эйлеров путь и цикл

Эйлеров путь(цепь) проходит через каждое ребро графа ровно по одному разу.

Эйлеров цикл — это замкнутый путь, проходящий через каждое ребро графа ровно по одному разу.

Алгоритм поиска Эйлеров цикла

Сервис использует алгоритм поиска Эйлеров цикла на основе циклов.

Будем рассматривать самый общий случай — случай ориентированного мультиграфа, возможно, с петлями. Также мы предполагаем, что эйлеров цикл в графе существует (и состоит хотя бы из одной вершины). Для поиска эйлерова цикла воспользуемся тем, что эйлеров цикл — это объединение всех простых циклов графа. Следовательно, наша задача — эффективно найти все циклы и эффективно объединить их в один.

Кроме того, перед поиском цикла проверяется его существование, для этого происходит поиск степени вершин.

Более подробно вы можете узнать об этом алгоритме
в Википедии.

Реализацию алгоритма на языке C++ вы можете найти в нашем репозитории на GitHub: Реализация поиска Эйлерового цикла в Graphoffline.

Алгоритм поиска Эйлервой цепи

Для поиска Эйлеров пути мы добавляем псевдо ребро соединяющие начальную и конечную вершину Эйлерова пути.

Начальная и конечная вершина для неориентированного графа будет иметь нечётные степени.

Для ориентированного графа начальная вершина имеет полустепень исхода на единицу больше полустепени захода. Для конечной вершины полустепень исхода на единицу меньше полустепени захода.

Как использовать

Создайте граф.
Выберите пункт меню Алгоритмы -> «Найти Эйлеров цикл» для поиска Эйлеров цикл.

Выберите пункт меню Алгоритмы -> «Найти Эйлерову цепь» для поиска Эйлеровой цепи.

Источник

#Нахождение эйлерова цикла

#Как удалять ребра

#Эйлеров путь

Definition[edit]

Properties[edit]

Constructing Eulerian trails and circuits[edit]

Fleury’s algorithm[edit]

Hierholzer’s algorithm[edit]

Counting Eulerian circuits[edit]

Complexity issues[edit]

Special cases[edit]

Applications[edit]

In infinite graphs[edit]

Undirected Eulerian graphs[edit]

Directed Eulerian graphs[edit]

Mixed Eulerian graphs[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Определение эйлерового пути в графе

Эйлеров путь и цикл

Алгоритм поиска Эйлеров цикла

Алгоритм поиска Эйлервой цепи

Как использовать