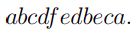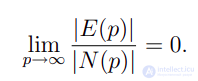Как найти эйлеров путь или эйлеров цикл - Исправление недочетов и поиск решений вместе с Examum.ru

import java.util.ArrayList;

import java.util.Arrays;

import java.util.List;

// Класс для хранения ребра Graph

class Edge

{

int source, dest;

public Edge(int source, int dest)

{

this.source = source;

this.dest = dest;

}

// Класс для представления graphического объекта

class Graph

{

// Список списков для представления списка смежности

List<List<Integer>> adjList;

// Конструктор

Graph(List<Edge> edges, int n)

{

adjList = new ArrayList<>();

for (int i = 0; i < n; i++) {

adjList.add(new ArrayList<>());

}

// добавляем ребра в неориентированный graph

for (Edge edge: edges)

{

adjList.get(edge.source).add(edge.dest);

adjList.get(edge.dest).add(edge.source);

}

class Main

{

// Вспомогательная функция для обхода DFS на Graphе

public static void DFS(Graph graph, int v, boolean[] discovered)

{

// помечаем текущий узел как обнаруженный

discovered[v] = true;

// делаем для каждого ребра (v, u)

for (int u: graph.adjList.get(v))

{

// если `u` еще не обнаружен

if (!discovered[u]) {

DFS(graph, u, discovered);

}

// Функция для проверки, все ли вершины с ненулевой степенью в Graph

// принадлежат одному связанному компоненту

public static boolean isConnected(Graph graph, int n)

{

// чтобы отслеживать, посещена ли вершина или нет

boolean[] visited = new boolean[n];

// запускаем поиск в глубину с первой вершины с ненулевой степенью

for (int i = 0; i < n; i++)

{

if (graph.adjList.get(i).size() > 0)

{

DFS(graph, i, visited);

break;

}

// если один вызов DFS не может посетить все вершины с ненулевой степенью,

// graph содержит более одной компоненты связности

for (int i = 0; i < n; i++)

{

if (!visited[i] && graph.adjList.get(i).size() > 0) {

return false;

}

return true;

}

// Вспомогательная функция для возврата общего количества вершин в Graph

// с нечетной степенью

public static int countOddVertices(Graph graph)

{

int count = 0;

for (List<Integer> list: graph.adjList)

{

if ((list.size() & 1) == 1) {

count++;

}

return count;

}

public static void main(String[] args)

{

// Список ребер Graph согласно приведенной выше диаграмме

List<Edge> edges = Arrays.asList(new Edge(0, 1), new Edge(0, 3),

new Edge(1, 2), new Edge(1, 3), new Edge(1, 4),

new Edge(2, 3), new Edge(3, 4));

// общее количество узлов в Graph (от 0 до 4)

int n = 5;

// создаем неориентированный graph из заданных ребер

Graph graph = new Graph(edges, n);

// проверяем, все ли вершины с ненулевой степенью принадлежат

// одиночный связный компонент

boolean is_connected = isConnected(graph, n);

// находим общее количество вершин с нечетной степенью

int odd = countOddVertices(graph);

// Эйлеров путь существует, если все вершины не нулевой степени соединены,

// и ноль или две вершины имеют нечетную степень

if (is_connected && (odd == 0 || odd == 2))

{

System.out.println(«The graph has an Eulerian path»);

// Связный graph имеет эйлеров цикл, если каждая вершина имеет

// четная степень

if (odd == 0) {

System.out.println(«The graph has an Eulerian cycle»);

}

// В Graph есть эйлеров путь, но нет эйлерова цикла

else {

System.out.println(«The Graph is Semi–Eulerian»);

}

else {

System.out.println(«The Graph is not Eulerian»);

}

Источник

Определение. Эйлеров путь — это путь в графе, проходящий через все его рёбра.

Определение. Эйлеров цикл — это эйлеров путь, являющийся циклом.

Для простоты в обоих случаях будем считать, что граф неориентированный.

Граф на пяти вершинах и один из его эйлеровых циклов: CDCBBADEBC

Также существует понятие гамильтонова пути и цикла — они посещают все вершины по разу, а не рёбра. Нахождение гамильтонова цикла (задача коммивояжера, англ. travelling salesman problem) — одна из самых известных NP-полных задач, в то время как нахождение эйлерова цика решается за линейное время, и мы сейчас покажем, как.

#Нахождение эйлерова цикла

Теорема. Эйлеров цикл существует тогда и только тогда, когда граф связный и степени всех вершин чётны.

Доказательство. Необходимость показывается так: можно просто взять эйлеров цикл и ориентировать все его ребра в порядке обхода. Тогда из каждой вершины будет выходить столько же рёбер, сколько входить, а значит степень у всех вершин исходного неориентированного графа была четной.

Достаточность докажем конструктивно — предъявим алгоритм нахождения цикла:

void euler(int v) {
    while (!g[v].empty()) {
        u = *g[v].begin(); // берем любое ребро
        remove_edge(v, u); // удаляем его
        euler(u);            // запускаемся от противоположного конца
    }
    cout << v <<  " ";     // выписываем текущую вершину
}

Заметим, что:

выведется последовательность из ровно $(m + 1)$ вершин,
между каждой соседней парой выписанных вершин есть ребро,
каждое ребро будет выписано ровно один раз.

Значит, если условия на связность и четность степеней выполняются, то выведенная последовательность вершин действительно будет эйлеровым циклом, причём и в случае ориентированного графа тоже.

#Как удалять ребра

Проще всего хранить все списки смежности в set-подобной структуре и удалять их напрямую там:

const int maxn = 1e5;
set<int> g[maxn];

void euler(int v) {
    while (!g[v].empty()) {
        u = *g[v].begin();
        g[v].erase(u);
        g[u].erase(v); // если граф ориентированный, обратное ребро удалять не надо
        euler(u);
    }
    cout << v <<  " ";
}

Это будет работать за $O(m log n)$, однако просто заменив дерево на хеш-таблицу (unordered_set) можно уменьшить время до линейного.

Также можно использовать более общий подход, который часто применяется в задачах, где ребра как-то изменяются. Создадим отдельный массив с мета-информацией о ребрах и будем хранить в списках смежности не номера вершин, а номера рёбер:

struct edge {
    int to;
    bool deleted;
};

vector<edge> edges;
stack<int> g[maxn];

void add_edge(int u, int v) {
    g[u].push(edges.size());
    edges.add({v, false});
    g[u].push(edges.size());
    edges.add({u, false});
}

Если добавлять каждое ребро неориентированного графа через add_edge, то у получившейся нумерации ребер будет интересное свойство: чтобы получить обратное к ребру e, нужно вычислить e^1.

Тогда во время обхода можно поддерживать эту информацию вместо какой-то сложной модификации структур:

void euler(int v) {
    while (!g[v].empty()) {
        e = g[v].top();
        g[v].pop();
        if (!edges[e].deleted) {
            edges[e].deleted = edges[e^1].deleted = true;
            euler(e.to);
        }
    }
    cout << v <<  " ";
}

Во всех вариантах реализации нужно быть чуть аккуратнее в случае, когда в графе есть петли и кратные ребра.

#Эйлеров путь

Поговорим теперь про эйлеровы пути. Может, всё-таки можно что-нибудь сделать, даже если степени не всех вершин чётные?

Заметим, что, так как каждое ребро меняет четность степеней ровно двух вершин, и в пустом графе все степени изначально нулевые, то число вершин с нечетными степенями будет четным.

Если нечетных вершин ровно две, то можно сделать следующее: соединить их ребром, построить эйлеров цикл (ведь теперь степени всех вершин четные), а затем удалить это ребро из цикла. Если правильно сдвинуть этот цикл, мы получили эйлеров путь.

Альтернативно, можно просто запустить обход из одной из нечетных вершин и получить такой же результат.

Если нечетных вершин больше двух, то мы уже построить эйлеров путь не сможем, потому что любой эйлеров путь входит или покидает каждую вершину четное число раз, кроме, возможно двух своих концов.

Следствие. Эйлеров путь существует тогда и только тогда, когда граф связен и количество вершин с нечётными степенями не превосходит 2.

Упражнение. Дан связный неориентированный граф. Требуется покрыть его ребра наименьшим количеством непересекающихся путей. Асимптотика $O(n + m)$.

Упражнение. Сформулируйте и докажите аналогичные утверждения для случая ориентированного графа.

Источник

Эйлеров путь и цикл

Эйлеров путь(цепь) проходит через каждое ребро графа ровно по одному разу.

Эйлеров цикл — это замкнутый путь, проходящий через каждое ребро графа ровно по одному разу.

Алгоритм поиска Эйлеров цикла

Сервис использует алгоритм поиска Эйлеров цикла на основе циклов.

Будем рассматривать самый общий случай — случай ориентированного мультиграфа, возможно, с петлями. Также мы предполагаем, что эйлеров цикл в графе существует (и состоит хотя бы из одной вершины). Для поиска эйлерова цикла воспользуемся тем, что эйлеров цикл — это объединение всех простых циклов графа. Следовательно, наша задача — эффективно найти все циклы и эффективно объединить их в один.

Кроме того, перед поиском цикла проверяется его существование, для этого происходит поиск степени вершин.

Более подробно вы можете узнать об этом алгоритме
в Википедии.

Реализацию алгоритма на языке C++ вы можете найти в нашем репозитории на GitHub: Реализация поиска Эйлерового цикла в Graphoffline.

Алгоритм поиска Эйлервой цепи

Для поиска Эйлеров пути мы добавляем псевдо ребро соединяющие начальную и конечную вершину Эйлерова пути.

Начальная и конечная вершина для неориентированного графа будет иметь нечётные степени.

Для ориентированного графа начальная вершина имеет полустепень исхода на единицу больше полустепени захода. Для конечной вершины полустепень исхода на единицу меньше полустепени захода.

Как использовать

Создайте граф.
Выберите пункт меню Алгоритмы -> «Найти Эйлеров цикл» для поиска Эйлеров цикл.

Выберите пункт меню Алгоритмы -> «Найти Эйлерову цепь» для поиска Эйлеровой цепи.

Источник

Эйлеров граф

Эйлеров граф
— граф, содержащий
эйлеров цикл.

Эйлеров цикл
— это эйлеров путь,
являющийся циклом.

Эйлеров путь
(эйлерова цепь)
в графе — это путь,
проходящий по всем рёбрам графа
и притом только по одному разу.

Полуэйлеров
граф — граф,
содержащий эйлеров путь (цепь).

Существование
эйлерова цикла и эйлерова пути.

Разумеется,
эйлеров цикл/путь существуют только в
связных графах или в графах, которые
после удаления всех одиночных вершин
превратятся в связные.

В неориентированном графе

Кроме того,
согласно теореме, доказанной Эйлером,
эйлеров цикл существует тогда и только
тогда, когда граф связный и в нём
отсутствуют вершины нечётной степени.

Эйлеров путь в
графе существует тогда и только тогда,
когда граф связный и содержит не более
чем две вершины нечётной степени.^[1][2]
Ввиду леммы
о рукопожатиях,
число вершин с нечётной степенью должно
быть четным. А значит Эйлеров путь
существует только тогда, когда это число
равно нулю или двум. Причём когда оно
равно нулю, эйлеров путь вырождается в
эйлеров цикл.

В ориентированном графе

Ориентированный
граф содержит эйлеров цикл тогда и
только тогда, когда он сильно-связан
и для каждой вершины графа её полустепень
захода равна её полустепени исхода, то
есть в вершину входит столько же ребер,
сколько из неё и выходит.

Поиск
эйлерова пути в графе

Можно всегда
свести задачу поиска эйлерова пути к
задаче поиска эйлерова цикла. Действительно,
предположим, что эйлерова цикла не
существует, а эйлеров путь существует.
Тогда в графе будет ровно 2 вершины
нечётной степени. Соединим эти вершины
ребром, и получим граф, в котором все
вершины чётной степени, и эйлеров цикл
в нём существует. Найдём в этом графе
эйлеров цикл (алгоритмом,
описанным ниже), а затем удалим из ответа
несуществующее ребро.

Поиск
эйлерова цикла в графе

Будем рассматривать
самый общий случай — случай
ориентированного мультиграфа,
возможно, с петлями.
Также мы предполагаем, что эйлеров цикл
в графе существует (и состоит хотя бы
из одной вершины). Для поиска эйлерова
цикла воспользуемся тем, что эйлеров
цикл — это объединение всех простых
циклов графа. Следовательно, наша
задача — эффективно найти все циклы
и эффективно объединить их в один.

Каждая вершина графа (рис.
8.??) имеет чётную степень, поэтому этот
граф — эйлеров. Обход рёбер в алфавитном
порядке даёт эйлеров цикл.

Рис. 8.??

Гамильтонов граф

Гамильтонов
граф — в теории
графов это
граф,
содержащий гамильтонову
цепь или гамильтонов
цикл.

Гамильтонов
путь (или гамильтонова
цепь) — путь
(цепь),
содержащий каждую вершину графа ровно
один раз. Гамильтонов путь, начальная
и конечная вершины которого совпадают,
называется гамильтоновым
циклом.

Гамильтоновы
путь, цикл и граф названы в честь
ирландского
математика У.
Гамильтона,
который впервые определил эти классы,
исследовав задачу «кругосветного
путешествия» по додекаэдру,
узловые вершины которого символизировали
крупнейшие города Земли,
а рёбра — соединяющие их дороги.

Рис. Граф додекаэдра с
выделенным циклом Гамильтона

Условия
существования

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Привет, сегодня поговорим про эйлеров цикл, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
эйлеров цикл, эйлеров граф, эйлеров цепь, эйлеров путь, полуэйлеровый граф, квазиэйлеровый граф , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

эйлеров путь (эйлерова цепь) в графе — это путь (цепь), проходящий по всем дугам (ребрам) графа и притом только по одному разу. (ср. Гамильтонов путь)

эйлеров цикл — это цикл графа, проходящий через каждое ребро (дугу) графа ровно по одному разу.

эйлеров граф — граф, содержащий эйлеров цикл.

Полуэйлеров граф — граф, содержащий эйлеров путь (цепь).

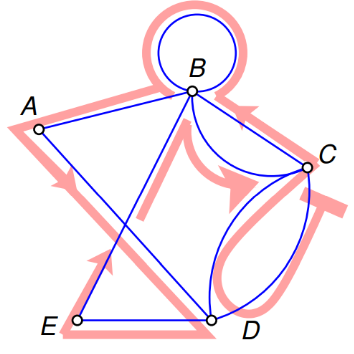
Граф Кенигсбергских мостов. Этот граф не является эйлеровым, поэтому решения не существует.

Каждая вершина этого графа имеет четную степень, поэтому этот граф — эйлеров. Обход ребер в алфавитном порядке дает эйлеров цикл.

Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называется эйлеровым циклом, а граф называется эйлеровым графом.

Если граф имеет цепь (не обязательно простую), содержащую все ребра графа по одному разу, то такая цепь называется эйлеровой цепью, а граф называется полуэйлеровым графом.

Определение 3
Цепь, содержащая все ребра графа, называется эйлеровой.

Определение 4
Граф, обладающий эйлеровой цепью, называется квазиэйлеровым.

Теорема 5

Граф является квазиэйлеровым, если в нем не более двух вершин нечетной степени.

Определение 1

Цикл называется эйлеровым, если он содержит все ребра графа. Цепь называется эйлеровой, если она содержит все ребра графа.

Определение 2

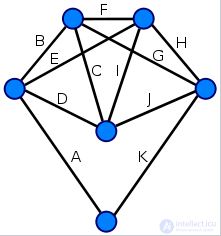
Граф называется эйлеровым, если в нем найдется эйлеров цикл.

Пример

Граф “Сабли Магомета” является эйлеровым, так как в нем есть эйлеров цикл 123475287651.

Существование эйлерова цикла и эйлерова пути

Эйлеров цикл/путь существуют только в связных графах или в графах, которые после удаления всех одиночных вершин превратятся в связные.

В неориентированном графе

Согласно теореме, доказанной Эйлером, в графе без одиночных вершин эйлеров цикл существует тогда и только тогда, когда графсвязный и в нем отсутствуют вершины нечетной степени.

Эйлерова цепь в графе существует тогда и только тогда, когда граф связный и содержит не более двух вершин нечетной степени. Ввиду леммы о рукопожатиях, число вершин с нечетной степенью должно быть четным . Об этом говорит сайт https://intellect.icu . А значит Эйлеров путь существует только тогда, когда это число равно нулю или двум. Причем когда оно равно нулю, эйлеров путь вырождается в эйлеров цикл.

В ориентированном графе

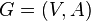
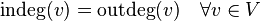
Ориентированный граф содержит эйлеров цикл тогда и только тогда, когда он сильно связан и для каждой вершины графа ее полустепень захода равна ее полустепени исхода, то есть в вершину входит столько же ребер, сколько из нее и выходит: .

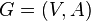
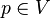
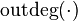
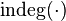
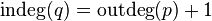
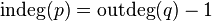
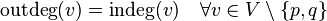
Ориентированный граф содержит эйлеров путь тогда и только тогда, когда он сильно связный и существуют две вершины и (начальная и конечная вершины пути соответственно) такие, что их полустепени захода и полустепени исхода связаны равенствами и , а все остальные вершины имеют одинаковые полустепени исхода и захода: .

Поиск эйлерова пути в графе

Можно всегда свести задачу поиска эйлерова пути к задаче поиска эйлерова цикла. Действительно, предположим, что эйлерова цикла не существует, а эйлеров путь существует. Тогда в графе будет ровно 2 вершины нечетной степени. Соединим эти вершины ребром, и получим граф, в котором все вершины четной степени, и эйлеров цикл в нем существует. Найдем в этом графе эйлеров цикл (алгоритмом, описанным ниже), а затем удалим из ответа несуществующее ребро.

Поиск эйлерова цикла в графе

Алгоритм Флери

Это хоть и элегантный, но неэффективный алгоритм, который был предложен Флери в 1883 году.

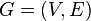
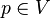
Пусть задан граф . Начинаем с некоторой вершины и каждый раз вычеркиваем пройденное ребро. Не проходим по ребру, если удаление этого ребра приводит к разбиению графа на две связные компоненты (не считая изолированных вершин), т.е. необходимо проверять, является ли ребро мостом или нет.

Алгоритм может быть распространен на орграфы.

Алгоритм на основе циклов

Реализовать это можно, например, так, рекурсивно:

procedure find_all_cycles (v)
var массив cycles
1. пока есть цикл, проходящий через v, находим его
    добавляем все вершины найденного цикла в массив cycles (сохраняя порядок обхода)
    удаляем цикл из графа
2. идем по элементам массива cycles
    каждый элемент cycles[i] добавляем к ответу
    из каждого элемента рекурсивно вызываем себя: find_all_cycles (cycles[i])

Достаточно вызвать эту процедуру из любой неодиночной вершины графа, и она найдет все циклы в графе, удалит их из графа и объединит их в один эйлеров цикл.

Для поиска цикла на шаге 1 используем поиск в глубину.

Сложность полученного алгоритма — O(M), то есть линейная относительно количества ребер М в данном графе.

Построение эйлерова цикла

Рассмотрим алгоритм построения эйлерова цикла в эйлеровом графе.
Алгоритм Флери.
Начиная с произвольной вершины, идем по ребрам графа, соблюдая следующие правила:
1. Удаляем ребра по мере их прохождения, и удаляем также изолированные вершины,
которые при этом образуются.
2. Идем по мосту только тогда, когда нет других возможностей.
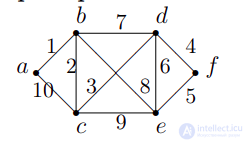
Пример.

По теореме граф является эйлеровым. На диаграмме ребра пронумерованы в порядке
их прохождения, таким образом эйлеров цикл

.Оценка числа эйлеровых графов

Лемма о числе вершин нечетной степени.

В любом графе число вершин нечетной степени четно. Доказательство. По теореме Эйлера сумма степеней вершин графа равна удвоенному количеству ребер, т. е. четному числу. Сумма степеней вершин четной степени четна, значит, сумма степеней вершин нечетной степени также четна, значит, их четное число. Пусть N(p) – множество всех графов с p вершинами, а E(p) – множество всех эйлеровых графов с p вершинами

Теорема. Эйлеровых графов почти нет, т. е

Задача почтальона

Неформальная постановка задачи звучит следующим образом: почтальон должен обойти все улицы по крайней мере один раз и вернуться в начальную точку, при этом его маршрут должен быть как можно более коротким. На языке теории графов ставится задача поиска кратчайшего замкнутого маршрута, содержащего все ребра взвешенного графа. Если граф является эйлеровым, решением задачи почтальона будет эйлеров цикл

при этом существуют

. Задача почтальона для не ориентированных графов
Задача почтальона для ориентированных графов
Задача почтальона для смешаных графов

Смешаный граф – граф, в котором часть ребер ориентирована, а часть – не ориентирована. Для смешаных графов возможны случаи:

1) граф четный, симметричный;
2) граф четный, несимметричный;
3) граф нечетный, несимметричный.

В первом случае оптимальным решением является эйлеров маршрут, который представляет собой объединение двух маршртов: эйлерова контура для ориентированной и эйлерова цикла для не ориентированной частей графа. Во втором случае неориентированные ребра ориентируются, в результате граф преобразуется в четный ориентированный граф. Однако из-за произвольности выбора направляния обхода неориентированных ребер возникает необходимость корректировки направлений некоторых из них.

Вау!! 😲 Ты еще не читал? Это зря!

Гамильтонов цикл
Граф (математика)
Задача о ходе коня
Дискретная математика
Проблема семи мостов Кенигсберга
Список объектов, названных в честь Леонарда Эйлера
Гамильтоновы графы
Покрытие ребер графа путями
Произвольно вычерчиваемые из заданной вершины графы

Напиши свое отношение про эйлеров цикл. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое эйлеров цикл, эйлеров граф, эйлеров цепь, эйлеров путь, полуэйлеровый граф, квазиэйлеровый граф
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.

Источник