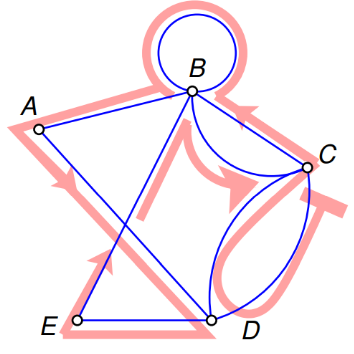
Как найти эйлеровы циклы - Исправление недочетов и поиск решений вместе с Examum.ru

Определение. Эйлеров путь — это путь в графе, проходящий через все его рёбра.

Определение. Эйлеров цикл — это эйлеров путь, являющийся циклом.

Для простоты в обоих случаях будем считать, что граф неориентированный.

Граф на пяти вершинах и один из его эйлеровых циклов: CDCBBADEBC

Также существует понятие гамильтонова пути и цикла — они посещают все вершины по разу, а не рёбра. Нахождение гамильтонова цикла (задача коммивояжера, англ. travelling salesman problem) — одна из самых известных NP-полных задач, в то время как нахождение эйлерова цика решается за линейное время, и мы сейчас покажем, как.

#Нахождение эйлерова цикла

Теорема. Эйлеров цикл существует тогда и только тогда, когда граф связный и степени всех вершин чётны.

Доказательство. Необходимость показывается так: можно просто взять эйлеров цикл и ориентировать все его ребра в порядке обхода. Тогда из каждой вершины будет выходить столько же рёбер, сколько входить, а значит степень у всех вершин исходного неориентированного графа была четной.

Достаточность докажем конструктивно — предъявим алгоритм нахождения цикла:

void euler(int v) {
    while (!g[v].empty()) {
        u = *g[v].begin(); // берем любое ребро
        remove_edge(v, u); // удаляем его
        euler(u);            // запускаемся от противоположного конца
    }
    cout << v <<  " ";     // выписываем текущую вершину
}

Заметим, что:

выведется последовательность из ровно $(m + 1)$ вершин,
между каждой соседней парой выписанных вершин есть ребро,
каждое ребро будет выписано ровно один раз.

Значит, если условия на связность и четность степеней выполняются, то выведенная последовательность вершин действительно будет эйлеровым циклом, причём и в случае ориентированного графа тоже.

#Как удалять ребра

Проще всего хранить все списки смежности в set-подобной структуре и удалять их напрямую там:

const int maxn = 1e5;
set<int> g[maxn];

void euler(int v) {
    while (!g[v].empty()) {
        u = *g[v].begin();
        g[v].erase(u);
        g[u].erase(v); // если граф ориентированный, обратное ребро удалять не надо
        euler(u);
    }
    cout << v <<  " ";
}

Это будет работать за $O(m log n)$, однако просто заменив дерево на хеш-таблицу (unordered_set) можно уменьшить время до линейного.

Также можно использовать более общий подход, который часто применяется в задачах, где ребра как-то изменяются. Создадим отдельный массив с мета-информацией о ребрах и будем хранить в списках смежности не номера вершин, а номера рёбер:

struct edge {
    int to;
    bool deleted;
};

vector<edge> edges;
stack<int> g[maxn];

void add_edge(int u, int v) {
    g[u].push(edges.size());
    edges.add({v, false});
    g[u].push(edges.size());
    edges.add({u, false});
}

Если добавлять каждое ребро неориентированного графа через add_edge, то у получившейся нумерации ребер будет интересное свойство: чтобы получить обратное к ребру e, нужно вычислить e^1.

Тогда во время обхода можно поддерживать эту информацию вместо какой-то сложной модификации структур:

void euler(int v) {
    while (!g[v].empty()) {
        e = g[v].top();
        g[v].pop();
        if (!edges[e].deleted) {
            edges[e].deleted = edges[e^1].deleted = true;
            euler(e.to);
        }
    }
    cout << v <<  " ";
}

Во всех вариантах реализации нужно быть чуть аккуратнее в случае, когда в графе есть петли и кратные ребра.

#Эйлеров путь

Поговорим теперь про эйлеровы пути. Может, всё-таки можно что-нибудь сделать, даже если степени не всех вершин чётные?

Заметим, что, так как каждое ребро меняет четность степеней ровно двух вершин, и в пустом графе все степени изначально нулевые, то число вершин с нечетными степенями будет четным.

Если нечетных вершин ровно две, то можно сделать следующее: соединить их ребром, построить эйлеров цикл (ведь теперь степени всех вершин четные), а затем удалить это ребро из цикла. Если правильно сдвинуть этот цикл, мы получили эйлеров путь.

Альтернативно, можно просто запустить обход из одной из нечетных вершин и получить такой же результат.

Если нечетных вершин больше двух, то мы уже построить эйлеров путь не сможем, потому что любой эйлеров путь входит или покидает каждую вершину четное число раз, кроме, возможно двух своих концов.

Следствие. Эйлеров путь существует тогда и только тогда, когда граф связен и количество вершин с нечётными степенями не превосходит 2.

Упражнение. Дан связный неориентированный граф. Требуется покрыть его ребра наименьшим количеством непересекающихся путей. Асимптотика $O(n + m)$.

Упражнение. Сформулируйте и докажите аналогичные утверждения для случая ориентированного графа.

Источник

import java.util.ArrayList;

import java.util.Arrays;

import java.util.List;

// Класс для хранения ребра Graph

class Edge

{

int source, dest;

public Edge(int source, int dest)

{

this.source = source;

this.dest = dest;

}

// Класс для представления graphического объекта

class Graph

{

// Список списков для представления списка смежности

List<List<Integer>> adjList;

// Конструктор

Graph(List<Edge> edges, int n)

{

adjList = new ArrayList<>();

for (int i = 0; i < n; i++) {

adjList.add(new ArrayList<>());

}

// добавляем ребра в неориентированный graph

for (Edge edge: edges)

{

adjList.get(edge.source).add(edge.dest);

adjList.get(edge.dest).add(edge.source);

}

class Main

{

// Вспомогательная функция для обхода DFS на Graphе

public static void DFS(Graph graph, int v, boolean[] discovered)

{

// помечаем текущий узел как обнаруженный

discovered[v] = true;

// делаем для каждого ребра (v, u)

for (int u: graph.adjList.get(v))

{

// если `u` еще не обнаружен

if (!discovered[u]) {

DFS(graph, u, discovered);

}

// Функция для проверки, все ли вершины с ненулевой степенью в Graph

// принадлежат одному связанному компоненту

public static boolean isConnected(Graph graph, int n)

{

// чтобы отслеживать, посещена ли вершина или нет

boolean[] visited = new boolean[n];

// запускаем поиск в глубину с первой вершины с ненулевой степенью

for (int i = 0; i < n; i++)

{

if (graph.adjList.get(i).size() > 0)

{

DFS(graph, i, visited);

break;

}

// если один вызов DFS не может посетить все вершины с ненулевой степенью,

// graph содержит более одной компоненты связности

for (int i = 0; i < n; i++)

{

if (!visited[i] && graph.adjList.get(i).size() > 0) {

return false;

}

return true;

}

// Вспомогательная функция для возврата общего количества вершин в Graph

// с нечетной степенью

public static int countOddVertices(Graph graph)

{

int count = 0;

for (List<Integer> list: graph.adjList)

{

if ((list.size() & 1) == 1) {

count++;

}

return count;

}

public static void main(String[] args)

{

// Список ребер Graph согласно приведенной выше диаграмме

List<Edge> edges = Arrays.asList(new Edge(0, 1), new Edge(0, 3),

new Edge(1, 2), new Edge(1, 3), new Edge(1, 4),

new Edge(2, 3), new Edge(3, 4));

// общее количество узлов в Graph (от 0 до 4)

int n = 5;

// создаем неориентированный graph из заданных ребер

Graph graph = new Graph(edges, n);

// проверяем, все ли вершины с ненулевой степенью принадлежат

// одиночный связный компонент

boolean is_connected = isConnected(graph, n);

// находим общее количество вершин с нечетной степенью

int odd = countOddVertices(graph);

// Эйлеров путь существует, если все вершины не нулевой степени соединены,

// и ноль или две вершины имеют нечетную степень

if (is_connected && (odd == 0 || odd == 2))

{

System.out.println(«The graph has an Eulerian path»);

// Связный graph имеет эйлеров цикл, если каждая вершина имеет

// четная степень

if (odd == 0) {

System.out.println(«The graph has an Eulerian cycle»);

}

// В Graph есть эйлеров путь, но нет эйлерова цикла

else {

System.out.println(«The Graph is Semi–Eulerian»);

}

else {

System.out.println(«The Graph is not Eulerian»);

}

Источник

Содержание

1 Алгоритм
- 1.1 Описание алгоритма
- 1.2 Псевдокод
- 1.3 Доказательство корректности
- 1.4 Рекурсивная реализация
- 1.5 Время работы
- 1.6 Рекурсивная реализация за [math]O(E)[/math]
2 См. также
3 Источники информации

Алгоритм

Описание алгоритма

Алгоритм находит Эйлеров цикл как в ориентированном, так и в неориентированном графе. Перед запуском алгоритма необходимо проверить граф на эйлеровость. Чтобы построить Эйлеров путь, нужно запустить алгоритм из вершины с нечетной степенью.
Алгоритм напоминает поиск в глубину. Главное отличие состоит в том, что пройденными помечаются не вершины, а ребра графа. Начиная со стартовой вершины строим путь, добавляя на каждом шаге не пройденное еще ребро, смежное с текущей вершиной. Вершины пути накапливаются в стеке . Когда наступает такой момент, что для текущей вершины все инцидентные ей ребра уже пройдены, записываем вершины из в ответ, пока не встретим вершину, которой инцидентны не пройденные еще ребра. Далее продолжаем обход по не посещенным ребрам.

Псевдокод

Код проверки графа на эйлеровость:

boolean checkForEulerPath():
   int OddVertex 
   for   
       if () mod 
           OddVertex++
   if OddVertex // если количество вершин с нечетной степенью больше двух, то граф не является эйлеровым
       return false
   boolean visited(, false) // массив инициализируется значениями false
   for   
       if () 
           dfs(, visited)
           break
   for   
       if ()  and not visited[]   // если количество компонент связности, содержащие ребра, больше одной,
           return false              // то граф не является эйлеровым
   return true   // граф является эйлеровым

Код построения эйлерова пути:

function findEulerPath():   // если граф является полуэйлеровым, то алгоритм следует запускать из вершины нечетной степени 
   for 
       if () mod 
           
           break
   .push()  //  — стек
   while not .empty()
        .top()
       found_edge = False
       for 
           if ()   // нашли ребро, по которому ещё не прошли
               .push()  // добавили новую вершину в стек
               .remove()
               found_edge = True
               break
       if not found_edge
           .pop()  // не нашлось инцидентных вершине  рёбер, по которым ещё не прошли
           print()

Доказательство корректности

Лемма:

Данный алгоритм проходит по каждому ребру, причем ровно один раз.

Доказательство:

Допустим, что в момент окончания работы алгоритма имеются еще не пройденные ребра. Поскольку граф связен, должно существовать хотя бы одно не пройденное ребро, инцидентное посещенной вершине. Но тогда эта вершина не могла быть удалена из стека , и он не мог стать пустым. Значит алгоритм пройдёт по всем рёбрам хотя бы один раз.

Но так как после прохода по ребру оно удаляется, то пройти по нему дважды алгоритм не может.

Вершина , с которой начат обход графа, будет последней помещена в путь . Так как изначально стек пуст, и вершина входит в стек первой, то после прохода по инцидентным ребрам, алгоритм возвращается к данной вершине, выводит ее и опустошает стек, затем выполнение программы завершается.

Лемма:

Напечатанный путь — корректный маршрут в графе, в котором каждые две соседние вершины и будут образовывать ребро .

Доказательство:

Будем говорить, что ребро представлено в или , если в какой-то момент работы алгоритма вершины и находятся рядом. Каждое ребро графа представлено в . Рассмотрим случай, когда из в перемещена вершина , а следующей в лежит . Возможны 2 варианта:

На следующем шаге для вершины не найдётся инцидентного ребра, тогда переместят в , и ребро будет представлено в .
Иначе будет пройдена некоторая последовательность ребер , начинающаяся в вершине и проходящая по ребру . Докажем, что данный проход закончится в вершине :

Ребро не может быть инцидентно вершинам , иначе степень вершины окажется нечетной.
Предположим, что инцидентно вершине, пройденной при обходе графа из вершины . Но это неверно, так как тогда бы данные вершины пройдены ранее.

Из этого следует, что мы закончим обход в вершине . Следовательно, данная вершина первой поместится в вслед за , и ребро будет представлено в .

Теорема:

Данный алгоритм находит корректный эйлеров путь.

Доказательство:

Из предыдущих лемм следует, что — искомый эйлеров путь и алгоритм работает корректно.

Рекурсивная реализация

function findEulerPath( : Vertex):
   for   
       remove 
       findEulerPath()
   print()

Время работы

Если реализовать поиск ребер инцидентных вершине и удаление ребер за , то алгоритм будет работать за .
Чтобы реализовать поиск за , для хранения графа следует использовать списки смежных вершин; для удаления достаточно добавить всем ребрам свойство бинарного типа.

Рекурсивная реализация за

Заведём 2 массива: и
— посещено ли ребро с индексом

(массив нужен, чтобы за проверять, доступно ребро или нет)
— индекс первой вершины в списке смежных вершин, такой что ребро не посещено
(массив нужен, чтобы в среднем за находить доступное ребро)

Изначально оба массива заполнены нулями.

Граф будем хранить в виде списков смежных вершин. Для каждой вершины построим список из пар вида
— индекс ребра
— номер смежной вершины

После ввода графа нужно запустить или от любой другой вершины.

function euler():
   while (first[] < g[].size()):  //если first[] = g[].size, рёбра во все смежные вершины уже посещены
      , = g[][first[]]
      first[] += 1
      if (!vis[]):
         vis[] = true
         euler()
         print()

См. также

Гамильтоновы графы
Покрытие рёбер графа путями
Произвольно вычерчиваемые из заданной вершины графы

Источники информации

Википедия — Эйлеров цикл
Статья про нахождение Эйлерова пути с реализацией на С++ на сайте e-maxx.ru
Статья про нахождение Эйлерова пути с реализацией на Pascal на сайте ивтб.рф
Видео-лекция А.С.Станкевича про нахождение Эйлерова цикла с реализацией на C++ на сайте youtube.com

Источник

Эйлеров путь и цикл

Эйлеров путь(цепь) проходит через каждое ребро графа ровно по одному разу.

Эйлеров цикл — это замкнутый путь, проходящий через каждое ребро графа ровно по одному разу.

Алгоритм поиска Эйлеров цикла

Сервис использует алгоритм поиска Эйлеров цикла на основе циклов.

Будем рассматривать самый общий случай — случай ориентированного мультиграфа, возможно, с петлями. Также мы предполагаем, что эйлеров цикл в графе существует (и состоит хотя бы из одной вершины). Для поиска эйлерова цикла воспользуемся тем, что эйлеров цикл — это объединение всех простых циклов графа. Следовательно, наша задача — эффективно найти все циклы и эффективно объединить их в один.

Кроме того, перед поиском цикла проверяется его существование, для этого происходит поиск степени вершин.

Более подробно вы можете узнать об этом алгоритме
в Википедии.

Реализацию алгоритма на языке C++ вы можете найти в нашем репозитории на GitHub: Реализация поиска Эйлерового цикла в Graphoffline.

Алгоритм поиска Эйлервой цепи

Для поиска Эйлеров пути мы добавляем псевдо ребро соединяющие начальную и конечную вершину Эйлерова пути.

Начальная и конечная вершина для неориентированного графа будет иметь нечётные степени.

Для ориентированного графа начальная вершина имеет полустепень исхода на единицу больше полустепени захода. Для конечной вершины полустепень исхода на единицу меньше полустепени захода.

Как использовать

Создайте граф.
Выберите пункт меню Алгоритмы -> «Найти Эйлеров цикл» для поиска Эйлеров цикл.

Выберите пункт меню Алгоритмы -> «Найти Эйлерову цепь» для поиска Эйлеровой цепи.

Источник

Эйлеров цикл: определение, условие существования, алгоритм нахождения

Эйлеров
путь (эйлерова цепь) в графе — это путь,
проходящий по всем рёбрам графа и притом
только по одному разу.

Эйлеров
цикл — это эйлеров путь, являющийся
циклом, то есть замкнутый путь, проходящий
через каждое ребро графа ровно по одному
разу.

Условие
существования:

В
неориентированном графе эйлеров цикл
существует тогда и только тогда, когда
граф связный или будет являться связным,
если удалить из него все изолированные
вершины, и в нём отсутствуют вершины
нечётной степени.

В
ориентированном графе эйлеров цикл
существует тогда и только тогда, когда
он сильно связан (то есть из любой
вершины графа существует ориентированный
путь в любую другую) или среди его
компонент сильной связности только
одна содержит ребра (а все остальные
являются изолированными вершинами) и
для каждой вершины графа её входящая
степень любой вершины равна её выходной
степени.

Алгоритм
нахождения:

Для
поиска эйлерова цикла воспользуемся
тем, что эйлеров цикл — это объединение
всех простых циклов графа. Следовательно,
задача — эффективно найти все циклы
и эффективно объединить их в один.

Реализовать
это можно, например, так, рекурсивно:

procedure
FindEulerPath (V)

1.
перебрать все рёбра, выходящие из
вершины V; каждое такое ребро удаляем
из графа, и вызываем FindEulerPath из второго
конца этого ребра;

2.
добавляем вершину V в ответ.

Сложность
полученного алгоритма — O(M), то есть
линейная относительно количества рёбер
М в данном графе.

Гамильтонов цикл: определение, алгоритм нахождения на основе динамического программирования

Гамильтонов
цикл – цикл проходящий через каждую
вершину графа ровно один раз. Граф
который имеет гамильтонов цикл называется
гамильтонов граф.

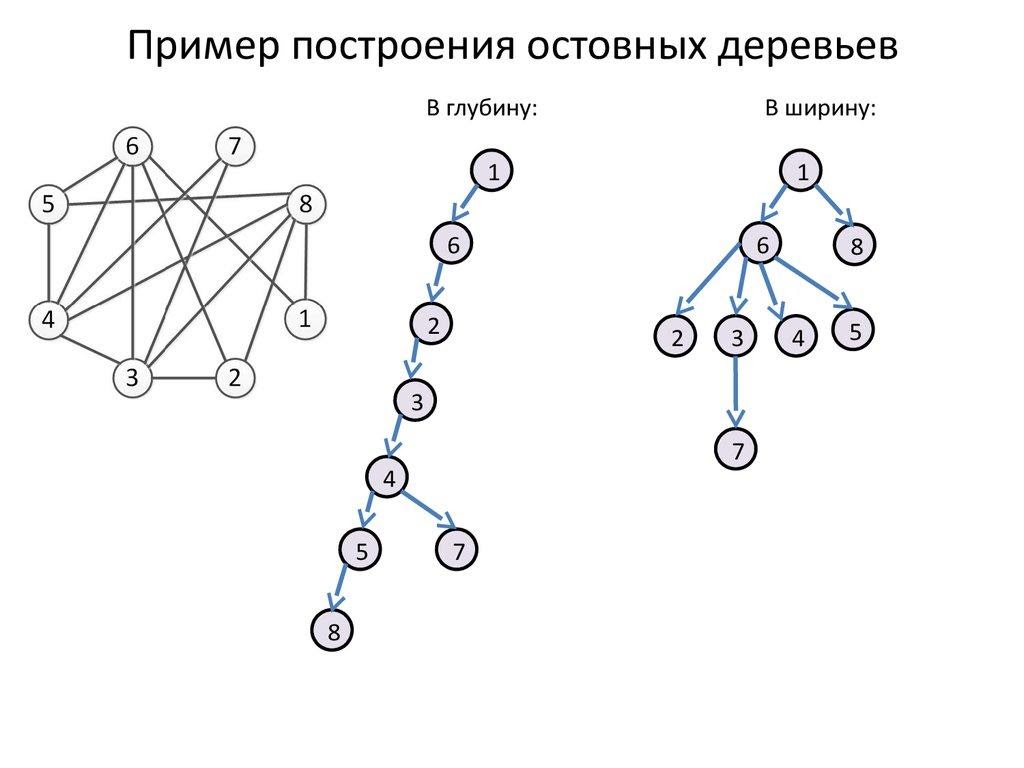
Деревья: остовное дерево, алгоритм Крускала

Остовное
дерево — ациклический связный подграф
данного связного неориентированного
графа, в который входят все его вершины.

Понятие
остовный лес неоднозначно, под ним
могут понимать один из следующих
подграфов:

любой
ациклический подграф, в который входят
все вершины графа, но не обязательно
связный;
в
несвязном графе — подграф, состоящий
из объединения остовных деревьев для
каждой его компоненты связности.

Остовное
дерево также иногда называют покрывающим
деревом, остовом или скелетом графа.
Ударение в слове «остовный» у разных
авторов указывается на первый (от слова
о́стов) или на второй слог.

П
ример
минимального остовного дерева.

Свойства

Любое
остовное дерево в графе с n вершинами
содержит ровно n-1 ребро.

Число
остовных деревьев в полном графе на n
вершинах равно n^{n-2}; это утверждение
называется формулой Кэли

Число
остовных деревьев в полном двудольном
графе Km.n
равно mn-1*nm-1

В
общем случае, число остовных деревьев
в произвольном графе может быть вычислено
при помощи так называемой матричной
теоремы о деревьях.

Остовное
дерево может быть построено практически
любым алгоритмом обхода графа, например
поиском в глубину или поиском в ширину.
Оно состоит из всех пар рёбер u,v), таких,
что алгоритм, просматривая вершину u,
обнаруживает в её списке смежности
новую, не обнаруженную ранее вершину
v.

Остовные
деревья, построенные при обходе графа
алгоритмом Дейкстры, начиная из вершины
s, обладают тем свойством, что кратчайший
путь в графе из s до любой другой вершины
— это (единственный) путь из s до этой
вершины в построенном остовном дереве.

Существует
также несколько параллельных и
распределённых алгоритмов нахождения
остовного дерева. Как практический
пример распределённого алгоритма можно
привести протокол STP.

Если
каждому ребру графа присвоен вес (длина,
стоимость и т. п.), то нахождением
оптимального остовного дерева, которое
минимизирует сумму весов входящих в
него рёбер, занимаются многочисленные
алгоритмы нахождения минимального
остовного дерева.

Задача
о нахождении остовного дерева, в котором
степень каждой вершины не превышает
некоторой наперёд заданной константы
k, является NP-полной/

Алгоритм
Краскала (англ. Kruskal’s algorithm) — алгоритм
поиска минимального остовного дерева
(англ. minimum spanning tree, MST) во взвешенном
неориентированном связном графе.

Будем
последовательно строить подграф F графа
G («растущий лес»), пытаясь на каждом
шаге достроить F до некоторого MST. Начнем
с того, что включим в F все вершины графа
G. Теперь будем обходить множество E(G)
в порядке неубывания весов ребер. Если
очередное ребро e соединяет вершины
одной компоненты связности F, то
добавление его в остов приведет к
возникновению цикла в этой компоненте
связности. В таком случае, очевидно, e
не может быть включено в F. Иначе e
соединяет разные компоненты связности
F, тогда существует ⟨S,T⟩
разрез такой, что одна из компонент
связности составляет одну его часть,
а оставшаяся часть графа — вторую.
Тогда e — минимальное ребро, пересекающее
этот разрез. Значит, из леммы о безопасном
ребре следует, что e является безопасным,
поэтому добавим это ребро в F. На последнем
шаге ребро соединит две оставшиеся
компоненты связности, полученный
подграф будет минимальным остовным
деревом графа G. Для проверки возможности
добавления ребра используется система
непересекающихся множеств.

Соседние файлы в предмете Государственный экзамен

Источник

#Нахождение эйлерова цикла

#Как удалять ребра

#Эйлеров путь

Содержание

Алгоритм

Описание алгоритма

Псевдокод

Доказательство корректности

Рекурсивная реализация

Время работы

Рекурсивная реализация за

См. также

Источники информации

Эйлеров путь и цикл

Алгоритм поиска Эйлеров цикла

Алгоритм поиска Эйлервой цепи

Как использовать

Эйлеров цикл: определение, условие существования, алгоритм нахождения

Гамильтонов цикл: определение, алгоритм нахождения на основе динамического программирования

Деревья: остовное дерево, алгоритм Крускала