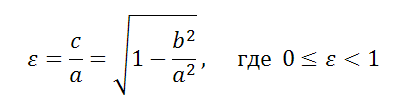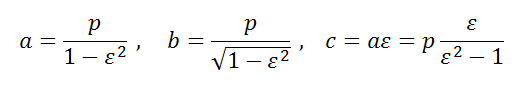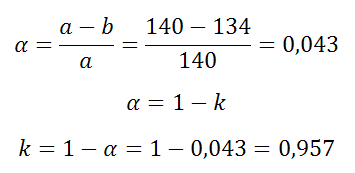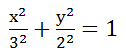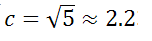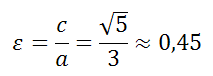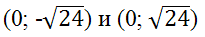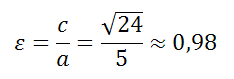| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
эксцентриситет:9x^2+4y^2=1
-
эксцентриситет:16x^2+25y^2=100
-
эксцентриситет:25x^2+4y^2+100x-40y=400
-
эксцентриситет:frac{(x-1)^2}{9}+frac{y^2}{5}=100
- Показать больше
Описание
Пошаговый расчет эксцентриситета эллипса по заданному уравнению
ellipse-function-eccentricity-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
My Notebook, the Symbolab way
Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Онлайн калькуляторы
Calculatorium.ru — это бесплатные онлайн калькуляторы для самых разнообразных целей: математические калькуляторы,
калькуляторы даты и времени, здоровья, финансов. Инструменты для работы с текстом. Конвертеры. Удобное решение различных задач — в учебе, работе, быту.
Актуальная информация
Помимо онлайн калькуляторов, сайт также предоставляет актуальную информацию по курсам валют и
криптовалют, заторах на дорогах, праздниках и значимых событиях, случившихся в этот день.
Информация из официальных источников, постоянное обновление.
Here is a simple calculator to solve ellipse equation and calculate the elliptical co-ordinates such as center, foci, vertices, eccentricity and area and axis lengths such as Major, Semi Major and Minor, Semi Minor axis lengths from the given ellipse expression. An ellipse is a figure consisting of all points for which the sum of their distances to two fixed points, (foci) is a constant.
Solve Ellipse Equation
Here is a simple calculator to solve ellipse equation and calculate the elliptical co-ordinates such as center, foci, vertices, eccentricity and area and axis lengths such as Major, Semi Major and Minor, Semi Minor axis lengths from the given ellipse expression. An ellipse is a figure consisting of all points for which the sum of their distances to two fixed points, (foci) is a constant.
Code to add this calci to your website 
Solving Ellipse Equation is just the inverse of finding the ellipse expression from the given elliptical co-ordinates such as center, foci, vertices, eccentricity and area.
Эксцентриситет эллипса Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Малая полуось эллипса: 6 метр —> 6 метр Конверсия не требуется
Большая полуось эллипса: 10 метр —> 10 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.8 метр —> Конверсия не требуется
8 Эксцентриситет эллипса Калькуляторы
4 Эксцентриситет и линейный эксцентриситет эллипса Калькуляторы
Эксцентриситет эллипса формула
Эксцентриситет эллипса = sqrt(1-(Малая полуось эллипса/Большая полуось эллипса)^2)
e = sqrt(1-(b/a)^2)
Что такое эллипс?
Эллипс в основном представляет собой коническое сечение. Если мы разрезаем прямой круговой конус плоскостью под углом, большим, чем полуугол конуса. Геометрически эллипс — это совокупность всех точек на плоскости, сумма расстояний до которых от двух фиксированных точек является константой. Эти фиксированные точки являются фокусами эллипса. Наибольшая хорда эллипса является большой осью, а хорда, проходящая через центр и перпендикулярно большой оси, является малой осью эллипса. Окружность является частным случаем эллипса, в котором оба фокуса совпадают в центре, и поэтому обе большие и малые оси становятся равными по длине, которая называется диаметром окружности.
Эллипс
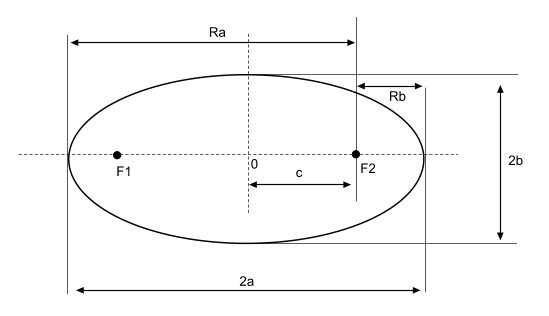
Эллипс – геометрическое место точек M(x;y), сумма расстояний которых до двух данных точек F1F2 имеет одно и то же значение 2a:
точки F1 и F2 – называются фокусами эллипса;
расстояние F1F2 – фокусное расстояние и равно F1F2=2с;
a — большая полуось;
b — малая полуось;
c — фокальный радиус, то есть полу расстояние между фокусами;
p — фокальный параметр;
Rmin – минимальное расстояние от фокуса до точки на эллипсе;
Rmax — максимальное расстояние от фокуса до точки на эллипсе;
Каноническое уравнение эллипса
где
Фокальный параметр находится
 Коэффициент сжатия эллипса (эллиптичность):
Коэффициент сжатия эллипса (эллиптичность):
Сжатие эллипса
Коэффициент сжатия и эксцентриситет эллипса связаны соотношением
 Эксцентриситет эллипса
Эксцентриситет эллипса
Полуоси a, b и полуфокусное расстояние c эллипса выражаются через ε следующим образом
Длина малой оси эллипса 134 м. Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса
Постройте кривую 4x 2 +9y 2 =36. Найдите фокусы, фокальный параметр и эксцентриситет.
Делим обе части на 36 и получаем каноническое уравнение эллипса
a=3, b=2
c 2 =a 2 -b 2 =3 2 -2 2 =9-4=5
Отсюда находим Фокусы F1(-2,2;0) F2(2,2;0)
Фокальный параметр находим следующим образом 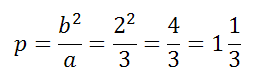
Эксцентриситет эллипса
Пример 3
Постройте кривую 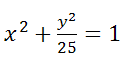
Решение
Уравнение запишем в виде 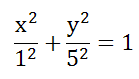
a=1, b=5
Это уравнение не является каноническим уравнением эллипса, так как b>a, а должно быть b c 2 =a 2 − b 2 =5 2 −1 2 =25 − 1=24
Следовательно, фокусы в системе координат (x’;y’) имеют координаты (-4,9;0) и (4,9;0), а в системе (x;y) координаты
Эксцентриситет эллипса равен
Каноническое уравнение эллипса по двум точкам
| Две точки с координатами |
| Первая координата |
| Вторая координата |
| Каноническое уравнение эллипса |
| Большая полуось эллипса |
| Малая полуось эллипса |
| Эксцентриситет эллипса |
| Фокусное/фокальное расстояние |
| Коэффициент сжатия |
| Координаты первого фокуса F1(x1:y1) |
| Координаты второго фокуса F2(x2:y2) |
| Фокальный параметр |
| Перифокусное расстояние |
| Апофокусное расстояние |
Уравнение эллипса в каноническом виде имеет вот такой вид.
Так как тут всего две переменных, то логично предположить, что по двум заданным точкам мы всегда сможем построить формулу эллипса.
Для расчета поставленной задачи воспользуемся материалом расчет кривой второго порядка на плоскости, который и позволит легко и быстро получить результат.
Кроме этого, на этой странице мы получим следующую информацию.
Фокальный параметр — половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса
Значение полуосей — большая полуось и малая полуось ( Естественно это в том случае, когда эллипс вытянут вдоль оси абсцисс)
Эксцентриситет — коэффициент, показывающий насколько его фигура отличается от окружности
Фокальное расстояние
Коэффициент сжатия — отношение длин малой и большой полуосей
Примеры задач
Cоставить каноническое уравнение эллипса по двум точкам
Ввводим данные в калькулятор, не забывая что квадратный корень у нас обозначается sqrt
и получаем результат
| Каноническое уравнение эллипса | |||
| Большая полуось эллипса | |||
| Малая полуось эллипса | |||
| Эксцентриситет эллипса | |||
| Фокусное/фокальное расстояние | |||
| Коэффициент сжатия | |||
| Координаты первого фокуса F1(x1:y1) | |||
| Координаты второго фокуса F2(x2:y2) | |||
| Фокальный параметр | |||
| Перифокусное расстояние | |||
| Апофокусное расстояние | |||
|
И еще один пример Даны две точки с координатами (3:2) и (4:-9) построить каноническое уравнение эллипса. Если мы введем данные в калькулятор получим
|




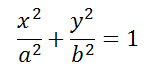
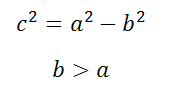
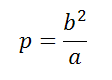 Коэффициент сжатия эллипса (эллиптичность):
Коэффициент сжатия эллипса (эллиптичность):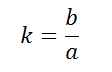

 Эксцентриситет эллипса
Эксцентриситет эллипса