-
Основные
определения
Граф
– это совокупность двух множеств: вершин
и ребер
,
между которыми определено отношениеинцидентности.
Каждое ребро e
из E
инцидентно ровно двум вершинам
и
,
которые оно соединяет. При этом вершинаи реброe
называются инцидентными
друг другу, а вершины
и
называютсясмежными.
Принято обозначение
n
для числа вершин графа (мощность множества
):
иm
для числа его ребер:
.
Говорят, что графG
есть (n,
m)
граф, где n
– порядок графа, m
– размер графа.
Если все ребра
графа неориентированные, т.е. пары
вершин, определяющие элементы множестваE,
неупорядочены, то такой граф называется
неориентированным графом, или неографом.
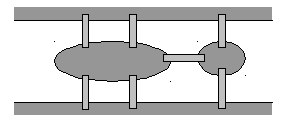
На рис. 12.1 показан пример неографа. Этот
граф имеет пять вершин и шесть ребер.
Рис. 12.1
Маршрут
– последовательность ребер, в которой
каждые два соседних ребра имеют общую
вершину. Граф связен,
если любые две вершины соединены хотя
бы одним маршрутом. Число ребер маршрута
определяет его длину.
Ребра, инцидентные
одной паре вершин, называются параллельными
или кратными.
Граф с кратными ребрами называется
мультиграфом.
Ребро
называетсяпетлей
(концевые вершины совпадают). Граф,
содержащий петли и кратные ребра,
называется псевдографом.
На рис. 12.2 показан псевдограф.
Рис. 12.2
Степень
deg(v)
вершины – это число ребер, инцидентных
v.
В неографе
сумма степеней всех вершин равна
удвоенному числу ребер
(лемма о рукопожатиях):
. (12.1)
Петля дает вклад,
равный 2, в степень вершины.
Степенная
последовательность
– последовательность степеней всех
вершин графа, записанная в определенном
порядке (по возрастанию или убыванию).
Пример
12.1. Степенная
последовательность неографа, изображенного
на рис. 12.1, записанная по возрастанию,
выглядит так:
=1,
=2,
=3,
=3,
=3.
Сумма степеней
всех вершин графа равна:
.
Этот результат
не противоречит лемме о рукопожатиях,
поскольку граф имеет шесть ребер (m
= 6).
Матрица
смежности
графа – квадратная матрица A
порядка n,
где элемент
равен числу ребер, соединяющих вершиныi
и j.
Пример 12.2.
Граф, показанный на рис. 12.1, имеет
следующую матрицу смежности
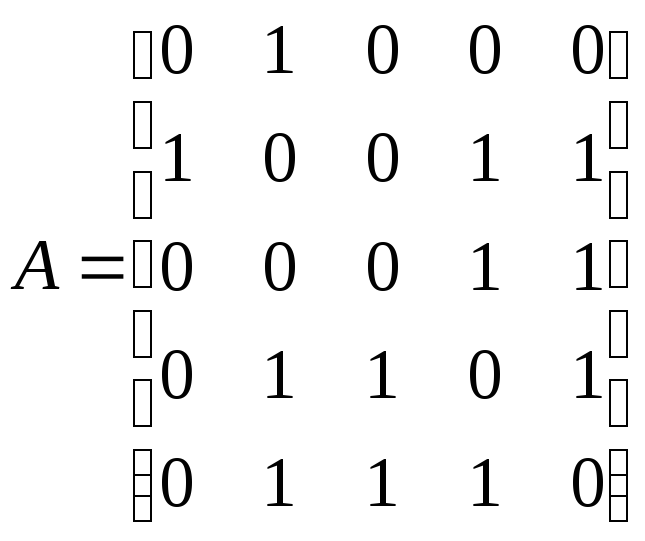
Матрица
инцидентности
I
– еще один способ описания графа. Число
строк этой матрицы равно числу вершин,
число столбцов – числу ребер;
=1,
если вершинаv
инцидентна ребру e;
в противном случае
=0.
В каждом столбце матрицы инцидентности
простого графа (без петель и без кратных
ребер) содержится по две единицы. Число
единиц в строке равно степени
соответствующей вершины.
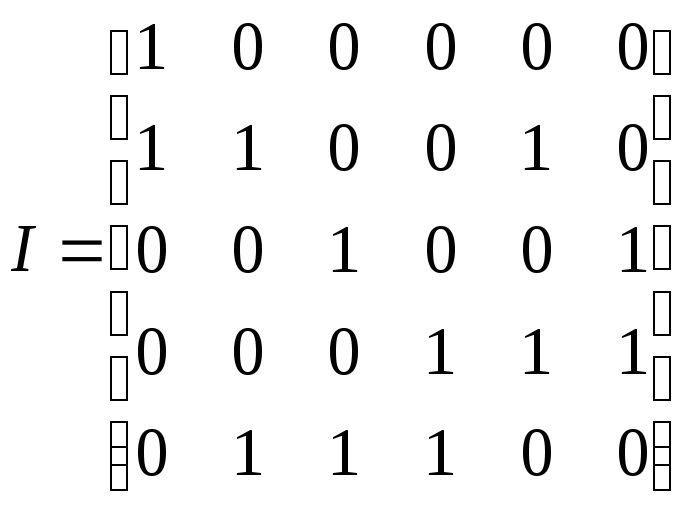
Пример 12.3.
Граф, показанный на рис. 12.1, имеет
следующую матрицу инцидентности
Граф
называетсяподграфом
графа
,
еслии
.
Если,
то подграф называетсяостовным.
Компонента
связности
графа – максимальный по включению
вершин и ребер связной подграф.
Ранг
графа
,
гдеk
– число компонент связности.
Дерево
– связной граф, содержащий n
– 1 ребро.
Пример 12.4.
На рис. 12.3 показано дерево, которое
одновременно является остовным подграфом
графа, показанного на рис. 12.1.
Рис. 12.3
-
Радиус, диаметр
и центр графа
Вычисление
расстояний и определение маршрутов в
графе являются одной из наиболее
очевидных и практичных задач, которые
возникают в теории графов. Введем
некоторые необходимые определения.
Эксцентриситет
вершины графа – расстояние до максимально
удаленной от нее вершины. Для графа, для
которого не определен вес
его ребер, расстояние определяется в
виде числа ребер.
Радиус
графа – минимальный эксцентриситет
вершин, а диаметр
графа – максимальный эксцентриситет
вершин.
Центр
графа образуют вершины, у которых
эксцентриситет равен радиусу. Центр
графа может состоять из одной, нескольких
или всех вершин графа.
Периферийные
вершины имеют эксцентриситет, равный
диаметру.
Простая цепь с
длиной, равной диаметру графа, называется
диаметральной.
Теорема 12.1.
В связном графе диаметр не больше ранга
его матрицы смежности.
Теорема 12.2.
(Жордана) Каждое дерево имеет центр,
состоящий из одной или двух смежных
вершин.
Теорема 12.3.
Если диаметр дерева четный, то дерево
имеет единственный центр, и все
диаметральные цепи проходят через него,
если диаметр нечетный, то центров два
и все диаметральные цепи содержат ребро,
их соединяющее.
Очевидно практическое
значение центра графа. Если, например,
речь идет о графе дорог с вершинами-городами,
то в математическом центре целесообразно
размещать административный центр,
складские помещения и т.п. Этот же подход
можно применять и для взвешенного графа,
где расстояния – это веса ребер. В
качестве веса можно брать евклидовое
расстояние, время или стоимость
передвижения между пунктами.
Пример 12.5.
Найти радиус, диаметр и центр графа,
изображенного на рис. 12.1.
Решение.
В данной задаче удобно использовать
матрицу
расстояний S.
Элемент этой квадратной симметричной
матрицы
равен расстоянию между вершинойi
и вершиной j.
Для графа, показанного на рис. 12.1, матрица
расстояний имеет следующий вид:

Вычислим
эксцентриситет
каждой вершины. Эту величину можно
определить как максимальный элемент
соответствующего столбца матрицы
расстояний (или строки – поскольку
матрицаS
симметрична).
Получаем
|
№ |
1 |
2 |
3 |
4 |
5 |
|
|
3 |
2 |
3 |
2 |
2 |
Радиус графа r
– минимальный эксцентриситет вершин.
В данном случае r
= 2. Такой эксцентриситет имеют вершины
№ 2, № 4 и № 5. Эти вершины образуют центр
графа. Диаметр графа d
– максимальный эксцентриситет вершин.
В данном случае d
= 3. Такой эксцентриситет имеют вершины
№ 1 и № 3, это периферия графа. В
исследованном графе вершины оказались
либо центральными, либо периферийными.
В графах большего порядка существуют
и другие вершины.
Эксцентриситеты
вершин небольшого графа легко вычислять
непосредственным подсчетом по рисунку.
Однако не всегда граф задан своим
рисунком. Кроме того, граф может иметь
большой размер. Поэтому необходим другой
способ решения предыдущей задачи.
Известна следующая теорема.
Теорема
12.4. Пусть
– матрица смежности графаG
без петель и
,
где.
Тогдаравно числу маршрутов длиныk
от вершины
к вершине
.
Решение задач
теории графов с помощью различных
преобразований матрицы смежности
называют алгебраическим
методом.
Пример 12.6.
Найти матрицу расстояний графа,
изображенного на рис. 12.1, алгебраическим
методом.
Решение.
Матрица смежности данного графа равна:

Будем заполнять
матрицу расстояний, рассматривая степени
матрицы смежности. Единицы матрицы
смежности показывают пары вершин,
расстояние между которыми равно единице
(т.е. они соединены одним ребром).

Диагональные
элементы матрицы расстояний – нули.
Умножаем матрицу смежности на себя:

Согласно теореме
между вершинами 2 и 3, 1 и 4 и т.д. имеется
некоторое число маршрутов длиной 2
(поскольку степень матрицы равна двум).
Число маршрутов здесь не используется,
важен сам факт наличия маршрута и его
длина, на что и указывает ненулевой
элемент степени матрицы, не совпадающий
с элементом, отмеченным при вычислении
маршрута меньшей длины. Проставляем 2
в незаполненные элементы матрицы
расстояний и получаем следующее
приближение:

Осталось неизвестным
расстояние между вершинами 1 и 3. Будем
умножать матрицу смежности
саму на себя до тех пор, пока в матрице
не появится ненулевой элемент
.
Тогда соответствующий элемент матрицы
расстояний равен степени матрицы
смежности:
.
На следующем шаге получаем

следовательно,
,
и окончательно

Полученная матрица
совпадает с матрицей расстояний S
(12.2), найденной непосредственными
вычислениями по рисунку.
-
Эйлерова цепь
Маршрут в неографе,
в котором все ребра разные, называется
цепью.
Цепь в графе называется эйлеровой,
если она содержит все ребра и все вершины
графа.
Рис. 12.4. Схема
Кенигсбергских мостов
Теория графов
многократно переоткрывалась разными
авторами при решении различных прикладных
задач. В их ряду – знаменитый математик
Леонард Эйлер (1707-1783). К созданию теории
графов его подтолкнула задача о
Кенигсберских мостах, которую он решил
в 1736 году. По условию задачи требовалось
пройти по всем семи мостам города
Кенигсберга через реку Преголь по одному
разу и вернуться к исходной точке. На
рис. 12.4 показана схема этих мостов (один
из них соединяет между собой два острова,
а остальные – острова с берегами). Этой
схеме соответствует приведенный на
следующем рисунке мультиграф с четырьмя
вершинами.
Рис. 12.5
Эйлер решил задачу
о Кенигсбергских мостах в отрицательном
смысле. Он доказал, что данная задача
не имеет решения. Для этого ему пришлось
доказать следующую теорему.
Теорема 12.5
(Эйлера).
Мультиграф обладает эйлеровой цепью
тогда и только тогда, когда он связен и
число вершин нечетной степени равно 0
или 2.
Вершины нечетной
степени в этой теореме, очевидно, являются
началом и концом цепи. Если таких вершин
нет, то эйлерова цепь становится эйлеровым
циклом.
Граф, обладающий эйлеровым циклом,
называется эйлеровым.
Если граф имеет эйлерову цепь, но не
обладает эйлеровым циклом (число вершин
нечетной степени равно 2), то он называется
полуэйлеровым
графом.
Предположим, что
граф имеет эйлеров цикл. Двигаясь по
нему, будем подсчитывать степени вершин,
полагая их до начала прохождения
нулевыми. Прохождение каждой вершины
вносит 2 в степень этой вершины. Поскольку
эйлеров цикл содержит все ребра, то
когда обход будет закончен, будут учтены
все ребра, а степени вершин – четные.
Все четыре вершины
мультиграфа, показанного на рис. 12.5,
имеют нечетные степени. Поэтому этот
граф не обладает эйлеровым циклом, а
задача о Кенигсбергских мостах не имеет
решения.
Рассмотрим для
сравнения граф, обладающий эйлеровой
цепью. В графе на рис. 12.6 только две
вершины имеют нечетную степень,
следовательно, эйлерова цепь есть.
Рис. 12.6
Цепей может быть
несколько. Например, граф на рис. 12.6
имеет две эйлеровы цепи: 1-2-3-4-1-3 и
1-2-3-1-4-3.
-
Реберный граф
Рассмотрим два
графа G
и L(G).
Граф G
имеет произвольную форму, а вершины
графа L(G)
расположены на ребрах графа G.
В этом случае граф L(G)
называется реберным
графом по
отношению к графу G.
Английское название
реберного графа – line
graph,
отсюда и обозначение графа – L(G).
На рис. 12.7 показан реберный граф (он
выделен жирными линиями), построенный
для графа с рис. 12.1.
Рис. 12.7. Реберный
граф
Теорема 12.6.
Если
– степенная последовательность (n,
m)
графа G,
то L(G)
является (m,
)-графом,
где
. (12.3)
Для графа G,
показанного на рис. 12.7 (и рис. 12.1), его
степенная последовательность: 1-3-2-3-3.
Поэтому
.
-
Раскраска графа,
хроматический полином
Предположим, что
перед нами стоит задача: раскрасить
карту мира так, чтобы каждая страна
имела свой собственный цвет. Поскольку
на свете существует несколько сотен
государств, то, естественно, потребуется
достаточно много разных красок.
Упростим задачу.
Будем использовать меньшее количество
красок, но при этом не будем допускать,
чтобы соседние страны, имеющие общие
границы, были окрашены в один цвет.
Возникает вопрос: какое минимальное
количество красок требуется, чтобы
удовлетворить этому условию?
Ответить на этот
вопрос можно с помощью теории графов.
Для этого нужно представить карту мира
в виде графа, каждая вершина которого
соответствует отдельной стране, а ребро
между смежными вершинами соответствует
наличию между странами общей границы.
Произвольная
функция
на множестве вершин графа называется
раскраской
графа. Раскраска называется правильной,
если
для любых смежных вершин
и
.
Минимальное числоk,
при котором граф G
является k-раскрашиваемым
называется хроматическим
числом
графа
.
Граф называется
пустым,
если в нем удалены все ребра и вершины
изолированы друг от друга. Граф называется
полным,
если в нем нельзя добавить новое ребро,
не добавив при этом одновременно новую
вершину.
Теорема 12.7
(Брукса).
Для любого графа G,
не являющегося полным,
,
если–максимальная
из степеней вершин графа.
Для определения
количества способов раскраски графа в
x
цветов, необходимо составить хроматический
полином
P(G,
x).
Значение полинома при некотором
конкретном
равно числу правильных раскрасок графа
вцветов.
Существует лемма,
утверждающая, что хроматический
полином графа имеет вид
,(12.4)
где
– граф, полученный изG
добавлением ребра (u,
v),
а граф
получается изG
отождествлением вершин u
и v.
Другой вариант
леммы:
, (12.5)
где
– граф, полученный изG
удалением ребра (u,
v),
а граф
получается изG
отождествлением вершин u
и v.
Операцию
отождествления вершин u
и
v
называют также стягиванием ребра (u,
v).
Оба варианта леммы
составляют основу для хроматической
редукции графа (reduction
– «сокращение» на английском).
Хроматическая редукция графа –
представление графа в виде нескольких
пустых или полных графов, сумма
хроматических полиномов которых равна
хроматическому полиному графа. Очевидно,
что хроматический полином пустого графа
равен
(каждая вершина может быть раскрашена
независимо от других), а для полного
графа.
Последнее выражение называютфакториальной
степенью
переменной x:
.
Разложения по
пустым и полным графам связаны.
Факториальную степень можно представить
в виде полинома:
, (12.6)
где
– числа Стирлинга первого рода. И
наоборот, степеньможно выразить через факториальные
степени:
, (12.7)
где
– числа Стирлинга второго рода, обладающие
следующими свойствами:
при
, (12.8)
при
,
при
.
При получении
хроматического полинома могут быть
полезны следующие теоремы.
Теорема 12.8.
Коэффициенты хроматического полинома
составляют знакопеременную
последовательность.
Теорема 12.9.
Абсолютная величина второго коэффициента
хроматического полинома равна числу
ребер графа.
Теорема 12.10.
Наименьшее число i,
для которого отличен от нуля коэффициент
при
в хроматическом полиноме графа G,
равно числу компонент связности графа
G.
Кроме вершинной
раскраски, существует еще реберная
раскраска и раскраска граней.
Пример 12.7.
Найти хроматический полином графа,
показанного на рис. 12.8.
Рис. 12.8
Решение.
В зависимости от числа ребер графа можно
использовать разложение (12.4) или (12.5).
Если граф почти полный, то, добавив
несколько ребер по разложению (12.4),
получим хроматический полином в виде
суммы факториальных степеней. Если же
ребер мало и для получения пустого графа
требуется удалить только несколько
ребер, то следует использовать разложение
(12.5) с удалением ребер. Такие действия
называются хроматической редукцией.
1. Хроматическая
редукция по пустым графам.
Воспользуемся вначале леммой (12.5). Удаляя
ребра и отождествляя соответствующие
вершины (стягивая ребра), сведем исходный
граф к пустым графам. Сначала разложим
граф на два, убрав, а затем стянув ребро
1-3. Выполненное действие запишем в виде
условного равенства:
Здесь
операция вычитания относится не к самому
графу, а к его хроматическому полиному.
Таким образом, последнее равенство
означает, что
.
Для сокращения записи обозначениеP(…)
будем опускать. Далее разложим каждый
из графов
и
,
пользуясь той же леммой.
Приведем подобные
члены:
(12.9)
В итоге получим
искомый хроматический полином:
. (12.10)
Разложение (12.9)
называется хроматической редукцией
графа по пустым графам.
Очевидно, что
результат соответствует утверждениям
теорем 12.8-12.10. Коэффициенты в (12.10) образуют
знакопеременную последовательность,
а коэффициент при
равен четырем – числу ребер. Наименьшая
степеньx
в полиноме равна 1, т.е. числу компонент
связности графа.
2. Хроматическая
редукция по полным графам.
Добавив к изображенному на рис. 12.8 графу
ребро 1–4, получим граф с большим числом
ребер. Затем в исходном графе отождествим
вершины 1 и 4. В результате получим два
графа.
Отождествление
вершин приводит к уменьшению порядка
и иногда размера графа. Второй граф –
это полный граф
,
его преобразовывать больше не требуется.
К первому графу добавим ребро 1–2 и
отождествим вершины 1 и 2:
В итоге получим

Хроматический
полином примет вид
(12.12)
Разложение (12.11)
называется хроматической редукцией
графа по полным графам.
Оба способа дали
один результат, и из редукции по полным
графам легко получить редукцию по
пустым. Для этого достаточно раскрыть
скобки и привести подобные члены, как
в (12.12). Однако обратное действие не
очевидно. Для того чтобы полином
,
полученный из пустых графов, выразить
в виде суммы факториальных степеней,
необходимы числа Стирлинга 2-го рода.
Согласно рекуррентным формулам (12.8)
имеем следующие числа:
,
,
,
.
Пользуясь (12.7) и
найденными числами Стирлинга 2-го рода,
получим
,
,
.
Произведем
преобразование хроматического полинома:
Хроматическое
число
графа лучше всего получить, разложив
хроматический полином на множители:
.
Минимальное
натуральное число x,
при котором
не обращается в нуль, равно 3. Отсюда
следует.
Так как максимальная степень вершин
графа,
выполняется оценка.
-
Ранг-полином
графа
Ранг графа
определяется как
,
гдеn
– число вершин, k
– число компонент связности графа.
Коранг графа, или цикломатический ранг,
есть
,
гдеm
– число ребер.
Ранг-полином графа
G
имеет вид
,
где
– ранг графаG
, а
– корангостовного
(т.е. включающего в себя все вершины
графа) подграфа H,
а
– его ранг. Суммирование ведется по
всем остовным подграфам графаG.
Ранг полином
служит для анализа множества остовных
подграфов. Так, например, коэффициент
при
в
есть число подграфов размераk,
а значение
равно числу подграфов (включая
несобственный подграф), ранг которых
равен рангу самого графа.
Пример
12.8. Найти
ранг-полином графа, изображенного на
рис. 12.8.
Решение.
Найдем все 16 остовных подграфов графа
G
(рис. 12.9). Множество представим в виде
четырех графов размера 1 (т.е. с одним
ребром), шести графов размера 2, четырех
графов размера 3 и двух несобственных
графов (пустой граф и граф G).
Рис. 12.9
Учитывая, что ранг
графа равен 3, получаем сумму:
-
Циклы
Маршрут, в котором
начало и конец совпадают, – циклический.
Циклический маршрут называется циклом,
если он – цепь.
Остовом
графа G
называется граф, не содержащий циклов
и состоящий из ребер графа G
и всех его вершин. Остов графа определяется
неоднозначно.
Ребра графа, не
входящие в остов, называются хордами.
Цикл, получающийся при добавлении к
остову графа его хорды, называется
фундаментальным
относительно
этой хорды.
Теорема 12.11.
Число ребер неографа, которые необходимо
удалить для получения остова, не зависит
от последовательности их удаления и
равно цикломатическому рангу графа.
Пример 12.8.
По заданной матрице смежности:
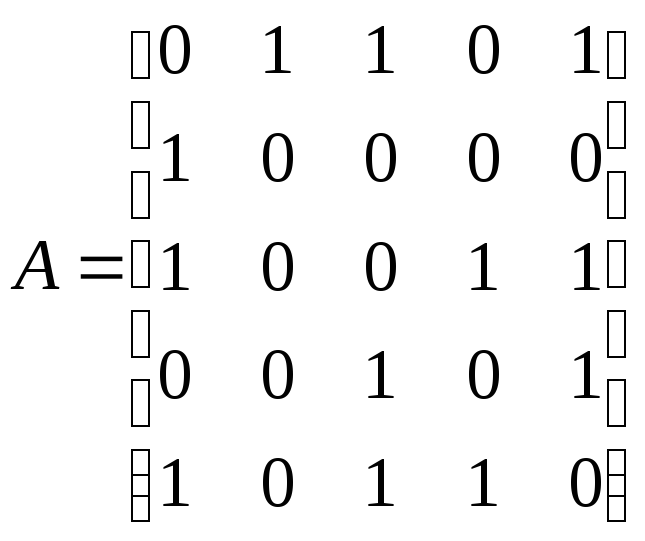
определить число
циклов длины 3 ()
и длины 4 ().
Записатьматрицу
фундаментальных циклов.
Решение.
Матрица смежности данного графа
симметричная, поэтому ей соответствует
неориентированный граф. Сумма ненулевых
элементов матрицы равна 12, следовательно,
по лемме о рукопожатиях в графе 6 ребер.
Построим этот граф (рис. 12.10). Очевидно,
в нем два цикла (3–4–5 и 1–3–5) длиной 3 и
один цикл (1–3–4–5) длиной 4. В данной
задаче решение получено прямым подсчетом
по изображению графа. Для более сложных
случаев существует алгоритм решения
задачи по матрице смежности.
Известно, что след
(trace)
матрицы смежности, возведенный в k-ю
степень, равен числу циклических
маршрутов длины k
(см. теорему 12.4). Это число включает в
себя и искомое число циклов. Цикл
отличается от циклического маршрута
тем, что в нем не повторяются ребра.
Кроме того, предполагается, что искомые
циклы не помечены, а в след матрицы
входят именно помеченные маршруты.
Рис. 12.10
Непомеченных
циклов длиной 3 в 6 раз меньше, чем
помеченных, так как каждый помеченный
цикл может отличаться началом (а их в
данном случае три) и двумя направлениями
обхода (по и против часовой стрелки).
Возведем заданную матрицу смежности в
третью степень:

и получим
.
Поскольку
циклических маршрутов длиной 3, отличных
от циклов длиной 3, не существует,
найденное число и есть ответ в поставленной
задаче.
С циклами длиной
4 немного сложнее. В след четвертой
степени матрицы смежности графа

входят не только
циклы, но и циклические маршруты с
двойным и четырехкратным прохождением
ребер. Обозначим количество таких
маршрутов через
и
соответственно. Очевидно, число маршрутов
с четырехкратным прохождением одного
ребра для вершиныравно степени этой вершины:
.
Число маршрутов с двукратным прохождением
ребра складывается из числас висячей вершиной
и числа
маршрутов с вершиной
в центре.
Легко заметить,
что
.
Числозависит от степеней вершин, соседних с
:
,
где
– ребро, инцидентное вершинамi
и k.
Для графа на рис.
12.10 получим
,
,
,
.
С учетом того, что
непомеченных циклов длиной 4 в 8 раз
меньше, получим
.
После преобразований
формула примет вид

Для нахождения
матрицы фундаментальных циклов
пронумеруем ребра графа, начиная
нумерацию с хорд, как показано на рис.
12.11 (а).
Рис. 12.11
Двум хордам, 1 и 2,
соответствуют два фундаментальных
цикла: 1–4–5 и 2–4–6 (рис. 12.11 (б и в)).
Матрица фундаментальных циклов имеет
две строки (число циклов) и шесть столбцов
(число ребер).
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
2 |
0 |
1 |
0 |
1 |
0 |
1 |
В первой строке
матрицы единицами отмечены столбцы с
номерами ребер, входящих в первый цикл,
а во второй строке – номера ребер из
второго цикла.
Графы имеют различные свойства, которые используются для характеристики графов в зависимости от их структуры. Эти свойства определены в конкретных терминах, относящихся к области теории графов. В этой главе мы обсудим несколько основных свойств, которые являются общими для всех графиков.
Расстояние между двумя вершинами
Это число ребер в кратчайшем пути между вершиной U и вершиной V. Если существует несколько путей, соединяющих две вершины, то кратчайший путь рассматривается как расстояние между двумя вершинами.
Обозначение – d (U, V)
Может быть любое количество путей из одной вершины в другую. Среди них вам нужно выбрать только самый короткий.
пример
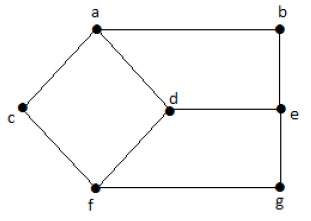
Посмотрите на следующий график –
Здесь расстояние от вершины ‘d’ до вершины ‘e’ или просто ‘de’ равно 1, поскольку между ними есть одно ребро. Существует много путей от вершины ‘d’ до вершины ‘e’ –
- да, а, бе
- дф, фг, гэ
- де (считается для расстояния между вершинами)
- дф, фц, ca, ab, be
- да, ac, cf, fg, ge
Эксцентриситет вершины
Максимальное расстояние между вершиной и всеми остальными вершинами рассматривается как эксцентриситет вершины.
Обозначение – e (V)
Расстояние от конкретной вершины до всех других вершин графа берется, и среди этих расстояний эксцентриситет является наибольшим из расстояний.
пример
На приведенном выше графике эксцентриситет «а» равен 3.
Расстояние от «a» до «b» равно 1 («ab»),
от ‘a’ до ‘c’ равно 1 (‘ac’),
от «а» до «d» равно 1 («объявление»),
от ‘a’ до ‘e’ равно 2 (‘ab’ – ‘be’) или (‘ad’ – ‘de’),
от ‘a’ до ‘f’ равно 2 (‘ac’ – ‘cf’) или (‘ad’ – ‘df’),
от ‘a’ до ‘g’ равно 3 (‘ac’ – ‘cf’ – ‘fg’) или (‘ad’ – ‘df’ – ‘fg’).
Таким образом, эксцентриситет равен 3, что является максимумом от вершины «а» от расстояния между «ag», которое является максимальным.
Другими словами,
е (б) = 3
е (с) = 3
е (д) = 2
е (е) = 3
е (е) = 3
е (г) = 3
Радиус связного графа
Минимальный эксцентриситет от всех вершин рассматривается как радиус графа G. Минимальный среди всех максимальных расстояний между вершиной до всех остальных вершин рассматривается как радиус графа G.
Обозначение – r (G)
Из всех эксцентриситетов вершин графа радиус связного графа является минимумом всех этих эксцентриситетов.
Пример – На приведенном выше графике r (G) = 2, что является минимальным эксцентриситетом для «d».
Диаметр графика
Максимальный эксцентриситет от всех вершин рассматривается как диаметр графа G. Максимальный из всех расстояний между вершиной до всех других вершин рассматривается как диаметр графа G.
Обозначение – d (G)
Из всех эксцентриситетов вершин графа диаметр связного графа является максимальным из всех этих эксцентриситетов.
Пример. На приведенном выше графике d (G) = 3; что является максимальным эксцентриситетом.
Центральная точка
Если эксцентриситет графа равен его радиусу, то он называется центральной точкой графа. Если
e (V) = r (V),
тогда «V» является центральной точкой графа «G».
Пример – в примере графика ‘d’ является центральной точкой графика.
e (d) = r (d) = 2
Центр
Множество всех центральных точек «G» называется центром графа.
Пример. В примере графика {‘d’} является центром графика.
Длина окружности
Число ребер в самом длинном цикле «G» называется окружностью «G».
Пример. На графике примера длина окружности равна 6, что мы получили из самого длинного цикла acfgeba или acfdeba.
обхват
Число ребер в кратчайшем цикле G называется его обхват.
Обозначения – g (G).
Пример – в примере графика обхват графа равен 4, который мы получили из кратчайшего цикла acfda или dfged или abeda.
Теорема о сумме степеней вершин
Если G = (V, E) ненаправленный граф с вершинами V = {V 1 , V 2 ,… V n }, то
n ∑ i = 1 градус (V i ) = 2 | E |
Следствие 1
Если G = (V, E) ориентированный граф с вершинами V = {V 1 , V 2 ,… V n }, то
n ∑ i = 1 градус + (V i ) = | E | = n ∑ i = 1 град – (V i )
Следствие 2
В любом неориентированном графе число вершин с нечетной степенью является четным.
Следствие 3
В неориентированном графе, если степень каждой вершины равна k, то
к | V | = 2 | E |
Следствие 4
В неориентированном графе, если степень каждой вершины не меньше k, то
к | V | ≤ 2 | E |
Следствие 5
В неориентированном графе, если степень каждой вершины не более k, то
к | V | ≥ 2 | E |
Определение
Эксцентриситетом вершины называется расстояние до самой дальней вершины графа.
Радиусом графа называется минимальный эксцентриситет среди всех вершин графа
Диаметром графа — это наибольшее расстояние между всеми парами вершин графа
Центральной вершиной графа является вершина чей эксцентриситет равен радиусу графа.
Периферийной вершиной графа является вершина чей эксцентриситет равен диаметру графа.
Поиск радиуса и диаметра
Сервис граф онлайн позволит вам найти радиус и диаметр, а также укажет центральные и периферийные вершины. Для этого выберете пункт меню Алгоритмы -> Поиск радиуса и диаметра графа.
Реализацию алгоритма на JavaScript можно найти по ссылке: http://graphonline.ru/script/plugins/RadiusAndDiameter.js
Содержание
- 1 Диаметр дерева
- 1.1 Алгоритм
- 1.2 Реализация
- 1.3 Обоснование корректности
- 1.4 Оценка времени работы
- 2 Центр дерева
- 2.1 Определения
- 2.2 Алгоритм
- 2.2.1 Наивный алгоритм
- 2.2.2 Алгоритм для дерева за O(n)
- 3 См. также
- 4 Источники информации
Диаметр дерева
| Определение: |
| Диаметр дерева (англ. diameter of a tree) — максимальная длина (в рёбрах) кратчайшего пути в дереве между любыми двумя вершинами. |
Пусть дан граф . Тогда диаметром называется , где — кратчайшее расстояние между вершинами.
Алгоритм
- Возьмём любую вершину и найдём расстояния до всех других вершин.
- Возьмём вершину такую, что для любого . Снова найдём расстояние от до всех остальных вершин. Самое большое расстояние — диаметр дерева.
Расстояние до остальных вершин будем искать алгоритмом .
Реализация
//граф g представлен списком смежности
int diameterTree(list<list<int>> g):
v = u = w = 0
d = bfs(g, v)
for i = 0, i < n, i++
if d[i] > d[u]
u = i
d = bfs(g, u)
for i = 0, i < n, i++
if d[i] > d[w]
w = i
return d[w]
Обоснование корректности
Будем пользоваться свойством, что в любом дереве больше одного листа. Исключительный случай — дерево из одной вершины, но алгоритм сработает верно и в этом случае.
| Теорема: |
|
Искомое расстояние — расстояние между двумя листами. |
| Доказательство: |
| Пусть искомое расстояние — расстояние между вершинами , где не является листом. Так как не является листом, то её степень больше единицы, следовательно, из неё существует ребро в непосещённую вершину (дважды посетить вершину мы не можем). |
После запуска алгоритма получим дерево .
| Теорема: |
|
В дереве не существует ребер между вершинами из разных поддеревьев некоторого их общего предка. |
| Доказательство: |
|
Предположим, существует ребро между соседними поддеревьями: Рассмотрим первую вершину, в которую приведет наш алгоритм, пусть это вершина , тогда в ходе рассмотрения всех смежных вершин мы добавим в список вершину , тем самым исключив возможность попадания их в разные поддеревья. |
Мы свели задачу к нахождению вершины , такой что сумма глубин поддеревьев максимальна.
Докажем, что одно из искомых поддеревьев содержит самый глубокий лист.
Пусть нет, тогда, взяв расстояние от до глубочайшего листа, мы можем улучшить ответ.
Таким образом мы доказали, что нам нужно взять вершину с наибольшей глубиной после первого , очевидно, что ей в пару надо сопоставить вершину , такую что максимально. Вершину можно найти запуском из .
Оценка времени работы
Все операции кроме — .
работает за линейное время, запускаем мы его два раза. Получаем .
Центр дерева
Определения
| Определение: |
| Эксцентриситет вершины (англ. eccentricity of a vertex) — , где — множество вершин связного графа . |
| Определение: |
| Радиус (англ. radius) — наименьший из эксцентриситетов вершин графа . |
| Определение: |
| Центральная вершина (англ. central vertex) — вершина графа , такая что |
| Определение: |
| Центр графа (англ. center of a graph) — множество всех центральных вершин графа . |
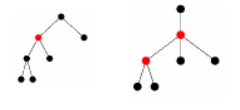
Примеры деревьев с одной и двумя центральными вершинами
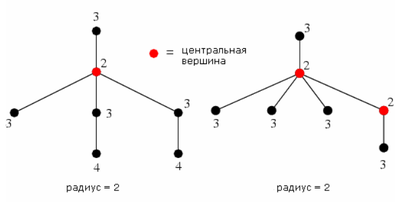
Графы, у которых показан эксцентриситет каждой вершины
Алгоритм
Наивный алгоритм
Найдём центр графа исходя из его определения.
- Построим матрицу ( — мощность множества ), где , то есть матрицу кратчайших путей. Для её построения можно воспользоваться алгоритмом Флойда-Уоршелла или Дейкстры.
- Подсчитаем максимум в каждой строчке матрицы . Таким образом, получим массив длины .
- Найдём наименьший элемент в этом массиве. Эта вершина и есть центр графа. В том случае, когда вершин несколько, все они являются центрами.
Асимптотика зависит от используемого способа подсчета кратчайших путей. При Флойде это будет , а при Дейкстре — максимум из асимптотики конкретной реализации Дейкстры и , за которую мы находим максимумы в матрице.
Алгоритм для дерева за O(n)
| Теорема: |
|
Каждое дерево имеет центр, состоящий из одной вершины или из двух смежных вершин. |
| Доказательство: |
| Утверждение очевидно для деревьев с одной и двумя вершинами. Покажем, что у любого другого дерева те же центральные вершины, что и у дерева , полученного из удалением всех его висячих вершин. Расстояние от данной вершины дерева до любой другой вершины достигает наибольшего значения, когда – висячая вершина. Таким образом, эксцентриситет каждой вершины дерева точно на единицу меньше эксцентриситета этой же вершины в дереве , следовательно, центры этих деревьев совпадают. Продолжим процесс удаления и получим требуемое. |
Собственно, алгоритм нахождения центра описан в доказательстве теоремы.
- Пройдёмся по дереву обходом в глубину и пометим все висячие вершины числом .
- Обрежем помеченные вершины.
- Образовавшиеся листья пометим числом и тоже обрежем.
- Будем повторять, пока на текущей глубине не окажется не более двух листьев, и при этом в дереве будет тоже не более двух листьев.
Оставшиеся листья являются центром дерева.
Для того, чтобы алгоритм работал за , нужно обрабатывать листья по одному, поддерживая в очереди два последовательных по глубине слоя.
См. также
- Дерево, эквивалентные определения
- Дополнительный, самодополнительный граф
Источники информации
- Wikipedia — Distance (graph theory)
- Ф. Харари: Теория графов
- А. Клебанов: Центры графов(нерабочая ссылка)
Пусть G = <V, U> — связный неорграф, Vi, Vj — две его несовпадающие вершины.
Длина кратчайшего (Vi, Vj)-маршрута называется расстоянием между вершинами Vi и Vj и обозначается через ? (Vi, Vj).
Положим ? (Vi, Vj) = 0. Очевидно, что введенное таким образом расстояние удовлетворяет следующим аксиомам метрики:
1) ? (Vi, Vj) ? 0;
2) ? (Vi, Vj) = 0 — Vi = Vj
3) ? (Vi, Vj) = ? (Vi, Vj) — симметричность
4) ? (Vi, Vj) ? ? (Vi, Vj) + ? (Vj, Vк) — неравенство треугольника.
Если V = {V1, V2,…, Vn}, то матрица Р = (рi,j) = ? (Vi, Vj), называется матрицей расстояний (где матрица Р симметрична).
Для фиксированной вершины V величина Е (v) = мах { ? (Vi, Vj) | Vj є V} называется эксцентриситетом вершины V. Таким образом, эксцентриситет вершины равен расстоянию от данной вершины до наиболее удаленной от нее.
Если Р-матрица расстояний, то эксцентриситет Е (Vi) равен наибольшему из числе, стоящих в i-й строке.
Максимальный среди всех эксцентриситетов вершин называется диаметром графа G и обозначается через d (G) : d (G) = vf[ {E(v) | v є V}. Вершина V называется периферийной, если Е (v) = d (G).
Рассмотрим пример. Найдем диаметр графа G, изображенный на рис.18. Матрица расстояний Р имеет вид:
Рис. 18
Отсюда Е (1) = 3, Е (2) = 2, Е (3) = 3, Е (4) = 2, Е (5) = 2 и, следовательно, d (G) = 3. Вершины 1 и 3 являются периферийными.
Минимальный из эксцентриситетов графа G называется его радиусом и обозначается через r (G) : r (G) = min {E (vi) | vi є V}.
Вершина V называется центральной, если Е (v) = r (G).
Множество всех центральных вершин графа называется его центром.
Рассмотрим соответствующий пример. Радиус графа, показанного на рис.18, равен 2, а его центром является множество {2, 4, 5}.
Задача нахождения центральных вершин возникает в практической деятельности людей. Пусть, например, граф представляет собой сеть дорог, т.е. вершины соответствуют населенным пунктам, а ребра — дорогам между ними. Требуется оптимально разместить больницы, пункты обслуживания и т.п. В подобных ситуациях оптимизация заключается в минимизации расстояния от места обслуживания до наиболее удаленного населенного пункта. Следовательно, местами размещения должны быть центральные вершины графа. Реальные задачи отличаются от этой идеальной темы, что приходится учитывать и другие обстоятельства — расстояния между населенными пунктами, стоимость, время проезда и т.д.
Дерево — одно из наиболее часто встречающихся в теории графов понятий (рис.19).
Ясно, что «особое место» в дереве занимают не только висячие вершины. Выделяются в этих деревьях и вершины, отмеченные двойным кружком. Такие вершины называют корневыми.
Корневую вершину нетрудно также выделить у деревьев на рисунках 20, 21, 22.
В первом случае корневой вершиной является единственная вершина графа А, во втором — вершина С, в третьем (такое дерево, все вершины которого, кроме одной, висячие, называют «звездой») — вершина А. Но какие вершины считать корневыми в графах, которые изображены на рисунках 23, 24 и 25?
Естественно считать, что все эти три дерева имеют по две корневые вершины. У дерева на рисунке 23 — это А и В, у дерева на рисунке 24 — это С и Д, у дерева на рисунке 25 — это А и В.
Расстоянием d (Vi, Vj) между вершинами Vi и Vj графа G называют длину кратчайшего пути, их соединяющего. (Если граф G-дерево, то путь соединяющий вершины Vi и Vj, единственный).
Подсчитаем для каждой вершины дерева, изображенного на рисунке 26, наибольшее из расстояний до всех остальных его вершин и запишем эти числа на рисунке возле вершин (рис.27).
Наибольшее из таких чисел называют диаметром графа (в данном случае дерева), наименьшее — радиусом графа.
Вершины дерева, для которых максимальное из расстояний до других вершин равно радиусу, называются корневыми. Для дерева, изображенного на рисунке 26, диаметр равен 5, а радиус равен 3; корневые вершины — А и В.
Задача. Подсчитайте диаметр и радиус графа, изображенного на рисунке:
а) 18; б) 24; в) 25.
Английский математик А.Кэли в 1875 году опубликовал первую работу по применению теории графов в органической химии. При этом он использовал понятие «висячая вершина» дерева для подсчета числа изомеров предельных (не имеющих циклов) углеводородов.
Решим еще одну задачу по химии: «Насыщенным углеводородом называется соединение углерода С, имеющего валентность 4 и водорода Н, имеющего валентность 1, в котором при заданном числе атомов углерода содержится наибольшее число атомов водорода. Найдите формулу насыщенного углеводорода, содержащего n атомов углерода».
Рассмотрим граф, в котором вершинами являются атомы, а ребрами — соответствующие валентные связи между ними. Покажем от противного, что в графе не существует цикла, т.е. возможности, переходя по ребрам графа из вершины в вершину, вернуться в исходную вершину. Если цикл есть, то должен быть составлен из атомов углерода, поскольку водород имеет валентность 1 и может соединяться только с одним атомом. В случае существования цикла разорвем связь между двумя атомами углерода и присоединим к каждому из них еще по одному водорода. Число атомов водорода увеличится, значит, исходный граф описывал не молекулу насыщенного углеводорода.
В построенном графе можно перейти по ребрам от любой вершины к любой другой, и в нем нет циклов. Такой граф называется деревом. Пусть молекула содержит n атомов углерода и m атомов водорода, тогда граф будет содержать n + m вершин. Далее, при решении задачи воспользуемся легко доказываемым соотношением: в дереве число ребер на единицу меньше числа вершин. Следовательно, в графе n + m — 1 ребер. Из вершин графа, обозначающих атомы углерода, выходит по 4 ребра, а из вершин, обозначающих атомы водорода, — одно. Используя простой факт, что сумма степеней вершин, т.е. сумма числа ребер, можно написать соотношение: 4n + m = 2 (n + m — 1). Отсюда получаем, что m = 2n + 2. Следовательно, формула насыщенного углеводорода, имеющего n атомов углерода: Сn H2n+n.
Т.е., можно получить формулу вещества с помощью математики, используя только определение и не проводя химических опытов.
К числу предельных (не имеющих цикла) углеводородов относится, например пентан С5Н12. Его структурная формула изображена на рисунке 28. Этой формуле можно поставить во взаимно однозначное соответствие однокорневое дерево (рис. 29), показывающее взаимное расположение только атомов углерода в молекуле пентана. Но тем самым определяется однозначно и расположение атомов водорода в этой молекуле. На рисунке 30 представлена структурная формула молекулы одного из изопентанов, а на рисунке 31 соответствующее ей двукорневое дерево.
По тем или иным причинам почти все работы по теории графов таят в себе семена возможных практических применений или по крайней мере потенциально полезны.
Графы эффективно используются в теории планирования и управления, теории расписаний, социологии, экономике, биологии, медицине, в областях прикладной математики.