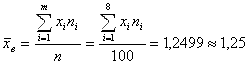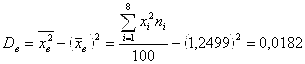Как найти экспериментальную частоту

  1. Теоретические и эмпирические частоты. Критерии согласия.

Эмпирические
частоты
получают в результате опыта (наблюдения).
Теоретические частоты рассчитывают по
формулам. Для нормального закона
распределения их можно найти следующим
образом:

,
(*)

где
–
сумма эмпирических (наблюдаемых) частот;
–
разность между двумя соседними вариантами
(то есть длина частичного интервала);
–
выборочное среднее квадратическое
отклонение;
;

–
выборочная средняя арифметическая;
–
середина
-го
частичного интервала; значения функции


находят по таблице (см. приложения).

Обычно эмпирические
и теоретические частоты различаются.
Возможно, что расхождение случайно и
связано с ограниченным количеством
наблюдений; возможно, что расхождение
неслучайно и объясняется тем, что для
вычисления теоретических частот
выдвинута статистическая гипотеза о
том, что генеральная совокупность
распределена нормально, а в действительности
это е так. Распределение генеральной
совокупности, которое она имеет в силу
выдвинутой гипотезы, называют
теоретическим.

Возникает
необходимость установить правило
(критерий), которое позволяло бы судить,
является ли расхождение между эмпирическим
и теоретическим распределениями
случайным или значимым. Если расхождение
окажется случайным, то считают, что
данные наблюдений (выборки) согласуются
с выдвинутой гипотезой о законе
распределения генеральной совокупности
и, следовательно, гипотезу принимают.
Если же расхождение окажется значимым,
то данные наблюдений не согласуются с
выдвинутой гипотезой, и её отвергают.

Критерием
согласия
называют критерий, который позволяет
установить, является ли расхождение
эмпирического и теоретического
распределений случайным или значимым,
то есть согласуются ли данные наблюдений
с выдвинутой статистической гипотезой
или не согласуются.

Имеются несколько
критериев согласия: критерий

(Пирсона), критерий Колмогорова, критерий
Романовского и др. Ограничимся описанием
того, как критерий

применяется к проверке гипотезы о
нормальном распределении генеральной
совокупности1
(предлагаем студентам
написать рефераты по различным критериям
согласия и их применению).

Допустим, что в
результате

наблюдений получена выборка:

Значения
признака

.
. .

Эмпирические
частота

.
. .

причём

Выдвинем
статистическую гипотезу: генеральная
совокупность, из которой извлечена
данная выборка, имеет нормальное
распределение. Требуется установить,
согласуется ли эмпирическое распределение
с этой гипотезой. Предположим, что по
формуле (*)
вычислены теоретические частоты
.
Обозначим

среднее арифметическое квадратов
разностей между эмпирическими и
теоретическим частотами, взвешенное
по обратным величинам теоретических
частот:

.

Чем больше
согласуются эмпирическое и теоретическое
распределения, тем меньше различаются
эмпирические и теоретические частоты
и тем меньше значение
.
Отсюда следует, что

характеризует близость эмпирического
и теоретического распределений. В разных
опытах

принимает различные, заранее неизвестные
значения, то есть является случайной
величиной. Плотность вероятности этого
распределения (для выборки достаточно
большого объёма) не зависит от проверяемого
закона распределения, а зависит от
параметра
,
называемого числом степеней свободы.
Так при проверке гипотезы о нормальном
распределении генеральной совокупности

,
где
–
число групп, на которые разбиты данные
наблюдений. Существуют таблицы (см.
приложения), в которых указана вероятность
того, что в результате влияния случайных
факторов величина

примет значение не меньше вычисленного
по данным выборки
.

Для определённости
примем уровень значимости 0,01. Если
вероятность, найденная по таблицам,
окажется меньше 0,01, то это означает, что
в результате влияния случайных причин
наступило событие, которое практически
невозможно. Таким образом, тот факт, что

приняло значение
,
нельзя объяснить случайными причинами;
его можно объяснить тем, что генеральная
совокупность не распределена нормально
и, значит, выдвинутая гипотеза о нормальном
распределении генеральной совокупности
должна быть отвергнута. Если вероятность,
найденная по таблицам, превышает 0,01, то
гипотеза о нормальном распределении
генеральной совокупности согласуется
с данными наблюдений и поэтому может
быть принята. Полученные выводы
распространяются и на другие уровни
значимости.

На практике надо,
чтобы объём выборки был достаточно
большим ()
и чтобы каждая группа содержала 5 – 8
значений признака.

Для проверки
гипотезы о нормальном распределении
генеральной совокупности нужно:

  1. вычислить
    теоретические частоты по формуле (*);

  2. вычислить
    ,
    где
    –
    соответственно частоты эмпирические
    и теоретические;

  3. вычислить число
    степеней свободы
    ,
    где
    –
    число групп, на которые разбита выборка;

  4. выбрать уровень
    значимости;

  5. найти по таблице
    (см. приложения) по найденным

    и

    вероятность
    ,
    причём, если эта вероятность меньше
    принятого уровня значимости, то гипотезу
    о нормальном распределении генеральной
    совокупности отвергают; если же
    вероятность больше уровня значимости,
    то гипотезу принимают.

ПРИМЕР 5.
Проверить, согласуются ли данные выборки
со статистической гипотезой о нормальном
распределении генеральной совокупности,
из которой извлечена выборка:

варианта

15

20

25

30

35

40

45

50

55

частота

6

13

38

74

106

85

30

10

4

Решение.
Вычислим выборочное среднее и выборочную
дисперсию:

;

.

Далее, вычислим
теоретические частоты по формуле (*):

15

6

– 19,7

– 2,67

0,0113

3

20

13

– 14,7

– 1,99

0,0551

14

25

38

– 9,7

– 1,31

0,1691

42

30

74

– 4,7

– 0,63

0,3271

82

35

106

0,3

0,05

0,3984

99

40

85

5,3

0,73

0,3056

76

45

30

10,3

1,41

0,1476

37

50

10

15,3

2,09

0,0449

11

55

4

20,3

2,77

0,0086

2

Найдём
.
Вычислим число степеней свободы,
учитывая, что число групп выборки
.
Уровень значимости примем равным 0,01.
По таблице (см. приложения) при

и

находим вероятность
;
при

вероятность
.
Используя линейную интерполяцию,
получаем приближённое значение искомой
вероятности 0,16 > 0,01.

Следовательно,
данные наблюдений согласуются с гипотезой
о нормальном распределении генеральной
совокупности.

1
Интервал

имеет случайные концы (их называют
доверительными границами). Действительно,
в разных выборках получаются различные
значения
.
Следовательно от выборки к выборке
будут изменяться и концы доверительного
интервала, то есть доверительные границы
сами являются случайными величинами
– функциями от
.
Так как случайной величиной является
не оцениваемый параметр
,
а доверительный интервал, то более
правильно говорить не о вероятности
попадания

в доверительный интервал, а о вероятности
того, что доверительный интервал покроет
.

1
Обычно при выполнении пп. 4 – 7 используют
статистику с нормальным распределением,
статистику Стьюдента, Фишера.

2
То есть – с математическим ожиданием.

1
Критерий применяется аналогично и для
других распределений

12

Соседние файлы в папке Теор.вер. (лекции)

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

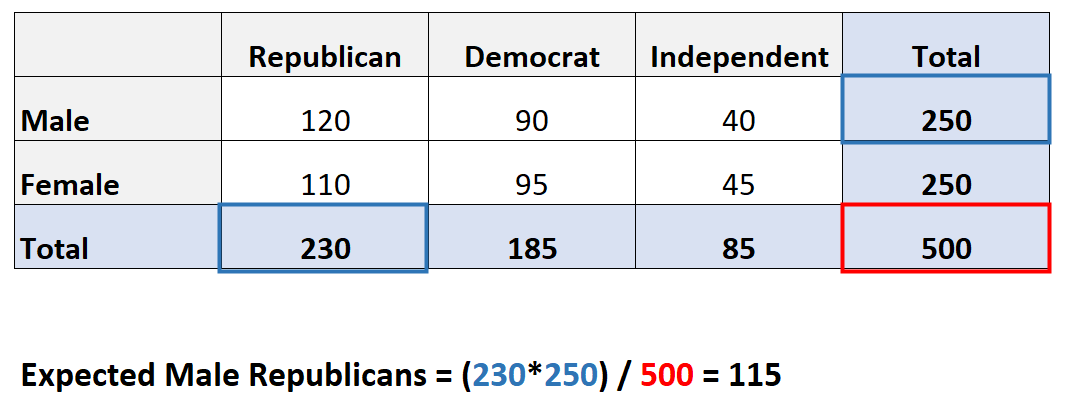
Как рассчитать ожидаемую частоту

  • Редакция Кодкампа

17 авг. 2022 г.
читать 2 мин

Ожидаемая частота — это теоретическая частота, которую мы ожидаем получить в эксперименте.

Этот тип частоты чаще всего встречается в двух типах тестов хи-квадрат:

  • Хи-квадрат критерия согласия
  • Хи-квадрат тест независимости

В этом руководстве объясняется, как рассчитать ожидаемую частоту для каждого из этих двух тестов.

Ожидаемая частота в тесте согласия хи-квадрат

Критерий согласия Хи-квадрат используется, чтобы определить, следует ли категориальная переменная гипотетическому распределению. С помощью этого типа теста мы сравниваем наблюдаемые частоты категориальной переменной с ожидаемыми частотами.

Например, предположим, что владелец магазина утверждает, что каждый будний день в его магазин заходит одинаковое количество покупателей. Чтобы проверить эту гипотезу, независимый исследователь записывает количество покупателей, которые заходят в магазин на определенной неделе, и обнаруживает следующее:

Чтобы рассчитать ожидаемую частоту клиентов каждый день, мы можем использовать следующую формулу:

Ожидаемая частота = ожидаемый процент * общее количество

В этом конкретном примере владелец магазина ожидает, что каждый день в магазин будет приходить одинаковое количество покупателей, поэтому ожидаемый процент покупателей, приходящих в данный день, составляет 20% от общего числа покупателей за неделю.

Это означает, что мы можем рассчитать ожидаемую частоту клиентов каждый день как:

Ожидаемая частота = 20% * 250 клиентов = 50

Ожидаемая частота в критерии качества независимости хи-квадрат

Критерий независимости Хи-квадрат используется для определения того, существует ли значительная связь между двумя категориальными переменными. С помощью этого типа теста мы также сравниваем набор наблюдаемых частот с набором ожидаемых частот.

Например, предположим, что мы хотим знать, связан ли пол с предпочтениями политической партии. Мы берем простую случайную выборку из 500 избирателей и опрашиваем их об их предпочтениях в отношении политических партий. В следующей таблице представлены результаты опроса:

Чтобы рассчитать ожидаемую частоту каждой ячейки в таблице, мы можем использовать следующую формулу:

Ожидаемая частота = (сумма строк * сумма столбцов) / сумма таблицы

Например, ожидаемое значение для мужчин-республиканцев: (230*250) / 500 = 115 .

Расчет ожидаемой частоты

Мы можем повторить эту формулу, чтобы получить ожидаемое значение для каждой ячейки в таблице:

Расчет ожидаемой частоты в тесте хи-квадрат

Вы можете найти больше руководств по статистике на нашей странице здесь .

Источник

Критерии согласия. Теоретические и эмпирические частоты

Эмпирические частоты получают в результате опыта (наблюдения). Теоретические частоты рассчитывают по формулам. Для нормального закона распределения их можно найти следующим образом:

n_i=frac{varphi(t_i),h}{sigma_text{v}}sumlimits_{j=1}^{n}m_j

где sumlimits_{j=1}^{n}m_j — сумма эмпирических частот; h — разность между двумя соседними вариантами; sigma_text{v} — выборочное среднеквадратическое отклонение; t_i=frac{x_i-overline{x}_text{v}}{sigma_text{v}}; overline{x}_text{v} — выборочная средняя арифметическая; varphi(t) — см. прил. 1.

Обычно эмпирические и теоретические частоты различаются. Возможно, что расхождение случайно и связано с ограниченным количеством наблюдений; возможно, что расхождение неслучайно и объясняется тем, что для вычисления теоретических частот выдвинута статистическая гипотеза о том, что генеральная совокупность распределена нормально, а в действительности это не так. Распределение генеральной совокупности, которое она имеет в силу выдвинутой гипотезы, называют теоретическим.

Возникает необходимость установить правило (критерий), которое позволяло бы судить, является ли расхождение между эмпирическим и теоретическим распределениями случайным или значимым. Если расхождение окажется случайным, то считают, что данные наблюдений (выборки) согласуются с выдвинутой гипотезой о законе распределения генеральной совокупности и, следовательно, гипотезу принимают; если же расхождение окажется значимым, то данные наблюдений не согласуются с гипотезой, и ее отвергают.

Критерием согласия называют критерий, который позволяет установить, является ли расхождение эмпирического и теоретического распределений случайным или значимым, т. е. согласуются ли данные наблюдений с выдвинутой статистической гипотезой или не согласуются.

Имеется несколько критериев согласия: критерий хи-квадрат chi^2 (Пирсона), критерий Колмогорова, критерий Романовского и др. Ограничимся описанием того, как критерий chi^2 применяется к проверке гипотезы о нормальном распределении генеральной совокупности (критерий применяется аналогично и для других распределений).

Допустим, что в результате n наблюдений получена выборка:

значение признака x_1~~~x_2~~~cdots~~~x_s;

эмпирическая частота m_1~~~m_2~~~cdots~~~m_s.

Выдвинем статистическую гипотезу: генеральная совокупность, из которой извлечена данная выборка, имеет нормальное распределение. Требуется установить, согласуется ли эмпирическое распределение с этой гипотезой. Предположим, что по формуле (11.3) вычислены теоретические частоты n_1,n_2,ldots,n_s.Обозначим chi_q^2 среднее арифметическое квадратов разностей между эмпирическими и теоретическими частотами, взвешенное по обратным величинам теоретических частот:

chi_q^2=sumlimits_{i=1}^{s}frac{(m_i-n_i)^2}{n_i}.

Чем больше согласуются эмпирическое и теоретическое распределения, тем меньше различаются эмпирические и теоретические частоты и тем меньше значение chi_q^2. Отсюда следует, что chi_q^2 характеризует близость эмпирического и теоретического распределений. В разных опытах chi_q^2 принимает различные, наперед неизвестные значения, т. е. является случайной величиной. Плотность вероятности этого распределения (для выборки достаточно большого объема) не зависит от проверяемого закона распределения, а зависит от параметра k, называемого числом степеней свободы. При проверке гипотезы о нормальном распределении генеральной совокупности k=s-3, где s — число групп, на которые разбиты данные наблюдений. Существуют таблицы (прил. 6), в которых указана вероятность того, что в результате влияния случайных факторов величина chi^2 примет значение не меньше вычисленного по данным выборки chi_q^2.

Для определенности примем уровень значимости 0,01. Если вероятность, найденная по таблицам, окажется меньше 0,01, то это означает, что в результате влияния случайных причин наступило событие, которое практически невозможно. Таким образом, тот факт, что chi^2 приняло значение chi_q^2 нельзя объяснить случайными причинами; его можно объяснить тем, что генеральная совокупность не распределена нормально и, значит, выдвинутая гипотеза о нормальном распределении генеральной совокупности должна быть отвергнута. Если вероятность, найденная по таблицам, превышает 0,01, то гипотеза о нормальном распределении генеральной совокупности согласуется с данными наблюдений и поэтому может быть принята. Полученные выводы распространяются и на другие уровни значимости.

На практике надо, чтобы объем выборки был достаточно большим (ngeqslant50) и чтобы каждая группа содержала не менее 5-8 значений признака.

Для проверки гипотезы о нормальном распределении генеральной совокупности нужно:

1) вычислить теоретические частоты по формуле (11.3);

2) вычислить chi_q^2=sumlimits_{i=1}^{s}frac{(m_i-n_i)^2}{n_i}, где m_i,n_i — соответственно частоты эмпирические и теоретические;

3) вычислить число степеней свободы k=s-3, где s — число групп, на которые разбита выборка;

4) выбрать уровень значимости;

5) найти по таблице прил. 6 по найденным k и chi_q^2 вероятность P{chi^2geqslantchi_q^2} причем если эта вероятность меньше принятого уровня значимости, то гипотезу о нормальном распределении генеральной совокупности отвергают; если вероятность больше уровня значимости, то гипотезу принимают.

Пример 5. Проверить, согласуются ли данные выборки со статистической гипотезой о нормальном распределении генеральной совокупности, из которой извлечена эта выборка:

begin{array}{|c|c|c|c|c|c|c|c|c|c|} hline{x_i}&15&20&25&30&35&40&45&50&55\ hline{m_i}&6&13&38&74&106&85&30&10&4\ hlineend{array}

Решение. Вычислим выборочное среднее и выборочную дисперсию по формулам из первой главы этой части: overline{x}_text{v}=34,!7;~D_text{v}=7,!38. Вычислим теоретические частоты по формулам (11.3)

begin{array}{|c|c|c|c|c|c|} hline{x_i}&{m_i}&overline{x}_i-overline{x}_text{v}&t_i&varphi(t_i)&n_i\hline 15&6&hfill-19,!7&hfill-2,!67&0,!0113&3\ 20&13&hfill-14,!7&hfill-1,!99&0,!0551&14\ 25&38&hfill-9,!7&hfill-1,!31&0,!1691&42\ 30&74&hfill-4,!7&hfill-0,!63&0,!3271&82\ 35&106&hfill0,!3&hfill0,!05&0,!3984&99\ 40&85&hfill5,!3&hfill0,!73&0,!3056&76\ 45&30&hfill10,!3&hfill1,!41&0,!1476&37\ 50&10&hfill15,!3&hfill2,!09&0,!0449&11\ 55&4&hfill20,!3&hfill2,!77&0,!0086&2\ hline{}&sum{m_i=366}&{}&{}&{}&sum{n_i=366}\hline end{array}

Найдём chi_q^2. Вычислим число степеней свободы, учитывая, что число групп выборки s=9;~k=s-3=6. Уровень значимости alpha примем равным 0,01. По таблице прил. 6 при k=6 и chi_q^2=9 находим вероятность P=0,!1736; при chi_q^2=10 вероятность P=0,!1247. Используя линейную интерполяцию, получаем приближённое значение искомой вероятности 0,!16>0,!01.

Следовательно, данные наблюдения согласуются с гипотезой о нормальном распределении генеральной совокупности.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Проверка гипотезы о нормальном распределении генеральной совокупности

  • Краткая теория
  • Примеры решения задач
  • Задачи контрольных и самостоятельных работ

Краткая теория

Проверка дискретного распределения на нормальность

Пусть
эмпирическое распределение задано в виде последовательности равноотстоящих
вариант и соответствующих им частот:

…

…

Требуется, используя критерий Пирсона, проверить
гипотезу о том, что генеральная совокупность

 распределена нормально.

Для того,
чтобы при заданном уровне значимости

 проверить гипотезу о нормальном распределении
генеральной совокупности, надо:

1. Вычислить
выборочную среднюю

 и выборочное среднее квадратическое отклонение

.

2.
Вычислить теоретические частоты

где

 – объем выборки,

 — шаг (разность между двумя соседними
вариантами)

3.  Сравнить эмпирические и теоретические частоты
с помощью критерия Пирсона. Для этого:

а)
составляют расчетную таблицу (см. пример), по которой находят наблюдаемое
значение критерия

б) по
таблице критических точек распределения

, по заданному уровню
значимости

 и числу степеней свободы

 (

 – число групп выборки) находят критическую
точку

 правосторонней критической области.

Если

 – нет оснований отвергнуть гипотезу о
нормальном распределении генеральной совокупности. Если

 — гипотезу отвергают.

Проверка интервального распределения на нормальность

Пусть
эмпирическое распределение задано в виде последовательности интервалов

 и соответствующих им частот

.

Требуется,
используя критерий Пирсона, проверить гипотезу о том, что генеральная
совокупность

 распределена нормально.

Для того,
чтобы при уровне значимости

 проверить гипотезу о нормальном распределении
генеральной совокупности, надо:

1.
Вычислить выборочную среднюю

 и выборочное среднее квадратическое отклонение

, причем в качестве вариант

 принимают среднее арифметическое концов
интервала:

2.
Пронормировать

, то есть перейти к
случайной величине

и
вычислить концы интервалов:

причем
наименьшее значение

, то есть

 полагают равным

, а наибольшее, то есть

 полагают равным

.

3. Вычислить теоретические
частоты:

где

 – объем выборки

 – вероятности попадания

 в интервалы

 – функция Лапласа.

4.  Сравнить эмпирические и
теоретические частоты с помощью критерия Пирсона. Для этого:

а)
составляют расчетную таблицу (см. пример), по которой находят наблюдаемое
значение критерия

б) по
таблице критических точек распределения

, по заданному уровню
значимости

 и числу степеней свободы

 (

 – число групп выборки) находят критическую
точку

 правосторонней критической области.

Если

 – нет оснований отвергнуть гипотезу о
нормальном распределении генеральной совокупности.  Если

 — гипотезу отвергают.

Замечание.

Малочисленные частоты

 следует объединить, в этом случае и
соответствующие им теоретические частоты также надо сложить. Если производилось
объединение частот, то при определении числа степеней свободы по формуле

 следует в качестве

 принять число групп выборки, оставшихся после
объединения частот.

Примеры решения задач

Пример 1

Используя
критерий Пирсона при уровне значимости 0,05, проверить, согласуется ли гипотеза
с нормальным распределением генеральной совокупности X с заданным эмпирическим
распределением:

xi -4.5 -3.5 -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 4.5
ni 1 4 21 30 63 59 34 18 5 2

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Вычислим
характеристики распределения. Для этого составим расчетную таблицу.

Выборочная средняя:

Средняя
квадратов:

Выборочная
дисперсия:

Среднее квадратическое
отклонение:

Вычислим
теоретические частоты.

Вероятность
попадания в соответствующий интервал:

Теоретические
частоты:

где

 -объем выборки

Составим
расчетную таблицу:

Проверим
степень согласия эмпирического и теоретического распределения по критерию
Пирсона. Объединяем малочисленные частоты (

).

Из
расчетной таблицы

Уровень
значимости

Число
степеней свободы

По
таблице критических точек распределения:

Нет
оснований отвергнуть гипотезу о нормальном распределении генеральной
совокупности.

Пример 2

Из большой партии по схеме случайной
повторной выборки было проверено 150 изделий с целью определения процента
влажности древесины, из которой изготовлены эти изделия. Получены следующие
результаты:

Процент влажности, xi

11-13

13-15

15-17

17-19

19-21

Число изделий, ni

8

42

51

37

12

На уровне значимости 0,05 проверить
гипотезу о нормальном законе распределения признака (случайной величины) X, используя критерий χ2 — Пирсона.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Составим расчетную таблицу

Средняя:

Средняя квадратов:

Дисперсия:

Исправленная дисперсия:

Исправленное среднее квадратическое
отклонение:

Вычислим теоретические частоты.

Составим расчетную таблицу:

Вероятность попадания в
соответствующий интервал:

, где

— функция Лапласа

Теоретические частоты:

, где

 -объем выборки

Составим расчетную таблицу:

Проверим степень согласия
эмпирического и теоретического распределения по критерию Пирсона:

Из расчетной таблицы

Уровень значимости

Число степеней свободы

По таблице критических точек
распределения:

Нет оснований отвергать гипотезу о
распределении случайной величины по нормальному закону.

Задачи контрольных и самостоятельных работ

Задача 1

Выборка X
объемом n=100 задана таблицей:

 0.8 1.1 1.4 1.7 2 2.3 2.6

5 13 25 25 19 10 3

1) Построить
полигон относительных частот

.

2) Вычислить
среднее выборочное

, выборочную дисперсию

 и среднее квадратическое отклонение

.

3) Вычислить
теоретические частоты

. Построить график

 на одном рисунке с полигоном.

4) С помощью
критерия χ2 проверить гипотезу о нормальном распределении
генеральной совокупности при уровне значимости α=0.05.

Задача 2

Построить
нормальную кривую по опытным данным. Рассчитать теоретические (выравнивающие) частоты
и сравнить с опытным распределением.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 3

Выборка X
объемом N=100 измерений задана таблицей:

 0.6 1.5 2.4 3.3 4.2 5.1 6

5 13 26 24 19 10 3

а)
Построить полигон относительных частот

б)
вычислить среднее выборочное

, выборочную дисперсию

 и среднее квадратическое отклонение

;

в) по
критерию χ2 проверить гипотезу о
нормальном распределении генеральной совокупности при уровне значимости α=0.05.

Задача 4

Для
изучения количественного признака

 из генеральной совокупности извлечена выборка

 объема n, имеющая данное
статистическое распределение.

а)
Построить полигон частот по данному распределению выборки.

б) Найти
выборочное среднее

, выборочное среднее
квадратическое отклонение

 и исправленное среднее квадратическое
отклонение

.

в) При
данном уровне значимости

 проверить по критерию Пирсона гипотезу о
нормальном распределении генеральной совокупности.

г) В
случае принятия гипотезы о нормальном распределении генеральной совокупности
найти доверительные интервалы для математического ожидания

 и среднего квадратического отклонения σ при
данном уровне надежности γ=1-α; α=0.05

 4 8 12 16 20 24 28 32

5 9 15 19 20 16 10 6

Задача 5

Для выборки
объема N=100, представленной вариационным рядом

 -1 0 1 2 3 4 5

3 8 11 19 37 17 5

построить
полигон относительных частот и гистограмму накопленных частот. Найти выборочное
среднее

 и выборочное среднее квадратичное отклонение

. Определить доверительный интервал с
доверительной вероятностью β=0,95 для оценки математического ожидания
генеральной совокупности в предположении, что среднее квадратическое отклонение
генеральной совокупности σ равно исправленному выборочному среднему s. Проверить
гипотезу о нормальности закона распределения генеральной совокупности,
используя критерий Пирсона с уровнем значимости α=0,05.

Задача 6

Для случайной величины X составить интервальный
вариационный ряд, вычислить выборочные средние характеристики, подобрать
теоретический закон распределения, проверить его согласование с теоретическим
критерием Пирсона при α=0,05.

7 4 4 15 1 1 7 15 19 4
0 4 8 14 10 0 1 11 8 2
6 2 5 3 12 2 9 6 2 5
13 5 7 3 3 10 0 11 17 11
9 6 11 7 20 1 14 6 7 4

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 7

Данные о
продолжительности телефонных разговоров, отобранные по схеме
собственно-случайной бесповторной выборки, приведены в таблице:

Время, мин 1.5-2.5 2.5-3.5 3.5-4.5 4.5-5.5 5.5-6.5 6.5-7.5 7.5-8.5 8.5-9.5 9.5-10.5 Итого
Число разговоров 3 4 9 14 37 12 8 8 5 100

Используя χ2-критерий Пирсона при уровне
значимости α=0.05 проверить гипотезу о том, что случайная величина X —
продолжительность телефонных разговоров — распределена по нормальному закону.
Построить на одном чертеже гистограмму и соответствующую нормальную кривую.

Задача 8

Распределение
случайной величины X – заработной платы сотрудников на фирме (в у.е.) –
задано в виде интервального ряда:

Найти:

. Построить теоретическое
нормальное распределение и сравнить его с эмпирическим с помощью критерия
согласия Пирсона χ2 при α=0,05.

Задача 9

Записать для выборки интервальное
распределение, построить гистограмму относительных частот. По критерию Пирсона
проверить гипотезу нормальном распределении.

7.81 3.15 2.27 32.64 4.72 5.33 8.51 7.72 30.23 20.12
9.83 8.33 9.61 31.83 8.52 27.22 27.22 8.43 15.91 25.46
24.82 26.54 46.73 17.31 13.05 53.24 5.23 18.28 40.93 17.44
32.34 28.26 9.75 3.72 8.16 22.91 0.74 12.97 12.05 1.53
43.15 45.57 2.02 32.23 8.67 4.83 9.12 6.77 6.48 19.22
36.42 47.81 40.64 5.45 0.21 26.51 17.36 3.62 15.57 23.21
58.73 62.52 10.15 38.36 35.55 6.10 3.04 4.54 1.95 5.24
64.71 67.63 1.21 0.81 2.03 10.17 5.51 8.35 43.76 8.74
4.72 17.54 17.32 29.43 5.91 6.92 4.72 16.04 57.54 15.46
13.31 36.45 3.45 16.15 15.77 2.43 14.24 2.25 15.63 23.72

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 10

Результаты наблюдений над случайной
величиной

 оказались
лежащими на отрезке

 и были
сгруппированы в 10 равновеликих интервалов. Значения

 и частоты
попадания в интервалы приведены в таблице. Построить: гистограмму частот,
эмпирическую функцию распределения, найти медиану. Найти выборочное среднее

 и исправленное
среднеквадратическое отклонение

. Указать 95-процентные доверительные интервалы для

. С помощью критерия Пирсона проверить гипотезу о
нормальном (с параметрами

) законе распределения (уровень значимости α=0.02

.

Задача 11

В таблице приведены результаты
измерения роста (см.) случайно отобранных 100 студентов:

Интервалы
роста 		154-158 158-162 162-166 166-170 170-174 174-178 178-182
Число
студентов,

10 14 26 28 12 8 2

С помощью критерия Пирсона при
уровне значимости α=0.05 проверить правдоподобие гипотезы о нормальном
распределении роста студентов.

Задача 12

При массовых стрельбах из пушек для
одинаковых общих условий были зафиксированы продольные ошибки (м) попадания
снарядов в цель:

На уровне значимости 0,05 проверить
гипотезу о нормальном законе распределения признака (случайной величины) L, используя критерий χ2— Пирсона.

  • Краткая теория
  • Примеры решения задач
  • Задачи контрольных и самостоятельных работ
Источник

При исследовании различных признаков объектов генеральной совокупности обычно заведомо предполагается, что исследуемый признак Х является случайной величиной, распределенной нормально. Но это можно подтвердить (или отвергнуть) с помощью выборки значений величины Х.

Итак, выдвигается нулевая гипотеза H0: исследуемый признак Х объектов генеральной совокупности распределен нормально. Альтернативная гипотеза Н1: это не так. Принимается некоторый уровень значимости α. Требуется указать критерий, по которому можно было бы решить, принимать или отвергать гипотезу H0.

Такой критерий, в частности, разработал американский математик Э. Пирсон. Чтобы воспользоваться этим критерием, сначала, естественно, нужно из генеральной совокупности сделать некоторую выборку. Причем выборку достаточно большую, по крайней мере объемом не менее 50. Полученное статистическое распределение выборки вида (1.1) или (1.3) затем несколько изменяют, приводя его к виду с равноотстоящими вариантами Хί И достаточно большими частотами Ni (Ni≥5, кроме разве что крайних частот). Для этого полученные в выборке варианты, если они неравноотстоящие, несколько сдвигают, а близлежащие малочисленные варианты объединяют в одну с объединением их частот. В дальнейшем будем считать, что такая предварительная работа проделана, так что статистическое распределение выборки

Xi

X1

X2

…

Xm

(N1+n2+…+nm=n) (3.28)

Ni

N1

N2

…

Nm

Уже удовлетворяет указанным выше требованиям. Будем также считать, что из (3.28) найдены и .

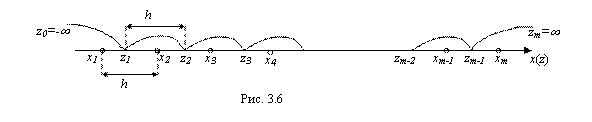
Пусть, в соответствии с гипотезой Н0, признак Х (случайная величина Х) распределена нормально с некоторыми неизвестными параметрами и . В качестве значений этих параметров примем их известные точечные оценки ≈ и ≈. Далее, разобьем ось Ох с нанесенными на нее M равноотстоящими с шагом H вариантами Хί (I=1, 2,…M) на M интервалов , окружающими эти варианты – так, как показано на рис. 3.6.

Если мы найдем вероятности РI Попадания значения исследуемой величины Х в интервалы , окружающие варианты Хί , и умножим эти вероятности на объем N выборки, то получим частоты , являющиеся математическими ожиданиями экспериментальных частот . То есть получим теоретические частоты Вариант Хί:

Xi

X1

X2

…

Xm

() (3.29)

…

Незначительное расхождение экспериментальных и теоретических частот и будет свидетельствовать в пользу принятия гипотезы H0. А если же они будут сильно различаться, то это будет означать, что гипотеза H0, скорее всего, неверна.

В качестве критерия близости (согласия) частот и Пирсоном было предложено использовать величину

(3.30)

Эта величина – случайная, так как ее значения от выборки к выборке меняются. Ясно, что все ее значения неотрицательны, и чем ближе она к нулю, тем ближе между собой и , а значит, тем в большей мере подтверждается гипотеза H0.

Доказано, что при N→ ∞ закон распределения случайной величины χ2, определенной равенством (3.30), стремится к закону распределения χ2 (хи-квадрат, см. часть I, главу 2, §4) с K=M-3 степенями свободы. Причем даже независимо от того, по какому закону распределен признак Х в генеральной совокупности. Поэтому случайная величина (3.30) и обозначена символом χ2. А сам критерий Пирсона называется еще «критерием «хи-квадрат».

Область принятия и критическую область проверяемой гипотезы H0 о нормальности распределения случайной величины Х Определяют следующим образом. По заданному уровню значимости α И числу K=M-3 с помощью таблицы критических точек распределения «хи-квадрат» (таблица 3 Приложения) находят такое критическое значение χ2кр(α; K) величины χ2, чтобы (см. рис.3.7)

(3.31)

И если χ2эксп, вычисленное по формуле (3.30), окажется больше χ2кр(α; K), то гипотезу H0 о нормальности распределения случайной величины Х отвергают. А если окажется, что χ2эксп< χ2кр(α; K), то гипотезу H0 принимают.

Нам осталось лишь указать, как найти вероятность РI попадания значений нормально распределенной случайной величины Х С параметрами и в интервалы , окружающие на рис. 3.6 варианты Хί (I=1,2,…M), ибо через эти вероятности РI по формуле Ni* = Npi находятся теоретические частоты Ni* (I=1,2,…M). Для нахождения указанных вероятностей следует применить формулу (4.10) (часть I, глава 2) для нормально распределенных случайных величин, согласно которой получаем:

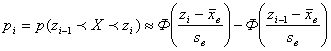
(3.32)

Здесь, как это следует из рис. 3.6,

(3.33)

Пример5. При исследовании некоторого признака Х объектов генеральной совокупности выборочным путем обследовано 100 объектов. Данные выборки представлены в таблице:

Хί

Ni

Хί

Ni

Хί

Ni

1,00

1

1,19

2

1,37

6

1,03

3

1,20

4

1,38

2

1,05

6

1,23

4

1,39

1

1,06

4

1,25

8

1,40

2

1,08

2

1,26

4

1,44

3

1,10

4

1,29

4

1,45

3

1,12

3

1,30

6

1,46

2

1,15

6

1,32

4

1,49

4

1,16

5

1,33

5

1,50

2

При уровне значимости α=0,05 проверить гипотезу Н0 О нормальности распределения признака Х В генеральной совокупности.

Решение. Варианты нашей выборки не равностоящие, причем малочисленные. Сведем их к небольшому числу равноотстоящих вариант с достаточно большими частотами. Для этого предварительно оформим данное статистическое распределение выборки в интервальном виде, чтобы затем принять середины получавшихся интервалов за новые равноотстоящие варианты.

Сначала определим минимальную и максимальную варианты исходного статистического распределения выборки:

Xmin=1,00; Xmax=1,50

Таким образом, размах вариации

∆= Xmax— Xmin=0,50

При этом N=100–количество вариант (объем выборки). А теперь разобьем промежуток вариации [Xmin; Xmax]=[1,00; 1,50] точками Хί* на несколько (M) промежутков одинаковой ширины H – Так, как показано на рис. 3.8. Для выбора оптимального (не слишком большого и не слишком малого) шага разбиения H применим Формулу Стэрджеса:

(3.34)

В нашем примере эта формула дает:

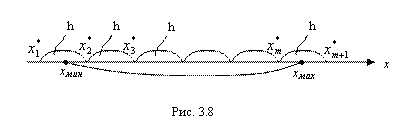
Теперь, в соответствии с рис. 3.8, добавляя к размаху вариации ∆ один шаг H (по полшага с обеих сторон), находим (округляя по недостатку до целого) оптимальное количество M интервалов, на которые мы разобьем интервал вариации:

А теперь, исходя из выбранного значения M=8 количества интервалов, получим и окончательное значение длины H каждого интервала:

(окончательное значение H для борьбы с накоплением погрешностей взято с двумя дополнительными десятичными знаками по сравнению с исходными вариантами, то есть в нашей задаче – до десятичных).

После того, как количество интервалов M=8 и шаг разбиения H=0,0714 определены, запишем и сами интервалы (I=1,2,…8):

(Х1* х2*)=(Xmin—H/2; Xmin+ H/2)=(1,00-0,0714/2; 1,00+0,0714/2)=(0,9643; 1,0357);

(Х2*; х3*)=(1,0357; 1,0357+H)=(1,0357; 1,1071);

(Х3*; х4*)=(1,1071; 1,1071+H)=(1,1071; 1,1785);

(Х4*; х5*)=(1,1785; 1,1785+H)=(1,1785; 1,2499);

(Х5*; х6*)=(1,2499; 1,2499+H)=(1,2499; 1,3213);

(Х6*; х7*)=(1,3213; 1,3213+H)=(1,3213; 1,3927);

(Х7*; х8*)=(1,3927; 1,3927+H)=(1,3927; 1,4641);

(Х8*; х9*)=(1,4641; 1,4641+H)=(1,4641; 1,5355).

В каждом из полученных восьми интервалов проведем подсчет количества вариант исходного распределения выборки, попавших в эти интервалы. Это будут новые частоты для новых вариант Хί – середин получившихся интервалов. Таким образом, приходим к следующей таблице:

№ интервала

Интервалы

Середины интервалов

(новые варианты Хί )

Частоты

Ni

1

0,9643 – 1,0357

1,0000

4

2

1,0357 – 1,1071

1,0714

16

3

1,1071 – 1,1785

1,1428

14

4

1,1785 – 1,2499

1,2142

10

5

1,2499 – 1,3213

1,2856

26

6

1,3213 – 1,3927

1,3570

14

7

1,3927 – 1,4641

1,4284

10

8

1,4641 – 1,5355

1,4998

6

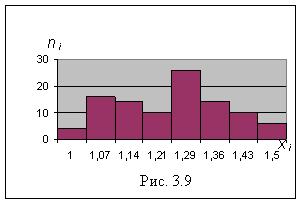
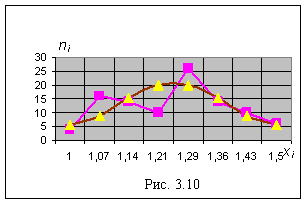
Данные этой таблицы можно, для наглядности, представить и в виде гистограммы частот, и в виде полигона частот (рис.3.9 и ломаная на рис.3.10):

И на гистограмме, и на полигоне частот обнаружился провал частот в их средней части, которого не должно быть, если исследуемый признак Х распределен нормально. То есть этот провал является доводом против выдвинутой гипотезы H0 о том, что признак Х Распределен нормально. Но этот провал мог образоваться и случайно – в силу случайности самой выборки. Так что пока неясно, принимать или отвергать гипотезу H0. Обоснованный вывод мы сделаем, если наряду с найденными экспериментальными частотами Ni вариант Хί найдем и их теоретические частоты Ni*, которые следуют из гипотезы H0, а затем сравним те и другие частоты по критерию Пирсона.

Для этого сначала по новым вариантам Хί и их частотам Ni найдем и – выборочную среднюю и исправленное выборочное среднее квадратическое отклонение:

Если исследуемая случайная величина Х распределена нормально, то заменяя ее неизвестные параметры и их точечными оценками и , получим:

Теперь, в соответствии с рис. 3.6, найдем по формулам (3.33) числа Zi (I=0, 1, 2,…8):

Zo = — ∞; Z1 = X1 + H/2 = 1,0000 + 0,0714/2 = 1,0357;

Z2 = X2 + H/2 = 1,0714 + 0,0714/2 = 1,1071; Z3 = 1,1785;

Z4 = 1,2499; Z5 = 1,3213; Z6 = 1,3927; Z7 = 1,4641; z8 = + ∞

После этого по формуле (3.32) подсчитаем вероятности Pi попадания значений величины Х в интервалы (I=1, 2,…8), а по ним по формулам Ni*=Npi (I=1, 2,…M) подсчитаем теоретические частоты Ni* наших новых вариант Хί (I=1, 2,…8). Подсчет этих теоретических частот оформим в виде таблицы, округляя, для точности, итоговые частоты Ni* до десятых, то есть до одного лишнего десятичного знака:

I

Pi

Ni*=npi =100 Pi

1

— ∞

1,0357

— ∞

-1,580

-0,5

-0,443

0,057

5,7

2

1,0357

1,1071

-1,580

-1,054

-0,443

-0,354

0,089

8,9

3

1,1071

1,1785

-1,054

-0,527

-0,354

-0,201

0,153

15,3

4

1,1785

1,2499

-0,527

0

-0,201

0

0,201

20,1

5

1,2499

1,3213

0

0,526

0

0,201

0,201

20,1

6

1,3213

1,3927

0,526

1,052

0,201

0,354

1,153

15,3

7

1,3927

1,4641

1,052

1,579

0,354

0,443

0,089

8,9

8

1,4641

+∞

1,579

+∞

0,443

0,5

0,057

5,7

∑

∑Ni*= 100,0

Полученные Для одних и тех же вариант Хί теоретические частоты Ni* и экспериментальные частоты Ni можем теперь сравнить. Сначала сделаем это визуально:

Ni

4

16

14

10

26

14

10

6

Ni*

5,7

8,9

15,3

20,1

20,1

15,3

8,9

5,7

Как видим, есть и небольшие расхождения, и существенные (особенно в паре 10 и 20,1) Особенно наглядно видны эти расхождения, если наряду с полигоном реальных частот Ni (ломаной) построить и полигон теоретических частот Ni* — плавную кривую нормального распределения (см. рис. 3.10).

Сравним, однако, частоты Ni И Ni* на согласованность с помощью критерия Пирсона. Так как условие «все частоты Ni должны быть не менее 5, кроме разве что крайних» у нас выполняется, то объединять частоты не будем. В соответствии с формулой (3.30) подсчитаем экспериментальное значение величины χ2:

χ2= χ2эксп=13,35

А теперь по таблице критических точек распределения «хи-квадрат» (таблица 3 Приложения) для уровня значимости α=0,05 и числа степеней свободы K=M-3=8-3=5 найдем критическое значение величины χ2:

Сравнивая χ2эксп И χ2кр видим, что χ2эксп> χ2кр. Таким образом, гипотезу H0 о нормальности исследуемого признака Х отвергаем – она не подтверждается экспериментальными данными. То есть расхождения между реальными и теоретическими частотами являются слишком существенными, чтобы, при справедливости гипотезы H0 , Их можно было отнести лишь на счет случайности самой выборки.

Впрочем, мы можем и ошибаться — гипотеза H0 О нормальности распределения признака Х объектов генеральной совокупности на самом деле может быть верна. В таком случае, отвергая ее, мы совершаем ошибку 1-го рода. И вероятность этой ошибки – это принятый нами уровень значимости α=0,05.

Упражнения

1. Станок-автомат должен изготовлять детали массой 20г. Известно, что средняя квадратичная ошибка в работе станка равна 0,1г. Из продукции станка наудачу отобрано 10 деталей. Средняя масса одной детали оказалась равной 20,08г. При уровне значимости а) α=0,05 и б) α=0,01 проверить гипотезу H0 о том, что станок настроен правильно при альтернативной гипотезе Н1, что станок настроен неправильно (производит в целом увеличенные или уменьшенные детали).

Ответ: а) гипотеза H0 отвергается; б) гипотеза H0 принимается.

2. Решить предыдущую задачу по проверке гипотезы H0 при альтернативной гипотезе H1, состоящей в том, что станок производит в целом увеличенные по массе детали.

Ответ: И в варианте а), и в варианте б) гипотеза H0 Отвергается.

3. Исследовались ошибки Х И Y двух однотипных приборов. Экспериментальные данные о допущенных ошибках измерений на этих приборах (они выявлены с помощью более точных приборов) таковы:

Xi

0,05

1,50

-1,35

-1,12

-0,52

Ni

1

1

1

1

1

Yi

1,82

0,10

-0,56

0,24

0,17

0,23

-0,31

Ni

1

1

1

1

1

1

1

При уровне значимости α=0,05 проверить гипотезу H0 О равной точности обоих приборов при альтернативной гипотезе Н1 О более высокой точности второго прибора.

Ответ: гипотеза H0 принимается.

4. В результате двух серий измерений с количеством измерений N1=25 и N2=50 получены следующие средние значения измеряемых величин А И B Соответственно: и . При уровне значимости α=0,01 проверить нулевую гипотезу H0 О равенстве А и B при альтернативной гипотезе Н1 о неравенстве А и B, если известно, что оба измерения равноточны со средним квадратическим отклонением σ = 0,30.

Ответ: гипотеза H0 отвергается.

5. Рассмотреть упражнение 3 с теми же данными, но при неизвестном σ. Взамен использовать исправленные выборочные дисперсии =0,28 и =0,33 указанных двух серий измерений.

Ответ: гипотеза H0 принимается.

6. Уровень исполнительского мастерства участников конкурса оценивался двумя судьями в баллах. Известны результаты оценки пяти первых участников конкурса:

Оценки первого судьи (Xi)

6

7

8

5

7

Оценки второго судьи (Yi)

7

6

8

7

8

При уровне значимости α=0,05 установить, значимо или незначимо различаются результаты оценок судей.

Ответ: оценки судей различаются незначимо.

Указание. Разность Z=X—Y оценок судей в силу большого числа факторов, влияющих на эту разность, можно, очевидно, считать случайной величиной, распределенной нормально. Если оценки судей различаются незначимо, то математическое ожидание величины Z равно нулю. А если значимо, то M(Z)≠0. Поэтому задача состоит в том, чтобы при уровне значимости α=0,05 проверить гипотезу о том, что M(Z)= А = 0 при альтернативной гипотезе Н1 о том, что M(Z)= а ≠ 0 при объеме выборки N=5.

7. Решить предыдущую задачу 6 по проверке гипотезы H0 о незначимости различия в оценках двух судей при альтернативной гипотезе Н1, Состоящей в том, что второй судья ставит в целом более высокие оценки, чем первый.

Ответ: гипотеза H0 принимается.

8. Для исследования массы Х клубней кормовой свеклы из урожая случайным образом отобрано 100 клубней. Статистическое распределение выборки оказалось таковым:

Xi(Кг)

0 — 1,0

1,0 – 2,0

2,0 – 3,0

3,0 – 4,0

4,0 – 5,0

5,0 – 6,0

Ni

20

20

28

22

12

8

Выдвинув гипотезу H0 О нормальном распределении массы Х клубней, найти соответствующие этой гипотезе теоретические частоты Ni* (I=1,2,…6) для указанной выше выборки. С помощью критерия Пирсона при уровне значимости а) α=0,05 и б) α=0,01 подтвердить или отвергнуть гипотезу H0.

Ответ:

Ni

20

20

28

22

12

8

Ni*

8

18

29

26

14

5

Гипотеза H0 Отклоняется при обоих уровнях значимости.

< Предыдущая   Следующая >
Источник

Понравилась статья? Поделить с друзьями:
  • Как найти где находится судно
  • Как найти файлы скачанные сегодня
  • War thunder как нашел танк
  • Как найти лицевой счет домофона
  • Как составить соп для аптеки