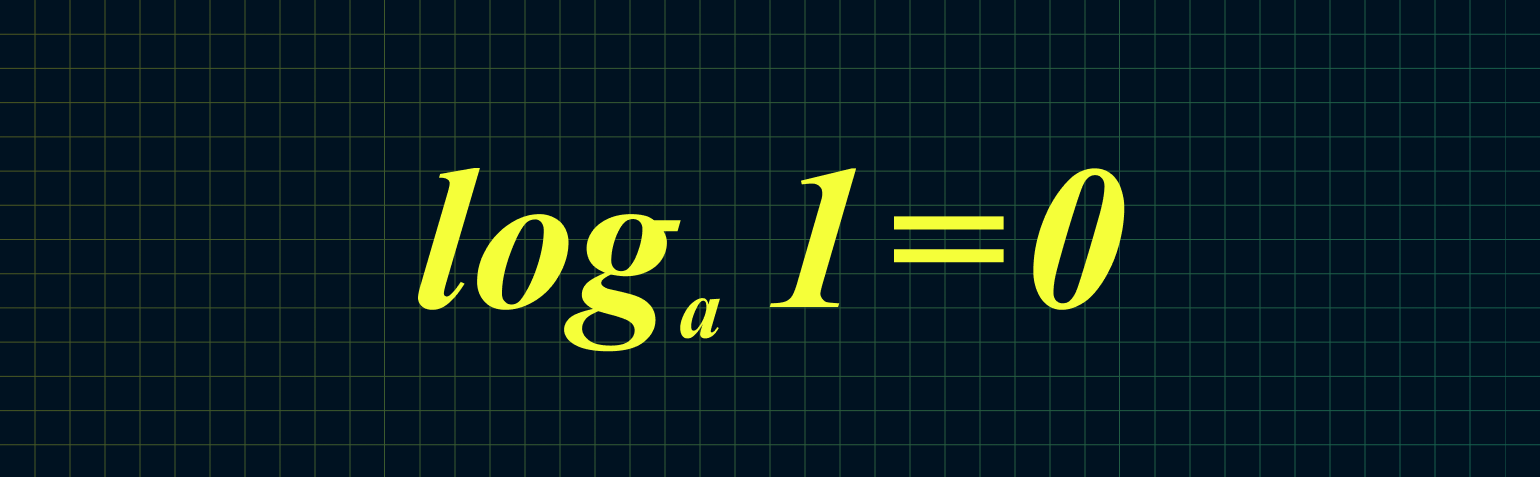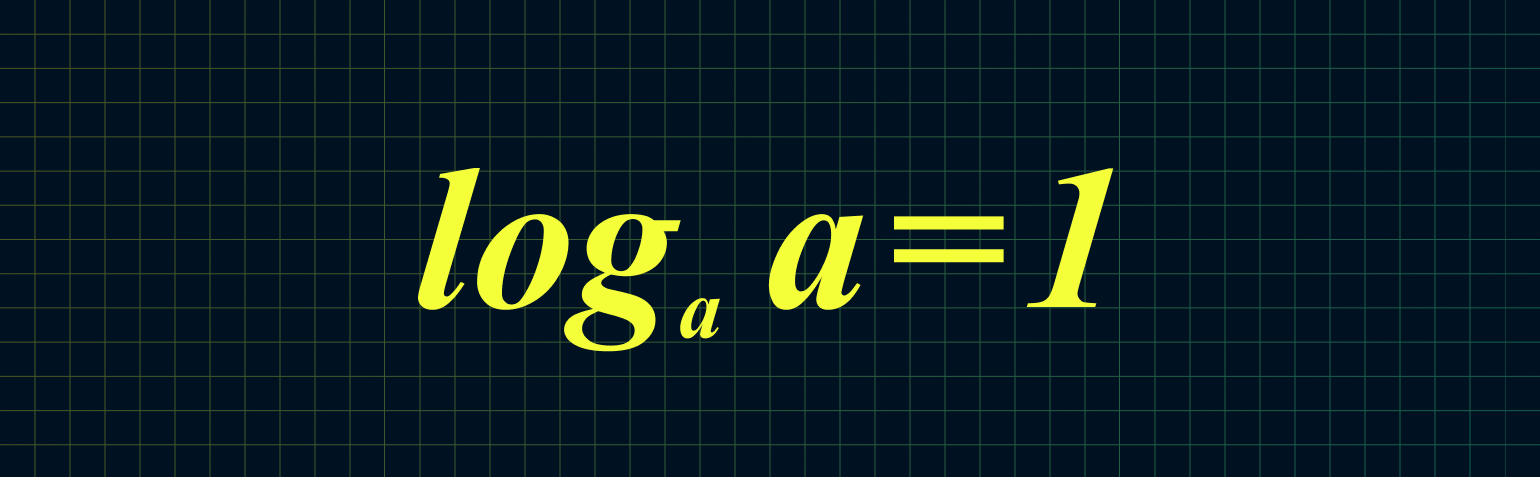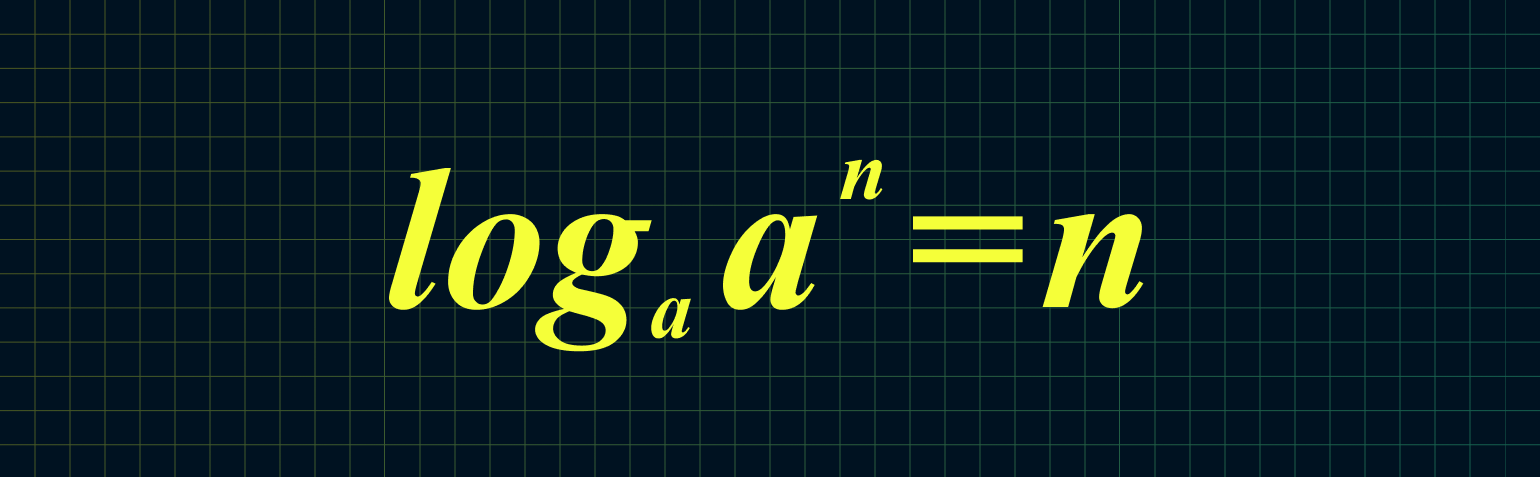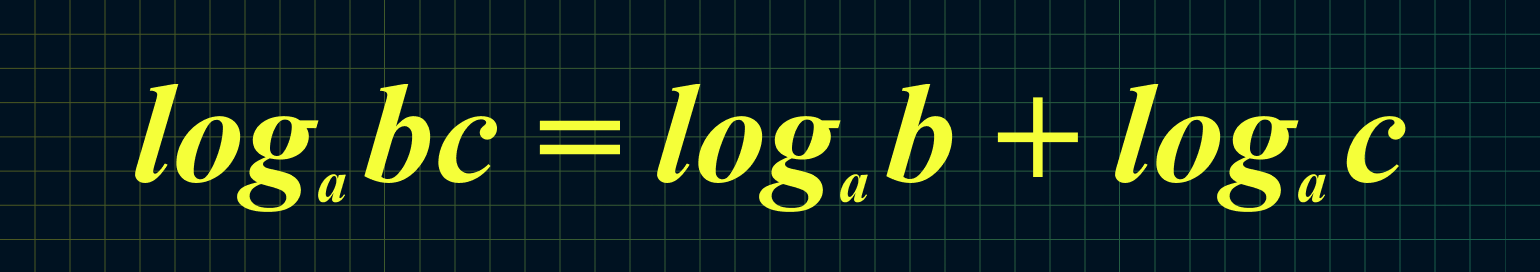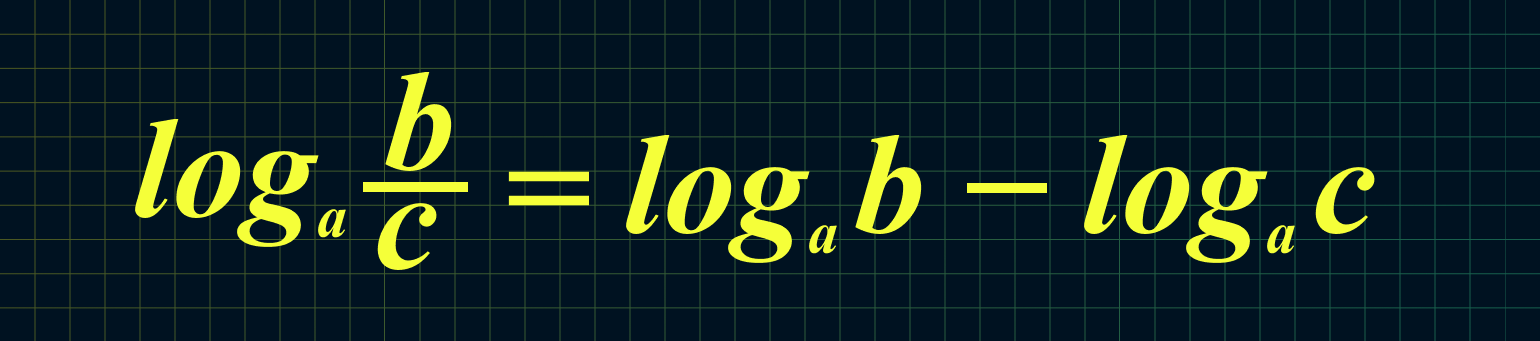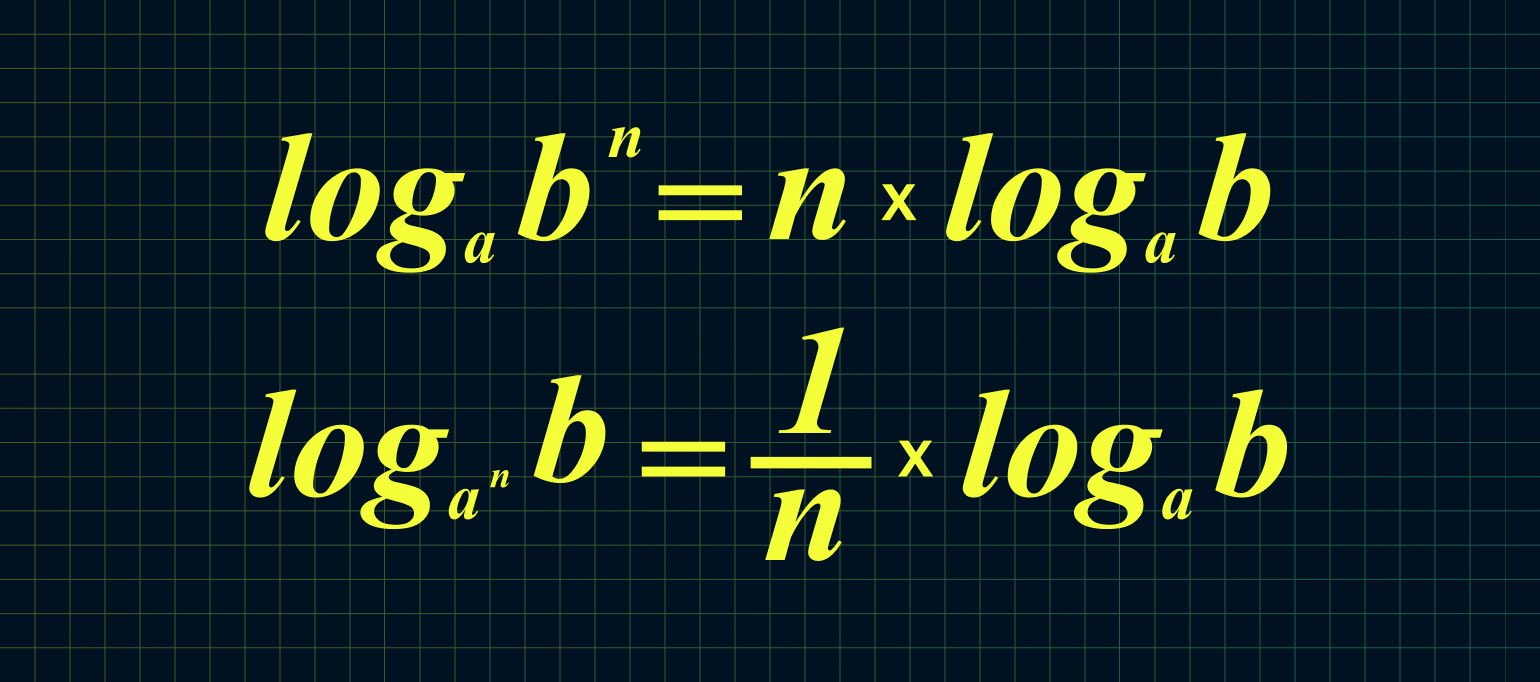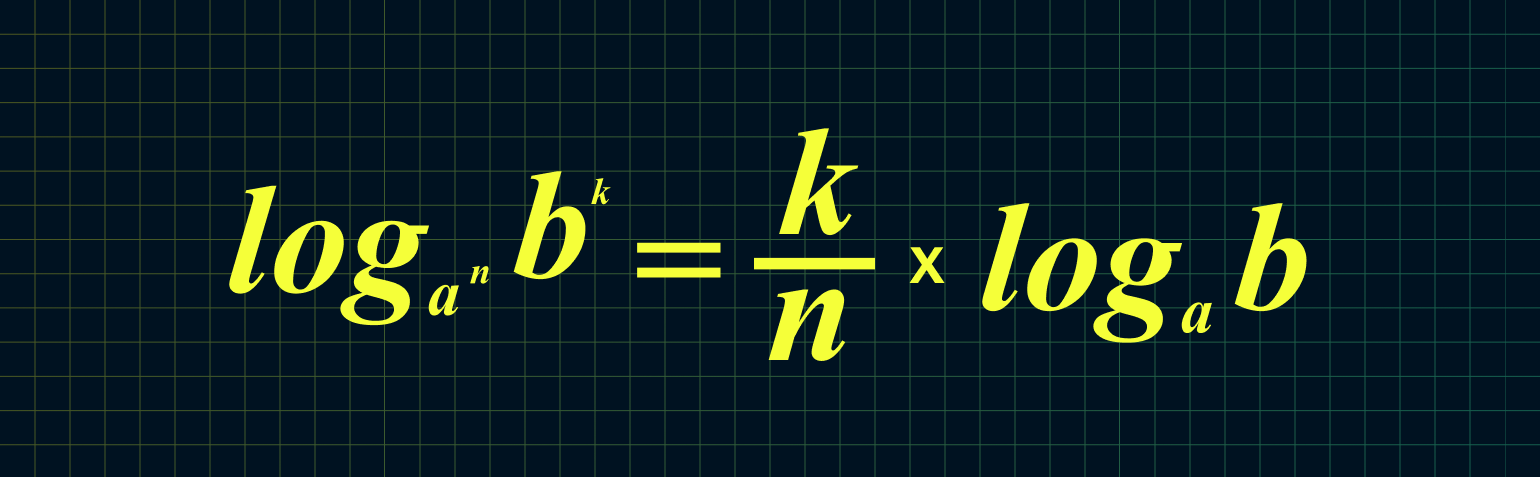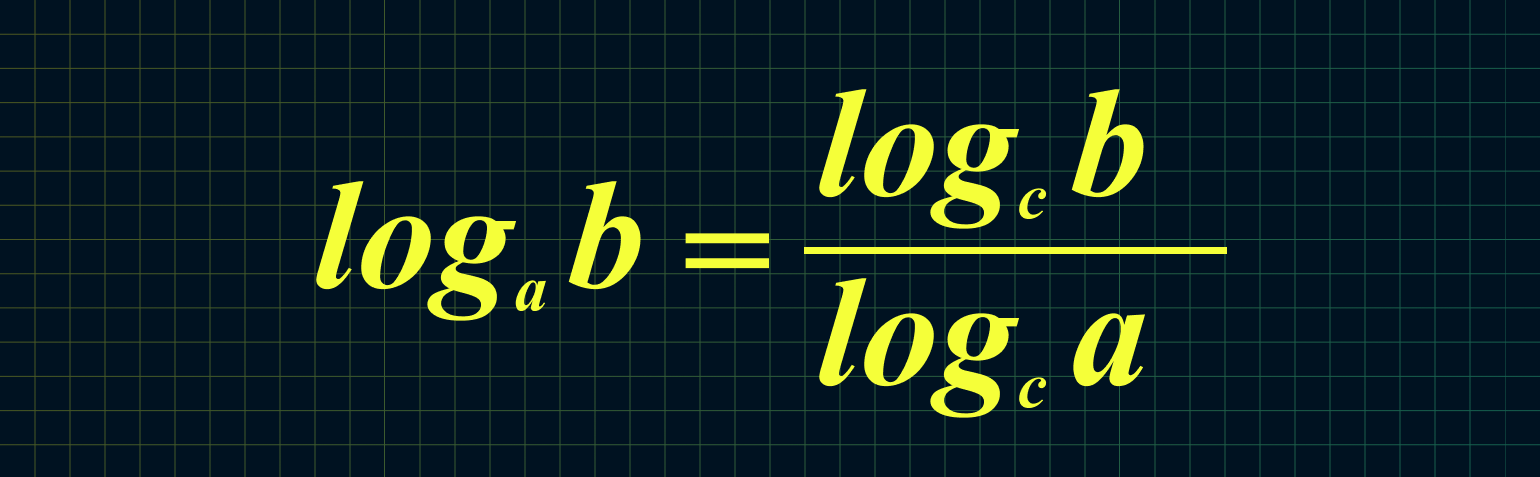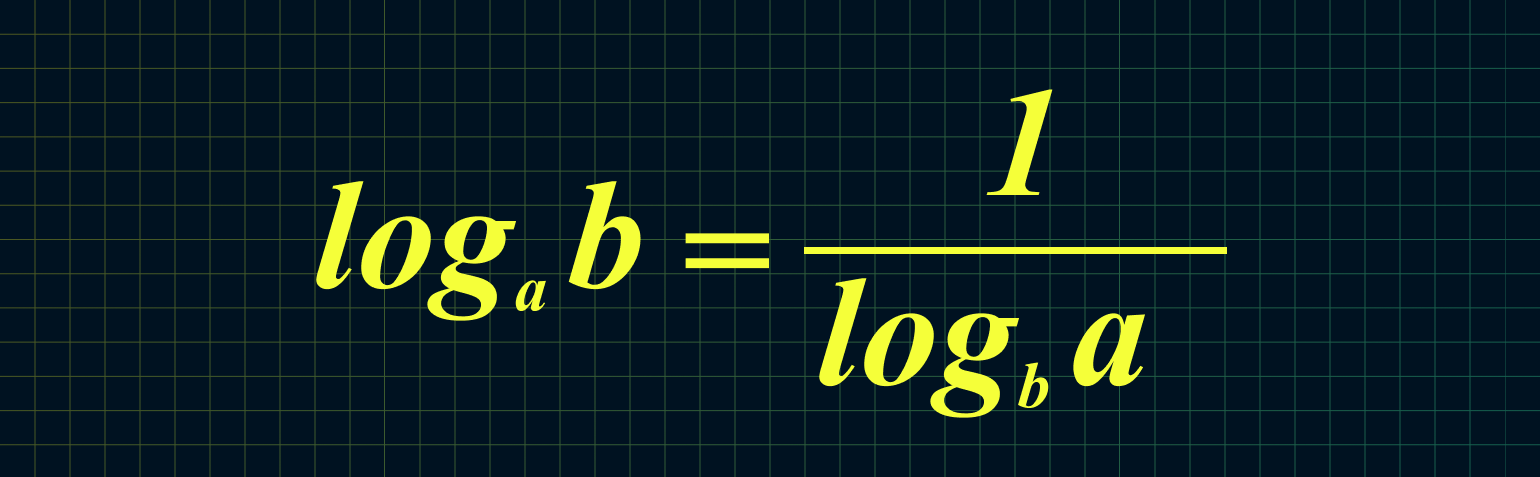С
показательных функций
выберем такую, график которой пересекает
ось
под углом
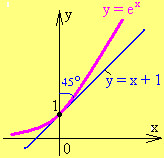
(рис. 19.1). Основание такой функции
обозначают
буквой
и пишут
или
.
Эту функцию и её
график называют экспонентой.
Равенства
равносильны. Логарифм
,
имеющий основание
,
принято обозначать
и называть
натуральным логарифмом.
Итак,
|
|
поэтому Рис. 19.1
Переставив буквы
и
вы получаете обратную функцию
График логарифмической
функции с основанием
показан на рис. 19.1. Отметим, что
.
Возьмём наши
равносильные равенства
Подставив первое
равенство во второе, будете иметь
А если подставить
второе равенство в первое, вы получите
Следовательно,
|
|
|
|
здесь |
здесь |
(19.2)
20. Вторая замечательная эквивалентность
|
|
Второй замечательной
эквивалентностью называется следующее
выражение
(20.1)
Докажем его.
♥
На рис. 20.1 вы видите,
что вблизи точки
обе линии
и
сливаются, совпадают,
поэтому
где
бесконечно малая
переменная. Получилась
формула (20.1). ■
Эта формула позволяет
раскрывать
неопределённости
вида
З
а д а ч а 1. Найдите
Рис.
20.1
□

■
Итак, получилось
Давайте сделаем в
этой формуле замену
Тогда
и
при
будет
теперь формула запишется так
Эта формула называется
вторым
замечательным пределом.
З
а д а ч а 2. Найдите
□
■
З
а д а ч а 3. Найдите
□
■
Из (20.1) получаются
полезные формулы
♥
отсюда
получилась первая формула;
получилась вторая
формула. ■
21. Сводка формул для раскрытия неопределённостей
Соберём вместе
формулы, применяемые для раскрытия
неопределённостей.
|
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
22. Непрерывная функция
Н
рис. 22.1 график непрерывен, его можно
нарисовать, не отрывая ручки от бу -маги.
Когда график функции непрерывен, то и
саму функцию будем называть непрерывной.
Но как выяснить, непрерывна ли функция,
не рисуя её график?
Пусть имеется функция
Если вы дадите переменной
приращение
то зависящая от неё функция тоже получит
приращение
На рис. 22.1 вы видите,
что при уменьшении
будет уменьшаться
т. е. при
будет
.
Поэтому можно ввести следующее
определение: Рис.
22.1
|
Если при
во всех точках |
|
то функция |
Иначе говоря, функция
непрерывна,
если при бесконечно малых
получаются бесконечно малые
.
Бесконечно малое
приращение переменной
принято обозначать
.
Можно доказать, что
каждая простейшая
функция непрерывна в своей области
определения.
(22.1)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Когда я думаю о задаче, которая касается степеней и логарифмов, я задаю себе два вопроса:
Речь идет о вводных параметрах (то, что вызвало конечное изменение) или о результате (собственно, произошедшем изменении)?
- Логарифмы раскрывают именно аргументы (входные параметры), которые вызвали рост
- Степени помогают вычислить конечный результат роста
Мы смотрим на задачу с позиции объекта роста или наблюдателя этого процесса?
- e и натуральный логарифм отражают рост с позиции объекта роста.
- Основание 10, основание 2 и т.д. — это измерения, удобные для наблюдателя.
В своей голове я упорядочиваю всё в таблицу:
| Найти причину | Найти следствие | |
|---|---|---|
| С точки зрения растущего | ln(x)натуральный логарифм |
exэкспонента с основанием e |
| С точки зрения наблюдателя | log10(x), log2(x)другие логарифмы |
10x, 2xдругие экспоненты |
У меня появляются мысли вроде «Мне нужна причина, с точки зрения того, кто растет… это натуральный логарифм.». (Натуральный логарифм на латыни звучит как logarithmus naturalis, отсюда пошло и сокращение, используемое в математике, — ln).
Я очень не любил уроки, на которых преподаватель описывал содержимое таблицы, эти функции, без каких-либо пояснений, когда и как их нужно применять!
Такой подход, увы, не срабатывает. Давайте попрактикуемся в том, как мыслить логарифмами и степенями, на реальных примерах.
Пример №1: Описание роста ВВП
Вот типичный пример роста:
- С 2000 по 2010 год ВВП страны изменился с 9,9 триллионов до 14,4 триллионов монет.
Хорошо, эти цифры показывают уже произошедшее изменение. Но нам бы, возможно, хотелось узнать составные части такого изменения: Какой средний ежегодный прирост привел к такому конечному изменению? И тут же мой мозг подсказывает мне: «логарифмы», потому что мы задаемся вопросом, что вызвало такой конечный рост. В голове срабатывает схема:
логарифм изменения → источник роста
Неплохой старт, но давайте его немного дополним.
Для начала, какой логарифм нам использовать?
По умолчанию я выбираю натуральный логарифм. Большинство событий касаются непосредственно предмета роста (а не наблюдателя), и я люблю «идти рядом» с растущим объектом, чтобы визуализировать происходящее. (Так же и с радианами: они измеряют углы с позиции того, кто движется).
Следующий вопрос: к какому изменению применить логарифм?
Мы всего лишь заинтересованы в отношении между стартом и финишем: 9,9 миллиардов к 14,4 миллиардам за 10 лет. Это такой же коэффициент роста, как если вырасти с 9.9 монет до 14.4 монет за тот же период времени.
Мы можем отточить нашу первоначальную мысль:
натуральный логарифм доли роста → источник роста
Хорошо, источником роста послужил коэффициент в 0,374 или 37,4%. Мы закончили?
Еще нет. Логарифмы ничего не знают о том, сколько времени понадобилось на такое изменение (мы же не включили в расчет 10 лет, верно?). У нас получился коэффициент, как если бы всё изменение целиком произошло за 1 единицу времени.
Такой прирост в 37,4% действительно мог случиться за один год, или за два года равномерного роста на 18,7%, или из любой другой комбинации.
По сценарию мы знаем, что изменение произошло за 10 лет, и коэффициент этого изменения должен быть:
С точки зрения постоянного, равномерного роста, экономика страны росла на 3,74% ежегодно.
Теперь мы закончили? Еще нет!
Этот постоянный коэффициент рассчитан с позиции растущего объекта (т.е. ВВП), как если бы мы постоянно шли рядом с экономикой на графике, пока она изменялась. Банкиру, вероятно, хотелось бы знать ежегодную разницу в приросте. Мы можем рассчитать этот показатель, дав постоянному росту поработать годик:
экспонента со скоростью и временем → эффект от роста
Ежегодный прирост составил 3,8%, немного выше, чем 3,74% — мгновенный коэффициент, без учета роста самого прироста. Получается, что:
- Данная часть экономики номинально растет на 3,74% , этот рост смоделирован функцией e0,0374 × годы
- Если считать по ежегодному базису, когда срабатывает составной рост ВВП (образовавшаяся часть прироста дает свой собственный прирост), то общий прирост составит уже 3,81%, смоделированный функцией 1,0381годы
В финансах актуальнее исследовать изменения по сравнению с предыдущим годом, которые можно сравнивать с другими трендами. В науке и технике предпочтительнее моделировать текущее поведение, исследуя мгновенные изменения.
Пример №2: Описание естественного роста
Я ненавижу надуманные примеры вроде «Предположим, что количество бактерий удваивается каждые 24 часа, вычислите формулу их роста». Неужели колонии бактерий размножаются четко по человеческим часам, и к конкретному времени мы ожидаем точное удвоение популяции?
Вот сценарий получше: «Я нашел немного бактерий, подождал часок, и в результате их общая масса увеличилась с 2,3 до 2,32 граммов. Сейчас я иду на обед. Вычислите, какое количество бактерий будет через 3 часа, когда я вернусь».
Давайте смоделируем эту ситуацию. Нам нужен логарифм для вычисления коэффициента роста, а затем степень, чтобы спроектировать будущий рост. Как и в предыдущий раз, давайте для начала придерживаться натуральных логарифмов.
Фактор роста таков:
логарифм изменения → источник роста
Это и есть коэффициент роста за один час, и общая модель будущего роста будет:
экспонента со скоростью и временем → эффект от роста
Если на старте у нас 2,32 грамма, то рост за 3 часа будет:
Ну и из спортивного интереса, через какое время бактерии удвоятся в количестве? Представьте, что мы ждем, пока 1 превратится в 2:
Мы можем механически вычислить натуральный логарифм обеих сторон уравнения, чтобы «отменить экспоненту», но давайте мыслить интуитивно.
Если 2 — это конечный результат, то ln(2) — это рост, который привел нас к этому результату (какой-то коэффициент x время). Мы знаем, что коэффициент равен 0,0086, так что время роста до 2 будет таким:
Колония удвоится через ~80 часов. (Не пропало желание дождаться этого результата?)
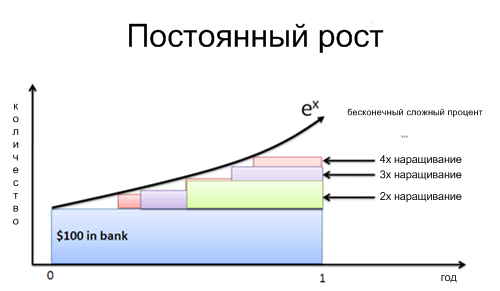
Что в действительности означает смена перспективы?
Выбор поиска входной величины (источника роста) или исхода (результат роста) очень прост. Но как Вы визуализируете процесс с точки зрения объекта роста?
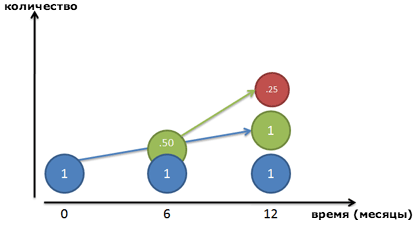
Представьте, что у нас есть два маленьких работника, которые строят финальную модель роста (помните графики из статьи про экспоненты и число е, где деньги были как пример?)
Если коэффициент роста 100%, мы говорим нашему работнику (синий кружок) работать старательно и создать 100% копию себя самого к концу года (зеленый кружок).
Но… новый работник (зеленый кружок) тоже начинает работать. Если Зеленый впервые появляется на графике на отметке в 6 месяцев, у него есть еще полгода на работу (при таком же ежегодном коэффициенте роста, как и Синего). Зеленый человечек начинает создавать Красного. Конечно, Красный будет сделан только наполовину к концу срока, потому что у Зеленого было в запасе только полгода.
А что, если Зеленый впервые появился не через полгода, а через 4 месяца? Месяц? День? Секунду? Если работники начали работу сразу, то у нас будет кривая мгновенных изменений, определенная ex:
Натуральный логарифм дает нам коэффициент роста с точки зрения того самого «человечка». Мы включаем этот коэффициент в ex, чтобы найти конечный результат, включая все составные роста.
Использование других оснований
Переключение на другой тип логарифма (с основанием 10, с основанием 2 и т.д.) означает, что мы ищем определенную закономерность в общем росте, а не что-то, касающееся конкретного работника. Каждый логарифм задается своим вопросом, когда происходит изменение:
- Логарифм с основанием e: Какова мгновенная скорость работы каждого работника?
- Логарифм с основанием 2: Как много удвоений требуется?
- Логарифм с основанием 10: Сколько удесятерений требуется?
Вот небольшой пример для анализа:
- За последние 30 лет количество транзисторов в типичных микросхемах увеличилось с 1000 до 1 миллиарда.
Как вы это проанализируете?
- Все эти микросхемы — это не совокупная единица, которая плавно растет с течением времени. Это разные схемы, произведенные разными конкурирующими компаниями, которые в совокупности определяют общий тренд развития.
- Так как мы не «идем рядом» с расширяющейся микросхемой, давайте использовать масштаб, созданный для удобства человека, чтобы проанализировать такой рост. Об удвоении как-то проще размышлять, чем об удесятерении, так что с него и начнем.
Получаем:
логарифм изменения → источник роста
«Источником роста» послужили 20 удвоений, которые, как мы знаем, произошли в течение 30 лет. В среднем это 2/3 удвоений за год или 1,5 года на каждое удвоение.
С позиции растущего объекта, мы вычислим ln(1 миллиард/1000)/30 лет=46% непрерывного роста (такой рост немного сложно представить в контексте данного примера). Мы можем резюмировать наш анализ в таблицу:
Ситуация: от тысячи к 1 млрд транзисторов за 30 лет
| Найти причину | Найти следствие | |
|---|---|---|
| С точки зрения растущего | ln(1 млрд/1000) = 13.8113.81 входящей причины / 30 лет = коэффициент 0.46 в годнайти коэффициент непрерывного роста |
e0.46 × годыпромоделировать непрерывный рост |
| С точки зрения наблюдателя | log2(1 млрд/1000) = 20 удвоений20 удвоений / 30 лет = 23 удвоения в годнайти коэффициент роста удвоениями |
223 × годыпромоделировать рост удвоениями |
Заключение
Изучение — это процесс поиска скрытого смысла за определенным понятием. Когда это понятие используется? С какого угла нужно посмотреть на задачу?
Данная интерпретация говорит о том, что показатели степени как бы спрашивают — причина или результат, объект роста или наблюдатель роста? Именно это и помогает мне понять суть логарифмов и степеней.
Приложение: Изменение базовой формулы
Вот как можно пояснить смену оснований. Взяв 100% непрерывный показатель прироста:
- ln(x) — это время роста до x
- ln(2) — это время роста до 2
Так как на удвоение у нас уйдет определенное время, мы можем вычислить, как много удвоений «поместится» в общее время роста до x:
Например, сколько удвоений происходит с 1 до 64?
Ну, ln(64)=4,158. А ln(2)=0,693. Количество удвоений равно:
В реальном мире калькуляторы могут быть не точными, так что по возможности используйте функцию логарифма с основанием 2. И, конечно, у нас может получиться дробное число: рост с 1 до квадратного корня 2 — это «половина» удвоения, или log2(1.414) = 0,5. Переход к логарифму с основанием 10 означает, что мы подсчитываем количество удесятерений, которое «помещается» в рост с 1 до х:
Здорово, правда?
Приятных вам вычислений!
Перевод статьи «How To Think With Exponents And Logarithms»
| Natural logarithm | |
|---|---|

Graph of part of the natural logarithm function. The function slowly grows to positive infinity as x increases, and slowly goes to negative infinity as x approaches 0 («slowly» as compared to any power law of x). |
|
| General information | |
| General definition |  |
| Motivation of invention | Analytic proofs |
| Fields of application | Pure and applied mathematics |
| Domain, Codomain and Image | |
| Domain |  |
| Codomain |  |
| Image |  |
| Specific values | |
| Value at +∞ | +∞ |
| Value at e | 1 |
| Specific features | |
| Asymptote |  |
| Root | 1 |
| Inverse |  |
| Derivative |  |
| Antiderivative |  |
The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, loge x, or sometimes, if the base e is implicit, simply log x.[1][2] Parentheses are sometimes added for clarity, giving ln(x), loge(x), or log(x). This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.
The natural logarithm of x is the power to which e would have to be raised to equal x. For example, ln 7.5 is 2.0149…, because e2.0149… = 7.5. The natural logarithm of e itself, ln e, is 1, because e1 = e, while the natural logarithm of 1 is 0, since e0 = 1.
The natural logarithm can be defined for any positive real number a as the area under the curve y = 1/x from 1 to a[3] (with the area being negative when 0 < a < 1). The simplicity of this definition, which is matched in many other formulas involving the natural logarithm, leads to the term «natural». The definition of the natural logarithm can then be extended to give logarithm values for negative numbers and for all non-zero complex numbers, although this leads to a multi-valued function: see Complex logarithm for more.
The natural logarithm function, if considered as a real-valued function of a positive real variable, is the inverse function of the exponential function, leading to the identities:
Like all logarithms, the natural logarithm maps multiplication of positive numbers into addition:
[4]
Logarithms can be defined for any positive base other than 1, not only e. However, logarithms in other bases differ only by a constant multiplier from the natural logarithm, and can be defined in terms of the latter, 
Logarithms are useful for solving equations in which the unknown appears as the exponent of some other quantity. For example, logarithms are used to solve for the half-life, decay constant, or unknown time in exponential decay problems. They are important in many branches of mathematics and scientific disciplines, and are used to solve problems involving compound interest.
History[edit]
The concept of the natural logarithm was worked out by Gregoire de Saint-Vincent and Alphonse Antonio de Sarasa before 1649.[5] Their work involved quadrature of the hyperbola with equation xy = 1, by determination of the area of hyperbolic sectors. Their solution generated the requisite «hyperbolic logarithm» function, which had the properties now associated with the natural logarithm.
An early mention of the natural logarithm was by Nicholas Mercator in his work Logarithmotechnia, published in 1668,[6] although the mathematics teacher John Speidell had already compiled a table of what in fact were effectively natural logarithms in 1619.[7] It has been said that Speidell’s logarithms were to the base e, but this is not entirely true due to complications with the values being expressed as integers.[7]: 152
Notational conventions[edit]
The notations ln x and loge x both refer unambiguously to the natural logarithm of x, and log x without an explicit base may also refer to the natural logarithm. This usage is common in mathematics, along with some scientific contexts as well as in many programming languages.[nb 1] In some other contexts such as chemistry, however, log x can be used to denote the common (base 10) logarithm. It may also refer to the binary (base 2) logarithm in the context of computer science, particularly in the context of time complexity.
Definitions[edit]
The natural logarithm can be defined in several equivalent ways.
Inverse of exponential[edit]
The most general definition is as the inverse function of 











Doing so yields:
This definition therefore derives its own principal branch from the principal branch of nth roots.
Integral definition[edit]
ln a as the area of the shaded region under the curve f(x) = 1/x from 1 to a. If a is less than 1, the area taken to be negative.
The area under the hyperbola satisfies the logarithm rule. Here A(s,t) denotes the area under the hyperbola between s and t.
The natural logarithm of a positive, real number a may be defined as the area under the graph of the hyperbola with equation y = 1/x between x = 1 and x = a. This is the integral[3]
If a is less than 1, then this area is considered to be negative.
This function is a logarithm because it satisfies the fundamental multiplicative property of a logarithm:[4]
This can be demonstrated by splitting the integral that defines ln ab into two parts, and then making the variable substitution x = at (so dx = a dt) in the second part, as follows:
In elementary terms, this is simply scaling by 1/a in the horizontal direction and by a in the vertical direction. Area does not change under this transformation, but the region between a and ab is reconfigured. Because the function a/(ax) is equal to the function 1/x, the resulting area is precisely ln b.
The number e can then be defined to be the unique real number a such that ln a = 1.
The natural logarithm also has an improper integral representation,[8] which can be derived with Fubini’s theorem as follows:

Properties[edit]
Derivative[edit]
The derivative of the natural logarithm as a real-valued function on the positive reals is given by[3]
How to establish this derivative of the natural logarithm depends on how it is defined firsthand. If the natural logarithm is defined as the integral
then the derivative immediately follows from the first part of the fundamental theorem of calculus.
On the other hand, if the natural logarithm is defined as the inverse of the (natural) exponential function, then the derivative (for x > 0) can be found by using the properties of the logarithm and a definition of the exponential function. From the definition of the number 


Also, we have:
so, unlike its inverse function 
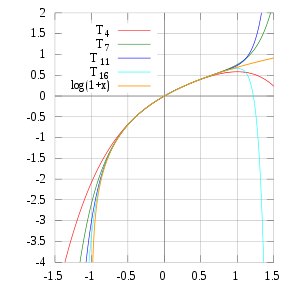
Series[edit]
The Taylor polynomials for ln(1 + x) only provide accurate approximations in the range −1 < x ≤ 1. Beyond some x > 1, the Taylor polynomials of higher degree are increasingly worse approximations.
Since the natural logarithm is undefined at 0, 

This is the Taylor series for ln x around 1. A change of variables yields the Mercator series:
valid for |x| ≤ 1 and x ≠ −1.
Leonhard Euler,[10] disregarding 
The figure is a graph of ln(1 + x) and some of its Taylor polynomials around 0. These approximations converge to the function only in the region −1 < x ≤ 1; outside this region, the higher-degree Taylor polynomials devolve to worse approximations for the function.
A useful special case for positive integers n, taking 
If 
Now, taking 
If 
Since
we arrive at
Using the substitution 
This is, by far, the fastest converging of the series described here.
The natural logarithm can also be expressed as an infinite product:[11]
Two examples might be:
From this identity, we can easily get that:
For example:
The natural logarithm in integration[edit]
The natural logarithm allows simple integration of functions of the form g(x) = f ‘(x)/f(x): an antiderivative of g(x) is given by ln(|f(x)|). This is the case because of the chain rule and the following fact:
In other words, when integrating over an interval of the real line that does not include 
where C is an arbitrary constant of integration.[12]
Likewise, when the integral is over an interval where 
For example, consider the integral of tan(x) over an interval that does not include points where tan(x) is infinite:
The natural logarithm can be integrated using integration by parts:
Let:
then:
Efficient computation[edit]
For ln(x) where x > 1, the closer the value of x is to 1, the faster the rate of convergence of its Taylor series centered at 1. The identities associated with the logarithm can be leveraged to exploit this:
Such techniques were used before calculators, by referring to numerical tables and performing manipulations such as those above.
Natural logarithm of 10[edit]
The natural logarithm of 10, which has the decimal expansion 2.30258509…,[13] plays a role for example in the computation of natural logarithms of numbers represented in scientific notation, as a mantissa multiplied by a power of 10:
This means that one can effectively calculate the logarithms of numbers with very large or very small magnitude using the logarithms of a relatively small set of decimals in the range [1, 10).
High precision[edit]
To compute the natural logarithm with many digits of precision, the Taylor series approach is not efficient since the convergence is slow. Especially if x is near 1, a good alternative is to use Halley’s method or Newton’s method to invert the exponential function, because the series of the exponential function converges more quickly. For finding the value of y to give exp(y) − x = 0 using Halley’s method, or equivalently to give exp(y/2) − x exp(−y/2) = 0 using Newton’s method, the iteration simplifies to
which has cubic convergence to ln(x).
Another alternative for extremely high precision calculation is the formula[14][15]
where M denotes the arithmetic-geometric mean of 1 and 4/s, and
with m chosen so that p bits of precision is attained. (For most purposes, the value of 8 for m is sufficient.) In fact, if this method is used, Newton inversion of the natural logarithm may conversely be used to calculate the exponential function efficiently. (The constants ln 2 and π can be pre-computed to the desired precision using any of several known quickly converging series.) Or, the following formula can be used:
where
are the Jacobi theta functions.[16]
Based on a proposal by William Kahan and first implemented in the Hewlett-Packard HP-41C calculator in 1979 (referred to under «LN1» in the display, only), some calculators, operating systems (for example Berkeley UNIX 4.3BSD[17]), computer algebra systems and programming languages (for example C99[18]) provide a special natural logarithm plus 1 function, alternatively named LNP1,[19][20] or log1p[18] to give more accurate results for logarithms close to zero by passing arguments x, also close to zero, to a function log1p(x), which returns the value ln(1+x), instead of passing a value y close to 1 to a function returning ln(y).[18][19][20] The function log1p avoids in the floating point arithmetic a near cancelling of the absolute term 1 with the second term from the Taylor expansion of the ln. This keeps the argument, the result, and intermediate steps all close to zero where they can be most accurately represented as floating-point numbers.[19][20]
In addition to base e the IEEE 754-2008 standard defines similar logarithmic functions near 1 for binary and decimal logarithms: log2(1 + x) and log10(1 + x).
Similar inverse functions named «expm1»,[18] «expm»[19][20] or «exp1m» exist as well, all with the meaning of expm1(x) = exp(x) − 1.[nb 2]
An identity in terms of the inverse hyperbolic tangent,
gives a high precision value for small values of x on systems that do not implement log1p(x).
Computational complexity[edit]
The computational complexity of computing the natural logarithm using the arithmetic-geometric mean (for both of the above methods) is O(M(n) ln n). Here n is the number of digits of precision at which the natural logarithm is to be evaluated and M(n) is the computational complexity of multiplying two n-digit numbers.
Continued fractions[edit]
While no simple continued fractions are available, several generalized continued fractions are, including:
These continued fractions—particularly the last—converge rapidly for values close to 1. However, the natural logarithms of much larger numbers can easily be computed, by repeatedly adding those of smaller numbers, with similarly rapid convergence.
For example, since 2 = 1.253 × 1.024, the natural logarithm of 2 can be computed as:
Furthermore, since 10 = 1.2510 × 1.0243, even the natural logarithm of 10 can be computed similarly as:
The reciprocal of the natural logarithm can be also written in this way:
For example:
Complex logarithms[edit]
The exponential function can be extended to a function which gives a complex number as ez for any arbitrary complex number z; simply use the infinite series with x=z complex. This exponential function can be inverted to form a complex logarithm that exhibits most of the properties of the ordinary logarithm. There are two difficulties involved: no x has ex = 0; and it turns out that e2iπ = 1 = e0. Since the multiplicative property still works for the complex exponential function, ez = ez+2kiπ, for all complex z and integers k.
So the logarithm cannot be defined for the whole complex plane, and even then it is multi-valued—any complex logarithm can be changed into an «equivalent» logarithm by adding any integer multiple of 2iπ at will. The complex logarithm can only be single-valued on the cut plane. For example, ln i = iπ/2 or 5iπ/2 or —3iπ/2, etc.; and although i4 = 1, 4 ln i can be defined as 2iπ, or 10iπ or −6iπ, and so on.
- Plots of the natural logarithm function on the complex plane (principal branch)
-
z = Re(ln(x + yi))
-
z = |(Im(ln(x + yi)))|
-
z = |(ln(x + yi))|
-
Superposition of the previous three graphs
See also[edit]
- Approximating natural exponents (log base e)
- Iterated logarithm
- Napierian logarithm
- List of logarithmic identities
- Logarithm of a matrix
- Logarithmic differentiation
- Logarithmic integral function
- Nicholas Mercator – first to use the term natural logarithm
- Polylogarithm
- Von Mangoldt function
Notes[edit]
- ^ Including C, C++, SAS, MATLAB, Mathematica, Fortran, and some BASIC dialects
- ^ For a similar approach to reduce round-off errors of calculations for certain input values see trigonometric functions like versine, vercosine, coversine, covercosine, haversine, havercosine, hacoversine, hacovercosine, exsecant and excosecant.
References[edit]
- ^ G.H. Hardy and E.M. Wright, An Introduction to the Theory of Numbers, 4th Ed., Oxford 1975, footnote to paragraph 1.7: «log x is, of course, the ‘Naperian’ logarithm of x, to base e. ‘Common’ logarithms have no mathematical interest«.
- ^ Mortimer, Robert G. (2005). Mathematics for physical chemistry (3rd ed.). Academic Press. p. 9. ISBN 0-12-508347-5. Extract of page 9
- ^ a b c Weisstein, Eric W. «Natural Logarithm». mathworld.wolfram.com. Retrieved 2020-08-29.
- ^ a b «Rules, Examples, & Formulas». Logarithm. Encyclopedia Britannica. Retrieved 2020-08-29.
- ^ Burn, R.P. (2001). Alphonse Antonio de Sarasa and Logarithms. Historia Mathematica. pp. 28:1–17.
- ^ O’Connor, J. J.; Robertson, E. F. (September 2001). «The number e». The MacTutor History of Mathematics archive. Retrieved 2009-02-02.
- ^ a b Cajori, Florian (1991). A History of Mathematics (5th ed.). AMS Bookstore. p. 152. ISBN 0-8218-2102-4.
- ^ An improper integral representation of the natural logarithm., retrieved 2022-09-24
- ^ ««Logarithmic Expansions» at Math2.org».
- ^ Leonhard Euler, Introductio in Analysin Infinitorum. Tomus Primus. Bousquet, Lausanne 1748. Exemplum 1, p. 228; quoque in: Opera Omnia, Series Prima, Opera Mathematica, Volumen Octavum, Teubner 1922
- ^ RUFFA, Anthony. «A PROCEDURE FOR GENERATING INFINITE SERIES IDENTITIES» (PDF). International Journal of Mathematics and Mathematical Sciences. International Journal of Mathematics and Mathematical Sciences. Retrieved 2022-02-27. (Page 3654, equation 2.6)
- ^ For a detailed proof see for instance: George B. Thomas, Jr and Ross L. Finney, Calculus and Analytic Geometry, 5th edition, Addison-Wesley 1979, Section 6-5 pages 305-306.
- ^ OEIS: A002392
- ^ Sasaki, T.; Kanada, Y. (1982). «Practically fast multiple-precision evaluation of log(x)». Journal of Information Processing. 5 (4): 247–250. Retrieved 2011-03-30.
- ^ Ahrendt, Timm (1999). «Fast Computations of the Exponential Function». Stacs 99. Lecture Notes in Computer Science. 1564: 302–312. doi:10.1007/3-540-49116-3_28. ISBN 978-3-540-65691-3.
- ^ Borwein, Jonathan M.; Borwein, Peter B. (1987). Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity (First ed.). Wiley-Interscience. ISBN 0-471-83138-7. page 225
- ^ Beebe, Nelson H. F. (2017-08-22). «Chapter 10.4. Logarithm near one». The Mathematical-Function Computation Handbook — Programming Using the MathCW Portable Software Library (1 ed.). Salt Lake City, UT, USA: Springer International Publishing AG. pp. 290–292. doi:10.1007/978-3-319-64110-2. ISBN 978-3-319-64109-6. LCCN 2017947446. S2CID 30244721.
In 1987, Berkeley UNIX 4.3BSD introduced the log1p() function
- ^ a b c d Beebe, Nelson H. F. (2002-07-09). «Computation of expm1 = exp(x)−1» (PDF). 1.00. Salt Lake City, Utah, USA: Department of Mathematics, Center for Scientific Computing, University of Utah. Retrieved 2015-11-02.
- ^ a b c d HP 48G Series – Advanced User’s Reference Manual (AUR) (4 ed.). Hewlett-Packard. December 1994 [1993]. HP 00048-90136, 0-88698-01574-2. Retrieved 2015-09-06.
- ^ a b c d HP 50g / 49g+ / 48gII graphing calculator advanced user’s reference manual (AUR) (2 ed.). Hewlett-Packard. 2009-07-14 [2005]. HP F2228-90010. Retrieved 2015-10-10. Searchable PDF
Решение показательных уравнений методом логарифмирования
Знакомство с логарифмом числа открывает возможность использования метода логарифмирования для решения уравнений. Преимущественно методом логарифмирования решаются показательные уравнения. В этой статье мы подробно разберем, как проводится решение показательных уравнений методом логарифмирования. Здесь мы дадим необходимую теорию и, конечно же, рассмотрим характерный пример решения показательного уравнения методом логарифмирования.
Теория
Решение каких показательных уравнений проводится методом логарифмирования
В основном, методом логарифмирования решаются показательные уравнения в двух следующих случаях:
- В одной части уравнения находится степень, произведение или частное степеней, а в другой – положительное число. Например, 2 x−1 =10 , и др.
- И в одной, и в другой части уравнения находится степень, произведение или частное степеней, возможно с положительным числовым коэффициентом. Например, 3 x 2 −1 =5·2 x+1 и др.
Как проводится решение
Во-первых, нужно убедиться, что обе части показательного уравнения принимают только положительные значения на ОДЗ для исходного уравнения. Во-вторых, проводится логарифмирование обеих частей уравнения по одному и тому же положительному и отличному от единицы основанию. В-третьих, решается уравнение, полученное в результате логарифмирования. Это дает решение исходного уравнения.
По какому основанию логарифмировать
В принципе, в качестве основания логарифма можно брать любое положительное и отличное от единицы число. Обычно логарифмирование проводят по основанию, равному основанию одной из степеней, фигурирующих в исходном уравнении. Также в ходу основание 10 . Это удобно тем, что дает возможность проводить некоторые попутные вычисления при помощи таблицы десятичных логарифмов.
Пример решения показательного уравнения
Рассмотрим характерный пример решения показательного уравнения методом логарифмирования.
Решите показательное уравнение .
Как решать
показательные уравнения?
Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Это поможет решить задания №5, 13 и 15 из профильного уровня математики.
Одна из их разновидностей – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие переменной (х) не в основании степени, а в самом показателе. Как это выглядит:
Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:
Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение (х). Познакомиться с понятием степени и ее свойствами можно тут и тут.
И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:
И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением. Кроме самой показательной функции в уравнении могут быть любые другие математические конструкции – тригонометрические функции, логарифмы, корни, дроби и т.д. Если вы видите степень, значит перед вам показательное уравнение.
Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.
Простейшие показательные уравнения
Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:
Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (х) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:
Значит, если (х=3), то мы получим верное равенство, а значит мы решили уравнение.
Решим что-нибудь посложнее.
Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:
Мы применили свойство отрицательной степени по формуле:
Теперь наше уравнение будет выглядеть так:
Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные – слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:
Такое мы решать умеем, ведь это обыкновенное линейное уравнение.
Поздравляю, мы нашли корень нашего показательного уравнения.
Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:
Воспользуемся одним из свойств степеней ((a^n)^m=a^):
И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:
И еще один пример:
Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.
Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.
Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.
Общий метод решения показательных уравнений
Пусть у нас есть вот такой пример:
Где (a,b) какие-то положительные числа. ((a>0, ; b>0).
Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.
Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:
Раз основания одинаковые, то мы можем просто приравнять степени:
Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:
Замечаем, что (16=2*2*2*2=2^4) это степень двойки:
Основания одинаковые, значит можно приравнять степени:
$$x=4.$$
Пример 6 $$5^<-x>=125 Rightarrow 5^<-x>=5*5*5 Rightarrow 5^<-x>=5^3 Rightarrow –x=3 Rightarrow x=-3.$$
Пример 7 $$9^<4x>=81 Rightarrow (3*3)^<4x>=3*3*3*3 Rightarrow(3^2)^<4x>=3^4 Rightarrow 3^<8x>=3^4 Rightarrow 8x=4 Rightarrow x=frac<1><2>.$$
Здесь мы заметили, что (9=3^2) и (81=3^4) являются степенями (3).
Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:
(3) и (2) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число (b>0), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице (a>0, ; a neq 1):
Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим (2) в виде (3) в какой-то степени, где (a=3), а (b=2):
Подставим данное преобразование в наш пример:
Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:
Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.
Кто забыл, что такое логарифм, можно посмотреть здесь.
Рассмотрим еще несколько аналогичных примеров.
Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:
Все эти варианты ответа верные, их можно смело писать в ответ.
И так, мы с вами научились решать любые показательные уравнения вот такого вида: (a^x=b), где (a>0; ; b>0).
Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа (a^x=b), где (a>0; ; b>0). Рассмотрим типы сложных уравнений, которые могут попасться:
Решение показательных уравнений при помощи замены
Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.
Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^<2x>=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^). Подставим:
Обратим внимание, что во всем уравнении все (х) «входят» в одинаковую функцию — (3^x). Сделаем замену (t=3^x, ; t>0), так как показательная функция всегда положительна.
Квадратное уравнение, которое решается через дискриминант:
Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:
И второй корень:
И еще один пример на замену:
Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Но если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):
Подставим в исходное уравнение:
Теперь показательные функции одинаковы и можно сделать замену:
Обратная замена, и наше уравнение сводится к простейшему:
И второе значение (t):
Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на (3^x):
Здесь нам придется воспользоваться свойствами степеней:
Разберем каждое слагаемое:
Теперь подставим получившееся преобразования в исходное уравнение:
Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену (t=(frac<7><3>)^x):
Сделаем обратную замену:
И последний пример на замену:
Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:
Разберем каждое слагаемое нашего уравнения:
Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!
И последнее слагаемое со степенью:
Подставим все наши преобразования в исходное уравнение:
Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):
Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера. Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.
И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут
Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2), (5) и (10). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:
Воспользуемся формулой ((a*b)^n=a^n*b^n):
И перекинем все показательные функции с основанием (2) влево, а с основанием (5) вправо:
Сокращаем и воспользуемся формулами (a^n*a^m=a^) и (frac=a^):
Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.
Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!
Экспонента, е в степени х
Определение
Экспоненту обозначают так , или .
Число e
Основанием степени экспоненты является число e . Это иррациональное число. Оно примерно равно
е ≈ 2,718281828459045.
Число e определяется через предел последовательности. Это, так называемый, второй замечательный предел:
.
Также число e можно представить в виде ряда:
.
График экспоненты
На графике представлена экспонента, е в степени х.
y ( x ) = е х
На графике видно, что экспонента монотонно возрастает.
Формулы
Основные формулы такие же, как и для показательной функции с основанием степени е .
Выражение показательной функции с произвольным основанием степени a через экспоненту:
.
Частные значения
Пусть y ( x ) = e x . Тогда
.
Свойства экспоненты
Экспонента обладает свойствами показательной функции с основанием степени е > 1 .
Область определения, множество значений
Экспонента y ( x ) = e x определена для всех x .
Ее область определения:
– ∞ .
Ее множество значений:
0 .
Экстремумы, возрастание, убывание
Экспонента является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.
| y = е х | |
| Область определения | – ∞ |
| Область значений | 0 |
| Монотонность | монотонно возрастает |
| Нули, y = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 1 |
| + ∞ | |
| 0 |
Обратная функция
Производная экспоненты
Производная е в степени х равна е в степени х:
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
Комплексные числа
Действия с комплексными числами осуществляются при помощи формулы Эйлера:
,
где есть мнимая единица:
.
Выражения через гиперболические функции
Выражения через тригонометрические функции
Разложение в степенной ряд
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов . Опубликовано: 25-02-2014 Изменено: 09-06-2018
http://sigma-center.ru/exponential_equations
http://1cov-edu.ru/mat_analiz/funktsii/eksponenta/
#статьи
- 6 окт 2022
-
0
Стыдные вопросы о логарифмах: всё, что нужно знать программисту
Объясняем, почему не стоит бояться логарифмов и как их считать в Python.
Иллюстрация: Оля Ежак для Skillbox Media
Журналист, изучает Python. Любит разбираться в мелочах, общаться с людьми и понимать их.
Прежде чем начать обсуждение, давайте немного освежим знания и решим несколько стандартных задачек:
- Чему равен log3 81?
- А lg 2 × lb 10?
- А сумма log216 2 + log216 3?
Если вы легко прорешали все три примера в уме, не пользуясь калькулятором, — можете сразу переходить к заключительной главе. Для тех же, кто слегка подзабыл школьные годы чудесные, — буквально пять минут ликбеза.
По большому счёту, логарифм — это просто перевёрнутая степень. Рассмотрим выражение 23 = 8. В нём:
- 2 — основание степени;
- 3 — показатель степени;
- 8 — результат возведения в степень.
У возведения в степень существует два обратных выражения. В одном мы ищем основание (это извлечение корня), в другом — показатель (это логарифмирование).
Таким образом, выражение 23 = 8 можно превратить в log2 8 = 3.
Закрепляем знания: логарифм — это число, в которое нужно возвести 2 (основание степени), чтобы получить 8 (результат возведения в степень).
Форма записи неинтуитивна, и поначалу можно легко спутать основание со степенью. Чтобы избежать этого, можно использовать следующее правило:
Основание у логарифма, как и у возведения в степень, находится внизу.
Чтобы лучше запомнить структуру записи, посмотрите на эти выражения и постарайтесь понять их смысл:
- log3 9 = 2
- log4 64 = 3
- log5 625 = 4
- log7 343 = 3
- log10 100 = 2
- log2 128 = 7
- log2 0,25 = −2
- log625 125 = 0,75
В общем виде запись logAB читается так: логарифм B по основанию A.
Главная часть любого логарифма — его основание. Именно наличие общего основания у нескольких логарифмических функций позволяет проводить с ними различные операции.
Основанием натурального логарифма является число Эйлера (e) — иррациональное число, приблизительно равное 2,71828.
На всякий случай напомним, что такое иррациональные числа. Так называют числа, которые нельзя записать в виде обыкновенной дроби с целыми числителем и знаменателем. При этом знаменатель не должен быть равен нулю.
Например, 0,333… — рациональное число, потому что его можно записать как 1/3. А вот число Пи или корень из 2 — иррациональны.
Так как натуральные логарифмы часто используются, для них ввели особый способ записи: ln x — это то же самое, что loge x.
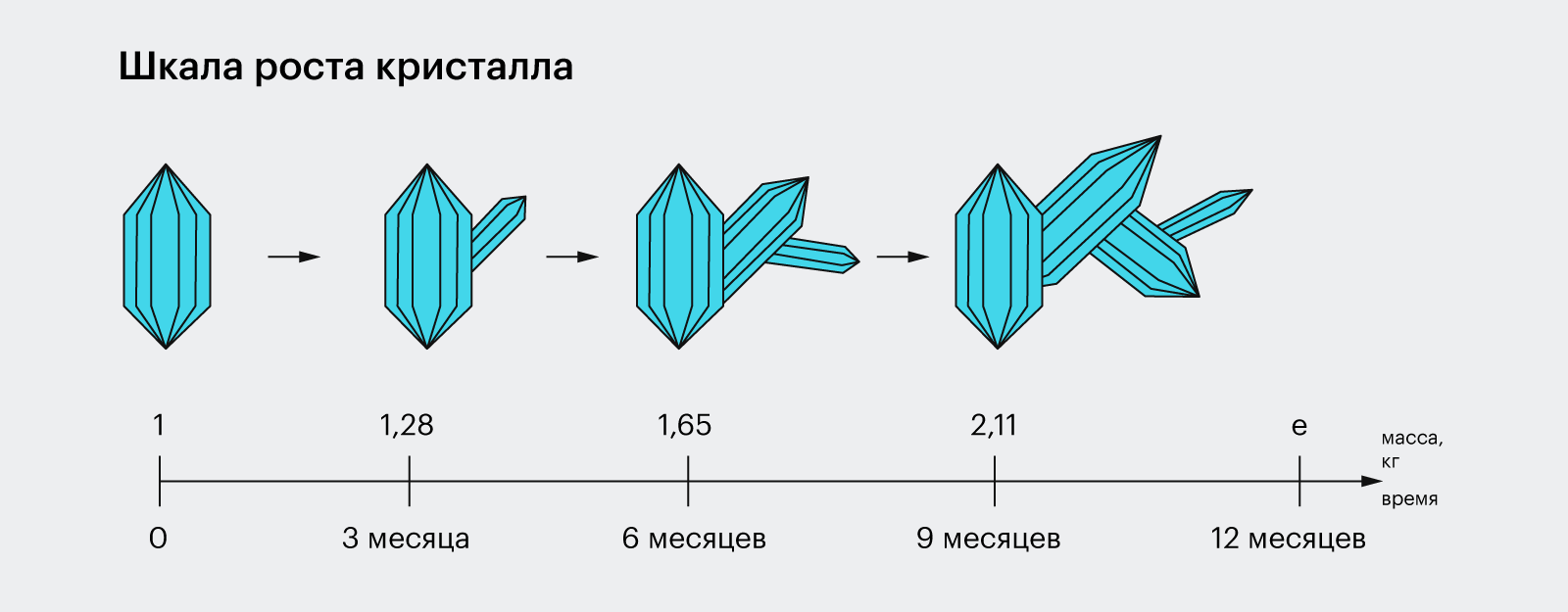
Представим кристалл, который весит 1 кг и растёт со скоростью 100% в год. Можно ожидать, что через год он будет весить 2 кг, но это не так.
Каждая новая выращенная часть начнёт растить свою собственную. Когда в кристалле будет 1,1 кг, он будет расти со скоростью 1,1 кг в год, а когда в нём будет 1,5 кг — со скоростью 1,5 кг в год. Математики подсчитали, что через год масса кристалла составит e, или ≈ 2,71828 кг.
Такой рост называется экспоненциальным. По экспоненте размножаются бактерии, увеличиваются популяции, приумножаются доходы, растут снежные комья, распадается радиоактивное вещество и остывают напитки.
Чтобы узнать, какой массы достигнет кристалл через три, пять, десять лет, нужно возвести e в соответствующую степень.
e3 ≈ 20,0855 кг
e5 ≈ 148,4132 кг
e10 ≈ 22 026,4658 кг
Но как рассчитать, когда кристалл будет весить тонну? Составим уравнение:
ex = 1000
Нам известны основание степени и результат возведения в степень — осталось найти её показатель. Ничего не напоминает? Это ведь и есть логарифм x = loge 1000! Или, если использовать сокращённую запись, x = ln 1000.
Подставим в калькулятор и выясним, что x ≈ 6,9. Именно столько лет потребуется кристаллу, чтобы его масса достигла тонны.
Десятичный логарифм — логарифм, основание которого равно 10. Он обозначается lg x и очень удобен, потому что с ним легко вычислять круглые числа.
Двоичный логарифм — логарифм, основание которого равно 2. Он обозначается lb x и часто используется программистами, потому что компьютеры думают и считают в двоичной системе.
Список операций, которые можно совершать с логарифмами, ограничен. Если вы запомните все и научитесь их выполнять, то сможете щёлкать логарифмические задачки, как семечки.
У всех логарифмов есть ограничения. Их основание и аргумент должны быть больше нуля, при этом основание не может быть равно единице. На математическом языке это звучит так:
Перейдём к свойствам логарифмов. Они работают в обе стороны, и их применяют как слева направо, так и справа налево.
1. Логарифм единицы по любому основанию всегда равен нулю:
Например: log17 1 = 0
2. Логарифм, где число и основание совпадают, равен единице:
Например: log17 17 = 1
3. Основное логарифмическое тождество:
Например: log17 175 = 5
4. Логарифм произведения чисел равен сумме их логарифмов:
Например: log5 12,5 + log5 10 = log5 (12,5 × 10) = log5 125 = 3
5. Логарифм дроби равен разности логарифмов числителя и знаменателя:
Например: log3 63 − log3 7 = log3 63/7 = log3 9 = 2
6. Если основание или аргумент возведены в степень, то их можно удобно выносить перед логарифмом:
Из этих двух формул следует:
Например: log23 49 = 9/3 × log2 4 = 3 × 2 = 6
7. Если нам неудобно основание логарифма, то его можно изменить:
Например: log25 125 = log5 125/log5 25 = 3/2 = 1,5
Из этой формулы следует, что мы можем поменять местами основание и аргумент вот так:
Например: log16 4 = 1/log4 16 = 1/2 = 0,5
А теперь возвращаемся к задачам, которые мы дали в начале статьи.
Пример 1
log3 81
Вспомните, что 81 — это 92. А 9 — это 32. Таким образом:
log3 81 = log3 92 = log3 32+2 = log3 34
Теперь логарифм не представляет для нас никаких сложностей. Воспользуемся свойством степени и вынесём четвёрку.
log3 34 = 4 × log3 3 = 4 × 1 =4
Ответ: 4.
Пример 2
lg 2 × lb 10
Переведём сокращённые записи в полный вид:
lg 2 × lb 10 = log10 2 × log2 10
Приведём оба логарифма к одному основанию.
log10 2 × log2 10 = 1/log2 10 × log2 10 = log2 10/log2 10 = 1
Ответ: 1.
Пример 3
log216 2 + log216 3
Воспользуемся свойством суммы.
log216 2 + log216 3 = log216 2 × 3 = log216 6
Представим 216 в виде степени числа 6 и вынесем с помощью свойства степени.
log216 6 = log63 6 = 1/3 × log6 6 = 1/3 × 1 = 1/3
Ответ: 1/3.
Чтобы работать с логарифмическими выражениями в Python, необходимо импортировать модуль math:
import math
И теперь посчитаем log2 8, используя метод math.log (b, a):
print (math.log (8, 2)) >>> 3.0
Обратите внимание на два момента. Во-первых, мы сначала передаём функции аргумент и только потом — основание. Во-вторых, функция всегда возвращает тип данных float, даже если результат целочисленный.
Если мы не передаём функции основание, то логарифм по умолчанию считается натуральным:
#math.e — метод для вызова числа Эйлера. print (math.log (math.e)) >>> 1.0
Для подсчёта десятичного и двоичного логарифма есть отдельные методы:
#Для десятичного. print (math.log10 (100)) >>> 2.0 #Для двоичного. print (math.log2 (512)) >>> 9.0
Ещё в Python есть специфичный метод, который прибавляет к аргументу единицу и считает натуральный логарифм от получившегося числа:
x = math.e print (math.log1p (x-1)) >>> 1.0
Когда х близок к нулю, этот метод даёт более точные результаты, чем math.log (1+x). Сравните:
x = 0.00001 print (math.log(x+1)) >>> 9.999950000398841e-06 print (math.log1p(x)) >>> 9.99995000033333e-06
Это все основные инструменты для работы с логарифмами в Python.

Научитесь: Профессия Python-разработчик
Узнать больше



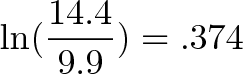
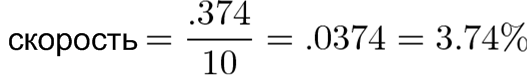

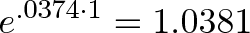
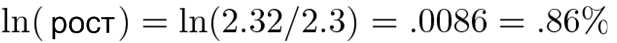
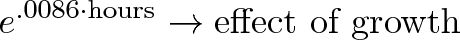
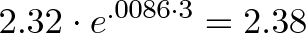

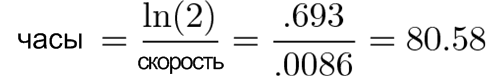
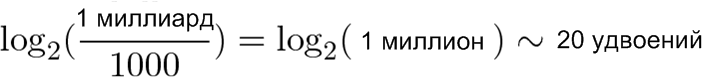
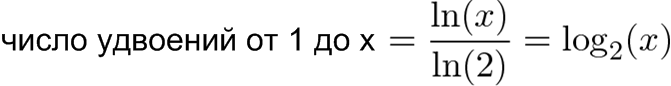
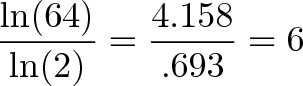
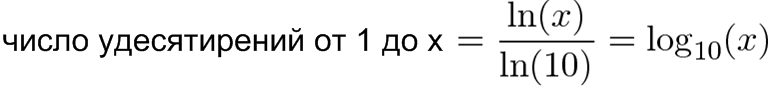



![{displaystyle ln(z)=lim _{nto infty }ncdot ({sqrt[{n}]{z}}-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bba681ea4108b1376919349999b5c3ae9bd08e3b)




![{displaystyle {begin{aligned}ln ab=int _{1}^{ab}{frac {1}{x}},dx&=int _{1}^{a}{frac {1}{x}},dx+int _{a}^{ab}{frac {1}{x}},dx\[5pt]&=int _{1}^{a}{frac {1}{x}},dx+int _{1}^{b}{frac {1}{at}}a,dt\[5pt]&=int _{1}^{a}{frac {1}{x}},dx+int _{1}^{b}{frac {1}{t}},dt\[5pt]&=ln a+ln b.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7210259ed243c3b86451e39eb2b50dccc7832e1)


![{displaystyle {begin{aligned}{frac {d}{dx}}ln x&=lim _{hto 0}{frac {ln(x+h)-ln x}{h}}\&=lim _{hto 0}left[{frac {1}{h}}ln left({frac {x+h}{x}}right)right]\&=lim _{hto 0}left[ln left(left(1+{frac {h}{x}}right)^{frac {1}{h}}right)right]quad &&{text{all above for logarithmic properties}}\&=ln left[lim _{hto 0}left(1+{frac {h}{x}}right)^{frac {1}{h}}right]quad &&{text{for continuity of the logarithm}}\&=ln e^{1/x}quad &&{text{for the definition of }}e^{x}=lim _{hto 0}(1+hx)^{1/h}\&={frac {1}{x}}quad &&{text{for the definition of the ln as inverse function.}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ac40a28d99ea3c3c0e2fbcfad73461fa5837fa6)










![{displaystyle ln(x)=(x-1)prod _{k=1}^{infty }left({frac {2}{1+{sqrt[{2^{k}}]{x}}}}right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19a685fc50f560fbfd45cd8c625c839137a0cb42)
![{displaystyle ln(2)=left({frac {2}{1+{sqrt {2}}}}right)left({frac {2}{1+{sqrt[{4}]{2}}}}right)left({frac {2}{1+{sqrt[{8}]{2}}}}right)left({frac {2}{1+{sqrt[{16}]{2}}}}right)...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7b509b3f7ce72ef554df0dfb48f10dbdc772055)
![{displaystyle pi =(2i+2)left({frac {2}{1+{sqrt {i}}}}right)left({frac {2}{1+{sqrt[{4}]{i}}}}right)left({frac {2}{1+{sqrt[{8}]{i}}}}right)left({frac {2}{1+{sqrt[{16}]{i}}}}right)...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/438561a80d9075271b2dcd15bea94412d2683e69)

![{displaystyle {frac {1}{ln(2)}}=2-{frac {sqrt {2}}{2+2{sqrt {2}}}}-{frac {sqrt[{4}]{2}}{4+4{sqrt[{4}]{2}}}}-{frac {sqrt[{8}]{2}}{8+8{sqrt[{8}]{2}}}}cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/def29e93c87165f8547949c7e10896c45dc22d2f)
















![{displaystyle {begin{aligned}ln(1+x)&={frac {x^{1}}{1}}-{frac {x^{2}}{2}}+{frac {x^{3}}{3}}-{frac {x^{4}}{4}}+{frac {x^{5}}{5}}-cdots \[5pt]&={cfrac {x}{1-0x+{cfrac {1^{2}x}{2-1x+{cfrac {2^{2}x}{3-2x+{cfrac {3^{2}x}{4-3x+{cfrac {4^{2}x}{5-4x+ddots }}}}}}}}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92f9f9bda019d60b5ac5d5fd29ea2dd952c5b90a)
![{displaystyle {begin{aligned}ln left(1+{frac {x}{y}}right)&={cfrac {x}{y+{cfrac {1x}{2+{cfrac {1x}{3y+{cfrac {2x}{2+{cfrac {2x}{5y+{cfrac {3x}{2+ddots }}}}}}}}}}}}\[5pt]&={cfrac {2x}{2y+x-{cfrac {(1x)^{2}}{3(2y+x)-{cfrac {(2x)^{2}}{5(2y+x)-{cfrac {(3x)^{2}}{7(2y+x)-ddots }}}}}}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90abfa2132828fc8eea5d3551dfa4df25dbdfa87)
![{displaystyle {begin{aligned}ln 2&=3ln left(1+{frac {1}{4}}right)+ln left(1+{frac {3}{125}}right)\[8pt]&={cfrac {6}{9-{cfrac {1^{2}}{27-{cfrac {2^{2}}{45-{cfrac {3^{2}}{63-ddots }}}}}}}}+{cfrac {6}{253-{cfrac {3^{2}}{759-{cfrac {6^{2}}{1265-{cfrac {9^{2}}{1771-ddots }}}}}}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc10de9595aca079ef56e7b76a2a23af56e453da)
![{displaystyle {begin{aligned}ln 10&=10ln left(1+{frac {1}{4}}right)+3ln left(1+{frac {3}{125}}right)\[10pt]&={cfrac {20}{9-{cfrac {1^{2}}{27-{cfrac {2^{2}}{45-{cfrac {3^{2}}{63-ddots }}}}}}}}+{cfrac {18}{253-{cfrac {3^{2}}{759-{cfrac {6^{2}}{1265-{cfrac {9^{2}}{1771-ddots }}}}}}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/931b5e1a786450547bd77e466677d9a983974886)