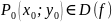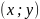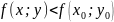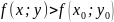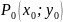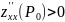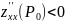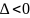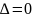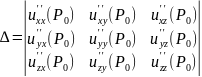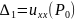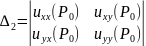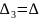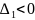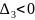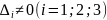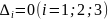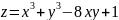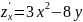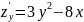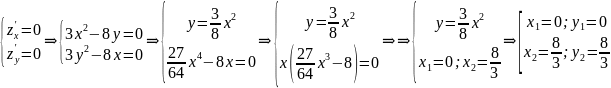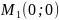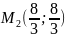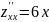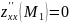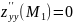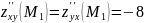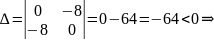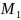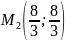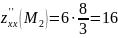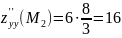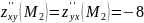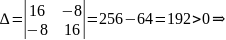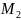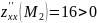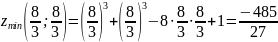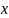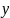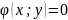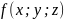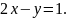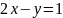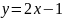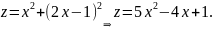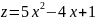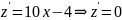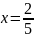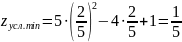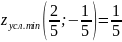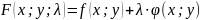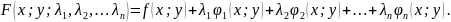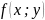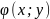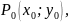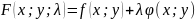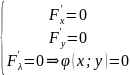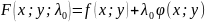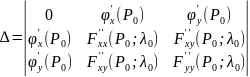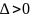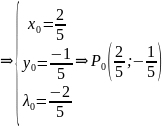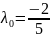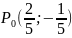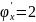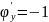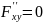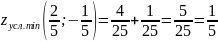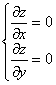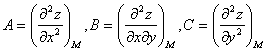Как найти экстремум функции на множестве

1. Экстремумы функций двух и трёх переменных

Определение
1

Точка



называется
точкой максимума функции

,
если
для любых точек


,
принадлежащих
окрестности точки

,
выполняется неравенство:


.

Определение
2

Точка

называется
точкой минимума функции

,
если
для любых точек

,
принадлежащих окрестности точки

,
выполняется
неравенство:



.

Определение
3

Точки
максимума и минимума называются
точками
экстремума
функции.

Теорема
1 (необходимое условие экстремума)

Если
точка

является точкой экстремума функции

,
то её частные производные в точке

равны нулю или не существуют.

При
доказательстве теоремы 1 используются
определения частных производных и
теорема о необходимых условиях экстремума
функции одной переменной.

Замечание
1.
Аналогично формулируются определения
1 и 2 и теорема 1 для функции трёх и более
переменных.

Теорема
2
(достаточные
условия экстремума функции двух
переменных)

Если
функция

дважды дифференцируема в критической
точке

и её окрестности и определитель

,
то в точке

есть экстремум. Причём, если

,
то точка

является точкой минимума функции, а
если

,
то точка

является точкой максимума.
Замечание
2.
Если определитель

,
то в точке

нет экстремума, при этом точку

называют седловой точкой. Если

,
то вопрос об экстремуме в точке

остаётся нерешённым, нужны исследования
функции

по её производным более высокого порядка.

Теорема
3
(достаточные
условия экстремума функции трёх
переменных)

Пусть
функция

дважды дифференцируема в
критической точке

и её окрестности. Определитель

имеет все главные диагональные миноры

,

,

положительные, то

–точка минимума функции

.
Если

,

и

, то точка

– точка максимума функции

.

Замечание
3.
Если


критическая точка функции

и

,
но не выполняются условия теоремы 3, то
в точке

нет экстремума, при этом точка

называется седловой точкой. Если все

,
то вопрос об экстремуме в точке

решается с помощью производных более
высокого порядка.

Пример
1.
Найти экстремумы функции:


.

Решение.

;

.

.

Получили
две точки

и

;

;

а)
Исследуем точку

:

;

;

.

Тогда

точка

не является точкой экстремума.

б)
Исследуем точку

:

;

;

.

Тогда

точка

является точкой экстремума. Причём так
как

,
то точка

является точкой минимума функции:

.

Ответ:

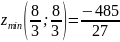
1. Условный экстремум

Пусть
задана функция

на множестве

.
Требуется найти экстремумы функции

,
если

и

связаны некоторым условием

,
называемым уравнением
связи.

Определение
4.
Точка

называется точкой
условного экстремума
функции

при выполнении дополнительных условий

– уравнений связи.

Для
нахождения точек условного экстремума
существует два метода: метод прямого
отыскания и метод Лагранжа. Прямой
метод состоит в том, что из уравнения
связи

выражается одна из переменных через
другую, и её подставляют в функцию

.
Получают функцию одной переменной, для
которой и решают задачу нахождения
обычного экстремума. Такой метод
применяют тогда, когда удаётся из
уравнения связи выразить одну переменную
через другую.

Пример
2.
Найти условный экстремум функции

при
условии

Решение.
Используем метод прямого отыскания
точек условного экстремума. Из условия

выразим

и подставим его в функцию

.
Тогда

Найдём
для функции

обычный экстремум.

,

– +
x

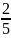
Следовательно,

– точка минимума функции

.

Подставляем

в функцию

и получим:

.

Ответ:

.

Определение
5.
Функция

называется функцией
Лагранжа,
а коэффициент λ
–
множителем
Лагранжа.

Замечание
4.
Если связи не одно уравнение, а несколько
(например,

),
то функция Лагранжа для функции

записывается с

множителями Лагранжа:

Теорема
4
(необходимое
условие поиска условного экстремума)

Пусть
функции

и

,
дифференцируемые в точке

а

является точкой условного экстремума
функции

при условии

.
Тогда найдется такое число

,
при котором точка

является критической для функции
Лагранжа

.

Метод
Лагранжа
поиска условного экстремума состоит в
следующем:

1)
составляют функцию Лагранжа

;

2)
находят её частные производные по

;

3)
приравнять частные производные к нулю
и решают систему уравнений

;

4)
исследуют найденную в результате решения
системы точку

при найденном значении

и решают задачу обычного экстремума
для

.

Теорема
5 (достаточное условие поиска условного
экстремума для случая одного уравнения
связи)

Пусть
точка

и

найдены из решения системы

.

Пусть
определитель

.

Если

,
то функция

имеет в точке

условный максимум.

Если

,
то функция

имеет в точке

условный минимум.

Пример
3.
Методом Лагранжа найти условный экстремум
для функции

при условии

.
Решение.
Составим функцию Лагранжа

.

Найдём
её частные производные по

:

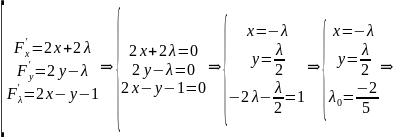
при

.

Выясним
характер точки

по теореме 5:

;

;

;

;

.

Составим
определитель:

.

Так
как

,
то

– точка условного минимума.

.

Ответ:

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Условный экстремум. Метод множителей Лагранжа. Первая часть.

Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции $z=f(x,y)$ в точке $M_0(x_0;y_0)$ называется экстремум этой функции, достигнутый при условии, что переменные $x$ и $y$ в окрестности данной точки удовлетворяют уравнению связи $varphi (x,y)=0$.

Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие $varphi(x,y)=0$. Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует $y=psi(x)$, то подставив $y=psi(x)$ в $z=f(x,y)$, получим функцию одной переменной $z=fleft(x,psi(x)right)$. В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма.

Метод множителей Лагранжа для функций двух переменных.

Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: $F(x,y)=f(x,y)+lambdavarphi(x,y)$ (параметр $lambda$ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:

$$
left { begin{aligned}
& frac{partial F}{partial x}=0;\
& frac{partial F}{partial y}=0;\
& varphi (x,y)=0.
end{aligned} right.
$$

Достаточным условием, из которого можно выяснить характер экстремума, служит знак $d^2 F=F_{xx}^{»}dx^2+2F_{xy}^{»}dxdy+F_{yy}^{»}dy^2$. Если в стационарной точке $d^2F > 0$, то функция $z=f(x,y)$ имеет в данной точке условный минимум, если же $d^2F < 0$, то условный максимум.

Есть и другой способ для определения характера экстремума. Из уравнения связи получаем: $varphi_{x}^{‘}dx+varphi_{y}^{‘}dy=0$, $dy=-frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dx$, поэтому в любой стационарной точке имеем:

$$d^2 F=F_{xx}^{»}dx^2+2F_{xy}^{»}dxdy+F_{yy}^{»}dy^2=F_{xx}^{»}dx^2+2F_{xy}^{»}dxleft( -frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dxright)+F_{yy}^{»}left( -frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dxright)^2=\
=-frac{dx^2}{left(varphi_{y}^{‘} right)^2}cdotleft( -(varphi_{y}^{‘})^2 F_{xx}^{»}+2varphi_{x}^{‘}varphi_{y}^{‘}F_{xy}^{»}-(varphi_{x}^{‘})^2 F_{yy}^{»} right)$$

Второй сомножитель (расположенный в скобке) можно представить в такой форме:

$$
H=left| begin{array} {ccc}
0 & varphi_{x}^{‘} & varphi_{y}^{‘}\
varphi_{x}^{‘} & normred{F_{xx}^{»}} & normred{F_{xy}^{»}} \
varphi_{y}^{‘} & normred{F_{xy}^{»}} & normred{F_{yy}^{»}} end{array} right|
$$

Красным цветом выделены элементы определителя $left| begin{array} {cc} F_{xx}^{»} & F_{xy}^{»} \ F_{xy}^{»} & F_{yy}^{»} end{array} right|$, который является гессианом функции Лагранжа. Если $H > 0$, то $d^2F < 0$, что указывает на условный максимум. Аналогично, при $H < 0$ имеем $d^2F > 0$, т.е. имеем условный минимум функции $z=f(x,y)$.

Примечание относительно формы записи определителя $H$. показатьскрыть

Алгоритм исследования функции двух переменных на условный экстремум

1. Составить функцию Лагранжа $F(x,y)=f(x,y)+lambdavarphi(x,y)$
2. Решить систему $
   left { begin{aligned}
   & frac{partial F}{partial x}=0;\
   & frac{partial F}{partial y}=0;\
   & varphi (x,y)=0.
   end{aligned} right.$
3. Определить характер экстремума в каждой из найденных в предыдущем пункте стационарных точек. Для этого применить любой из указанных способов:
   • Составить определитель $H$ и выяснить его знак
   • С учетом уравнения связи вычислить знак $d^2F$

Метод множителей Лагранжа для функций n переменных

Допустим, мы имеем функцию $n$ переменных $z=f(x_1,x_2,ldots,x_n)$ и $m$ уравнений связи ($n > m$):

$$varphi_1(x_1,x_2,ldots,x_n)=0; ; varphi_2(x_1,x_2,ldots,x_n)=0,ldots,varphi_m(x_1,x_2,ldots,x_n)=0.$$

Обозначив множители Лагранжа как $lambda_1,lambda_2,ldots,lambda_m$, составим функцию Лагранжа:

$$F(x_1,x_2,ldots,x_n,lambda_1,lambda_2,ldots,lambda_m)=f+lambda_1varphi_1+lambda_2varphi_2+ldots+lambda_mvarphi_m$$

Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа:

$$left{begin{aligned}
& frac{partial F}{partial x_i}=0; (i=overline{1,n})\
& varphi_j=0; (j=overline{1,m})
end{aligned} right.$$

Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака $d^2F$. Если в найденной точке $d^2F > 0$, то функция имеет условный минимум, если же $d^2F < 0$, – то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:

Определитель матрицы

$$left| begin{array} {ccccc} frac{partial^2F}{partial x_{1}^{2}} & frac{partial^2F}{partial x_{1}partial x_{2}} & frac{partial^2F}{partial x_{1}partial x_{3}} &ldots & frac{partial^2F}{partial x_{1}partial x_{n}}\
frac{partial^2F}{partial x_{2}partial x_1} & frac{partial^2F}{partial x_{2}^{2}} & frac{partial^2F}{partial x_{2}partial x_{3}} &ldots & frac{partial^2F}{partial x_{2}partial x_{n}}\
frac{partial^2F}{partial x_{3} partial x_{1}} & frac{partial^2F}{partial x_{3}partial x_{2}} & frac{partial^2F}{partial x_{3}^{2}} &ldots & frac{partial^2F}{partial x_{3}partial x_{n}}\
ldots & ldots & ldots &ldots & ldots\
frac{partial^2F}{partial x_{n}partial x_{1}} & frac{partial^2F}{partial x_{n}partial x_{2}} & frac{partial^2F}{partial x_{n}partial x_{3}} &ldots & frac{partial^2F}{partial x_{n}^{2}}\
end{array} right|,$$

выделенной в матрице $L$ красным цветом, есть гессиан функции Лагранжа. Используем следующее правило:

• Если знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ матрицы $L$ совпадают с знаком $(-1)^m$, то исследуемая стационарная точка является точкой условного минимума функции $z=f(x_1,x_2,x_3,ldots,x_n)$.
• Если знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ чередуются, причём знак минора $H_{2m+1}$ совпадает с знаком числа $(-1)^{m+1}$, то исследуемая стационарная точка является точкой условного максимума функции $z=f(x_1,x_2,x_3,ldots,x_n)$.

Пример №1

Найти условный экстремум функции $z(x,y)=x+3y$ при условии $x^2+y^2=10$.

Решение

Геометрическая интерпретация данной задачи такова: требуется найти наибольшее и наименьшее значение аппликаты плоскости $z=x+3y$ для точек ее пересечения с цилиндром $x^2+y^2=10$.

Выразить одну переменную через другую из уравнения связи и подставить ее в функцию $z(x,y)=x+3y$ несколько затруднительно, поэтому будем использовать метод Лагранжа.

Обозначив $varphi(x,y)=x^2+y^2-10$, составим функцию Лагранжа:

$$
F(x,y)=z(x,y)+lambda varphi(x,y)=x+3y+lambda(x^2+y^2-10);\
frac{partial F}{partial x}=1+2lambda x; frac{partial F}{partial y}=3+2lambda y.
$$

Запишем систему уравнений для определения стационарных точек функции Лагранжа:

$$
left { begin{aligned}
& 1+2lambda x=0;\
& 3+2lambda y=0;\
& x^2+y^2-10=0.
end{aligned} right.
$$

Если предположить $lambda=0$, то первое уравнение станет таким: $1=0$. Полученное противоречие говорит о том, что $lambdaneq 0$. При условии $lambdaneq 0$ из первого и второго уравнений имеем: $x=-frac{1}{2lambda}$, $y=-frac{3}{2lambda}$. Подставляя полученные значения в третье уравнение, получим:

$$

left( -frac{1}{2lambda} right)^2+left( -frac{3}{2lambda} right)^2-10=0;\
frac{1}{4lambda^2}+frac{9}{4lambda^2}=10; lambda^2=frac{1}{4}; left[ begin{aligned} & lambda_1=-frac{1}{2};\ & lambda_2=frac{1}{2}. end{aligned} right.\
begin{aligned}
& lambda_1=-frac{1}{2}; ; x_1=-frac{1}{2lambda_1}=1; ; y_1=-frac{3}{2lambda_1}=3;\
& lambda_2=frac{1}{2}; ; x_2=-frac{1}{2lambda_2}=-1; ; y_2=-frac{3}{2lambda_2}=-3.end{aligned}
$$

Итак, система имеет два решения: $x_1=1;; y_1=3;; lambda_1=-frac{1}{2}$ и $x_2=-1;; y_2=-3;; lambda_2=frac{1}{2}$. Выясним характер экстремума в каждой стационарной точке: $M_1(1;3)$ и $M_2(-1;-3)$. Для этого вычислим определитель $H$ в каждой из точек.

$$
varphi_{x}^{‘}=2x;; varphi_{y}^{‘}=2y;; F_{xx}^{»}=2lambda;; F_{xy}^{»}=0;; F_{yy}^{»}=2lambda.\

H=left| begin{array} {ccc} 0 & varphi_{x}^{‘} & varphi_{y}^{‘}\ varphi_{x}^{‘} & F_{xx}^{»} & F_{xy}^{»} \ varphi_{y}^{‘} & F_{xy}^{»} & F_{yy}^{»} end{array} right|=
left| begin{array} {ccc} 0 & 2x & 2y\ 2x & 2lambda & 0 \ 2y & 0 & 2lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|
$$

В точке $M_1(1;3)$ получим:

$$H=8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & 1 & 3\ 1 & -1/2 & 0 \ 3 & 0 & -1/2 end{array} right|=40 > 0.$$

Следовательно, в точке $M_1(1;3)$ функция $z(x,y)=x+3y$ имеет условный максимум, $z_{max}=z(1;3)=10$.

Аналогично, в точке $M_2(-1;-3)$ найдем:

$$H=8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & -1 & -3\ -1 & 1/2 & 0 \ -3 & 0 & 1/2 end{array} right|=-40$$

Так как $H < 0$, то в точке $M_2(-1;-3)$ имеем условный минимум функции $z(x,y)=x+3y$, а именно: $z_{min}=z(-1;-3)=-10$.

Отмечу, что вместо вычисления значения определителя $H$ в каждой точке, гораздо удобнее раскрыть его в общем виде. Дабы не загромождать текст подробностями, этот способ скрою под примечание.

Запись определителя $H$ в общем виде. показатьскрыть

Вопрос о характере экстремума в стационарных точках $M_1(1;3)$ и $M_2(-1;-3)$ можно решить и без использования определителя $H$. Найдем знак $d^2F$ в каждой стационарной точке:

$$
d^2 F=F_{xx}^{»}dx^2+2F_{xy}^{»}dxdy+F_{yy}^{»}dy^2=2lambda left( dx^2+dy^2right)
$$

Отмечу, что запись $dx^2$ означает именно $dx$, возведённый в вторую степень, т.е. $left( dx right)^2$. Отсюда имеем: $dx^2+dy^2>0$, посему при $lambda_1=-frac{1}{2}$ получим $d^2F < 0$. Следовательно, функция имеет в точке $M_1(1;3)$ условный максимум. Аналогично, в точке $M_2(-1;-3)$ получим условный минимум функции $z(x,y)=x+3y$. Отметим, что для определения знака $d^2F$ не пришлось учитывать связь между $dx$ и $dy$, ибо знак $d^2F$ очевиден без дополнительных преобразований. В следующем примере для определения знака $d^2F$ уже будет необходимо учесть связь между $dx$ и $dy$.

Ответ: в точке $(-1;-3)$ функция имеет условный минимум, $z_{min}=-10$. В точке $(1;3)$ функция имеет условный максимум, $z_{max}=10$.

Пример №2

Найти условный экстремум функции $z(x,y)=3y^3+4x^2-xy$ при условии $x+y=0$.

Решение

Первый способ (метод множителей Лагранжа)

Обозначив $varphi(x,y)=x+y$ составим функцию Лагранжа:

$$F(x,y)=z(x,y)+lambda varphi(x,y)=3y^3+4x^2-xy+lambda(x+y).$$

$$
frac{partial F}{partial x}=8x-y+lambda; ; frac{partial F}{partial y}=9y^2-x+lambda.\

left { begin{aligned} & 8x-y+lambda=0;\ & 9y^2-x+lambda=0; \ & x+y=0. end{aligned} right.

$$

Решив систему, получим: $x_1=0$, $y_1=0$, $lambda_1=0$ и $x_2=frac{10}{9}$, $y_2=-frac{10}{9}$, $lambda_2=-10$. Имеем две стационарные точки: $M_1(0;0)$ и $M_2 left(frac{10}{9};-frac{10}{9} right)$. Выясним характер экстремума в каждой стационарной точке с использованием определителя $H$.

$$
H=left| begin{array} {ccc} 0 & varphi_{x}^{‘} & varphi_{y}^{‘}\ varphi_{x}^{‘} & F_{xx}^{»} & F_{xy}^{»} \ varphi_{y}^{‘} & F_{xy}^{»} & F_{yy}^{»} end{array} right|=
left| begin{array} {ccc} 0 & 1 & 1\ 1 & 8 & -1 \ 1 & -1 & 18y end{array} right|=-10-18y
$$

В точке $M_1(0;0)$ $H=-10-18cdot 0=-10 < 0$, поэтому $M_1(0;0)$ есть точка условного минимума функции $z(x,y)=3y^3+4x^2-xy$, $z_{min}=0$. В точке $M_2left(frac{10}{9};-frac{10}{9}right)$ $H=10 > 0$, посему в данной точке функция имеет условный максимум, $z_{max}=frac{500}{243}$.

Исследуем характер экстремума в каждой из точек иным методом, основываясь на знаке $d^2F$:

$$
d^2 F=F_{xx}^{»}dx^2+2F_{xy}^{»}dxdy+F_{yy}^{»}dy^2=8dx^2-2dxdy+18ydy^2
$$

Из уравнения связи $x+y=0$ имеем: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.

$$
d^2 F=8dx^2-2dxdy+18ydy^2=8dx^2-2dx(-dx)+18y(-dx)^2=(10+18y)dx^2
$$

Так как $ d^2F Bigr|_{M_1}=10 dx^2 > 0$, то $M_1(0;0)$ является точкой условного минимума функции $z(x,y)=3y^3+4x^2-xy$. Аналогично, $d^2F Bigr|_{M_2}=-10 dx^2 < 0$, т.е. $M_2left(frac{10}{9}; -frac{10}{9} right)$ – точка условного максимума.

Второй способ

Из уравнения связи $x+y=0$ получим: $y=-x$. Подставив $y=-x$ в функцию $z(x,y)=3y^3+4x^2-xy$, получим некоторую функцию переменной $x$. Обозначим эту функцию как $u(x)$:

$$
u(x)=z(x,-x)=3cdot(-x)^3+4x^2-xcdot(-x)=-3x^3+5x^2.
$$

Таким образом задачу о нахождении условного экстремума функции двух переменных мы свели к задаче определения экстремума функции одной переменной.

$$
u_{x}^{‘}=-9x^2+10x;\
-9x^2+10x=0; ; xcdot(-9x+10)=0;\
x_1=0; ; y_1=-x_1=0;\
x_2=frac{10}{9}; ; y_2=-x_2=-frac{10}{9}.
$$

Получили точки $M_1(0;0)$ и $M_2left(frac{10}{9}; -frac{10}{9}right)$. Дальнейшее исследование известно из курса дифференциального исчисления функций одной переменой. Исследуя знак $u_{xx}^{»}$ в каждой стационарной точке или проверяя смену знака $u_{x}^{‘}$ в найденных точках, получим те же выводы, что и при решении первым способом. Например, проверим знак $u_{xx}^{»}$:

$$u_{xx}^{»}=-18x+10;\
u_{xx}^{»}(M_1)=10;;u_{xx}^{»}(M_2)=-10.$$

Так как $u_{xx}^{»}(M_1)>0$, то $M_1$ – точка минимума функции $u(x)$, при этом $u_{min}=u(0)=0$. Так как $u_{xx}^{»}(M_2)<0$, то $M_2$ – точка максимума функции $u(x)$, причём $u_{max}=uleft(frac{10}{9}right)=frac{500}{243}$.

Значения функции $u(x)$ при заданном условии связи совпадают с значениями функции $z(x,y)$, т.е. найденные экстремумы функции $u(x)$ и есть искомые условные экстремумы функции $z(x,y)$.

Ответ: в точке $(0;0)$ функция имеет условный минимум, $z_{min}=0$. В точке $left(frac{10}{9}; -frac{10}{9} right)$ функция имеет условный максимум, $z_{max}=frac{500}{243}$.

Рассмотрим еще один пример, в котором характер экстремума выясним посредством определения знака $d^2F$.

Пример №3

Найти наибольшее и наименьшее значения функции $z=5xy-4$, если переменные $x$ и $y$ положительны и удовлетворяют уравнению связи $frac{x^2}{8}+frac{y^2}{2}-1=0$.

Решение

Составим функцию Лагранжа: $F=5xy-4+lambda left( frac{x^2}{8}+frac{y^2}{2}-1 right)$. Найдем стационарные точки функции Лагранжа:

$$
F_{x}^{‘}=5y+frac{lambda x}{4}; ; F_{y}^{‘}=5x+lambda y.\

left { begin{aligned}
& 5y+frac{lambda x}{4}=0;\
& 5x+lambda y=0;\
& frac{x^2}{8}+frac{y^2}{2}-1=0;\
& x > 0; ; y > 0.
end{aligned} right.
$$

Все дальнейшие преобразования осуществляются с учетом $x > 0; ; y > 0$ (это оговорено в условии задачи). Из второго уравнения выразим $lambda=-frac{5x}{y}$ и подставим найденное значение в первое уравнение: $5y-frac{5x}{y}cdot frac{x}{4}=0$, $4y^2-x^2=0$, $x=2y$. Подставляя $x=2y$ в третье уравнение, получим: $frac{4y^2}{8}+frac{y^2}{2}-1=0$, $y^2=1$, $y=1$.

Так как $y=1$, то $x=2$, $lambda=-10$. Характер экстремума в точке $(2;1)$ определим, исходя из знака $d^2F$.

$$
F_{xx}^{»}=frac{lambda}{4}; ; F_{xy}^{»}=5; ; F_{yy}^{»}=lambda.
$$

Так как $frac{x^2}{8}+frac{y^2}{2}-1=0$, то:

$$
dleft( frac{x^2}{8}+frac{y^2}{2}-1right)=0; ; dleft( frac{x^2}{8} right)+dleft( frac{y^2}{2} right)=0; ; frac{x}{4}dx+ydy=0; ; dy=-frac{xdx}{4y}.
$$

В принципе, здесь можно сразу подставить координаты стационарной точки $x=2$, $y=1$ и параметра $lambda=-10$, получив при этом:

$$
F_{xx}^{»}=frac{-5}{2}; ; F_{xy}^{»}=-10; ; dy=-frac{dx}{2}.\

d^2 F=F_{xx}^{»}dx^2+2F_{xy}^{»}dxdy+F_{yy}^{»}dy^2=-frac{5}{2}dx^2+10dxcdot left(-frac{dx}{2} right)-10cdot left(-frac{dx}{2} right)^2=\
=-frac{5}{2}dx^2-5dx^2-frac{5}{2}dx^2=-10dx^2.

$$

Однако в других задачах на условный экстремум стационарных точек может быть несколько. В таких случаях лучше $d^2F$ представить в общем виде, а потом подставлять в полученное выражение координаты каждой из найденных стационарных точек:

$$
d^2 F=F_{xx}^{»}dx^2+2F_{xy}^{»}dxdy+F_{yy}^{»}dy^2=frac{lambda}{4}dx^2+10cdot dxcdot frac{-xdx}{4y} +lambdacdot left(-frac{xdx}{4y} right)^2=\
=frac{lambda}{4}dx^2-frac{5x}{2y}dx^2+lambda cdot frac{x^2dx^2}{16y^2}=left( frac{lambda}{4}-frac{5x}{2y}+frac{lambda cdot x^2}{16y^2} right)cdot dx^2
$$

Подставляя $x=2$, $y=1$, $lambda=-10$, получим:

$$
d^2 F=left( frac{-10}{4}-frac{10}{2}-frac{10 cdot 4}{16} right)cdot dx^2=-10dx^2.
$$

Так как $d^2F=-10cdot dx^2 < 0$, то точка $(2;1)$ есть точкой условного максимума функции $z=5xy-4$, причём $z_{max}=10-4=6$.

Ответ: в точке $(2;1)$ функция имеет условный максимум, $z_{max}=6$.

В следующей части рассмотрим применение метода Лагранжа для функций большего количества переменных.

Экстремум функции двух переменных

Назначение сервиса. Онлайн-калькулятор используется для нахождения в онлайн режиме наибольшего и наименьшего значения функции двух переменных (см. пример). Решение оформляется в формате Word.

• Решение онлайн
• Видеоинструкция
• Оформление Word

Для функции трех переменных можно использовать матрицу Гессе.

Алгоритм исследования функции двух переменных на экстремум

Функция z = f(x,y) имеет максимум в точке M₀(x₀;y₀), если f(x₀;y₀) > f(x;y) для всех точек (x;y), достаточно близких к точке (x₀;y₀) и отличных от неё. Функция z = f(x,y) имеет минимум в точке M₀(x₀;y₀), если f(x₀;y₀) < f(x;y) для всех точек (x;y), достаточно близких к точке (x₀;y₀) и отличных от неё. Максимум и минимум функции называются экстремумами функции.

Исследование функции двух переменных на экстремум проводят по следующей схеме.

1. Находят частные производные dz/dx и dz/dy.

2. Решают систему уравнений:

и таким образом находят критические точки функции.

3. Находят частные производные второго порядка:

4. Вычисляют значения этих частных производных второго порядка в каждой из найденных в п.2 критических точках M(x₀;y₀).

5. Делаю вывод о наличии экстремумов:

а) если AC – B² > 0 и A < 0 , то в точке M имеется максимум;

б) если AC – B² > 0 и A > 0 , то в точке M имеется минимум;

в) если AC – B² < 0, то экстремума нет;

г) если AC – B² = 0, то вопрос о наличии экстремума остается открытым;

Пример №1. Найти экстремумы функции f(x,y)=x³+xy²+x²+y² и определить по критерию Сильвестра их тип.

Решение.

1. Найдем первые частные производные.





2. Решим систему уравнений.

3x²+2x+y²=0

2xy+2y=0

Получим:

а) Из первого уравнения выражаем x и подставляем во второе уравнение:

x = -1

y²+1=0

Данная система уравнений не имеет решения.

б) Из первого уравнения выражаем y и подставляем во второе уравнение:





или





или

Откуда x₁ = -2/3; x₂ = 0; x₃ = -2/3; x₄ = 0

Данные значения x подставляем в выражение для y. Получаем: y₁ = 0; y₂ = 0; y₃ = 0; y₄ = 0

Количество критических точек равно 2: M₁(-2/3;0), M₂(0;0)

3. Найдем частные производные второго порядка.







4. Вычислим значение этих частных производных второго порядка в критических точках M(x₀;y₀).

Вычисляем значения для точки M₁(-2/3;0)







AC — B² = -4/3 < 0, то глобального экстремума нет.

Вычисляем значения для точки M₂(0;0)







AC — B² = 4 > 0 и A > 0 , то в точке M₂(0;0) имеется минимум z(0;0) = 0

Вывод: В точке M₂(0;0) имеется минимум z(0;0) = 0

Пример №2. Исследовать функцию на экстремум классическим методом: Z=8x2+2xy-5x+6.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).