Как найти экстремум функции python

Время на прочтение
5 мин

Количество просмотров 56K

Метод Нелдера — Мида — метод оптимизации (поиска минимума) функции от нескольких переменных. Простой и в тоже время эффективный метод, позволяющий оптимизировать функции без использования градиентов. Метод надежен и, как правило, показывает хорошие результаты, хотя и отсутствует теория сходимости. Может использоваться в функции optimize из модуля scipy.optimize популярной библиотеки для языка python, которая используется для математических расчетов.

Алгоритм заключается в формировании симплекса (simplex) и последующего его деформирования в направлении минимума, посредством трех операций:

1) Отражение (reflection);
2) Растяжение (expansion);
3) Сжатие (contract);

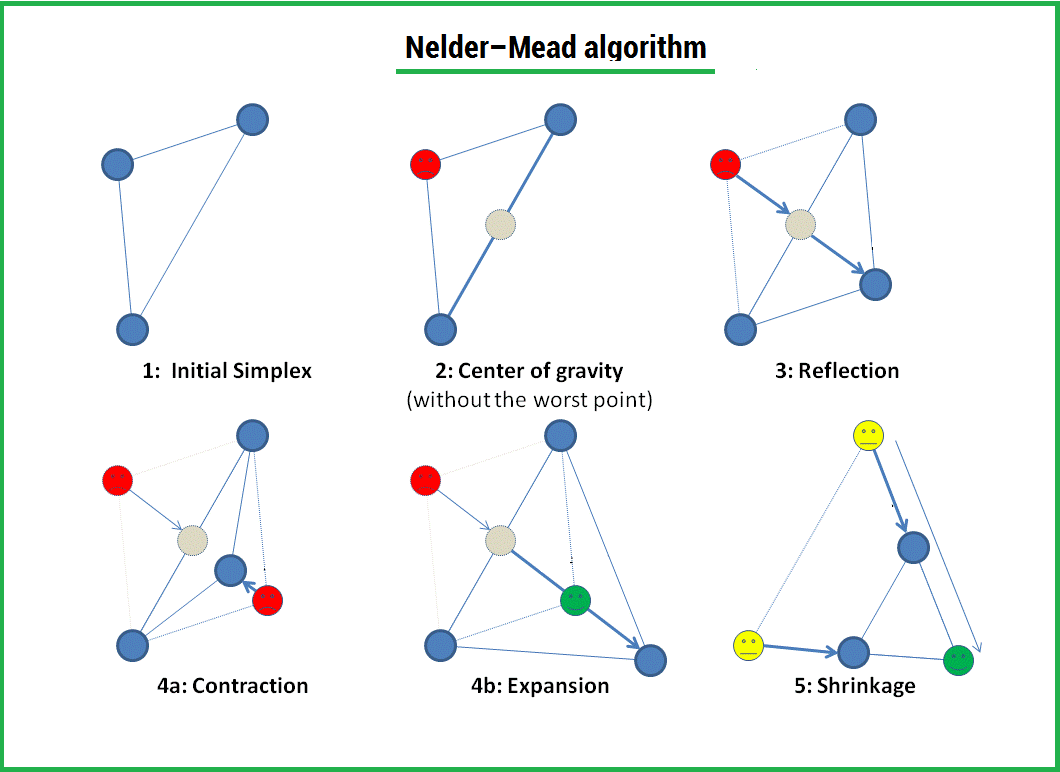
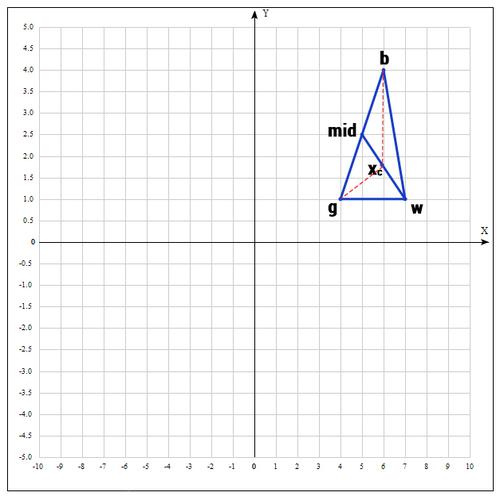
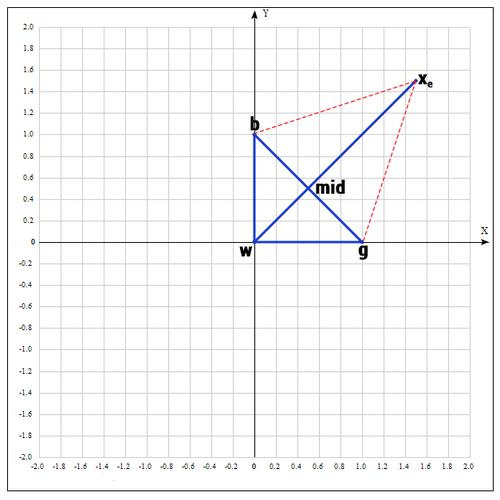
Симплекс представляет из себя геометрическую фигуру, являющуюся n — мерным обобщением треугольника. Для одномерного пространства — это отрезок, для двумерного — треугольник. Таким образом n — мерный симплекс имеет n + 1 вершину.

Алгоритм

1) Пусть

функция, которую необходимо оптимизировать. На первом шаге выбираем три случайные точки (об этом чуть позже) и формируем симплекс (треугольник). Вычисляем значение функции в каждой точке:

,

,

.

Сортируем точки по значениям функции

в этих точках, таким образом получаем двойное неравенство:

Мы ищем минимум функции, а следовательно, на данном шаге лучшей будет та точка, в которой значение функции минимально. Для удобства переобозначим точки следующим образом:

b =

, g =

, w =

, где best, good, worst — соответственно.

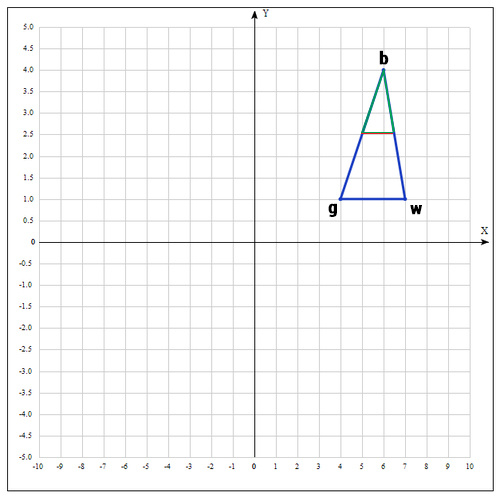
2) На следующем шаге находим середину отрезка, точками которого являются g и b. Т.к. координаты середины отрезка равны полусумме координат его концов, получаем:

В более общем виде можно записать так:

3) Применяем операцию отражения:
Находим точку

, следующим образом:

Т.е. фактически отражаем точку w относительно mid. В качестве коэффициента берут как правило 1. Проверяем нашу точку: если

, то это хорошая точка. А теперь попробуем расстояние увеличить в 2 раза, вдруг нам повезет и мы найдем точку еще лучше.

4) Применяем операцию растяжения:
Находим точку

следующим образом:

В качестве γ принимаем γ = 2, т.е. расстояние увеличиваем в 2 раза.

Проверяем точку

:

Если

, то нам повезло и мы нашли точку лучше, чем есть на данный момент, если бы этого не произошло, мы бы остановились на точке

.

Далее заменяем точку w на

, в итоге получаем:

5) Если же нам совсем не повезло и мы не нашли хороших точек, пробуем операцию сжатия.
Как следует из названия операции мы будем уменьшать наш отрезок и искать хорошие точки внутри треугольника.

Пробуем найти хорошую точку

:

Коэффициент β принимаем равным 0.5, т.е. точка

на середине отрезка wmid.

Существует еще одна операция — shrink (сокращение). В данном случае, мы переопределяем весь симплекс. Оставляем только «лучшую» точку, остальные определяем следующим образом:

Коэффициент δ берут равным 0.5.

По существу передвигаем точки по направлению к текущей «лучшей» точке. Преобразование выглядит следующим образом:

Необходимо отметить, что данная операция дорого обходится, поскольку необходимо заменять точки в симплексе. К счастью было установлено, при проведении большого количества экспериментов, что shrink — трансформация редко случается на практике.

Алгоритм заканчивается, когда:

1) Было выполнено необходимое количество итераций.
2) Площадь симплекса достигла определенной величины.
3) Текущее лучшее решение достигло необходимой точности.

Как и в большинстве эвристических методов, не существует идеального способа выбора инициализирующих точек. Как уже было сказано, можно брать случайные точки, находящиеся недалеко друг от друга для формирования симплекса; но есть решение и получше, которое используется в реализации алгоритма в MATHLAB:

Выбор первой точки

поручаем пользователю, если он имеет некоторое представление о возможном хорошем решении, в противном случае выбирается случайным образом. Остальные точки выбираются исходя из

, на небольшом расстоянии вдоль направления каждого измерения:

где

— единичный вектор.

определяется таким образом:

= 0.05, если коэффициент при

в определении

не нулевой.

= 0.00025, если коэффициент при

в определении нулевой.

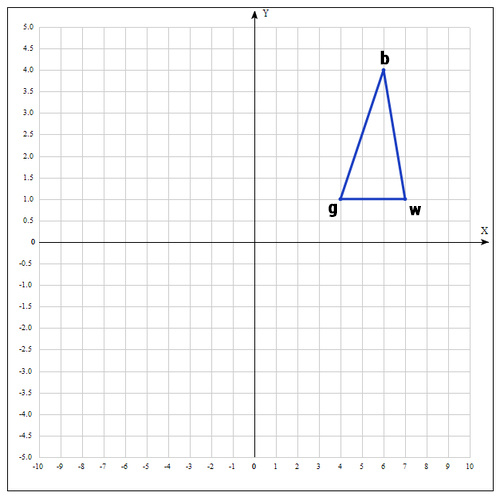
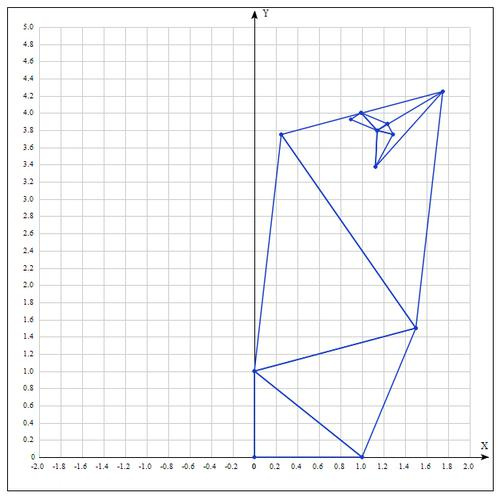
Пример:

Найти экстремум следующей функции:

В качестве начальных возьмем точки:

Вычислим значение функции в каждой точке:

Переобозначим точки следующим образом:

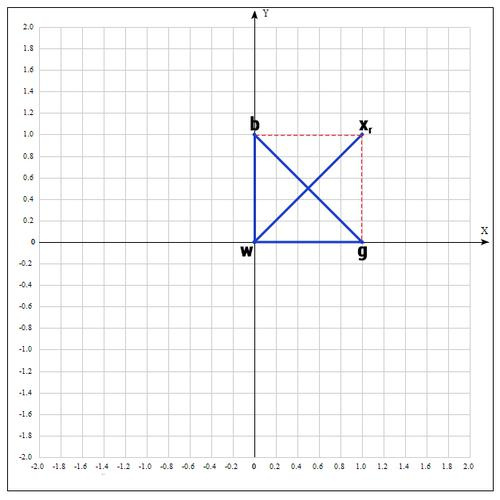
Находим середину отрезка bg:

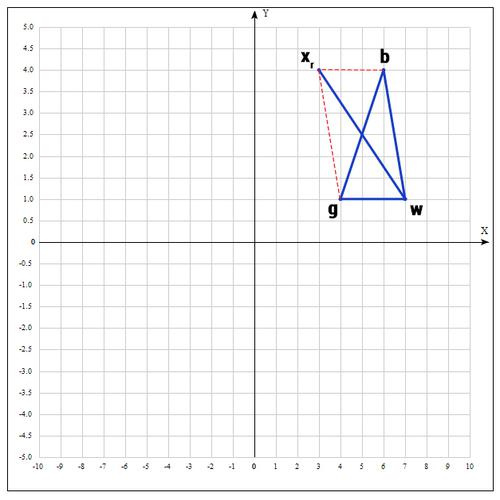
Находим точку

(операция отражения):

если α=1, тогда:

Проверяем точку

:

, т.к.

пробуем увеличить отрезок (операция растяжения).

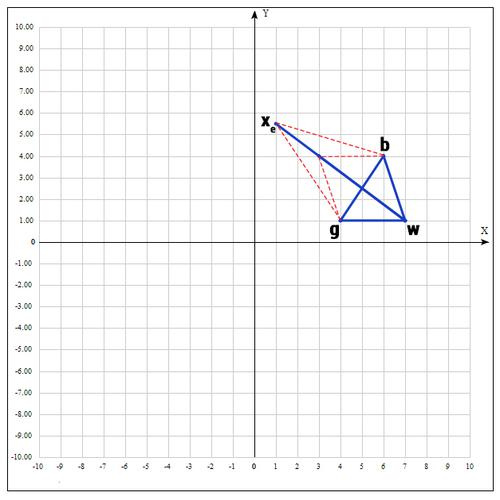
если γ = 2, тогда:

Проверяем значение функции в точке

:

Оказалось, что точка

«лучше» точки b. Следовательно мы получаем новые вершины:

И алгоритм начинается сначала.

Таблица значений для 10 итераций:

Best	Good	Worst

Аналитически находим экстремум функции, он достигается в точке

.
После 10 итераций мы получаем достаточно точное приближение:

Еще о методе:

Алгоритм Нелдера — Мида в основном используется для выбора параметра в машинном обучении. В сущности, симплекс-метод используется для оптимизации параметров модели. Это связано с тем, что данный метод оптимизирует целевую функцию довольно быстро и эффективно (особенно там, где не используется shrink — модификация).

С другой стороны, в силу отсутствия теории сходимости, на практике метод может приводить к неверному ответу даже на гладких (непрерывно дифференцируемых) функциях. Также возможна ситуация, когда рабочий симплекс находится далеко от оптимальной точки, а алгоритм производит большое число итераций, при этом мало изменяя значения функции. Эвристический метод решения этой проблемы заключается в запуске алгоритма несколько раз и ограничении числа итераций.

Реализация на языке программирования python:

Создаем вспомогательный класс Vector и перегружаем операторы для возможности производить с векторами базовые операции. Я намерено не использовал вспомогательные библиотеки для реализации алгоритма, т.к. в таком случае зачастую снижается восприятие.

#!/usr/bin/python
# -*- coding: utf-8 -*-
class Vector(object):
    def __init__(self, x, y):
        """ Create a vector, example: v = Vector(1,2) """
        self.x = x
        self.y = y

    def __repr__(self):
        return "({0}, {1})".format(self.x, self.y)

    def __add__(self, other):
        x = self.x + other.x
        y = self.y + other.y
        return Vector(x, y)

    def __sub__(self, other):
        x = self.x - other.x
        y = self.y - other.y
        return Vector(x, y)

    def __rmul__(self, other):
        x = self.x * other
        y = self.y * other
        return Vector(x, y)

    def __truediv__(self, other):
        x = self.x / other
        y = self.y / other
        return Vector(x, y)

    def c(self):
        return (self.x, self.y)
        
# objective function
def f(point):
    x, y = point
    return x**2 + x*y + y**2 - 6*x - 9*y

def nelder_mead(alpha=1, beta=0.5, gamma=2, maxiter=10):
    
    # initialization
    v1 = Vector(0, 0)
    v2 = Vector(1.0, 0)
    v3 = Vector(0, 1)

    for i in range(maxiter):
        adict = {v1:f(v1.c()), v2:f(v2.c()), v3:f(v3.c())}
        points = sorted(adict.items(), key=lambda x: x[1])
        
        b = points[0][0]
        g = points[1][0]
        w = points[2][0]
        
        
        mid = (g + b)/2

        # reflection
        xr = mid + alpha * (mid - w)
        if f(xr.c()) < f(g.c()):
            w = xr
        else:
            if f(xr.c()) < f(w.c()):
                w = xr
            c = (w + mid)/2
            if f(c.c()) < f(w.c()):
                w = c
        if f(xr.c()) < f(b.c()):

            # expansion
            xe = mid + gamma * (xr - mid)
            if f(xe.c()) < f(xr.c()):
                w = xe
            else:
                w = xr
        if f(xr.c()) > f(g.c()):
            
            # contraction
            xc = mid + beta * (w - mid)
            if f(xc.c()) < f(w.c()):
                w = xc

        # update points
        v1 = w
        v2 = g
        v3 = b
    return b

print("Result of Nelder-Mead algorithm: ")
xk = nelder_mead()
print("Best poits is: %s"%(xk))

Спасибо за чтение статьи. Надеюсь она была Вам полезна и Вы узнали много нового.
С вами был FUNNYDMAN. Удачной оптимизации!)

The bounds argument goes [(lower1,upper1),(lower2,upper2)], not [(lower1,lower2),(upper1,upper2)]. If you look at your result (max_x) you will see «ERROR: NO FEASIBLE SOLUTION», which I am guessing is because your bounds specify an empty set.

Here is a correct way to call the function. I assume the square root is just an example. I used -x**2 instead.

import scipy.optimize as opt
import scipy
from numpy import *
def f(x):
    print x
    return -x**(2)

max_x = opt.fmin_l_bfgs_b(lambda x: -f(x), 1.0, bounds=[(-9,9)],approx_grad=True)

Because you are not specifying a gradient function, you need to set approx_grad=True. The 1.0 is my initial guess for the maximum (although it is obviously zero for this example). I added a print statement so I can see each time the function is called, but that’s normally not necessary. For more details on different ways to call fmin_l_bfgs_b, see here.

The above code results in:

[ 1.]
[ 1.]
[ 1.00000001]
[-0.99999999]
[-0.99999999]
[-0.99999998]
[ 0.001]
[ 0.001]
[ 0.00100001]
[ -5.01108742e-09]
[ -5.01108742e-09]
[  4.98891258e-09]

And max_x looks like this:

(array([ -5.01108742e-09]),
 array([  2.51109971e-17]),
 {'funcalls': 4,
  'grad': array([ -2.21748344e-11]),
  'task': 'CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL',
  'warnflag': 0})