Как найти экстремумы функции графическим методом - Исправление недочетов и поиск решений вместе с Examum.ru

Применение поверхностей первого и второго порядков
в задачах на экстремум функций

Общая постановка задачи поиска экстремума функций приведена здесь. Рассмотрим задачу поиска безусловного экстремума функций двух переменных.

Аналитический метод поиска локального безусловного экстремума

Пусть задана дважды непрерывно дифференцируемая функция f(x)=f(x_1,x_2) двух переменных.

Точка $x^{ast}$ называется точкой локального минимума, если существует такая окрестность этой точки, для всех точек которой выполняется условие

$f(x^{ast})leqslant f(x).$

Если знак неравенства заменить на знак , то получится определение локального максимума. Точки локального минимума или максимума называются точками локального экстремума функции.

Требуется найти точки локального экстремума функции f(x) .

Порядок решения поставленной задачи содержит два этапа.

На первом этапе при помощи необходимых условий экстремума первого порядка:

$left.frac{partial f(x)}{partial x_1}right|_{x=x^{ast}}=0,quad left.frac{partial f(x)}{partial x_2}right|_{x=x^{ast}}=0,$

(4.74)

находятся стационарные точки $x^{ast}$ , «подозрительные» на наличие локального экстремума (частные производные первого порядка в точке $x^{ast}$ равны нулю).

На втором этапе проверяются достаточные условия экстремума, а если они не выполняются, то и необходимые условия второго порядка. Они следуют из формулы Тейлора для приращения функции в точке $x^{ast}$ (учитывая члены до второго порядка включительно):

$Delta f=f(x_1^{ast}+Delta x_1,,x_2^{ast}+Delta x_2)-f(x_1^{ast},x_2^{ast})= frac{1}{2}Bigl[a_{11}cdotDelta x_1^2+2cdot a_{12}cdotDelta x_1Delta x_2+a_{22}cdotDelta x_2^2Bigr],$

где

$a_{11}=left.frac{partial^2f(x)}{partial x_1^2}right|_{x=x^{ast}},quad a_{12}=left.frac{partial^2f(x)}{partial x_1partial x_2}right|_{x=x^{ast}},quad a_{22}=left.frac{partial^2f(x)}{partial x_2^2}right|_{x=x^{ast}},$

а члены с производными первого порядка отсутствуют, так как точка $x^{ast}$ удовлетворяет (4.74).

Равенство

$Delta f=frac{1}{2}Bigl[a_{11}cdotDelta x_1^2+2cdot a_{12}cdotDelta x_1Delta x_2+a_{22}cdotDelta x_2^2Bigr]$

(4.75)

можно рассматривать как уравнение поверхности второго порядка относительно неизвестных Delta x_1, Delta x_2, Delta f . Уравнение (4.75) можно записать в матричной форме

$Delta f=frac{1}{2}begin{pmatrix}Delta x_1&Delta x_2end{pmatrix}cdot H(x^{ast})cdot begin{pmatrix}Delta x_1\Delta x_2end{pmatrix},$

(4.76)

где $H(x^{ast})$ — матрица квадратичной формы, называемая матрицей Гессе.

Она составлена из частных производных второго порядка, вычисленных в стационарной точке $x^{ast}:$

$H(x^{ast})= begin{pmatrix}a_{11}&a_{12}\a_{12}&a_{22}end{pmatrix}= left.{begin{pmatrix}dfrac{partial^2f(x)}{partial x_1^2}&dfrac{partial^2f(x)}{partial x_1partial x_2}\ dfrac{partial^2f(x)}{partial x_1partial x_2}& dfrac{partial^2f(x)}{partial x_1^2}end{pmatrix}}right|_{Large{x=x^{ast}}}$

Как показано в разд.4.4.1, при помощи поворота системы координат вокруг оси Delta f можно квадратичную форму в правой части (4.76) привести к каноническому виду

$Delta f=frac{1}{2}Bigl[lambda_1cdot(Delta x'_1)^2+lambda_2cdot(Delta x'_2)^2Bigr],$

(4.77)

где lambda_1,,lambda_2 — собственные значения матрицы Гессе $H(x^{ast})$ .

В зависимости от знаков собственных значений возможны следующие случаи:

1) если собственные значения одного знака, то поверхность (4.77) представляет собой эллиптический параболоид: выпуклый при lambda_1>0, lambda_2>0 (рис.4.58,а), или вогнутый при lambda_1<0, lambda_2<0 (рис.4.58,б);

2) если собственные значения имеют разные знаки, то поверхность (4.77) представляет собой гиперболический параболоид (рис.4.58,в при lambda_1>0, lambda_2<0 );

3) если одно из собственных значений равно нулю (например, при lambda_2=0 ), то поверхность (4.77) представляет собой параболический цилиндр: выпуклый при lambda_1>0 (рис.4.58,2) или вогнутый при lambda_1<0 (рис.4.58,д).

Критические (стационарные) точки поверхностей второго порядка

В случае эллиптического параболоида стационарная точка $x^{ast}$ является либо точкой локального минимума функции при lambda_1>0, lambda_2>0 , либо точкой локального максимума функции при lambda_1<0, lambda_2<0 . В случае гиперболического параболоида ( и имеют разные знаки) в стационарной точке $x^{ast}$ нет экстремума. В случае выпуклого параболического цилиндра можно сказать, что точка $x^{ast}$ не может быть точкой максимума, но может быть точкой минимума, в случае вогнутого параболического цилиндра точка $x^{ast}$ не может быть точкой минимума, но может быть точкой максимума. Таким образом, если хотя бы одно собственное значение равно нулю, судить о наличии экстремума в точке $x^{ast}$ нельзя, так как нужны дополнительные исследования, учитывающие в формуле Тейлора члены выше второго порядка.

Алгоритм исследования функции на локальный экстремум

1. Составить и решить систему (4.74) — найти стационарные точки $x^{ast}$ . Если система не имеет решения, то точек локального экстремума нет.

2. Составить матрицу Гессе $H(x^{ast})$ и найти ее собственные значения lambda_1 и lambda_2 , решая характеристическое уравнение

$detBigl(H(x^{ast})-lambdacdot EBigr)=0.$

3. Проверить выполнение следующих условий.

а) Если lambda_1>0, lambda_2>0 , то $x^{ast}$ — точка локального минимума.

б) Если lambda_1<0, lambda_2<0 , то $x^{ast}$ — точка локального максимума.

в) Если lambda_1geqslant0, lambda_2geqslant0 , то $x^{ast}$ может быть точкой локального минимума (требуется дополнительное исследование).

г) Если lambda_1leqslant0, lambda_2leqslant0 , то $x^{ast}$ может быть точкой локального максимума (требуется дополнительное исследование).

д) Если lambda_1 и lambda_2 разных знаков (lambda_1cdotlambda_2<0) , то $x^{ast}$ не является точкой локального экстремума.

Пример 4.25. Найти экстремумы функции f(x)=x_1^3+x_2^3-3x_1x_2 .

Решение.. Решая систему уравнений

$frac{partial f(x)}{partial x_1}=3cdot x_1^2-3cdot x_2=0,quad frac{partial f(x)}{partial x_2}=3cdot x_2^2-3cdot x_1=0,$

находим стационарные точки O(0,0) и M(1,1) .

Составляем матрицу Гессе $H(x)=begin{pmatrix}6x_1&-3\-3&6x_2end{pmatrix}$ .

В стационарной точке O(0,0) матрица Гессе $H(x)|_{O}=begin{pmatrix}0&-3\-3&0end{pmatrix}$ . Найдем собственные значения матрицы Гессе. Характеристическое уравнение

$begin{vmatrix},-lambda&-3\-3&-lambda,end{vmatrix}=0 quadLeftrightarrowquad lambda^2-9=0$

имеет корни lambda_1=3,~lambda_2=-3 разных знаков. Следовательно, точка O(0,0) не является точкой экстремума (см. п.3,»д» алгоритма).

В стационарной точке M(1,1) матрица Гессе $H(x)|_{M}=begin{pmatrix}6&-3\-3&6end{pmatrix}$ . Характеристическое уравнение

$begin{vmatrix},6&-3\-3&6,end{vmatrix} quadLeftrightarrowquad (6-lambda)^2-9=0$

имеет два положительных корня lambda_1=3,~lambda_2=9 . Следовательно, точка M(1,1) является точкой минимума (см. п.3,»а» алгоритма).

Применение графических методов поиска экстремума функции

Рассмотрим постановку задачи поиска условного экстремума функции трех переменных. Пусть заданы:

а) функция f(x)=f(x_1,x_2,x_3) трех переменных $(xinmathbb{R}^3)$ ;

б) множество допустимых решений $M~(Msubsetmathbb{R}^3)$ .

Требуется найти такую точку $x^{ast}$ из множества допустимых решений, которой соответствует минимальное значение функции f(x) на этом множестве:

$f(x^{ast})=min_{xin M}f(x).$

Алгоритм графического метода поиска условного (или безусловного экстремума) функции аналогичен алгоритму, рассмотренному ранее для функции двух переменных. Однако его применение на практике ограничивается возможностями изображения пространственных фигур. Как правило, используется плоское изображение пространственных фигур, т.е. проекции этих фигур на плоскость, что не дает полного представления о взаимном их расположении.

Ниже рассматриваются задачи, в которых минимизируемая функция и функции, задающие ограничения, являются многочленами трех переменных первой или второй степени. Построение множества допустимых решений и поверхностей уровня функции f(x) сводится к построению алгебраических поверхностей первого или второго порядков. В этих задачах применение графического метода упрощается.

Напомним, что поверхностью уровня функции f(x)=f(x_1,x_2,x_3) называется геометрическое место точек пространства, в которых функция принимает постоянное значение, т.е. f(x)=text{const} .

Если функция f(x)=f(x_1,x_2,x_3) является многочленом первой степени, то ее поверхности уровня f(x)=text{const} при разных значениях постоянной (text{const}) представляют собой семейство параллельных плоскостей (несобственный пучок плоскостей).

Если функция f(x)=f(x_1,x_2,x_3) является многочленом второй степени, то ее поверхности уровня f(x)=text{const} при разных значениях постоянной (text{const}) представляют собой поверхности второго порядка. Поскольку уравнения разных поверхностей уровня отличаются только свободными членами, то собственные векторы, собственные значения lambda_1,,lambda_2,,lambda_3 , а также инварианты tau_1,,tau_2,,delta остаются постоянными для всех поверхностей уровня f(x)=text{const} . Следовательно, тип поверхности и канонический базис остаются постоянными для всех поверхностей уровня квадратичной функции.

Пример 4.26. Графическим методом найти экстремумы:

$mathsf{1)}~f(x)=x_1^2+frac{x_2^2}{4}+x_3^2totext{extr},;quad mathsf{2)},begin{cases}f(x)=x_3totext{extr},\dfrac{x_1}{2}+dfrac{x_2}{3}+x_3=1,\ x_1,x_2,x_3geqslant0;end{cases}mathsf{3)},begin{cases}f(x)=x_1^2+x_2^2-x_3^2totext{extr},\x_1^2+x_2^2+x_3^2=1.end{cases}$

Решение.

1) 1. Множество допустимых решений строить не нужно, так как оно совпадает со всем пространством: $M=mathbb{R}^3$ .

2. Поверхность уровня $x_1^2+frac{x_2^2}{4}+x_3^2=text{const}$ при text{const}>0 представляет собой эллипсоид (рис.4.59,а), при text{const}=0 — мнимый конус с единственной вещественной точкой O(0,0,0) , при text{const}<0 — мнимый эллипсоид. При увеличении постоянной (text{const}) полуоси эллипсоида пропорционально увеличиваются. На рис.4.59,а изображены эллипсоиды

$x_1^2+frac{x_2^2}{4}+x_3^2=1~(a=1,~b=2,~c=1)$ и $frac{x_1^2}{4}+frac{x_2^2}{16}+frac{x_3^2}{4}=1~(a=2,~b=4,~c=2).$

Стрелками указаны направления наискорейшего возрастания функции.

3. Из пункта 2 следует, что допустимые значения функции определяются не равенством 0leqslant f(x)<+infty .

4. В точке O(0,0,0) достигается безусловный минимум функции, так как в этой точке функция принимает наименьшее значение по сравнению со значениями в других точках пространства, а наибольшего значения функция не достигает.

Поверхности уровня эллипсоида и плоскости

2) Решается задача поиска условного экстремума с ограничениями типа равенств и неравенств.

1. Строим множество допустимых решений — часть плоскости $frac{x_1}{2}+frac{x_2}{3}+x_3=1$ в первом октанте, т.е. плоский треугольник с вершинами A(2,0,0), B(0,3,0), C(0,0,1) (рис.4.59,б).

2. Поверхности уровня $x_3=text{const}$ функции f(x_1,x_2,x_3)=x^3 представляют собой семейство параллельных плоскостей, каждая из которых перпендикулярна оси аппликат. На рис.4.59,б изображены три плоскости уровня x_3=0, x_3=1, x_3=2 . При text{const}<0 или text{const}>1 плоскость $x_3=text{const}$ не имеет общих точек с треугольником ABC ; при 0leqslanttext{const}leqslant1 плоскость $x_3=text{const}$ имеет общие точки с треугольником ABC , в частности, при text{const}=0 плоскости x_3=0 принадлежит сторона треугольника, при text{const}=1 плоскости x_3=1 принадлежит вершина треугольника.

3. Из пункта 2 следует, что допустимые значения функции определяются неравенством 0leqslant f(x)leqslant1 .

4. Наименьшее значение на множестве , равное нулю, функция достигает в любой точке отрезка ; наибольшее значение на множестве , равное единице, функция достигает в точке C(0,0,1) .

3) Решается задача поиска условного экстремума с ограничением типа равенств.

1. Строим множество допустимых решений — сфера x_1^2+x_2^2+x_3^2=1 единичного радиуса с центром в начале координат (рис.4.60).

2. Поверхности уровня $x_1^2+x_2^2-x_3^2=text{const}$ представляют собой либо однополостный гиперболоид вращения при text{const}>0 (например, однополостный гиперболоид x_1^2+x_2^2-x_3^2=1 (рис.4.60,а)), либо круговой конус x_1^2+x_2^2-x_3^2=0 при text{const}=0 (рис.4.60,б), либо двуполостный гиперболоид вращения при text{const}<0 (например, двуполостный гиперболоид x_1^2+x_2^2-x_3^2=-1 (рис.4.60,в)). При text{const}>1 поперечные полуоси однополостного гиперболоида $x_1^2+x_2^2-x_3^2=text{const}$ больше единицы, и он не имеет общих точек со сферой единичного радиуса. При text{const}<-1 продольная полуось двуполостного гиперболоида $x_1^2+x_2^2-x_3^2=text{const}$ больше единицы, и он не имеет общих точек со сферой x_1^2+x_2^2+x_3^2=1 . При -1leqslanttext{const}leqslant1 поверхность уровня $x_1^2+x_2^2-x_3^2=text{const}$ имеет общие точки с заданной сферой.

3. Из п.2 следует, что допустимые значения функции определяются неравенством -1leqslant f(x)leqslant1 .

4. Наименьшее значение на множестве , равное –1, функция достигает в точках (0,0,pm1) — вершинах двуполостного гиперболоида x_1^2+x_2^2-x_3^2=-1 (рис.4.60,в); наибольшее значение на множестве , равное единице, функция достигает в точках окружности $begin{cases}x_1^2+x_2^2=1,\x_3=0,end{cases}$ т.е. в точках горлового эллипса (в данном случае окружности) однополостного гиперболоида вращения x_1^2+x_2^2-x_3^2=1 (рис.4.60,а).

Поверхности уровня гиперболоидов и конуса

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Графическим методом
можно решать задачи, заданные в
неканоническом виде с двумя переменными
или сводящиеся к ним. Рассмотрим задачу
следующего вида: найти экстремум функции

при ограничениях:

х₁>0,
х₂>0.

Надо построить
область допустимых решений системы
ограничений. При этом возможны случаи:

1) область
допустимых решений — пустое множество;

2) область
допустимых решений — единственная точка;

3) область
допустимых решений — выпуклый многоугольник;

4) область
допустимых решений — выпуклая неограниченная
область.

В первом случае
ЗЛП не имеет оптимального решения из-за
несовместности системы ограничений.

Во втором случае
— это единственное решение и будет
оптимальным решением.

В третьем случае,
чтобы найти оптимальное решение задачи,
можно найти координаты всех угловых
точек многоугольника, вычислить значения
целевой функции во всех угловых точках.
Наибольшее из этих значений и будет
максимальным значением целевой функции,
а наименьшее — минимальным, а координаты
соответствующей угловой точки —
оптимальным решением.

Существует другой
способ, который позволяет графически
сразу найти угловую точку, соответствующую
оптимальному решению.

Пусть
с₀
— некоторое число. Прямая является
линией уровня целевой функции. В каждой
точке этой прямой целевая функция
принимает одно и то же значение, равное
с₀.
Вектор — градиент целевой функции

перпендикулярен
к линиям уровня и показывает направление,
в котором эта функция возрастает с
наибольшей скоростью. Выбирая из линий
уровня, проходящих через область
допустимых решений, наиболее удаленную
в направлениях вектора (в
случае минимизации — в противоположном
направлении), определим угловую точку,
в которой целевая функция принимает
максимальное (минимальное) значение.

Если экстремум
достигается в двух угловых точках, то,
по теореме об альтернативном оптимуме,
оптимальным решением будет любая точка
отрезка, соединяющего эти точки:

,
.

В четвертом случае,
когда область допустимых решений системы
ограничений задачи неограниченная
выпуклая область, оптимальное решение
находится аналогично описанному выше.
В данном случае оптимальное решение
может совпадать с одной угловой точкой,
с двумя угловыми точками и оптимальное
решение может и не существовать из-за
неограниченности целевой функции сверху
в задаче на максимум или снизу в задаче
на минимум.

Пример
1. Решить
графически следующую задачу:

х₁
>0, х₂
>0.

Построим область
допустимых решений системы ограничений:

Х₂

30
А

D
Х₁

40 50 80

l₂
l₁

l₃

Областью
допустимых решений системы ограничений
является выпуклый пятиугольник ОАВCD.

Построим
вектор и
линию уровня, перпендикулярную вектору
.
Наибольшее значение целевая функция
достигает в угловой точке В.
Найдем координаты точки В,
для этого решим систему из уравнений
первой и второй прямой.

Решая
систему, получим: ,
.

Пример
2. Найти
наибольшее и наименьшее значения функции

при ограничениях:

х₁+х₂
> 8,

-5х₁+2х₂
<
10,

х₁-3х₂
<
0,

х₁
>0, х₂
>0

Построим ОДР.

Областью
допустимых решений системы ограничений
является выпуклая многоугольная
неограниченная область. Наименьшее
значение целевой функции достигается
в угловой точке А,
а наибольшее значение функции найти
нельзя, так как функция не ограничена
сверху, т.е. max
L
= ∞.

Найдем
координаты точки А, для этого решим
систему из уравнений первой и третьей
прямой:

х₁+х₂
= 8,

х₁-3х₂
=0

х₁
= 6,

х₂= 2.

т.е.
.

Соседние файлы в папке ПОСОБИЕ МСС

Источник

Графический метод решения задач нелинейного программирования

Графический метод можно использовать для решения задачи нелинейного программирования (НП), которая содержит две переменных х₁ и х₂, например задачи следующего вида:

Z = f(x₁, x₂) → min (max);

g_i(x₁, x₂) ≤ b_i, i=1,m

Чтобы найти ее оптимальное решение, нужно выполнить следующие действия:

Найти ОДР, определяемую ограничениями задачи. Если окажется, что эта область пуста, то это означает, что задача не имеет решения.
Построить семейство линий уровня целевой функции f(х₁, х₂) = C при различных значениях числового параметра С.
При решении задачи на минимум определить направление убывания, а для задачи на максимум — направление возрастания линий уровня ЦФ.
Найти точку ОДР, через которую проходит линия уровня с наименьшим в задаче на минимум (соответственно, наибольшим в задачи на максимум) значением параметра С. Эта точка будет оптимальным решением. Если ЦФ не ограничена снизу в задаче на минимум (сверху — в задаче на максимум), то это означает, что задача не имеет оптимального решения.
Найти координаты точки оптимума и определить в ней значение ЦФ.

Отметим, что в отличие от задачи ЛП точка оптимума в задаче НП не обязательно находится на границе ОДР. Ею также может быть внутренняя точка этого множества.

Пример. В задаче выпуклого программирования требуется:

найти решение графическим методом;
написать функцию Лагранжа и найти ее седловую точку, используя решение, полученное графически.

F(X) = x₁²+(x₂-2)²

2x₁+x₂ ≥ 7

x₁+2x₂ ≥ 5

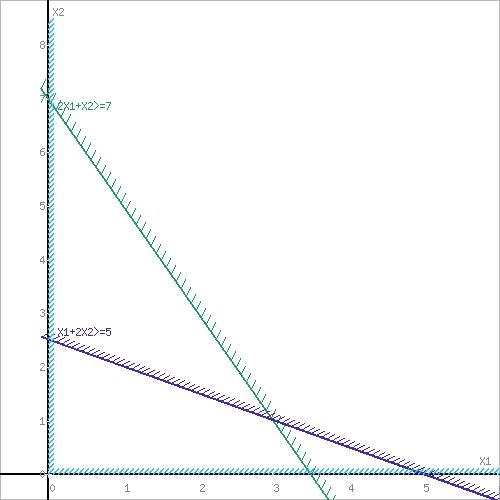
Решение. 1) Строим два ограничения, тем самым определяя ОДР. Можно использовать этот калькулятор. Также удобно строить ограничения через этот сервис.

Затем строим функцию цели. В данном случае это окружность.

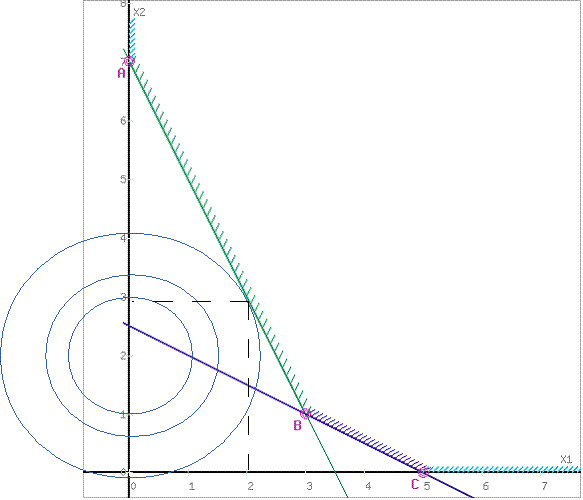
Поскольку задача минимума, то ищем первое касание линии уровня области ОДР. В данном случае это точка пересечения с прямой 2x₁+x₂-7=0.

Найдем точку пересечения. Для этого построим уравнение касательной, проходящей через центр окружности O(0;2) и перпендикулярно прямой 2x₁+x₂-7=0 (можно использовать этот калькулятор). Получаем: 2x₂-x₁-4=0. Решая систему уравнений:

2x₁+x₂-7=0

2x₂-x₁-4=0,

получаем: x₁=2, x₂=3.

2) Найдем экстремум функции F(X) = x₁²+(x₂-2)², используя калькулятор Функция Лагранжа:

L(X, λ)=F(X)+∑(λ_i·φ_i)

где F(X) — целевая функция вектора X; φ_i(X) — ограничения в неявном виде (i=1..n)

В качестве целевой функции, подлежащей оптимизации, в этой задаче выступает функция: F(X) = x₁²+(x₂-2)²

Перепишем ограничение задачи в неявном виде:

φ₁(X) = 7 — (2*x₁+x₂) = 0 (X₁)

φ₂(X) = 5 — (x₁+2*x₂) = 0 (X₂)

Составим вспомогательную функцию Лагранжа: L(X, λ) = x₁²+(x₂-2)² — λ₁*(7 — (2*x₁+x₂)) — λ₂*(5 — (x₁+2*x₂))

Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным х_i и неопределенным множителям λ.

Составим систему:

∂L/∂x₁ = 2*λ₁+λ₂+2*x₁ = 0

∂L/∂x₂ = λ₁+2*λ₂+2*x₂-4 = 0

∂L/∂λ₁ = 2*x₁+x₂-7 = 0

∂L/∂λ₂ = x₁+2*x₂-5 = 0

Решив данную систему, получаем:

а) для случая X₁: x₁ = λ₁/2 + λ₂ + 2; x₂ = 7 — 2x₁

Откуда можно найти такие λ₁ ≥ 0, λ₂ ≥ 0. Пусть λ₂ = 0. Тогда λ₁ = 2; x₁ = 2; x₂ = 3.

Поскольку λ₂ ≥ 0, то данное решение удовлетворяет условиям Куна-Таккера. Z_min(2;3)=5

б) для случая X₂: x₂ = λ₁/2 + λ₂ + 2; x₁ = 5 — 2x₂

Откуда можно найти такие λ₁ ≥ 0, λ₂ ≥ 0. Пусть λ₂ = 0. Тогда λ₁ = 2/5; x₁ = 11/5; x₂ = 3/5.

Поскольку λ₁ ≥ 0, то данное решение удовлетворяет условиям Куна-Таккера. Z_min(11/5;3/5)=6.8

Минимальное значение составит Z_min(2;3)=5.

см. также прикладное использование метода Лагранжа

см. также Решение задачи безусловной оптимизации, Решение классической задачи условной оптимизации.

Пример. Фирма выпускает два вида изделий А и В, которые обрабатываются на станках двух типов. Известны нормативы a_ij времени, требуемого для обработки одного изделия j-го вида на станке i-го типа (ст./час.), общие фонды рабочего времени каждого типа станков b_i (ст./час.). Фирма имеет контракт, согласно которому должна ежедневно поставлять заказчику d₁ изделий А и d₂ изделий В.

Анализ продаж фирмы показал, что с увеличением объема выпуска из-за роста расходов по реализации изделий их удельная прибыль р_j (руб.) уменьшается, причем для ее определения может быть использована формула р_j = c_j – lх_j, где х_j — количество проданных изделий j-го вида, а c_j и l — фиксированные величины.

Нужно определить, сколько изделий каждого вида следует изготовить фирме, чтобы прибыль от их реализации была максимальной.

Исходные значения параметров представлены в таблице:

а₁₁	a₁₂	a₂₁	a₂₂	b₁	b₂	d₁	d₂	c₁	c₂	l
2	2	6	2	160	220	10	20	320	280	2

Требуется:

1. Составить математическую модель нахождения оптимального плана выпуска продукции.

2. Определить оптимальный план выпуска обобщенным методом множителей Лагранжа и дать экономическую интерпретацию полученных результатов.

Решение:

1. Построение математической модели

В рассматриваемой задаче следует определить

х₁ — план выпуска изделий А;

х₂ — план выпуска изделий В.

Эти величины являются переменными модели. Обязательства по контракту дают следующие ограничения на их значения: х₁ ≥ 10 и х₂ ≥ 20. Так как время работы станков каждого типа, затрачиваемое на обработку деталей, не должно превосходить их общего лимита времени работы, то получаем еще два ограничения:

2х₁ + 2х₂≤ 160,

6х₁ + 2х₂ ≤ 220.

Прибыль Z, получаемая от продажи продукции, вычисляется по формуле

Z = (320 – 2х₁) х₁+ (280 – 2х₂) х₂ = 320 х₁ – 2x₁² + 280 х₂ – 2x₂².

Таким образом, математическая модель задачи фирмы имеет вид:

Z = 320х₁ – 2x₁² + 280 х₂ – 2x₂² → max, (1)

2х₁ + 2х₂≤ 160, (2)

6х₁ + 2х₂ ≤ 220, (3)

х₁ ≥ 10, х₂ ≥ 20. (4)

2. Нахождение оптимального плана обобщенным методом множителей Лагранжа.

Сначала проверим, что задача (1) – (4) является задачей ВП. Так как все ограничения модели линейны, для этого достаточно убедиться в том, что ЦФ — вогнутая функция. Для этого вычислим ее гессиан.

Найдем первые частные производные ЦФ:

и ,

а затем ее вторые частные производные:

;

;

.

Следовательно, гессиан Н функции f имеет следующий вид:

.

Главные миноры первого порядка равны –4, а главный минор второго порядка равен

= (-4)·(-4) – 0·0 = 16.

Значения этих миноров не зависят от точки х = (x₁, x₂), причем минор первого (нечетного) порядка отрицателен, а минор второго (четного) порядка положителен. Поэтому ЦФ — строго вогнутая функция (см. теорему 1) Это означает, что задача (1) – (3) является задачей ВП и имеет единственное оптимальное решение.

Для нахождения оптимального решения этой задачи обобщенным методом множителей Лагранжа нужно выполнить следующие действия.

Шаг 1. Сначала решим задачу без учета ограничений, т.е. как задачу отыскания глобального максимума ЦФ. Назовем ее «задача 2.1». Она имеет следующий вид.

Z = 320х₁ – 2x₁² + 280 х₂ – 2x₂² → max.

Для ее решения нужно найти стационарную точку ЦФ, координаты которой являются решением системы

Отсюда, x₁¹=80, x₂²=70. Таким образом, стационарная точка ЦФ — точка x¹=(80,70). В силу вогнутости Z она является точкой ее глобального максимума. Поэтому, если окажется, что эта точка является допустимой в исходной задаче, то она будет ее точкой оптимума. Проверим выполнение ограничения (2):

2×80 + 2×70 = 160 + 140 = 300 > 160.

Найденная точка не является допустимой и, следовательно, не может являться оптимальным решением задачи (1) – (4).

Шаг 2. Согласно схеме обобщенного метода множителей Лагранжа решим задачу максимизации ЦФ («задача 2.2») с учетом первого из ограничений исходной задачи фирмы, которое следует записывать в виде равенства.

Задача 2.2 имеет следующий вид:

Z = 320х₁ – 2x₁² + 280х₂ – 2x₂² → max, (5)

2х₁ + 2х₂ = 160. (6)

Сформируем функцию Лагранжа

L(x₁, x₂, λ) = 320х₁ – 2x₁² + 280х₂ – 2x₂² + λ(160– 2х₁ – 2х₂)

и найдем ее стационарные точки. Для этого нужно решить систему

Из первого уравнения имеем

4x₁=320-2λ → x₁=80-0.5λ,

а из второго уравнения

4x₂=280-2λ → x₂=70-0.5λ,

Подставив найденные выражения х₁ и х₂ от λ в третье уравнение, получим

160 – 2×(80 – 0.5λ) – 2×(70 – 0.5λ) = 0 → 2λ – 140 = 0 → λ = 70.

Тогда х₁ = 80 – 70/2 = 45, а х₂ = 70 – 70/2 = 35, т.е. решение системы:

x₁² = 45, x₂² = 35, λ² = 70.

Найденная точка х² = (45, 35) является оптимальным решением задачи 2.2. Проверим, является ли она допустимой в исходной задаче (1) – (4). Для этого подставим ее координаты в ограничение (3). Получаем, что

6×45 + 2×35 = 270 + 70 = 340 > 220.

Следовательно, найденное решение не является допустимым.
Шаг 3. Решим задачу максимизации ЦФ («задача 2.3») с учетом второго ограничения задачи фирмы, которое также запишем в виде равенства. Она имеет следующий вид:

Z = 320х₁ – 2x₁² + 280 х₂ – 2x₂² → max, (7)

6х₁ + 2х₂ = 220. (8)

Снова сформируем функцию Лагранжа:

L(x₁, x₂, λ) = 320х₁ – 2x₁² + 280 х₂ – 2x₂² + λ(220– 6х₁ – 2х₂)

и найдем ее стационарные точки. Для этого нужно решить систему

Из первого уравнения имеем

4x₁=320-6λ → x₁=80-1.5λ,

а из второго уравнения

4x₂=280-2λ → x₂=70-0.5λ,

Подставив найденные выражения х₁ и х₂ от λ в третье уравнение, получим

220 – 6 (80 – 1.5λ) – 2×(70 – 0.5λ) = 10λ – 400 = 0 → λ = 40.

Тогда х₁ = 80 – 1.5×40 = 20, а х₂ = 70 – 40/2 = 50. Итак, решение системы:

x₁³ = 20, x₂³ = 50, λ³ = 40.

Найденная точка х³ = (20, 50) является оптимальным решением задачи 3. Проверим, является ли она допустимой в исходной задаче. Для этого подставим ее координаты в ограничение (2). Получаем, что

2×20 + 2×50 = 40 + 100 = 140 < 160,

т.е. это ограничение выполнено. Очевидно, что выполнены и остальные ограничения задачи (1) – (4). Так как она является задачей ВП, это означает, что найдено оптимальное решение задачи фирмы х^* = (20, 50). Вычислим оптимальное значение ЦФ:

Z^* = 320×20 – 2×20² + 280×50 – 2×50² = 14 600.

Итак, оптимальным решением является выпуск 20 изделий вида А и 50 изделий вида А. Реализация выпущенных изделий даст фирме максимальную прибыль, равную 14 600 руб. Выполнение этой производственной программы требует затрат 140 ст./час. из фонда рабочего времени станков первого типа и 220 ст./час. из фонда рабочего времени станков второго типа. Это означает, что первый вид оборудования недоиспользуется, а второй вид оборудования используется полностью.

Множитель Лагранжа ограничения по станкам второго типа λ^* = 40 характеризует предельную полезность этого ресурса. Его величина показывает, что при увеличении фонда рабочего времени станков этого типа на 1 ст./час. прибыль фирмы возрастет примерно на 40 руб.

Геометрическая интерпретация используемого метода решения

С геометрической точки зрения ОДР задачи фирмы представляет собой выпуклый четырехугольник АВCD (см. рис. 2). Линии уровня ЦФ представляют собой концентрические окружности, имеющие общий центр в точке О (80, 70), причем чем дальше от центра находится линия уровня, тем меньшее значение имеет на ней ЦФ.

Рис. 2. Геометрическая интерпретация решения задачи фирмы

Решение задачи 2.1 — точка О, в которой находится глобальный безусловный максимум ЦФ. Она находится вне ОДР и, следовательно, не является допустимой в задаче фирмы.

Решение задачи 2.2 — точка Е (45, 35), в которой линия уровня ЦФ касается граничной прямой ограничения (2). Эта точка также находится вне ОДР и не является допустимой в задаче фирмы.

Решение задачи 2.3 — точка F (20, 50), в которой линия уровня ЦФ касается граничной прямой ограничения (3). Она лежит на границе ОДР и является «первой» общей точкой ОДР и линии уровня ЦФ. Это оптимальное решение задачи фирмы.

С геометрической точки зрения решение задач 2.2 и 2.3 аналогично графическому решению предыдущей задачи.

Замечание. Если при решении задачи фирмы оказалось бы, что точка О лежит внутри ОДР, то в этом случае точка оптимума была бы глобальным максимумом ЦФ. Возможна ситуация, когда точкой оптимума является угловая точка (одна из вершин ОДР). Она будет стационарной точкой функции Лагранжа в задаче максимизации ЦФ, содержащей два ограничения, активных (выходящих на равенство) в этой точке.

Источник

Применение поверхностей первого и второго порядковв задачах на экстремум функций

Аналитический метод поиска локального безусловного экстремума

Алгоритм исследования функции на локальный экстремум

Применение графических методов поиска экстремума функции

Графический метод решения задач нелинейного программирования

Геометрическая интерпретация используемого метода решения

Применение поверхностей первого и второго порядков
в задачах на экстремум функций