Как найти экстремумы функции матлаб

Main Content

syms x
num = 3*x^2 + 6*x -1;
denom = x^2 + x - 3;
f = num/denom

f1 = 
6 x+6x2+x-3-2 x+1 3 x2+6 x-1x2+x-32

f1 = 
-3 x2+16 x+17x2+x-32

crit_pts = 
(-133-83133-83)

fplot(f)
hold on
plot(double(crit_pts), double(subs(f,crit_pts)),'ro')
title('Maximum and Minimum of f')
text(-4.8,5.5,'Local minimum')
text(-2,4,'Local maximum')
hold off

f2 = diff(f1);
inflec_pt = solve(f2,'MaxDegree',3);
double(inflec_pt)

ans = 3×1 complex

  -5.2635 + 0.0000i
  -1.3682 - 0.8511i
  -1.3682 + 0.8511i

idx = imag(double(inflec_pt)) == 0;
inflec_pt = inflec_pt(idx)

inflec_pt = 
-139 16954-2197181/3-16954-2197181/3-83

fplot(f,[-9 6])
hold on
plot(double(inflec_pt), double(subs(f,inflec_pt)),'ro')
title('Inflection Point of f')
text(-7,1,'Inflection point')
hold off

Здравствуйте, уважаемые читатели. Продолжаем разбираться в Matlab. И сегодня наша тема связанна с численной оптимизацией — нахождением локальных и глобальных экстремумов функций одной или нескольких переменных в среде Matlab.

Общие сведения

Итак, в этом блоке ничего про Matlab не будет, лишь информация о понятии оптимизации. Это понятие сводится к терминам минимума и максимума функции, или, если коротко — экстремумам.

Под минимумом понимают такое значение функции, которое в некоторой окрестности этой функции, принимает наименьшее значение из всех возможных значений в этой окрестности. Соответственно максимум — это наибольшее значение функции в какой-либо окрестности.

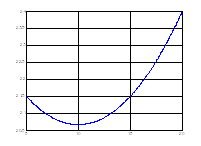
Если не понятно — вот простой пример с всеми известной параболой:

У этой функции есть один минимум, и он находится в точке x = 0. Эта точка называется точкой минимума, а само значение этой функции есть минимум (он тоже равен 0). Максимумов у этой функции нет, но если бы функцию перевернули вверх ногами, то он бы появился.

Часто встречаются сложные функции, у которых есть несколько и минимумов и максимумов. И в таком случае, разделяют понятия локального и глобального экстремума. Локальный — это тот экстремум, который определен в некоторой области, а глобальный — на всей области определения функции. На рисунке выше представлен глобальный минимум параболы.

И теперь, когда вы хоть как то познакомились с понятиями оптимизации и нахождения экстремумов функции, можем перейти к нахождению максимумов и минимумов в Matlab. Далее, как обычно мы будем разбирать примеры различной сложности. Часть примеров будет содержать в себе стандартные команды Matlab для нахождения минимума и максимума функции, а другая часть — это реализация метода с нуля.

Стандартные методы Matlab

Разберем 2 задачи нахождения минимума в Matlab:

1 пример. Вычислить минимум функции f(x)=-x^1/x, определив графически интервал его локализации. Вычисления провести с минимальным шагом по аргументу 1*10^-5

Для начала создадим скрипт, который отобразит эту функцию. Вот код для этого:

x = 0.00001:0.00001:10;
y = -x.^(x.^(-1));
plot (x,y);
hold on;
grid on;

Запускаем скрипт и получаем:
По графику функции делаем вывод, что имеется один минимум, и его координаты находятся в интервале 2.5 — 3, то есть мы сократим интервал поиска минимума.

Теперь создадим еще один скрипт, дадим ему название first.m и пропишем в него функцию:

function fun=first(x)
fun = -x.^(x.^(-1));
end

Таким образом в этом m-файле мы определили функцию. Теперь в командном окне мы пропишем следующий код:

>> [x,y] = fminbnd(@first,2.5,3)

И получаем такие значения:
x = 2.7183 — координата точки минимума
y = -1.4447 — значение минимума

В этой части кода мы использовали стандартный метод Matlab для нахождения минимума функции — fminbnd. мы передаем 3 параметра — саму функцию и интервалы для поиска минимума. Стоит отметить, что этот метод подходит только для функций, зависящих от одной переменной.

Итак, для этой задачи мы создали 2 скрипт-файла, которые вы можете скачать в конце статьи.

2 пример. Вычислить минимум функции двух переменных x⁴+y⁴-2x²+4xy-2y²+1 с точность 1*10-5.
Координаты начальной точки поиска [1.0,-1.0].

Для начала построим график функции от двух переменных — для этого создадим новый скрипт и пропишем там этот код:

[x y] = meshgrid(-2:0.1:2, -2:0.1:2);
z = x.^4 + y.^4 - 2*x.^2 + 4 * x.*y - 2*y.^2 + 1;
surf(x,y,z);

Функция surf позволяет строить трехмерные графики и отображать глубину значений функции для лучшего понимания. Запускаем скрипт — в итоге получился такой график:
Как видно из графика, имеется два участка, где присутствует локальный минимум (темно-синие участки), и наша задача найти координаты и значения двух этих точек. Воспользуемся стандартными инструментами Matlab и создадим новый скрипт с именем second.m, в котором и пропишем код:

function fun=second(x)
fun = x(1)^4 + x(2)^4 - 2*x(1)^2 + 4 * x(1)*x(2) - 2*x(2)^2 + 1;
end

После этого, в командной строке, как и для первой задачи, прописываем стандартную функцию Matlab:

>> [z,f,exitflag,output] = fminsearch(@second, [1.0,-1.0], optimset('TolX',1e-5))

Получаем такой вывод:

z = 1.4142   -1.4142
f = -7.0000
exitflag = 1
output = 
    iterations: 40
    funcCount: 74
    algorithm: 'Nelder-Mead simplex direct search'
    message: [1x196 char]

Для нахождение минимумов в Matlab на этот раз мы использовали функцию fminsearch. Эта функция реализует симплекс — метод Нелдера-Мида. В выводе мы получили несколько переменных: в z записались значения координат точек минимума, в f само значение этого минимума. А в переменных exitflag и output помещены условия прерывания процесса поиска и информация об оптимизации соответственно.

В итоге у нас опять получилось 2 m-файла.

Метод Ньютона Matlab

А теперь попробуем сами реализовать метод Ньютона для оптимизации функции.

3 пример. Методом Ньютона найти точку минимума x* и минимальное значение f* функции f(x)=(x-2)⁴-lnx на отрезке xє[2;3] c точностью 10^-7

Начнем с того, что создадим новый скрипт и назовем его Newton.m. Затем пропишем в нем код:

function [Xk, Yk] = Newton(f,diap)
    a = diap(1); % границы
    b = diap(2);
    df = char(diff(sym(f))); % символьно ищем первую 
    ddf = char(diff(sym(df))); % и вторую производные
    F = inline(f); % преобразуем в функции
    F1 = inline(df);
    F2 = inline(ddf);
    eps = 0.0000001; % задаем точность
    if F(a)*F2(a) > 0 % проверка с какой границы начинать искать
        Xk = b;
    else
        Xk = a;
    end
    while abs(F1(Xk)) > eps
        X0 = Xk; % X0 - значение предыдущего шага
        Xk =  X0 - (F1(X0)/(F2(X0))); % расчет нового значения
        Yk = F(Xk);
    end
end

Вполне понятная функция, которая работает с первой и второй производной символьной функции, которую получает в качестве параметра. Также в параметрах принимается диапазон. Эта функция возвращает координаты точки и значение экстремума.
Теперь нам осталось вызвать эту функцию в командном окне:

>> fun = '(x-2)^4 - log(x)';
>> diap = [2,3];
>> [Xk, Yk] = Newton(fun, diap);

В итоге получилось:
Xk = 2.4663
Yk = -0.8554

Не будем приводить график, но вы сами можете проверить, что значения найдены правильно. Важно сказать, что этот метод позволяет найти только локальный экстремум, и если на выбранном диапазоне есть несколько экстремумов, то метод может найти не тот, который нужен вам.

Также, очень важно задавать как можно узкий диапазон поиска, иначе метод может работать некорректно, особенно это проявляется с периодическими функциями по типу cos(x) и т.п.

Заключение

Ну что ж, в этой статье мы рассмотрели некоторые методы для нахождения экстремумов в Matlab. Мы использовали как стандартные методы, так и реализовали метод Ньютона в среде Matlab. Их исходники чуть ниже.
Скачать исходники

На этом сегодня все, оставляйте ваши комментарии и задавайте вопросы.

Тема
5.6. Технология решения задач одномерной
оптимизации средствами MatLab

Пакет MatLab,
также
как и пакет MathCad,
с помощью встроенных функций решает
задачу нахождения только локального
экстремума. Для нахождения глобального
экстремума необходимо вычислить все
локальные экстремумы и выбрать среди
них наибольший (наименьший).

В MatLab
поиск локального минимума осуществляет
функция:

[x,y]=fminbnd(name,a,b,[,options]),

где
name
– имя m-функции,
вычисляющей значение f(x);

a,
b
– границы интервала, на котором
осуществляется поиск минимума;

Options–
параметр, управляющий ходом решения;

x,
y
– координаты точки, в которой
достигается минимум функции на заданном
интервале.

Пример 4.6-1. Найти
локальные экстремумы функции
f(x)=x⁴-0.5x³-28x²+140.

Пример 4.6-2. Найти
минимальное значение функции f(x)=24–2x
/3+x²/
30 наотрезке [5;20].

[Введите текст] Страница
22

Соседние файлы в папке Учебное пособие

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Определение 1(
локальный экстремум). Говорят, что функция f имеет локальный минимум в точке x = p, если существует такой открытый
интервал I,
содержащий p,
что  f(p)<=f(x) для всех  xÎI. Аналогично говорят, что функция f имеет локальный максимум в точке x = p, если  f(x) <= f(p) для всех x∈I. Если функция f имеет или локальный минимум, или
локальный максимум в точке x
= p,
то говорят, что она имеет локальный экстремум в точке x = p.

Определение 2(возрастание
и убывание функции). Предположим, что функция f(x) определена на интервале I.

·       
Если из неравенства x1<x2 следует, что f( x1)<f(x2) для всех x1, x2∈I, то говорят, что функция f возрастает на интервале I.

·       
Если из неравенства x1<x2 вытекает, что f( x1)>f(x2) для всех x1, x2∈I, то говорят, что функция f убывает на интервале I.

Теорема 1.
Предположим, что функция f(x) непрерывна на интервале I=[a,b] и дифференцируема на (a,b).

·       
Если f ‘(x)>0 для всех x∈(a,b), то функция  f(x) является возрастающей на
интервале I.

·       
Если f ‘(x)<0 для всех x∈(a,b), то функция  f(x) является убывающей на интервале I.

Теорема 2.
Предположим, что функция f(x) определена на отрезке I=[a,b] и имеет локальный экстремум во
внутренней точке p∈(a,b). Если f(x) дифференцируема в точке x=p, то f ‘(x)=0.

Теорема 3(критерий
первой производной). Предположим, что функция f(x) непрерывна на отрезке I=[a,b]. Кроме того, предположим, что

f ‘(x) определена для всех x∈(a,b) за исключением, возможно точки x=p.

·       
Если f ‘(x)<0 на интервале (a,p) и f ‘(x)>0 на (p,b), то f(p) – локальный минимум.

·       
Если f ‘(x)>0 на интервале (a,p) и f ‘(x)<0 на (p,b), то f(p) – локальный максимум.

Теорема 4(критерий
второй производной). Предположим, что функция f
непрерывна на отрезке [a,b] и f ‘ и f » определены на (a,b). Также предположим, что p(a,b) – критическая точка, в которой f ‘ (p)=0.

·       
Если f »(p)>0, то значение f(p) является локальным минимумом f.

·       
Если f »(p)<0 то значение f(p) является локальным максимумом f.

·       
Если f »(p)=0, то этот критерий не является
окончательным.

Пример 1.
Используем критерий второй производной, чтобы 
классифировать локальный экстремум функции f(x)= x^3 +x^2 — x+1 на интервале [-2,2].

Первая
производная равна f ‘(x)=3x^2+2x-1= (3x-1)(x+1), а вторая — f »(x) = 6x+2. Существуют две точки,
в которых f ‘(x)=0 (т. е. x=1/3, -1).

Случай
(1). Находим, что в точке x=1/3
f ‘(1/3)=0
и f »(1/3)=4>0;
таким образом, функция f(x) имеет локальный минимум в точке x=1/3.

Случай
(2). Находим, что в точке x=-1 f ‘(-1)=0 и f »(-1)=-4<0; таким образом,
функция f(x) имеет в точке x=-1 локальный максимум.