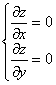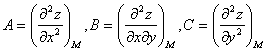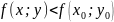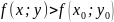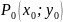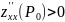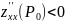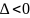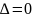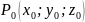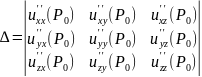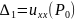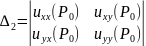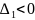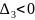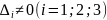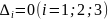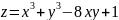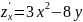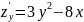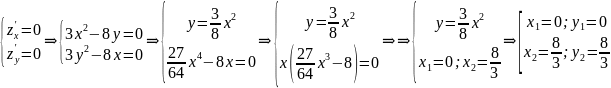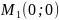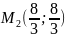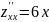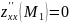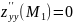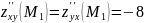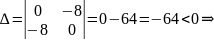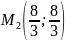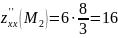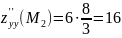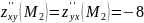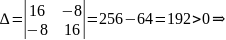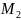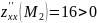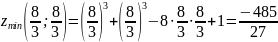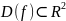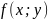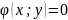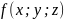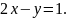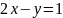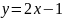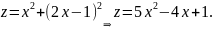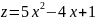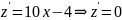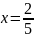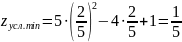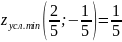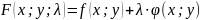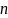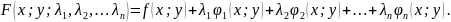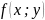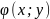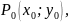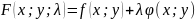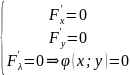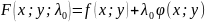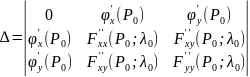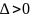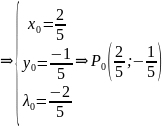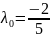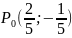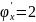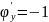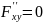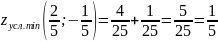Экстремум функции двух переменных
Назначение сервиса. Онлайн-калькулятор используется для нахождения в онлайн режиме наибольшего и наименьшего значения функции двух переменных (см. пример). Решение оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Оформление Word
Для функции трех переменных можно использовать матрицу Гессе.
Алгоритм исследования функции двух переменных на экстремум
Функция z = f(x,y) имеет максимум в точке M0(x0;y0), если f(x0;y0) > f(x;y) для всех точек (x;y), достаточно близких к точке (x0;y0) и отличных от неё. Функция z = f(x,y) имеет минимум в точке M0(x0;y0), если f(x0;y0) < f(x;y) для всех точек (x;y), достаточно близких к точке (x0;y0) и отличных от неё. Максимум и минимум функции называются экстремумами функции.
Исследование функции двух переменных на экстремум проводят по следующей схеме.
1. Находят частные производные dz/dx и dz/dy.
2. Решают систему уравнений:
и таким образом находят критические точки функции.
3. Находят частные производные второго порядка:
4. Вычисляют значения этих частных производных второго порядка в каждой из найденных в п.2 критических точках M(x0;y0).
5. Делаю вывод о наличии экстремумов:
а) если AC – B2 > 0 и A < 0 , то в точке M имеется максимум;
б) если AC – B2 > 0 и A > 0 , то в точке M имеется минимум;
в) если AC – B2 < 0, то экстремума нет;
г) если AC – B2 = 0, то вопрос о наличии экстремума остается открытым;
Пример №1. Найти экстремумы функции f(x,y)=x3+xy2+x2+y2 и определить по критерию Сильвестра их тип.
Решение.
1. Найдем первые частные производные.
2. Решим систему уравнений.
3x2+2x+y2=0
2xy+2y=0
Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
x = -1
y2+1=0
Данная система уравнений не имеет решения.
б) Из первого уравнения выражаем y и подставляем во второе уравнение:
или
или
Откуда x1 = -2/3; x2 = 0; x3 = -2/3; x4 = 0
Данные значения x подставляем в выражение для y. Получаем: y1 = 0; y2 = 0; y3 = 0; y4 = 0
Количество критических точек равно 2: M1(-2/3;0), M2(0;0)
3. Найдем частные производные второго порядка.
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(-2/3;0)
AC — B2 = -4/3 < 0, то глобального экстремума нет.
Вычисляем значения для точки M2(0;0)
AC — B2 = 4 > 0 и A > 0 , то в точке M2(0;0) имеется минимум z(0;0) = 0
Вывод: В точке M2(0;0) имеется минимум z(0;0) = 0
Пример №2. Исследовать функцию на экстремум классическим методом: Z=8x2+2xy-5x+6.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
-
Экстремумы функций двух и трёх переменных
Определение
1
Точка
называется
точкой максимума функции
,
если
для любых точек
,
принадлежащих
окрестности точки
,
выполняется неравенство:
.
Определение
2
Точка
называется
точкой минимума функции
,
если
для любых точек
,
принадлежащих окрестности точки
,
выполняется
неравенство:
.
Определение
3
Точки
максимума и минимума называются
точками
экстремума
функции.
Теорема
1 (необходимое условие экстремума)
Если
точка
является точкой экстремума функции
,
то её частные производные в точке
равны нулю или не существуют.
При
доказательстве теоремы 1 используются
определения частных производных и
теорема о необходимых условиях экстремума
функции одной переменной.
Замечание
1.
Аналогично формулируются определения
1 и 2 и теорема 1 для функции трёх и более
переменных.
Теорема
2
(достаточные
условия экстремума функции двух
переменных)
Если
функция
дважды дифференцируема в критической
точке
и её окрестности и определитель
,
то в точке
есть экстремум. Причём, если
,
то точка
является точкой минимума функции, а
если
,
то точка
является точкой максимума.
Замечание
2.
Если определитель
,
то в точке
нет экстремума, при этом точку
называют седловой точкой. Если
,
то вопрос об экстремуме в точке
остаётся нерешённым, нужны исследования
функции
по её производным более высокого порядка.
Теорема
3
(достаточные
условия экстремума функции трёх
переменных)
Пусть
функция
дважды дифференцируема в
критической точке
и её окрестности. Определитель
имеет все главные диагональные миноры
,
,
положительные, то
–точка минимума функции
.
Если
,
и
, то точка
– точка максимума функции
.
Замечание
3.
Если
критическая точка функции
и
,
но не выполняются условия теоремы 3, то
в точке
нет экстремума, при этом точка
называется седловой точкой. Если все
,
то вопрос об экстремуме в точке
решается с помощью производных более
высокого порядка.
Пример
1.
Найти экстремумы функции:
.
Решение.
;
.
.
Получили
две точки
и
;
;

а)
Исследуем точку
:
;
;
.
Тогда
точка
не является точкой экстремума.
б)
Исследуем точку
:
;
;
.
Тогда
точка
является точкой экстремума. Причём так
как
,
то точка
является точкой минимума функции:
.
Ответ:
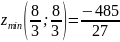
-
Условный экстремум
Пусть
задана функция
на множестве
.
Требуется найти экстремумы функции
,
если
и
связаны некоторым условием
,
называемым уравнением
связи.
Определение
4.
Точка
называется точкой
условного экстремума
функции
при выполнении дополнительных условий
– уравнений связи.
Для
нахождения точек условного экстремума
существует два метода: метод прямого
отыскания и метод Лагранжа. Прямой
метод состоит в том, что из уравнения
связи
выражается одна из переменных через
другую, и её подставляют в функцию
.
Получают функцию одной переменной, для
которой и решают задачу нахождения
обычного экстремума. Такой метод
применяют тогда, когда удаётся из
уравнения связи выразить одну переменную
через другую.
Пример
2.
Найти условный экстремум функции
при
условии
Решение.
Используем метод прямого отыскания
точек условного экстремума. Из условия
выразим
и подставим его в функцию
.
Тогда
Найдём
для функции
обычный экстремум.
,

– +
x
Следовательно,
– точка минимума функции
.
Подставляем
в функцию
и получим:
.
Ответ:
.
Определение
5.
Функция
называется функцией
Лагранжа,
а коэффициент λ
–
множителем
Лагранжа.
Замечание
4.
Если связи не одно уравнение, а несколько
(например,
),
то функция Лагранжа для функции
записывается с
множителями Лагранжа:
Теорема
4
(необходимое
условие поиска условного экстремума)
Пусть
функции
и
,
дифференцируемые в точке
а
является точкой условного экстремума
функции
при условии
.
Тогда найдется такое число
,
при котором точка
является критической для функции
Лагранжа
.
Метод
Лагранжа
поиска условного экстремума состоит в
следующем:
1)
составляют функцию Лагранжа
;
2)
находят её частные производные по
;
3)
приравнять частные производные к нулю
и решают систему уравнений
;
4)
исследуют найденную в результате решения
системы точку
при найденном значении
и решают задачу обычного экстремума
для
.
Теорема
5 (достаточное условие поиска условного
экстремума для случая одного уравнения
связи)
Пусть
точка
и
найдены из решения системы
.
Пусть
определитель
.
Если
,
то функция
имеет в точке
условный максимум.
Если
,
то функция
имеет в точке
условный минимум.
Пример
3.
Методом Лагранжа найти условный экстремум
для функции
при условии
.
Решение.
Составим функцию Лагранжа
.
Найдём
её частные производные по
:
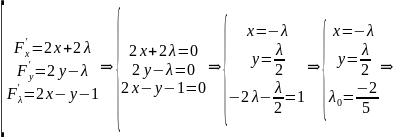
при
.
Выясним
характер точки
по теореме 5:
;
;
;
;
.
Составим
определитель:
.
Так
как
,
то
– точка условного минимума.
.
Ответ:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Экстремумы функций многих переменных
2 раздела
от теории до практики
1 пример
Примеры решения задач
видео
Примеры решения задач
-
Необходимые условия экстремума.
Начать изучение
-
Достаточные условия экстремума.
Начать изучение
Необходимые условия экстремума.
Пусть функция (f(x)) определена в области (G subset boldsymbol{R}^{n}) и пусть (x^{0} = (x_{1}^{0}, ldots, x_{n}^{0}) in G). Назовем (x_{0}) точкой (локального) минимума функции (f(x)), если найдется такой шар (S_{delta}(x^{0}) subset G), что для всех (x subset S_{delta}(x^{0})) выполнено неравенство (f(x) geq f(x^{0})). Назовем точку (x^{0}) точкой строгого минимума функции (f(x)), если найдется такой шар (S_{delta}(x^{0}) in G), что для всех (x in S_{delta}(x^{0})) (то есть для всех точек шара, не совпадающих с его центром) выполнено неравенство (f(x) geq f(x^{0})).
Аналогично определяются точки максимума (строгого максимума) функции (f(x)). Точки максимума и минимума функции называются точками экстремума.
Теорема 1.
Если в точке экстремума (x^{0}) функции (f(x)) существует частная производная (displaystylefrac{partial f}{partial x_{k}} (x^{0})), то она равна нулю.
Доказательство.
(circ) Пусть, например, существует (displaystylefrac{partial f}{partial x_{1}} (x^{0})). Рассмотрим функцию одной переменной
$$
varphi(x_{1}) = f(x_{1}, x_{2}^{0}, ldots, x_{n}^{0}).nonumber
$$
Так как (x^{0}) — точка экстремума (пусть, например, минимума), то существует шар (S_{delta}(x^{0})) такой, что (f(x) geq f(x^{0})) для всех точек этого шара. В частности, для любого (x_{1} in (x_{1}^{0} — delta, x_{1}^{0} + delta)) должно быть выполнено неравенство
$$
varphi(x_{1}) = f(x_{1}, x_{2}^{0}, ldots, x_{n}^{0}) geq f(x_{1}^{0}, ldots, x_{n}^{0}) = varphi(x_{1}^{0}).nonumber
$$
Функция одной переменной (varphi(x_{1})) имеет в точке (x_{1}^{0}) минимум. Поэтому
$$
frac{dvarphi}{dx_{1}} (x_{1}^{0}) = 0, mbox{то есть} frac{partial f}{partial x_{1}} (x^{0}) = 0. bulletnonumber
$$
Следствие.
Если в точке экстремума (x^{0}) функция (f(x)) дифференцируема, то
$$
df(x^{0}) = sum_{i=1}^{n} frac{partial f}{partial x_{i}} (x^{0}) dx_{i} = 0.label{ref1′}
$$
(circ) Действительно, так как в точке (x^{0}) функция (f(x)) дифференцируема, то в этой точке существуют частные производные (displaystylefrac{partial f}{partial x_{i}} (x^{0})), (i = overline{1, n}), а так как (x^{0}) есть точка экстремума, то (displaystylefrac{partial f}{partial x_{i}} (x^{0}) = 0). Отсюда следует равенство eqref{ref1′}. (bullet)
Если функция (f(x)) дифференцируема в точке (x^{0}) и (df(x^{0}) = 0), то точка (x^{0}) называется стационарной точкой функции (f(x)). Точка экстремума дифференцируемой функции в силу необходимых условий экстремума будет стационарной точкой. Обратное утверждение неверно. Стационарная точка может не быть точкой экстремума.
Пример 1.
Показать, что (0,0) является стационарной точкой функции (f(x, y) = xy), но (0,0) не есть точка экстремума этой функции.
Решение.
(vartriangle) Так как (df (x, y) = y dx + x dy), то (df(0, 0) = 0) и (0, 0) есть стационарная точка функции (f(x, y)). Но для любого (delta > 0) точки ((delta, delta)) и ((delta, -delta)) лежат в круге (S_{2delta}(0, 0)) и
$$
f(delta, delta) = delta^{2} > f(0, 0) = 0,quad f(delta, -delta) = -delta^{2} < f(0, 0) = 0.nonumber
$$
Поэтому (0, 0) не есть точка экстремума функции (f(x, y)). График функции (z = xy) изображен на рис. 59.1. (blacktriangle)
Лемма 1.
Если функция одной переменной (varphi(t)) имеет производные первого и второго порядков в точке минимума (t = 0), то (varphi″(0) geq 0).
Доказательство.
(circ) Пусть (t = 0) является точкой минимума функции (varphi(t)). Тогда найдется число (varepsilon > 0) такое, что для всех (|t| < varepsilon) выполняется неравенство (varphi(t) — varphi(0) geq 0). Применяя разложение функции (varphi(t)) по формуле Тейлора с остаточным членом в форме Пеано, получаем, воспользовавшись тем, что в точке минимума (varphi'(0) = 0):
$$
0 leq frac{varphi(t) — varphi(0)}{t^{2}} = frac{1}{t^{2}} left[varphi'(0)t + varphi″(0)frac{t^{2}}{2} + o(t^{2})right] = frac{1}{2} varphi″(0) + o(1)label{ref1}
$$
при (t rightarrow 0).
Переходя в этом неравенстве к пределу при (t rightarrow 0), получаем, что (varphi″(0) geq 0). (bullet)
Теорема 2.
(Необходимое условие минимума).
Пусть функция (f(x)) имеет в окрестности точки минимума (x^{0} in boldsymbol{R}^{n}) непрерывные частные производные первого и второго порядка. Тогда
$$
df(x^{0}) = 0,quad d^{2}f(x^{0}) = sum_{i=1}^{n} sum_{j=1}^{n} frac{partial^{2}f}{partial x_{i} partial x_{j}} (x^{0}) dx_{i} dx_{j} geq 0.label{ref2}
$$
Доказательство.
(circ) Пусть (x^{0}) — точка минимума функции (f(x)). Тогда найдется шар (S_{delta}(x^{0})) такой, что при всех (xi in S_{delta}(x^{0})) выполнено неравенство (f(xi) — f(x^{0}) geq 0). Пусть (x in boldsymbol{R}^{n}) и (x neq x^{0}), тогда (|Delta x| = rho (x, x^{0}) > 0). При любом (t) таком, что (|t| < displaystylefrac{delta}{|Delta x|}), точка (x^{0} + tDelta x in S_{delta}(x^{0})), и поэтому (varphi(t) = f(x^{0} + tDelta x) — f(x^{0}) geq 0). Функция (varphi(t)) определена в окрестности точки (t = 0) и имеет при (t = 0) минимум. В силу формул (4) и (5) отсюда функция (varphi(t)) имеет в точке (t = 0) производные первого и второго порядков, причем
$$
varphi'(0) = sum_{i=1}^{n} frac{partial f}{partial x_{i}} (x^{0}) dx_{i} = df(x^{0}),nonumber
$$
$$
varphi″(0) = sum_{i=1}^{n} sum_{j=1}^{n} frac{partial^{2}f(x^{0})}{partial x_{i} partial x_{j}} dx_{i} dx_{j} = d^{2} f(x^{0}).nonumber
$$
Так как в силу леммы 1 должно выполняться неравенство (varphi″(0) geq 0), то (d^{2} f(x^{0}) geq 0). (bullet)
Аналогично доказывается, что для функции (f(x)), дважды непрерывно дифференцируемой в окрестности точки максимума (x^{0}), выполняются условия
$$
df(x^{0}) = 0,quad d^{2} f(x^{0}) leq 0.nonumber
$$
Замечание.
Условия (df(x^{0}) = 0) и (d^{2} f(x^{0}) geq 0) необходимы, но не достаточны для того, чтобы точка (x^{0}) была точкой минимума. Например, функция (f(x, y) = x^{3} + y^{3}) имеет единственную стационарную точку (x = y = 0), и в этой точке (d^{2}f(0, 0) = 0). Легко убедиться, что функция (f(x, y)) не имеет экстремума в точке (0,0).
Достаточные условия экстремума.
При доказательстве достаточных условии потребуются некоторые сведения о квадратичных формах. Напомним, что квадратичная форма
$$
Phi(xi) = sum_{i=1}^{n} sum_{j=1}^{n} a_{ij}xi_{i}xi_{j},label{ref3}
$$
где (xi = (xi_{1}, ldots, xi_{n}) in boldsymbol{R}^{n}), (a_{ij} = a_{ji}), называется:
- положительно определенной, если (Phi(xi) > 0) для любого (xi neq 0);
- отрицательно определенной, если (Phi(xi) < 0) для любого (xi neq 0);
- неопределенной, если существуют (xi) и (xi’) такие, что (Phi(xi) > 0), а (Phi(xi’) < 0).
Квадратичная форма положительно определена в том и только том случае, когда все главные миноры ее матрицы положительны (критерий Сильвестра положительной определенности квадратичной формы), то есть
$$
Delta_{1} = a_{11} > 0,quad Delta_{2} = begin{vmatrix}a_{11}&a_{12}\a_{21}&a_{22}end{vmatrix} >0, ldots,quad Delta_{n} = begin{vmatrix}a_{11}&ldots& a_{1n}\….&….&….\a_{n1}&ldots&a_{nn}end{vmatrix} > 0.label{ref4}
$$
Заметим также, что квадратичная форма (Phi(xi)) отрицательно определена в том и только том случае, когда квадратичная форма (-Phi(xi)) положительно определена.
Лемма 2.
Если квадратичная форма (Phi(xi)) положительно определена, то найдется такое положительное число (gamma), что
$$
Phi(xi) geq gamma|xi|^{2}, mbox{где} |xi| = sqrt{xi_{1}^{2} + ldots + xi_{n}^{2}}.label{ref5}
$$
Доказательство.
(circ) Рассмотрим квадратичную форму (Phi(eta)) на сфере
$$
S = {eta: eta_{1}^{2} + ldots + eta_{1}^{2} = 1}.nonumber
$$Так как точка (0 notin S), а квадратичная форма положительно определена, то (Phi(eta) > 0) в любой точке (eta in S).Очевидно, что (S) есть замкнутое и ограниченное множество в (boldsymbol{R}^{n}). Непрерывная на компакте (S) функция (Phi(eta)) принимает в некоторой точке (overline{eta} in S) свое наименьшее на (S) значение (теорема Вейерштрасса). Поэтому, полагая (gamma = Phi(overline{eta})), получаем, что (gamma > 0) и что для любой точки (eta in S) выполняется неравенство (Phi(eta) geq gamma).Если (xi neq 0), то точка (xi/|xi|) принадлежит сфере (S). Поэтому
$$
Phi left(frac{xi}{|xi|}right) geq gamma.nonumber
$$
Пользуясь однородностью квадратичной формы, получаем
$$
frac{1}{|xi|^{2}} Phi(xi) = Phi left(frac{xi}{|xi|}right) geq gamma. bulletnonumber
$$
Теорема 3.
(Достаточные условия экстремума).
Пусть функция (f(x)) имеет в окрестности точки (x^{0} in boldsymbol{R}^{n}) непрерывные частные производные второго порядка, и пусть (df(x^{0}) = 0). Тогда если второй дифференциал (d^{2}f(x^{0})) есть положительно определенная квадратичная форма (см. формулу eqref{ref2}), то (x^{0}) — точка строгого минимума функции (f(x)), если (d^{2}f(x^{0})) — отрицательно определенная квадратичная форма, то (x^{0}) — точка строгого максимума функции (f(x)), если (d^{2}f(x^{0})) — неопределенная квадратичная форма, то функция (f(x)) не имеет экстремума в точке (x^{0}).
Доказательство.
(circ) Воспользуемся формулой Тейлора с остаточным членом в форме Пеано (m = 2). Учитывая, что (df(x^{0}) = 0), получаем
$$
f(x) — f(x^{0}) = frac{1}{2} d^{2}f(x^{0}) + o(|Delta x|^{2}) mbox{при} |Delta x| rightarrow 0,label{ref6}
$$
где
$$
|Delta x|^{2} = Delta x_{1}^{2} + ldots + Delta x_{n}^{2}.nonumber
$$
Пусть
$$
d^{2}f(x^{0}) = sum_{i=1}^{n} sum_{j=1}^{n} frac{partial^{2}f(x^{0})}{partial x_{i} partial x_{j}} Delta x_{i} Delta x_{j}nonumber
$$
есть положительно определенная квадратичная форма. В силу леммы 2 существует такое положительное число (gamma), что
$$
d^{2}f(x^{0}) geq gamma |Delta x|^{2}.nonumber
$$
Применяя это неравенство к формуле eqref{ref6}, получаем
$$
f(x) — f(x^{0}) = frac{gamma}{2} |Delta x|^{2} + o(|Delta x|^{2}) = frac{gamma}{2} |Delta x|^{2} (1 + alpha(Delta x)),label{ref7}
$$
где (alpha(Delta x) rightarrow 0) при (Delta x rightarrow 0), откуда следует, что найдется шар (S_{delta}(x^{0})) такой, что (forall x in S_{delta}(x^{0})) выполнено неравенство (|alpha(Delta x)| < displaystylefrac{1}{2}).
Тогда из формулы eqref{ref7} следует, что (forall x in dot{S}_{delta}(x^{0})) выполнено неравенство
$$
f(x) — f(x^{0}) geq frac{gamma}{2} |Delta x|^{2} (1 — |alpha(Delta x)|) geq frac{gamma}{4} |Delta x|^{2} > 0.
$$
Следовательно, (x^{0}) — точка строгого минимума функции (f(x)).
Аналогично доказывается, что в том случае, когда (d^{2}f(x^{0})) есть отрицательно определенная квадратичная форма, (x^{0}) — точка строгого максимума функции (f(x)).
Если (d^{2}f(x^{0})) есть неопределенная квадратичная форма, то не выполняется необходимое условие минимума (d^{2}f(x^{0}) geq 0) (см. теорему 2). Поэтому (x^{0}) не есть точка минимума функции (f(x)). Аналогично доказывается, что (x^{0}) не есть точка минимума функций (-f(x)), то есть точка максимума функции (f(x)). (bullet)
Пример 2.
Исследовать на экстремум функцию
$$
f(x, y, z) = x^{2} + 2xy + 4xz + 8yz + 5y^{2} + 9z^{2}.nonumber
$$
Решение.
(vartriangle) Найдем стационарные точки функции (f(x, y, z)). Они определяются из системы уравнений
$$
frac{partial f}{partial x} = 2x + 2y + 4z = 0,quad frac{partial f}{partial y} = 2x + 10y + 8z = 0,quad frac{partial f}{partial z} = 4x + 8y + 18z = 0.nonumber
$$
Определитель этой системы
$$
begin{vmatrix}2&2&4\2&10&8\4&8&18end{vmatrix} = 8begin{vmatrix}1&1&2\1&5&4\2&4&9end{vmatrix} = 8 cdot 16 > 0.nonumber
$$
Поэтому единственное решение однородной системы есть (x = y = z = 0).
Итак, функция (f(x, y, z)) имеет единственную стационарную точку (0,0,0). Найдем (d^{2}f(0, 0, 0)). Имеем
$$
d^{2}f(0, 0, 0) = 2 dx^{2} + 4 dx dy + 8 dx dz + 16 dy dz + 10 dy^{2} + 18 dz^{2}.nonumber
$$
Так как
$$
Delta_{1} = 2 > 0,quad Delta_{2} = begin{vmatrix}2&2\2&10end{vmatrix} > 0,quad Delta_{3} = begin{vmatrix}2&2&4\2&10&8\4&8&18end{vmatrix} = 8 cdot 16 > 0,nonumber
$$
то в силу критерия Сильвестра квадратичная форма (d^{2}f(0, 0, 0)) положительно определена. Точка (0,0,0) является точкой строгого минимума функции (f(x, y, z)). (blacktriangle)